Conservation Laws and Exact Solutions for Time-Delayed Burgers–Fisher Equations

Abstract

A generalization of the time-delayed Burgers–Fisher equation is studied. This partial differential equation appears in many physical and biological problems describing the interaction between reaction, diffusion, and convection. New travelling wave solutions are obtained. The solutions are derived in a systematic way by applying the multi-reduction method to the symmetry-invariant conservation laws. The translation-invariant conservation law yields a first integral, which is a first-order Chini equation. Under certain conditions on the coefficients of the equation, the Chini type equation obtained can be solved, yielding travelling wave solutions expressed in terms of the Lerch transcendent function. For a special case, the first integral becomes a Riccati equation, whose solutions are given in terms of Bessel functions, and for a special case of the parameters, the solutions are given in terms of exponential, trigonometric, and hyperbolic functions. Furthermore, a complete classification of the zeroth-order local conservation laws is obtained. To the best of our knowledge, our results include new solutions that have not been previously reported in the literature.

1. Introduction

The interaction between convection and diffusion, or reaction and diffusion, describes several nonlinear phenomena including physical, biochemical, and biological processes.

The simplest convection–diffusion partial differential equation (PDE) is the Burgers equation describing wave propagation in dissipative systems [1]. Another important PDE is the Fisher equation. This reaction–diffusion equation was first studied by Fisher, Kolmogorov, Petrovsky, and Piscounov as a model for the transmission of a mutant gene [2,3].

A PDE governing a wide range of these processes is the well-known Burgers–Fisher equation [4],

$$u_t+pu{u}_x-u_{xx}=qu(1-u),p,q\in (0,\infty ),$$

(1)

which describes the interplay of the reaction mechanism, convection effect, and diffusion transport. If $q=0$, PDE (1) transforms into the Burgers equation; if $p=0$, PDE (1) becomes the Fisher equation. The Burgers–Fisher Equation (1) has important applications in different fields such as gas dynamics [5] and traffic flow [6], among other problems in mathematical physics.

Later on, a generalized Burgers–Fisher equation was presented,

$$u_t+p{u}^s{u}_x-u_{xx}=qu(1-u^s),p,q,s\in (0,\infty ).$$

(2)

Both equations have been widely studied. Many works have been conducted to find exact solutions of the generalized Burgers–Fisher Equation (2) by using direct methods [7,8,9,10,11] and by applying nonlinear transformations [12].

Memory effects are an important feature in reaction–diffusion and convection–diffusion systems. If memory effects are considered, i.e., if particle dispersal is not mutually independent, diffusion processes are drastically altered. Therefore, for a given concentration gradient, successive movements of the diffusing particles might be interpreted as a delay in the flow. Recent works have been published including a time delay in this type of systems [13,14,15,16,17].

In real-world applications, it is of interest to consider more general models including a time delay, such as the time-delayed Burgers–Fisher equation

$$\tau u_{tt}+[1-\tau f_u]u_t=u_{xx}-pu{u}_x+f\left(u\right),f\left(u\right)=qu(1-u).$$

(3)

This motivates the study in this paper of the generalized time-delayed Burgers–Fisher equation

$$\tau u_{tt}+[1-\tau f_u]u_t=u_{xx}-g\left(u\right)u_x+f\left(u\right),$$

(4)

where $\tau >0$ is the time-delayed constant and $f\left(u\right)$, $g\left(u\right)$ are arbitrary functions. Another so-called generalized time-delayed Burgers–Fisher equation is

$$\tau u_{tt}+[1-\tau f_u]u_t=u_{xx}-p{u}^s{u}_x+f\left(u\right),f\left(u\right)=qu(1-u^s),$$

(5)

where s, p, and q are positive constants.

The widespread existence of wave phenomena in biomedical sciences motivates studying travelling waves. Travelling wave solutions were determined for the generalized time-delayed Burgers–Fisher Equation (5) through factorizations [18] and by using the $G^{\prime }/G$ [19] and the first-integral [20] methods. In Ref. [21], travelling wave solutions were studied for PDE (5) with $s=1$, again by using the $G^{\prime }/G$ method. In Ref. [22], travelling waves were derived for fractional power terms. Nevertheless, as far as we know, there has not been any complete work conducted on travelling wave solutions for the generalized time-delayed Burgers–Fisher Equation (4) with $f\left(u\right)$ and $g\left(u\right)$ arbitrary functions.

The aim of this work is to find new classes of travelling wave solutions for the generalized time-delayed Burgers–Fisher Equation (4) in a systematic way by using the symmetry-invariance of conservation laws. This is achieved by applying the multi-reduction method [23]. We also provide a complete classification of zeroth-order conservation laws in order to use the relation between them and symmetries admitted by PDE (4) to find exact solutions for the generalized time-delayed Burgers–Fisher Equation (4).

In Section 2, the multiplier method [24,25] is applied to seek conservation laws. A complete classification of zeroth-order conservation laws is presented. It is worth noting that in this classification problem, no physical or biological considerations have been made to model $f\left(u\right)$ and $g\left(u\right)$.

In Section 3, a second-order ordinary differential equation (ODE) is derived for travelling waves. Then, by applying the multi-reduction theory [23], the translation-invariant conservation law is reduced to a first integral of the travelling wave ODE. The first integral corresponds to a Chini type equation, which can be solved for some particular values of the parameters. Finally, considering special forms for $f\left(u\right)$ and $g\left(u\right)$, Equation (4) becomes an equation of biological interest. This case is discussed and new travelling wave solutions are obtained. Shock wave solutions are also shown and their basic physical feature is described. For $s=1$, the reduced first-order ODE becomes a Ricatti type equation, which is completely solved.

A general treatment of conservation laws and symmetries for nonlinear PDEs can be found in [26,27,28,29].

All computations have been performed using Maple 2021 software.

2. Conservation Laws

Conservation laws are essential in the analysis of PDEs, providing physical conserved quantities for all solutions. They are also employed for detecting integrability and linearizations, as well as checking numerical solution methods’ accuracy.

For further details on multipliers, conservation laws, and their applications to PDEs, see Refs. [28,29].

A conservation law of the generalized time-delayed Burgers–Fisher Equation (4) is a continuity equation

$$(D_{t}T+D_x\Phi ){|}_{\mathcal{E}}=0,$$

(6)

which holds for all solutions $u(t,x)$, with $D_t$ and $D_x$ denoting total derivatives. Here, T represents the conserved density and $\Phi$ the spatial flux, which are functions of t, x, u, and u derivatives. A conserved current is the pair $(T,\Phi )$.

If $T=D_x\Theta$ and $\Phi =-D_t\Theta$ are satisfied for all solutions, with $\Theta$ a function of t, x, u, and u derivatives, then the continuity equation holds identically, and such conservation law is called trivial (it provides no interesting information about $u(t,x)$ solutions). Two conservation laws are said to be locally equivalent if they differ by a trivial conservation law. Hence, only nontrivial conservation laws (up to local equivalence) are of interest.

On the space of solutions $\mathcal{E}$, the integral of a nontrivial conservation law over the spatial domain $\Omega \subseteq \mathbb{R}$ yields a conserved integral

$$C={\int }_{\Omega }Tdx{|}_{\mathcal{E}}$$

(7)

satisfying

$$\frac{dC}{dt}{=-\Phi |}_{\partial \Omega }{|}_{\mathcal{E}}.$$

(8)

This states that the rate of change of the density integral on $\Omega$ (7) is equal to the negative of the net spatial flux passing through the boundary points $\partial \Omega$ as measured by the flux integral. Under suitable boundary conditions, the net flux vanishes, and the conserved integral C is time-independent.

Any local conservation law has an equivalent characteristic form, given by a divergence identity

$$(\tau u_{tt}+[1-\tau f_u]u_t-u_{xx}+g\left(u\right)u_x-f\left(u\right))Q=D_t\tilde{T}+D_x\tilde{\Phi }$$

(9)

holding for the solutions of the generalized time-delayed Burgers–Fisher Equation (4), where $\tilde{T}$ and $\tilde{\Phi }$ are, respectively, a conserved density and a spatial flux locally equivalent to T and $\Phi$, and Q is a function of t, x, u, and u derivatives, called a multiplier.

Multipliers are extremely important since conservation laws (up to local equivalence) and multipliers have a one-to-one correspondence. All nontrivial conservation laws are derived from multipliers [28,29].

A determining equation for multipliers is given by applying the Euler operator with respect to u to the divergence expression (9),

$$E_u\left((\tau u_{tt}+[1-\tau f_u]u_t-u_{xx}+g\left(u\right)u_x-f\left(u\right))Q\right)=0$$

(10)

holding identically for all $u(t,x)$ and not only for solutions of Equation (4). Equation (10) splits with respect to the u derivatives not appearing in Q, yielding an overdetermined linear system for Q.

Conservation laws for basic physical quantities such as energy and momentum arise from multipliers of lower order than the order of the equation [29]. A classification of all low-order conservation laws is, in principle, possible by the multiplier method [24,25]. However, in the present problem, we seek zeroth-order multipliers of the form $Q(t,x,u)$. It is straightforward to solve the full system using Maple software, leading to the following result.

Proposition 1.

The generalized time-delayed Burgers–Fisher Equation (4), with $f\left(u\right)$ and $g\left(u\right)$ arbitrary functions satisfying $f^{\prime }\left(u\right)\ne 0$ and $g^{\prime }\left(u\right)\ne 0$, admits only a zeroth-order multiplier

$$\begin{array}{cc}\hfill Q_1& =e^{t/\tau }.\hfill \end{array}$$

(11)

Additional zeroth-order multipliers are admitted in the following cases.

(i) 

For $f\left(u\right)=f_1(u+f_0)$, with $f_0$, $f_1\ne 0$ arbitrary constants, and $g\left(u\right)$ arbitrary function,

$$\begin{array}{cc}\hfill Q_2& =e^{-f_{1}t}.\hfill \end{array}$$

(12)

(ii) 

For $f\left(u\right)$ nonlinear function and $g\left(u\right)=g_1{f}^{\prime }\left(u\right)+g_0$, with $g_0$, $g_1\notin \{0,\pm \tau \}$ arbitrary constants,

$$\begin{array}{cc}\hfill Q_3& =e^{\frac{(g_0\tau -g_1)x+(g_0{g}_1-1)t}{g_1^2-\tau }}.\hfill \end{array}$$

(13)

(iii) 

For $f\left(u\right)$ nonlinear function and $g\left(u\right)=\pm \sqrt{\tau }{f}^{\prime }\left(u\right)\pm \frac{1}{\sqrt{\tau }}$,

$$\begin{array}{cc}\hfill Q_{4\pm }& =e^{t/\tau }F(x\pm \frac{t}{\sqrt{\tau }}),\hfill \end{array}$$

(14)

with F an arbitrary function of its argument.

The use of any of the methods described in Ref. [29] yields the conserved currents coming from these multipliers.

Theorem 1.

For the generalized time-delayed Burgers–Fisher Equation (4), with $f\left(u\right)$ and $g\left(u\right)$ arbitrary functions satisfying $f^{\prime }\left(u\right)\ne 0$, $g^{\prime }\left(u\right)\ne 0$, the admitted local conservation law is

$$\begin{array}{cc}\hfill & \begin{array}{cc}\hfill T_1& =e^{t/\tau }\tau (u_t-f\left(u\right)),\hfill \end{array}\hfill \end{array}$$

(15a)

$$\begin{array}{cc}\hfill & \begin{array}{cc}\hfill {\Phi }_1& =e^{t/\tau }\left(-u_x+\int g\left(u\right)du\right).\hfill \end{array}\hfill \end{array}$$

(15b)

Additional zeroth-order local conservation laws are admitted in the following cases.

(i) 

For $f\left(u\right)=f_1(u+f_0)$, with $f_0$, $f_1\ne 0$ arbitrary constants, and $g\left(u\right)$ arbitrary function,

$$\begin{array}{cc}\hfill & \begin{array}{cc}\hfill T_2& =e^{-f_{1}t}(\tau u_t+u+f_0),\hfill \end{array}\hfill \end{array}$$

(16a)

$$\begin{array}{cc}\hfill & \begin{array}{cc}\hfill {\Phi }_2& =e^{-f_{1}t}\left(-u_x+\int g\left(u\right)du\right).\hfill \end{array}\hfill \end{array}$$

(16b)

(ii) 

For $f\left(u\right)$ nonlinear function and $g\left(u\right)=g_1{f}^{\prime }\left(u\right)+g_0$, with $g_0$, $g_1\notin \{0,\pm \tau \}$ arbitrary constants,

$$\begin{array}{cc}\hfill & \begin{array}{cc}\hfill T_3& =e^{\frac{(g_0\tau -g_1)x+(g_0{g}_1-1)t}{g_1^2-\tau }}\left(\tau (u_t-f\left(u\right))+\frac{g_1(g_1-g_0\tau )}{g_1^2-\tau }u\right),\hfill \end{array}\hfill \end{array}$$

(17a)

$$\begin{array}{cc}\hfill & \begin{array}{cc}\hfill {\Phi }_3& =e^{\frac{(g_0\tau -g_1)x+(g_0{g}_1-1)t}{g_1^2-\tau }}\left(-u_x+g_{1}f\left(u\right)+\frac{g_1(g_0{g}_1-1)}{g_1^2-\tau }u\right).\hfill \end{array}\hfill \end{array}$$

(17b)

(iii) 

For $f\left(u\right)$ nonlinear function and $g\left(u\right)=\pm \sqrt{\tau }{f}^{\prime }\left(u\right)\pm \frac{1}{\sqrt{\tau }}$,

$$\begin{array}{cc}\hfill & \begin{array}{cc}\hfill T_{4\pm }& =e^{t/\tau }\sqrt{\tau }\left(\sqrt{\tau }F(x\pm \frac{t}{\sqrt{\tau }})(u_t-f\left(u\right))\mp F^{\prime }(x\pm \frac{t}{\sqrt{\tau }})u\right),\hfill \end{array}\hfill \end{array}$$

(18a)

$$\begin{array}{cc}\hfill & \begin{array}{cc}\hfill {\Phi }_{4\pm }& =e^{t/\tau }\left(F(x\pm \frac{t}{\sqrt{\tau }})\left(-u_x\pm \sqrt{\tau }f\left(u\right)\pm \frac{1}{\sqrt{\tau }}u\right)+F^{\prime }(x\pm \frac{t}{\sqrt{\tau }})u\right),\hfill \end{array}\hfill \end{array}$$

(18b)

with F an arbitrary function of its argument.

3. Travelling Waves

A travelling wave is defined by

$$u(t,x)=U(x-ct),$$

(19)

where c is the constant speed of the wave. This expression results from a group invariance with respect to the translation symmetry

$$X={\partial }_t+c{\partial }_x,$$

(20)

with $\zeta =x-ct$ and $u=U$ being the invariants.

The substitution of the travelling wave expression (19) into the generalized time-delayed Burgers–Fisher Equation (4) yields a second-order nonlinear ODE for $U\left(\zeta \right)$,

$$(c^2\tau -1)U^{″}+(c\tau f^{\prime }\left(U\right)+g\left(U\right)-c)U^{\prime }-f\left(U\right)=0.$$

(21)

Here, a prime denotes a differentiation with respect to $\zeta$.

It is known that any translation-invariant conservation law reduces to a first integral of the travelling wave ODE [23]. This first integral has the form

$${\Psi =(\Phi -cT)|}_{u=U\left(\zeta \right)},{\Psi }^{\prime }=0,$$

(22)

where $(T,\Phi )$ is the conserved current.

Let us now focus on the case from Theorem 1 with the translation-invariant conservation law (17). For this case, $g\left(U\right)$ must satisfy

$$g\left(U\right)=g_1{f}^{\prime }\left(U\right)+g_0,g_0=\frac{c{g}_1+1}{c\tau +g_1},c\tau +g_1\ne 0.$$

(23)

The associated conserved current (17) yields a first integral of ODE (21). The resulting first integral is given by

$$U^{\prime }+\frac{c\tau +g_1}{c^2\tau -1}f\left(U\right)-\frac{C_0}{c^2\tau -1}{e}^{\frac{\zeta }{c\tau +g_1}}=0,$$

(24)

where $C_0$ is an arbitrary constant and $c^2\tau -1\ne 0$. Now, two cases are distinguished: $C_0=0$ and $C_0\ne 0$.

3.1. For $C_0=0$

The first-order ODE (24) is a Bernoulli equation, and each solution $U\left(\zeta \right)$ can be implicitly given by the quadrature

$${\int }_{U_0}^U\frac{c^2\tau -1}{(c\tau +g_1)f\left(U\right)}dU=-(\zeta -{\zeta }_0),$$

(25)

where $U_0=U\left({\zeta }_0\right)$ is an arbitrary constant, and ${\zeta }_0$ can be set to 0 by translation invariance.

Proposition 2.

The quadrature (25) gives an implicit solution $U\left(\zeta \right)$ of the travelling wave ODE (21), $f\left(U\right)$ being an arbitrary function, $g\left(U\right)$ a related function given by (23), and c, τ, $g_1$, and ${\zeta }_0$ arbitrary constants satisfying $c^2\tau -1\ne 0$ and $c\tau +g_1\ne 0$.

3.2. For $C_0\ne 0$

The first-order ODE (24) is a Chini type equation. As far as we know, there is no general solution known for this type of equation. However, a family of these equations appearing in Ref. [30] as I-55 can be solved. In order for ODE (24) to belong to this Chini family, $f\left(U\right)$ must satisfy

$$f\left(U\right)=\frac{c^2\tau -1}{c\tau +g_1}(f_2{U}^n+f_{1}U),$$

(26)

where $f_1$ and $f_2$ are arbitrary constants. Thus, the first-order ODE (24) becomes

$$U^{\prime }+f_2{U}^n+f_{1}U-\frac{C_0}{c^2\tau -1}{e}^{\frac{\zeta }{c\tau +g_1}}=0.$$

(27)

Following Ref. [30] (p. 303), in order for ODE (27) to be solved, there should exist two constants $\alpha$ and $\beta$ such that

$${\left(-\frac{C_0}{(c^2\tau -1)f_2}\right)}^{1/n}{e}^{\frac{\zeta }{n(c\tau +g_1)}}=e^{-f_1\zeta }\left(\beta +\alpha \int \frac{C_0}{c^2\tau -1}{e}^{\left(f_1+\frac{1}{c\tau +g_1}\right)\zeta }d\zeta \right)$$

(28)

is satisfied. Consequently,

$$\alpha =0,\beta ={\left(-\frac{C_0}{(c^2\tau -1)f_2}\right)}^{1/n},f_1=-\frac{1}{n(c\tau +g_1)}$$

(29)

must be verified. Therefore, the local change for the dependent variable $U\left(\zeta \right)$ given by

$$U\left(\zeta \right)={\left(-\frac{C_0}{(c^2\tau -1)f_2}\right)}^{1/n}{e}^{\frac{\zeta }{n(c\tau +g_1)}}Z\left(\zeta \right),$$

(30)

transforms Equation (27) into the first-order separable ODE

$$Z^{\prime }=\kappa e^{\frac{(n-1)\zeta }{n(c\tau +g_1)}}(1+Z^n),\kappa =f_2^{1/n}{\left(-\frac{C_0}{c^2\tau -1}\right)}^{\frac{n-1}{n}},$$

(31)

or, equivalently,

$$\int \frac{dZ}{Z^n+1}+C_1=\kappa \frac{n(c\tau +g_1)}{n-1}{e}^{\frac{(n-1)\zeta }{n(c\tau +g_1)}},$$

(32)

where $C_1$ is an integration constant. The solution of Equation (31) or (32) is given by

$$\frac{1}{n}L(-Z^n,1,\frac{1}{n})Z+C_1=\kappa \frac{n(c\tau +g_1)}{n-1}{e}^{\frac{(n-1)\zeta }{n(c\tau +g_1)}},$$

(33)

where L represents the Lerch transcendent function [31].

Proposition 3.

The change of variables (30) transforms the first-order ODE (21) into the separable ODE (31) whose general solution is given in terms of the Lerch transcendent function, with $f\left(U\right)$ and $g\left(U\right)$ given by (26) and (23), respectively, and $n>1$, c, τ, $g_1$, $f_2$, $C_0$, and $C_1$ are arbitrary constants satisfying $c^2\tau -1\ne 0$ and $c\tau +g_1\ne 0$.

4. Equations of Biological Interest: Exact Solutions

For $f\left(u\right)=qu(1-u^s)$ and $g\left(u\right)=p{u}^s$, with s, p, and q positive parameters, Equation (4) becomes an equation of biological interest. These types of functions are considered because they introduce both the features of convective phenomena from the Burgers equation and the diffusion transport as well as reaction from the Fisher equation.

For these special forms of $f\left(u\right)$ and $g\left(u\right)$, the generalized time-delayed Burgers–Fisher Equation (4) is written as

$$\tau u_{tt}+[1-\tau q(1-(s+1)u^s)]u_t=u_{xx}-p{u}^s{u}_x+qu(1-u^s).$$

(34)

The first integral (24) becomes

$$U^{\prime }+\frac{cq\tau (s+1)-p}{(c^2\tau -1)(s+1)}(U-U^{s+1})+\frac{C_0}{c^2\tau -1}{e}^{\frac{q(s+1)\zeta }{cq\tau (s+1)-p}}=0,$$

(35)

where $C_0$ is a constant, and c must satisfy

$$c=\frac{p^2+q{(s+1)}^2}{p(q\tau +1)(s+1)}.$$

(36)

This relation for the speed of the wave comes from holding the previous condition (23) for these special forms of $f\left(u\right)$ and $g\left(u\right)$. It is clear from the previous relation (36) that the soliton’s velocity is affected by the time-delayed constant $\tau$. As the time-delayed constant $\tau$ increases, the speed of the wave decreases.

In the particular case in which the time delay is not considered, i.e., $\tau =0$, this first integral (35) coincides with the first integral appearing in Ref. [32], and (36) coincides with the condition appearing in [10,11] for the existence of travelling wave solutions for PDE (34).

Setting $C_0=0$, the first-order ODE (35) is obviously a Bernoulli equation. It is straightforward to solve it, explicitly obtaining a solution for $U\left(\zeta \right)$,

$$U\left(\zeta \right)={\left(1+e^{\frac{\left(q\right(s+1)c\tau -p)s\zeta }{(s+1)(c^2\tau -1)}}{U}_0\right)}^{-1/s},$$

(37)

where $U_0$ is an integration constant. This solution has already been obtained using a factorization technique [18] and a first-integral method [20].

Physically, this solution describes a bright kink soliton (shock wave) solution. This type of solution is distinguished by the feature that the wave amplitude transitions exponentially between two asymptotically constant values. These waves are characterized by an almost vertical front. Figure 1 (left) shows a plot of the shock wave profile for different values of $\tau$. The effect of the time delay is to smooth the shock wave nature of the shock wave solution. The wave leads to a less smooth behaviour with a larger slope when the time-delayed constant $\tau$ increases. Figure 1 (right) shows a space-time plot of the shock wave front.

For s = 1

This model describes a density-dependent diffusion with a logistically growing population [33].

The first integral (35) becomes

$$U^{\prime }+\frac{2cq\tau }{2(c^2\tau -1)}(U-U^2)+\frac{C_0}{c^2\tau -1}{e}^{\frac{2q\zeta }{2cq\tau -p}}=0,$$

(38)

which is of Ricatti type.

The transformation

$$U=k\frac{V^{\prime }}{V},$$

(39)

where

$$k=-\frac{2(c^2\tau -1)}{2cq\tau -p},$$

(40)

maps ODE (38) into the linear second-order ODE

$$V^{″}+\frac{2cq\tau -p}{2(c^2\tau -1)}{V}^{\prime }-\frac{C_0(2cq\tau -p)}{2{(c^2\tau -1)}^2}{e}^{\frac{2q\zeta }{2cq\tau -p}}V=0.$$

(41)

Setting

$$\nu =\pm 2cq\tau \mp p,\mu =c^2\tau -1,$$

(42)

ODE (41) can be rewritten as

$$V^{″}\pm \frac{\nu }{2\mu }{V}^{\prime }\mp \frac{C_0\nu }{2{\mu }^2}{e}^{\frac{\pm 2q\zeta }{\nu }}V=0.$$

(43)

Then, setting ${\delta }^2=\frac{C_0\nu }{2{\mu }^2}$, this ODE can be again rewritten as

$$V^{″}\pm \frac{\nu }{2\mu }{V}^{\prime }\mp {\delta }^2{e}^{\frac{\pm 2q\zeta }{\nu }}V=0.$$

(44)

It is straightforwardly solved, giving its general solution in terms of Bessel [34] or elementary functions.

(i)

For ${\nu }^2\pm 2q\mu \ne 0$:

•

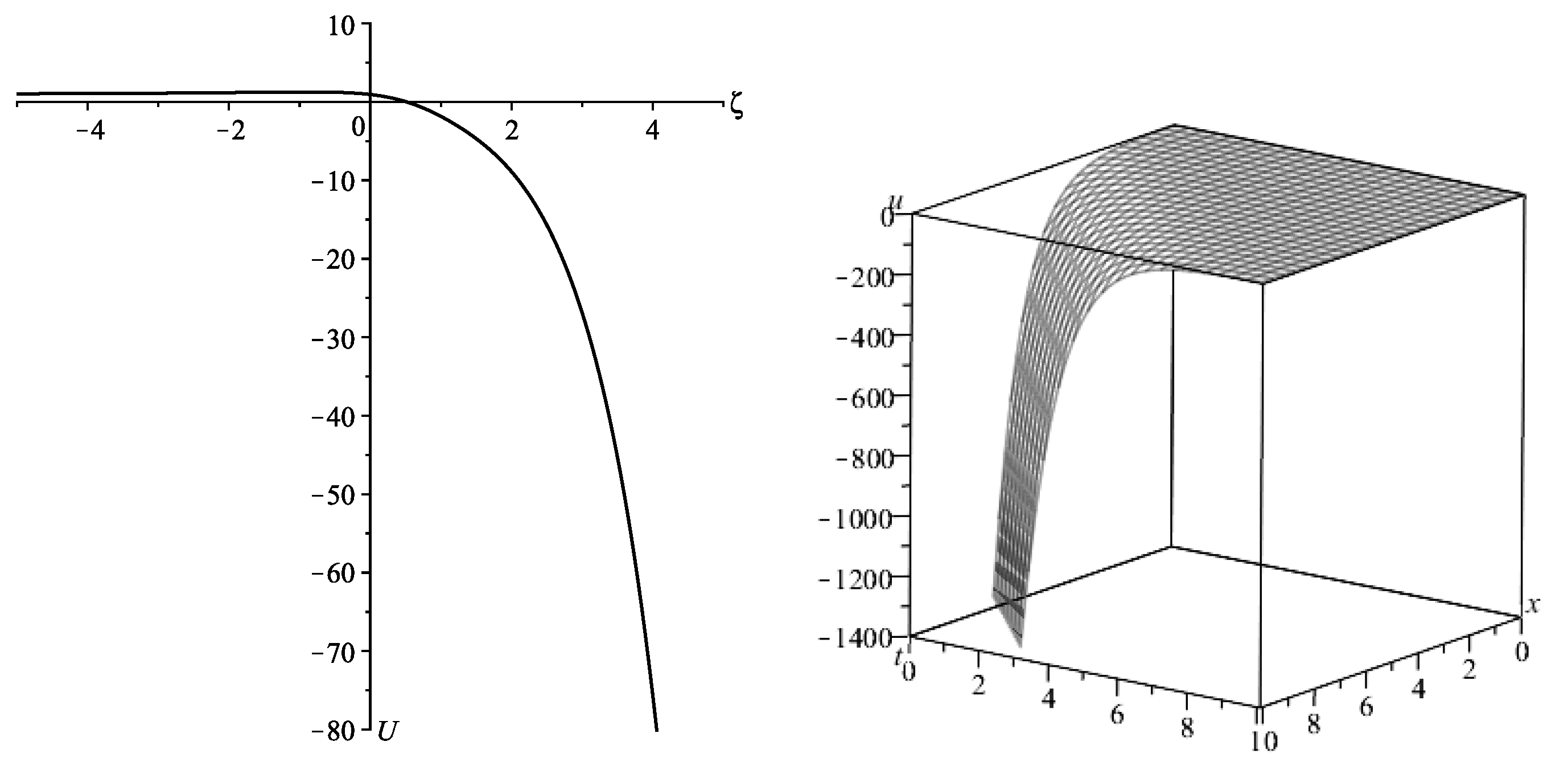
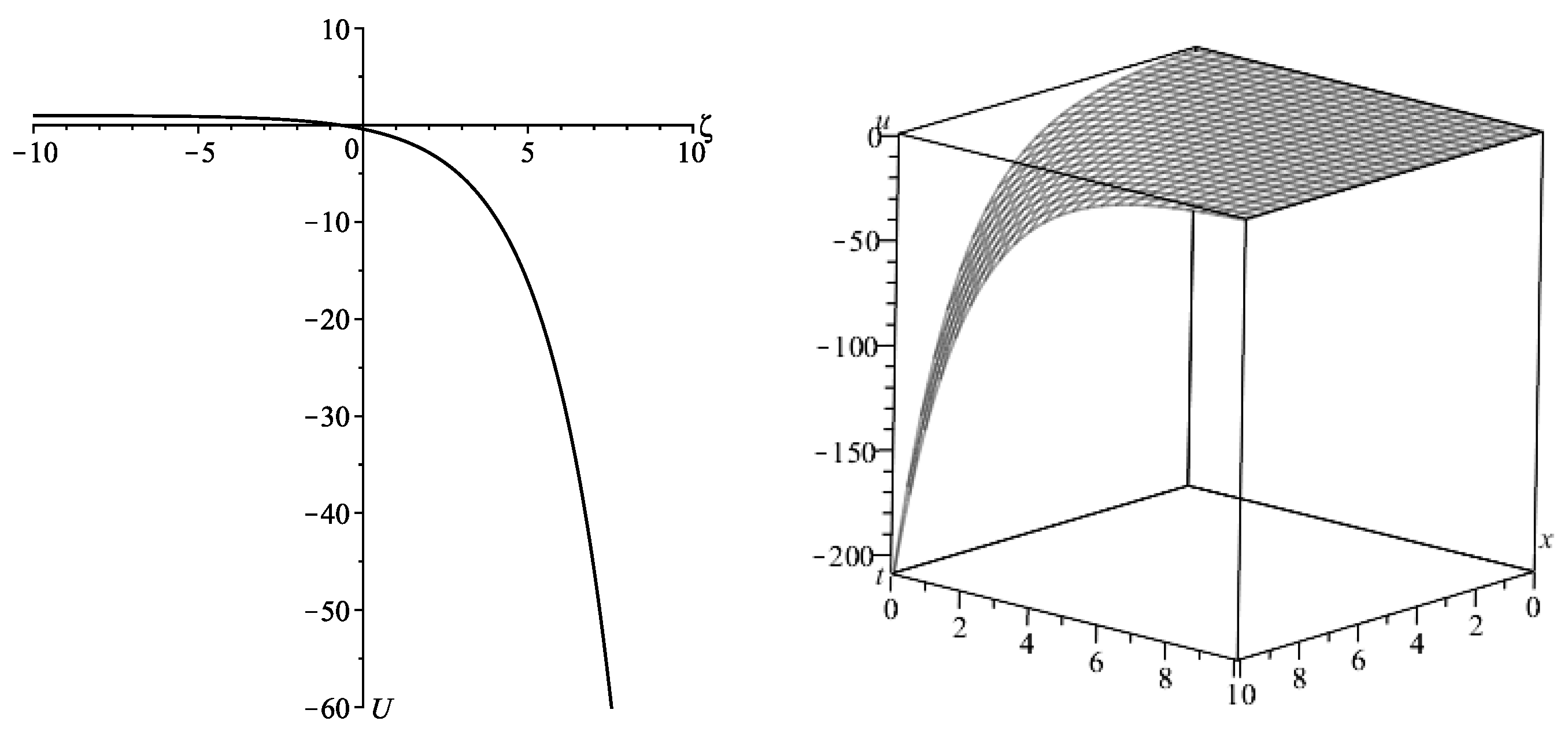
If $\nu =2cq\tau -p$, the general solution to ODE (44) is

$$V\left(\zeta \right)=C_1{e}^{-\frac{\nu \zeta }{4\mu }}I\left(\frac{{\nu }^2}{4q\mu },\frac{\delta \nu }{q}{e}^{\frac{q\zeta }{\nu }}\right)+C_2{e}^{-\frac{\nu \zeta }{4\mu }}K\left(\frac{{\nu }^2}{4q\mu },\frac{\delta \nu }{q}{e}^{\frac{q\zeta }{\nu }}\right).$$

(45)

Hence, the solution to ODE (38) is

$$U\left(\zeta \right)=-\frac{2\mu \delta }{\nu }{e}^{\frac{q\zeta }{\nu }}\frac{C_{1}I\left(\frac{4q\mu +{\nu }^2}{4q\mu },\frac{\delta \nu }{q}{e}^{\frac{q\zeta }{\nu }}\right)-C_{2}K\left(\frac{4q\mu +{\nu }^2}{4q\mu },\frac{\delta \nu }{q}{e}^{\frac{q\zeta }{\nu }}\right)}{C_{1}I\left(\frac{{\nu }^2}{4q\mu },\frac{\delta \nu }{q}{e}^{\frac{q\zeta }{\nu }}\right)+C_{2}K\left(\frac{{\nu }^2}{4q\mu },\frac{\delta \nu }{q}{e}^{\frac{q\zeta }{\nu }}\right)}$$

(46)

where I and K denote the modified Bessel functions of first and second kind, respectively, and $C_1$ and $C_2$ are integration constants.

Figure 2 shows a solitary wave solution given in terms of modified Bessel functions, decaying from an asymptotically constant value.

•

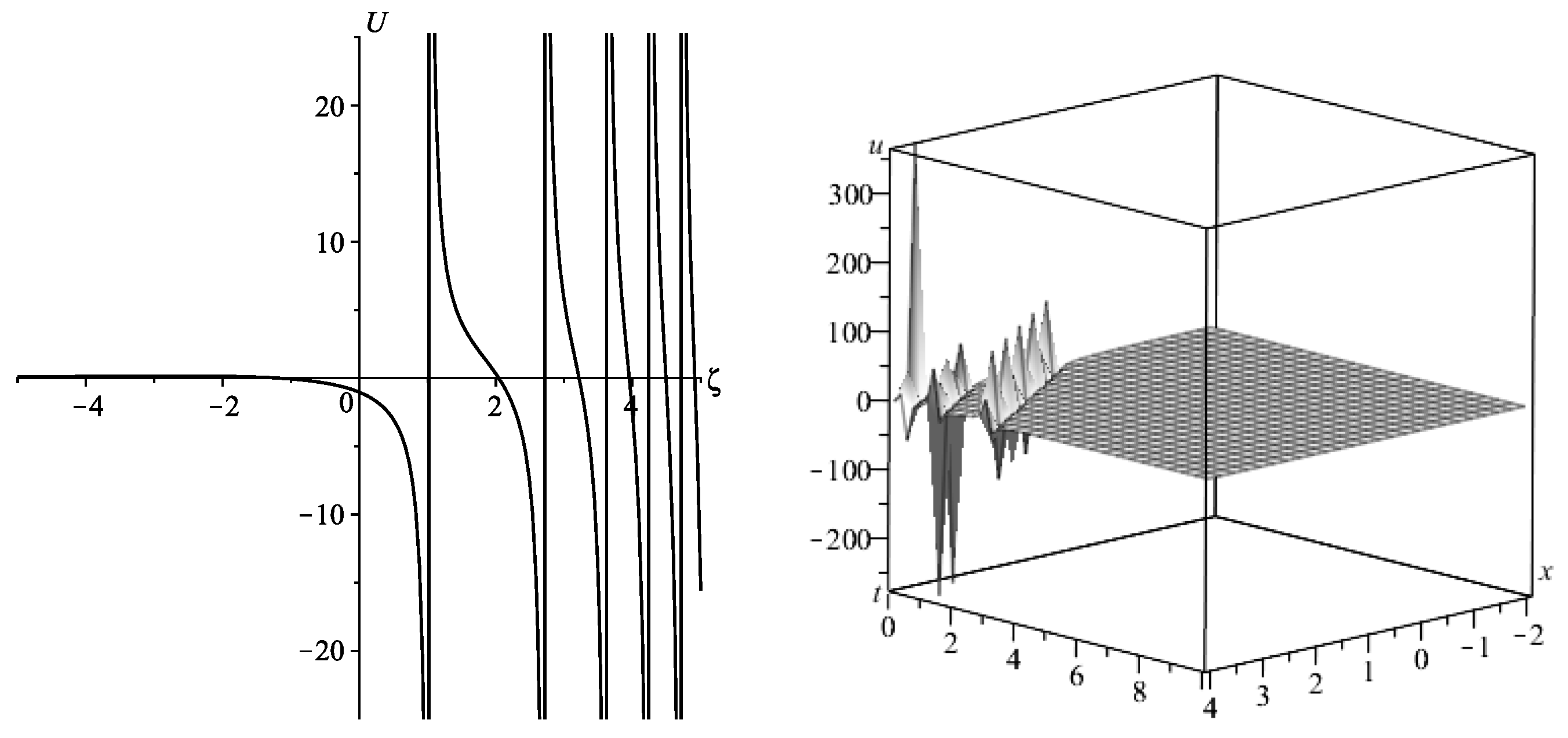
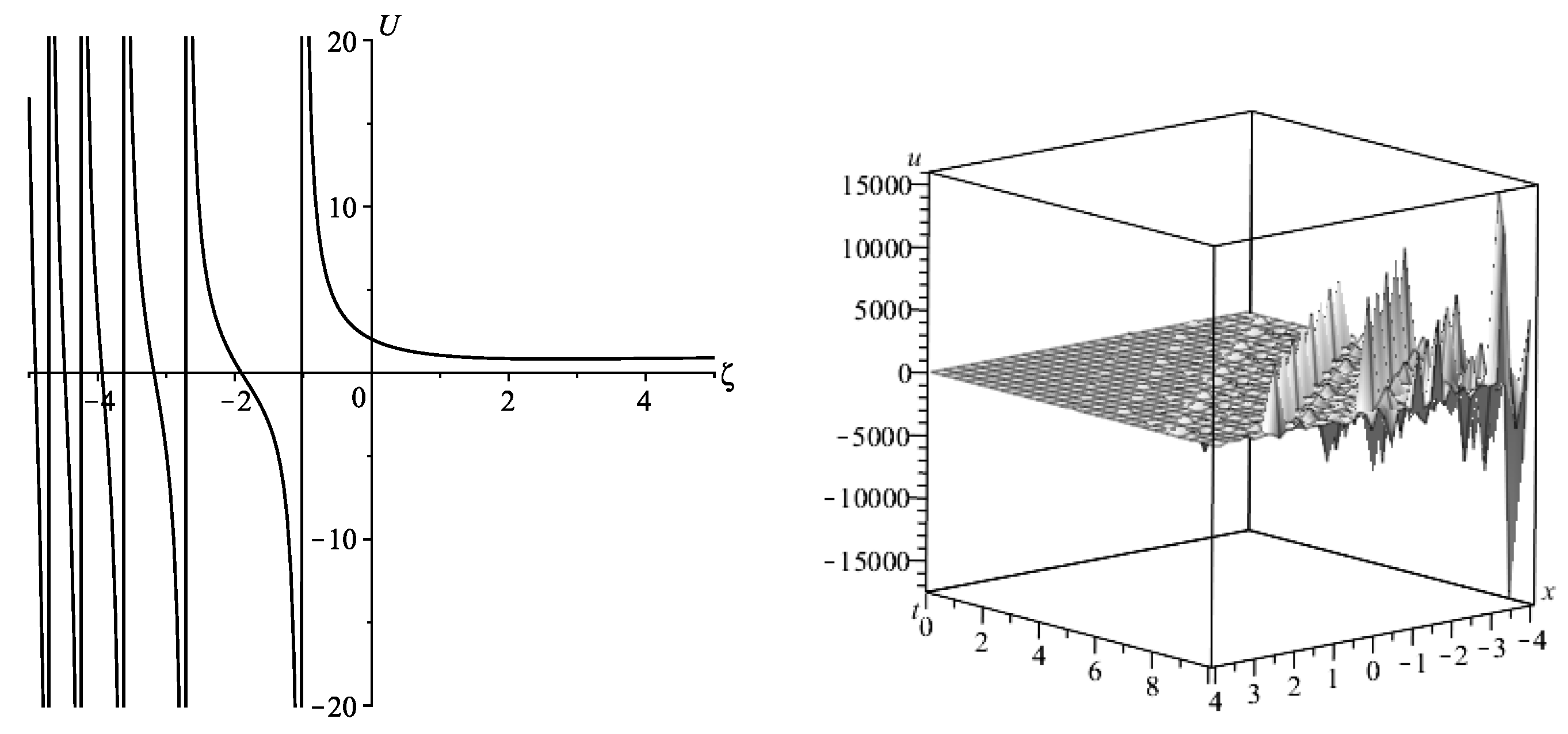
If $\nu =-2cq\tau +p$, the general solution to ODE (44) is

$$V\left(\zeta \right)=C_1{e}^{\frac{\nu \zeta }{4\mu }}J\left(\frac{{\nu }^2}{4q\mu },\frac{\delta \nu }{q}{e}^{-\frac{q\zeta }{\nu }}\right)+C_2{e}^{\frac{\nu \zeta }{4\mu }}Y\left(\frac{{\nu }^2}{4q\mu },\frac{\delta \nu }{q}{e}^{-\frac{q\zeta }{\nu }}\right).$$

(47)

Hence, the solution to ODE (38) is

$$U\left(\zeta \right)=\frac{2\mu \delta }{\nu }{e}^{-\frac{q\zeta }{\nu }}\frac{C_{1}J\left(\frac{4q\mu +{\nu }^2}{4q\mu },\frac{\delta \nu }{q}{e}^{-\frac{q\zeta }{\nu }}\right)+C_{2}Y\left(\frac{4q\mu +{\nu }^2}{4q\mu },\frac{\delta \nu }{q}{e}^{-\frac{q\zeta }{\nu }}\right)}{C_{1}J\left(\frac{{\nu }^2}{4q\mu },\frac{\delta \nu }{q}{e}^{-\frac{q\zeta }{\nu }}\right)+C_{2}Y\left(\frac{{\nu }^2}{4q\mu },\frac{\delta \nu }{q}{e}^{-\frac{q\zeta }{\nu }}\right)}$$

(48)

where J and Y denote the Bessel functions of first and second kind, respectively, and $C_1$ and $C_2$ are integration constants.

Figure 3 represents a solution given in terms of ordinary Bessel functions. This solution becomes a singular solution if the denominator is equal to zero. Thus, depending on the choice of the parameters, it leads to a singular solution. The solution behaves as a rogue wave holding elevation peaks and deep humps.

(ii)

For ${\nu }^2\pm 2q\mu =0$:

•

If ${\nu }^2=2q\mu$ and $\nu =2cq\tau -p$, the general solution to ODE (44) is

$$V\left(\zeta \right)=C_1{e}^{-\frac{\nu \zeta }{2\mu }}sinh(\frac{2\delta \mu }{\nu }{e}^{\frac{\nu \zeta }{2\mu }})+C_2{e}^{-\frac{\nu \zeta }{2\mu }}cosh(\frac{2\delta \mu }{\nu }{e}^{\frac{\nu \zeta }{2\mu }}).$$

(49)

Hence, the solution to ODE (38) is

$$U\left(\zeta \right)=\frac{(C_1\nu -2C_2\delta \mu e^{\frac{\nu \zeta }{2\mu }})sinh(\frac{2\delta \mu }{\nu }{e}^{\frac{\nu \zeta }{2\mu }})+(C_2\nu -2C_1\delta \mu e^{\frac{\nu \zeta }{2\mu }})cosh(\frac{2\delta \mu }{\nu }{e}^{\frac{\nu \zeta }{2\mu }})}{\nu (C_{1}sinh(\frac{2\delta \mu }{\nu }{e}^{\frac{\nu \zeta }{2\mu }})+C_{2}cosh(\frac{2\delta \mu }{\nu }{e}^{\frac{\nu \zeta }{2\mu }}))}$$

(50)

where $C_1$ are $C_2$ are integration constants.

Figure 4 shows a behaviour similar to Figure 2 and corresponds to the case ${\nu }^2-2q\mu =0$.

•

If ${\nu }^2=2q\mu$ and $\nu =-2cq\tau +p$, the general solution to ODE (44) is

$$V\left(\zeta \right)=C_1{e}^{\frac{\nu \zeta }{2\mu }}sin(\frac{2\delta \mu }{\nu }{e}^{-\frac{\nu \zeta }{2\mu }})+C_2{e}^{\frac{\nu \zeta }{2\mu }}cos(\frac{2\delta \mu }{\nu }{e}^{\frac{-\nu \zeta }{2\mu }}).$$

(51)

Hence, the solution to ODE (38) is

$$U\left(\zeta \right)=\frac{(C_1\nu +2C_2\delta \mu e^{-\frac{\nu \zeta }{2\mu }})sin(\frac{2\delta \mu }{\nu }{e}^{-\frac{\nu \zeta }{2\mu }})+(C_2\nu -2C_1\delta \mu e^{-\frac{\nu \zeta }{2\mu }})cos(\frac{2\delta \mu }{\nu }{e}^{-\frac{\nu \zeta }{2\mu }})}{\nu (C_{1}sin(\frac{2\delta \mu }{\nu }{e}^{-\frac{\nu \zeta }{2\mu }})+C_{2}cos(\frac{2\delta \mu }{\nu }{e}^{-\frac{\nu \zeta }{2\mu }}))}$$

(52)

where $C_1$ and $C_2$ are integration constants.

Figure 5 shows a behaviour similar to Figure 3 and corresponds to the case ${\nu }^2-2q\mu =0$.

•

If ${\nu }^2=-2q\mu$ and $\nu =2cq\tau -p$, the general solution to ODE (44) is

$$V(\zeta )=C_{1}sinh(\frac{2\delta \mu }{\nu }{e}^{-\frac{\nu \zeta }{2\mu }})+C_{2}cosh(\frac{2\delta \mu }{\nu }{e}^{-\frac{\nu \zeta }{2\mu }}).$$

(53)

Hence, the solution to ODE (38) is

$$U\left(\zeta \right)=\frac{2\delta \mu }{\nu }{e}^{-\frac{\nu \zeta }{2\mu }}\frac{C_{2}sinh(\frac{2\delta \mu }{\nu }{e}^{-\frac{\nu \zeta }{2\mu }})+C_{1}cosh(\frac{2\delta \mu }{\nu }{e}^{-\frac{\nu \zeta }{2\mu }})}{C_{1}sinh(\frac{2\delta \mu }{\nu }{e}^{-\frac{\nu \zeta }{2\mu }})+C_{2}cosh(\frac{2\delta \mu }{\nu }{e}^{-\frac{\nu \zeta }{2\mu }})}$$

(54)

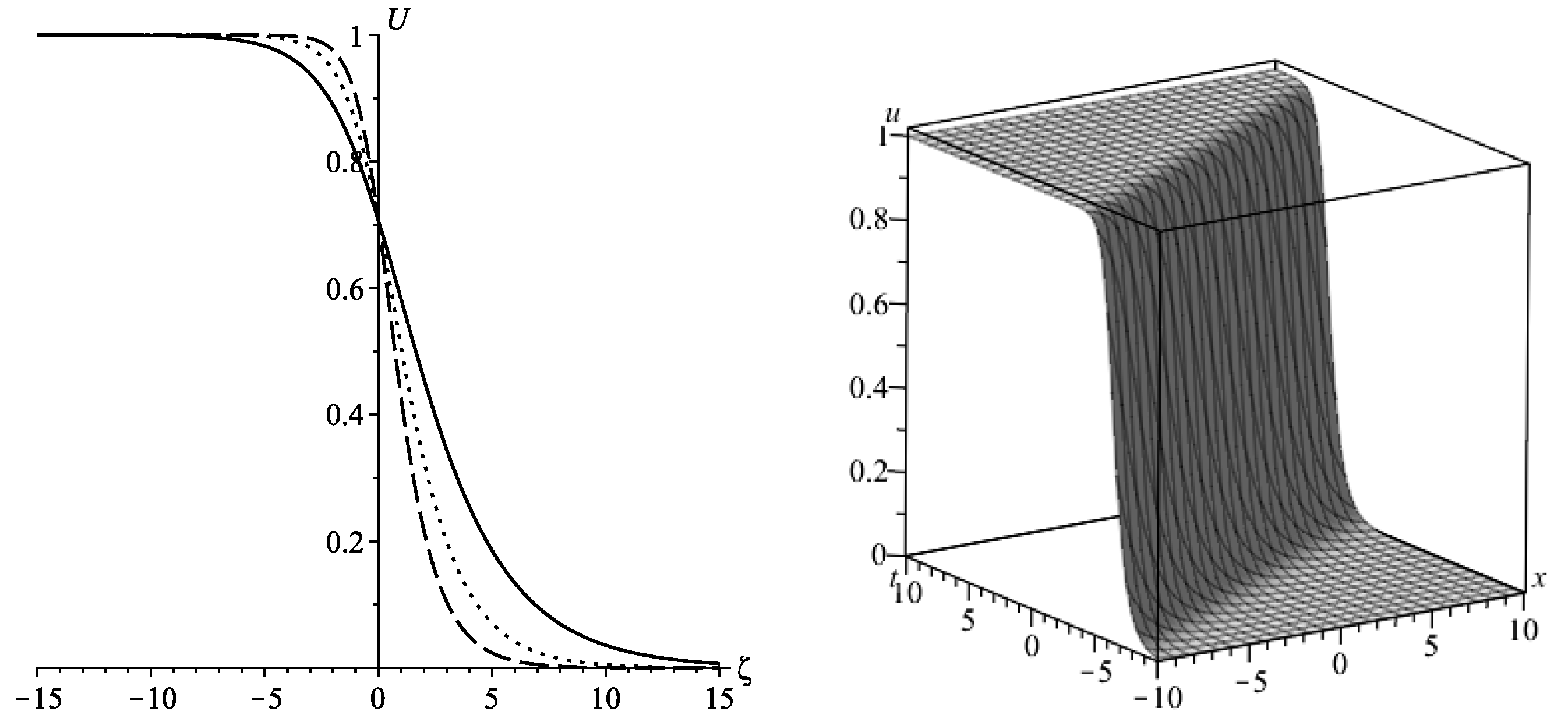
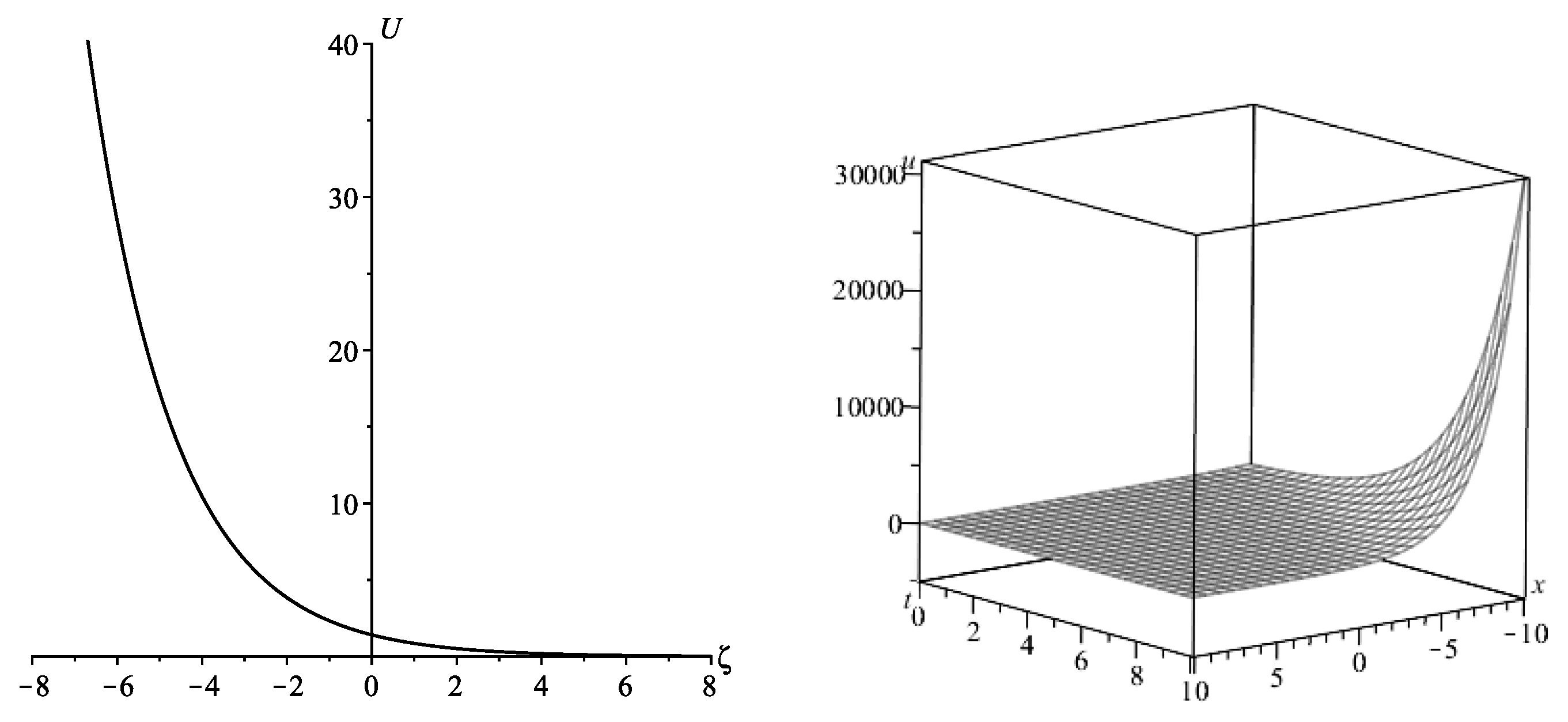
where $C_1$ and $C_2$ are integration constants.

Figure 6 shows a solitary wave solution decaying to an asymptotically constant value and corresponds to the case ${\nu }^2+2q\mu =0$. This solution is an exponential sheet.

•

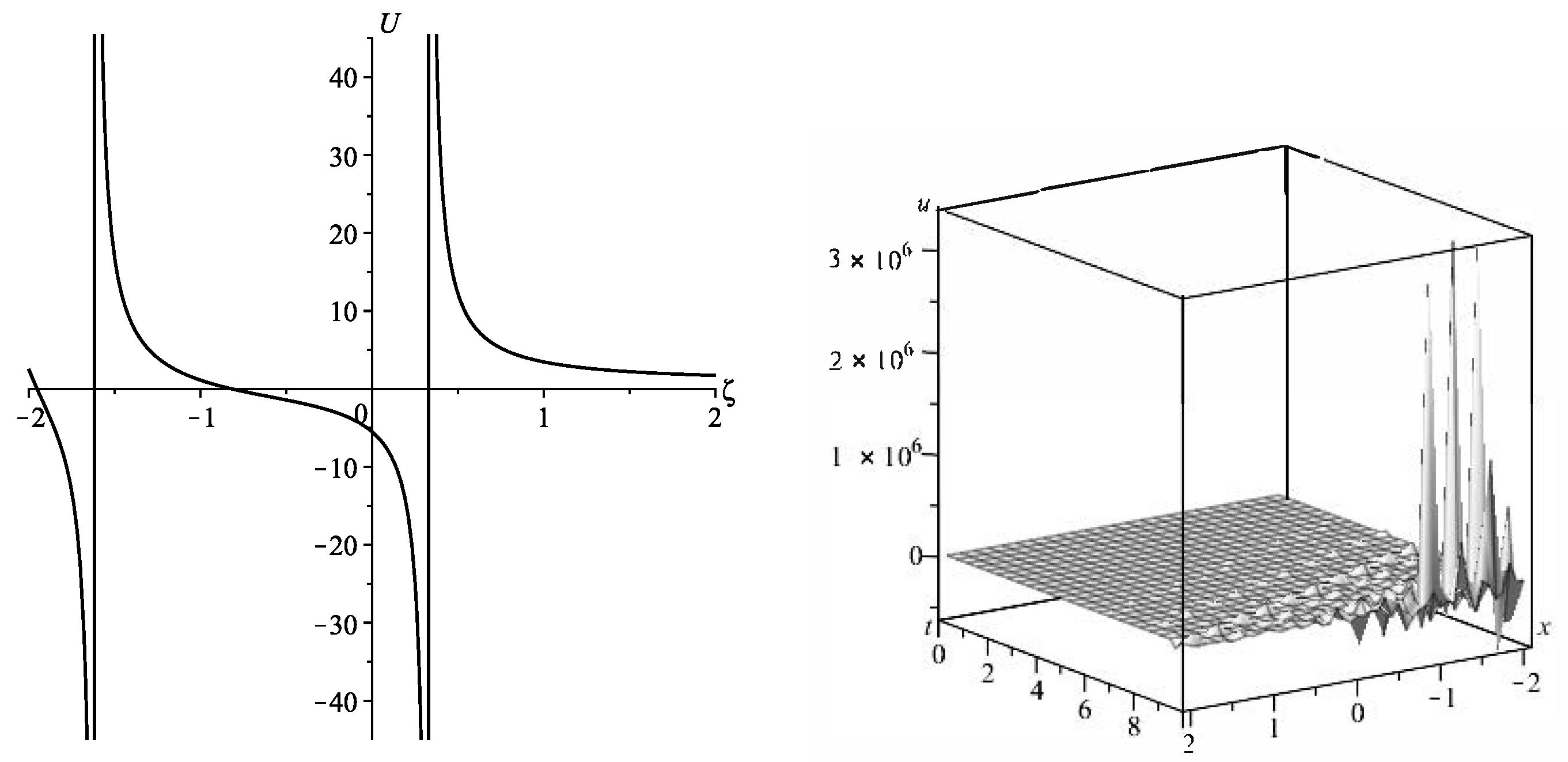
If ${\nu }^2=-2q\mu$ and $\nu =-2cq\tau +p$, the general solution to ODE (44) is

$$V\left(\zeta \right)=C_{1}sin(\frac{2\delta \mu }{\nu }{e}^{\frac{\nu \zeta }{2\mu }})+C_{2}cos(\frac{2\delta \mu }{\nu }{e}^{\frac{\nu \zeta }{2\mu }}).$$

(55)

Hence, the solution to ODE (38) is

$$U\left(\zeta \right)=-\frac{2\delta \mu }{\nu }{e}^{\frac{\nu \zeta }{2\mu }}\frac{C_{2}sin(\frac{2\delta \mu }{\nu }{e}^{\frac{\nu \zeta }{2\mu }})-C_{1}cos(\frac{2\delta \mu }{\nu }{e}^{\frac{\nu \zeta }{2\mu }})}{C_{1}sin(\frac{2\delta \mu }{\nu }{e}^{\frac{\nu \zeta }{2\mu }})+C_{2}cos(\frac{2\delta \mu }{\nu }{e}^{\frac{\nu \zeta }{2\mu }})}$$

(56)

where $C_1$ and $C_2$ are integration constants.

Figure 7 represents a solution given in terms of trigonometric functions and corresponds to the case ${\nu }^2+2q\mu =0$. This solution becomes a singular solution if the denominator is equal to zero. Thus, depending on the choice of the parameters, it leads to a singular solution. The solution behaves as a rogue wave holding elevation peaks and deep humps.

The change of variable (19) yields exact travelling wave solutions of PDE (34). The exact solutions (33), (46), (48), (50), (52), (54) and (56) with $\tau >0$ and $C_0\ne 0$, as far as we know, are new and have not appeared in the literature before.

5. Conclusions

In this paper, travelling wave solutions of the generalized time-delayed Burgers–Fisher Equation (4) were studied. This PDE has a wide applicability, especially in biological phenomena. New travelling wave solutions were obtained by using the multi-reduction theory.

The symmetry-invariant conservation law was reduced to a first integral that corresponded to a first-order Chini equation. This ODE was solved under some conditions leading to solutions written in terms of the Lerch transcendent function.

For a particular case of biological interest, the equation became a Bernoulli equation, whose solution was implicitly given by a quadrature, yielding a one-parameter exact solution corresponding to a shock wave. For $s=1$, the equation described a density-dependent diffusion with a logistically growing population and the first integral became a Ricatti equation, whose solutions were given in terms of exponential, trigonometric, hyperbolic, and Bessel functions.

To the best of our knowledge, solutions (33), (46), (48), (50), (52), (54) and (56) are new and have not been previously obtained.

Additionally, a complete classification of zeroth-order conservation laws was presented with all specific time-delayed Burgers–Fisher equations of the general form (4) for which a conserved quantity of the zeroth-order derivatives of $u(t,x)$ was admitted.