Multivariate Bayesian Semiparametric Regression Model for Forecasting and Mapping HIV and TB Risks in West Java, Indonesia
Abstract
1. Introduction
2. Multivariate Bayesian Semiparametric Regression Model for Forecasting and High-Resolution Mapping
2.1. Generalized Additive Mixed Model via Log Linear Model
2.2. Bayesian Specification
2.3. Model Fitting Using INLA
- (i)
- First, obtain the approximation of the marginal posterior distribution of the hyperparameter:
- (ii)
- Second, approximate the conditional posterior of the l-th (for ) parameter of interest that is needed for calculating the marginal posterior of the parameter of interest. The simplified Laplace approximation of on Taylor’s series expansion is defined as [33]:
2.4. Multivariate Forecasting
2.5. Spatiotemporal Autocorrelation
2.6. High-Resolution Mapping
2.7. Bayesian Model Selection Criteria
- Deviance information criteria (DIC)
- Watanabe Akaike information criteria (WAIC)
- Marginal predicted likelihood (MPL)
- Mean absolute error (MAE)
- Root means square error (RMSE)
3. Results
3.1. Descriptive Analysis
3.2. Model Selection
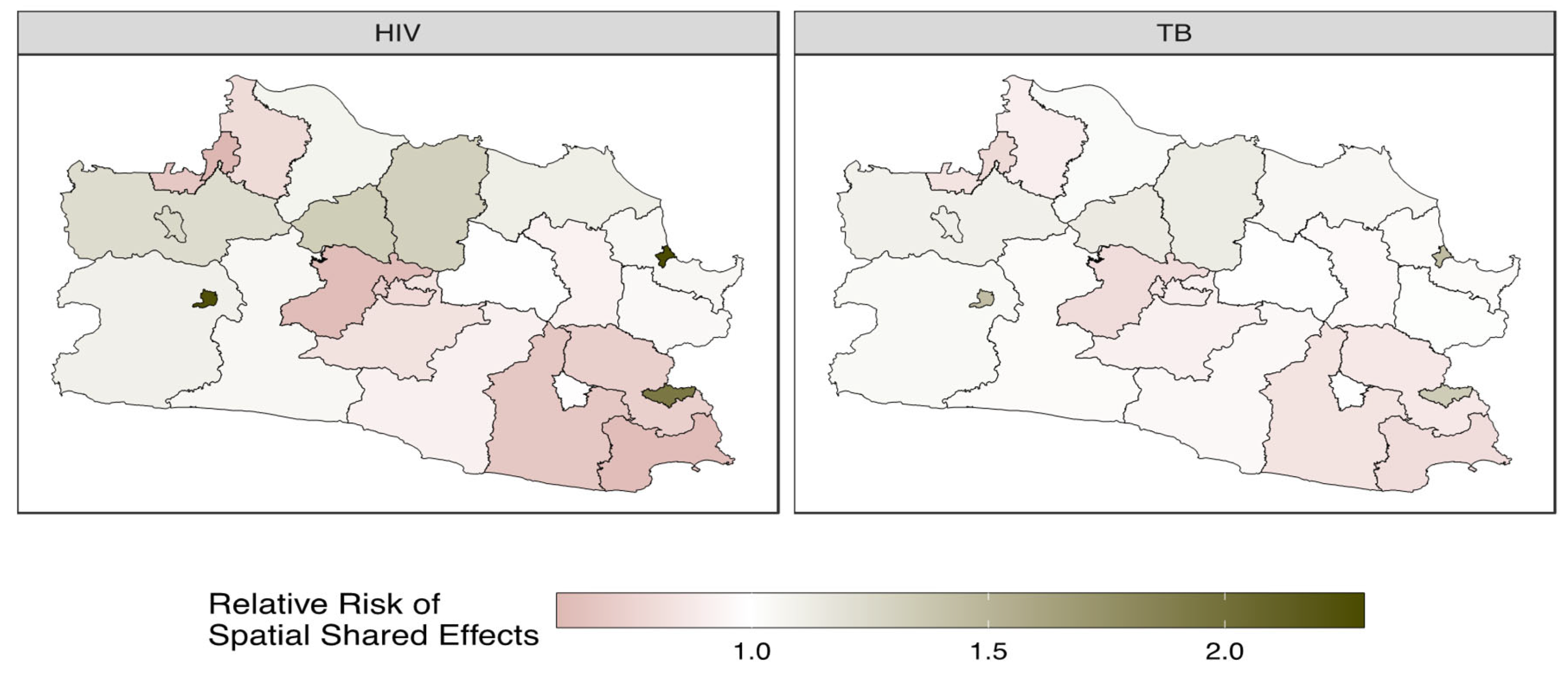
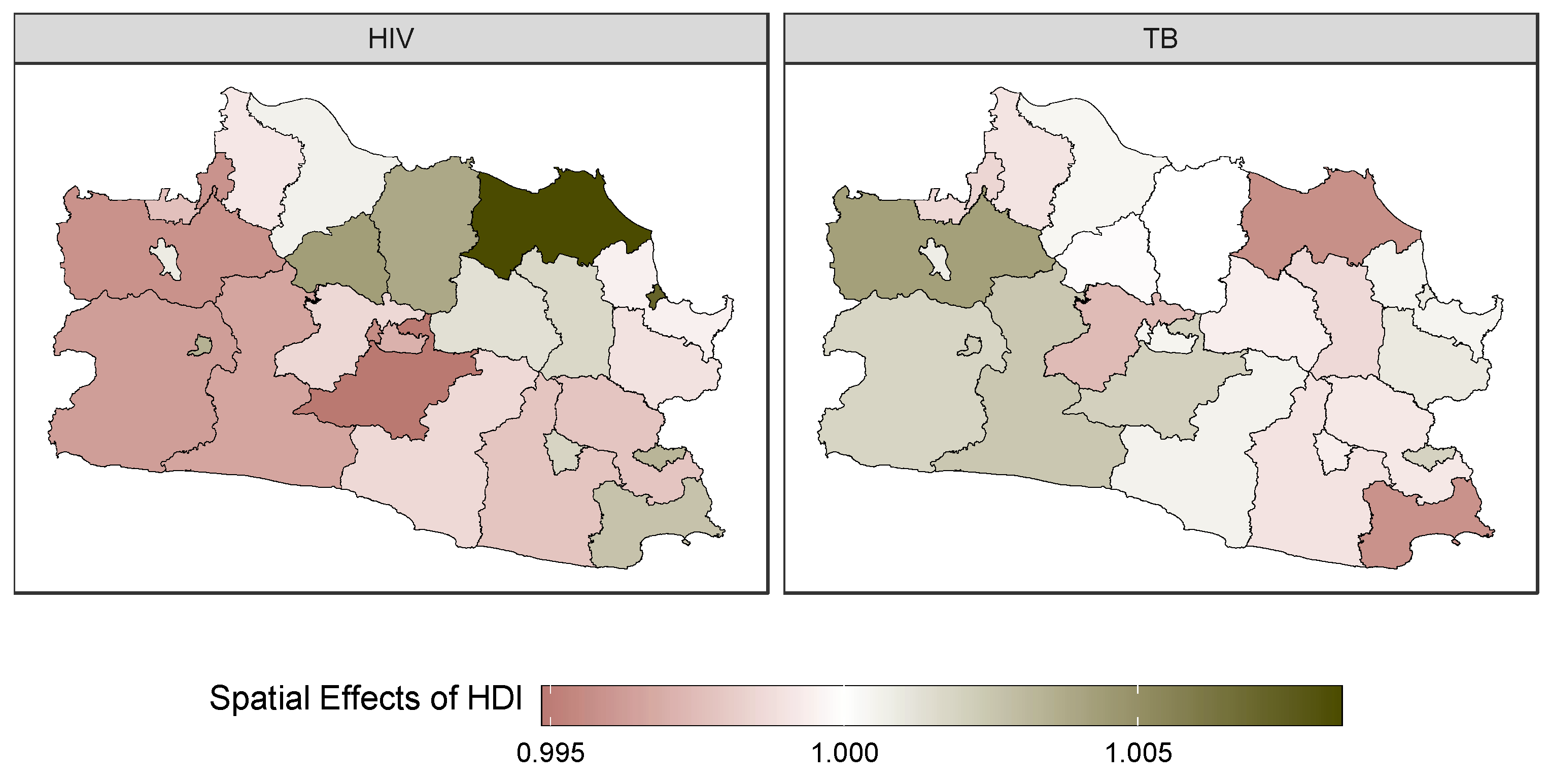
3.3. Final Model Inference
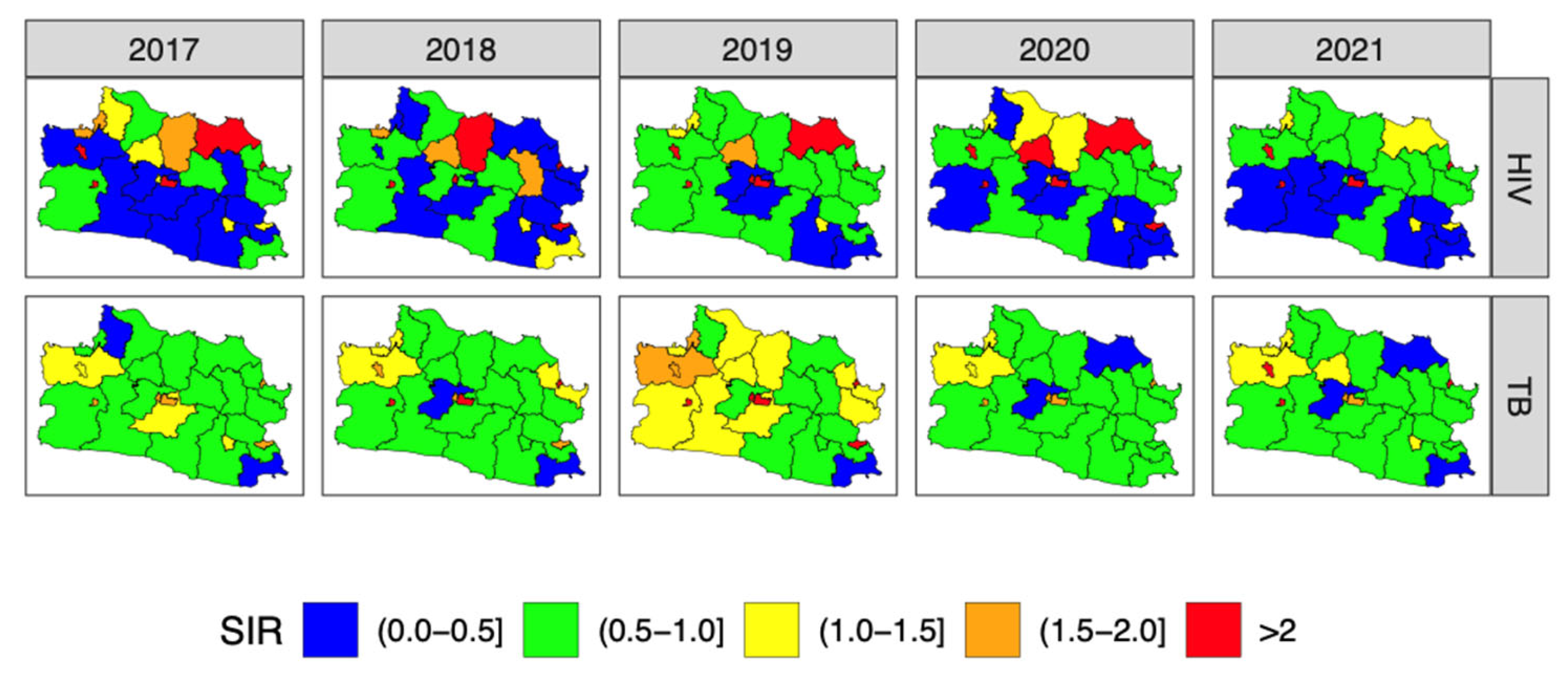
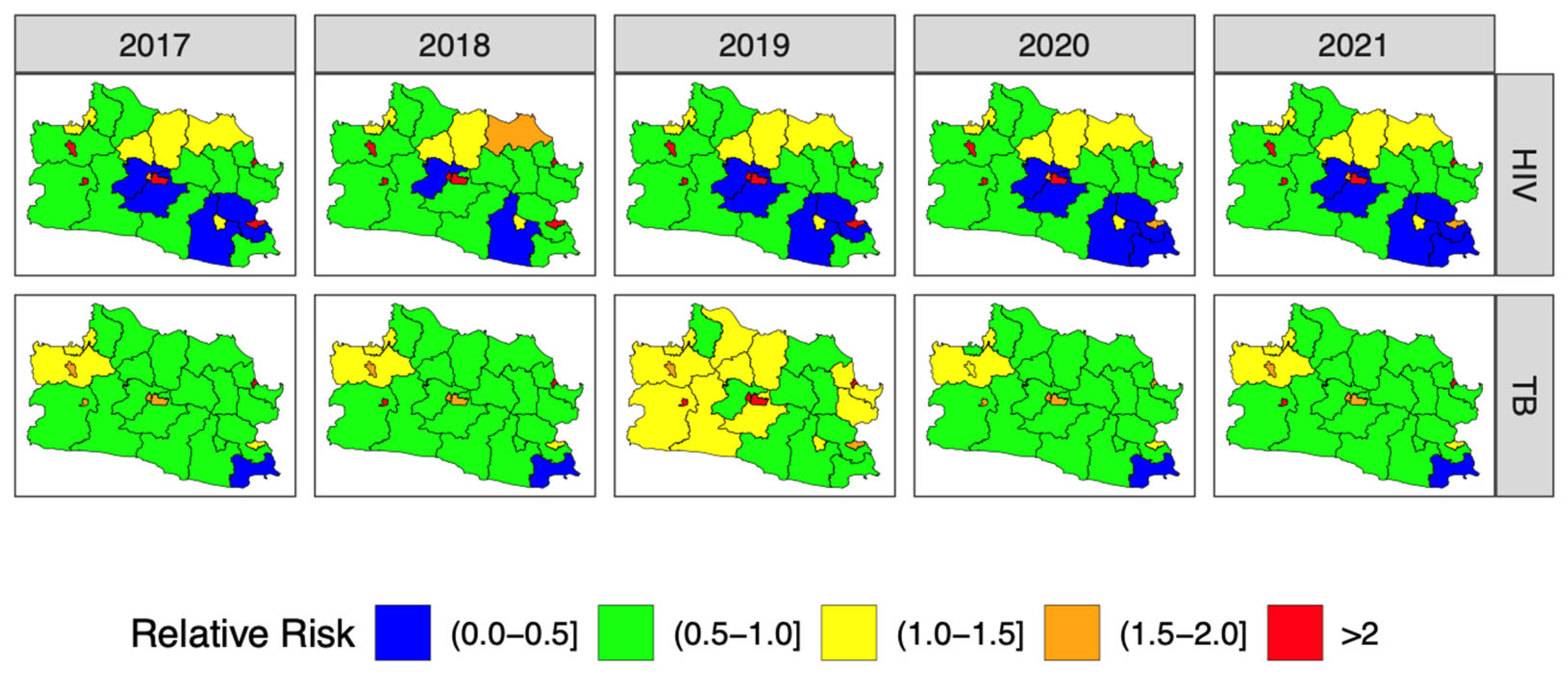
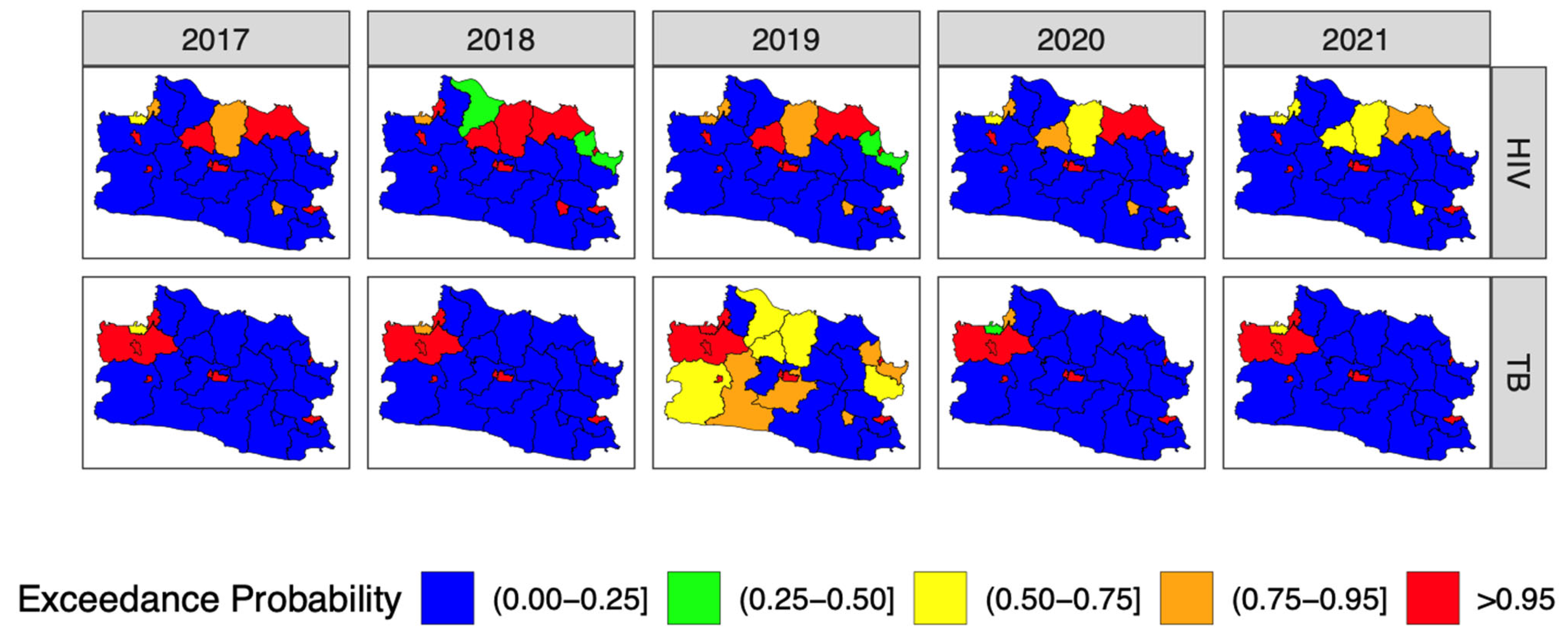
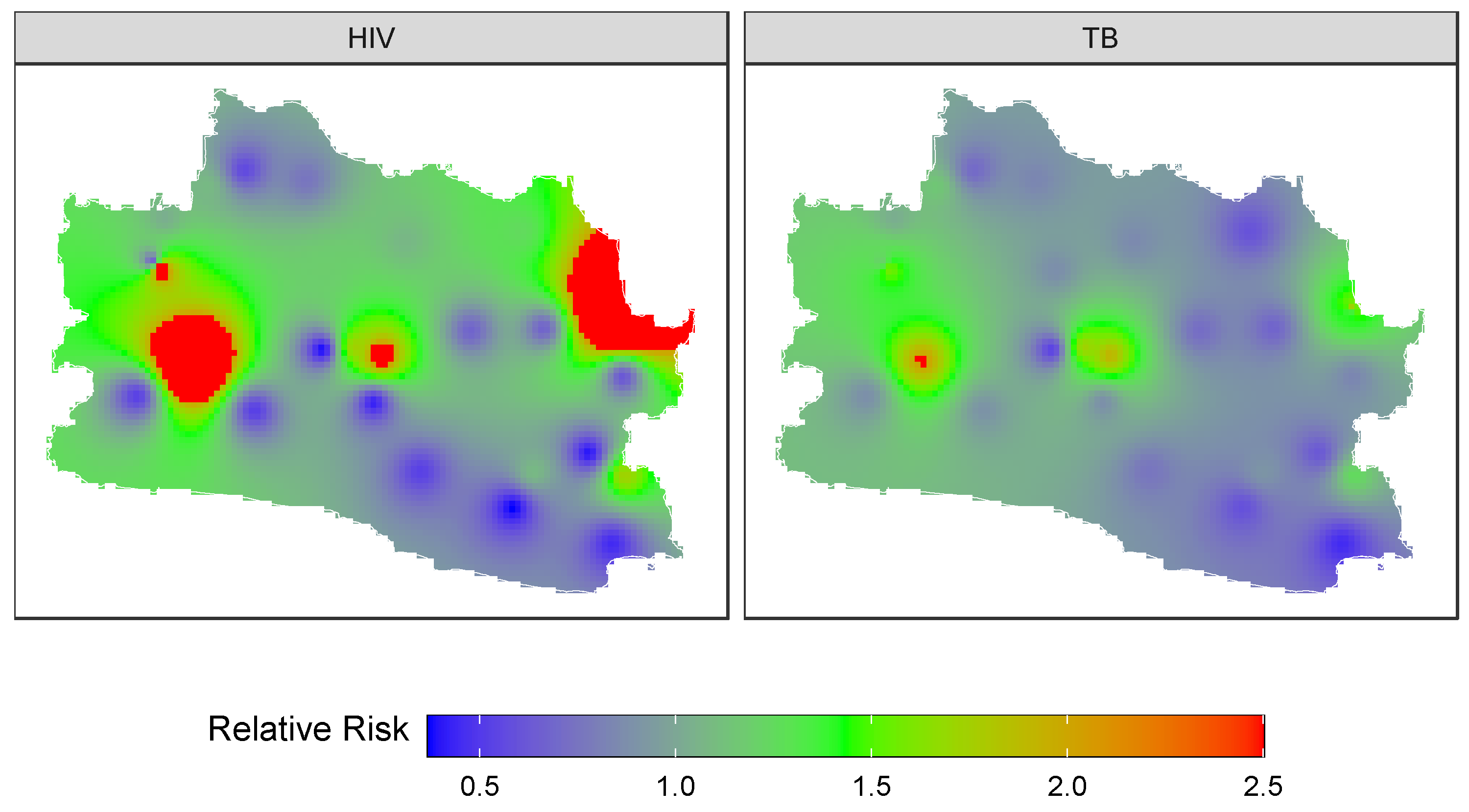
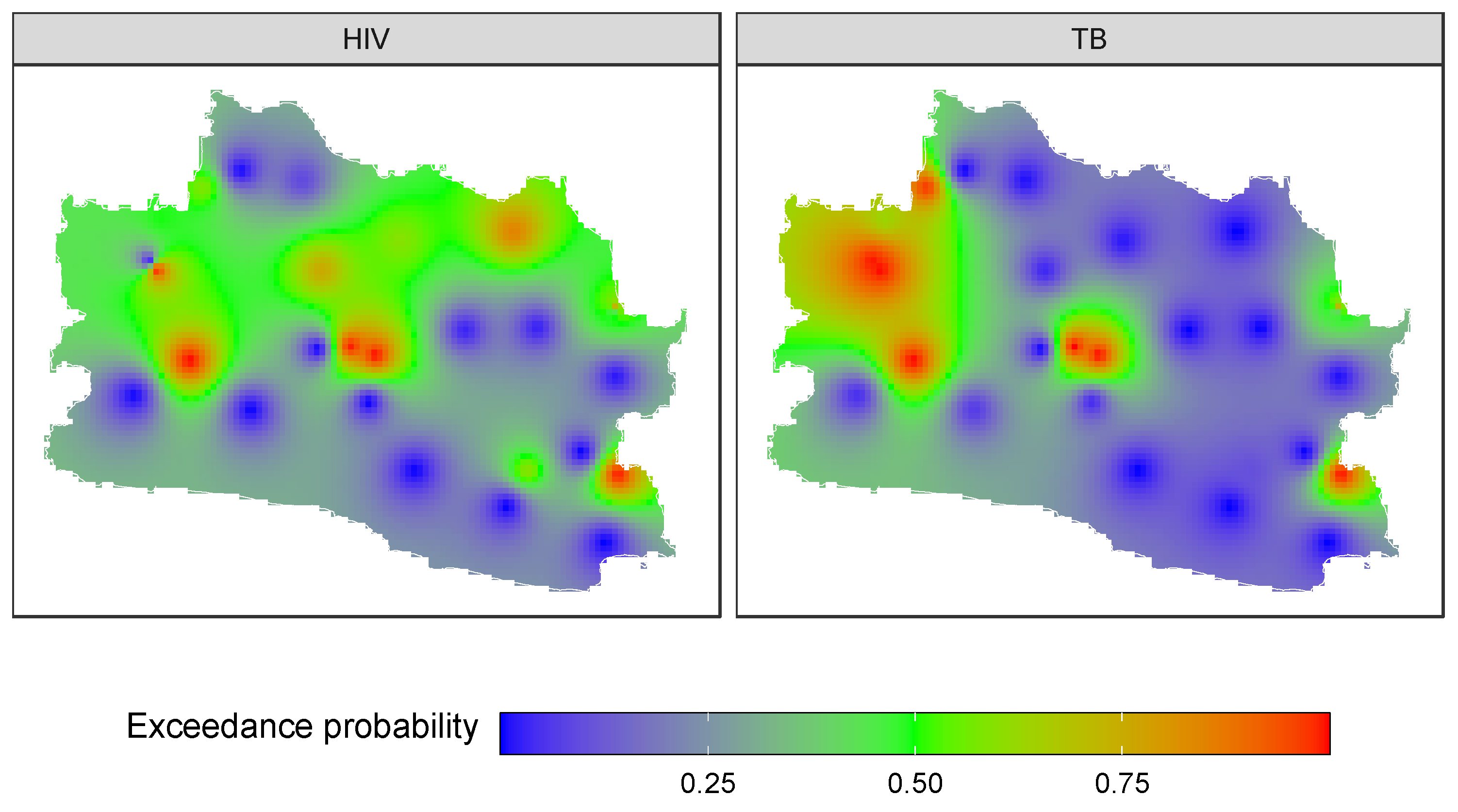
3.4. Forecasting and High-Resolution Mapping
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
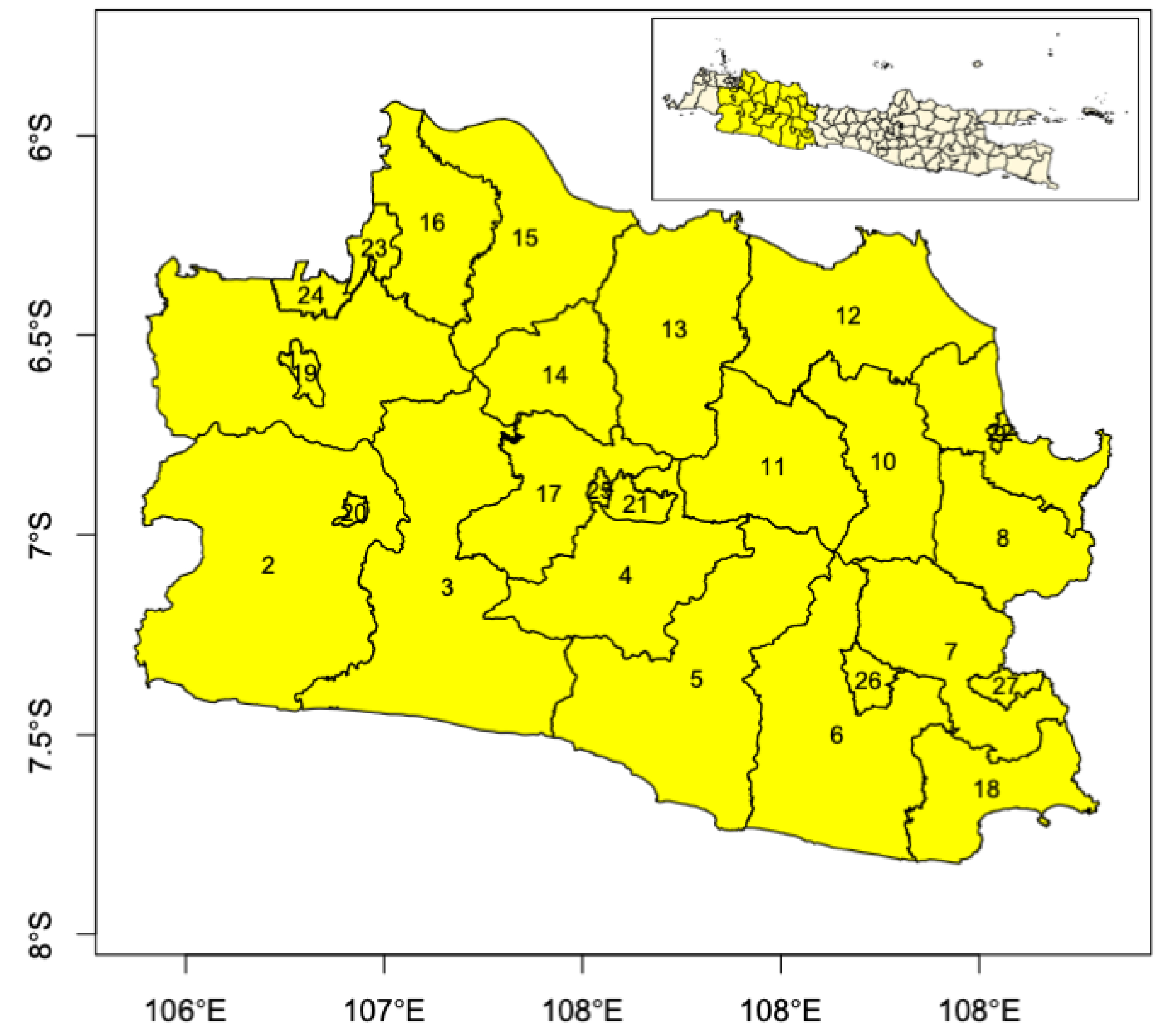
Appendix A
| ID | District | ID | District |
|---|---|---|---|
| 1 | Regency Bogor | 14 | Regency Purwakarta |
| 2 | Regency Sukabumi | 15 | Regency Karawang |
| 3 | Regency Cianjur | 16 | Regency Bekasi |
| 4 | Regency Bandung | 17 | Regency Bandung Barat |
| 5 | Regency Garut | 18 | Regency Pangandaran |
| 6 | Regency Tasikmalaya | 19 | City Bogor |
| 7 | Regency Ciamis | 20 | City Sukabumi |
| 8 | Regency Kuningan | 21 | City Bandung |
| 9 | Regency Cirebon | 22 | City Cirebon |
| 10 | Regency Majalengka | 23 | City Bekasi |
| 11 | Regency Sumedang | 24 | City Depok |
| 12 | Regency Indramayu | 25 | City Cimahi |
| 13 | Regency Subang | 26 | City Tasikmalaya |
| 27 | City Banjar |
References
- Coly, S.; Garrido, M.; Abrial, D.; Yao, A.F. Bayesian hierarchical models for disease mapping applied to contagious pathologies. PLoS ONE 2021, 6, e0222898. [Google Scholar] [CrossRef]
- MacNab, Y.C. Bayesian disease mapping: Past, present, and future. Spat. Stat. 2022, 50, 100593. [Google Scholar] [CrossRef] [PubMed]
- Coly, S.; Charras-Garrido, M.; Abriala, D.; YaoLafourcade, A.F. Spatiotemporal Disease Mapping Applied to Infectious Diseases. Procedia Environ. Sci. 2015, 26, 32–37. [Google Scholar] [CrossRef]
- Schrodle, B.; Held, L. Spatio-Temporal Disease Mapping Using INLA. Environmetrics 2011, 22, 725–734. [Google Scholar] [CrossRef]
- Otiende, V.A.; Achia, T.N.; Mwambi, H.G. Bayesian Hierarchical Modeling of Joint Spatiotemporal Risk Patterns for Human Immunodeficiency Virus (HIV) and Tuberculosis (TB) in Kenya. PLoS ONE 2020, 15, e0234456. [Google Scholar] [CrossRef]
- Baptista, H.; Congdon, P.; Mendes, J.M.; Rodrigues, A.M.; Canhão, H.; Dias, S.S. Disease mapping models for data with weak spatial dependence or spatial discontinuities. Epidemiol. Methods 2020, 9, 20190025. [Google Scholar] [CrossRef]
- MacNab, Y.C. On identification in Bayesian disease mapping and ecological−spatial regression models. Stat. Methods Med. Res. 2014, 23, 134–155. [Google Scholar] [CrossRef] [PubMed]
- Lawson, A.B. Bayesian Disease Mapping Hierarchical Modeling in Spatial Epidemiology, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Lee, S.A.; Economou, T.; Lowe, R. A Bayesian Modelling Framework to Quantify Multiple Sources of Spatial Variation for Disease Mapping. J. R. Soc. Interface 2022, 19, 20220440. [Google Scholar] [CrossRef]
- Chamanpara, P.; Moghimbeigi, A.; Faradmal, J.; Poorolajal, J. Joint Disease Mapping of Two Digestive Cancers in Golestan Province, Iran Using a Shared Component Model. Osong Public Health Res. Perspect. 2015, 6, 205–210. [Google Scholar] [CrossRef]
- Manda, S.; Feltbower, R.; Gilthorpe, M. Review and Empirical Comparison of Joint Mapping of Multiple Diseases. S. Afr. J. Epidemiol. Infect. 2012, 27, 169–182. [Google Scholar] [CrossRef]
- Held, L.; Natario, I.; Fenton, S.E.; Rue, H.; Becker, N. Towards Joint Disease Mapping. Stat. Methods Med. Res. 2005, 14, 61–82. [Google Scholar] [CrossRef]
- Tesema, G.A.; Tessema, Z.T.; Heritier, S.; Stirling, R.G.; Earnest, A. A Systematic Review of Joint Spatial and Spatiotemporal Models in Health Research. Int. J. Environ. Res. Public Health 2023, 20, 5295. [Google Scholar] [CrossRef]
- Downing, A.; Forman, D.; Gilthorpe, M.S.; Edwards, K.L.; Manda, S.O. Joint Disease Mapping Using Six Cancers in The Yorkshire Region of England. Int. J. Health Geogr. 2008, 7, 41. [Google Scholar] [CrossRef]
- Earnest, A.; Beard, J.R.; Morgan, G.; Lincoln, D.; Summerhayes, R.; Dunn, T.; Muscatello, D.; Mengersen, K. Small Area Estimation of Sparse Disease Counts Using Shared Component Models-Application to Birth Defect Registry Data in New South Wales, Australia. Health Place 2010, 16, 684–693. [Google Scholar] [CrossRef]
- Ibáñez-Beroiz, B.; Librero-López, J.; Peiró-Moreno, S.; Bernal-Delgado, E. Shared Component Modelling as an Alternative to Assess Geographical Variations in Medical Practice: Gender Inequalities in Hospital Admissions for Chronic Diseases. BMC Med. Res. Methodol. 2011, 11, 172. [Google Scholar] [CrossRef] [PubMed]
- Knorr-Held, L. Bayesian Modelling of Inseparable Space-Time Variation in Disease Risk. Stat. Med. 2000, 19, 2555–2567. [Google Scholar] [CrossRef]
- Mahaki, B.; Mehrabi, Y.; Kavousi, A.; Schmid, V.J. Joint Spatio-Temporal Shared Component Model with an Application in Iran Cancer Data. Asian Pac. J. Cancer Prev. 2018, 19, 1553–1560. [Google Scholar] [PubMed]
- Meliker, J.R.; Sloan, C.D. Spatio-Temporal Epidemiology: Principles and Opportunities. Spat. Spatio-Temporal Epidemiol. 2011, 2, 1–9. [Google Scholar] [CrossRef]
- Richardson, S.; Abellan, J.J.; Best, N. Bayesian Spatio-Temporal Analysis of Joint Patterns of Male and Female Lung Cancer Risks in Yorkshire (UK). Stat. Methods Med. Res. 2006, 15, 385–407. [Google Scholar] [CrossRef]
- Oleson, J.J.; Smith, B.J.; Kim, H. Joint Spatio-Temporal Modeling of Low Incidence Cancers Sharing Common Risk Factors. Data Sci. J. 2008, 6, 105–123. [Google Scholar] [CrossRef] [PubMed]
- Lee, D. A Comparison of Conditional Autoregressive Models Used in Bayesian Disease Mapping. Spat. Spatio-Temporal Epidemiol. 2011, 2, 79–89. [Google Scholar] [CrossRef]
- Giacomini, R.; Kitagawa, T. Robust Bayesian Inference for Set-Identified Models. Econometrica 2021, 89, 1519–1556. [Google Scholar] [CrossRef]
- Wasserman, L.A. A Robust Bayesian Interpretation of Likelihood Regions. Ann. Stat. 1989, 17, 1387–1393. [Google Scholar] [CrossRef]
- Tzala, E.; Best, N. Bayesian Latent Variable Modelling of Multivariate Spatio-Temporal Variation in Cancer Mortality. Stat. Methods Med. Res. 2007, 97, 97–118. [Google Scholar] [CrossRef]
- Banerjee, S.; Carlin, B.P. Semiparametric Spatio-Temporal Frailty Modeling. Environmetrics 2003, 14, 523–535. [Google Scholar] [CrossRef]
- Okango, E.; Mwambi, H.; Ngesa, O.; Achia, T. Semi-Parametric Spatial Joint Modeling of HIV and HSV-2 among Women in Kenya. PLoS ONE 2015, 10, e0135212. [Google Scholar] [CrossRef] [PubMed]
- Rong, Y.; Zhao, S.D.; Zhu, J.; Yuan, W.; Cheng, W.; Li, Y. More Accurate Semiparametric Regression in Pharmacogenomics. Stat. Interface 2018, 11, 573–580. [Google Scholar] [CrossRef]
- Luan, J.; Ba, J.; Liu, B.; Xu, X.; Shu, D. 2021–2022 Monitoring, Early Warning, and Forecasting of Global Infectious Diseases. J. Biosaf. Biosecur. 2022, 4, 98–104. [Google Scholar] [CrossRef]
- Wang, A.S. The Early Warning and Forecasting System (EWFS) for the Reduction of Serious Atmosphere-Hydrosphere Disasters. In Early Warning Systems for Natural Disaster Reduction; Zschau, J., Küppers, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 399–402. [Google Scholar]
- Tchuente, L.A.T.; Stothard, J.R.; Rollinson, D.; Reinhard-Rupp, J. Precision Mapping: An Innovative Tool and Way Forward to Shrink the Map, Better Target Interventions, and Accelerate toward the Elimination of Schistosomiasis. PLoS Negl. Trop. Dis. 2018, 12, e0006563. [Google Scholar] [CrossRef]
- Jaya, I.G.N.M.; Folmer, H. Spatiotemporal High-Resolution Prediction and Mapping: Methodology and Application to Dengue Disease. J. Geogr. Syst. 2022, 24, 527–581. [Google Scholar] [CrossRef]
- Blangiardo, M.; Cameletti, M. Spatial and Spatio-Temporal Bayesian Models with R-INLA; John Wiley& Sons: Chennai, India, 2015; pp. 105–200. [Google Scholar]
- Utazi, C.E.; Thorley, J.; Alegana, V.A.; Ferrari, M.J.; Nilsen, K.; Takahashi, S.; Metcalf, C.J.E.; Lessler, J.; Tatem, A.J. A Spatial Regression Model for the Disaggregation of Areal Unit Based Data to High-Resolution Grids with Application to Vaccination Coverage Mapping. Stat. Methods Med. Res. 2019, 28, 3226–3241. [Google Scholar] [CrossRef] [PubMed]
- Haider, M.S.; Salih, S.K.; Hassan, S.; Taniwall, N.J.; Moazzam, M.F.U.; Lee, B.G. Spatial Distribution and Mapping of COVID-19 Pandemic in Afghanistan using GIS Technique. SN Soc. Sci. 2022, 2, 59. [Google Scholar] [CrossRef] [PubMed]
- Berke, O. Exploratory Disease Mapping: Kriging the Spatial Risk Function from Regional Count Data. Int. J. Health Geogr. 2004, 3, 18. [Google Scholar] [CrossRef][Green Version]
- Goovaerts, P. Geostatistical Analysis of Disease Data: Accounting for Spatial Support and Population Density in the Isopleth Mapping of Cancer Mortality Risk Using Area-To-Point Poisson Kriging. Int. J. Health Geogr. 2006, 5, 52. [Google Scholar] [CrossRef]
- Tobler, W. A Computer Movie Simulating Urban Growth in The Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Yoo, E.H.; Kyriakidis, P.C.; Tobler, W. Reconstructing Population Density Surfaces from Areal Data: A Comparison of Tobler’s Pycnophylactic Interpolation Method and Area-to-Point Kriging. Geogr. Anal. 2010, 42, 78–98. [Google Scholar] [CrossRef]
- Jaya, I.G.N.M.; Ruchjana, B.N.; Abdullah, A.S.; Andriyana, Y. Comparison of IDW and GP Models with Application to Spatiotemporal Interpolation of Rainfall in Bali Province, Indonesia. J. Phys. Conf. Ser. 2021, 1722, 012080. [Google Scholar] [CrossRef]
- Jaya, I.G.N.M.; Folmer, H. Bayesian Spatiotemporal Mapping of Relative Dengue Disease Risk in Bandung, Indonesia. J. Geogr. Syst. 2020, 22, 105–142. [Google Scholar] [CrossRef]
- Berridge, D.M.; Crouchley, R. Multivariate Generalized Linear Mixed Models Using R; CRC Press: Boca Raton, FL, USA, 2011; pp. 1–20. [Google Scholar]
- Khazaei, S.; Rezaeian, S.; Baigi, V.; Saatchi, M.; Molaeipoor, L.; Khazaei, Z.; Khazaei, S.; Raza, O. Incidence and Pattern of Tuberculosis Treatment Success Rates in Different Levels of The Human Development Index: A Global Perspective. S. Afr. J. Epidemiol. Infect. 2017, 32, 100–104. [Google Scholar]
- Taylan, M.; Demir, M.; Yılmaz, S.; Kaya, H.; Sen, H.S.; Oruc, M.; Icer, M.; Gunduz, E.; Sezgi, C. Effect of Human Development Index Parameters on Tuberculosis Incidence in Turkish Provinces. J. Infect. Dev. Ctries. 2016, 10, 1183–1190. [Google Scholar] [CrossRef]
- Zille, A.I.; Werneck, G.L.; Luiz, R.R.; Conde, M.B. Social Determinants of Pulmonary Tuberculosis in Brazil: An Ecological Study. BMC Pulm. Med. 2019, 19, 87. [Google Scholar] [CrossRef]
- Maciel, E.M.G.d.S.; Amancio, J.d.S.; Castro, D.B.d.; Braga, J.U. Social Determinants of Pulmonary Tuberculosis Treatment Non-Adherence in Rio de Janeiro, Brazil. PLoS ONE 2018, 13, e0190578. [Google Scholar] [CrossRef]
- Jaya, I.G.N.M.; Folmer, H.; Lundberg, L. A joint Bayesian spatiotemporal risk prediction model of COVID-19 incidence, IC admission, and death with application to Sweden. Ann. Reg. Sci. 2022, 1, 1–34. [Google Scholar] [CrossRef] [PubMed]
- Mohebbi, M.; Wolfe, R.; Forbes, A. Disease Mapping and Regression with Count Data in the Presence of Overdispersion and Spatial Autocorrelation: A Bayesian Model Averaging Approach. Int. J. Environ. Res. Public Health 2014, 11, 883–902. [Google Scholar] [CrossRef] [PubMed]
- Clayton, D.; Kaldor, J. Empirical Bayes Estimates of Age-Standardized Relative Risks for Use in Disease Mapping. Biometrics 1987, 43, 671–681. [Google Scholar] [CrossRef] [PubMed]
- Rue, H.; Martino, S.; Chopin, N. Approximate Bayesian Inference for Latent Gaussian Models by Using Integrated Nested Laplace Approximations. J. R. Stat. Soc. B Stat. 2009, 71, 319–392. [Google Scholar] [CrossRef]
- Leroux, B.; Lei, X.; Breslow, N. Estimation of Disease Rates in Small Areas: A New Mixed Model for Spatial Dependence. In Statistical Models in Epidemiology, the Environment and Clinical Trials; Halloran, M., Berry, D., Eds.; Springer: New York, NY, USA, 1999; pp. 135–178. [Google Scholar]
- Bivand, R.; Gómez-Rubio, V.; Rue, H. Spatial Data Analysis with R-INLA with Some Extensions. J. Stat. Softw. 2015, 63, 1–31. [Google Scholar] [CrossRef]
- Gelman, A. Prior Distributions for Variance Parameters in Hierarchical Models. Bayesian Anal. 2006, 1, 515–534. [Google Scholar] [CrossRef]
- Osei, F.; Stein, A. Diarrhea Morbidities in Small Areas: Accounting for Non-Stationarity in Sociodemographic Impacts Using Bayesian Spatially Varying Coefficient Modelling. Sci. Rep. 2017, 7, 9908. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Yue, Y.R.; Faraway, J. Bayesian Regression Modeling with INLA; CRC Press: Boca Raton, FL, USA, 2018; pp. 1–20. [Google Scholar]
- Barbulescu, A.; Bautu, A.; Bautu, E. Optimizing Inverse Distance Weighting with Particle Swarm Optimization. Appl. Sci. 2020, 10, 2054. [Google Scholar] [CrossRef]
- Gelman, A.; Hwang, J.; Vehtari, A. Understanding Predictive Information Criteria for Bayesian Models. Stat. Comput. 2014, 24, 997–1016. [Google Scholar] [CrossRef]
- Watanabe, S. Asymptotic Equivalence of Bayes Cross Validation and Widely Applicable Information Criterion in Singular Learning Theory. J. Mach. Learn. Res. 2010, 11, 3571–3594. [Google Scholar]
- West Java. Health Profile of West Java 2017; West Java Health Office: Bandung, Indonesia, 2017; pp. 83–99. [Google Scholar]
- West Java. Health Profile of West Java 2018; West Java Health Office: Bandung, Indonesia, 2018; pp. 82–98. [Google Scholar]
- West Java. Health Profile of West Java 2019; West Java Health Office: Bandung, Indonesia, 2019; pp. 81–97. [Google Scholar]
- West Java. Health Profile of West Java 2020; West Java Health Office: Bandung, Indonesia, 2020; pp. 84–98. [Google Scholar]
- West Java. Health Profile of West Java 2021; West Java Health Office: Bandung, Indonesia, 2021; pp. 81–96. [Google Scholar]
- Mabaso, M.; Zama, T.; Mlangeni, L.; Mbiza, S.; Mkhize-Kwitshana, Z. Association between the Human Development Index and Millennium Development Goals 6 Indicators in Sub-Saharan Africa from 2000 to 2014: Implications for the New Sustainable Development Goals. J. Epidemiol. Glob. Health 2018, 8, 77–81. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Li, X.; Xuan, K.; Jiang, Y.; Jia, R.; Ji, J.; Liu, J. Interpolation of Soil Properties from Geostatistical Priors and DCT-Based Compressed Sensing. Ecol. Indic. 2022, 40, 109013. [Google Scholar] [CrossRef]


| Year | HIV | TB | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Q1 | Mean | Q3 | Max | SD | CV (%) | Min | Q1 | Mean | Q3 | Max | SD | CV (%) | |
| 2017 | 33 | 85.5 | 217.7 | 292.5 | 986 | 222.8 | 102.3 | 384 | 1732.0 | 3098.4 | 3602.0 | 10,943 | 2515.1 | 81.2 |
| 2018 | 38 | 85.0 | 207.5 | 255.0 | 1063 | 206.5 | 99.5 | 336 | 1583.5 | 3364.4 | 4158.0 | 13,567 | 2917.7 | 86.7 |
| 2019 | 4 | 111.0 | 240.1 | 252.0 | 1186 | 233.6 | 97.3 | 318 | 2117.0 | 4086.7 | 4959.0 | 15,886 | 3452.8 | 84.5 |
| 2020 | 16 | 101.5 | 218.0 | 283.5 | 813 | 169.3 | 77.7 | 332 | 1512.5 | 3173.4 | 4372.5 | 11,166 | 2532.6 | 79.8 |
| 2021 | 4 | 103.5 | 201.6 | 238.5 | 869 | 175.5 | 87.1 | 267 | 1670.5 | 3430.0 | 4695.0 | 11,991 | 2636.4 | 76.9 |
| Correlation | Min | Q1 | Mean | Q3 | Max | SD | SV |
|---|---|---|---|---|---|---|---|
| Spatial pattern | 0.540 | 0.608 | 0.689 | 0.756 | 0.877 | 0.131 | 19.013 |
| Temporal pattern | −0.810 | −0.393 | −0.131 | 0.196 | 0.641 | 0.419 | −319.847 |
| Model | Likelihood | DIC | WAIC | NPL | MAP | RMSE | R2 |
|---|---|---|---|---|---|---|---|
| Parametric models | |||||||
| M1.1 | Poisson | 17,813 | 15,184 | −9366 | 0.371 | 1.187 | 0.824 |
| M1.2 | NB | 3677 | 3678 | −1846 | 0.372 | 1.210 | 0.832 |
| Semiparametric models | |||||||
| M2.1 | Poisson | 11,912 | 12,223 | −6740 | 0.353 | 1.236 | 0.824 |
| M2.2 | NB | 3655 | 3655 | −1833 | 0.353 | 1.175 | 0.834 |
| Parameters | Mean | SD | q(0.025) | Median | q(0.975) | Relative Risk (RR) |
|---|---|---|---|---|---|---|
| Intercept HIV | −0.463 | 0.123 | −0.703 | −0.463 | −0.221 | 0.6294 |
| Intercept TB | −0.308 | 0.054 | −0.413 | −0.308 | −0.203 | 0.7349 |
| Population density on HIV | 0.131 | 0.031 | 0.070 | 0.131 | 0.191 | 1.1400 |
| Population density on TB | 0.072 | 0.014 | 0.044 | 0.072 | 0.099 | 1.0747 |
| Hyperparameters | Mean | SD | q(0.025) | Median | q(0.975) | % Fraction of Variance |
|---|---|---|---|---|---|---|
| Overdispersion parameter for HIV | 3.770 | 0.499 | 2.882 | 3.738 | 4.835 | |
| Overdispersion parameter for TB | 37.075 | 5.259 | 27.676 | 36.760 | 48.248 | |
| Spatial autoregressive of shared component on HIV () | 0.546 | 0.206 | 0.143 | 0.560 | 0.889 | |
| Scaling parameter on TB () | 0.500 | 0.249 | 0.039 | 0.488 | 1.013 | |
| Spatial autoregressive of spatial effect on HIV () | 0.456 | 0.239 | 0.069 | 0.440 | 0.903 | |
| Spatial autoregressive of spatial effect on TB () | 0.399 | 0.186 | 0.109 | 0.374 | 0.797 | |
| SD shared component on HIV () | 0.585 | 0.187 | 0.283 | 0.565 | 1.008 | 99.971 |
| SD temporal effects of HDI on HIV () | 0.003 | 0.002 | 0.001 | 0.002 | 0.007 | 0.002 |
| SD temporal effects of HDI on TB () | 0.003 | 0.002 | 0.001 | 0.003 | 0.007 | 0.003 |
| SD spatial effects of HDI on HIV () | 0.008 | 0.003 | 0.004 | 0.008 | 0.016 | 0.020 |
| SD spatial effects of HDI on TB () | 0.004 | 0.001 | 0.002 | 0.003 | 0.007 | 0.004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaya, I.G.N.M.; Handoko, B.; Andriyana, Y.; Chadidjah, A.; Kristiani, F.; Antikasari, M. Multivariate Bayesian Semiparametric Regression Model for Forecasting and Mapping HIV and TB Risks in West Java, Indonesia. Mathematics 2023, 11, 3641. https://doi.org/10.3390/math11173641
Jaya IGNM, Handoko B, Andriyana Y, Chadidjah A, Kristiani F, Antikasari M. Multivariate Bayesian Semiparametric Regression Model for Forecasting and Mapping HIV and TB Risks in West Java, Indonesia. Mathematics. 2023; 11(17):3641. https://doi.org/10.3390/math11173641
Chicago/Turabian StyleJaya, I. Gede Nyoman Mindra, Budhi Handoko, Yudhie Andriyana, Anna Chadidjah, Farah Kristiani, and Mila Antikasari. 2023. "Multivariate Bayesian Semiparametric Regression Model for Forecasting and Mapping HIV and TB Risks in West Java, Indonesia" Mathematics 11, no. 17: 3641. https://doi.org/10.3390/math11173641
APA StyleJaya, I. G. N. M., Handoko, B., Andriyana, Y., Chadidjah, A., Kristiani, F., & Antikasari, M. (2023). Multivariate Bayesian Semiparametric Regression Model for Forecasting and Mapping HIV and TB Risks in West Java, Indonesia. Mathematics, 11(17), 3641. https://doi.org/10.3390/math11173641







