Cumulative Incidence Functions for Competing Risks Survival Data from Subjects with COVID-19
Abstract
:1. Introduction
2. Materials and Methods
2.1. Non-Parametric Estimation Technique: CSH Approach
2.2. Semi-Parametric Regression Models for the CSH Approach
2.3. Non-Parametric Estimation Technique: The SDH Approach
2.4. Semi-Parametric Regression Models for the SDH Approach
3. Application to COVID-19 Data
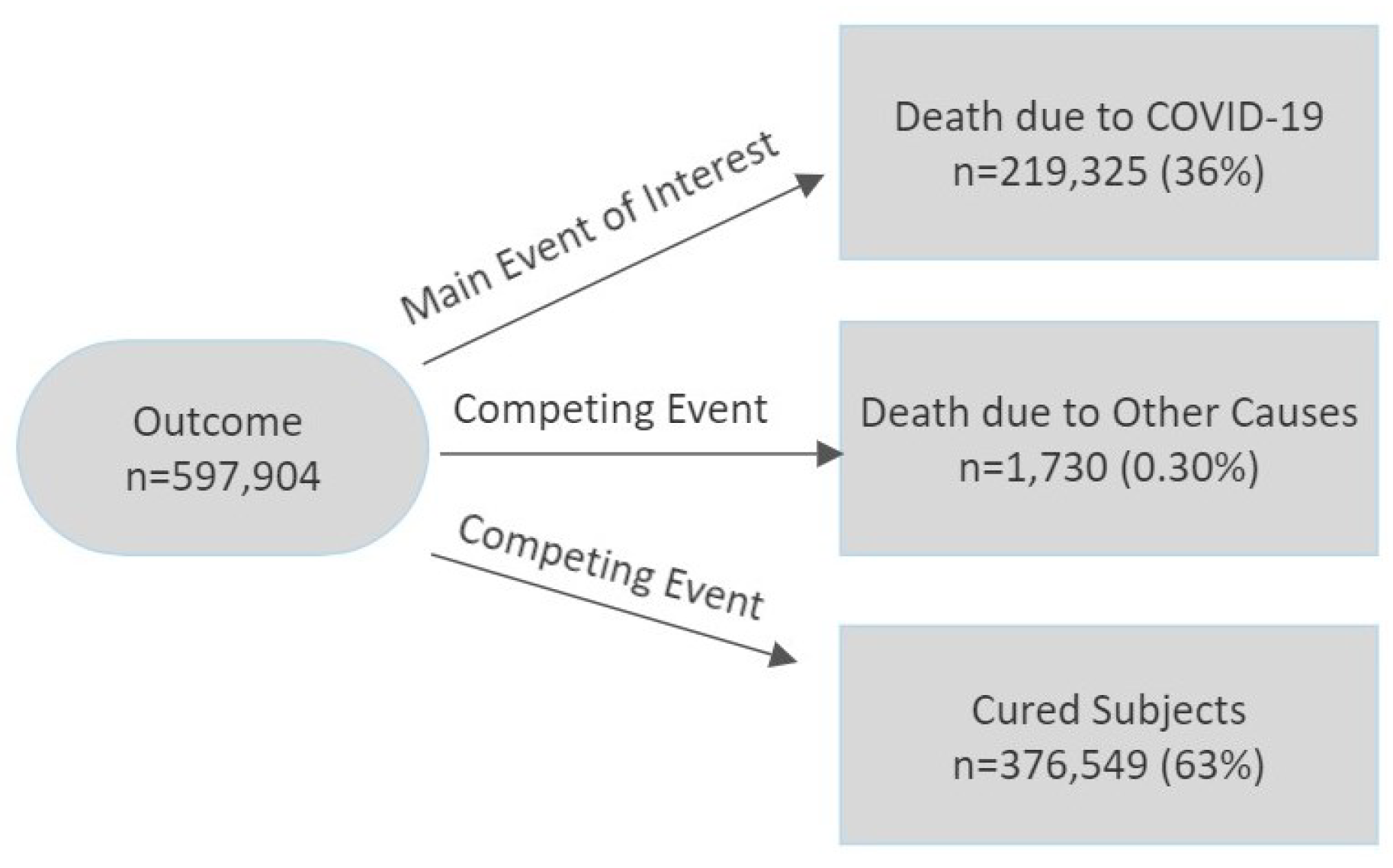
3.1. Data Sources and Variables
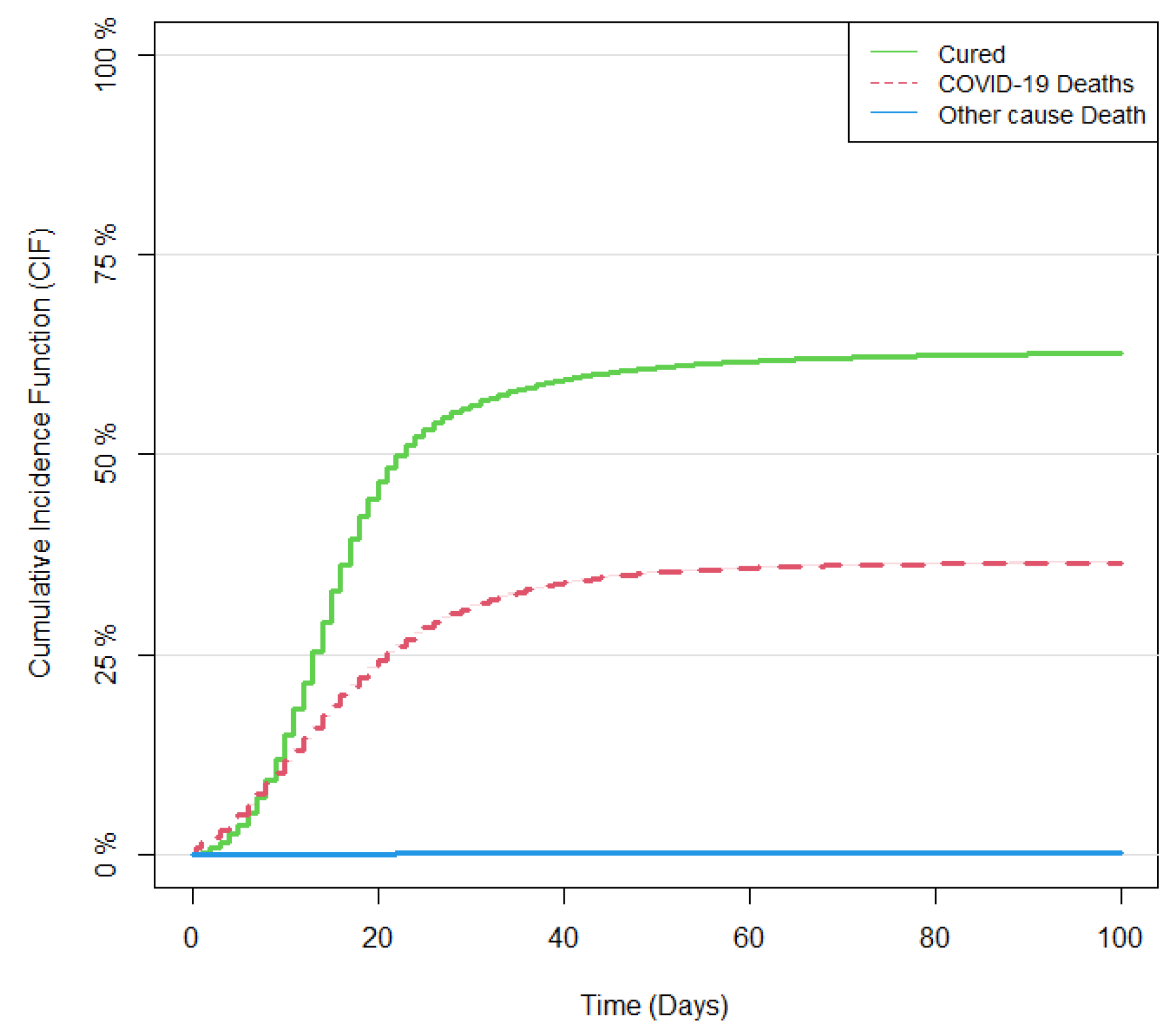
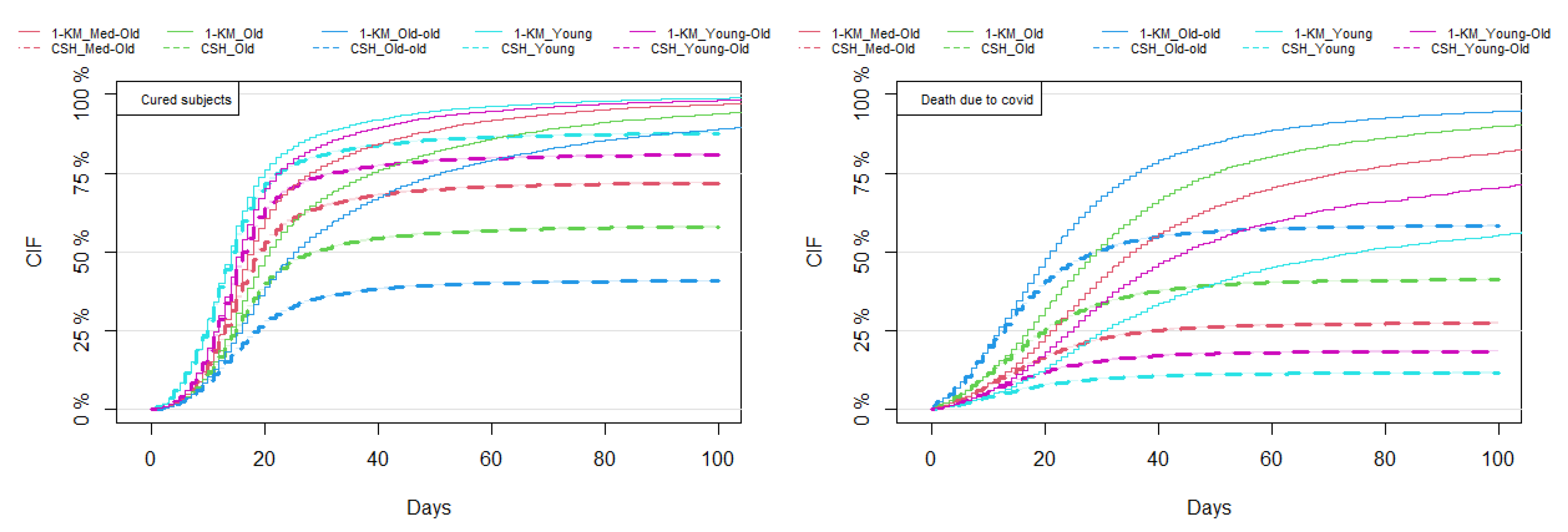
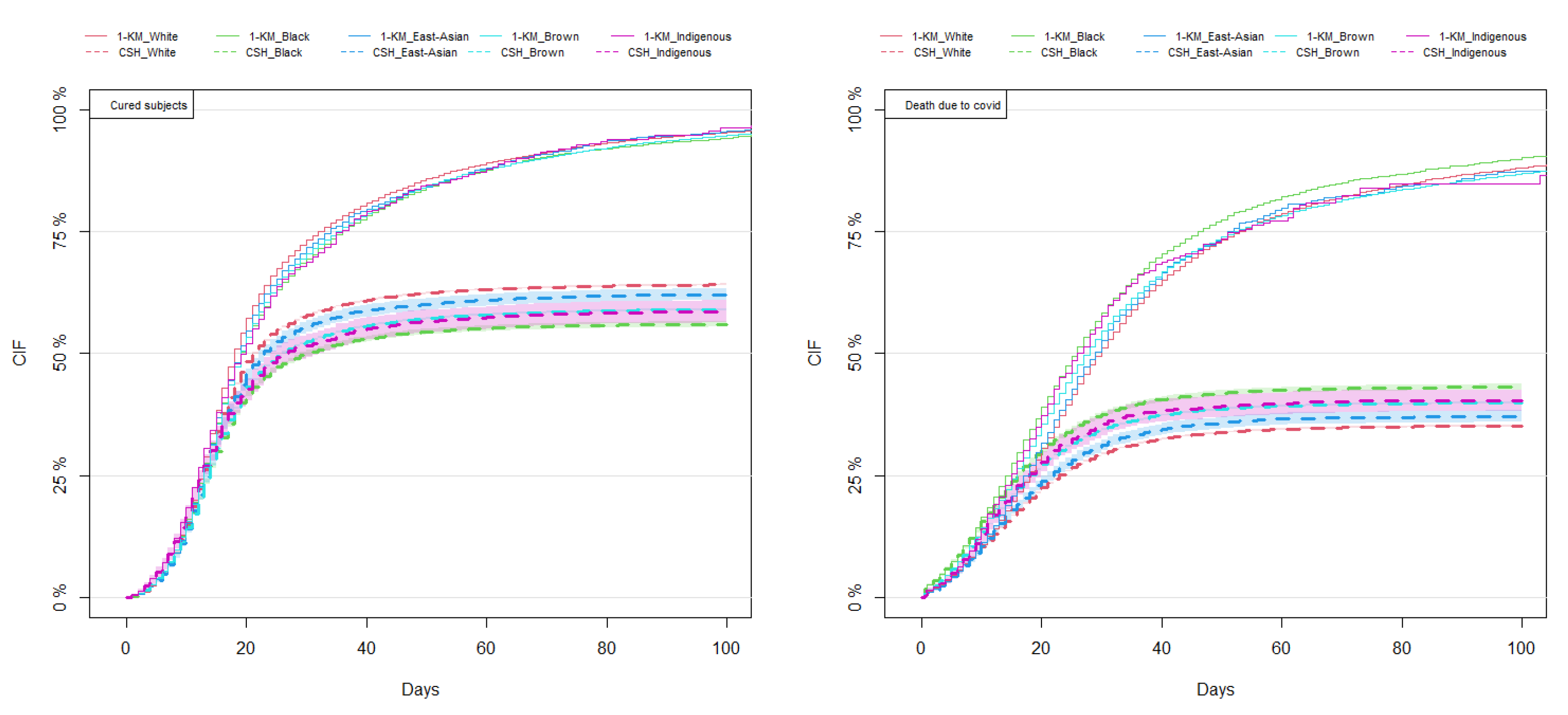
3.2. Results of Non-Parametric Estimation of the CIF
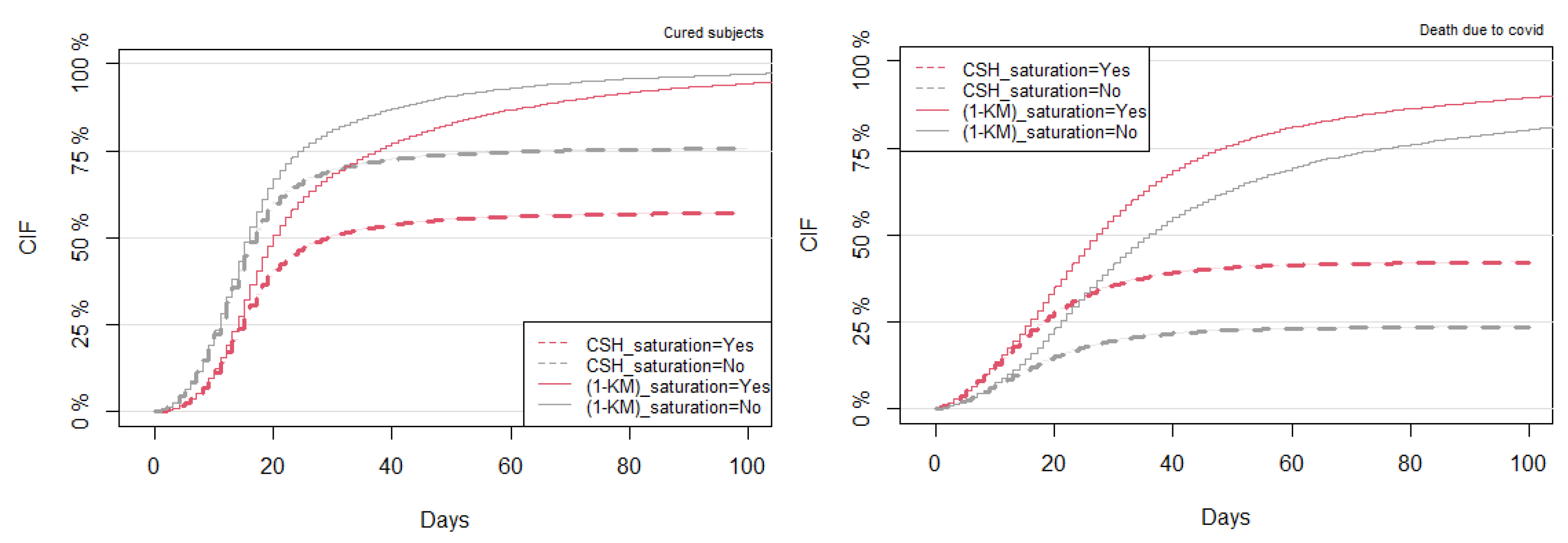
3.3. Comparison between the Kaplan–Meier and CSH Approaches
3.4. Regression Analysis under the CSH and SDH Approaches
3.4.1. Regression Analysis for the CSH Approach
3.4.2. Regression Analysis for the SDH Approach
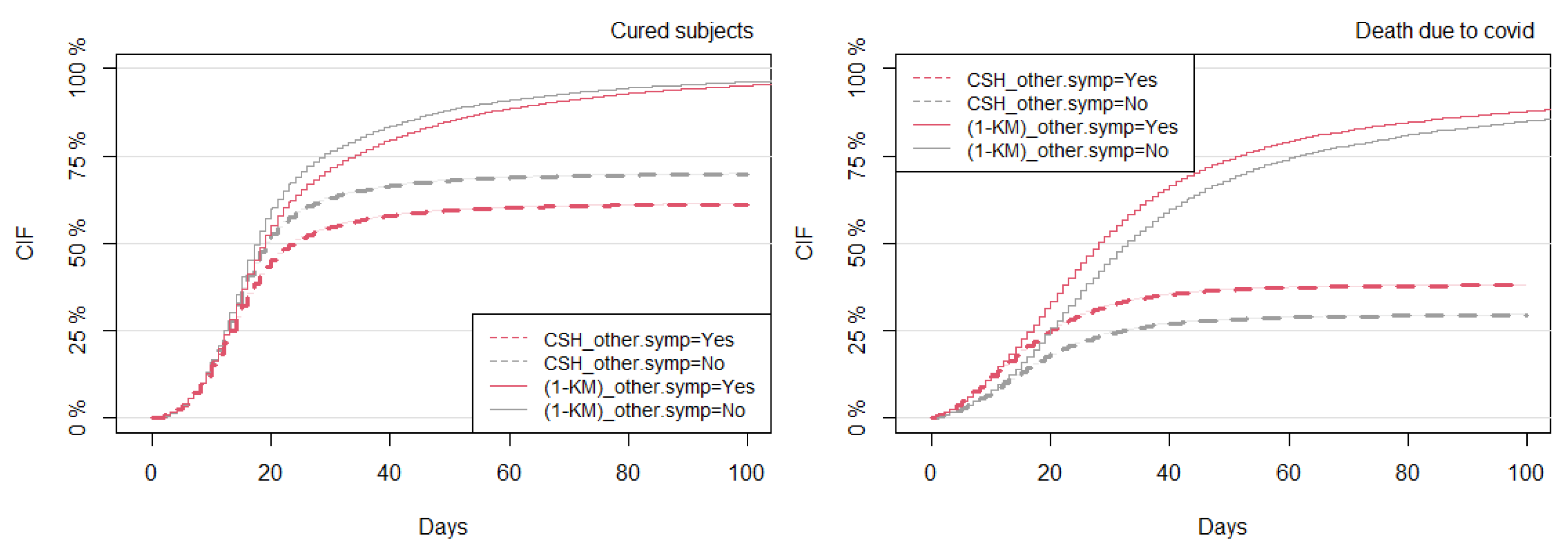
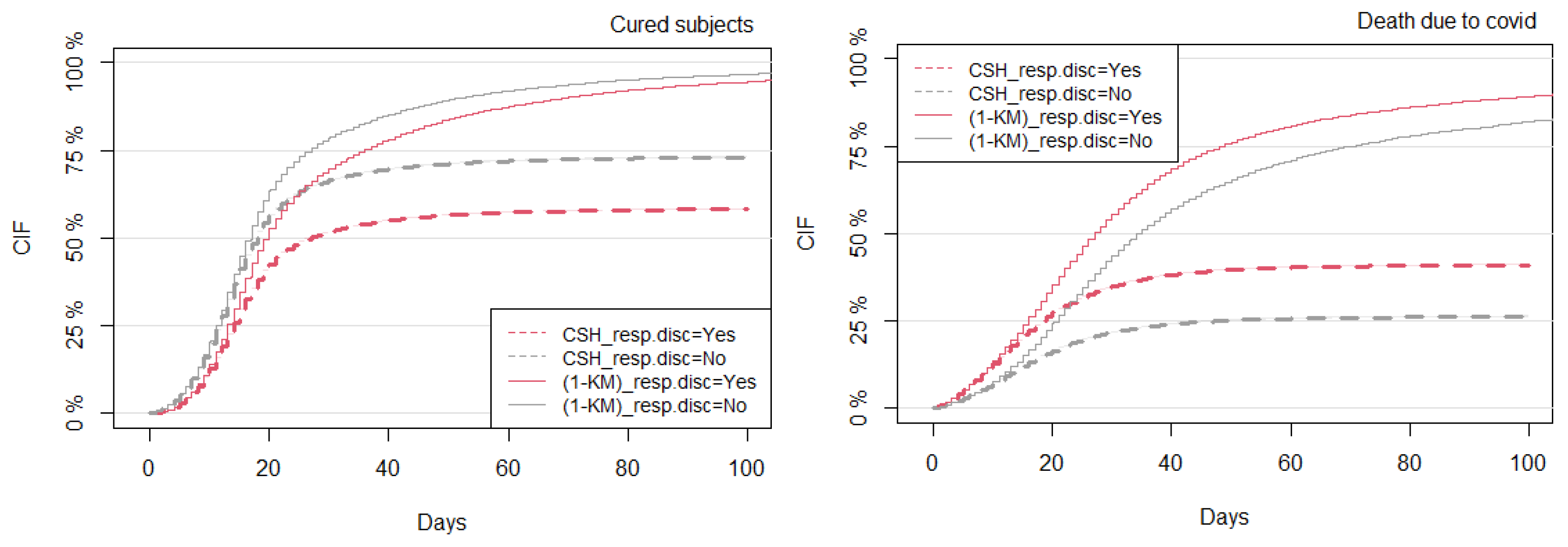
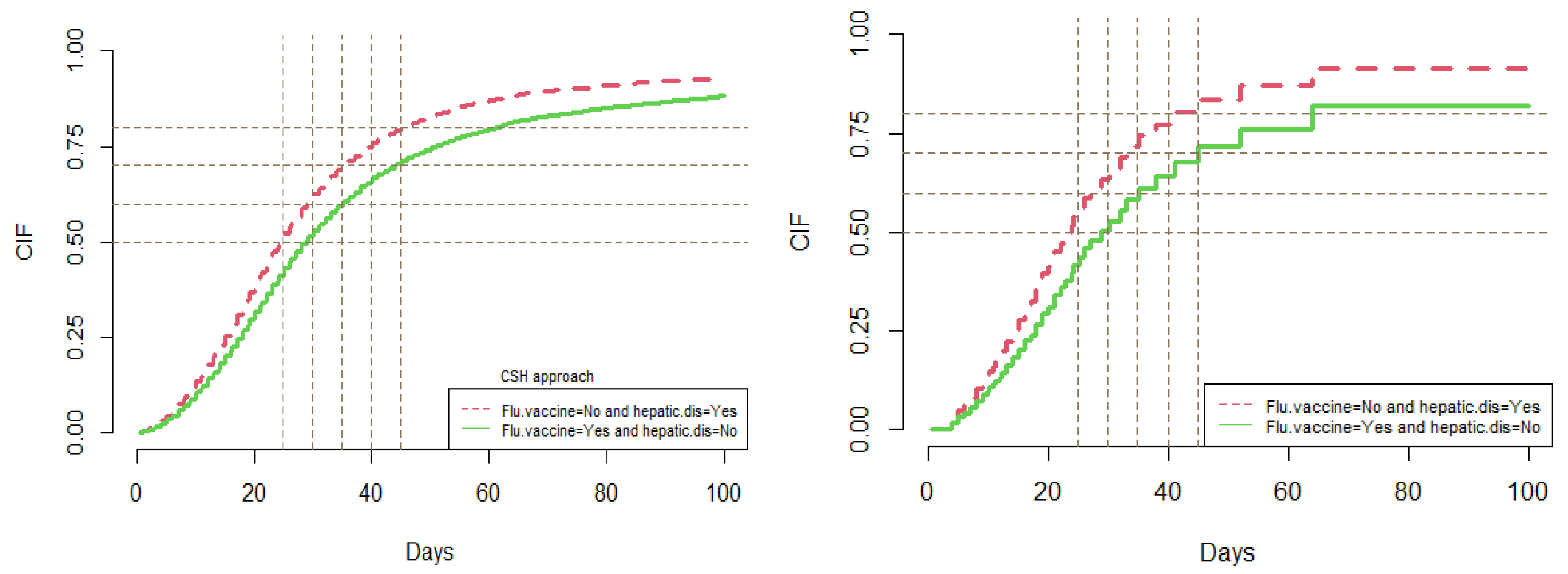
3.5. Comparison of Model Predictions between the CSH and SDH Approaches
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| COVID-19 | Coronavirus Disease-2019 |
| SARS-CoV2 | Severe Acute Respiratory Syndrome Coronavirus 2 |
| CRs | Competing Risks |
| CIF | Cumulative Incidence Function |
| K–M | Kaplan–Meier |
| CSH | Cause-Specific Hazard |
| SDH | Sub-Distribution Hazard |
| AIC | Akaike information criterion |
| ICU | Intensive Care Unit |
| HR | Hazard Ratio |
| IPCW | Inverse of the Probability of Censoring Weights |
References
- Ge, H.; Wang, X.; Yuan, X.; Xiao, G.; Wang, C.; Deng, T.; Yuan, Q.; Xiao, X. The epidemiology and clinical information about COVID-19. Eur. J. Clin. Microbiol. Infect. Dis. 2020, 39, 1011–1019. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; Samanta, G.P.; Mubayi, A. Comparison of regression approaches for analyzing survival data in the presence of competing risks. Lett. Biomath. 2021, 8, 29–47. [Google Scholar]
- Zuccaro, V.; Celsa, C.; Sambo, M.; Battaglia, S.; Sacchi, P.; Biscarini, S.; Valsecchi, P.; Pieri, T.C.; Gallazzi, I.; Colaneri, M.; et al. Competing-risk analysis of coronavirus disease 2019 in-hospital mortality in a Northern Italian centre from SMAtteo COVID-19 REgistry (SMACORE). Sci. Rep. 2021, 11, 1137. [Google Scholar] [CrossRef] [PubMed]
- Salinas-Escudero, G.; Carrillo-Vega, M.F.; Granados-García, V.; Martínez-Valverde, S.; Toledano-Toledano, F.; Garduño-Espinosa, J. A survival analysis of COVID-19 in the Mexican population. BMC Public Health 2020, 20, 1616. [Google Scholar]
- Nijman, G.; Wientjes, M.; Ramjith, J.; Janssen, N.; Hoogerwerf, J.; Abbink, E.; Blaauw, M.; Dofferhoff, T.; van Apeldoorn, M.; Veerman, K.; et al. Risk factors for in-hospital mortality in laboratory-confirmed COVID-19 patients in the Netherlands: A competing risk survival analysis. PLoS ONE 2021, 16, e0249231. [Google Scholar] [CrossRef]
- Rathouz, P.J.; Valencia, V.; Chang, P.; Morton, D.; Yang, H.; Surer, O.; Fox, S.; Meyers, L.A.; Matsui, E.C.; Haynes, A.B. Survival analysis methods for analysis of hospitalization data: Application to COVID-19 patient hospitalization experience. medRxiv, 2021; Preprint. [Google Scholar] [CrossRef]
- Kim, H.T. Cumulative incidence in competing risks data and competing risks regression analysis. Clin. Cancer Res. 2007, 13, 559–565. [Google Scholar] [CrossRef]
- Guo, C.; So, Y. Cause-specific analysis of competing risks using the PHREG procedure. SAS Glob. Forum 2018, 2018, 18. [Google Scholar]
- Kaplan, E.L.; Meier, P. Nonparametric estimation from incomplete observations. JASA 1958, 53, 457–481. [Google Scholar] [CrossRef]
- Andersen, P.K.; Borgan, Ø.; Gill, R.D.; Keiding, N. Statistical Models Based on Counting Processes; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Fine, J.P.; Gray, R.J. A proportional hazards model for the subdistribution of a competing risk. JASA 1999, 94, 496–509. [Google Scholar] [CrossRef]
- Satagopan, J.M.; Ben-Porat, L.; Berwick, M.; Robson, M.; Kutler, D.; Auerbach, A.D. A note on competing risks in survival data analysis. Br. J. Cancer 2004, 9, 1229–1235. [Google Scholar] [CrossRef] [PubMed]
- Bender, R.; Augustin, T.; Blettner, M. Generating survival times to simulate Cox proportional hazards models. Stat. Med. 2005, 24, 1713–1723. [Google Scholar] [CrossRef] [PubMed]
- Klein, J.P.; Van, H.; Hans, C.; Ibrahim, J.G.; Scheike, T.H. Handbook of Survival Analysis; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Haller, B. The Analysis of Competing Risks Data with a Focus on Estimation of Cause-Specific and Subdistribution Hazard Ratios from a Mixture Model. Ph.D. Thesis, LMU School, Munchen, Germany, 2014. [Google Scholar]
- Aalen, O. Nonparametric inference for a family of counting processes. Ann. Stat. 1978, 6, 701–726. [Google Scholar] [CrossRef]
- Aalen, O.O.; Johansen, S. An empirical transition matrix for non-homogeneous Markov chains based on censored observations. Scand. J. Statist. 1978, 5, 141–150. [Google Scholar]
- Prentice, R.L.; Kalbfleisch, J.D.; Peterson, A.V., Jr.; Flournoy, N.; Farewell, V.T.; Breslow, N.E. The analysis of failure times in the presence of competing risks. Biometrics 1978, 34, 541–554. [Google Scholar] [CrossRef]
- Cheng, S.; Fine, J.P.; Wei, L. Prediction of cumulative incidence function under the proportional hazards model. Biometrics 1998, 54, 219–228. [Google Scholar] [CrossRef]
- Bickel, P.J.; Doksum, T. Mathematical Statistics, 2nd ed.; Springer Prentice-Hall: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Demidenko, E. Mixed Models: Theory and Applications with R; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Demidenko, E. Sample size determination for logistic regression revisited. Stat. Med. 2007, 26, 3385–3397. [Google Scholar] [CrossRef]
- Gray, R.J. A class of K-sample tests for comparing the cumulative incidence of a competing risk. Ann. Stat. 1988, 16, 1141–1154. [Google Scholar] [CrossRef]
- R Core Team: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019; Available online: Https://www.R-project.org/ (accessed on 19 August 2023).
- Lai, C.C.; Shih, T.P.; Ko, W.C.; Tang, H.J.; Hsueh, P.R. Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) and coronavirus disease-2019 (COVID-19): The epidemic and the challenges. Int. J. Antimicrob. Agents 2020, 55, 105924. [Google Scholar] [CrossRef]
- Cortese, G.; Gerds, T.A.; Andersen, P.K. Comparing predictions among competing risks models with time–Dependent covariates. Stat. Med. 2013, 32, 3089–3101. [Google Scholar] [CrossRef]
- Scheike, T.H.; Mei-Jie, Z.; Gerds, T.A. Cumulative Incidence Probability by Direct Binomial Regression. Biometrika 2008, 49, 205–220. [Google Scholar] [CrossRef]





| Exposures | Estimates | HR | SE | Lower CI | Upper CI | p-Value |
|---|---|---|---|---|---|---|
| Asthma (Yes) | −0.115 | 0.891 | 0.029 | 0.842 | 0.943 | <0.001 |
| Diabetes (Yes) | 0.077 | 1.080 | 0.011 | 1.058 | 1.104 | <0.001 |
| Obesity (Yes) | 0.034 | 1.034 | 0.018 | 0.998 | 1.072 | 0.060 |
| Other.risk (Yes) | 0.058 | 1.060 | 0.011 | 1.038 | 1.082 | <0.001 |
| Immuno (Yes) | 0.252 | 1.286 | 0.024 | 1.227 | 1.348 | <0.001 |
| Kidney (Yes) | 0.238 | 1.269 | 0.019 | 1.222 | 1.317 | <0.001 |
| Neuro (Yes) | 0.270 | 1.310 | 0.019 | 1.262 | 1.360 | <0.001 |
| Flu.vaccine (Yes) | −0.063 | 0.939 | 0.011 | 0.918 | 0.960 | <0.001 |
| Hepatic.dis (Yes) | 0.247 | 1.280 | 0.040 | 1.184 | 1.384 | <0.001 |
| Age: Old (60–70 Years) | 0.276 | 1.318 | 0.018 | 1.272 | 1.366 | <0.001 |
| Age: Old-old (>70 Years) | 0.712 | 2.038 | 0.017 | 1.973 | 2.104 | <0.001 |
| Age: Young (<40 Years) | −0.333 | 0.717 | 0.031 | 0.675 | 0.761 | <0.001 |
| Age: Young-Old (40–50 Years) | −0.120 | 0.887 | 0.026 | 0.844 | 0.933 | <0.001 |
| Sex (Male) | 0.060 | 1.062 | 0.011 | 1.040 | 1.085 | <0.001 |
| ICU (Yes) | 0.430 | 1.537 | 0.011 | 1.504 | 1.571 | <0.001 |
| Pneumo (Yes) | 0.133 | 1.143 | 0.019 | 1.100 | 1.187 | <0.001 |
| Race: Black | 0.198 | 1.219 | 0.023 | 1.165 | 1.275 | <0.001 |
| Race: East Asian | 0.064 | 1.066 | 0.049 | 0.968 | 1.174 | 0.194 |
| Race: Brown | 0.149 | 1.160 | 0.011 | 1.135 | 1.187 | <0.001 |
| Race: Indigenous | 0.315 | 1.370 | 0.096 | 1.136 | 1.653 | <0.001 |
| Exposures | Estimates | HR | SE | Lower CI | Upper CI | p-Value |
|---|---|---|---|---|---|---|
| Asthma (Yes) | −0.115 | 0.891 | 0.029 | 0.842 | 0.943 | <0.001 |
| Diabetes (Yes) | 0.078 | 1.081 | 0.011 | 1.058 | 1.105 | <0.001 |
| Obesity (Yes) | 0.037 | 1.037 | 0.018 | 1.001 | 1.075 | <0.050 |
| Other.risk (Yes) | 0.056 | 1.058 | 0.011 | 1.036 | 1.081 | <0.001 |
| Immuno (Yes) | 0.241 | 1.272 | 0.025 | 1.211 | 1.338 | <0.001 |
| Kidney (Yes) | 0.235 | 1.265 | 0.021 | 1.216 | 1.317 | <0.001 |
| Neuro (Yes) | 0.267 | 1.306 | 0.021 | 1.253 | 1.361 | <0.001 |
| Flu.vaccine (Yes) | −0.062 | 0.940 | 0.011 | 0.919 | 0.961 | <0.001 |
| Hepatic.dis (Yes) | 0.244 | 1.276 | 0.044 | 1.171 | 1.391 | <0.001 |
| Age: Old (60–70 Years) | 0.278 | 1.321 | 0.017 | 1.277 | 1.367 | <0.001 |
| Age: Old-old (>70 Years) | 0.710 | 2.035 | 0.016 | 1.971 | 2.101 | <0.001 |
| Age: Young (<40 Years) | −0.335 | 0.715 | 0.030 | 0.674 | 0.759 | <0.001 |
| Age: Young-Old (40–50 Years) | −0.120 | 0.887 | 0.025 | 0.845 | 0.931 | <0.001 |
| Sex (Male) | 0.061 | 1.063 | 0.011 | 1.041 | 1.086 | <0.001 |
| ICU (Yes) | 0.434 | 1.543 | 0.011 | 1.510 | 1.577 | <0.001 |
| Pneumo (Yes) | 0.132 | 1.141 | 0.020 | 1.097 | 1.188 | <0.001 |
| Race: Black | 0.198 | 1.219 | 0.024 | 1.164 | 1.277 | <0.001 |
| Race3: East Asian | 0.053 | 1.054 | 0.047 | 0.961 | 1.157 | 0.264 |
| Race4: Brown | 0.144 | 1.155 | 0.012 | 1.129 | 1.181 | <0.001 |
| Race: Indigenous | 0.323 | 1.381 | 0.106 | 1.121 | 1.701 | <0.003 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haque, M.A.; Cortese, G. Cumulative Incidence Functions for Competing Risks Survival Data from Subjects with COVID-19. Mathematics 2023, 11, 3772. https://doi.org/10.3390/math11173772
Haque MA, Cortese G. Cumulative Incidence Functions for Competing Risks Survival Data from Subjects with COVID-19. Mathematics. 2023; 11(17):3772. https://doi.org/10.3390/math11173772
Chicago/Turabian StyleHaque, Mohammad Anamul, and Giuliana Cortese. 2023. "Cumulative Incidence Functions for Competing Risks Survival Data from Subjects with COVID-19" Mathematics 11, no. 17: 3772. https://doi.org/10.3390/math11173772
APA StyleHaque, M. A., & Cortese, G. (2023). Cumulative Incidence Functions for Competing Risks Survival Data from Subjects with COVID-19. Mathematics, 11(17), 3772. https://doi.org/10.3390/math11173772






