Time-Optimal Problem in the Roto-Translation Group with Admissible Control in a Circular Sector
Abstract
1. Introduction
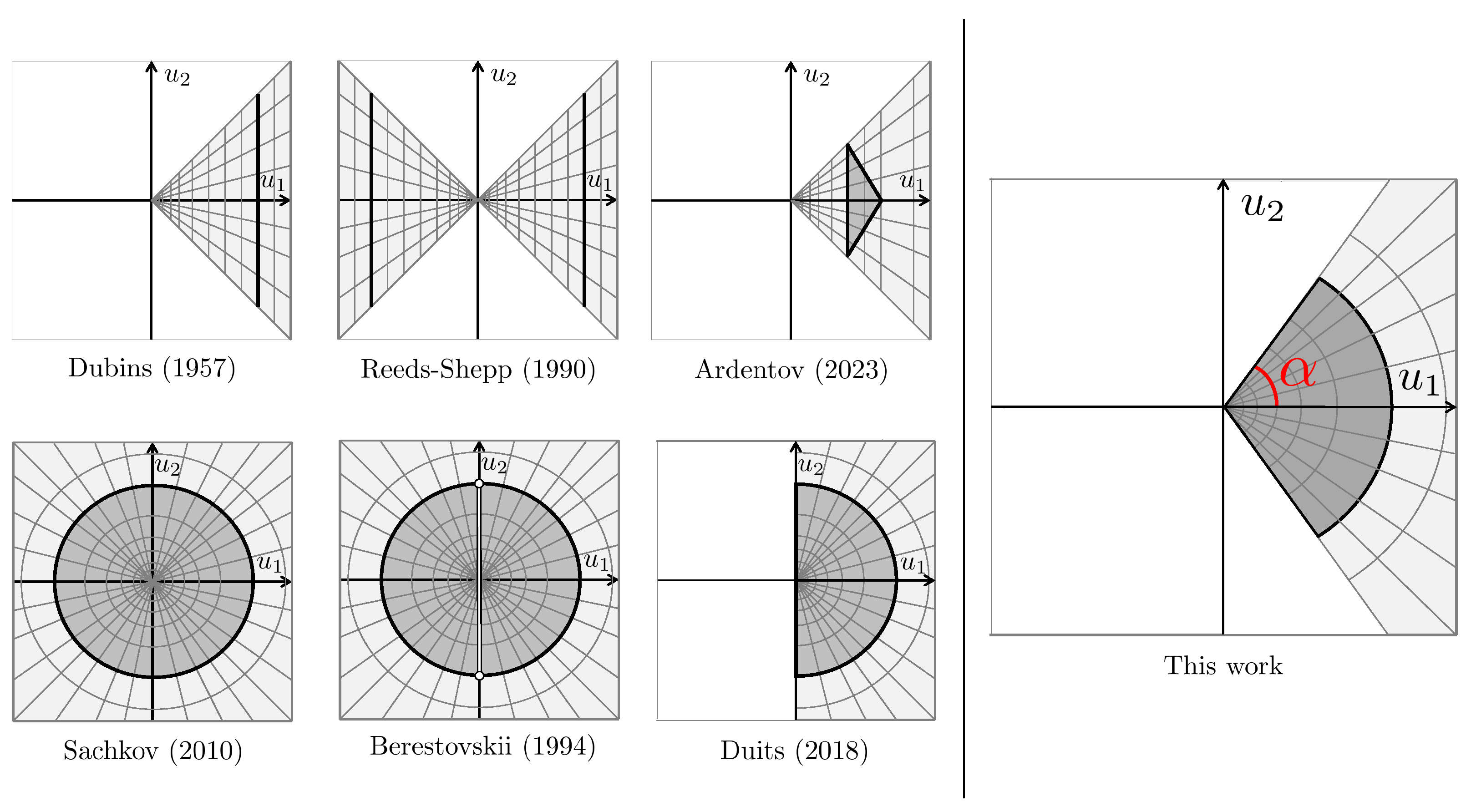
- , , leads to Dubins car [1];
- , , leads to Reeds–Shepp car [2];
- , leads to a generalized Dubins car, studied by Ardentov [3];
- leads to the model whose solutions are sub-Riemannian length minimals, studied by Sachkov [4];
- , leads to the model studied by Berestovskii [5];
- , leads to the model of a car moving forward and turning in place, proposed by Duits [6];
- , , , leads to the general model of a car with control in a circular sector, which is studied in this paper.
2. Preliminaries
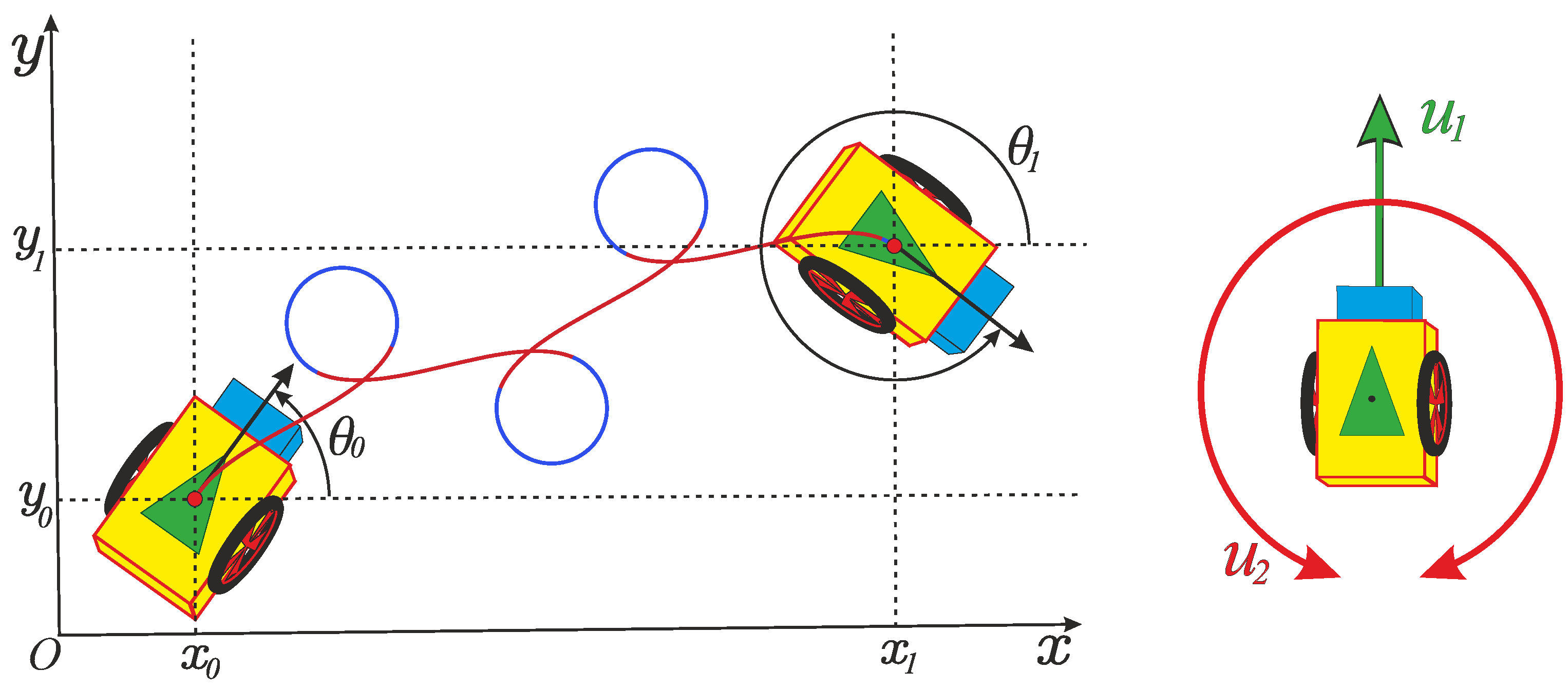
3. Statement of the Problem
4. Existence of the Solution
4.1. Controllability and Existence of Optimal Controls
- 1.
- For , the system is not globally controllable. The attainable set is . For any , there exists a unique optimal trajectory;
- 2.
- For , the system is globally controllable, but not small-time locally controllable. For any , there exists an optimal trajectory;
- 3.
- For , the system is globally controllable and small-time locally controllable. An optimal trajectory does not exist for some boundary conditions;
- 4.
- For , the system is globally and small-time locally controllable. For any , there exists an optimal trajectory.
- (a)
- ;
- (b)
- A trajectory , s.t. does not exist.
4.2. Local Controllability
- By , the attainable set of System (2) from Id for a time ;
- By , the attainable set of System (2) from Id for time not greater than t;
- By , the attainable set of System (2) from for time not greater than t.
5. Pontryagin Maximum Principle
5.1. Hamiltonian System and Maximality Condition
- 1.
- The Hamiltonian system
- 2.
- The maximality condition
5.2. Abnormal Case
5.3. Normal Case
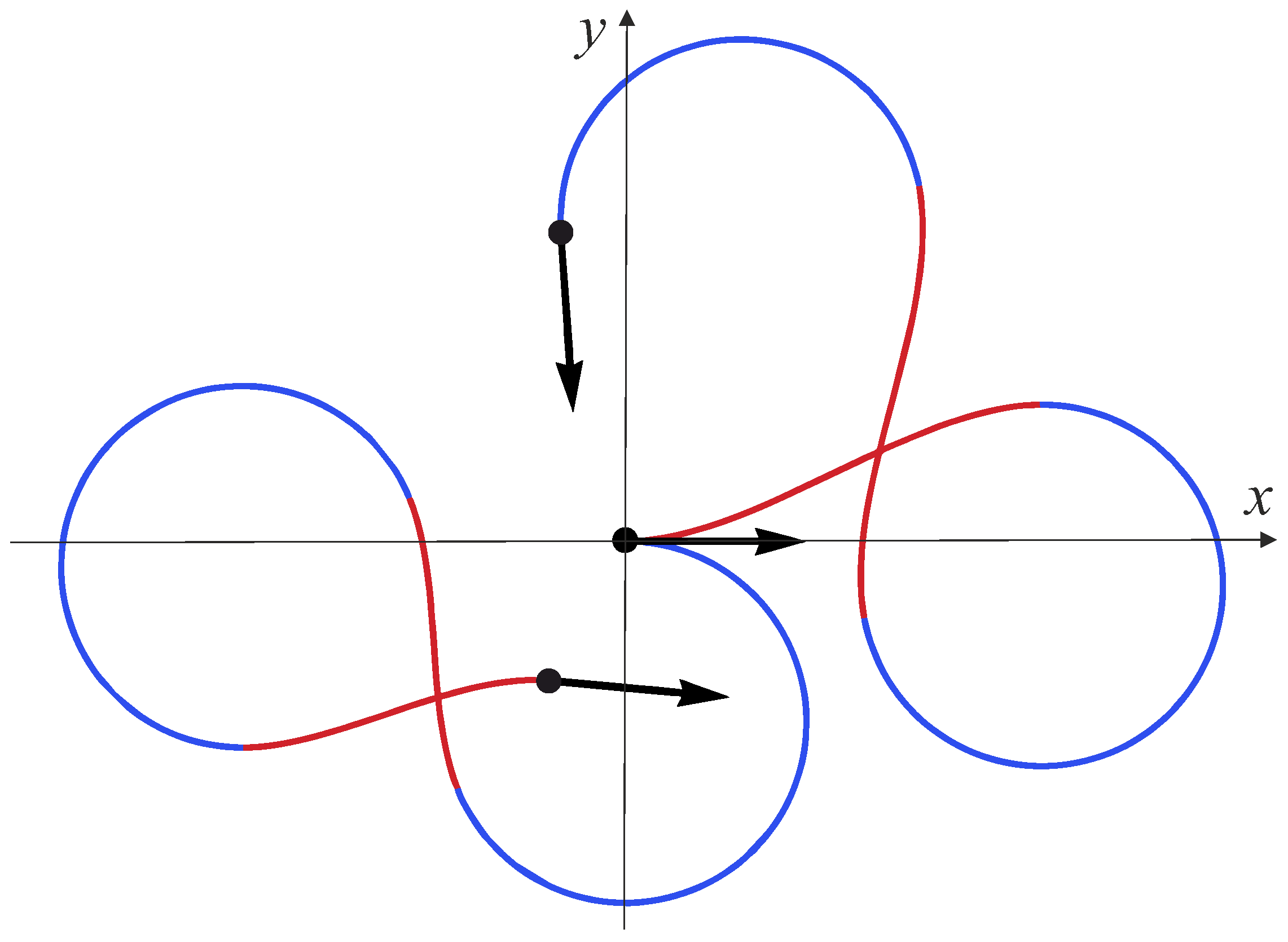
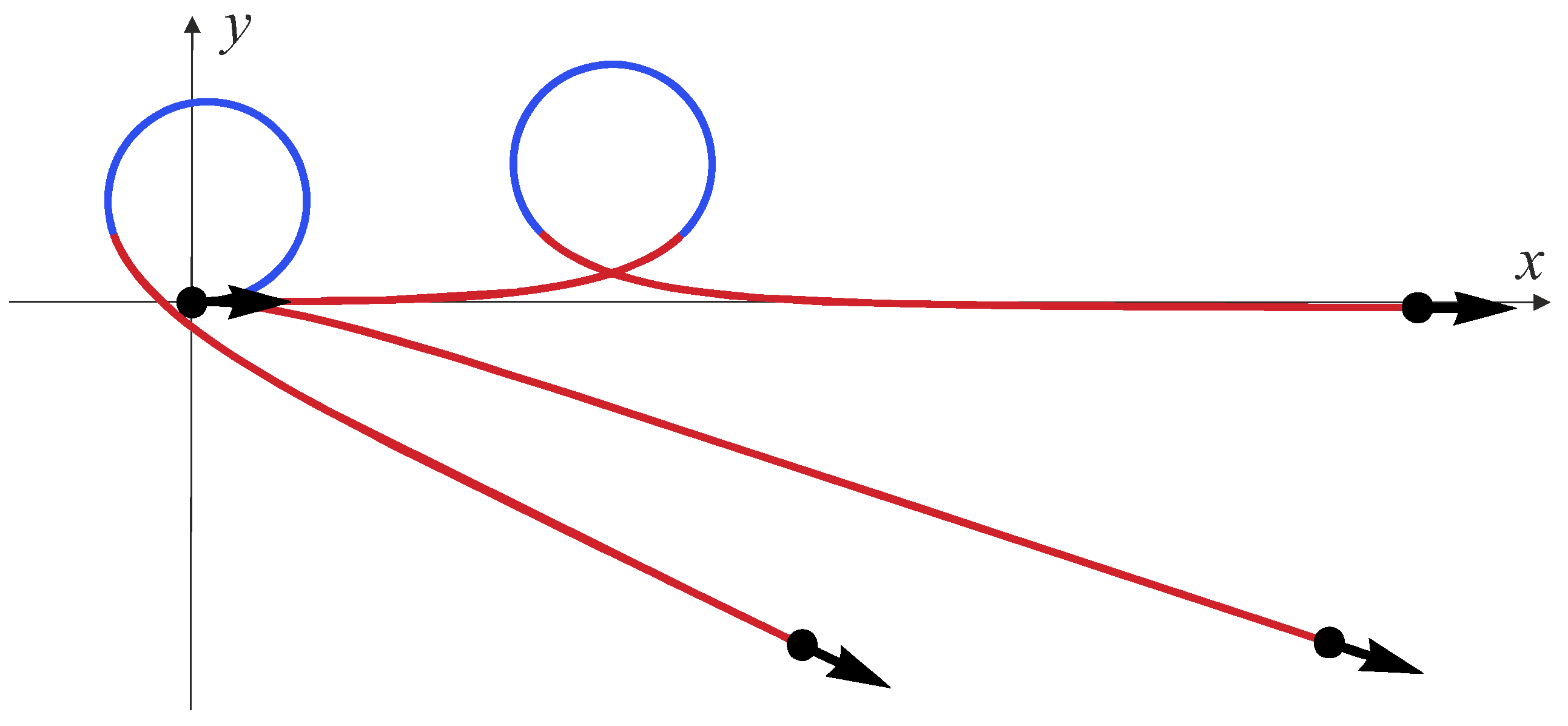
6. Explicit Expression for Normal Extremals
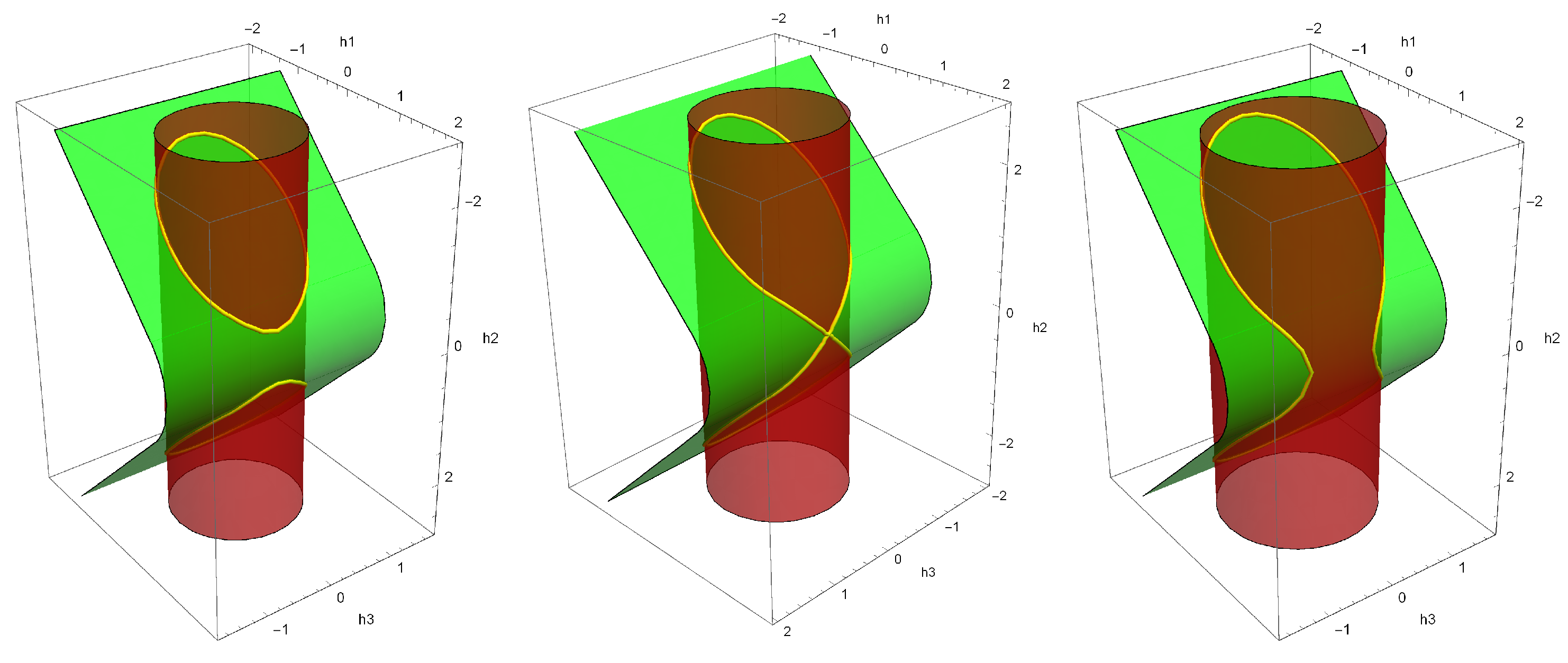
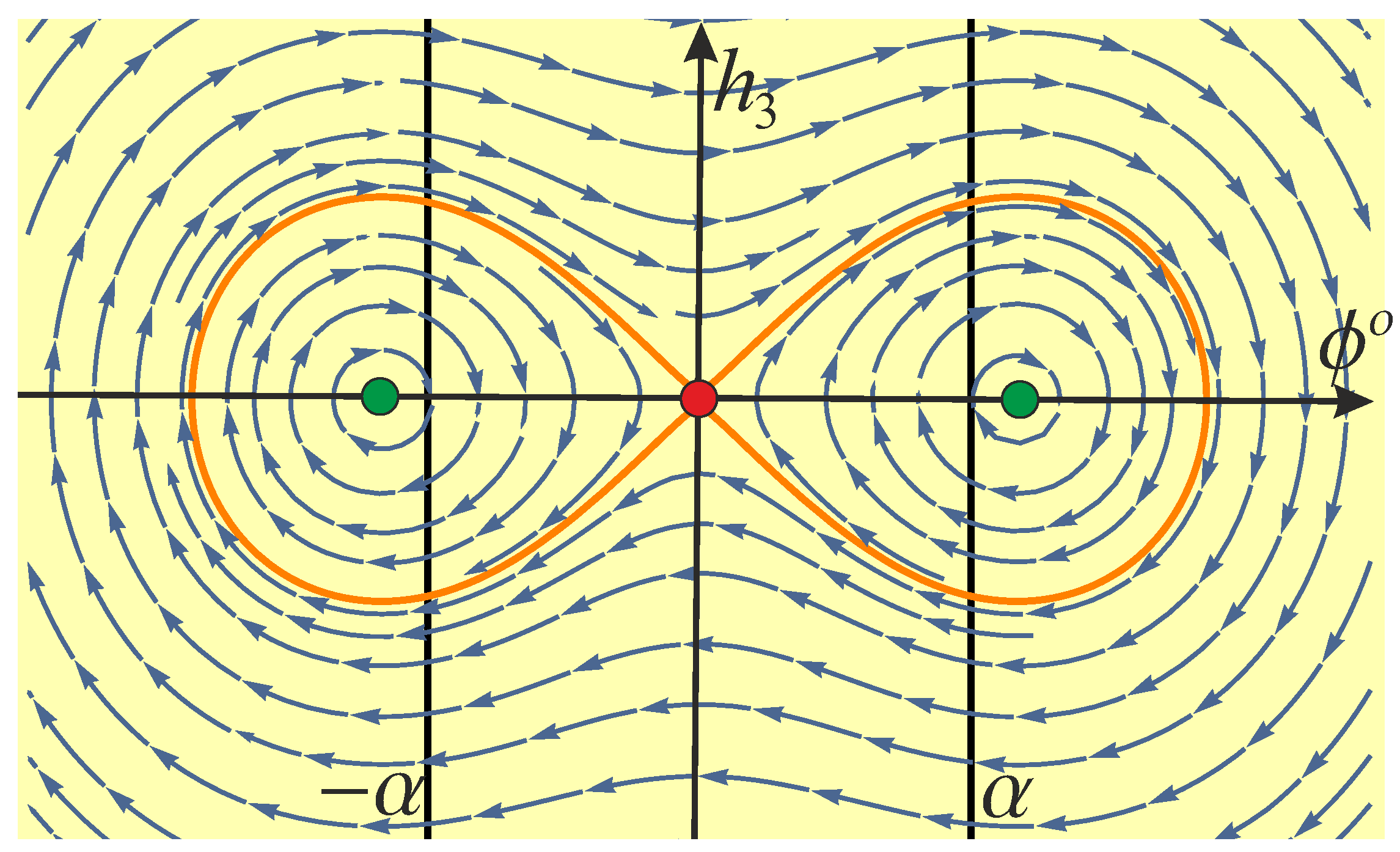
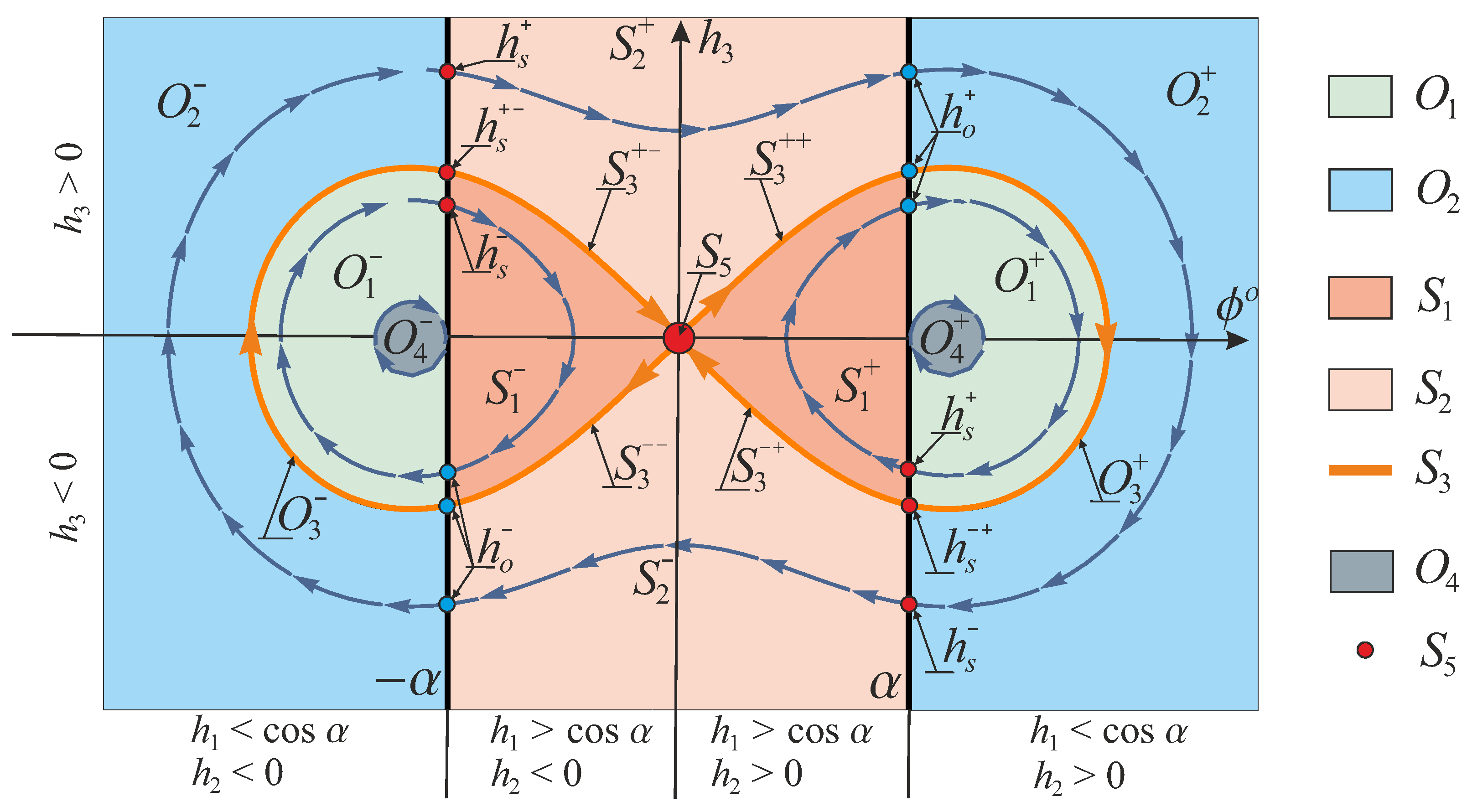
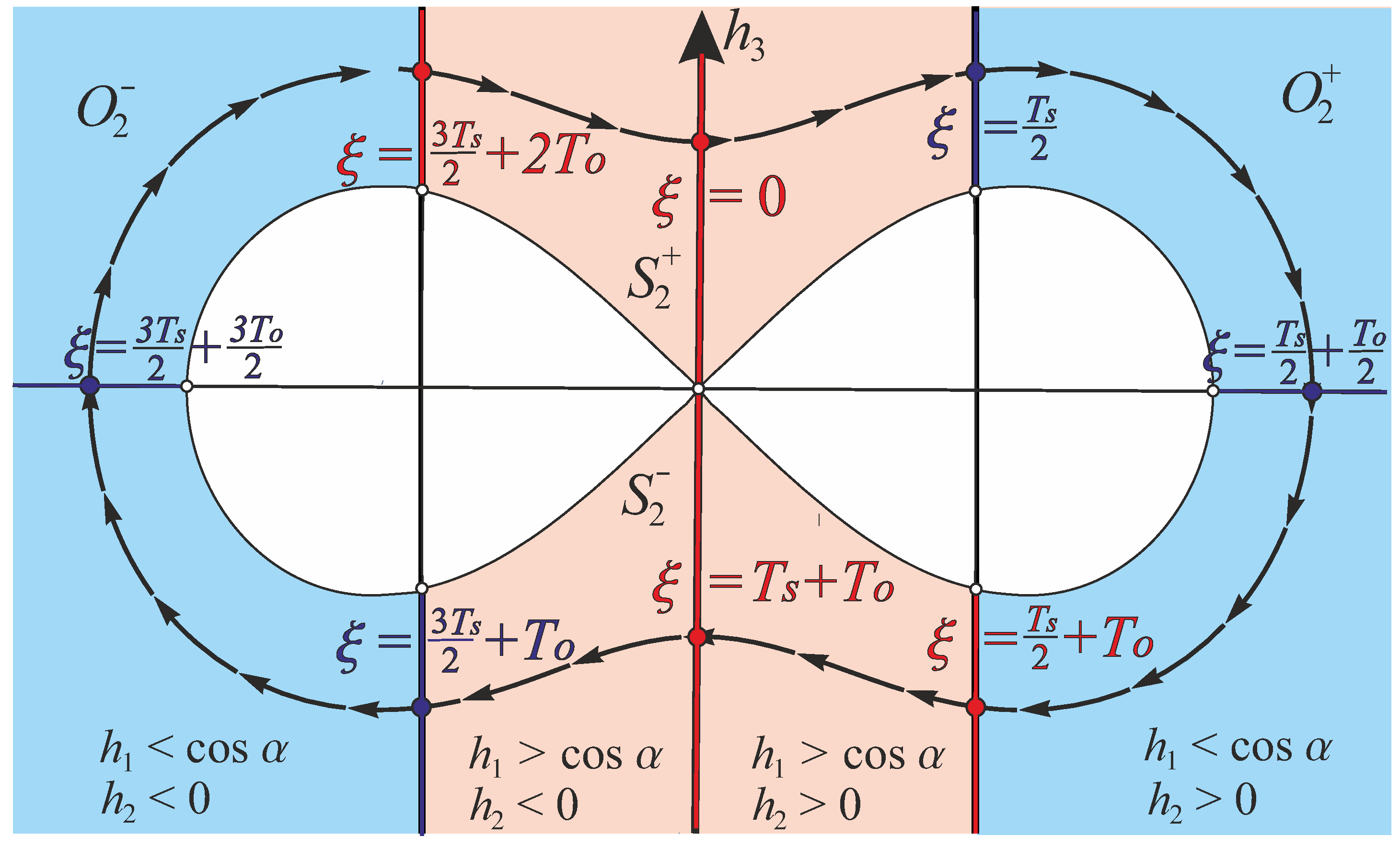
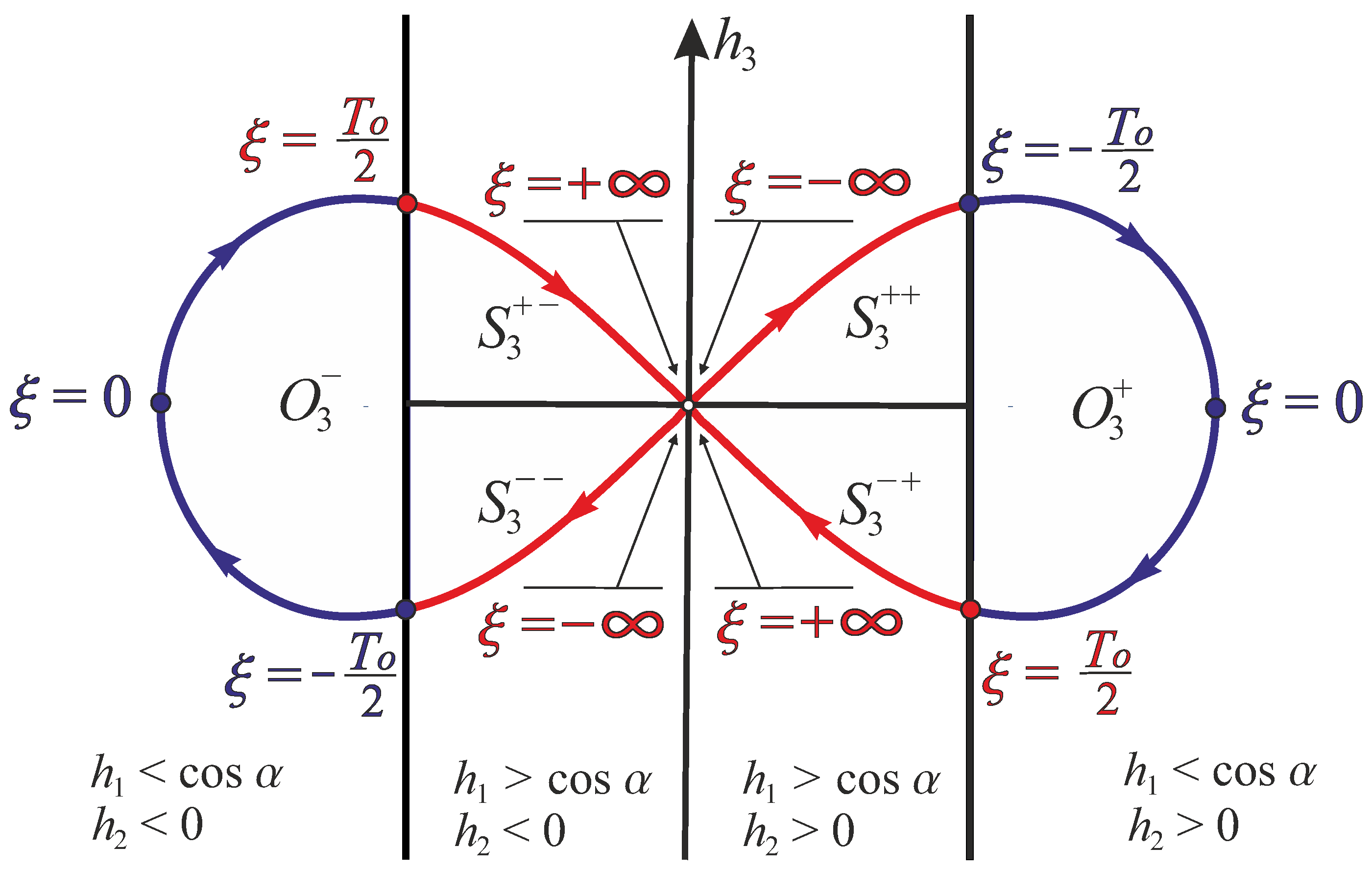
6.1. Stratification of the Hamiltonian System Adjoint Variables Domain
- 1.
- Arcs of noninflectional sub-Riemannian geodesics in , joined by arcs of the circular extremals, when (the subdomain ; );
- 2.
- Arcs of inflectional sub-Riemannian geodesics in joined by arcs of the circular extremals, when (the subdomain ; here, in the S-domain, and in the O-domain);
- 3.
- Arcs of the separatrix sub-Riemannian geodesics in joined by an arc of the circular extremal, when and (the subdomain ; here, in the S-domain, and in the O-domain);
- 4.
- The circular extremals, when (the subdomains ; here, correspond to the motion of the car clockwise or counterclockwise);
- 5.
- The straight extremal (the ray), when and (the subdomain ).
6.2. The Domain
6.3. The Domain
6.4. The Domain and
6.5. The Domain
6.6. The Domain and
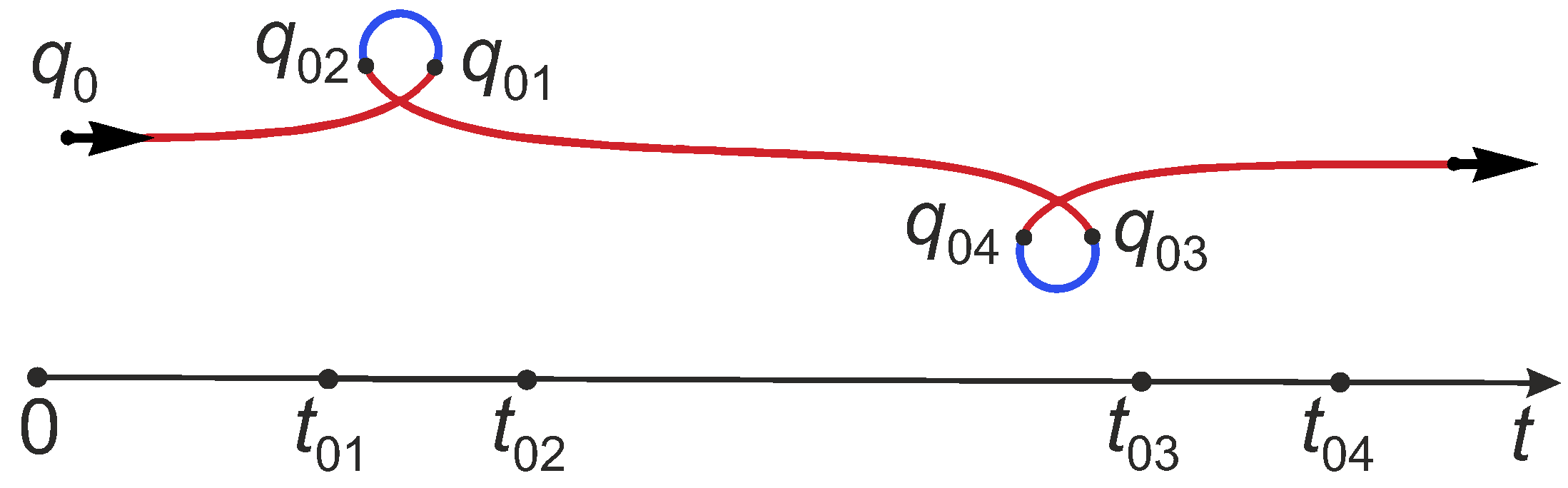
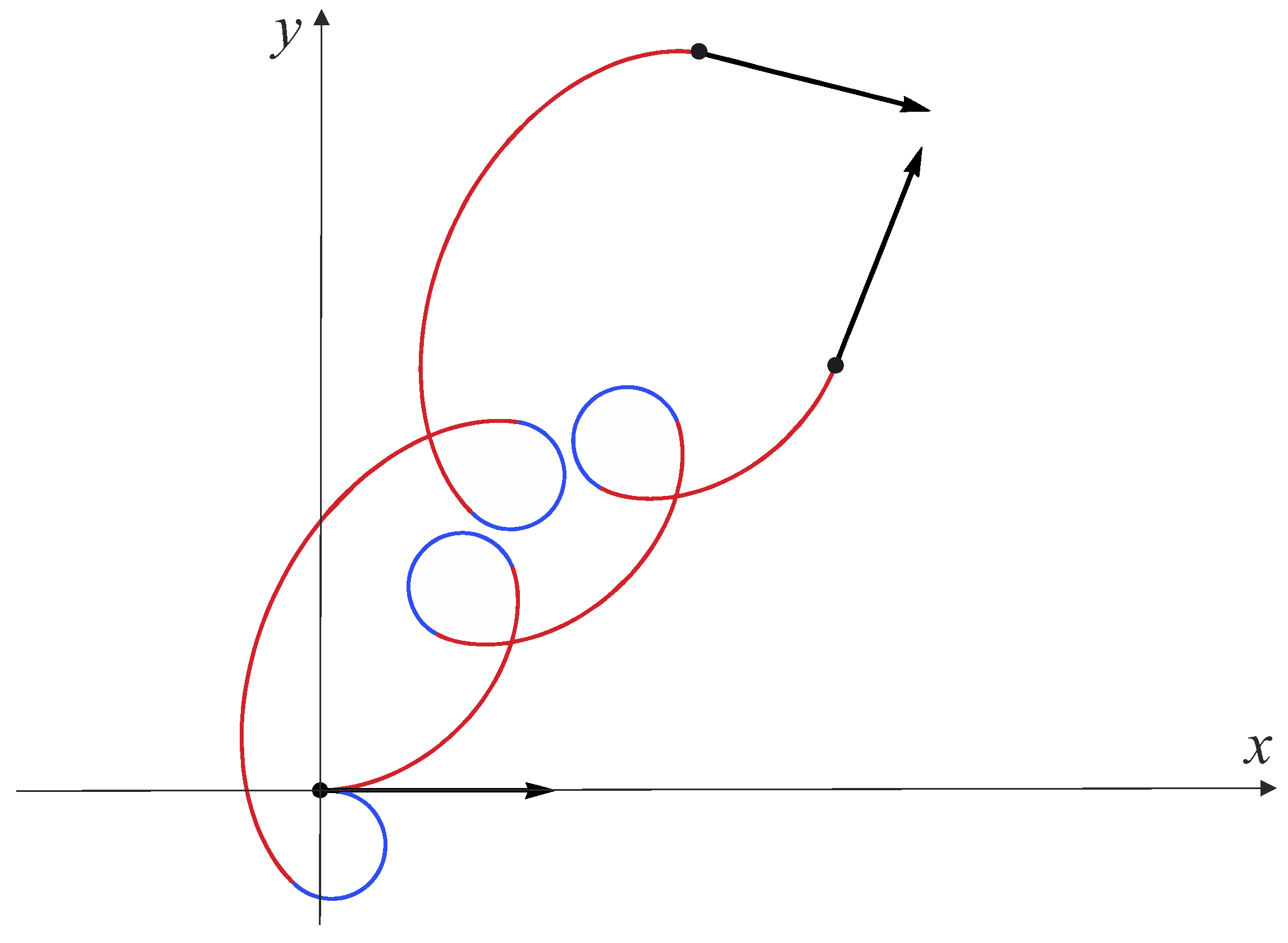
7. Optimality of Extremal Trajectories
7.1. General Upper Bound of Cut Time
- (1)
- for all ;
- (2)
- There exists a linear function , such that
- (1)
- and for any ;
- (2)
- .
7.2. Optimality of Extremals for
7.3. Optimality of Extremals for
7.4. Optimality of Separatrix Extremals (, )
7.5. Optimality of Circular Trajectories, cos
7.6. Optimality of the Straight Trajectory (, )
7.7. Lower Bound of Cut Time
8. Conclusions
- 1.
- For , the system is not globally controllable.
- 2.
- For , the system is globally but not small-time locally controllable.
- 3.
- For , the problem is ill-posed. The system is globally and small-time locally controllable, but an optimal trajectory does not exist for some boundary conditions.
- 4.
- For , the system is globally and small-time locally controllable. This case coincides with the sub-Riemannian length minimizers problem in .
- 1.
- Arcs of noninflectional sub-Riemannian geodesics in , joined by arcs of circular extremals. The exact expression is given by Theorem 4. An upper bound for the cut time is given by Proposition 3.
- 2.
- Arcs of inflectional sub-Riemannian geodesics in , joined by arcs of circular extremals. The exact expression is given by Theorem 5. An upper bound for the cut time is given by Proposition 4.
- 3.
- Arcs of the separatrix sub-Riemannian geodesics in joined by an arc of the circular extremal. The exact expression is given by Theorem 6. The extremals before the first switching are optimal (see Proposition 5).
- 4.
- The circular extremals. The exact expression is given by Theorem 7. The cut time is given by Proposition 6.
- 5.
- The straight extremal. The exact expression is given by Theorem 8. It is optimal up to infinity (see Proposition 7).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PMP | Pontryagin maximum principle |
References
- Dubins, L.E. On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents. Am. J. Math. 1975, 79, 497–516. [Google Scholar] [CrossRef]
- Reeds, J.A.; Shepp, L.A. Optimal paths for a car that goes both forwards and backwards. Pac. J. Math. 1990, 145, 367–393. [Google Scholar] [CrossRef]
- Ardentov, A.A. Markov–Dubins problem with Control on a Triangle. In Proceedings of the International Voronezh Spring Mathematical School Dedicated to the 115th Anniversary of the Birth of Academician L.S. Pontryagin, Voronezh, Russia, 3–9 May 2023; pp. 43–44. (In Russian). [Google Scholar]
- Sachkov, Y.L. Cut locus and optimal synthesis in the sub-Riemannian problem on the group of motions of a plane. ESAIM: Control. Optim. Calc. Var. 2011, 17, 293–321. [Google Scholar] [CrossRef][Green Version]
- Berestovskii, V.N. Geodesics of a left-invariant nonholonomic Riemannian metric on the group of motions of the Euclidean plane. Sib. Math. J. 1994, 35, 1083–1088. [Google Scholar] [CrossRef]
- Duits, R.; Meesters, S.P.L.; Mirebeau, J.-M.; Portegies, J.M. Optimal Paths for Variants of the 2D and 3D Reeds–Shepp Car with Applications in Image Analysis. J. Math. Imaging Vis. 2018, 60, 816–848. [Google Scholar] [CrossRef]
- Mashtakov, A.P. Time minimization problem on the group of motions of a plane with admissible control in a half-disk. Mat. Sb. 2022, 213, 100–122. (In Russian) [Google Scholar]
- Lynch, K.M.; Park, F.C. Modern Robotics. Mechanics, Planning, and Control; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Arismendi, C.; Alvarez, D.; Garrido, S.; Moreno, L. Nonholonomic Motion Planning Using the Fast Marching Square Method. Int. J. Adv. Robot. Syst. 2015, 12, 60129. [Google Scholar] [CrossRef]
- Boscain, U.V.; Chitour, Y. Time-Optimal Synthesis for Left-Invariant Control Systems on SO(3). SIAM J. Control Optim. 2005, 44, 111–139. [Google Scholar] [CrossRef]
- Hubel, D.H.; Wiesel, T.N. Receptive fields of single neurones in the cat’s striate cortex. J. Physiol. 1959, 148, 574. [Google Scholar] [CrossRef]
- Petitot, J. The neurogeometry of pinwheels as a sub-Riemannian contact structure. J. Physiol. 2003, 97, 265–309. [Google Scholar] [CrossRef]
- Citti, G.; Sarti, A. A cortical based model of perceptual completion in the roto-translation space. J. Math. Imaging Vis. 2006, 24, 307–326. [Google Scholar] [CrossRef]
- Duits, R.; Boscain, U.; Rossi, F.; Sachkov, Y.L. Association Fields via Cuspless Sub-Riemannian Geodesics in SE(2). J. Math. Imaging Vis. 2014, 49, 384–417. [Google Scholar] [CrossRef] [PubMed]
- Franceschiello, B.; Mashtakov, A.; Citti, G.; Sarti, A. Geometrical optical illusion via sub-Riemannian geodesics in the roto-translation group. Differ. Geom. Appl. 2019, 65, 55–77. [Google Scholar] [CrossRef]
- Baspinar, E.; Calatroni, L.; Franceschi, V.; Prandi, D. A Cortical-Inspired Sub-Riemannian Model for Poggendorff-Type Visual Illusions. J. Imaging 2021, 7, 41. [Google Scholar] [CrossRef] [PubMed]
- Boscain, U.; Gauthier, J.; Prandi, D.; Remizov, A. Image reconstruction via non-isotropic diffusion in Dubins/Reed-Shepp-like control systems. In Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; pp. 4278–4283. [Google Scholar]
- Bekkers, E.J.; Duits, R.; Mashtakov, A.; Sanguinetti, G.R. A PDE Approach to Data-driven Sub-Riemannian Geodesics in SE(2). Siam J. Imaging Sci. 2015, 8, 2740–2770. [Google Scholar] [CrossRef]
- Chen, D.; Mirebeau, J.-M.; Shu, M.; Cohen, L.D. Computing geodesic paths encoding a curvature prior for curvilinear structure tracking. Proc. Natl. Acad. Sci. USA 2023, 120, e2218869120. [Google Scholar] [CrossRef]
- Agrachev, A.A.; Sachkov, Y.L. Control Theory from the Geometric Viewpoint; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Jurdjevic, V. Rolling Geodesics, Mechanical Systems and Elastic Curves. Mathematics 2022, 10, 4827. [Google Scholar] [CrossRef]
- Jurdjevic, V. Integrable Systems: In the Footprints of the Greats. Mathematics 2023, 11, 1063. [Google Scholar] [CrossRef]
- Mashtakov, A.P.; Sachkov, Y.L. Extremal Trajectories in a Time Minimization Problem on the Group of Motions of a Plane with Admissible Control in a Circular Sector. Tr. Mat. Instituta Im. V.A. Steklova 2023, 321, 215–222. [Google Scholar]
- Bonnard, B.; Jurdjevic, V.; Kupka, I.; Sallet, G. Transitivity of families of invariant vector fields on the semidirect products of Lie groups. Trans. Am. Math. Soc. 1982, 271, 525–535. [Google Scholar] [CrossRef]
- Agrachev, A.; Barilari, D.; Boscain, U. A Comprehensive Introduction to Sub-Riemannian Geometry; Cambridge Studies in Advanced Mathematics; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Lokutsievskiy, L.V. Convex trigonometry with applications to sub-Finsler geometry. Sb. Math. 2019, 210, 1179–1205. [Google Scholar] [CrossRef]
- Arnold, V.I. Ordinary Differential Equations; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Sachkov, Y.L. Left-invariant optimal control problems on Lie groups that are integrable by elliptic functions. Uspekhi Mat. Nauk. 2023, 78, 67–166. [Google Scholar] [CrossRef]





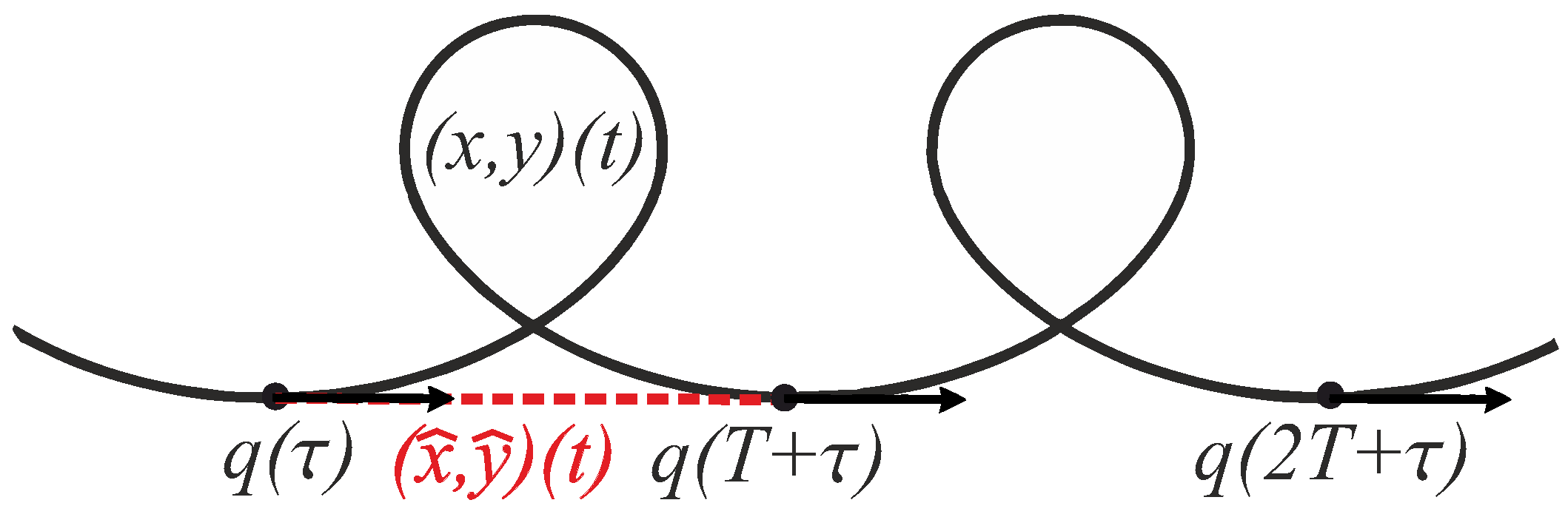
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mashtakov, A.; Sachkov, Y. Time-Optimal Problem in the Roto-Translation Group with Admissible Control in a Circular Sector. Mathematics 2023, 11, 3931. https://doi.org/10.3390/math11183931
Mashtakov A, Sachkov Y. Time-Optimal Problem in the Roto-Translation Group with Admissible Control in a Circular Sector. Mathematics. 2023; 11(18):3931. https://doi.org/10.3390/math11183931
Chicago/Turabian StyleMashtakov, Alexey, and Yuri Sachkov. 2023. "Time-Optimal Problem in the Roto-Translation Group with Admissible Control in a Circular Sector" Mathematics 11, no. 18: 3931. https://doi.org/10.3390/math11183931
APA StyleMashtakov, A., & Sachkov, Y. (2023). Time-Optimal Problem in the Roto-Translation Group with Admissible Control in a Circular Sector. Mathematics, 11(18), 3931. https://doi.org/10.3390/math11183931






