Efficient Monitoring of a Parameter of Non-Normal Process Using a Robust Efficient Control Chart: A Comparative Study
Abstract
:1. Introduction
2. Material and Methods: Memory-Type Control Charts Modified to the Case of LTS Distribution
2.1. Classical Cumulative Sum Control Chart
2.2. Classical Exponentially Weighted Moving Average Control Chart
2.3. Mixed Exponentially Weighted Moving Average—Cumulative Sum Control Chart
3. LTS Distribution, Lloyd’s Estimator, and Proposed Design Scheme for MEC Control Chart under Non-normality
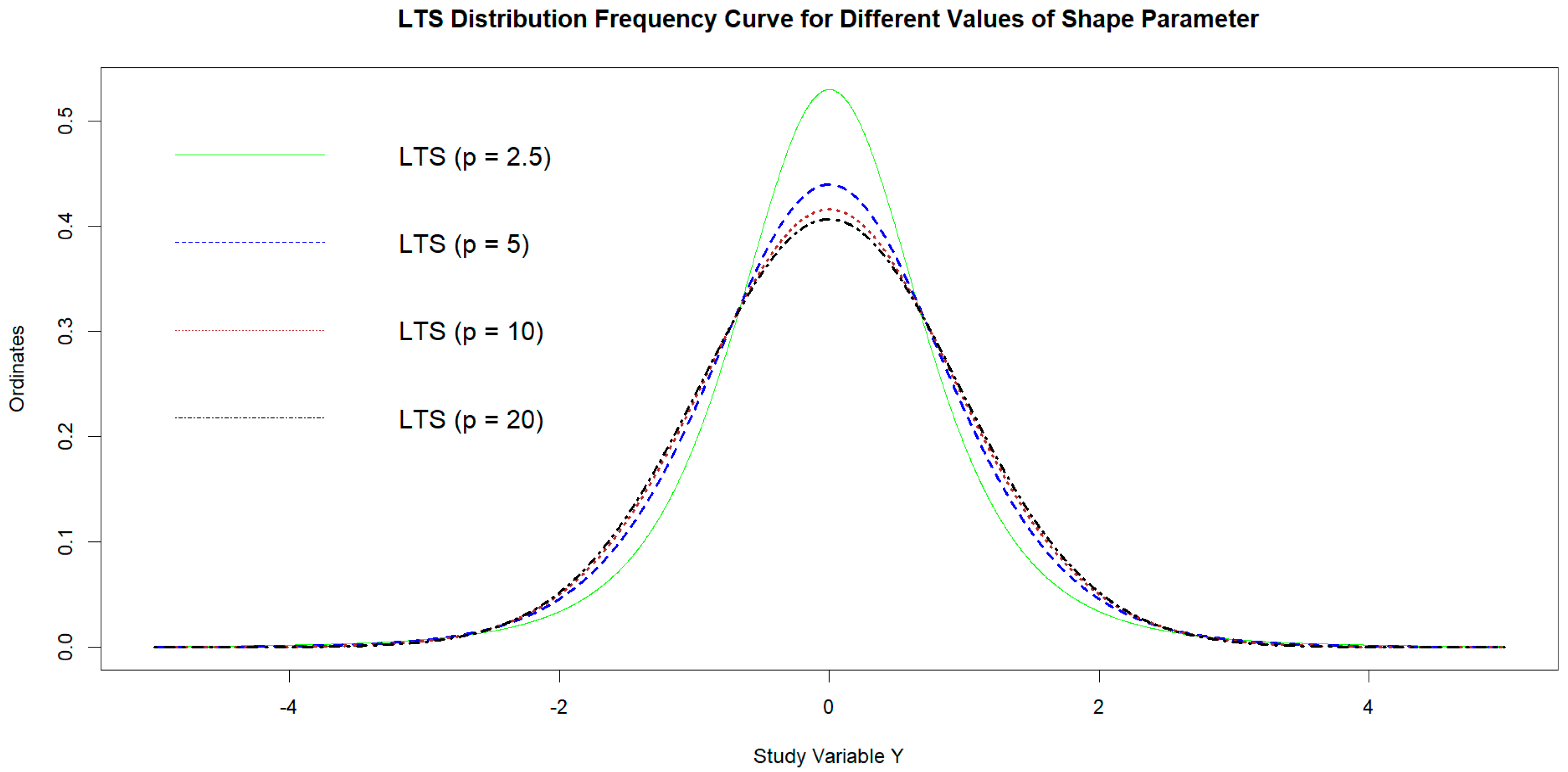
3.1. Long-Tailed Symmetric Family of Distribution
3.2. Lloyd BLUE Estimator
3.3. Proposed Scheme of Mixed Exponentially Weighted Moving Average—Cumulative Sum Control Chart
4. Performance Measure of Proposed and Conventional Control Charts
- The value of ARL increases with the increase in control limit () (see Table 16).
- When the smoothing constant () increases, then the control limit () decreases, to achieve the fixed ARL0 (Table 16).
- The value of ARL1 decreases with the increase in smoothing constant () (Table 16).
- The value of ARL1 goes down with the decrease in control limit () (see Table 16).
- The ARL values represent the average number of observations or samples required for the control chart to signal an out-of-control condition. The control chart scheme triggers an alarm within a few samples, as evidenced by the small ARL values, particularly for large shift sizes. The control chart scheme exhibits high sensitivity to small shifts in the process mean, as indicated by the ARL values of 15.15 and 6.43 for shift sizes of 0.25 and 0.5, respectively. This suggests that even relatively small deviations from the mean will be promptly detected by the control chart (Table 15).
- The control chart scheme achieves very low ARL values of 4.19 and 3.30 for shift sizes of 0.75 and 1, respectively, for a fixed ARL0 values of 400 (Table 14). This indicates that moderate shifts in the process mean can be detected efficiently with a relatively small number of samples.
5. Comparisons
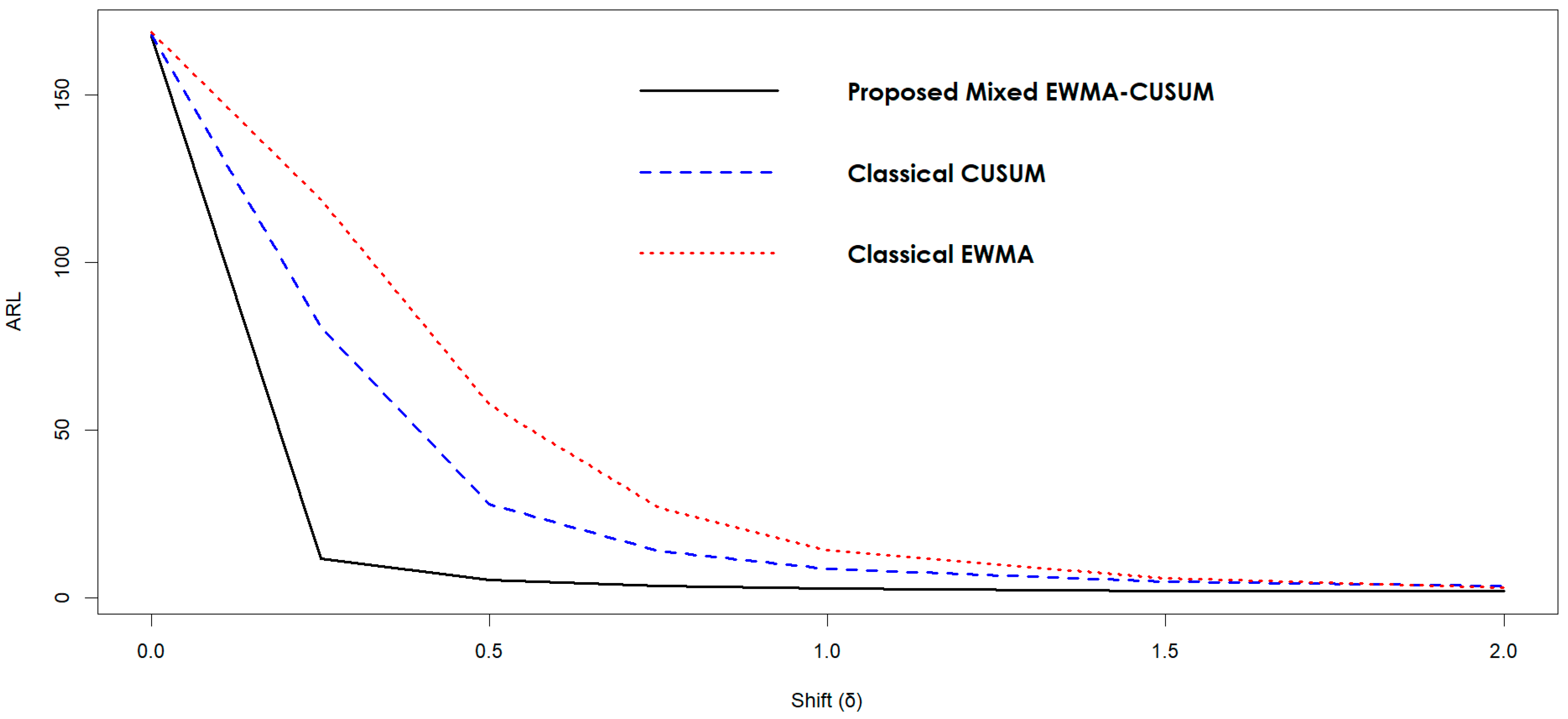
5.1. Proposed Mixed EWMA-CUSUM (MxEC) vs. Classical CUSUM
5.2. Proposed Mixed EWMA-CUSUM (MxEC) vs. FIR-CUSUM
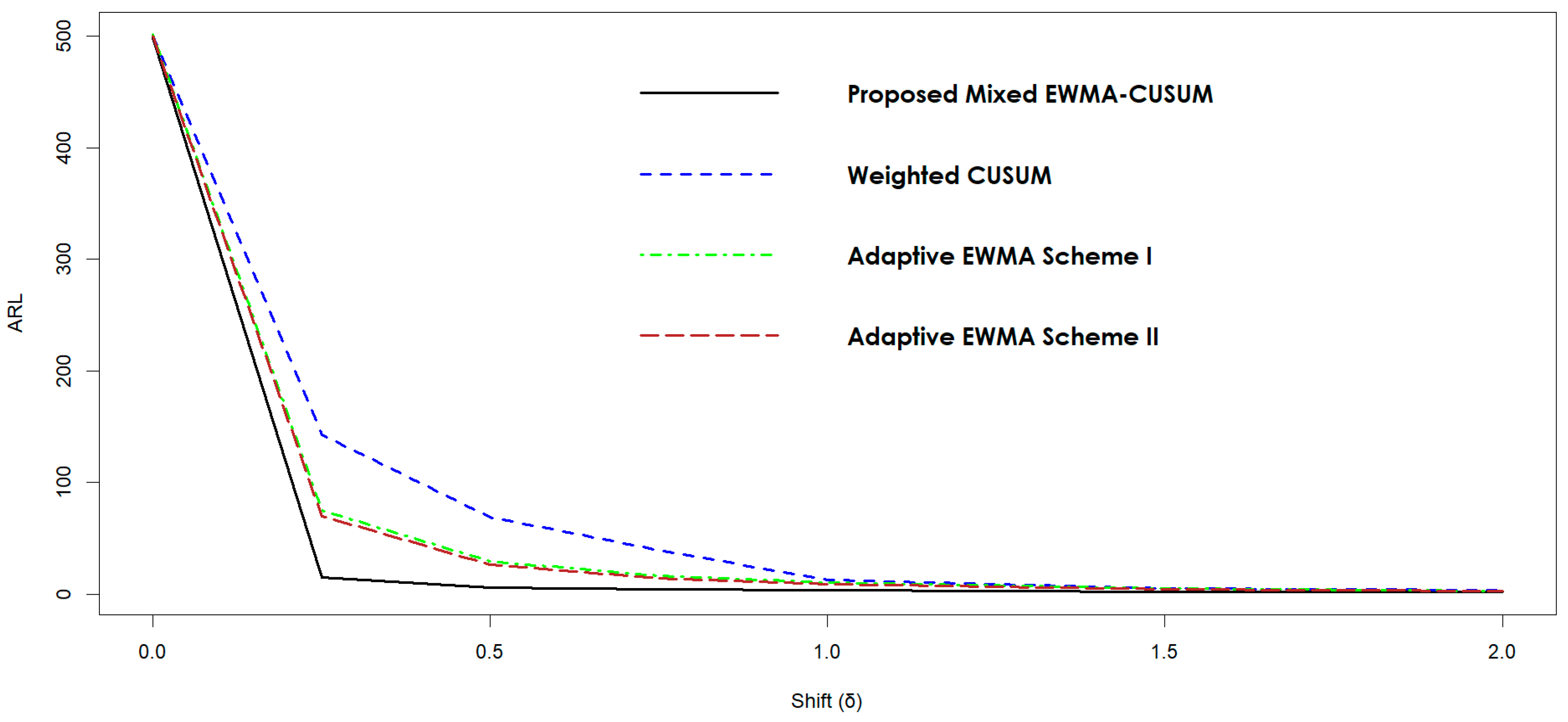
5.3. Proposed Mixed EWMA-CUSUM (MxEC) vs. Weighted CUSUM
5.4. Proposed Mixed EWMA-CUSUM (MxEC) vs. Adaptive CUSUM
5.5. Proposed Mixed EWMA-CUSUM (MxEC) vs. Run Rules-Based CUSUM
- Scheme I: A process is considered out of control if any of the following conditions are met:
- A single data point of the positive CUSUM (S+) falls outside the AL.
- A single data point of the negative CUSUM (S-) falls outside the AL.
- Two consecutive data points of S+ fall between the WL and the AL.
- Two consecutive data points of S- fall between the WL and the AL.
- Scheme II: A process is deemed out of control if any of the following conditions are met:
- A single data point of S+ falls outside the AL.
- A single data point of S- falls outside the AL.
- Two out of three consecutive data points of S+ fall between the WL and the AL.
- Two out of three consecutive data points of S- fall between the WL and the AL.
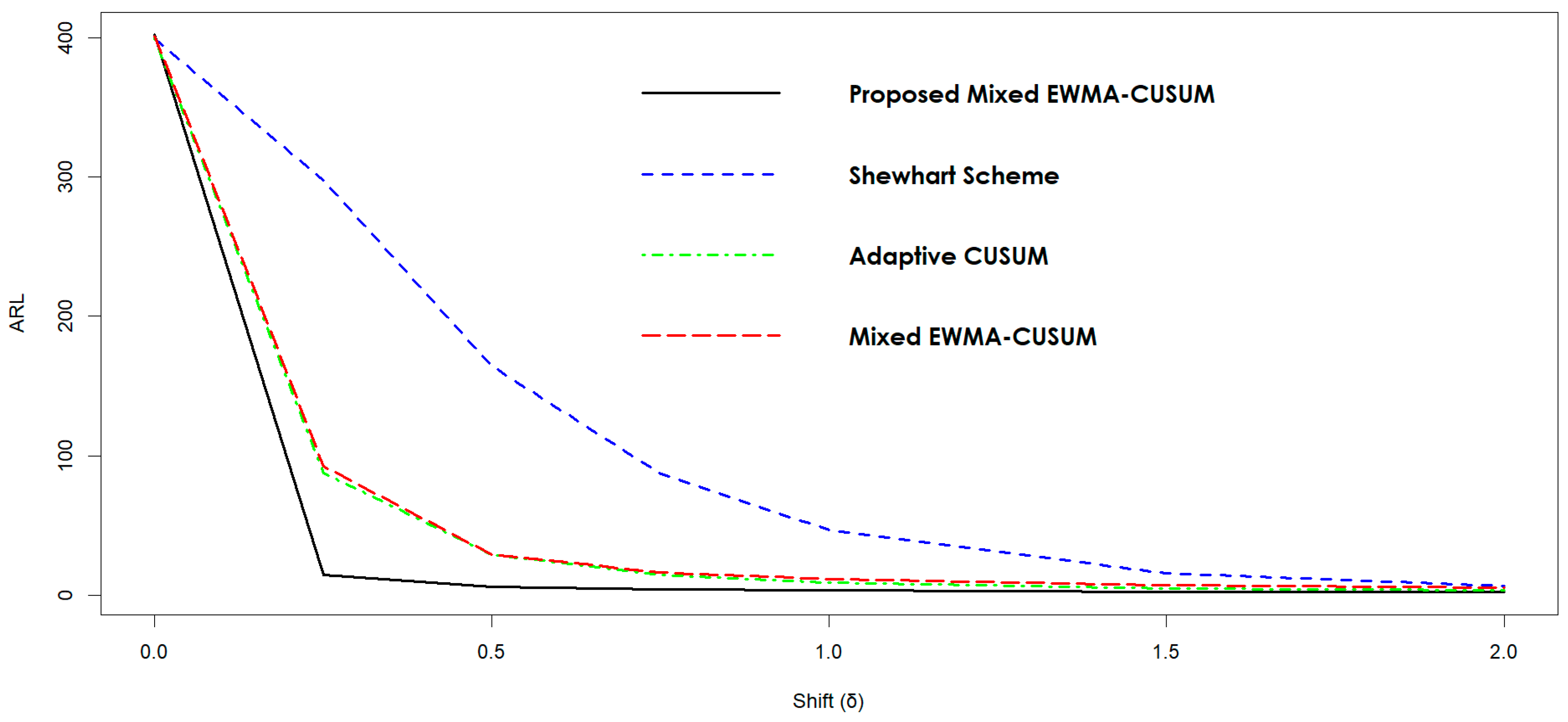
5.6. Proposed Mixed EWMA-CUSUM (MxEC) vs. Shewhart Scheme
5.7. Proposed Mixed EWMA-CUSUM (MxEC) vs. Classical Time-Varying EWMA
5.8. Proposed Mixed EWMA-CUSUM (MxEC) vs. FIR-EWMA
5.9. Proposed Mixed EWMA-CUSUM (MxEC) vs. Adaptive EWMA
5.10. Proposed Mixed EWMA-CUSUM (MxEC) vs. Runs Rules-Based EWMA
5.11. Proposed Mixed EWMA-CUSUM (MxEC) vs. Mixed EWMA-CUSUM
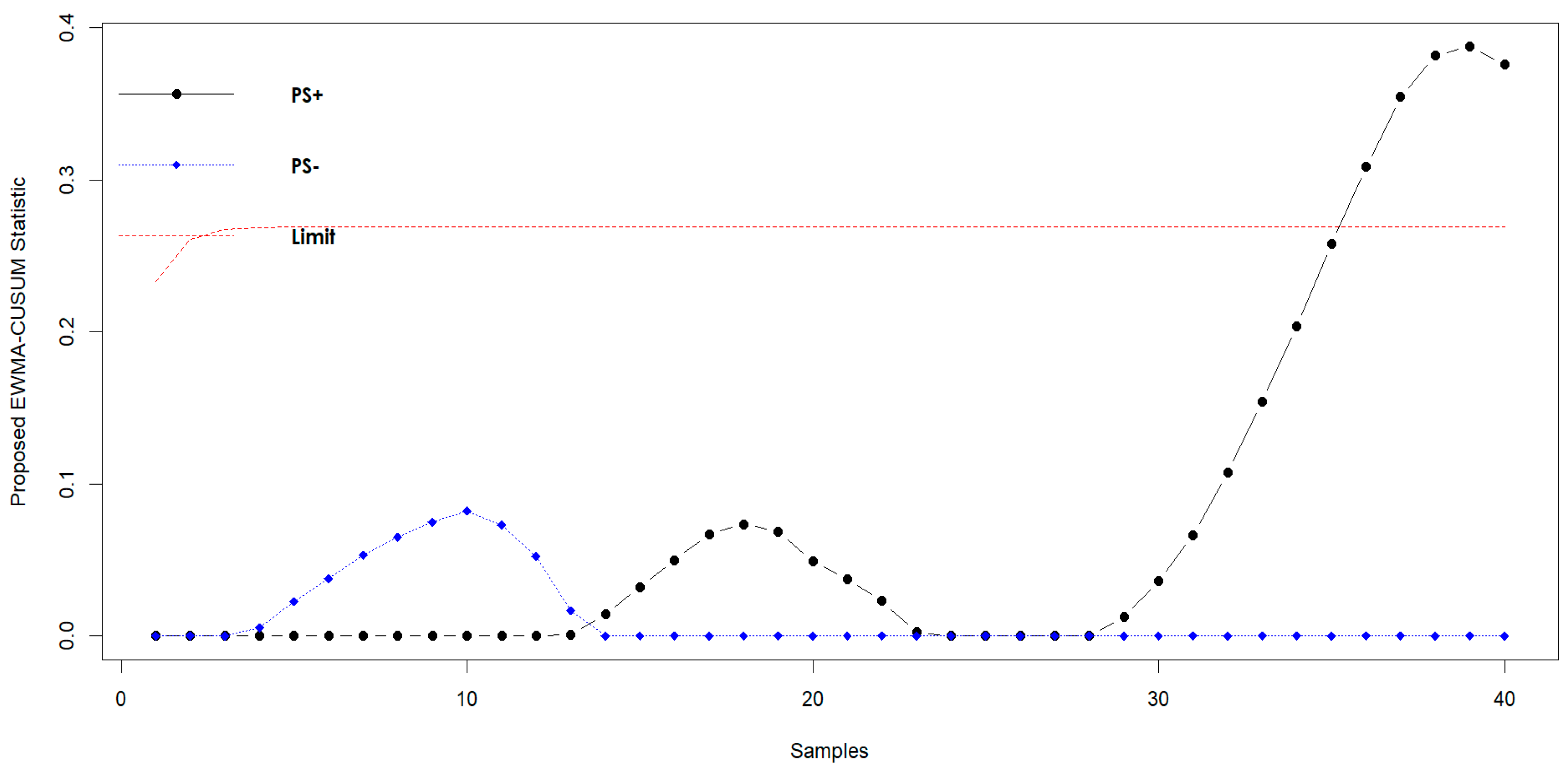
5.12. Graphical Presentation
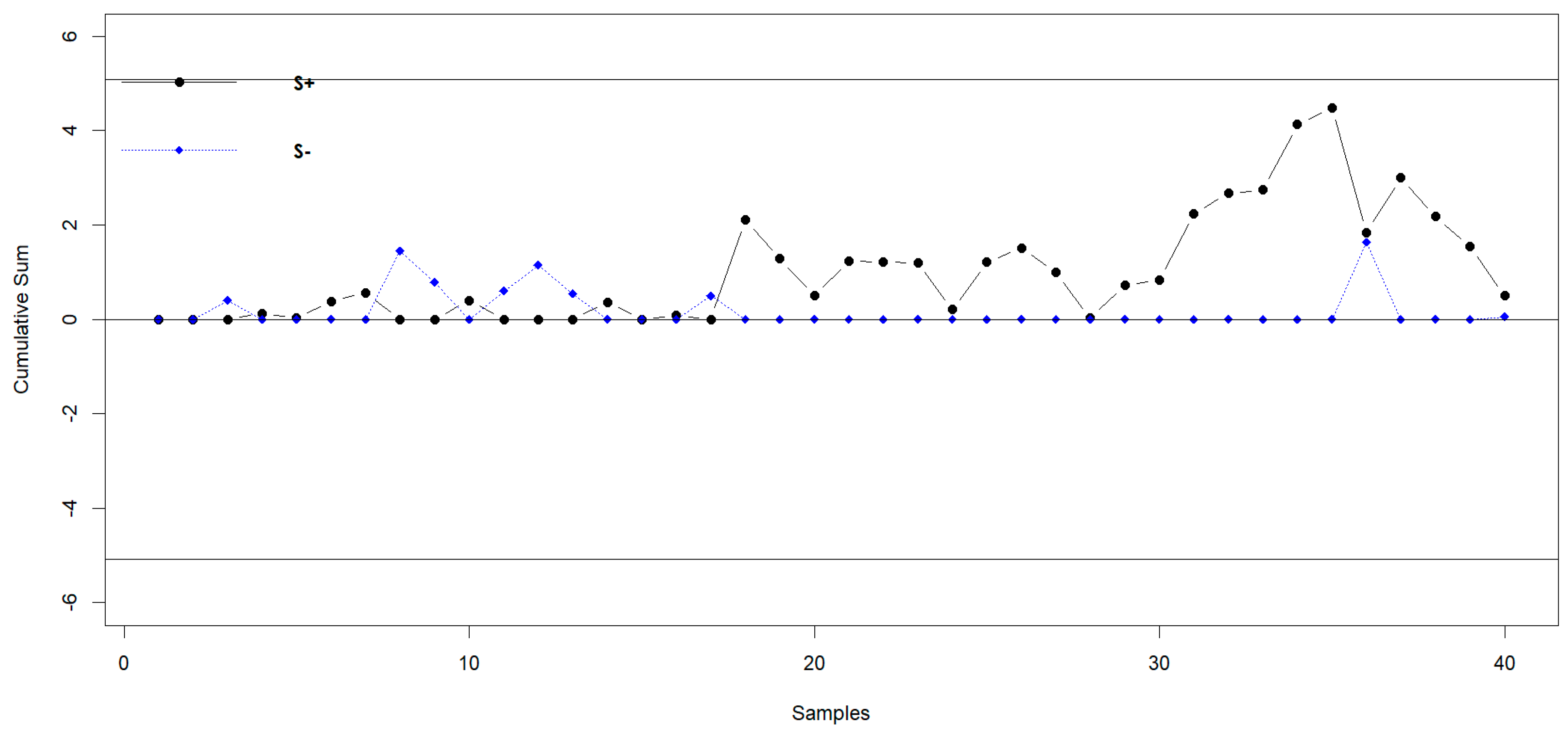
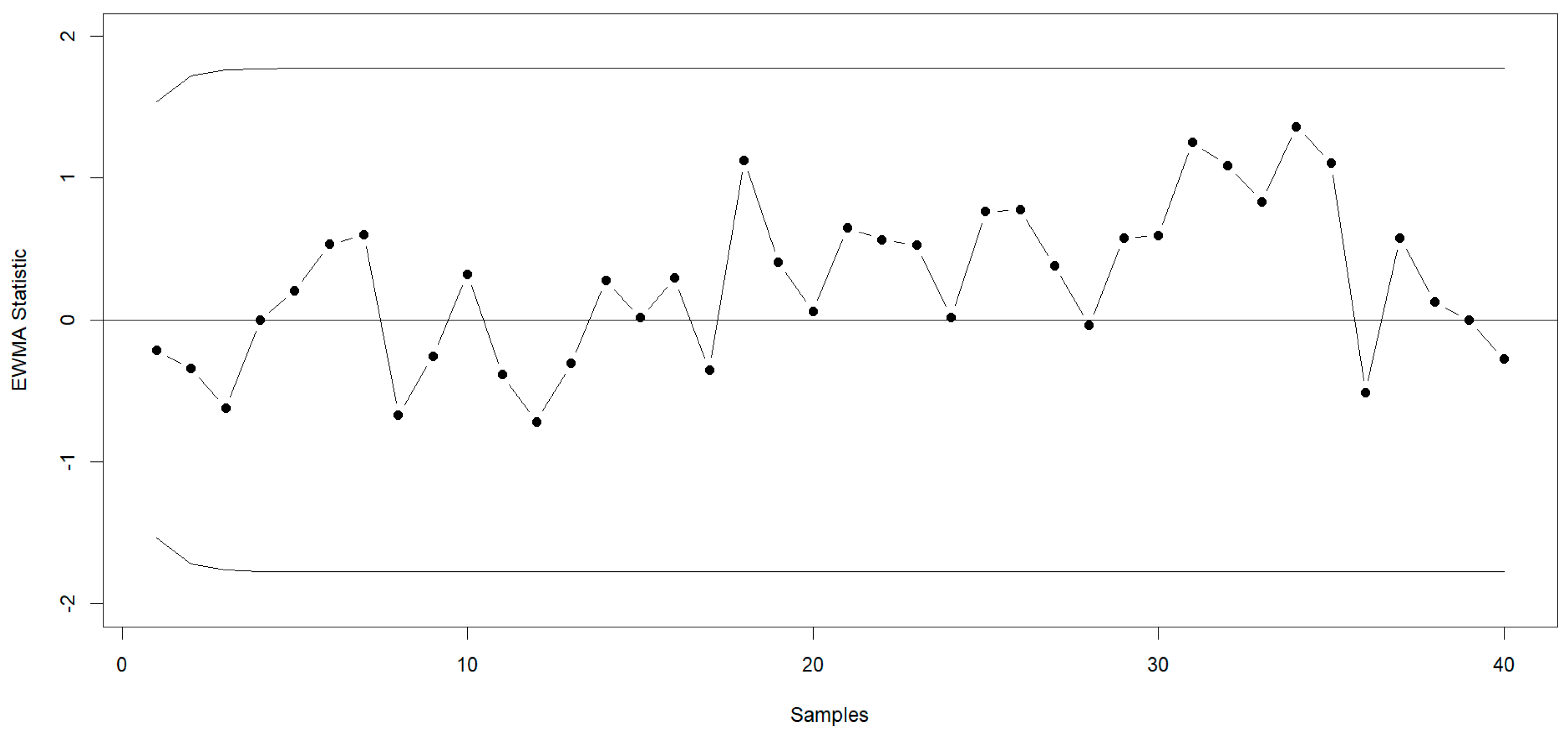
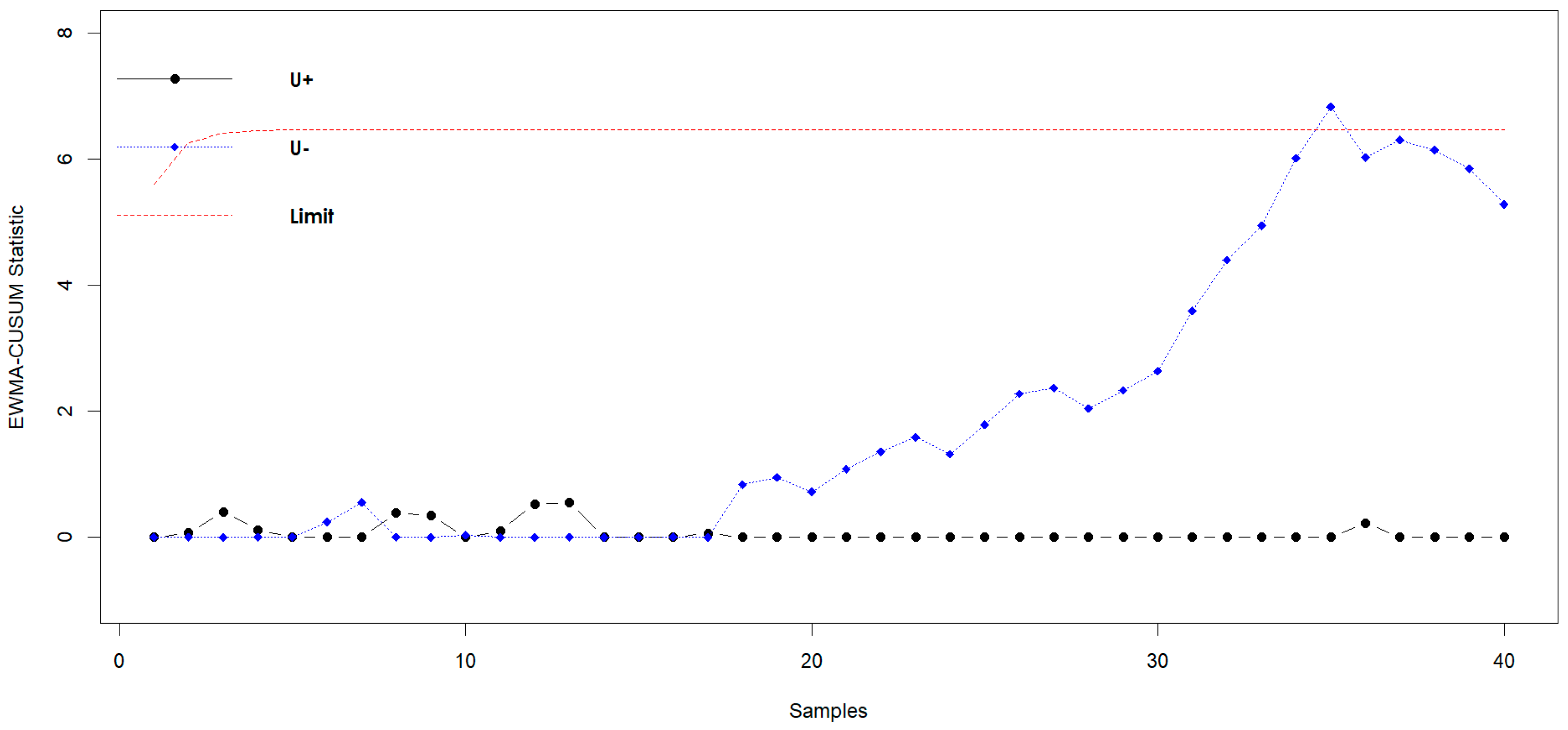
6. Real-Life Application
7. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shewhart, W.A. The Economic Control of Quality of Manufactured Product. J. R. Stat. Soc. 1932, 95, 546. [Google Scholar] [CrossRef]
- Montgomery, D.C. Introduction to Statistical Quality Control; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Page, E.S. Continuous Inspection Schemes. Biometrika 1954, 41, 100–115. [Google Scholar] [CrossRef]
- Roberts, S.W. Control Chart Tests Based on Geometric Moving Averages. Technometrics 2000, 42, 97–101. [Google Scholar] [CrossRef]
- Lucas, J.M. Combined Shewhart-CUSUM Quality Control Schemes. J. Qual. Technol. 1982, 14, 51–59. [Google Scholar] [CrossRef]
- Lucas, J.M.; Saccucci, M.S. Exponentially Weighted Moving Average Control Schemes: Properties and Enhancements. Technometrics 1990, 32, 1–12. [Google Scholar] [CrossRef]
- Lucas, J.M.; Crosier, R.B. Fast Initial Response for CUSUM Quality-Control Schemes: Give Your CUSUM A Head Start. Technometrics 2000, 42, 102–107. [Google Scholar] [CrossRef]
- Steiner, S.H. EWMA Control Charts with Time-Varying Control Limits and Fast Initial Response. J. Qual. Technol. 1999, 31, 75–86. [Google Scholar] [CrossRef]
- Riaz, M.; Abbas, N.; Does, R.J.M.M. Improving the Performance of CUSUM Charts. Qual. Reliab. Eng. Int. 2011, 27, 415–424. [Google Scholar] [CrossRef]
- Abbas, N.; Riaz, M.; Does, R.J.M.M. Enhancing the Performance of EWMA Charts. Qual. Reliab. Eng. Int. 2011, 27, 821–833. [Google Scholar] [CrossRef]
- Abbas, N.; Riaz, M.; Does, R.J.M.M. Mixed Exponentially Weighted Moving Average-Cumulative Sum Charts for Process Monitoring. Qual. Reliab. Eng. Int. 2013, 29, 345–356. [Google Scholar] [CrossRef]
- Zaman, B.; Riaz, M.; Abbas, N.; Does, R.J.M.M. Mixed Cumulative Sum-Exponentially Weighted Moving Average Control Charts: An Efficient Way of Monitoring Process Location. Qual. Reliab. Eng. Int. 2015, 31, 1407–1421. [Google Scholar] [CrossRef]
- Zaman, B.; Abbas, N.; Riaz, M.; Lee, M.H. Mixed CUSUM-EWMA Chart for Monitoring Process Dispersion. Int. J. Adv. Manuf. Technol. 2016, 86, 3025–3039. [Google Scholar] [CrossRef]
- Abid, M.; Mei, S.; Nazir, H.Z.; Riaz, M.; Hussain, S. A Mixed HWMA-CUSUM Mean Chart with an Application to Manufacturing Process. Qual. Reliab. Eng. Int. 2021, 37, 618–631. [Google Scholar] [CrossRef]
- Abid, M.; Mei, S.; Nazir, H.Z.; Riaz, M.; Hussain, S.; Abbas, Z. A Mixed Cumulative Sum Homogeneously Weighted Moving Average Control Chart for Monitoring Process Mean. Qual. Reliab. Eng. Int. 2021, 37, 1758–1771. [Google Scholar] [CrossRef]
- Riaz, M.; Khaliq, Q.-U.-A.; Gul, S. Mixed Tukey EWMA-CUSUM Control Chart and Its Applications. Qual. Technol. Quant. Manag. 2017, 14, 378–411. [Google Scholar] [CrossRef]
- Ahmed, A.; Sanaullah, A.; Hanif, M. A Robust Alternate to the HEWMA Control Chart under Non-Normality. Qual. Technol. Quant. Manag. 2020, 17, 423–447. [Google Scholar] [CrossRef]
- Nazir, H.; Abid, M.; Akhtar, N.; Riaz, M.; Qamar, S. An Efficient Mixed-Memory-Type Control Chart for Normal and Non-Normal Processes. Sci. Iran. 2021, 28, 1736–1749. [Google Scholar] [CrossRef]
- Aslam, M. A Mixed EWMA—CUSUM Control Chart for Weibull-Distributed Quality Characteristics. Qual. Reliab. Eng. Int. 2016, 32, 2987–2994. [Google Scholar] [CrossRef]
- Rao, G.S.; Aslam, M.; Rasheed, U.; Jun, C.-H. Mixed EWMA–CUSUM chart for COM-Poisson distribution. J. Stat. Manag. Syst. 2020, 23, 511–527. [Google Scholar] [CrossRef]
- Hussain, S.; Wang, X.; Ahmad, S.; Riaz, M. On a class of mixed EWMA-CUSUM median control charts for process monitoring. Qual. Reliab. Eng. Int. 2020, 36, 910–946. [Google Scholar] [CrossRef]
- Sales, L.O.F.; Pinho, A.L.S.; Bourguignon, M.; Medeiros, F.M.C. Control charts for monitoring the median in non-negative asymmetric data. Stat. Methods Appl. 2022, 31, 1037–1068. [Google Scholar] [CrossRef]
- Guh, R.S.; Hsieh, Y.C. A neural network-based model for abnormal pattern recognition of control charts. Comput. Ind. Eng. 1999, 36, 97–108. [Google Scholar] [CrossRef]
- Zan, T.; Liu, Z.; Wang, H.; Wang, M.; Gao, X. Control chart pattern recognition using the convolutional neural network. J. Intell. Manuf. 2020, 31, 703–716. [Google Scholar] [CrossRef]
- Chen, S.; Yu, J. Deep recurrent neural network-based residual control chart for autocorrelated processes. Qual. Reliab. Eng. Int. 2019, 35, 2687–2708. [Google Scholar] [CrossRef]
- Pugh, G.A. Synthetic neural networks for process control. Comput. Ind. Eng. 1989, 17, 24–26. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Statistics: Huber/Robust Statistics; Wiley Series in Probability and Statistics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1981. [Google Scholar] [CrossRef]
- Hampel, F.; Ronchetti, E.; Rousseeuw, P.J.; Stahel, W.A. Robust Statistics: The Approach Based on Influence Functions. J. R. Stat. Society. Ser. A (Gen.) 1987, 150, 281. [Google Scholar] [CrossRef]
- Lloyd, E.H. Least-Squares Estimation of Location and Scale Parameters using Order Statistics. Biometrika 1952, 39, 88–95. [Google Scholar] [CrossRef]
- Tiku, M.L.; Kumra, S. Expected Values and Variances and Covariances of Order Statistics for a Family of Symmetric Distributions (Student’st). Sel. Tables Math. Stat. 1985, 8, 141–270. [Google Scholar]
- Vaughan, D.C. Expected Values, Variances and Covariances of Order Statistics for Student’s t-Distribution with Two Degrees of Freedom. Commun. Stat.—Simul. Comp. 1992, 21, 391–404. [Google Scholar] [CrossRef]
- Yashchin, E. Weighted Cumulative Sum Technique. Technometrics 1989, 31, 321–338. [Google Scholar] [CrossRef]
- Jiang, W.; Shu, L.; Apley, D.W. Adaptive CUSUM Procedures with EWMA-Based Shift Estimators. IIE Trans. 2008, 40, 992–1003. [Google Scholar] [CrossRef]
- Zaman, B.; Lee, M.H.; Riaz, M.; Abujiya, M.R. An Adaptive EWMA Scheme-Based CUSUM Accumulation Error for Efficient Monitoring of Process Location. Qual. Reliab. Eng. Int. 2017, 33, 2463–2482. [Google Scholar] [CrossRef]


| = 4.1, n = 10 | ||||||
|---|---|---|---|---|---|---|
| ARL | SDRL | P25 | P50 | P75 | P90 | |
| 0 | 168.15 | 162.50 | 50 | 119 | 234 | 386 |
| 0.25 | 80.59 | 76.28 | 26 | 57 | 110 | 179 |
| 0.5 | 27.81 | 22.51 | 12 | 21 | 37 | 58 |
| 0.75 | 13.89 | 9.33 | 7 | 11 | 18 | 26 |
| 1 | 8.63 | 4.70 | 5 | 8 | 11 | 15 |
| 1.5 | 4.85 | 1.98 | 3 | 4 | 6 | 7 |
| 2 | 3.38 | 1.15 | 3 | 3 | 4 | 5 |
| = 5.065, n = 10 | ||||||
|---|---|---|---|---|---|---|
| ARL | SDRL | P25 | P50 | P75 | P90 | |
| 0 | 401.02 | 397.69 | 119 | 280 | 555.25 | 918 |
| 0.25 | 143.04 | 136.06 | 46 | 101 | 197 | 322 |
| 0.5 | 39.67 | 32.58 | 17 | 30 | 53 | 82 |
| 0.75 | 17.34 | 11.25 | 9 | 14 | 22 | 32 |
| 1 | 10.49 | 5.44 | 7 | 9 | 13 | 18 |
| 1.5 | 5.80 | 2.24 | 4 | 5 | 7 | 9 |
| 2 | 4.05 | 1.28 | 3 | 4 | 5 | 6 |
| = 5.32, n = 10 | ||||||
|---|---|---|---|---|---|---|
| ARL | SDRL | P25 | P50 | P75 | P90 | |
| 0 | 499.50 | 495.22 | 147 | 345.5 | 686 | 1129 |
| 0.25 | 164.61 | 155.48 | 52 | 119 | 225 | 368 |
| 0.5 | 42.17 | 34.78 | 18 | 32 | 56 | 88 |
| 0.75 | 18.52 | 11.78 | 10 | 16 | 24 | 34 |
| 1 | 10.97 | 5.61 | 7 | 10 | 14 | 18 |
| 1.5 | 6.08 | 2.28 | 4 | 6 | 7 | 9 |
| 2 | 4.20 | 1.30 | 3 | 4 | 5 | 6 |
| = 0.5 | = 0.5 | = 0.5 | = 0.5 | |
|---|---|---|---|---|
| = 4 | = 4.85 | = 5 | = 5.07 | |
| 0 | 169.61 | 400.78 | 465.74 | 501.72 |
| 0.25 | 74.52 | 127.52 | 139.30 | 146.35 |
| 0.5 | 26.91 | 36.89 | 38.30 | 38.95 |
| 0.75 | 13.17 | 16.59 | 17.30 | 17.23 |
| 1 | 8.38 | 10.06 | 10.37 | 10.47 |
| 1.5 | 4.74 | 5.63 | 5.73 | 5.82 |
| 2 | 3.36 | 3.90 | 4.01 | 4.05 |
| = 2.91, n = 10 | ||||||
|---|---|---|---|---|---|---|
| ARL | SDRL | P25 | P50 | P75 | P90 | |
| 0 | 168.89 | 168.04 | 49 | 117 | 233 | 391.1 |
| 0.25 | 118.72 | 118.75 | 35 | 84 | 163 | 271.1 |
| 0.5 | 57.51 | 56.39 | 17 | 40 | 79 | 132 |
| 0.75 | 26.96 | 25.18 | 9 | 19 | 37 | 60 |
| 1 | 14.22 | 12.66 | 5 | 10 | 19 | 30 |
| 1.5 | 5.64 | 4.09 | 3 | 5 | 7 | 11 |
| 2 | 3.05 | 1.78 | 2 | 3 | 4 | 5 |
| = 3.34, n = 10 | ||||||
|---|---|---|---|---|---|---|
| ARL | SDRL | P25 | P50 | P75 | P90 | |
| 0 | 399.09 | 402.25 | 115 | 276 | 552 | 917 |
| 0.25 | 282.81 | 283.55 | 81 | 199 | 388 | 649.1 |
| 0.5 | 134.59 | 132.32 | 41 | 94 | 183 | 312 |
| 0.75 | 58.68 | 57.31 | 18 | 41 | 80 | 133 |
| 1 | 27.99 | 25.85 | 10 | 20 | 38 | 61 |
| 1.5 | 8.60 | 6.64 | 4 | 7 | 11 | 17 |
| 2 | 4.21 | 2.65 | 2 | 4 | 5 | 8 |
| = 3.455, n = 10 | ||||||
|---|---|---|---|---|---|---|
| ARL | SDRL | P25 | P50 | P75 | P90 | |
| 0 | 498.34 | 498.73 | 143 | 345 | 691 | 1149.1 |
| 0.25 | 356.66 | 355.44 | 101 | 248 | 497 | 809 |
| 0.5 | 168.84 | 163.76 | 50 | 120 | 237 | 385 |
| 0.75 | 73.65 | 71.56 | 23 | 51 | 101 | 168.1 |
| 1 | 33.58 | 30.99 | 12 | 24 | 45 | 74 |
| 1.5 | 9.86 | 7.83 | 4 | 8 | 13 | 20 |
| 2 | 4.56 | 2.92 | 3 | 4 | 6 | 8 |
| = 0.1 = 2.824 | = 0.25 = 3 | = 0.5 = 3.072 | = 0.75 = 3.088 | |
|---|---|---|---|---|
| 0 | 500.77 | 499.29 | 499.37 | 500.57 |
| 0.25 | 103.58 | 170.45 | 255.19 | 325.24 |
| 0.5 | 28.88 | 48.37 | 88.71 | 143.44 |
| 0.75 | 13.60 | 19.24 | 34.97 | 63.14 |
| 1 | 8.29 | 10.31 | 17.04 | 30.29 |
| 1.5 | 4.14 | 4.76 | 6.33 | 9.96 |
| 2 | 2.66 | 2.94 | 3.38 | 4.47 |
| = 8.12, n = 10 | ||||||
|---|---|---|---|---|---|---|
| ARL | SDRL | P25 | P50 | P75 | P90 | |
| 0 | 169.54 | 160.64 | 55 | 120.5 | 233 | 382 |
| 0.25 | 60.22 | 51.30 | 24 | 45 | 80 | 127 |
| 0.5 | 22.39 | 14.39 | 12 | 19 | 28 | 41 |
| 0.75 | 12.77 | 6.34 | 8 | 11 | 16 | 21 |
| 1 | 9.02 | 3.62 | 6 | 8 | 11 | 14 |
| 1.5 | 5.78 | 1.68 | 5 | 5 | 7 | 8 |
| 2 | 4.41 | 1.04 | 4 | 4 | 5 | 6 |
| = 10.63, n = 10 | ||||||
|---|---|---|---|---|---|---|
| ARL | SDRL | P25 | P50 | P75 | P90 | |
| 0 | 401.16 | 391.52 | 122 | 276 | 552 | 917.1 |
| 0.25 | 92.20 | 77.95 | 36 | 69 | 123 | 196 |
| 0.5 | 29.17 | 18.32 | 16 | 24 | 37 | 53 |
| 0.75 | 16 | 7.63 | 11 | 14 | 19 | 26 |
| 1 | 11.05 | 4.18 | 8 | 10 | 13 | 17 |
| 1.5 | 7.04 | 1.91 | 6 | 7 | 8 | 10 |
| 2 | 5.34 | 1.15 | 5 | 5 | 6 | 7 |
| = 11.33, n = 10 | ||||||
|---|---|---|---|---|---|---|
| ARL | SDRL | P25 | P50 | P75 | P90 | |
| 0 | 501.21 | 497.16 | 153 | 344 | 686 | 1144.1 |
| 0.25 | 104.25 | 91.01 | 41 | 77 | 138 | 221 |
| 0.5 | 31.26 | 19.60 | 18 | 26 | 39 | 57 |
| 0.75 | 16.88 | 7.83 | 11 | 15 | 21 | 27 |
| 1 | 11.55 | 4.22 | 9 | 11 | 14 | 17 |
| 1.5 | 7.35 | 1.97 | 6 | 7 | 8 | 10 |
| 2 | 5.55 | 1.18 | 5 | 5 | 6 | 7 |
| = 0.1 = 21.3 | = 0.25 = 13.29 | = 0.75 = 5.48 | = 0.1 = 33.54 | = 0.25 = 18.7 | = 0.75 = 6.94 | = 0.1 = 37.42 | = 0.25 = 20.16 | = 0.75 = 7.32 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 168.15 | 169.18 | 170.83 | 399.84 | 401.27 | 398.63 | 502.33 | 502.75 | 505.26 |
| 0.25 | 52.74 | 55.23 | 68.34 | 74.37 | 79.38 | 104.91 | 79.98 | 83.78 | 120.46 |
| 0.5 | 24.96 | 23.72 | 24.16 | 33.98 | 32.68 | 31.36 | 35.40 | 30.78 | 33.36 |
| 0.75 | 17.38 | 15.94 | 12.62 | 23.04 | 18.79 | 15.58 | 23.97 | 18.83 | 16.43 |
| 1 | 13.56 | 11.74 | 8.25 | 18.19 | 14.23 | 10.16 | 18.85 | 13.89 | 10.76 |
| 1.5 | 9.86 | 8.54 | 4.89 | 13.54 | 9.88 | 6.08 | 13.79 | 9.57 | 6.31 |
| 2 | 7.98 | 6.08 | 3.56 | 10.76 | 7.09 | 4.41 | 11.17 | 7.59 | 4.59 |
| = 5.61, n = 10 | ||||||
|---|---|---|---|---|---|---|
| ARL | SDRL | P25 | P50 | P75 | P90 | |
| 0 | 167.50 | 160.97 | 52 | 117 | 230 | 380 |
| 0.25 | 11.61 | 6.24 | 7 | 10 | 14 | 20 |
| 0.5 | 5.12 | 1.54 | 4 | 5 | 6 | 7 |
| 0.75 | 3.53 | 0.79 | 3 | 3 | 4 | 5 |
| 1 | 2.79 | 0.56 | 2 | 3 | 3 | 3 |
| 1.5 | 2.05 | 0.23 | 2 | 2 | 2 | 2 |
| 2 | 1.86 | 0.34 | 2 | 2 | 2 | 2 |
| = 7.32, n = 10 | ||||||
|---|---|---|---|---|---|---|
| ARL | SDRL | P25 | P50 | P75 | P90 | |
| 0 | 402.67 | 394.23 | 122.75 | 280 | 553 | 902 |
| 0.25 | 14.55 | 14.55 | 9 | 13 | 18 | 24.1 |
| 0.5 | 6.15 | 6.15 | 5 | 6 | 7 | 8 |
| 0.75 | 4.19 | 4.19 | 4 | 4 | 5 | 5 |
| 1 | 3.30 | 3.30 | 3 | 3 | 4 | 4 |
| 1.5 | 2.37 | 2.37 | 2 | 2 | 3 | 3 |
| 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| = 7.77, n = 10 | ||||||
|---|---|---|---|---|---|---|
| ARL | SDRL | P25 | P50 | P75 | P90 | |
| 0 | 498.81 | 484.28 | 155 | 348 | 687 | 1120.1 |
| 0.25 | 15.15 | 7.54 | 10 | 13 | 19 | 25 |
| 0.5 | 6.43 | 1.78 | 5 | 6 | 7 | 9 |
| 0.75 | 4.36 | 0.88 | 4 | 4 | 5 | 5 |
| 1 | 3.43 | 0.59 | 3 | 3 | 4 | 4 |
| 1.5 | 2.51 | 0.50 | 2 | 3 | 3 | 3 |
| 2 | 2.02 | 0.13 | 2 | 2 | 2 | 2 |
| = 0.1 = 14.49 | = 0.25 = 9.17 | = 0.75 = 3.87 | = 0.1 = 23.33 | = 0.25 = 12.83 | = 0.75 = 4.85 | = 0.1 = 25.92 | = 0.25 = 14.12 | = 0.75 = 5.10 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 168.98 | 168.40 | 167.80 | 401.15 | 399.88 | 401.08 | 499.96 | 500.82 | 500.41 |
| 0.25 | 15.18 | 12.70 | 11.56 | 20.15 | 15.81 | 14.34 | 21.42 | 16.92 | 15.31 |
| 0.5 | 8.59 | 6.49 | 4.52 | 11.46 | 8.02 | 5.38 | 12.20 | 8.55 | 5.59 |
| 0.75 | 6.32 | 4.71 | 2.93 | 8.49 | 5.77 | 3.44 | 9.04 | 6.13 | 3.55 |
| 1 | 5.13 | 3.77 | 2.25 | 6.91 | 4.66 | 2.61 | 7.39 | 4.96 | 2.70 |
| 1.5 | 3.88 | 2.88 | 1.73 | 5.19 | 3.45 | 1.98 | 5.56 | 3.74 | 2.01 |
| 2 | 3.06 | 2.16 | 1.16 | 4.18 | 2.96 | 1.58 | 4.57 | 3.02 | 1.70 |
| 0 | 0.25 | 0.5 | 0.75 | 1 | 1.5 | 2 | |
|---|---|---|---|---|---|---|---|
| = 4, S0 = 1 | 162.56 | 71.16 | 24.38 | 11.74 | 7.16 | 3.87 | 2.71 |
| = 4, S0 = 2 | 148.93 | 62.77 | 20.21 | 8.99 | 5.32 | 2.91 | 2.04 |
| = 4.14, S0 = 1 | = 4.21, S0 = 2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ARL | SDRL | P25 | P50 | P75 | P90 | ARL | SDRL | P25 | P50 | P75 | P90 | |
| 0 | 167.08 | 164.23 | 50 | 118 | 231 | 375 | 166.97 | 178.26 | 39 | 111 | 235 | 403 |
| 0.25 | 78.57 | 77.70 | 23 | 54 | 109 | 181 | 73.24 | 78.13 | 16.75 | 49 | 104 | 173 |
| 0.5 | 26.73 | 23.84 | 10 | 20 | 36 | 57 | 22.67 | 23.06 | 6 | 15 | 32 | 53 |
| 0.75 | 12.08 | 8.99 | 6 | 10 | 16 | 24 | 9.95 | 8.89 | 4 | 7 | 13 | 22 |
| 1 | 7.27 | 4.59 | 4 | 6 | 9 | 13 | 5.65 | 4.16 | 3 | 4 | 7 | 11 |
| 1.5 | 3.95 | 1.85 | 3 | 4 | 5 | 6 | 3.08 | 1.67 | 2 | 3 | 4 | 5 |
| 2 | 2.79 | 1.06 | 2 | 3 | 3 | 4 | 2.16 | 0.94 | 2 | 2 | 3 | 3 |
| = 5.08, S0 = 1 | = 5.09, S0 = 2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ARL | SDRL | P25 | P50 | P75 | P90 | ARL | SDRL | P25 | P50 | P75 | P90 | |
| 0 | 400.42 | 401.65 | 115 | 277 | 554 | 915 | 400.09 | 406.43 | 109 | 278 | 555 | 937 |
| 0.25 | 143.07 | 142.17 | 43 | 99 | 196 | 321 | 133.79 | 136.15 | 36 | 91 | 185 | 318 |
| 0.5 | 37.69 | 32.85 | 14 | 28 | 50 | 81 | 33.56 | 31.75 | 11 | 24 | 46 | 75 |
| 0.75 | 15.79 | 11.43 | 8 | 12 | 20 | 31 | 13.18 | 10.59 | 6 | 10 | 17 | 28 |
| 1 | 9.31 | 5.40 | 5.75 | 8 | 12 | 16 | 7.57 | 5.02 | 4 | 6 | 10 | 14 |
| 1.5 | 4.90 | 2.07 | 3 | 4 | 6 | 8 | 3.93 | 1.89 | 3 | 4 | 5 | 6 |
| 2 | 3.42 | 1.18 | 3 | 3 | 4 | 5 | 2.77 | 1.06 | 2 | 3 | 3 | 4 |
| = 5.34, S0 = 1 | = 5.35, S0 = 2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ARL | SDRL | P25 | P50 | P75 | P90 | ARL | SDRL | P25 | P50 | P75 | P90 | |
| 0 | 501.05 | 498.24 | 145 | 347 | 701 | 1143.1 | 500.73 | 501.65 | 140 | 345 | 701 | 1164.1 |
| 0.25 | 163.25 | 160.12 | 51 | 114 | 225 | 367 | 157.81 | 162.21 | 42 | 108 | 219 | 373 |
| 0.5 | 40.79 | 34.65 | 16 | 31 | 55 | 85.1 | 37.40 | 35.93 | 12 | 26 | 51 | 85 |
| 0.75 | 16.72 | 11.66 | 8 | 14 | 22 | 32 | 14.15 | 11.38 | 6 | 11 | 18 | 29 |
| 1 | 9.75 | 5.59 | 6 | 8 | 12 | 17 | 7.92 | 5.06 | 4 | 7 | 10 | 15 |
| 1.5 | 5.21 | 2.17 | 4 | 5 | 6 | 8 | 4.20 | 1.95 | 3 | 4 | 5 | 7 |
| 2 | 3.61 | 1.24 | 3 | 3 | 4 | 5 | 2.94 | 1.10 | 2 | 3 | 3 | 4 |
| = 0.5 | |||||
|---|---|---|---|---|---|
| Υ | 0.5 | 1 | 1.5 | 2 | |
| 0.7 | 3.16 | 85.94 | 15.78 | 6.05 | 3.50 |
| 0.8 | 3.46 | 69.37 | 13.27 | 5.63 | 3.49 |
| 0.9 | 3.97 | 53.93 | 11.29 | 5.49 | 3.58 |
| 1.0 | 5.09 | 38.98 | 10.42 | 5.72 | 4.00 |
| = 1.5 = 5.07 | = 2 = 4.79 | = 3 = 4.425 | = 4 = 4.355 | = 4.345 | |
|---|---|---|---|---|---|
| 0 | 398.32 | 401.93 | 400.36 | 398.97 | 401.03 |
| 0.25 | 92.73 | 91.64 | 87.41 | 85.92 | 85.82 |
| 0.5 | 30.24 | 30.17 | 28.88 | 28.54 | 28.37 |
| 0.75 | 14.68 | 14.54 | 14.23 | 13.79 | 13.43 |
| 1 | 9.13 | 8.97 | 8.78 | 8.54 | 8.21 |
| 1.5 | 4.92 | 4.78 | 4.87 | 4.81 | 4.78 |
| 2 | 3.25 | 3.23 | 3.32 | 3.28 | 3.26 |
| Scheme I | |||||||
|---|---|---|---|---|---|---|---|
| Limits | |||||||
| WL | AL | 0.25 | 0.5 | 0.75 | 1 | 1.5 | 2 |
| 3.42 | 4.8 | 71.97 | 25.65 | 13.54 | 8.66 | 5.17 | 3.68 |
| 3.44 | 4.6 | 72.38 | 25.72 | 13.5 | 8.57 | 5.11 | 3.61 |
| 3.48 | 4.4 | 71.94 | 25.62 | 13.49 | 8.52 | 4.94 | 3.53 |
| 3.53 | 4.2 | 71.48 | 25.34 | 13.33 | 8.41 | 4.83 | 3.43 |
| Scheme II | |||||||
| 3.5 | 4.44 | 71.49 | 25.38 | 13.40 | 8.46 | 4.94 | 3.54 |
| 3.6 | 4.19 | 72.94 | 25.37 | 13.35 | 8.38 | 4.83 | 3.44 |
| 3.7 | 4.08 | 73.11 | 25.37 | 13.31 | 8.34 | 4.78 | 3.38 |
| 3.8 | 4.03 | 73.59 | 25.41 | 13.28 | 8.32 | 4.75 | 3.35 |
| Scheme I | |||||||
|---|---|---|---|---|---|---|---|
| Limits | |||||||
| WL | AL | 0.25 | 0.5 | 0.75 | 1 | 1.5 | 2 |
| 4.8 | 5.12 | 141.12 | 38.60 | 17.39 | 10.52 | 5.91 | 4.06 |
| 4.7 | 5.2 | 150.38 | 38.62 | 17.63 | 10.61 | 5.90 | 4.15 |
| 4.6 | 5.39 | 145.21 | 38.21 | 17.47 | 10.56 | 6.01 | 4.24 |
| 4.5 | ∞ | 146.74 | 38.47 | 17.73 | 10.83 | 6.32 | 4.71 |
| Scheme II | |||||||
| 4.8 | 5.11 | 139.72 | 38.87 | 17.48 | 10.53 | 5.83 | 4.11 |
| 4.7 | 5.2 | 142.17 | 37.98 | 17.28 | 10.59 | 5.87 | 4.10 |
| 4.6 | 5.5 | 145.79 | 38.34 | 17.39 | 10.76 | 6.08 | 4.28 |
| 4.55 | ∞ | 149.13 | 39.93 | 17.59 | 10.98 | 6.47 | 4.88 |
| 0 | 0.25 | 0.5 | 0.75 | 1 | 1.5 | 2 | |
|---|---|---|---|---|---|---|---|
| ARL at L = 2.75 | 168.55 | 131.38 | 77.65 | 43.58 | 25.05 | 9.38 | 4.40 |
| ARL at L = 3.024 | 399.74 | 297.59 | 164.39 | 87 | 46.63 | 15.69 | 6.50 |
| ARL at L = 3.09 | 501.13 | 370.83 | 201.60 | 101.63 | 55.54 | 17.98 | 7.18 |
| % Head Start | = 0.1 = 2.824 | = 0.25 = 3 | = 0.5 = 3.072 | = 0.75 = 3.088 | |
|---|---|---|---|---|---|
| 0 | 25 | 489 | 494 | 496 | 499.15 |
| 50 | 471 | 486 | 488 | 496.54 | |
| 0.5 | 25 | 29.45 | 47.34 | 88.13 | 141.05 |
| 50 | 26.39 | 44.07 | 86.89 | 139.67 | |
| 1 | 25 | 8.97 | 10.38 | 17.27 | 30.48 |
| 50 | 6.88 | 8.97 | 16.38 | 29.83 | |
| 2 | 25 | 3.64 | 3.23 | 3.74 | 4.47 |
| 50 | 2.91 | 2.56 | 2.98 | 4.26 |
| = 0.5, = 0.1, Υ = 4.15, = 4.865 (Scheme I) | = 0.2, = 0.05, Υ = 31.12, = 8.95 (Scheme II) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ARL | SDRL | P25 | P50 | P75 | P90 | ARL | SDRL | P25 | P50 | P75 | P90 | |
| 0 | 501.29 | 498.75 | 139 | 348 | 695 | 1168 | 500.01 | 497.62 | 135 | 344 | 689 | 1154 |
| 0.25 | 75.38 | 73.18 | 26 | 55 | 112 | 178 | 70.17 | 62.59 | 26 | 53 | 109 | 172 |
| 0.5 | 29.47 | 26.94 | 11 | 22 | 37 | 49 | 26.23 | 22.36 | 12 | 21 | 35 | 48 |
| 0.75 | 16.68 | 13.67 | 6 | 10 | 16 | 22 | 14.17 | 10.82 | 6 | 11 | 14 | 21 |
| 1 | 10.25 | 8.51 | 3 | 6 | 11 | 15 | 8.98 | 4.12 | 4 | 7 | 9 | 12 |
| 1.5 | 5.25 | 3.79 | 2 | 3 | 5 | 7 | 4.82 | 1.98 | 2 | 4 | 5 | 7 |
| 2 | 3.26 | 1.18 | 1 | 2 | 3 | 4 | 2.99 | 1.09 | 1 | 2 | 3 | 4 |
| Scheme I | Scheme II | |||||||
|---|---|---|---|---|---|---|---|---|
| = 0.1 = 2.556 | = 0.25 = 2.554 | = 0.5 = 2.36 | = 0.75 = 2.115 | = 0.1 = 2.3 | = 0.25 = 2.345 | = 0.5 = 2.202 | = 0.75 = 1.982 | |
| 0 | 500.76 | 502.25 | 499.02 | 502.18 | 501.88 | 498.43 | 500.68 | 501.59 |
| 0.25 | 103.34 | 169.15 | 237.12 | 280.17 | 66.87 | 96.87 | 133.77 | 155.72 |
| 0.5 | 29.75 | 47.32 | 79.46 | 108.89 | 21.62 | 32.24 | 46.39 | 56.88 |
| 0.75 | 14.27 | 18.38 | 30.85 | 45.35 | 11.83 | 14.49 | 20.26 | 26.46 |
| 1 | 8.98 | 10.84 | 15.07 | 22.13 | 7.85 | 7.98 | 11.29 | 13.82 |
| 1.5 | 4.97 | 5.29 | 6.14 | 7.79 | 4.48 | 4.73 | 5.18 | 5.84 |
| 2 | 3.45 | 3.56 | 3.72 | 3.98 | 3.54 | 3.58 | 3.62 | 3.78 |
| Sample No. | ||||||
|---|---|---|---|---|---|---|
| 1 | −0.4349 | 0.0063 | 0.0150 | 0 | 0 | 0.2333 |
| 2 | −0.4739 | 0.0032 | 0.0168 | 0 | 0 | 0.2608 |
| 3 | −0.9013 | −0.0085 | 0.0172 | 0 | 0 | 0.2673 |
| 4 | 0.6214 | −0.0226 | 0.0173 | 0 | 0.0053 | 0.2689 |
| 5 | 0.4051 | −0.0346 | 0.0173 | 0 | 0.0225 | 0.2692 |
| 6 | 0.8579 | −0.0326 | 0.0173 | 0 | 0.0378 | 0.2693 |
| 7 | 0.6719 | −0.0325 | 0.0173 | 0 | 0.0530 | 0.2694 |
| 8 | −1.9477 | −0.0293 | 0.0173 | 0 | 0.0650 | 0.2694 |
| 9 | 0.1620 | −0.0273 | 0.0173 | 0 | 0.0749 | 0.2694 |
| 10 | 0.8997 | −0.0248 | 0.0173 | 0 | 0.0824 | 0.2694 |
| 11 | −1.0975 | −0.0078 | 0.0173 | 0 | 0.0729 | 0.2694 |
| 12 | −1.0499 | 0.0032 | 0.0173 | 0 | 0.0523 | 0.2694 |
| 13 | 0.1022 | 0.0183 | 0.0173 | 0.0009 | 0.0167 | 0.2694 |
| 14 | 0.8610 | 0.0306 | 0.0173 | 0.0142 | 0 | 0.2694 |
| 15 | −0.2477 | 0.0354 | 0.0173 | 0.0323 | 0 | 0.2694 |
| 16 | 0.5758 | 0.0351 | 0.0173 | 0.0500 | 0 | 0.2694 |
| 17 | −1.0004 | 0.0343 | 0.0173 | 0.0670 | 0 | 0.2694 |
| 18 | 2.6021 | 0.0239 | 0.0173 | 0.0735 | 0 | 0.2694 |
| 19 | −0.3164 | 0.0124 | 0.0173 | 0.0686 | 0 | 0.2694 |
| 20 | −0.2892 | −0.0023 | 0.0173 | 0.0490 | 0 | 0.2694 |
| 21 | 1.2362 | 0.0058 | 0.0173 | 0.0375 | 0 | 0.2694 |
| 22 | 0.4803 | 0.0029 | 0.0173 | 0.0231 | 0 | 0.2694 |
| 23 | 0.4866 | −0.0033 | 0.0173 | 0.0024 | 0 | 0.2694 |
| 24 | −0.4928 | −0.0101 | 0.0173 | 0 | 0 | 0.2694 |
| 25 | 1.5063 | −0.0135 | 0.0173 | 0 | 0 | 0.2694 |
| 26 | 0.7896 | −0.0110 | 0.0173 | 0 | 0 | 0.2694 |
| 27 | −0.0107 | −0.0059 | 0.0173 | 0 | 0 | 0.2694 |
| 28 | −0.4599 | 0.0168 | 0.0173 | 0 | 0 | 0.2694 |
| 29 | 1.1920 | 0.0297 | 0.0173 | 0.0123 | 0 | 0.2694 |
| 30 | 0.6065 | 0.0409 | 0.0173 | 0.0359 | 0 | 0.2694 |
| 31 | 1.9126 | 0.0477 | 0.0173 | 0.0663 | 0 | 0.2694 |
| 32 | 0.9250 | 0.0584 | 0.0173 | 0.1074 | 0 | 0.2694 |
| 33 | 0.5797 | 0.0641 | 0.0173 | 0.1542 | 0 | 0.2694 |
| 34 | 1.8840 | 0.0666 | 0.0173 | 0.2034 | 0 | 0.2694 |
| 35 | 0.8481 | 0.0717 | 0.0173 | 0.2579 | 0 | 0.2694 |
| 36 | −2.1358 | 0.0679 | 0.0173 | 0.3084 | 0 | 0.2694 |
| 37 | 1.6618 | 0.0634 | 0.0173 | 0.3545 | 0 | 0.2694 |
| 38 | −0.3279 | 0.0447 | 0.0173 | 0.3818 | 0 | 0.2694 |
| 39 | −0.1319 | 0.0233 | 0.0173 | 0.3878 | 0 | 0.2694 |
| 40 | −0.5497 | 0.0054 | 0.0173 | 0.3759 | 0 | 0.2694 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaudhary, A.M.; Sanaullah, A.; Hanif, M.; Almazah, M.M.A.; Albasheir, N.A.; Al-Duais, F.S. Efficient Monitoring of a Parameter of Non-Normal Process Using a Robust Efficient Control Chart: A Comparative Study. Mathematics 2023, 11, 4157. https://doi.org/10.3390/math11194157
Chaudhary AM, Sanaullah A, Hanif M, Almazah MMA, Albasheir NA, Al-Duais FS. Efficient Monitoring of a Parameter of Non-Normal Process Using a Robust Efficient Control Chart: A Comparative Study. Mathematics. 2023; 11(19):4157. https://doi.org/10.3390/math11194157
Chicago/Turabian StyleChaudhary, Aamir Majeed, Aamir Sanaullah, Muhammad Hanif, Mohammad M. A. Almazah, Nafisa A. Albasheir, and Fuad S. Al-Duais. 2023. "Efficient Monitoring of a Parameter of Non-Normal Process Using a Robust Efficient Control Chart: A Comparative Study" Mathematics 11, no. 19: 4157. https://doi.org/10.3390/math11194157
APA StyleChaudhary, A. M., Sanaullah, A., Hanif, M., Almazah, M. M. A., Albasheir, N. A., & Al-Duais, F. S. (2023). Efficient Monitoring of a Parameter of Non-Normal Process Using a Robust Efficient Control Chart: A Comparative Study. Mathematics, 11(19), 4157. https://doi.org/10.3390/math11194157






