Homogeneously Weighted Moving Average Control Charts: Overview, Controversies, and New Directions
Abstract
1. Introduction
- (i)
- (ii)
- (iii)
- (iv)
- (v)
2. The Weight Function of the Most Popular Charts
3. The Basic Properties of the HWMA and Enhanced HWMA Charts
3.1. Design of the HWMA and Enhanced HWMA Charts
3.2. Performance Evaluation
| Chart | Charting Statistics | Design Parameters | Time-Varying Control Limits | Asymptotic Control Limits |
|---|---|---|---|---|
| HWMA | and | > 0, | and | and |
| HHWMA | where and | 0, | and where | and with |
| THWMA | > 0, | and where | and | |
| HWMA–CUSUM | and | 0, , 0 | ||
| CUSUM–HWMA | and where and | > 0, , | and | and |
3.3. Outline of the Review
- (i)
- The process characteristic being monitored, i.e., the location (L), variability (V), both the location and variability (LV), or profile monitoring (P), e.g., for monitoring regression parameters and/or the regression error variance;
- (ii)
- Whether the charts are parametric (Par) or nonparametric (NPar);
- (iii)
- The design of the chart, i.e., economic (E), statistical (S), or economic statistical design (ESD);
- (iv)
- Whether the underlying process parameters are known or unknown, i.e., Case K or Case U;
- (v)
- The dimension of the process, i.e., univariate (Uni) or multivariate (Multi);
- (vi)
- Whether the observations are i.i.d (IID) or autocorrelated (AC);
- (vii)
- With measurement error (ME);
- (viii)
- The mode, i.e., either zero-state (ZS) or steady-state (SS);
- (ix)
- The type of data used in the illustrative examples, i.e., simulated (Sim) or real-life (Real) data;
- (x)
- The number of citations (NC);
- (xi)
- The performance metrics as discussed and used in the design;
- (xii)
- The type of chart;
- (xiii)
- The journal where the paper was published.
| Articles | L, V, LV, P | Par or NPar | E, SD, ESD | K | U | Dimension | IID | AC | ME | NC | Data | Mode | Performance Metrics | Type of HWMA Chart | Journal |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Abbas [3] | L | Par | SD | 🗸 | 🗸 | Uni | 🗸 | 94 | Real | ZS | ARL, SDRL | HWMA | CIE | ||
| Adegoke et al. [43] | L | Par | SD | 🗸 | 🗸 | Uni | 🗸 | 52 | Sim | ZS | ARL, SDRL | HWMA with AIB | IEEE Access | ||
| Adegoke et al. [48] | L | Par | SD | 🗸 | Multi | 🗸 | 43 | Sim, Real | ZS | ARL, SDRL | IEEE Access | ||||
| Nawaz and Han [49] | L | Par | SD | 🗸 | Uni | 🗸 | 32 | Real | ZS | ARL | HWMA using RSS | QTQM | |||
| Abbas et al. [42] | L | Par | SD | 🗸 | Multi | 🗸 | 🗸 | 12 | Real | ZS | ARL | Mathematics | |||
| Abid et al. [25] | L | Par | SD | 🗸 | 🗸 | Uni | 🗸 | 35 | Real | ZS | ARL, SDRL, MRL | DHWMA | QREI | ||
| Abid et al. [26] | L | Par | SD | 🗸 | Uni | 🗸 | 25 | Real | ZS | ARL, SDRL, PRL | HWMA–CUSUM | QREI | |||
| Abid et al. [50] | L | Par | SD | 🗸 | Uni | 🗸 | 8 | Real | ZS | ARL, SDRL, PRL | CUSUM–HWMA | QREI | |||
| Adeoti and Koleoso [51] | L | Par | SD | 🗸 | Uni | 🗸 | 24 | Sim | ZS | ARL, SDRL | HHWMA | QREI | |||
| Raza et al. [52] | L | NPar | SD | 🗸 | Uni | 🗸 | 19 | Real | ZS | ARL, SDRL, MRL, EQL | HWMA SN and SR | JTE | |||
| Riaz et al. [53] | L | NPar | SD | 🗸 | Uni | 🗸 | 16 | Real | ZS | ARL | DHWMA SN | QREI | |||
| Riaz et al. [41] | V | Par | SD | 🗸 | Uni | 🗸 | 17 | Real | ZS | ARL, SDRL, MDRL | Mathematics | ||||
| Dawod et al. [54] | P | Par | SD | 🗸 | Multi | 🗸 | 14 | Real | ZS | ARL | HWMA profiles | CLS | |||
| Thanwane et al. [36] | L | Par | SD | 🗸 | Uni | 🗸 | 🗸 | 11 | Real | ZS | ARL, EARL | HWMA | TIMC | ||
| Thanwane et al. [40] | L | Par | SD | 🗸 | Uni | 🗸 | 🗸 | 🗸 | 7 | Real | ZS | ARL, SDRL, EARL, ESDRl | HWMA | IEEE Access | |
| Thanwane et al. [37] | L | Par | SD | 🗸 | Uni | 🗸 | 6 | Real | ZS | ARL, SDRL, EARL, ESDRl | HWMA with FIR | QREI | |||
| Thanwane et al. [38] | L | Par | SD | 🗸 | Uni | 🗸 | 2 | Real | ZS | ARL, SDRL, EARL, ESDRl, PCI | HWMA | IJIEC | |||
| Thanwane et al. [39] | L | Par | SD | 🗸 | Uni | 🗸 | 🗸 | 13 | Real | ZS | ARL, EARL | HWMA | JSCS | ||
| Alevizakos et al. [22] | L | Par | SD | 🗸 | Uni | 🗸 | 13 | Real, Sim | ZS | ARL, SDRL, AEQL, PCI, RMI | DHWMA & HHWMA | QREI | |||
| Alevizakos et al. [23] | L | NPar | SD | 🗸 | Uni | 🗸 | 2 | Real, Sim | ZS | ARL, SDRL, MRL, AEQL | DHWMA SN | QREI | |||
| Riaz et al. [24] | L | Par | SD | 🗸 | Uni | 🗸 | 14 | Real | ZS,SS | ARL, SDRL, MDRL | THWMA | Symmetry | |||
| Malela-Majika et al. [35] | L | Par | SD | 🗸 | Multi | 🗸 | 3 | - | ZS | ARL, SDRL, MRL | HHWMA | QREI | |||
| Adegoke et al. [55] | L | Par | SD | 🗸 | Uni | 🗸 | 0 | Real | ZS | ARL, SDRL | DSHWMA | QREI | |||
| Adegoke et al. [56] | L | Par | SD | 🗸 | Multi | 🗸 | 2 | Real | ZS,SS | ARL, SDRL | MHWMA | IEEE Access | |||
| Noor-ul-Amin and Noor [57] | L | Par | SD | 🗸 | Uni | 🗸 | 1 | Real | ZS | ARL, SDRL | HWMA BTB | QREI | |||
| Adeoti et al. [58] | LV | Par | SD | 🗸 | Uni | 🗸 | 10 | Real, Sim | ZS | ARL, SDRL, MRL | HWMA (COM-Poisson) | JAS | |||
| Knoth et al. [44] | L | Par | SD | 🗸 | Uni | 🗸 | 24 | - | ZS,SS | ARL (CED) | HWMA with PM | QREI | |||
| Chan et al. [59] | LV | NPar | SD | 🗸 | Uni | 🗸 | 16 | Real | ZS | ARL, EARL, PRL | DEWMA–HWMA | CIE | |||
| Abbasi et al. [60] | V | Par | SD | 🗸 | Uni | 🗸 | 3 | Real | ARL, SDRL, MRL, EQL, RARL | HWMA dispersion | QREI | ||||
| Abbasi et al. [61] | P | Par | SD | 🗸 | Uni | 🗸 | 3 | Real | ZS | ARL | HWMA profile | QREI | |||
| Rasheed et al. [62] | L | Par | SD | 🗸 | Multi | 🗸 | 10 | Real | ZS | ARL, EQL, RARL, PCI | MHWHC, MHCHW | MPE | |||
| Riaz et al. [63] | L | Par | SD | 🗸 | Uni | 🗸 | 8 | - | ZS,SS | ARL | HWMA | Processes | |||
| Aslam et al. [64] | L | Par | SD | 🗸 | Uni | 🗸 | 1 | Real | ZS | ARL, SDRL, EQL, RARL, PCI | HWMA TBE | QREI | |||
| Anwar et al. [65] | L | Par | SD | 🗸 | Uni | 🗸 | 14 | Real | ZS | ARL, RARL, EQL, PCI | DHWMA | QREI | |||
| Letshedi et al. [7] | L | NPar | SD | 🗸 | Uni | 🗸 | 0 | Real | ZS | ARL, SDRL, EARL, ESDRL | HWMA and HHWMA | PLoS one | |||
| Anwar et al. [66] | L | Par | SD | 🗸 | Uni | 🗸 | 0 | Real | ZS | ARL, SDRL, MRL, EQL, RARL, PCI | THWMA AIB | MPE | |||
| Al-Sayed et al. [67] | LV | Par | SD | 🗸 | Uni | 🗸 | 0 | Real | ZS | ARL, RMI | PR–HWMA, PR–DHWMA (ZIP) | IEEE ICIEEM | |||
| Rasheed et al. [68] | L | NPar | SD | 🗸 | Uni | 🗸 | 8 | Real | ZS | ARL, SDRL, MRL | DHWMA SR (RSS) | MPE | |||
| Chong et al. [69] | L | Par | SD | 🗸 | Uni | 🗸 | 0 | - | ZS | ARL, SDRL, PRL, EARL, EMRL | HWMA, DHWMA | IEEE ICIEEM | |||
| Iqbal et al. [70] | LV | Par | SD | 🗸 | Uni | 🗸 | 13 | Real | ZS | ARL, SDRL | HWMA and DHWMA DR, SDR | Symmetry | |||
| Zhang et al. [71] | L | NPar | SD | 🗸 | Uni | 🗸 | 2 | Real | ZS | ARL, SDRL, MRL | THWMA SR | MPE | |||
| Lone et al. [72] | L | Par | SD | 🗸 | Uni | 🗸 | 3 | Real | ZS | ARL, SDRL, EQL, RARL, PCI | THWMA TBE | AIMS Mathematics | |||
| Arslan et al. [73] | L | Par | SD | 🗸 | Multi | 🗸 | 3 | Real, Sim | ZS | ARL, EQL, RMI | TAHWMA | Symmetry | |||
| Yousefi et al. [74] | L | Par | SD | 🗸 | Multi | 🗸 | 🗸 | 4 | Real | ZS | ARL, SDRL | MHWMA | JAMS | ||
| Almanjahie et al. [75] | L | NPar | SD | 🗸 | Uni | 🗸 | 1 | Real | ZS | ARL, SDRL, MRL, EQL, RARL, PCI | HWMA SR | CMES | |||
| Noor-ul-Amin and Arshad [76] | L | Par | SD | 🗸 | Uni | 🗸 | 0 | Real | ZS | ARL, SDRL | HWMA AIB | CS-SC | |||
| Anwer et al. [77] | L | Par | SD | 🗸 | Uni | 🗸 | 1 | Real | ZS | ARL, PDARL | HWMA–CUSUM AIB | JSCS | |||
| Knoth [78] | L | Par | SD | 🗸 | Uni | 🗸 | 0 | - | SS | ARL, CED | HWMA | QREI | |||
| Knoth et al. [47] | L | Par | SD | 🗸 | Uni | 🗸 | 16 | - | ZS,SS | CED | Memory-type | JQT | |||
| Khan et al. [79] | V | Par | SD | 🗸 | Uni | 🗸 | 0 | Real | ZS | ARL, SDRL, EQL, RARL, PCI | THWMAV | MPE | |||
| Pieters et al. [80] | L | Par | SD | 🗸 | Multi | 🗸 | 1 | Real | ZS,SS | ARL, SDRL | MEHWMA | QREI | |||
| Ghasemi et al. [81] | P | Par | SD | 🗸 | Multi | 🗸 | 0 | Sim | ZS | ARL | MHWMA | CS-SC | |||
| Zubair et al. [82] | L | Par | SD | 🗸 | Uni | 🗸 | 0 | Sim | ZS | ARL, SDRL, MRL | HWMA–CUSUM: AIB | PLoS one | |||
| Shafqat et al. [83] | L | NPar | SD | 🗸 | 🗸 | Uni | 🗸 | 0 | Sim | ZS | ARL, SDRL, MRL | EWMA and HWMA SR: RS and AIB | Scientific Report | ||
| Sunthornwat et al. [84] | L | Par | SD | 🗸 | Uni | 🗸 | 0 | Real | ZS | ARL, SDRL, MRL, EARL, EMRL | Max HWMA | Symmetry |
4. HWMA and Enhanced HWMA Charts
4.1. HWMA Charts
- -
- Parametric HWMA Charts
4.1.1. Location
4.1.2. Variability
4.1.3. Joint Location and Variability
4.1.4. Profile
- -
- Nonparametric HWMA Charts
4.1.5. Location
4.1.6. Joint Location and Scale
4.2. DHWMA and HHWMA Charts
- -
- Parametric DHWMA and HHWMA Charts
4.2.1. Location
4.2.2. Joint Location and Variability
- -
- Nonparametric DHWMA and HHWMA Charts
4.2.3. Location
4.3. THWMA Charts
- -
- Parametric THWMA Charts
4.3.1. Location
4.3.2. Variability
- -
- Nonparametric THWMA and HHWMA Charts
4.3.3. Location
4.4. HWMA–CUSUM and CUSUM–HWMA Charts
- -
- Parametric HWMA Charts
4.4.1. Location
4.5. Multivariate Classical and Enhanced HWMA Charts
4.5.1. Location
4.5.2. Profile
4.6. Other HWMA-Type Charts
5. Controversies on the Practicality of the HWMA Chart
5.1. Mathematical Background of the CED Metric
5.2. CED Performance Comparison
6. Conclusions, Recommendation, Future Research Work, and New Directions
- (i)
- Most quality characteristics are dependent on one or more independent variables. In this case, profile monitoring can be used. However, only three articles on profile monitoring are available in the literature; hence, researchers interested in profile monitoring can construct charts using different regression models and investigate their performance.
- (ii)
- Parametric and nonparametric HWMA charts with unknown process parameters under the assumption of i.i.d. and correlated observations are scarce. More research and thorough investigations regarding the performances of these types of charts are required.
- (iii)
- No publications in nonparametric statistical monitoring for compound HWMA-type charts exist; hence, more research needs to be conducted to address this gap.
- (iv)
- To enhance the literature on HWMA charts, researchers are encouraged to conduct additional research focusing on parametric and nonparametric HWMA charts with unknown process parameters, particularly under the assumptions of i.i.d. and correlated observations. A comprehensive exploration study about the zero- and steady-state performances of these types of charts would significantly contribute to the existing body of knowledge.
- (v)
- The literature has various parametric and nonparametric synthetic charts using structured and unstructured sampling techniques (e.g., RSS, VSS, variable sample size and interval (VSSI), etc.). However, there is no work on synthetic HWMA and HWMA-related charts. Interested researchers can investigate this topic using different sampling structures.
- (vi)
- Measurement errors (or imperfect measurements) are widespread in SPC applications and have been shown to harm the performance of any chart. Only the performance of the standard HWMA chart has been investigated under imperfect measurements. Thus, researchers are encouraged to consider this when designing extended and compound HWMA-type charts.
- (vii)
- There are few parametric and nonparametric HWMA-type charts for joint monitoring of the process mean and variability (or process location and scale). Researchers are encouraged to use different test statistics to construct new HWMA-type charts.
- (viii)
- Evaluating the characteristics of the run-length of charts using exact formulae, is critical; hence, more research on these topics is needed to simplify the evaluation of the run-length properties of the HWMA and HWMA-related charts.
- (ix)
- The application of the HWMA-type charts in practice in various disciplines such as healthcare services and engineering is recommended.
- (x)
- Only a few attribute HWMA charts have been proposed in the literature. More investigations on attribute HWMA charts as well as high-yield processes are needed.
- (xi)
- There is no study on the economic and economic–statistical designs of the HWMA-type charts. Therefore, researchers are encouraged to investigate these topics under the assumption of i.i.d, serial dependency, perfect and imperfect measurements, and the combined effect of autocorrelation and measurement errors.
- (xii)
- Only three publications on multivariate HWMA charts are available in the literature. Given the relevance of multivariate charts in applications, there is a lot of research on HWMA-type charts that can be conducted based on parametric and nonparametric settings for monitoring the location, variability, profile, joint location, and variability of multivariate processes.
- (xiii)
- Researchers are advised to consider the weight structure when designing memory-type charts. The best weight structure will likely be the one that allocates small weights to previous samples.
- (xiv)
- In practice, most applications are characterized by several quality characteristics that depend on one or several variables; in such cases, charts for multivariate profiles are more appropriate. Table 2 and Table 3 show that there is a significant gap in the literature concerning the HWMA-related charts for monitoring multivariate processes. Thus, researchers are encouraged to design efficient classical multivariate charts as well as linear and nonlinear profile HWMA charts considering the effect of multicollinearity and dependence structure.
- (xv)
- Recent advances in information technology (IT) have enabled researchers to collect, store, and easily access large volumes of data at a modest cost. Researchers are encouraged to look at the design of multivariate HWMA-related charts for monitoring high-dimensional profile data.
- (xvi)
- Researchers are encouraged to continue the collaborative dialogue between critics and proponents of the HWMA chart, fostering a comprehensive understanding of its strengths and limitations. This inclusive approach will contribute to addressing research gaps and improve the overall quality of research in the field of SPC.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Simulation Algorithm
| Step | Zero-State Mode | Steady-State Mode | |
| Stage 1—Search for the optimal value of : | |||
| 1 | Specify the value, the sample size (n), the number of simulations (), the smoothing parameter (), and the parameters of the distribution. | Specify the value of , the value, the sample size (n), the number of simulations (), the smoothing parameter (), and the parameters of the distribution. | |
| 2 | (a) Set to some value, compute the control limits, and proceed to Step 3. (b) Whenever necessary, increase (or decrease) the value, then recompute the control limits to attain an IC value that approaches . | ||
| 3 | Generate a random sample from the N(0,1) distribution. Compute the charting statistic and compare it to the control limits found in Step 2. When the charting statistic plots between the control limits, generate the next sample, calculate its charting statistic, and compare it with the control limits. Continue this process until a charting statistic plots on or outside the control limits. This means that the process has gone OOC. Record the number of samples generated until an OOC signal occurs. This number represents one simulated value of the IC run-length distribution. | Generate a random sample from the N(0,1) distribution. Compute the charting statistic and compare it to the control limits found in Step 2. When the charting statistic plots between the control limits, generate the next sample, calculate its charting statistic, and compare it with the control limits. Continue this process until a charting statistic plots on or outside the control limits provided . This means that the process has gone OOC. Record the number of samples, , generated until an OOC signal occurs. Then, calculate . This value represents one simulated value of the IC run-length distribution. | |
| 4 | Repeat Step 3 a total of times to find the IC run-length vector of simulated observations () | ||
| 5 | Once the vector is obtained, we compute the average, which we call the attained IC value, i.e., | ||
| (A1) | |||
| If the attained IC value is equal or much closer to the , go to Step 6. Otherwise, if the attained IC is considerably smaller (greater) than the value, then go back to Step 2 (b) to update the control limits to be wider (narrower) by increasing (decreasing) the value. Note that the variance of the point estimator in Equation (A1) decreases as the number of simulations increases. | |||
| 6 | The latest value of used in Step 5 is considered as the optimal design parameter. Record the optimal value and the corresponding control limits. Thus, the search for the optimal is completed. | ||
| Stage 2—Computation of the characteristics of the OOC run-length: | |||
| 7 | Specify a nonzero value of i.e., 0, which represents the size of the shift in the process mean. | ||
| 8 | Generate a random sample from the N(,1) distribution. Then, compute its charting statistic and compare it to the control limits found in Step 6. When the charting statistic plots between the control limit, generate the next sample, calculate its charting statistic, and compare it with the control limits. Continue this process until a charting statistic plots on or outside the control limits. When this happens, record the number of samples generated until an OOC signal occurs. This number represents one value of the OOC run-length distribution. | Generate a random sample from the N(,1) distribution. Then, compute its charting statistic and compare it to the control limits found in Step 6. When the charting statistic plots between the control limits then generate the next sample, calculate its charting statistic, and compare it with the control limits. Continue this process until a charting statistic plots on or outside the control limits provided . When this happens, record the number of samples, , generated until an OOC signal occurs. Then, calculate . This number represents one simulated value of the OOC run-length distribution. | |
| 9 | Repeat Step 8 a total of times to find the OOC run-length vector of simulated observations (). | ||
| 10 | One the vector is obtained, compute the attained OOC () value as | ||
| (A2) | |||
| This value represents the value for a shift of standard deviation. | |||
Appendix B. List of Acronyms
| Acronyms | Description |
| AEQL | Average extra quadratic loss |
| AIB | Auxiliary information based |
| ARL | Average run-length |
| CED | Conditional expected delay |
| CIE | Computers & Industrial Engineering |
| CLS | Chemometrics and Laboratory Systems |
| CMES | Computer Modeling in Engineering & Sciences |
| CMP | Conway–Maxwell–Poisson |
| CS-SC | Communications in Statistics-Simulation and Computation |
| CUSUM | Cumulative sum |
| DEWMA | Double exponentially weighted moving average |
| DGWMA | Double generally weighted moving average |
| DHWMA | Double homogeneously weighted moving average |
| DR | Deviance residuals |
| EARL | Expected average run-length |
| EEWMA | Extended exponentially weighted moving average |
| EMRL | Expected median run-length |
| EQL | Extra quadratic loss |
| ESD | Economic statistical design |
| ESDRL | Expected standard deviation of the run-length |
| EWMA | Exponentially weighted moving average |
| GLM | Generalized linear model |
| GWMA | Generally weighted moving average |
| HHWMA | Hybrid homogeneously weighted moving average |
| HWMA | Homogeneously weighted moving average |
| IC | In-control |
| IEEE ICIEEM | IEEE International Conference on Industrial Engineering and Engineering Management |
| i.i.d. | Independent and identically distributed |
| IJIEC | International Journal of Industrial Engineering Computations |
| JAMS | Journal of Advanced Manufacturing Systems |
| JAS | Journal of Applied Statistics |
| JCR | Journal citation reports |
| JQT | Journal of Quality Technology |
| JSCS | Journal of Statistical Computation and Simulation |
| JTE | Journal Testing and Evaluation |
| MCE | Mixed CUSUM–EWMA |
| MCH | Mixed CUSUM–HWMA |
| MCUSUM | Multivariate cumulative sum |
| ME | Measurement error |
| MEC | Mixed EWMA–CUSUM |
| MEEWMA | Multivariate extended exponentially weighted moving average |
| MEHWMA | Multivariate extended homogeneously weighted moving average |
| MHC | Mixed HWMA–CUSUM |
| MHWMA | Multivariate homogeneously weighted moving average |
| ModEWMA | Modified exponentially weighted moving average |
| MPE | Mathematical Problems in Engineering |
| MRL | Median run-length |
| NC | Number of citations |
| OOC | Out-of-control |
| PCI | Performance comparison index |
| PDARL | Percentage decrease average run-length |
| PR | Pearson residual |
| PRL | Percentile of the run-length |
| QEWMA | Quadruple exponentially weighted moving average |
| QREI | Quality and Reliability Engineering International |
| QTQM | Quality Technology & Quantitative Management |
| RARL | Relative average run-length |
| RMI | Relative mean index |
| RS | Repetitive sampling |
| RSS | Ranked set sampling |
| SD | Statistical design |
| SDRL | Standard deviation of the run-length |
| SPC | Statistical process control |
| SPM | Statistical process monitoring |
| SR | Signed-rank |
| SS | Steady-state |
| SSARL | Steady-state average run-length |
| TBE | Time between events |
| TEWMA | Triple exponentially weighted moving average |
| THWMA | Triple homogeneously weighted moving average |
| TIMC | Transactions of the Institute of Measurement and Control |
| WRS | Wilcoxon rank-sum |
| ZIP | Zero-inflated Poisson |
| ZS | Zero-state |
| ZSARL | Zero-state average run-length |
References
- Page, E. Continuous inspection schemes. Biometrika 1954, 41, 100–115. [Google Scholar] [CrossRef]
- Roberts, S.W. Control chart tests based on geometric moving averages. Technometrics 1959, 1, 239–250. [Google Scholar] [CrossRef]
- Abbas, N. Homogeneously weighted moving average control chart with an application in substrate manufacturing process. Comput. Ind. Eng. 2018, 120, 460–470. [Google Scholar] [CrossRef]
- Haq, A.; Munir, T.; Khoo, M.B.C. Dual multivariate CUSUM mean charts. Comput. Ind. Eng. 2019, 137, 106028. [Google Scholar] [CrossRef]
- Haq, A.; Munir, T.; Shah, B.A. Dual multivariate CUSUM charts with auxiliary information for process mean. Qual. Reliab. Eng. Int. 2020, 36, 861–875. [Google Scholar] [CrossRef]
- Lee, M.H.; Khoo, M.B.C. Optimal statistical designs of a multivariate CUSUM chart based on ARL and MRL. Int. J. Reliab. Qual. Saf. Eng. 2006, 13, 479–497. [Google Scholar] [CrossRef]
- Letshedi, T.I.; Malela-Majika, J.-C.; Shongwe, S.C. New extended distribution-free homogenously weighted monitoring schemes for monitoring abrupt shifts in the location parameter. PLoS ONE 2022, 17, e0261217. [Google Scholar] [CrossRef] [PubMed]
- Lowry, C.A.; Woodall, W.H.; Champ, C.W.; Rigdon, S.E. A multivariate exponentially weighted moving average control chart. Technometrics 1992, 34, 46–53. [Google Scholar] [CrossRef]
- Montgomery, D.C. Introduction to Statistical Quality Control, 8th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2020; ISBN 978-1-119-72309-7. [Google Scholar]
- Shamma, S.E.; Shamma, A.K. Development and evaluation of control charts using double exponentially weighted moving averages. Int. J. Qual. Reliab. Manag. 1992, 9, 18–26. [Google Scholar] [CrossRef]
- Sheu, S.-H.; Lin, T.-C. The generally weighted moving average control chart for detecting small shifts in the process mean. Qual. Eng. 2003, 16, 209–231. [Google Scholar] [CrossRef]
- Srivastava, M.S.; Wu, Y. Evaluation of optimum weights and average run lengths in EWMA control schemes. Commun. Stat. Theory Methods 1997, 26, 1253–1267. [Google Scholar] [CrossRef]
- Alevizakos, V.; Chatterjee, K.; Koukouvinos, C. The triple exponentially weighted moving average control chart. Qual. Technol. Quant. Manag. 2021, 18, 326–354. [Google Scholar] [CrossRef]
- Alevizakos, V.; Chatterjee, K.; Koukouvinos, C. The quadruple exponentially weighted moving average control chart. Qual. Technol. Quant. Manag. 2022, 19, 50–73. [Google Scholar] [CrossRef]
- Alkahtani, S.; Schaffer, J.A. Double multivariate exponentially weighted moving average (dEWMA) control chart for a process location monitoring. Commun. Stat.-Simul. Comput. 2012, 41, 238–252. [Google Scholar] [CrossRef]
- Crosier, R.B. Multivariate generalizations of cumulative sum quality-control schemes. Technometrics 1988, 30, 291–303. [Google Scholar] [CrossRef]
- Haq, A.; Ali, Q. A maximum dual CUSUM chart for joint monitoring of process mean and variance. Qual. Technol. Quant. Manag. 2023. [Google Scholar] [CrossRef]
- Haq, A.; Syed, E.A. New CUSUM and dual CUSUM mean charts. Qual. Reliab. Eng. Int. 2021, 37, 1355–1372. [Google Scholar] [CrossRef]
- Wang, T.; Huang, S. An adaptive multivariate CUSUM control chart for signaling a range of location shifts. Commun. Stat. Theory Methods 2016, 45, 4673–4691. [Google Scholar] [CrossRef]
- Sheu, S.H.; Hsieh, Y.T. The extended GWMA control chart. J. Appl. Stat. 2009, 36, 135–147. [Google Scholar] [CrossRef]
- Phengsalae, Y.; Areepong, Y.; Sukparungsee, S. An Approximation of ARL for Poisson GWMA using Markov Chain Approach. Thail. Stat. 2015, 13, 111–124. [Google Scholar]
- Alevizakos, V.; Chatterjee, K.; Koukouvinos, C. The extended homogeneously weighted moving average control chart. Qual. Reliab. Eng. Int. 2021, 37, 2134–2155. [Google Scholar] [CrossRef]
- Alevizakos, V.; Chatterjee, K.; Koukouvinos, C. The extended nonparametric homogeneously weighted moving average sign control chart. Qual. Reliab. Eng. Int. 2021, 37, 3395–3416. [Google Scholar] [CrossRef]
- Riaz, M.; Abbas, Z.; Nazir, H.Z.; Abid, M. On the development of triple homogeneously weighted moving average control chart. Symmetry 2021, 13, 360. [Google Scholar] [CrossRef]
- Abid, M.; Mei, S.; Nazir, H.Z.; Riaz, M.; Hussain, S. A mixed HWMA-CUSUM mean chart with an application to manufacturing process. Qual. Reliab. Eng. Int. 2020, 37, 618–631. [Google Scholar] [CrossRef]
- Abid, M.; Shabbir, A.; Nazir, H.Z.; Sherwani, R.A.K.; Riaz, M. A double homogeneously weighted moving average control chart for monitoring of the process mean. Qual. Reliab. Eng. Int. 2020, 36, 1513–1527. [Google Scholar] [CrossRef]
- Ajadi, J.O.; Riaz, M. Mixed multivariate EWMA-CUSUM control charts for an improved process monitoring. Commun. Stat. Theory Methods 2017, 46, 6980–6993. [Google Scholar] [CrossRef]
- Osei-Aning, R.; Abbasi, S.A.; Riaz, M. Mixed EWMA-CUSUM and mixed CUSUM-EWMA for monitoring first order autoregressive processes. Qual. Technol. Quant. Manag. 2017, 14, 429–453. [Google Scholar] [CrossRef]
- Ottenstreuer, S.; Weiß, C.H.; Knoth, S. A combined Shewhart-CUSUM chart with switching limit. Qual. Eng. 2019, 31, 255–268. [Google Scholar] [CrossRef]
- Snyder, H. Literature Review as a Research Methodology: An Overview and Guidelines. J. Bus. Res. 2019, 104, 333–339. [Google Scholar] [CrossRef]
- Suman, G.; Prajapati, D.R. Control chart applications in healthcare: A literature review. Int. J. Metrol. Qual. Eng. 2018, 9, 5. [Google Scholar] [CrossRef]
- Císar, P.; Cisar, S.M. Optimization Methods of EWMA Statistics. Acta Polytech. Hung. 2012, 8, 73–87. [Google Scholar]
- Neuburger, J.; Walker, K.; Sherlaw-Johnson, C.; van der Meulen, J.; Cromwell, D.A. Comparison of control charts for monitoring clinical performance using binary data. BMJ Qual. Saf. 2017, 26, 919–928. [Google Scholar] [CrossRef]
- Vera do Carmo, C.; Lopes, L.F.D.; Souza, A.M. Comparative study of the performance of the CUSUM and EWMA control charts. Comput. Ind. Eng. 2004, 46, 707–724. [Google Scholar]
- Malela-Majika, J.-C.; Shongwe, S.C.; Adeoti, O.A. A hybrid homogeneously weighted moving average control chart for process monitoring: Discussion. Qual. Reliab. Eng. Int. 2021, 37, 3314–3322. [Google Scholar] [CrossRef]
- Thanwane, M.; Abbasi, S.A.; Malela-Majika, J.-C.; Aslam, M.; Shongwe, S.C. The use of fast initial response features on the homogeneously weighted moving average chart with estimated parameters under the effect of measurement errors. Qual. Reliab. Eng. Int. 2021, 37, 2568–2586. [Google Scholar] [CrossRef]
- Thanwane, M.; Malela-Majika, J.-C.; Castagliola, P.; Shongwe, S.C. The effect of measurement errors on the performance of the homogenously weighted moving average monitoring scheme with estimated parameters. J. Stat. Comput. Simul. 2021, 91, 1306–1330. [Google Scholar] [CrossRef]
- Thanwane, M.; Malela-Majika, J.-C.; Castagliola, P.; Shongwe, S.C. The effect of measurement errors on the performance of the homogenously weighted moving average monitoring scheme. Trans. Inst. Meas. Control 2021, 43, 728–745. [Google Scholar] [CrossRef]
- Thanwane, M.; Sandile, S.C.; Aslam, M.; Malela-Majika, J.-C.; Albassam, M. A homogenously weighted moving average scheme for observations under the effect of serial dependence and measurement inaccuracy. Int. J. Ind. Eng. Comput. 2021, 12, 401–414. [Google Scholar] [CrossRef]
- Thanwane, M.; Shongwe, S.C.; Malela-Majika, J.-C.; Aslam, M. Parameter estimation effect of the homogeneously weighted moving average chart to monitor the mean of autocorrelated observations with measurement errors. IEEE Access 2020, 8, 221352–221366. [Google Scholar] [CrossRef]
- Riaz, M.; Abbasi, S.A.; Abid, M.; Hamzat, A.K. A new HWMA dispersion control chart with an application to wind farm data. Mathematics 2020, 8, 2136. [Google Scholar] [CrossRef]
- Abbas, N.; Riaz, M.; Ahmad, S.; Abid, M.; Zaman, B. On the efficient monitoring of multivariate processes with unknown parameters. Mathematics 2020, 8, 823. [Google Scholar] [CrossRef]
- Adegoke, N.A.; Abbasi, S.A.; Smith, A.N.H.; Anderson, M.J.; Pawley, M.D.M. A multivariate homogeneously weighted moving average control chart. IEEE Access 2019, 7, 9586–9597. [Google Scholar] [CrossRef]
- Knoth, S.; Tercero-Gómez, V.G.; Khakifirooz, M.; Woodall, W.H. The impracticality of homogeneously weighted moving average and progressive mean control chart approaches. Qual. Reliab. Eng. Int. 2021, 37, 3779–3794. [Google Scholar] [CrossRef]
- Knoth, S. Steady-state average run length(s): Methodology, formulas, and numerics. Seq. Anal. 2012, 40, 405–426. [Google Scholar] [CrossRef]
- Kenett, R.; Pollak, M. On assessing the performance of sequential procedures for detecting a change. Qual. Reliab. Eng. Int. 2012, 28, 500–507. [Google Scholar] [CrossRef]
- Knoth, S.; Saleh, N.A.; Mahmoud, M.A.; Woodall, W.H.; Tercero-Gómez, V.G. A critique of a variety of “memory-based” process monitoring methods. J. Qual. Technol. 2023, 55, 18–42. [Google Scholar] [CrossRef]
- Adegoke, N.A.; Smith, A.N.H.; Anderson, M.J.; Sanusi, R.A.; Pawley, M.D.M. Efficient homogeneously weighted moving average chart for monitoring process mean using an auxiliary variable. IEEE Access 2019, 7, 94021–94032. [Google Scholar] [CrossRef]
- Nawaz, T.; Han, D. Monitoring the process location by using new ranked set sampling-based memory control charts. Qual. Technol. Quant. Manag. 2020, 17, 255–284. [Google Scholar] [CrossRef]
- Abid, M.; Mei, S.; Nazir, H.Z.; Riaz, M.; Hussain, S.; Abbas, Z. A mixed cumulative sum homogeneously weighted moving average control chart for monitoring process mean. Qual. Reliab. Eng. Int. 2021, 37, 1758–1771. [Google Scholar] [CrossRef]
- Adeoti, O.A.; Koleoso, S.O. A hybrid homogeneously weighted moving average control chart for process monitoring. Qual. Reliab. Eng. Int. 2020, 36, 2170–2186. [Google Scholar] [CrossRef]
- Raza, M.; Nawaz, T.; Han, D. On designing distribution-free homogeneously weighted moving average control charts. J. Test. Eval. 2020, 48, 3154–3171. [Google Scholar] [CrossRef]
- Riaz, M.; Abid, M.; Shabbir, A.; Nazir, H.Z.; Abbas, Z.; Abbasi, S.A. A non-parametric double homogeneously weighted moving average control chart under sign statistic. Qual. Reliab. Eng. Int. 2021, 37, 1544–1560. [Google Scholar] [CrossRef]
- Dawod, A.; Adegoke, N.A.; Abbasi, S.A. Efficient linear profile schemes for monitoring bivariate correlated processes with applications in the pharmaceutical industry. Chemom. Lab. Syst. 2020, 206, 104137. [Google Scholar] [CrossRef]
- Adegoke, N.A.; Ganiyu, K.O.; Abbasi, S.A. Directionally sensitive homogeneously weighted moving average control charts. Qual. Reliab. Eng. Int. 2021, 37, 3465–3492. [Google Scholar] [CrossRef]
- Adegoke, N.A.; Riaz, M.; Ganiyu, K.O.; Abbasi, S.A. One-sided and two one-sided multivariate homogeneously weighted moving charts for monitoring process mean. IEEE Access 2021, 9, 80388–80404. [Google Scholar] [CrossRef]
- Noor-ul-Amin, M.; Noor, S. Homogeneously weighted moving average control chart based on Bayesian theory. Qual. Reliab. Eng. Int. 2021, 37, 3617–3637. [Google Scholar] [CrossRef]
- Adeoti, O.A.; Malela-Majika, J.-C.; Shongwe, S.C.; Aslam, M. A homogeneously weighted moving average control chart for Conway–Maxwell Poisson distribution. J. Appl. Stat. 2022, 49, 3090–3119. [Google Scholar] [CrossRef] [PubMed]
- Chan, K.M.; Mukherjee, A.; Chong, Z.L.; Lee, H.C. Distribution-free double exponentially and homogeneously weighted moving average lepage schemes with an application in monitoring exit rate. Comput. Ind. Eng. 2021, 161, 107370. [Google Scholar] [CrossRef]
- Abbasi, S.A.; Nassar, S.H.; Aldosari, M.M.; Adeoti, O.A. Efficient homogeneously weighted dispersion control charts with an application to distillation process. Qual. Reliab. Eng. Int. 2021, 37, 3221–3241. [Google Scholar] [CrossRef]
- Abbasi, S.A.; Abbas, T.; Adegoke, N.A. Improved simple linear profiling method with application to chemical gas sensors. Qual. Reliab. Eng. Int. 2021, 37, 3179–3191. [Google Scholar] [CrossRef]
- Rasheed, Z.; Zhang, H.; Anwar, S.M.; Zaman, B. Homogeneously mixed memory charts with application in the substrate production process. Math. Probl. Eng. 2021, 2582210. [Google Scholar] [CrossRef]
- Riaz, M.; Ahmad, S.; Mahmood, T.; Abbas, N. On reassessment of the HWMA chart for process monitoring. Processes 2022, 10, 1129. [Google Scholar] [CrossRef]
- Aslam, M.; Khan, M.; Anwar, S.M.; Zaman, B. A homogeneously weighted moving average control chart for monitoring time between events. Qual. Reliab. Eng. Int. 2022, 38, 1013–1044. [Google Scholar] [CrossRef]
- Anwar, S.M.; Aslam, M.; Zaman, B.; Riaz, M. An enhanced double homogeneously weighted moving average control chart to monitor process location with application in automobile field. Qual. Reliab. Eng. Int. 2022, 38, 174–194. [Google Scholar] [CrossRef]
- Anwar, S.M.; Komal, S.; Cheema, A.N.; Abiodun, N.L.; Rasheed, Z.; Khan, M. Efficient control charting scheme for the process location with application in automobile Industry. Math. Probl. Eng. 2022, 2938878. [Google Scholar] [CrossRef]
- Al-Sayed, A.M.; Mahmood, T.; Saleh, H.H. Residual Based Control Charts for Zero-inflated Poisson Processes. In Proceedings of the 2022 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Kuala Lumpur, Malaysia, 7–10 December 2022; pp. 482–486. [Google Scholar] [CrossRef]
- Rasheed, Z.; Khan, M.; Abiodun, N.L.; Anwar, S.M.; Khalaf, G.; Abbasi, S.A. Improved nonparametric control chart based on ranked set sampling with application of chemical data modelling. Math. Probl. Eng. 2022, 2022, 7350204. [Google Scholar] [CrossRef]
- Chong, Z.L.; Chan, K.M.; Wang, J.; Malela-Majika, J.-C.; Shongwe, S.C. Overall performance comparison of homogeneously weighted moving average and double homogeneously weighted moving average schemes. In Proceedings of the 2021 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 13–16 December 2021; pp. 1225–1229. [Google Scholar]
- Iqbal, A.; Mahmood, T.; Ali, Z.; Riaz, M. On enhanced GLM-Based monitoring: An application to additive manufacturing process. Symmetry 2022, 14, 122. [Google Scholar] [CrossRef]
- Zhang, H.; Rasheed, Z.; Khan, M.; Namangale, J.J.; Anwar, S.M.; Hamid, A. A distribution-free THWMA control chart under ranked set sampling. Math. Probl. Eng. 2022, 2022, 3823013. [Google Scholar] [CrossRef]
- Lone, S.A.; Rasheed, Z.; Anwar, S.; Khan, M.; Anwar, S.M.; Shahab, S. Enhanced fault detection models with real-life applications. AIMS Math. 2023, 8, 19595–19636. [Google Scholar] [CrossRef]
- Arslan, M.; Anwar, S.; Gunaime, N.M.; Shahab, S.; Lone, S.A.; Rasheed, Z. An improved charting scheme to monitor the process mean using two supplementary variables. Symmetry 2023, 15, 482. [Google Scholar] [CrossRef]
- Yousefi, S.; Maleki, M.R.; Salmasnia, A.; Anbohi, M.K. Performance of multivariate homogeneously weighted moving average chart for monitoring the process mean in the presence of measurement errors. J. Adv. Manuf. Syst. 2023, 22, 27–40. [Google Scholar] [CrossRef]
- Almanjahie, I.M.; Rasheed, Z.; Khan, M.; Anwar, S.M.; Cheema, A.N. Ranked-set sampling based distribution free control chart with application in CSTR process. Comput. Model. Eng. Sci. 2023, 135, 2091–2118. [Google Scholar] [CrossRef]
- Noor-ul-Amin, M.; Arshad, A. Homogeneously weighted moving average-variance control chart using auxiliary information. Commun. Stat. Simul. Comput. 2023, 52, 4891–4908. [Google Scholar] [CrossRef]
- Anwer, F.; Sanaullah, A.; Ahmad, A.; Asghar, A. An improved mixed-homogeneously weighted moving average-CUSUM control chart for efficient monitoring of a process mean. J. Stat. Comput. Simul. 2023, 93, 1644–1666. [Google Scholar] [CrossRef]
- Knoth, S. Another objection to the homogeneously weighted moving average control chart. Qual. Reliab. Eng. Int. 2023, 39, 353–362. [Google Scholar] [CrossRef]
- Khan, M.; Rasheed, Z.; Anwar, S.M.; Namangale, J.J. Triple homogeneously weighted moving average charts for monitoring Process Dispersion. Math. Probl. Eng. 2023, 6996280. [Google Scholar] [CrossRef]
- Pieters, L.; Malela-Majika, J.-C.; Human, S.W.; Castagliola, P. A new multivariate extended homogeneously weighted moving average monitoring scheme incorporated with a support vector machine. Qual. Reliab. Eng. Int. 2023, 39, 2454–2475. [Google Scholar] [CrossRef]
- Ghasemi, Z.; Hamadani, A.H.; Yazdi, A.A. New methods for phase II monitoring of multivariate simple linear profiles. Commun. Stat. Simul. Comput. 2023, 1–25. [Google Scholar] [CrossRef]
- Zubair, F.; Sherwani, R.A.K.; Abid, M. Enhanced performance of mixed HWMA-CUSUM charts using auxiliary information. PLoS ONE 2023, 18, e0290727. [Google Scholar] [CrossRef]
- Shafqat, A.; Zhensheng, H.; Aslam, M. Efficient signed-rank based EWMA and HWMA repetitive control charts for monitoring process mean with and without auxiliary information. Sci. Rep. 2013, 13, 16459. [Google Scholar] [CrossRef] [PubMed]
- Sunthornwat, R.; Sukparungsee, S.; Areepong, Y. Analytical explicit formulas of average run length of homogenously weighted moving average control chart based on a MAX process. Symmetry 2023, 15, 2112. [Google Scholar] [CrossRef]

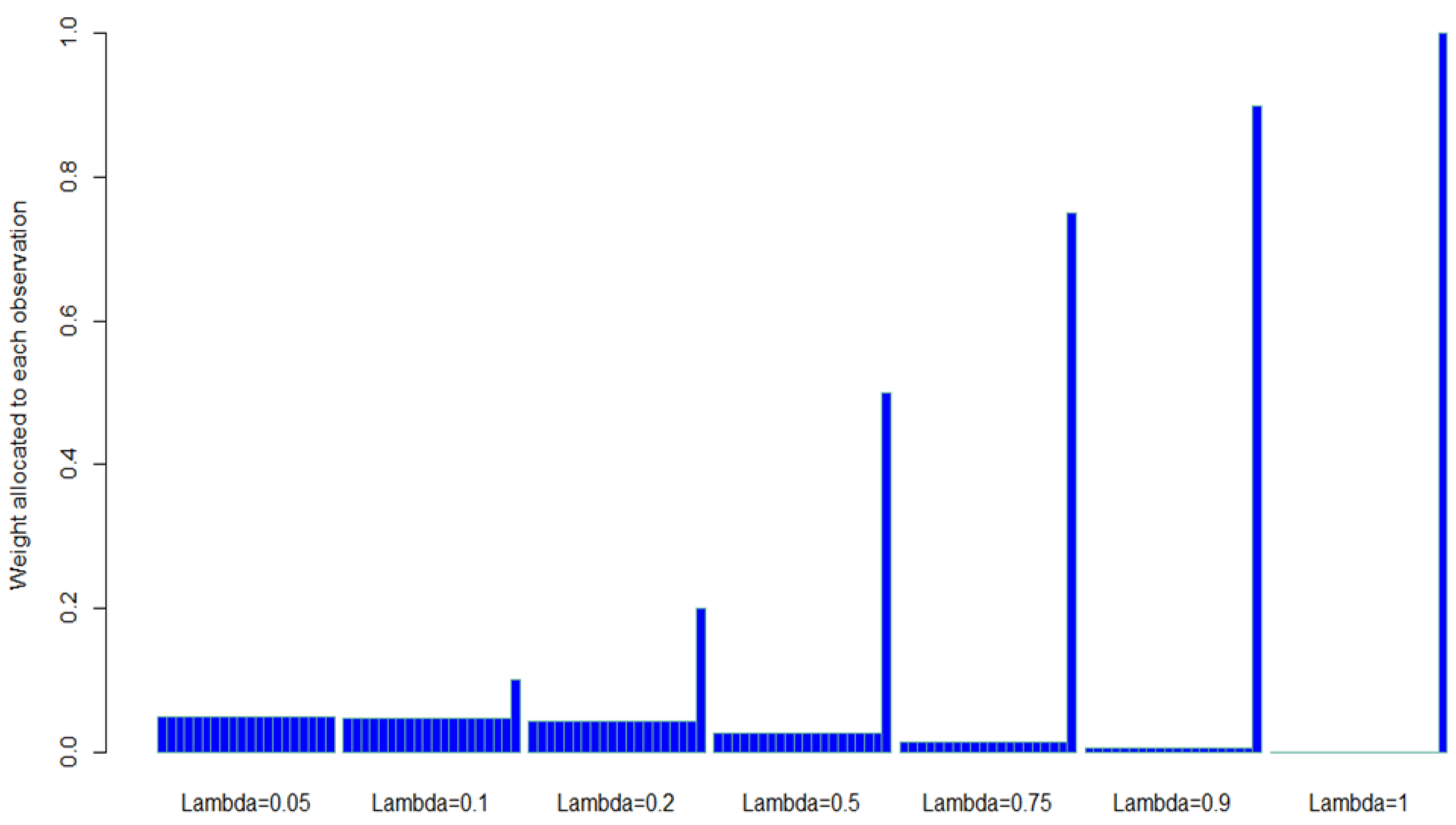
| Chart | Distribution | Section | Process Characteristic | Uni | Multi | |
|---|---|---|---|---|---|---|
| Section 4.1 | HWMA | Parametric | Section 4.1.1 | Location | 🗸 | 🗸 |
| Section 4.1.2 | Variability | 🗸 | ||||
| Section 4.1.3 | Joint Location and Variability | 🗸 | ||||
| Section 4.1.4 | Profile | 🗸 | 🗸 | |||
| Nonparametric | Section 4.1.5 | Location | 🗸 | 🗸 | ||
| Scale | × | |||||
| Section 4.1.6 | Joint Location and Scale | 🗸 | ||||
| Profile | ||||||
| Section 4.2 | DHWMA and HHWMA | Parametric | Section 4.2.1 | Location | 🗸 | |
| Variability | × | |||||
| Section 4.2.2 | Joint Location and Variability | 🗸 | ||||
| Profile | ||||||
| Nonparametric | Section 4.2.3 | Location | 🗸 | |||
| Scale | ||||||
| Joint Location and Scale | ||||||
| Profile | × | |||||
| Section 4.3 | THWMA | Parametric | Section 4.3.1 | Location | 🗸 | |
| Section 4.3.2 | Variability | 🗸 | ||||
| Joint Location and Variability | × | × | ||||
| Profile | ||||||
| Nonparametric | Section 4.3.3 | Location | 🗸 | |||
| Scale | × | |||||
| Joint Location and Scale | × | |||||
| Profile | × | |||||
| Section 4.4 | HWMA-CUSUM & CUSUM-HWMA | Parametric | Section 4.4.1 | Location | 🗸 | |
| Variability | ||||||
| Joint Location and Variability | ||||||
| Profile | ||||||
| Nonparametric | Location | |||||
| Scale | ||||||
| Joint Location and Scale | × | |||||
| Profile |
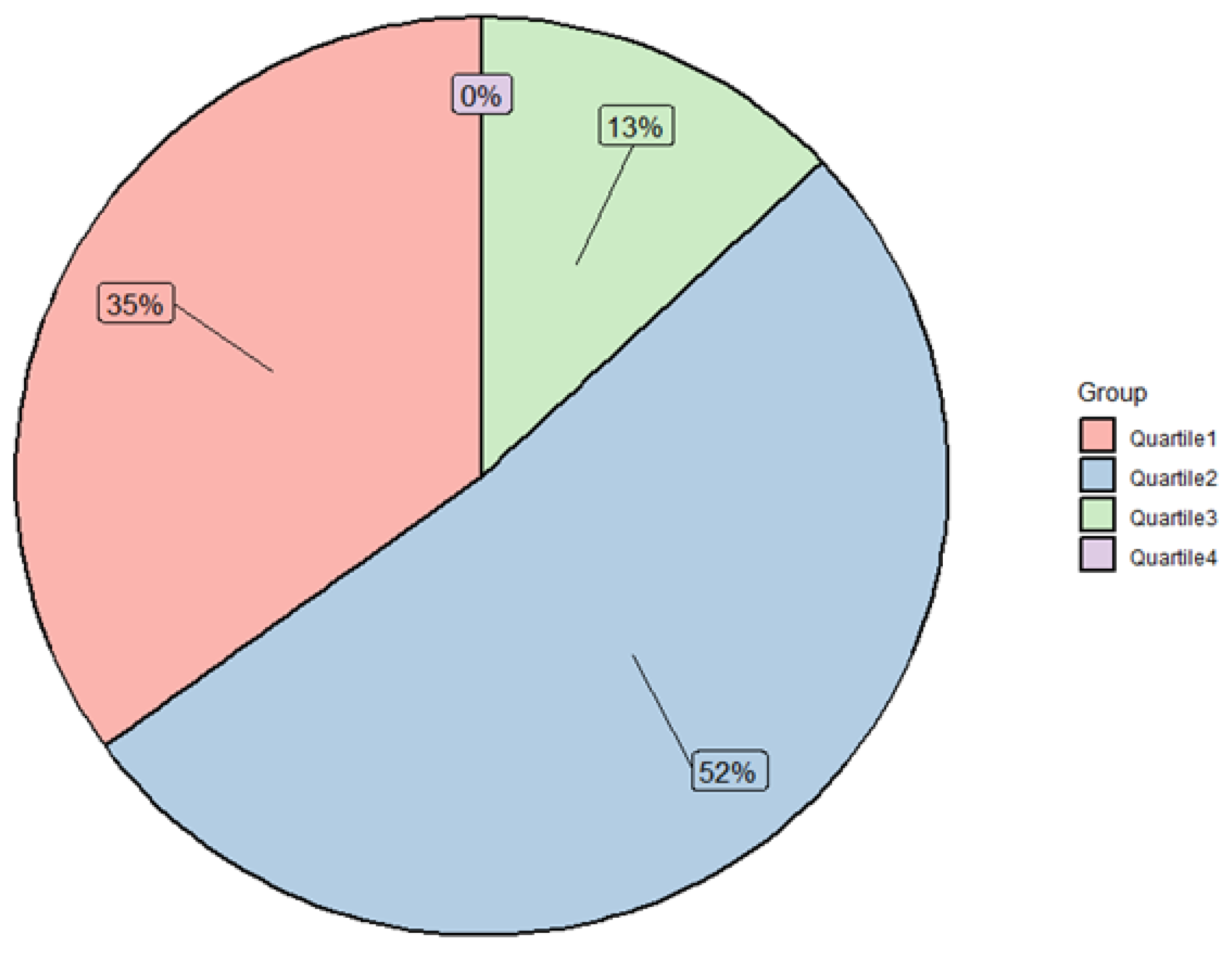
| Journal/Conference Proceedings | Open Access/Hybrid | JCR Quartile | Number of Publications |
|---|---|---|---|
| Computers & Industrial Engineering (CIE) | Hybrid | 1 | 2 |
| Mathematics | Open access | 1 | 2 |
| Quality and Reliability Engineering International (QREI) | Hybrid | 2 | 18 |
| IEEE Access | Open Access | 1 | 4 |
| Journal of Applied Statistics (JAS) | Hybrid | 2 | 1 |
| IEEE International Conference on Industrial Engineering and Engineering Management (IEEE ICIEEM) | Open access | 2 | 2 |
| Computer Modeling in Engineering & Sciences (CMES) | Open access | 3 | 1 |
| Mathematical Problems in Engineering (MPE) | Open access | 2 | 5 |
| Journal of Statistical Computation and Simulation (JSCS) | Hybrid | 2 | 2 |
| Chemometrics and Laboratory Systems (CLS) | Hybrid | 2 | 1 |
| Symmetry | Open access | 2 | 4 |
| PLoS ONE | Open access | 1 | 2 |
| AIMS Mathematics | Open access | 2 | 1 |
| Quality Technology & Quantitative Management (QTQM) | Hybrid | 1 | 1 |
| Communications in Statistics-Simulation and Computation (CS-SC) | Hybrid | 1 | 2 |
| Journal Testing and Evaluation (JTE) | Open access | 3 | 1 |
| Processes | Open access | 2 | 1 |
| Scientific Reports | Open access | 1 | 1 |
| Transactions of the Institute of Measurement and Control (TIMC) | Hybrid | 2 | 1 |
| International Journal of Industrial Engineering Computations (IJIEC) | Hybrid | 1 | 1 |
| Journal of Advanced Manufacturing Systems (JAMS) | Hybrid | 3 | 1 |
| Journal of Quality Technology (JQT) | Hybrid | 1 | 1 |
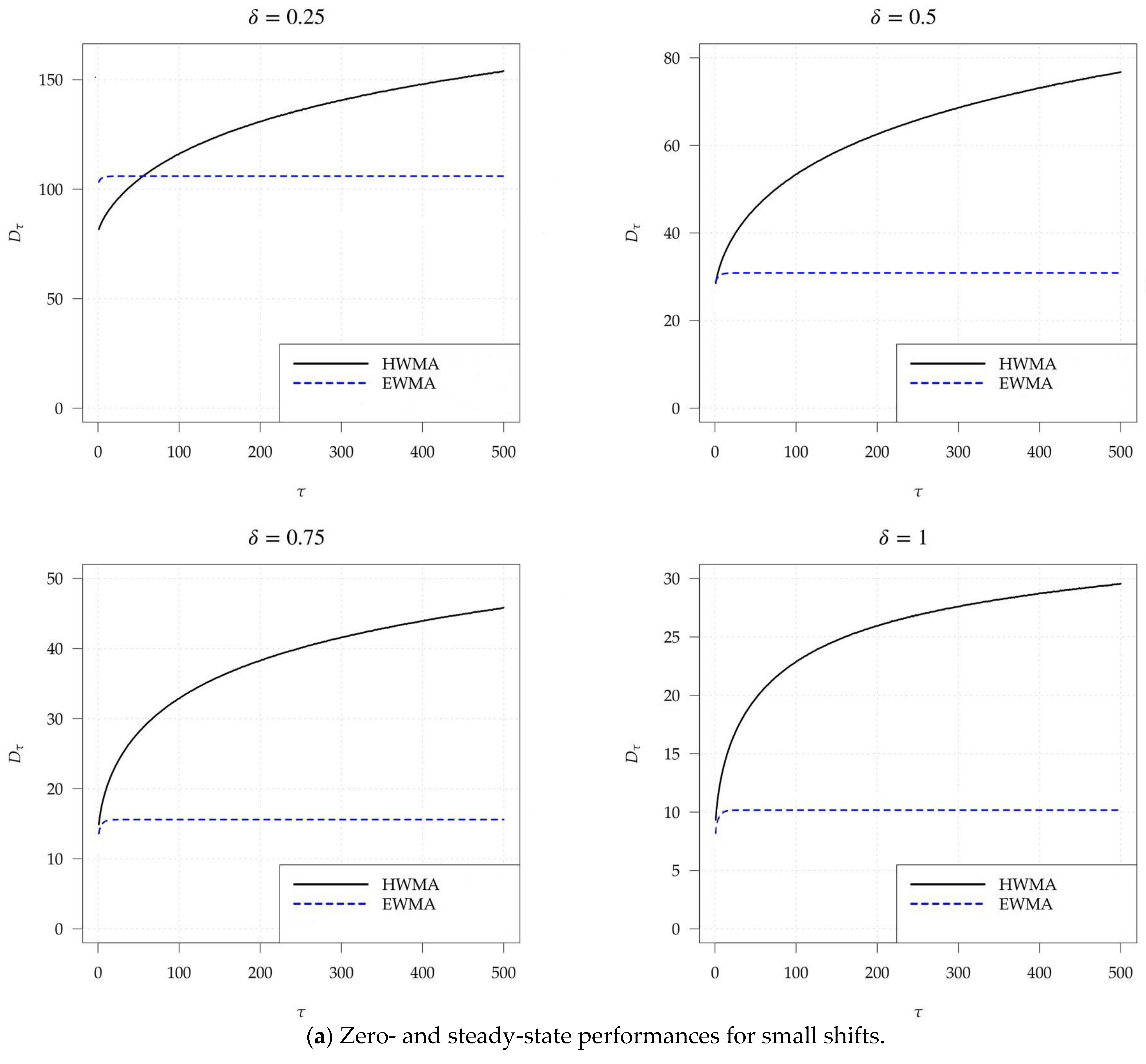
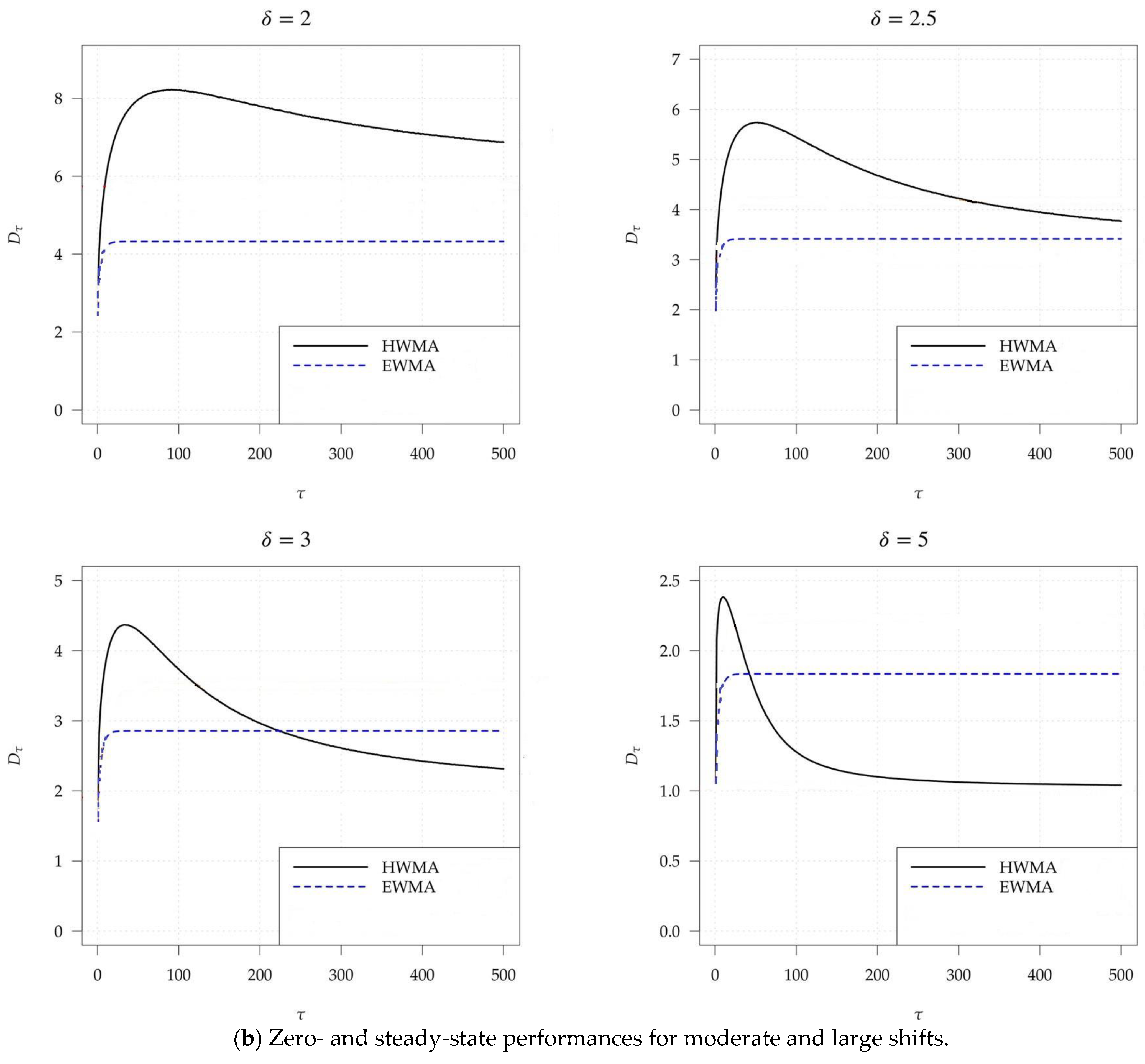
| Shift | 0.05) | EWMA (λ = 0.05) | CUSUM (k = 0.125) | HWMA (λ = 0.1) | EWMA (λ = 0.1) | CUSUM (k = 0.225) |
|---|---|---|---|---|---|---|
| 0.25 | 73.01 | 77.76 | 83.39 | 81.48 | 103.32 | 91.16 |
| 0.5 | 24.92 | 23.71 | 34.65 | 28.61 | 28.81 | 31.19 |
| 0.75 | 12.78 | 11.87 | 21.68 | 14.85 | 13.61 | 18.01 |
| 1 | 8.04 | 7.31 | 15.78 | 9.35 | 8.21 | 12.63 |
| 1.5 | 4.4 | 3.77 | 10.26 | 4.98 | 4.17 | 7.94 |
| 2 | 2.98 | 2.43 | 7.64 | 3.32 | 2.66 | 5.83 |
| 2.5 | 2.2 | 1.77 | 6.12 | 2.45 | 1.92 | 4.65 |
| 3 | 1.67 | 1.41 | 5.13 | 1.87 | 1.51 | 3.89 |
| 5 | 1.01 | 1.01 | 3.19 | 1.03 | 1.02 | 2.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malela-Majika, J.-C.; Human, S.W.; Chatterjee, K. Homogeneously Weighted Moving Average Control Charts: Overview, Controversies, and New Directions. Mathematics 2024, 12, 637. https://doi.org/10.3390/math12050637
Malela-Majika J-C, Human SW, Chatterjee K. Homogeneously Weighted Moving Average Control Charts: Overview, Controversies, and New Directions. Mathematics. 2024; 12(5):637. https://doi.org/10.3390/math12050637
Chicago/Turabian StyleMalela-Majika, Jean-Claude, Schalk William Human, and Kashinath Chatterjee. 2024. "Homogeneously Weighted Moving Average Control Charts: Overview, Controversies, and New Directions" Mathematics 12, no. 5: 637. https://doi.org/10.3390/math12050637
APA StyleMalela-Majika, J.-C., Human, S. W., & Chatterjee, K. (2024). Homogeneously Weighted Moving Average Control Charts: Overview, Controversies, and New Directions. Mathematics, 12(5), 637. https://doi.org/10.3390/math12050637






