Cooperative Guidance Strategy for Active Spacecraft Protection from a Homing Interceptor via Deep Reinforcement Learning

Abstract

The cooperative active defense guidance problem for a spacecraft with active defense is investigated in this paper. An engagement between a spacecraft, an active defense vehicle, and an interceptor is considered, where the target spacecraft with active defense will attempt to evade the interceptor. Prior knowledge uncertainty and observation noise are taken into account simultaneously, which are vital for traditional guidance strategies such as the differential-game-based guidance method. In this set, we propose an intelligent cooperative active defense (ICAAI) guidance strategy based on deep reinforcement learning. ICAAI effectively coordinates defender and target maneuvers to achieve successful evasion with less prior knowledge and observational noise. Furthermore, we introduce an efficient and stable convergence (ESC) training approach employing reward shaping and curriculum learning to tackle the sparse reward problem in ICAAI training. Numerical experiments are included to demonstrate ICAAI’s real-time performance, convergence, adaptiveness, and robustness through the learning process and Monte Carlo simulations. The learning process showcases improved convergence efficiency with ESC, while simulation results illustrate ICAAI’s enhanced robustness and adaptiveness compared to optimal guidance laws.

1. Introduction

Spacecraft such as satellites, space stations, and space shuttles play an important role in both civil and military activities. They are also at risk of being intercepted in the exo-atmosphere. The pursuit-evasion game between the spacecraft and the interceptor will be critical in the competition for space resources and has been widely studied in recent years. The trajectory of spacecraft can be accurately predicted [1] since the dynamics of the spacecraft is generally described in terms of a two-body problem. With the development of accurate sensors, guidance technology, small-sized propulsion systems, and fast servo-mechanism techniques, the Kinetic Kill Vehicle (KKV), which can be used for direct-hit killing, has superior maneuverability compared to the other spacecraft. In other words, it is not practical for targeted spacecraft involved in the pursuit-evasion game to rely solely on orbital maneuvering.

Among the many available countermeasures, launching an Active Defense Vehicle (ADV) as a defender to intercept the incoming threat has proven to be an effective approach to compensate for the inferior target maneuverability [2,3,4]. In an initial study [2], Boyell proposed the active defense strategy of launching a defensive missile to protect the target from a homing missile. Boyell proposed an approximate normalized curve of game results under the condition of constant or static target velocity based on the relative motion relationship among the three participants. The dynamic three-body framework was introduced by Rusnak in Ref. [4], inspired by the narrative of a “lady-bodyguard-bandit” situation. This framework was later transformed into a “target-interceptor-defender” (TID) three-body spacecraft active defense game scenario as described in Ref [3]. In the TID scenario, the defender aims to reduce the distance from the interceptor, while the interceptor endeavors to increase the distance from the defender and successfully intercept the target. In Refs. [3,4], Rusnak proposed a game guidance method under the TID scenario based on Multiple Objective Optimization and differential games theories. It was proven that the proposed active defense method significantly reduces the miss distance and the required acceleration level between interceptor and defender.

The efficacy of the active defense method has garnered increased attention to the collaborative strategy between the target and defender in the TID scenario. Traditional methods for solving optimal strategies in this context include Optimal Control [5,6,7] and differential games theories [8,9,10]. In Ref. [7], Weiss employed the Optimal Control theory to independently design the guidance for both the target and defender. This approach considered the influence of target maneuvers on the interceptor’s effectiveness as a defender. Furthermore, in Ref. [6], collaborative game strategies for the target and defender were proposed, emphasizing their combined efforts in the TID scenario. Aiming at the multi-member TID scenario in which a single target carries two defenders against two interceptors, Ref. [5] designed a multi-member cooperative game guidance strategy and considered the fuel consumption of target and defender. However, Optimal-Control-based strategies rely on perfect information, demanding accurate maneuvering details of the interceptor. In contrast, Differential Game approaches require prior knowledge instead of accurate target acceleration information, enhancing algorithm robustness [11]. In Ref. [8], optimal cooperative pursuit and evasion strategies were proposed using Pontryagin’s minimum principle. A similar scenario was studied in Ref. [9] for both continuous and discrete domains using the linear–quadratic differential game method. It is worth noting that the differential game control strategies proposed in Ref. [9] solve the fuel cost and saturation problem. However, they introduce computational problems and make the selection of weight parameters more difficult. A switching surface [10], designed with zero-effort miss distance, was introduced to divide the multi-agent engagement into two one-on-one differential games, thereby achieving a balance between performance and usability. Nonetheless, using the differential game method to solve the multi-agent pursuit-evasion game problem still faces shortcomings [11,12,13]. First, it is difficult to establish a scene model of a multi-member, multi-role game due to the extremely large increase in the dimension of the state quantity; second, it has high requirements for the accuracy of the prior knowledge, and the success rate of the game is low if the prior knowledge of the players in the game cannot be obtained accurately; third, the differential game algorithm is complicated, involving a high-dimensional matrix operation, power function operation, integral calculation, etc., which places a high demand on the computational resources of the spacecraft. More on this topic can be found in [14,15,16,17,18,19,20].

With the advancement of machine learning technology, Deep Reinforcement Learning (DRL) has emerged as a promising approach for addressing active defense guidance problems. In DRL, an agent interacts with the environment and receives feedback in the form of rewards, enabling it to improve its performance and achieve specific tasks. This mechanism has led to successful applications of DRL in various decision-making domains, including robot control, MOBA games, autonomous driving, and navigation [21,22,23,24,25]. In Ref. [26], the DRL was utilized to learn an adaptive homing phase control law, accounting for sensor and actuator noise and delays. Another work [27] proposed an adaptive guidance system to address the landing problem using Reinforcement Meta-Learning, adapting agent training from one environment to another with limited steps, showcasing robust policy optimization in the presence of parameter uncertainties. In the context of the TID scenario, Lau [28] demonstrated the potential of using reinforcement learning for active defense guidance rating, although an optimal strategy was not obtained in their preliminary investigation.

It is worthy to point out that, on one hand, to better align with real-world engineering applications, research in guidance methods often needs to consider the presence of various information gaps and noise [29,30]. However, most of the existing optimal active defense guidance methods rely on perfect information assumptions, leading to subpar performance when faced with unknown prior knowledge or observation noise. Additionally, these methods often struggle to meet the real-time requirements of spacecraft applications. On the other hand, the majority of reinforcement learning algorithms have been applied to non-adversarial or weak adversarial flight missions, where mission objectives and process rewards are clear and intuitive. However, in the highly competitive TID game scenario, obtaining effective reward information becomes challenging due to the intense confrontation between agents, leading to sparse reward problems or “Plateau Phenomenon” [31].

Given these observations, there is a strong motivation to develop an active defense guidance method based on reinforcement learning that possesses enhanced real-time capabilities, adaptiveness, and robustness, while addressing the challenges posed by adversarial scenarios and sparse reward issues.

In this paper, we focus on the cooperative active defense guidance strategy design of a target spacecraft with active defense attempting to evade an interceptor in space. This TID scenario holds significant importance in the domains of space attack-defense and ballistic missile penetration. The paper begins by deriving the kinematic and first-order dynamic models of the engagement scenario. Subsequently, an intelligent cooperative active defense (ICAAI) guidance method for active defense is proposed, utilizing the twin-delay deep deterministic policy gradient (TD3) algorithm. To address the challenge of sparse rewards, an efficient and stable convergence (ESC) training approach is introduced. Furthermore, benchmark comparisons are made using Optimal Guidance Laws (OGLs), and simulation analyses are presented to validate the performance of the proposed method.

The paper is organized as follows. In Section 2, the problem formulation is provided. In Section 3, the guidance law is developed. In Section 4, experiments are presented where the proposed method has been compared with its analytical counterpart, followed by the conclusions presented in Section 5.

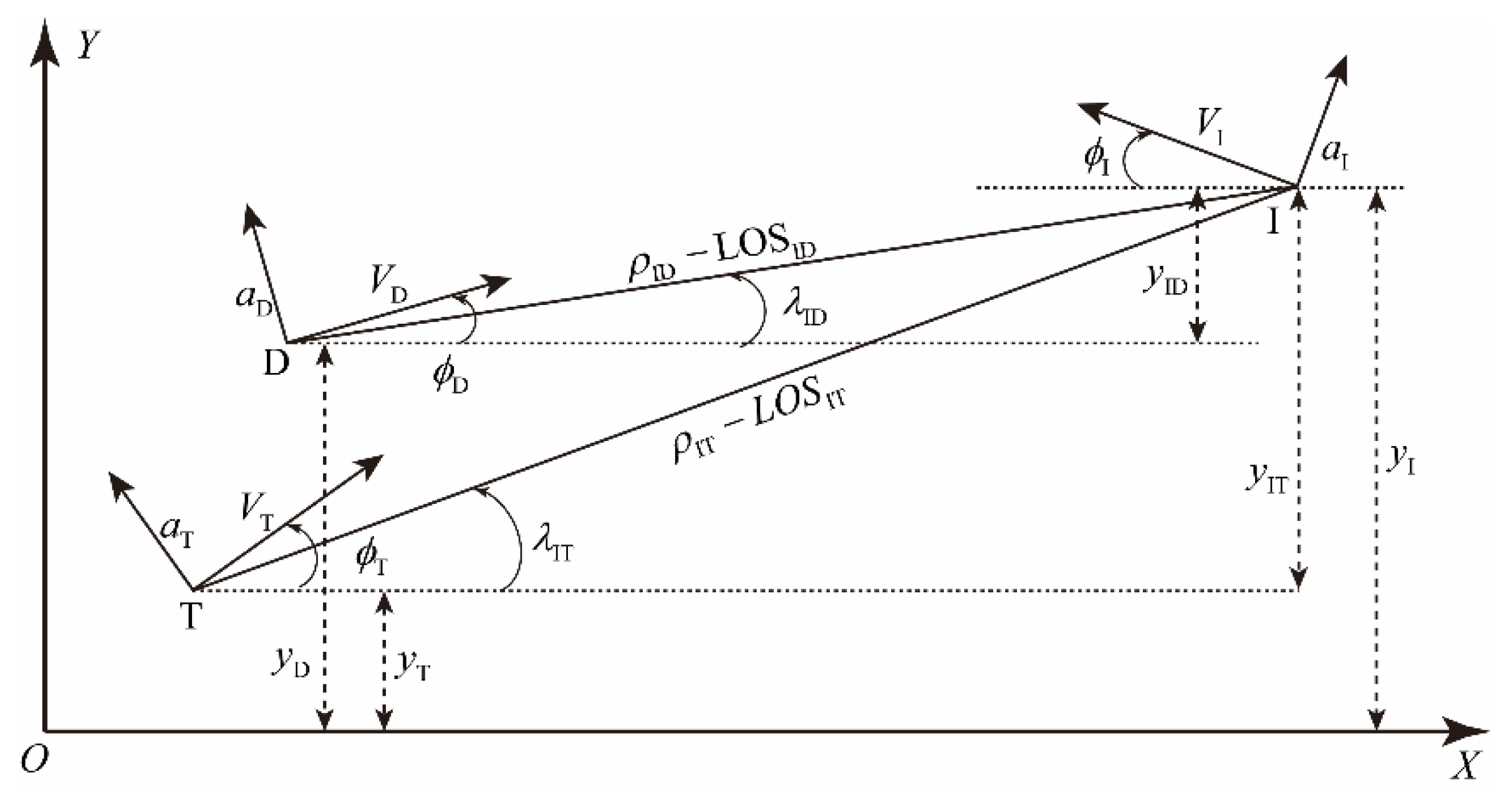
2. Problem Formulation

Consider a multi-agent game with a spacecraft as the main target (T), an active defense vehicle as the defender (D), and a highly maneuverable small spacecraft as the interceptor (I). In this battle, the interceptor chases the target, which launches the defender to protect itself by destroying the interceptor. During the endgame, all players are considered as constant-speed mass points whose trajectories can be linearized around the initial line of sight. As a consequence of trajectory linearization, the engagement, a three-dimensional process, can be simplified and will be analyzed in one plane. However, it should be noted that in most cases these assumptions do not affect the generality of the results [11].

A schematic view of the engagement is shown in Figure 1, where $X-O-Y$ is a Cartesian inertial reference frame. The distances between the players are denoted as ${\rho }_{\mathrm{ID}}$ and ${\rho }_{\mathrm{IT}}$, respectively. Each player’s velocity is indicated as $V_{\mathrm{I}}$, $V_{\mathrm{T}}$, and $V_{\mathrm{D}}$, while their accelerations are represented as $a_{\mathrm{I}}$, $a_{\mathrm{T}}$, and $a_{\mathrm{D}}$. The flight path angles of the players are defined as ${\varphi }_{\mathrm{I}}$, ${\varphi }_{\mathrm{T}}$, and ${\varphi }_{\mathrm{D}}$, respectively. The line of sight (LOS) between the players is described by ${\mathrm{LOS}}_{\mathrm{ID}}$ and ${\mathrm{LOS}}_{\mathrm{IT}}$, and the angles between the LOS and the X-axis are denoted as ${\lambda }_{\mathrm{ID}}$ and ${\lambda }_{\mathrm{IT}}$. The lateral displacements of each player relative to the X-axis are represented as $y_{\mathrm{I}}$, $y_{\mathrm{T}}$, and $y_{\mathrm{D}}$, while the relative displacements between the players are defined as $y_{\mathrm{IT}}$ and $y_{\mathrm{ID}}$.

Considering the collective mission objectives, the target’s priority is to evade the interceptor with defender support. Simultaneously, the interceptor aims to avoid the defender while chasing the target. Consequently, the target’s guidance law strives for maximum convergence, while the defender’s aims for convergence to zero. Conversely, the interceptor’s guidance law assumes the opposite role (as depicted in Figure 1). This scenario can thus be segmented into two collision triangles: one involving the interceptor and the target, and the other between the interceptor and the defender.

2.1. Equations of Motion

Consider the I-T collision triangle and the I-D collision triangle in a multi-agent pursuit-evasion engagement. The kinematics are expressed using the polar coordinate system attached in the target and defender as follows:

$$\begin{array}{l}{\dot{\rho }}_{\mathrm{IT}}=-V_{\mathrm{I}}\cos \left({\varphi }_{\mathrm{I}}+{\lambda }_{\mathrm{IT}}\right)-V_{\mathrm{T}}\cos \left({\varphi }_{\mathrm{T}}-{\lambda }_{\mathrm{IT}}\right)\\ {\dot{y}}_{\mathrm{IT}}=V_{\mathrm{I}}\sin {\varphi }_{\mathrm{I}}-V_{\mathrm{T}}\sin {\varphi }_{\mathrm{T}}\\ {\dot{\lambda }}_{\mathrm{IT}}=\frac{V_{\mathrm{I}}\sin \left({\varphi }_{\mathrm{I}}+{\lambda }_{\mathrm{IT}}\right)-V_{\mathrm{T}}\sin \left({\varphi }_{\mathrm{T}}-{\lambda }_{\mathrm{IT}}\right)}{{\rho }_{\mathrm{IT}}}\end{array}$$

(1)

$$\begin{array}{l}{\dot{\rho }}_{\mathrm{ID}}=-V_{\mathrm{I}}\cos \left({\varphi }_{\mathrm{I}}+{\lambda }_{\mathrm{ID}}\right)-V_{\mathrm{D}}\cos \left({\varphi }_{\mathrm{D}}-{\lambda }_{\mathrm{ID}}\right)\\ {\dot{y}}_{\mathrm{ID}}=V_{\mathrm{I}}\sin {\varphi }_{\mathrm{I}}-V_{\mathrm{D}}\sin {\varphi }_{\mathrm{D}}\\ {\dot{\lambda }}_{\mathrm{ID}}=\frac{V_{\mathrm{I}}\sin \left({\varphi }_{\mathrm{I}}+{\lambda }_{\mathrm{ID}}\right)-V_{\mathrm{D}}\sin \left({\varphi }_{\mathrm{D}}-{\lambda }_{\mathrm{ID}}\right)}{{\rho }_{\mathrm{ID}}}\end{array}$$

(2)

Furthermore, the flight path angles associated with dynamics can be defined for each of the players:

$${\dot{\varphi }}_i=\frac{a_i}{V_i}, i=\left\{\mathrm{I}, \mathrm{T}, \mathrm{D}\right\}$$

(3)

2.2. Linearized Equations of Motion

In the research context, both the LOS angle $\lambda$ and fight path angle $\varphi$ are small quantities, and the inter-spacecraft distances are much larger than the spacecraft velocities. Furthermore, during the terminal guidance phase, the rate of change in spacecraft velocity magnitude approaches zero. Therefore, the equations of motion can be linearized around the initial line-of-sight:

$$\begin{array}{cc}{\dot{\rho }}_{\mathrm{IT}}& =-V_{\mathrm{I}}\cos \left({\varphi }_{\mathrm{I}}+{\lambda }_{\mathrm{IT}}\right)-V_{\mathrm{T}}\cos \left({\varphi }_{\mathrm{T}}-{\lambda }_{\mathrm{IT}}\right)\approx -\left(V_{\mathrm{I}}+V_{\mathrm{T}}\right)\hfill \\ {\ddot{y}}_{\mathrm{IT}}& ={\left(V_{\mathrm{I}}\sin {\varphi }_{\mathrm{I}}-V_{\mathrm{T}}\sin {\varphi }_{\mathrm{T}}\right)}^{\prime }\approx {\left(V_{\mathrm{I}}{\varphi }_{\mathrm{I}}-V_{\mathrm{T}}{\varphi }_{\mathrm{T}}\right)}^{\prime }\hfill \\ & ={\dot{V}}_{\mathrm{I}}{\varphi }_{\mathrm{I}}-{\dot{V}}_{\mathrm{T}}{\varphi }_{\mathrm{T}}+V_{\mathrm{I}}{\dot{\varphi }}_{\mathrm{I}}-V_{\mathrm{T}}{\dot{\varphi }}_{\mathrm{T}}={\dot{V}}_{\mathrm{I}}{\varphi }_{\mathrm{I}}-{\dot{V}}_{\mathrm{T}}{\varphi }_{\mathrm{T}}+a_{\mathrm{I}}-a_{\mathrm{T}}\hfill \\ & \approx a_{\mathrm{I}}-a_{\mathrm{T}}\hfill \\ {\dot{\lambda }}_{\mathrm{IT}}& =\frac{V_{\mathrm{I}}\sin \left({\varphi }_{\mathrm{I}}+{\lambda }_{\mathrm{IT}}\right)-V_{\mathrm{T}}\sin \left({\varphi }_{\mathrm{T}}-{\lambda }_{\mathrm{IT}}\right)}{{\rho }_{\mathrm{IT}}}\approx \frac{V_{\mathrm{I}}\left({\varphi }_{\mathrm{I}}+{\lambda }_{\mathrm{IT}}\right)-V_{\mathrm{T}}\left({\varphi }_{\mathrm{T}}-{\lambda }_{\mathrm{IT}}\right)}{{\rho }_{\mathrm{IT}}}\approx 0\hfill \end{array}$$

(4)

$$\begin{array}{cc}{\dot{\rho }}_{\mathrm{ID}}& =-V_{\mathrm{I}}\cos \left({\varphi }_{\mathrm{I}}+{\lambda }_{\mathrm{ID}}\right)-V_{\mathrm{D}}\cos \left({\varphi }_{\mathrm{D}}-{\lambda }_{\mathrm{ID}}\right)\approx -\left(V_{\mathrm{I}}+V_{\mathrm{D}}\right)\hfill \\ {\ddot{y}}_{\mathrm{ID}}& ={\left(V_{\mathrm{I}}\sin {\varphi }_{\mathrm{I}}-V_{\mathrm{D}}\sin {\varphi }_{\mathrm{D}}\right)}^{\prime }\approx {\left(V_{\mathrm{I}}{\varphi }_{\mathrm{I}}-V_{\mathrm{D}}{\varphi }_{\mathrm{D}}\right)}^{\prime }\hfill \\ & ={\dot{V}}_{\mathrm{I}}{\varphi }_{\mathrm{I}}-{\dot{V}}_{\mathrm{D}}{\varphi }_{\mathrm{D}}+V_{\mathrm{I}}{\dot{\varphi }}_{\mathrm{I}}-V_{\mathrm{D}}{\dot{\varphi }}_{\mathrm{D}}={\dot{V}}_{\mathrm{I}}{\varphi }_{\mathrm{I}}-{\dot{V}}_{\mathrm{D}}{\varphi }_{\mathrm{D}}+a_{\mathrm{I}}-a_{\mathrm{D}}\hfill \\ & \approx a_{\mathrm{I}}-a_{\mathrm{D}}\hfill \\ {\dot{\lambda }}_{\mathrm{ID}}& =\frac{V_{\mathrm{I}}\sin \left({\varphi }_{\mathrm{I}}+{\lambda }_{\mathrm{ID}}\right)-V_{\mathrm{D}}\sin \left({\varphi }_{\mathrm{D}}-{\lambda }_{\mathrm{ID}}\right)}{{\rho }_{\mathrm{ID}}}\approx \frac{V_{\mathrm{I}}\left({\varphi }_{\mathrm{I}}+{\lambda }_{\mathrm{ID}}\right)-V_{\mathrm{D}}\left({\varphi }_{\mathrm{D}}-{\lambda }_{\mathrm{ID}}\right)}{{\rho }_{\mathrm{ID}}}\approx 0\hfill \end{array}$$

(5)

The dynamics for each of the players is assumed to be a first-order process:

$${\dot{a}}_i=-\frac{a_i-u_i}{{\tau }_i}, i=\left\{\mathrm{I}, \mathrm{T}, \mathrm{D}\right\}$$

(6)

Furthermore, the variable vector can be defined as follows:

$$\mathit{x}=\left[\begin{array}{ccccccc}{y}_{\mathrm{IT}}& {\dot{y}}_{\mathrm{IT}}& y_{\mathrm{ID}}& {\dot{y}}_{\mathrm{ID}}& a_{\mathrm{I}}& a_{\mathrm{T}}& a_{\mathrm{D}}\end{array}\right]$$

(7)

while the linearized equations of motion in the state space form can be written as follows:

$$\dot{\mathit{x}}=\mathit{A}\mathit{x}+\mathit{B}{\left[\begin{array}{ccc}{u}_{\mathrm{I}}& u_{\mathrm{T}}& u_{\mathrm{D}}\end{array}\right]}^T$$

(8)

where

$$\mathit{A}=\left[\begin{array}{ccccccc}0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& -1& 0\\ 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& -1\\ 0& 0& 0& 0& -1/{\tau }_{\mathrm{I}}& 0& 0\\ 0& 0& 0& 0& 0& -1/{\tau }_{\mathrm{T}}& 0\\ 0& 0& 0& 0& 0& 0& -1/{\tau }_{\mathrm{D}}\end{array}\right]$$

(9)

$$\mathit{B}=\left[\begin{array}{c}{0}_{5\times 3}\\ {\mathit{B}}_1\end{array}\right], {\mathit{B}}_1=\left[\begin{array}{ccc}1/{\tau }_{\mathrm{I}}& 0& 0\\ 0& 1/{\tau }_{\mathrm{T}}& 0\\ 0& 0& 1/{\tau }_{\mathrm{D}}\end{array}\right]$$

(10)

Since the velocity of each player is assumed to be constant, the engagement can be formulated as a fixed-time process. Thus, the interception time can be calculated using the following:

$$\begin{array}{l}{t}_{\mathrm{f},\mathrm{IT}}=-{\rho }_{\mathrm{IT}}^0/{\dot{\rho }}_{\mathrm{IT}}={\rho }_{\mathrm{IT}}^0/\left(V_{\mathrm{I}}+V_{\mathrm{T}}\right)\\ t_{\mathrm{f},\mathrm{ID}}=-{\rho }_{\mathrm{ID}}^0/{\dot{\rho }}_{\mathrm{ID}}={\rho }_{\mathrm{ID}}^0/\left(V_{\mathrm{I}}+V_{\mathrm{D}}\right)\end{array}$$

(11)

where ${\rho }_{\mathrm{IT}}^0$ represents the initial relative distance between the interceptor and the target, while ${\rho }_{\mathrm{ID}}^0$ is the distance between the interceptor and the defender, allowing us to define the time-to-go of each engagement by

$$\begin{array}{l}{t}_{\mathrm{go},\mathrm{IT}}=t_{\mathrm{f},\mathrm{IT}}-t\\ t_{\mathrm{go},\mathrm{ID}}=t_{\mathrm{f},\mathrm{ID}}-t\end{array}$$

(12)

which represents the expected remaining game time for the interceptor in the “Interceptor vs. Target” and “Interceptor vs. Defender” game scenarios, respectively.

2.3. Zero-Effort Miss

A well-known zero-effort miss (ZEM) is introduced in the guidance law design and reward function design. It is obtained from the homogeneous solutions of equations of motion and is only affected by the current state and interception time. It can be calculated as follows:

$$\begin{array}{l}{Z}_{\mathrm{IT}}(t)={\mathit{L}}_1\Phi (t,t_{\mathrm{f},\mathrm{IT}})\mathit{x}(t)\\ Z_{\mathrm{ID}}(t)={\mathit{L}}_2\Phi (t,t_{\mathrm{f},\mathrm{ID}})\mathit{x}(t)\end{array}$$

(13)

where

$$\begin{array}{l}{\mathit{L}}_1=\left[\begin{array}{lllllll}1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right]\\ {\mathit{L}}_2=\left[\begin{array}{lllllll}0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right]\end{array}$$

(14)

Thus, the ZEM and its derivative with respect to time are given as follows:

$$\begin{array}{l}{Z}_{\mathrm{IT}}(t)=x_1+t_{\mathrm{goIT}}{x}_2+a_{\mathrm{I}}{\tau }_{\mathrm{I}}^2\phi \left(t_{\mathrm{goIT}}/{\tau }_{\mathrm{I}}\right)x_5-a_{\mathrm{T}}{\tau }_{\mathrm{T}}^2\phi \left(t_{\mathrm{goIT}}/{\tau }_{\mathrm{T}}\right)x_6\\ Z_{\mathrm{ID}}(t)=x_3+t_{\mathrm{goID}}{x}_4+a_{\mathrm{I}}{\tau }_{\mathrm{I}}^2\phi \left(t_{\mathrm{goID}}/{\tau }_{\mathrm{I}}\right)x_5-a_{\mathrm{D}}{\tau }_{\mathrm{D}}^2\phi \left(t_{\mathrm{goID}}/{\tau }_{\mathrm{D}}\right)x_7\end{array}$$

(15)

$$\begin{array}{l}{\dot{Z}}_{\mathrm{IT}}(t)={\tau }_{\mathrm{I}}\phi \left(t_{\mathrm{goIT}}/{\tau }_{\mathrm{I}}\right)u_{\mathrm{I}}-{\tau }_{\mathrm{T}}\phi \left(t_{\mathrm{goIT}}/{\tau }_{\mathrm{T}}\right)u_{\mathrm{T}}\\ {\dot{Z}}_{\mathrm{ID}}(t)={\tau }_{\mathrm{I}}\phi \left(t_{\mathrm{goID}}/{\tau }_{\mathrm{I}}\right)u_{\mathrm{I}}-{\tau }_{\mathrm{D}}\phi \left(t_{\mathrm{goID}}/{\tau }_{\mathrm{D}}\right)u_{\mathrm{D}}\end{array}$$

(16)

where

$$\phi \left(\chi \right){=\mathrm{e}}^{-\chi }+\chi -1$$

(17)

2.4. Problem Statement

This research focuses on the terminal guidance task of evading a homing interceptor for a maneuvering target with active defense. We design a cooperative active defense guidance to facilitate coordinated maneuvers between the target and the defender based on DRL. This enables the target to evade the interceptor’s interception while allowing the defender to counter-intercept the incoming threat.

3. Guidance Law Development

In this section, we develop the Intelligent Cooperative Active Defense (ICAAI) guidance strategy and design an efficient and stable convergence (ESC) training approach. The target and defender utilize ICAAI guidance, while the interceptor employs OGL. We describe the game scenario using a Markov process, present the ICAAI guidance strategy, and design an ESC training approach based on reward shaping and curriculum learning.

3.1. Markov Decision Process

The sequential decision making that an autonomous RL agent interacts with the environment (e.g., the engagement) can be formally described as an MDP, which is required to properly set up the mathematical framework of an DRL problem. A generic time-discrete MDP can be represented as a 6-tuple $\{s,o,a,P_{sa},\gamma ,R\}$. $s_t\in S\in {ℝ}^n$ is a vector that completely identifies the state of the system (e.g., the EOM) at time t. Generally, the complete state is not available to the agent at each time t; the decision-making relies on an observation vector $o_t\in O\in {ℝ}^m$. In the present paper, the observations are defined as an uncertain (e.g., imperfect and noisy) version of the true state, which can be written as a function $\Omega$ of the current state $s_t$. The action $a\in A\in {ℝ}^l$ of the agent is given by a state-feedback policy $\pi :O\to A$, that is, $a_t=\pi (o_t)$. $P_{sa}$ is time-discrete dynamic model describing the transformation led by the state–action pair $(s_t,a_t)$. As a result, the evolution rule of the dynamic system can be described as follows:

$$\begin{array}{l}{s}_{t+1}=P_{sa}(s_t,a_t)\\ o_t=\Omega (s_t)\\ a_t=\pi (o_t)\end{array}$$

(18)

Since a fixed-time engagement is considered, the interaction between the agent and the environment gives rise to a trajectory ${\rm I}$:

$$\begin{array}{l}{\rm I}=\left[{\iota }_1,{\iota }_2,\cdots ,{\iota }_t,\cdots ,{\iota }_{T-1},{\iota }_T\right]\\ {\iota }_t={\left[o_t,a_t,r_t\right]}^T\end{array}$$

(19)

where the trajectory information at each time step ${\iota }_t$ is composed of observational $o_t$, action $a_t$, and reward signal $r_t$ generated through the interaction between the agent and the environment.

The return, the agent received at time $t$ in the trajectory ${\rm I}$, is defined as a discounted sum of rewards:

$$R_t^{{\rm I}}={\displaystyle {\sum }_{i=t}^T{\gamma }^{i-t}{r}_i}$$

(20)

where $\gamma \in (0,1]$ is a discount rate determining whether the agent has a long-term vision ($\gamma =1$) or is short-sighted ($\gamma \ll 1$).

Prior to deriving the current guidance law, we outline the key elements of the MDP: state space, action space, and observations. We present the reward design separately by highlighting a crucial aspect of the configuration.

3.1.1. Perfect Information Model

In a deterministic model, the basic assumption is that each player has perfect information about the interceptor (e.g., states, maximum acceleration, and time constant). The communication of this information between the defender and the protected target is assumed to be ideal and without delay. Thus, the state space can be identified by states, maximum acceleration, and time constant:

$${\mathit{s}}_t={[\begin{array}{ccccccc}t& {\mathit{x}}_t& {\mathit{y}}_t& {\mathit{V}}_t& {\mathit{a}}_{\mathit{t}}& {\mathit{a}}_{\max }& \mathbf{\tau }\end{array}]}^T$$

(21)

$${\mathit{x}}_t=\left[\begin{array}{ccc}{x}_{t,\mathrm{T}}& x_{t,\mathrm{D}}& x_{t,\mathrm{I}}\end{array}\right],{\mathit{y}}_t=\left[\begin{array}{ccc}{y}_{t,\mathrm{T}}& y_{t,\mathrm{D}}& y_{t,\mathrm{I}}\end{array}\right]$$

(22)

$${\mathit{V}}_t=\left[\begin{array}{ccc}{V}_{t,\mathrm{T}}& V_{t,\mathrm{D}}& V_{t,\mathrm{I}}\end{array}\right]$$

(23)

$${\mathbf{a}}_t=\left[\begin{array}{ccc}{a}_{t,\mathrm{T}}& a_{t,\mathrm{D}}& a_{t,\mathrm{I}}\end{array}\right]$$

(24)

$${\mathbf{a}}_{\max }=\left[\begin{array}{ccc}{a}_{\max ,\mathrm{T}}& a_{\max ,\mathrm{D}}& a_{\max ,\mathrm{I}}\end{array}\right]$$

(25)

$$\mathbf{\tau }=\left[\begin{array}{ccc}{\tau }_{\mathrm{T}}& {\tau }_{\mathrm{D}}& {\tau }_{\mathrm{I}}\end{array}\right]$$

(26)

As with the multi-agent system, interactions introduce uncertainty into the environment, which significantly affects the stability of the RL algorithm. Given the full cooperation between defender and target due to communication assumptions, the model must learn a shared guidance law for both. This effectively mitigates environmental uncertainty and enhances model convergence. In practical application, the same trained agent is assigned to the target pair, yielding the following action space:

$$\mathrm{action}=[\begin{array}{cc}{u}_{\mathrm{T}}& u_{\mathrm{D}}\end{array}]$$

(27)

Since the dynamics of the scenario are formulated in Section 2.1, the state can be propagated implicitly as the linearized equation of motion presented in Equations (4)–(6).

3.1.2. Imperfect Information Model

The imperfection of information is usually due to the limitations of radar measurement and the erasure of prior knowledge. However, in existing studies, perfect information is a strong assumption, which leads to implementation difficulties in practice. To address this dilemma, this thesis considers information degradation. On the one hand, the interceptor is assumed to have perfect information (i.e., the relative states and maneuverability of the target and the defender). On the other hand, the observation of the target and defender is imperfect and even noise-corrupted. The observation uncertainty is modeled as observation noise and a mask on the perfect information.

$$o_t=\Omega (s_t)=\Gamma s_t\times (\mathit{I}+{\omega }_{o,t})=\left[\begin{array}{c}t\\ {\mathit{x}}_t\\ {\mathit{y}}_t\\ {\mathit{V}}_t\\ {\mathit{a}}_t\end{array}\right]+\left[\begin{array}{c}0\\ \delta {\mathit{x}}_{o,t}\\ \delta {\mathit{y}}_{o,t}\\ \delta {\mathit{V}}_{o,t}\\ \delta {\mathit{a}}_{o,t}\end{array}\right]$$

(28)

where $\Gamma$ is the mask matrix and ${\omega }_{o,t}$ is the observation noise vector. ${\omega }_{o,t}$ can be calculated by Equations (29)–(32).

$${\mathbf{\omega }}_{o,t}=\left[\begin{array}{c}0\\ \delta {\mathit{x}}_{o,t}\\ \delta {\mathit{y}}_{o,t}\\ \delta {\mathit{V}}_{o,t}\\ \delta {\mathit{a}}_{o,t}\end{array}\right]~U(0_{13},\Sigma )\in {ℝ}^{13}$$

(29)

$$\Sigma ={\left[0,0,0,{\sigma }_{\mathrm{xI}},0,0,{\sigma }_{\mathrm{yI}},0,0,{\sigma }_v,0,0,{\sigma }_a\right]}^T$$

(30)

$${\sigma }_{\mathrm{xI}}=\cos \left({\sigma }_{\mathrm{LOS}}+{\lambda }_{\mathrm{IT}}\right)\left({\rho }_{\mathrm{IT}}+{\sigma }_{\rho }\right)-x_{\mathrm{I}}\approx 0$$

(31)

$${\sigma }_{\mathrm{yI}}=\sin \left({\sigma }_{\mathrm{LOS}}+{\lambda }_{\mathrm{IT}}\right)\left({\rho }_{\mathrm{IT}}+{\sigma }_{\rho }\right)-y_{\mathrm{I}}\approx {\sigma }_{\mathrm{LOS}}\cdot {\rho }_{\mathrm{IT}}$$

(32)

where $\Sigma$ represents the noise amplitude, with ${\sigma }_{\rho }\left(\mathrm{m}\right)$, ${\sigma }_{LOS}\left(\mathrm{mrad}\right)$, ${\sigma }_v\left(\mathrm{m}/\mathrm{s}\right)$, and ${\sigma }_a({\mathrm{m}/\mathrm{s}}^2)$ the nonnegative parameters.

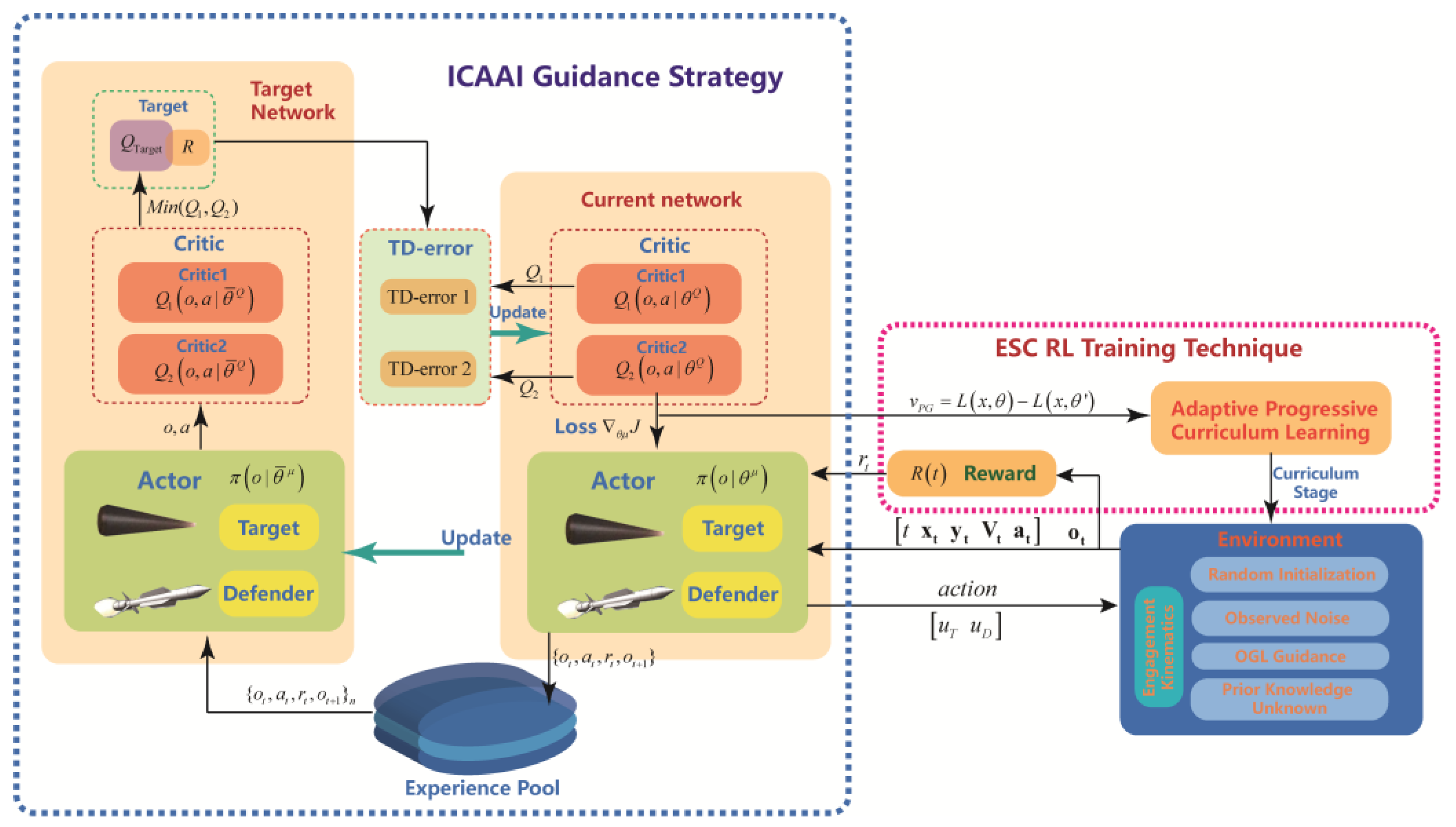
3.2. ICAAI Guidance Law Design

In this section, we present the mathematical framework of actor–critic RL algorithms, focusing on the algorithm used in ICAAI guidance: Twin-Delay Deep Deterministic Policy Gradient (TD3) [32]. TD3 is an advanced deterministic policy gradient reinforcement learning algorithm. In comparison to stochastic policy gradient algorithms like Proximal Policy Optimization (PPO) [33] and Asynchronous Advantage Actor–Critic (A3C) [34], TD3 exhibits a higher resistance to converging into local optima. Furthermore, when compared to traditional deterministic policy gradient RL algorithms such as Deep Deterministic Policy Gradient (DDPG) [35], TD3 achieves superior training stability and convergence efficiency. This assertion is supported by our prior RL algorithm selection experiments, as illustrated in Figure 2.

Without loss of generality, throughout the entire section the MDP is supposed to be perfectly observable (i.e., with $o_t=s_t$) to conform with the standard notation of RL. However, the perfect information state $s_t$ can be replaced by observation $o_t$ whenever the observations differ from the state.

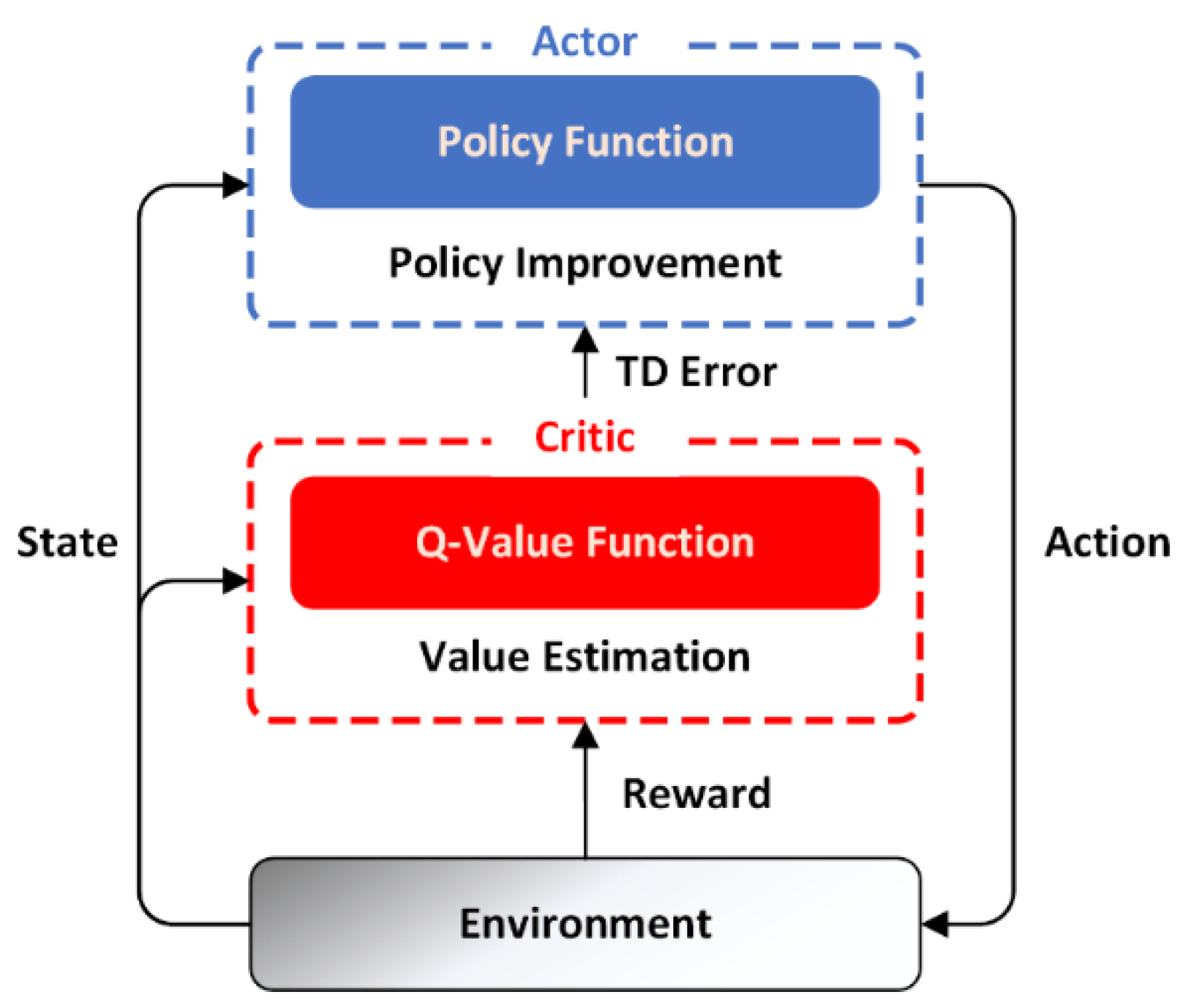
3.2.1. Actor–Critic Algorithms

The RL problem’s goal is to find the optimal policy ${\pi }_{\varphi }$ with parameters $\varphi$ that maximizes the expected return, which can be formulated as follows:

$$J(\varphi )=\underset{\tau ~{\pi }_{\varphi }}{\mathbb{E}}\left[R_0^{\tau }\right]=\underset{\tau ~{\pi }_{\varphi }}{\mathbb{E}}\left[{\displaystyle \sum _{i=0}^T{\gamma }^{i-0}{r}_i}\right]$$

(33)

where $\underset{\tau ~\pi }{\mathbb{E}}$ denotes the expectation taken over the trajectory $\tau$. In actor–critic algorithms, the policy, known as the actor, can be updated by using a deterministic policy gradient algorithm [36]:

$${\nabla }_{\varphi }J(\varphi )={\mathbb{E}}_{P_{sa}}\left[{\nabla }_a{Q}^{\pi }(s,a){|}_{a=\pi (s)}\nabla \varphi \pi \varphi (s)\right]$$

(34)

The expected return, when performing action $a$ in state $s$ and following $\pi$ after, is called the critic or the value function, which can be formulated as follows:

$$Q^{\pi }(s,a)=\underset{\tau ~{\pi }_{\varphi }}{\mathbb{E}}\left[R_t^{\tau }|s,a\right]$$

(35)

The value function can be learned through off-policy temporal differential learning, an update rule based on the Bellman equation which describes the relationship between the value of the state–action pair $(s,a)$ and the value of the subsequent state–action pair $(s^{\prime },a^{\prime })$:

$$Q^{\pi }(s,a)=r+\gamma \underset{s^{\prime },a^{\prime }}{\mathbb{E}}\left[Q^{\pi }(s^{\prime },a^{\prime })\right]$$

(36)

In deep Q-learning [37], the value function can be estimated with a neural network approximator $Q_{\theta }(s,a)$ with parameters $\theta$, and the network is updated by using temporary differential learning with a secondary frozen target network $Q_{{\theta }^{\prime }}(s,a)$ to maintain a fixed objective $U$ over multiple updates:

$$U=r+\gamma Q_{{\theta }^{\prime }}(s^{\prime },a^{\prime }), a^{\prime }={\pi }_{{\varphi }^{\prime }}(s^{\prime })$$

(37)

where the actions $a^{\prime }$ are determined by a target actor network ${\pi }_{{\varphi }^{\prime }}$. Generally, the loss function and update rule can be formulated as follows:

$$J(\theta )=U-Q_{\theta }(s,a)$$

(38)

$${\nabla }_{\theta }J(\theta )=\left[U-Q_{\theta }(s,a)\right]{\nabla }_{\theta }{Q}_{\theta }(s,a)$$

(39)

The parameters of target networks are updated periodically to exactly match the parameters of the corresponding current networks, which is called delayed update. This leads to the original actor–critic method, the basic structure of which is shown in Figure 3.

3.2.2. Twin-Delayed Deep Deterministic Policy Gradient Algorithm

To address the common RL issues in actor-critic algorithms (i.e., overestimation bias and accumulation of errors), in the TD3 algorithm, the actor–critic framework is modified from three aspects.

A novel variant of double Q-learning [38] called clipped double Q-learning is developed to limit possible overestimation. This provides the update objective of the critic:

$$U=r+\gamma \underset{i=1,2}{\min }{Q}_{{{\theta }^{\prime }}_i}(s^{\prime },{\pi }_{{{\varphi }^{\prime }}_1}(s^{\prime }))$$

(40)

The parameters of policy networks are updated periodically to match the value network, which is called delayed policy update, and the soft update approach is adopted, which can be formulated as follows:

$${\theta }^{\prime }\leftarrow \kappa \theta +(1-\kappa ){\theta }^{\prime }$$

(41)

where $\kappa$ is a proportion parameter.

Target policy smoothing regularization is adopted to alleviate the overfitting phenomenon, which can be explicated as follows:

$$y=r+\gamma Q_{{\theta }^{\prime }}(s^{\prime },{\pi }_{{\varphi }^{\prime }}(s^{\prime })+\epsilon )$$

(42)

where $\epsilon$ is a clipped Gaussian noise.

An overview of the TD3 algorithm is demonstrated in Figure 4.

3.2.3. Implementation Details

As for the network architecture setting, the agent observations are vectors with 13 dimensions. Both the guidance policy estimation (actor) and the value function estimation (critic) consist of three fully connected layers with sizes of 64, 256, and 512, respectively, along with layer normalization. The output layer has two units for the actor, representing the unified command of the target and defender, respectively, and one unit for the critic. The activation function is ReLU for the hidden layer neurons and linear for the output layer neuron. This structure is heuristically designed and can be generalized for efficient function approximation. Deeper and wider networks are avoided for real-time performance and fast convergence.

The hyperparameters of TD3 have been devised and validated by empirical experiments, which are reported in

Table 1. TD3 hyperparameters.

Hyperparameter	Symbol	Value
Discount factor	$\gamma$	0.99
Learning rate	$\alpha$	$3\times {10}^{-4}$
Buffer size	$\mathbb{B}$	5120
Batch size	$n_{\mathrm{batch}}$	128
Soft update coefficient	$\zeta$	$5\times {10}^{-3}$
Policy delay	$n_{\mathrm{opt}}$	2
Train frequency	$\omega$	6000

.

3.3. ESC Traning Technique

Aiming at the sparse reward problem in the multi-agent pursuit-evasion game, an efficient and stable convergence (ESC) training approach of reinforcement learning is proposed based on reward shaping [39] and curriculum learning [40].

3.3.1. Reward Shaping

The design of a reward function is the most challenging part of solving this multi-agent pursuit-evasion game through RL, as the function had to be adaptive to engagement with a sparse reward setting. It is found that, except for the common leadership mission, the pursuit-evasion game can be formulated as a strictly competitive zero-sum game. In addition, the agent policy network weights were randomly initiated at the beginning of training, while the interceptor was deployed with optimal guidance and is sufficiently aggressive.

In [41], a shaping technique was presented as a particularly effective approach to solving sparse reward problems through a series of biological experiments. The researchers divided a difficult task into several simple units and trained the animals according to an easy-to-hard schedule. This approach requires adjusting the reward signal to cover the entire training process, followed by gradual changes in task dynamics as training progresses. In [40], researchers took this idea further and proposed curriculum learning, a type of training strategy. In this work, the shaping technique and curriculum learning were used to speed up the convergence of neural networks and to increase the stability and performance of the algorithm.

The goal of the target and the defender is to converge $Z_{\mathrm{ID}}$ to zero as $t\to t_{f2}$ while keeping $Z_{\mathrm{IT}}$ as large as possible. On the contrary, the interceptor control law is designed to make $Z_{\mathrm{IT}}$ converge to zero while maintaining $Z_{\mathrm{ID}}$ as large as possible.

For this reason, a non-sparse reward function is defined in Equations (43) and(44):

$$r_{\mathrm{medium}}=\gamma \Phi \left(s’\right)-\Phi \left(s\right)$$

(43)

$$\Phi \left(s\right)={\left|\frac{Z_{\mathrm{IT}}}{{\alpha }_1}\right|}^{{\beta }_1}-{\left|\frac{Z_{\mathrm{ID}}}{{\alpha }_2}\right|}^{{\beta }_2}$$

(44)

$$r_{\mathrm{terminal}}=\{\begin{array}{l}\sigma , \mathrm{if} \mathrm{succeed}\hfill \\ -\sigma , \mathrm{else}\hfill \end{array}$$

(45)

where $\gamma$ is the discount factor in the Markov decision process and ${\alpha }_1$, ${\alpha }_2$, ${\beta }_1$, ${\beta }_2$, and $\sigma$ are the positive hyperparameters.

It must be stressed that, since both the number and maneuverability of players completely change the environment, the hyperparameter values used in this paper may be not universal. Thus, in the following subsection, the focus will be on the applied design method instead of the specific hyperparameter values. The $r_{\mathrm{terminal}}$ is the terminal reward signal given to the terminal behavior of the agent, which is sparse but intuitive. Situations in which the interceptor is destroyed by the defender (when $t=t_{\mathrm{f},\mathrm{ID}}$) or when the interceptor is driven away by the defender and misses the target are judged as a success. Furthermore, the $r_{\mathrm{medium}}$ is a non-sparse reward function based on the difference form of a potential function $\Phi \left(s\right)$ which ensures the consistency of the optimal strategy [42,43,44]. It is important to emphasize that the design of $\Phi \left(s\right)$ relies on a fractional exponential function. This function provides a continuous reward signal for the agent’s evaluation of each state. Notably, this model exhibits a unique property: as the base number approaches infinity, the gradient decreases to zero, and as the base number approaches zero, the gradient increases infinitely. This specific characteristic significantly aids the agent in converging towards states where the base number is either greater than zero or approaches zero.

In this paper, the defined reward function carries the physical meaning of the mission—the target must escape from the interceptor, while the defender has to get close to the interceptor. The $r_{\mathrm{medium}}$ value increases as $Z_{\mathrm{ID}}$ converges to zero, or when $Z_{\mathrm{IT}}$ increases. On the other hand, it decreases when $Z_{\mathrm{ID}}$ is divergent or when $Z_{\mathrm{IT}}$ converges to zero.

Generally, reward normalization is beneficial to neural network convergence. However, determining the bounds of $Z_{\mathrm{IT}}$ and $Z_{\mathrm{ID}}$ is a complex task. For this reason, hyperparameters ${\alpha }_1$, ${\alpha }_2$, ${\beta }_1$, and ${\beta }_2$ are tuned, aiming to scale the $r_{\mathrm{medium}}$ close to $[-c, c]$, in which c is a positive constant. In the following step, the design of $\rho$ is considered, which introduces the expectation of agent foresight. If the agent is expected to predict the terminal reward $r_{\mathrm{terminal}}$ n steps before, the discounted terminal reward must be larger than the $r_{\mathrm{medium}}$ bounds. Thus, the hyperparameter $\rho$ satisfies the following expression:

$$\rho \ge \frac{c}{{\gamma }^n}$$

(46)

3.3.2. Curriculum Learning

After hyperparameter tuning, we enhance the training stability of intelligent algorithms using an adaptive progressive curriculum learning approach. This method incrementally raises training complexity to enhance agent capability and performance. The agent’s training level is adaptively assessed through changes in network loss, determining appropriate training difficulty. The $v_{\mathrm{PG}}$ calculation formula is as follows:

$$v_{\mathrm{PG}}=L\left(x,\theta \right)-L\left(x,\theta ’\right)$$

(47)

where $L(\cdot )$ represents the calculation function of network loss; $\theta$ is the current network parameter and $\theta ’$ is the new network parameter obtained after data $x$ training. Given a small amount $\epsilon (1\gg \epsilon >0)$, when

$$\left|v_{\mathrm{PG}}\right|<\epsilon$$

(48)

the agent training enters the next stage. A sequence of increasingly difficult tasks is allocated to the agent, as shown in

Table 2. Curriculum learning.

Curriculum	Stage 1	Stage 2	Stage 3
Interceptor guidance command	None	Square wave signal	OGL
Maximum interceptor acceleration	0	8 g	4 g/6 g/8 g

. The curriculum was divided into three stages:

• The agent is required to combat the interceptors employing non-maneuvering;
• Square wave signal;
• OGL.

Finally, it is possible to complete the reward shaping process.

In summary, the block diagram of ICAAI guidance strategy is shown in Figure 5.

4. Experiments

In this section, we demonstrate the efficacy of the proposed guidance method and the effectiveness of the shaping technique through learning processes and Monte Carlo simulations. We establish benchmark comparisons by including OGLs and evaluating application requirements. To illustrate, we consider a scenario [10] involving a maneuverable small spacecraft (Interceptor, I), a defensive vehicle (Defender, D), and an evading spacecraft (Target, T), all in circular Earth orbits. Gravity effects are incorporated in the simulations. Assumptions include the interceptor’s superior maneuverability and time constant compared to the target and defender.

4.1. Optimal Pursuit and Evasion Guidance Laws

Lemma 1.

The linear–quadratic optimal guidance law (LQOGL) [10]:

$$u_I^{*}=\{\begin{array}{l}-\frac{K(t)Z_{\mathrm{ID}}(t)}{{\omega }_1}{u}_{\mathrm{I}}^{\max }{\tau }_{\mathrm{I}}\phi \left(\frac{t_{\mathrm{f},\mathrm{ID}}-t}{{\tau }_{\mathrm{I}}}\right) \mathrm{for} \Vert Z_{\mathrm{ID}}(t)\Vert <\eta \hfill \\ -\frac{P(t)Z_{\mathrm{IM}}(t)}{{\xi }_1}{u}_{\mathrm{I}}^{\max }{\tau }_{\mathrm{I}}\phi \left(\frac{t_{\mathrm{f},\mathrm{IT}}-t}{{\tau }_{\mathrm{I}}}\right) \mathrm{else}\hfill \end{array}$$

(49)

where$\eta$ is a positive constant representing the limit-collision radius between the interceptor and the defender, and $u_{\mathrm{I}}^{\max }$ is the maximum control force provided by the interceptor. Furthermore, variable K(t) and P(t) can be defined as follows:

$$K(t)=\frac{1}{{\displaystyle {\int }_t^{t_{\mathrm{fID}}}\left[\frac{1}{{\omega }_1}{\left(u_{\mathrm{I}}^{\max }{\tau }_{\mathrm{I}}\phi \left(\frac{t_{\mathrm{f},\mathrm{ID}}-t}{{\tau }_1}\right)\right)}^2-\frac{1}{{\omega }_2}{\left(u_D^{\max }{\tau }_{\mathrm{D}}\phi \left(\frac{t_{\mathrm{f},\mathrm{ID}}-t}{{\tau }_{\mathrm{D}}}\right)\right)}^2\right]}\mathrm{d}t-1}$$

(50)

$$P(t)=\frac{1}{{\displaystyle {\int }_t^{t_{\mathrm{fIM}}}\left[\frac{1}{{\xi }_1}{\left(u_{\mathrm{I}}^{\max }{\tau }_{\mathrm{I}}\phi \left(\frac{t_{\mathrm{f},\mathrm{IM}}-t}{{\tau }_1}\right)\right)}^2-\frac{1}{{\xi }_2}{\left(u_{\mathrm{M}}^{\max }{\tau }_{\mathrm{M}}\phi \left(\frac{t_{\mathrm{f},\mathrm{IM}}-t}{{\tau }_{\mathrm{M}}}\right)\right)}^2\right]}\mathrm{d}t-1}$$

(51)

where${\omega }_1$, ${\omega }_2$, ${\xi }_1$, and ${\xi }_2$ are nonnegative constants ensuring the interceptor converges towards the target, guaranteeing its escape from the defender.

Proof. 

The detailed proof of similar results can be found in [10]; see Theorem 1 and the associated proof. □

Lemma 2.

Standard optimal guidance law (SOGL) [45]:

$$\begin{array}{l}{u}_{\mathrm{I}}^{*}=u_{\mathrm{I}}^{\max }\mathrm{sgn}\left[Z_{\mathrm{ID}}\left(t_{\mathrm{f},\mathrm{ID}}\right)\right]\mathrm{sgn}\left[\phi \left(\frac{t_{\mathrm{f},\mathrm{ID}}-t}{{\tau }_{\mathrm{I}}}\right)\right] \mathrm{for} \Vert Z_{\mathrm{ID}}\left(t\right)\Vert <\eta \\ u_{\mathrm{I}}^{*}=-u_{\mathrm{I}}^{\max }\mathrm{sgn}\left[Z_{\mathrm{IT}}\left(t_{\mathrm{f},\mathrm{IT}}\right)\right]\mathrm{sgn}\left[\phi \left(\frac{t_{\mathrm{f},\mathrm{IT}}-t}{{\tau }_{\mathrm{I}}}\right)\right] \mathrm{else}\end{array}$$

(52)

where$\eta$ is a positive constant representing the switching condition always equal to the defender kill radius.

Proof. 

Consider the following cost function:

$$\begin{array}{l}{J}_1=-\frac{1}{2}{Z}_{\mathrm{ID}}^2\left(t_{\mathrm{fID}}\right) \mathrm{for} \Vert Z_{\mathrm{ID}}\left(t\right)\Vert <\eta \\ J_2=\frac{1}{2}{Z}_{\mathrm{IT}}^2\left(t_{\mathrm{fIT}}\right) \mathrm{else}\end{array}$$

(53)

For $J_1$, the Hamiltonian of the problem is defined as follows:

$$H_1={\lambda }_1{\dot{Z}}_{\mathrm{ID}}\left(t\right)$$

(54)

The costate equation and transversality condition are provided by the following:

$${\dot{\lambda }}_1\left(t\right)=-\frac{\partial H_1}{\partial Z_{\mathrm{ID}}}=0$$

(55)

$${\lambda }_1\left(t_{\mathrm{fID}}\right)=\frac{\partial J_1}{\partial Z_{\mathrm{ID}}\left(t_{\mathrm{fID}}\right)}=-Z_{\mathrm{ID}}\left(t_{\mathrm{fID}}\right)$$

(56)

The optimal interceptor controller minimizes the Hamiltonian satisfying the following:

$$u_{\mathrm{I}}^{*}=\underset{u_{\mathrm{I}}}{\arg }\min \left(H_1\right)$$

(57)

The interceptor guidance law can thus be obtained:

$$u_{\mathrm{I}}^{*}=u_{\mathrm{I}}^{\max }\mathrm{sgn}\left[Z_{\mathrm{ID}}\left(t_{\mathrm{fID}}\right)\right]\mathrm{sgn}\left[\phi \left(\frac{t_{\mathrm{fID}}-t}{{\tau }_{\mathrm{I}}}\right)\right]$$

(58)

For $J_2$, a similar interceptor guidance law can be found:

$$u_{\mathrm{I}}^{*}=-u_{\mathrm{I}}^{\max }\mathrm{sgn}\left[Z_{\mathrm{IT}}\left(t_{f\mathrm{IT}}\right)\right]\mathrm{sgn}\left[\phi \left(\frac{t_{f\mathrm{IT}}-t}{{\tau }_{\mathrm{I}}}\right)\right]$$

(59)

Finally, the interceptor guidance schemes for evading the defender and pursuing the target are proposed after combining Equations (58) and (59):

$$\begin{array}{l}{u}_{\mathrm{I}}^{*}=u_{\mathrm{I}}^{\max }\mathrm{sgn}\left[Z_{\mathrm{ID}}\left(t_{f\mathrm{ID}}\right)\right]\mathrm{sgn}\left[\phi \left(\frac{t_{f\mathrm{ID}}-t}{{\tau }_{\mathrm{I}}}\right)\right] \mathrm{for} \Vert Z_{\mathrm{ID}}\left(t\right)\Vert <\eta \\ u_{\mathrm{I}}^{*}=-u_{\mathrm{I}}^{\max }\mathrm{sgn}\left[Z_{\mathrm{IT}}\left(t_{f\mathrm{IT}}\right)\right]\mathrm{sgn}\left[\phi \left(\frac{t_{f\mathrm{IT}}-t}{{\tau }_{\mathrm{I}}}\right)\right] \mathrm{else}\end{array}$$

(60)

□

4.2. Engagement Setup

In this scenario, a target carrying an active anti-interceptor is threatened by a KKV interceptor in orbit at an altitude of 500 km. The defender maintains an initial safe distance of approximately 50 m longitudinally and 10 km transversely to the target. Given that the detection range of the interceptor’s guided warhead is about 100 km, the initial transverse distance between the interceptor and the target is set at 100 km, and the initial longitudinal position is random in the range 499.8–500.2 km. In addition, the maneuverability and control response speed of the interceptor are better than those of the target and defender, and the OGL is used for guidance.

The comprehensive list of engagement parameters is shown in

Table 3. Engagement parameters.

	Interceptor	Interceptor	Target	Defender
Parameters
Horizonal location (km)		100	0	0~15
Vertical location (km)		499.8~500.2	500	500.05
Horizonal velocity (km/s)		−3	2	2
Vertical velocity		0	0	0
Maximum acceleration (g)		8	2	6
Time constant (s)		0.02	0.1	0.05
Kill radius (m)		0.25	0.5	0.15

.

Furthermore, Gaussian noise with standard variance of ${\sigma }_{LOS}=1 \mathrm{mrad}$, ${\sigma }_v=0.2 \mathrm{m}/\mathrm{s}$, and ${\sigma }_a=1 {\mathrm{m}/\mathrm{s}}^2$ is considered in the interceptor information obtained by the target and defender through a radar seeker.

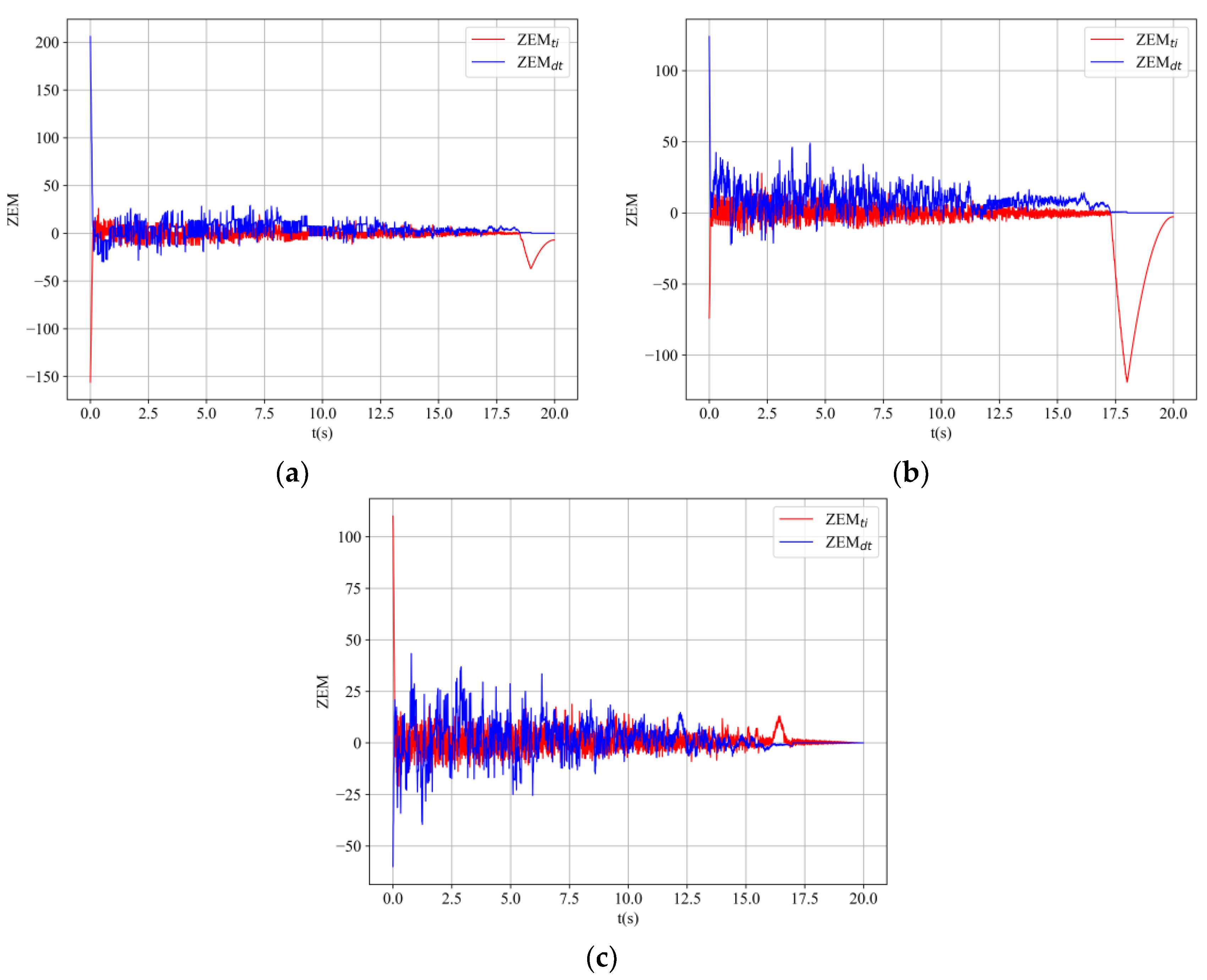
4.3. Experiment 1: Real-Time Performance of the Guidance Policy

To verify that the proposed RL training approach ESC can improve convergence efficiency and stability, the learning processes were demonstrated using the sparse reward (SR) signal and ESC, respectively, with the same hyperparameters. During the learning process, the weights of the neural network model were stored every 100 episodes for subsequent analysis. In addition, to remove stochasticity as a confounding factor, six random seeds were set for each case. Meanwhile, the real-time performance of the optimized agent is evaluated by comparing it with the traditional OGLs.

The agents were obtained after a training of 20,000 episodes, which took 12 h with 8 parallel workers on a computer equipped with a 104-core Intel Core Xeon Platinum 8270 CPU @2.70 GHz. Similarly, both the traditional methods and the proposed method are provided a current state or observation and return the required action.

Table 4. Statistics of time consumption with different guidance methods.

Metrics	LQOGL	SOGL	ICAAI
Duration (1e3 step)	2.773 s	0.0145 s	0.910 s
Update frequency	$\approx 360 \mathrm{HZ}$	$\approx 6.9\times {10}^4 \mathrm{HZ}$	$\approx 1.1\times {10}^3 \mathrm{HZ}$

shows the comparison of computational cost and update frequency obtained by using SOGL, LQOGL, and the proposed method. It can be seen from the table that LQOGL is time-consuming due to the calculation of the Riccati function, which is the reason why it has not been applied in practice. As a proven approach, the SOGL has excellent real-time performance. The proposed method achieved an update frequency of 10³ Hz and showed great potential for on-board applications. While a variety of approaches (e.g., pruning and distillation) were effective to compress the policy network and further improve its real-time performance, it is not the main work of this research.

Remark 1.

As shown in Equations (18) and (19), the LQOGL has to solve the Riccati differential equation. However, the experimental results show that its update frequency cannot meet the real-time requirements of spacecraft guidance. Compared to the LQOGL, the SOGL in Equation (60) does not need to solve the Riccati differential equation and has no hyperparameter. This improves both its computational efficiency and robustness at the cost of flexibility and the occurrence of the chattering phenomenon. To take into account the practical situation, the SOGL was chosen as an OGL benchmark.

4.4. Experiment 2: Convergence and Performance of the Guidance Policy

The performance of the trained agent in the fully observable game was investigated by comparing the escape success rate corresponding to an optimized policy ${\pi }_{\varphi }(s)$, obtained by performing Monte Carlo simulation in the fully observable (deterministic and with default engagement parameters) environment, with the solution of the SOGL.

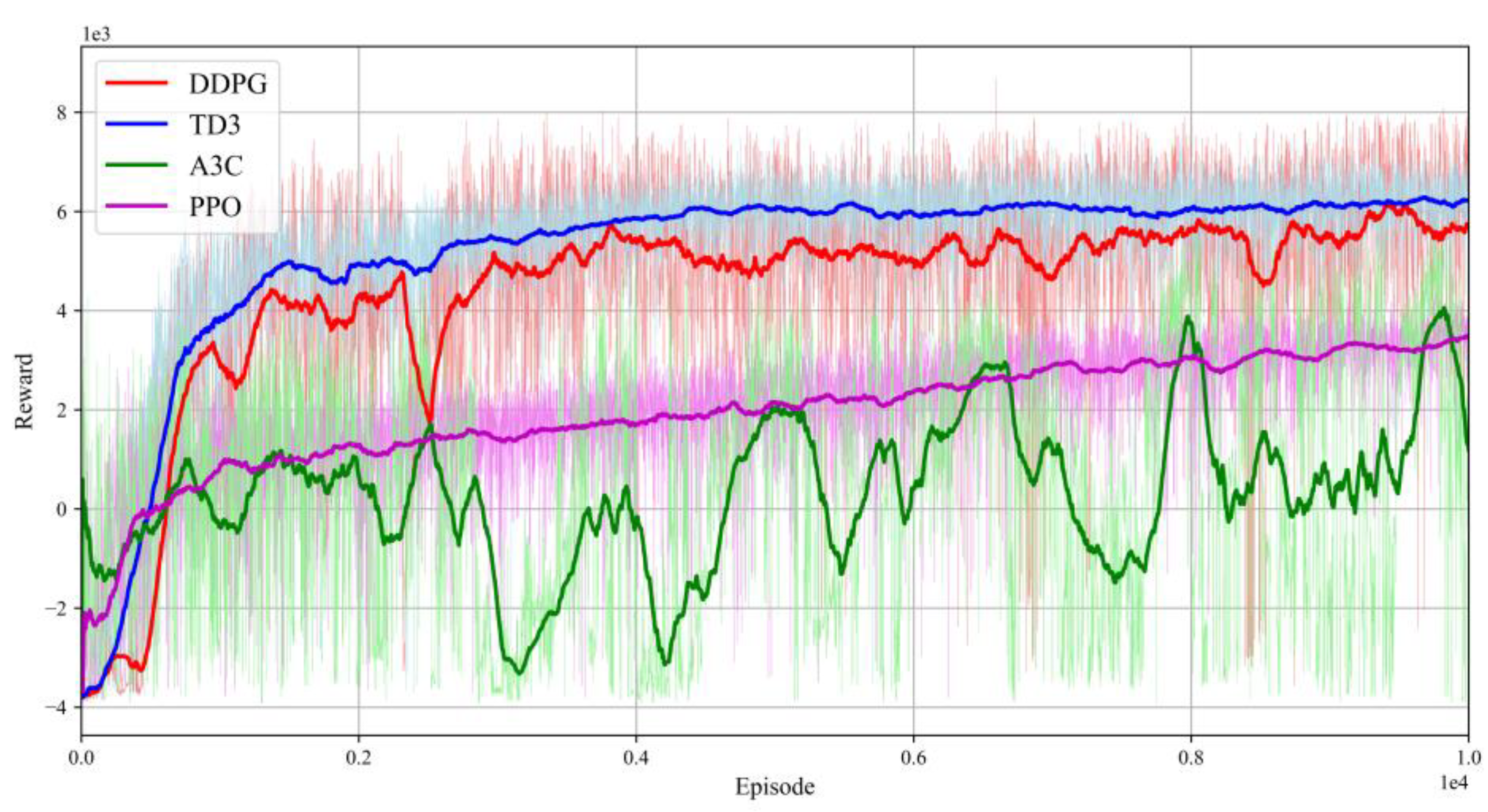
4.4.1. Baselines

The SOGL for the target and the defender were considered as an OGL benchmark. Through a brief derivation similar to that in Section 3, it can be proven that the SOGLs for the target and the defender are as follows:

$$\begin{array}{l}{u}_{\mathrm{T}}=-u_{\mathrm{T}}^{\max }\mathrm{sgn}\left[Z_{\mathrm{IT}}\left(t_{f\mathrm{IT}}\right)\right]\mathrm{sgn}\left[\phi \left(\frac{t_{f\mathrm{IT}}-t}{{\tau }_{\mathrm{T}}}\right)\right]\\ u_{\mathrm{D}}=u_{\mathrm{D}}^{\max }\mathrm{sgn}\left[Z_{\mathrm{ID}}\left(t_{f\mathrm{ID}}\right)\right]\mathrm{sgn}\left[\phi \left(\frac{t_{f\mathrm{ID}}-t}{{\tau }_{\mathrm{D}}}\right)\right]\end{array}$$

(61)

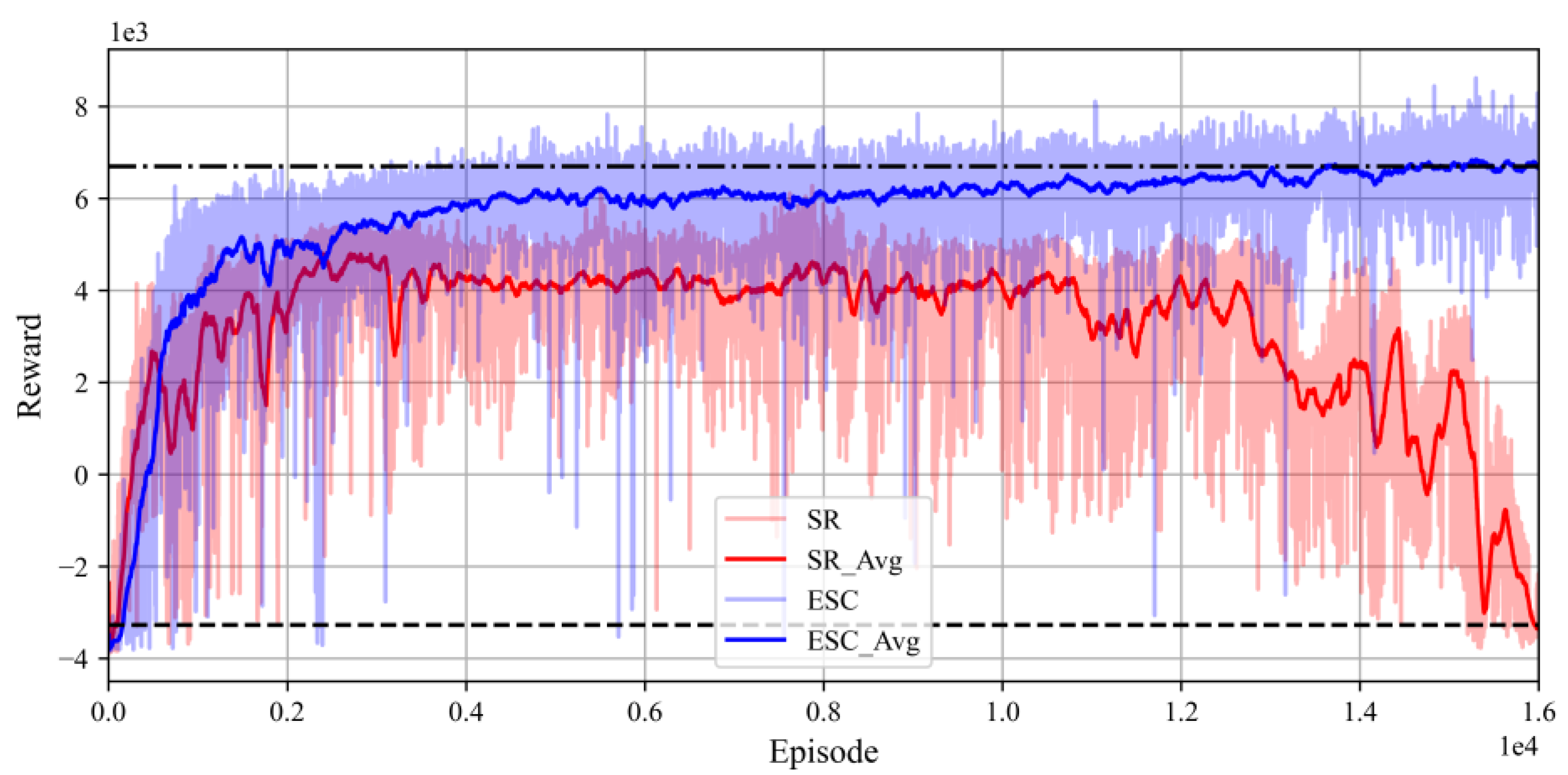
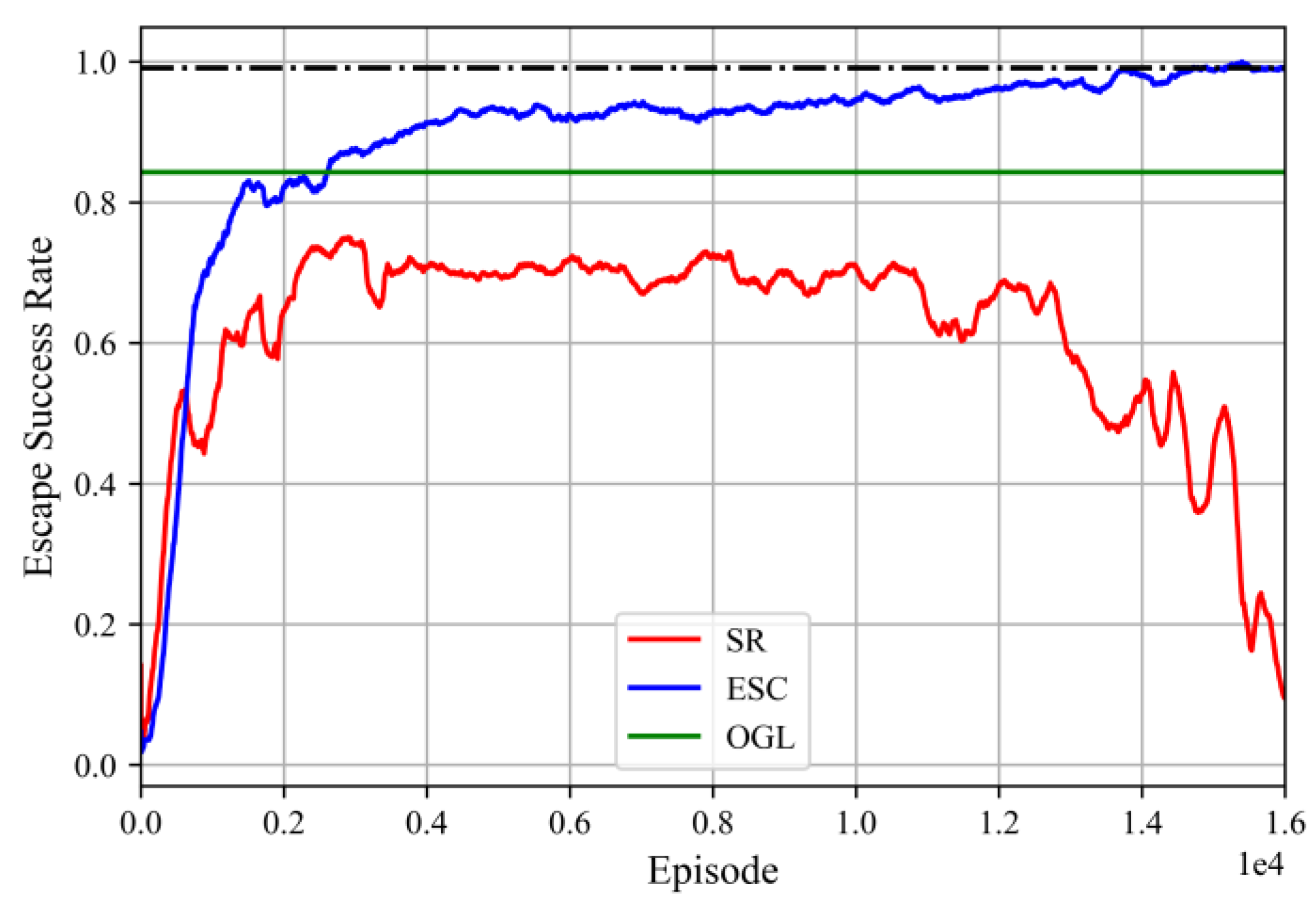
4.4.2. Convergence and Escape Success Rate

Figure 6 displays the learning curves depicting the mean accumulated reward across learning episodes for various scenarios. As depicted, in the ESC case, the agent’s reward consistently escalated throughout the training episodes, ultimately stabilizing at around 6000 after 4000 iterations. Conversely, within the sparse reward (SR) framework, the ICAAI encountered a plateau phenomenon during training, resulting in an unstable convergence process for the associated reward function and eventual convergence failure.

Figure 7 presents success rate curves for target evasion over learning episodes, comparing agents trained with and without ESC. The green line denotes OGL’s deterministic environment success rate of 83.4%. The ESC-trained agent surpassed the baseline by 2700 episodes, achieving a peak performance of 99% after around 13,800 episodes. Conversely, the agent without ESC exhibited a gradual decline in performance after reaching a zenith of 77%, signifying policy network overfitting during continued training. The ESC-trained agent demonstrated accelerated convergence and improved local optima. It can be inferred that the proposed ESC training approach effectively organizes exploration, addressing sparse reward issues and showcasing heightened learning efficiency and asymptotic performance. Furthermore, the proposed methodology adeptly mitigates overfitting phenomena.

4.4.3. Performance Test

Figure 8 depicts spacecraft trajectories, featuring the interceptor’s actual path (blue curve) and the observed trajectory from the target’s perspective (yellow curve). Figure 9 displays the lateral acceleration profiles for each spacecraft, while Figure 10 illustrates the ZEM measurements between the target and interceptor and between the defender and interceptor. The simulation results presented in Figure 11 reaffirm the impact of the relative distance between the target and defender $di{s}_{\mathrm{DT}}$ on the game outcomes for the target.

Figure 8, Figure 9 and Figure 10 illustrate the evident cooperation between the target and the defender, utilizing relative state information. Taking the simulation results at $di{s}_{\mathrm{DT}}=10\mathrm{km}$ as an example, the miss distance between the target and the interceptor was approximately 15 m. The defender maintained a miss distance of less than 1 m from the interceptor, confirming its successful interception threat. Figure 9 and Figure 10 depict that, within 16 s of the scenario’s initiation, the target collaborated with the defender, executing subtle maneuvers to intercept the interceptor. At around the 16 s mark, the interceptor perceived the threat and initiated an escape strategy. Simultaneously, the target executed an evasive maneuver in the opposite direction, utilizing its maximum maneuverability, which resulted in an increase in distance. Ultimately, the interceptor managed to evade the defender’s interception attempt but failed to intercept the target in time, leading to the target’s successful evasion.

In addition, the above simulation results show that the relative distance between the target and defender $di{s}_{\mathrm{DT}}$ directly determines the time it takes for the interceptor to intercept the target after evading the defender. Consequently, $di{s}_{\mathrm{DT}}$ significantly influences the game outcomes for the target, including the success rate of evasion and miss distance. Therefore, to explore the effect of $di{s}_{\mathrm{DT}}$ on the performance of ICAAI, the game results for $di{s}_{\mathrm{DT}}$ ranging from 0 to 15 km are introduced in Figure 11.

As evident from Figure 11, employing the ICAAI intelligent game algorithm results in the target achieving success rates of no less than approximately 90% when the relative distance to the defender is less than 10 km. However, as the $di{s}_{\mathrm{DT}}$ increases from 10 to 15 km, the success rate of target evasion decreases from 90% to 0%. These simulation results illustrate that a smaller relative distance leads to an increased evasion success rate. Additionally, the curve depicting the average miss distance for the target reveals that the miss distance follows a pattern of initially increasing and then decreasing with $di{s}_{\mathrm{DT}}$. The miss distance reaches its maximum value of approximately 50 m around a relative distance of 5 km. The occurrence of this phenomenon can be attributed to the fact that, when $di{s}_{\mathrm{DT}}$ is less than 5 km, the miss distance increases with the target’s evasion time. Moreover, at this point, the interceptor has not had sufficient time to alter its trajectory to intercept the target. Conversely, when $di{s}_{\mathrm{DT}}$ exceeds 5 km, the interceptor has ample time to intercept the target after evading the defender. Consequently, the miss distance decreases with an increasing $di{s}_{\mathrm{DT}}$.

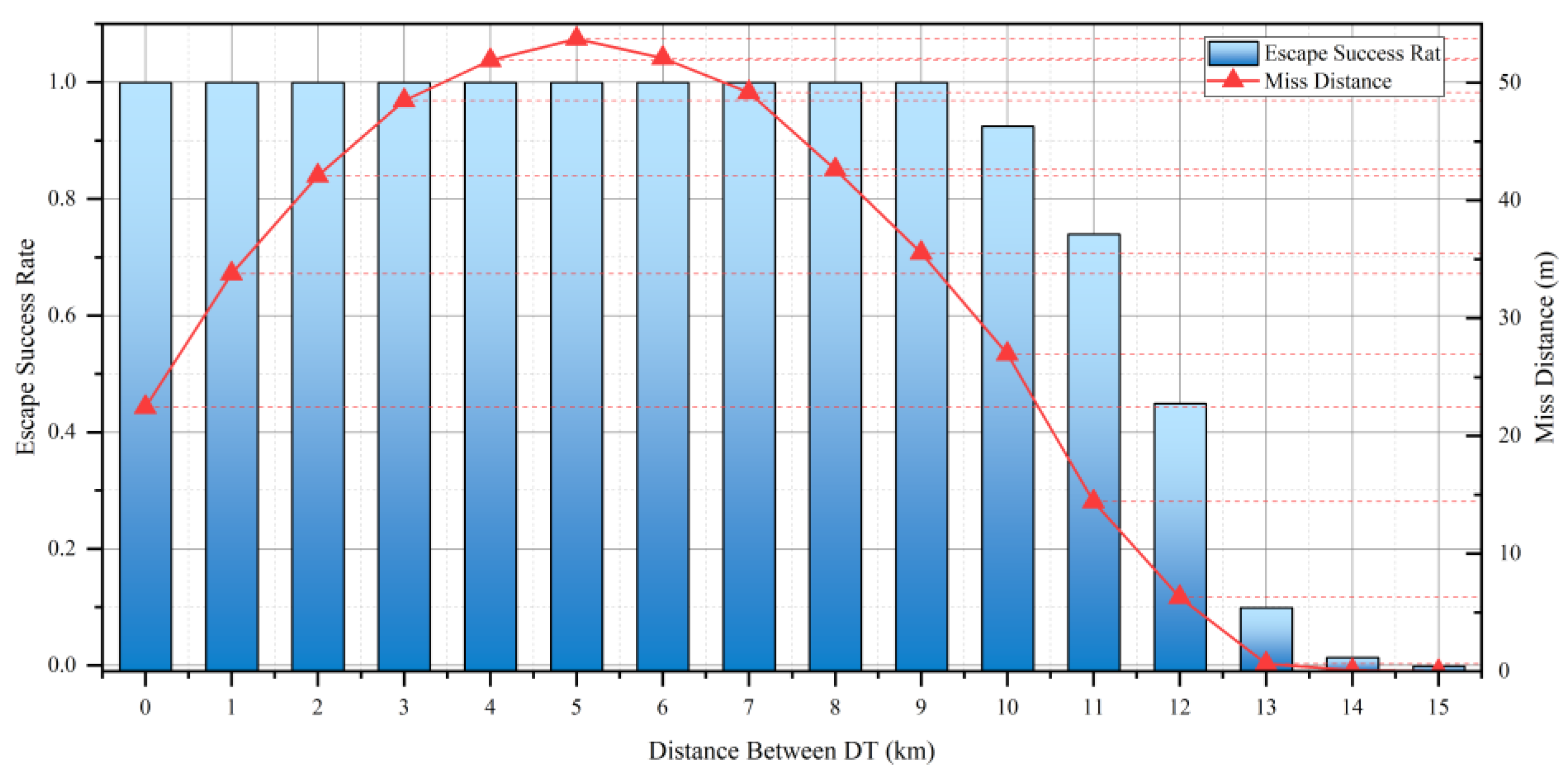
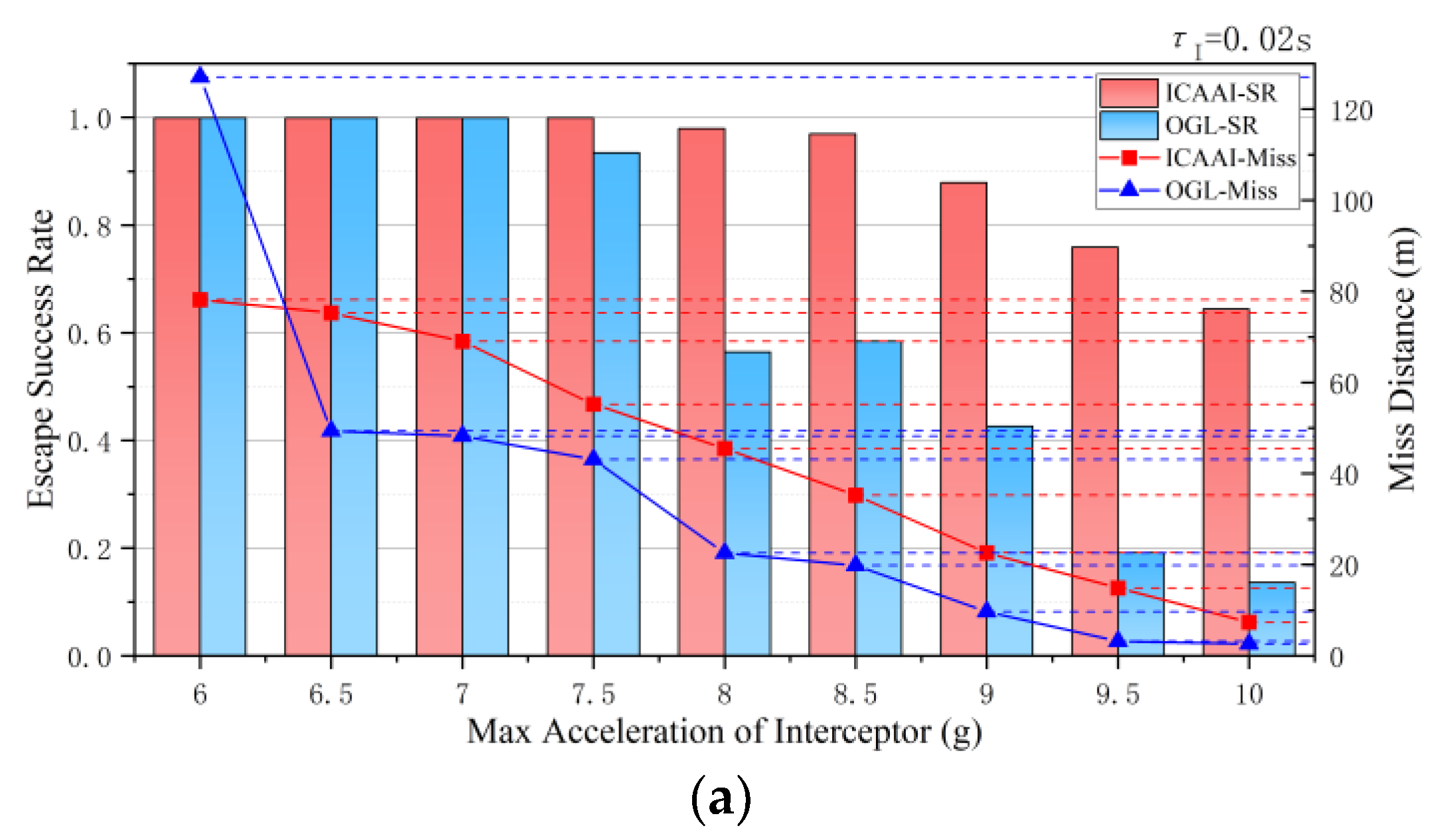
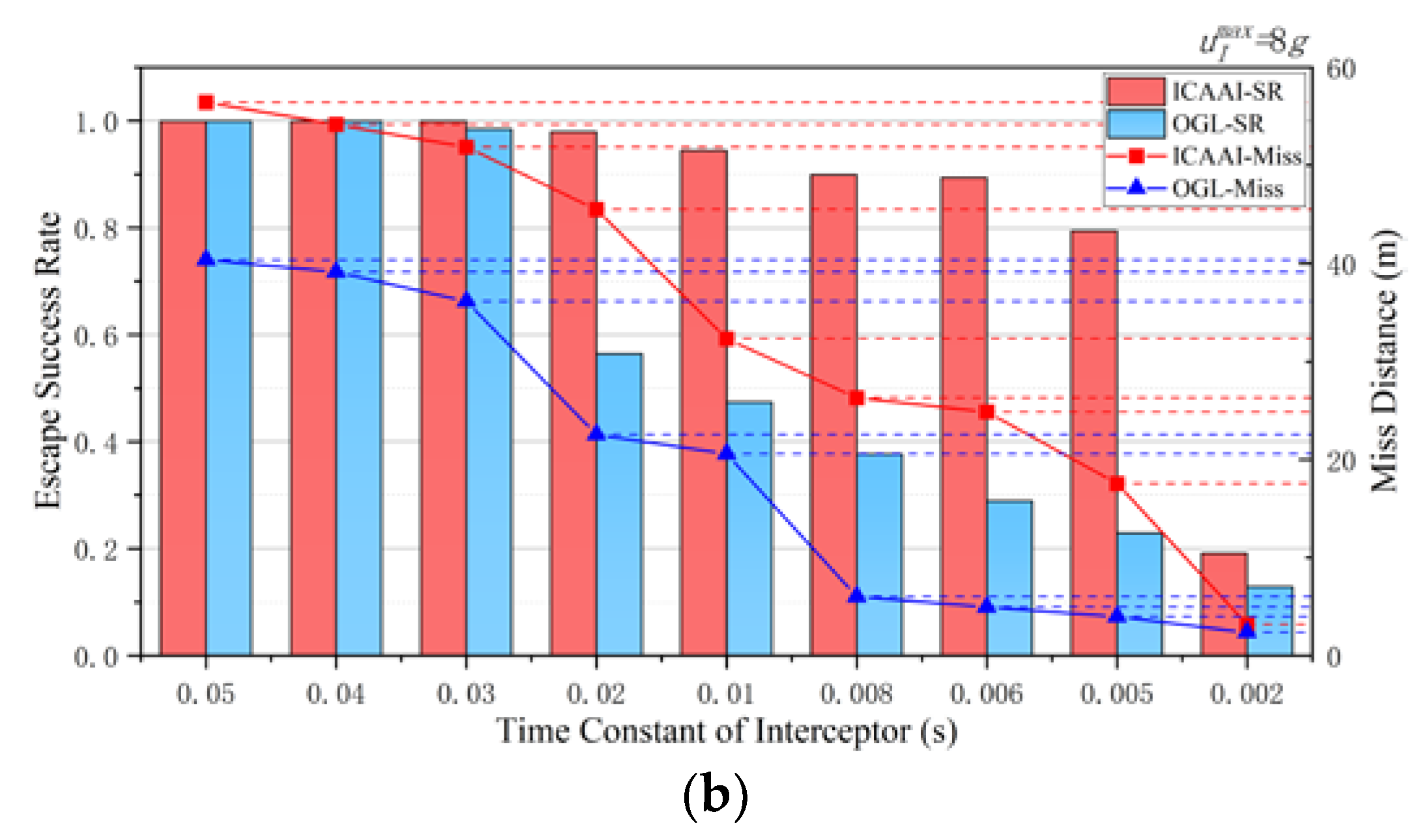
4.5. Experiment 3: Adaptiveness of the ICAAI Guidance

In the real-world game confrontation process, obtaining the opponent’s prior knowledge, such as the maximum acceleration and time constant, is often impractical. To assess the proposed ICAAI guidance method’s superior adaptability compared to the OGL method under conditions of unknown opponent knowledge, several comparison conditions were designed and evaluated using the Monte Carlo target shooting method. The adaptive capabilities of both methods were analyzed based on the game results (escape success rate and miss distance) of the target spacecraft employing the two strategies.

While the target utilized OGL guidance, we considered it adopting ${\overline{u}}_I^{\max }=8$ g, ${\overline{\tau }}_I=0.02$ s as the prediction of the prior knowledge of the interceptor, while the actual $u_I^{\max }=6~10$ g, $\tau =0.05~0.002$ s. The simulation results are shown in Figure 12.

As depicted in Figure 12a, as the interceptor’s maneuverability improves, the target’s escape ability decreases for both guidance methods. However, it is evident that, when employing the ICAAI guidance, the rate of decline in the target’s escape ability is significantly lower compared to the OGL guidance method. Similarly, Figure 12b demonstrates that an increase in the interceptor’s response speed yields a similar trend in the target’s escape ability as in Figure 12a. Specifically, when accurately estimating the prior knowledge of the target, the escape abilities of both methods are comparable. However, when the prior knowledge error exceeds 25%, the OGL guidance leads to a reduction of over 75% in the target’s escape ability, while the ICAAI guidance results in less than a 34% decrease. In conclusion, the proposed ICAAI guidance exhibits superior adaptability compared to the OGL guidance when the interceptor’s prior knowledge is unknown.

Remark 2.

As an analytical method, the SOGL is stable but inflexible due to its theoretical framework [46] and stringent assumptions [47]. Correspondingly, the ICAAI control strategies are flexible and can be continuously optimized. The proposed method is independent of the time constant, which means that it performs better with less prior knowledge than the OGL. Furthermore, the adaptability of the proposed method can be improved by considering the tolerance of the maximum interceptor acceleration.

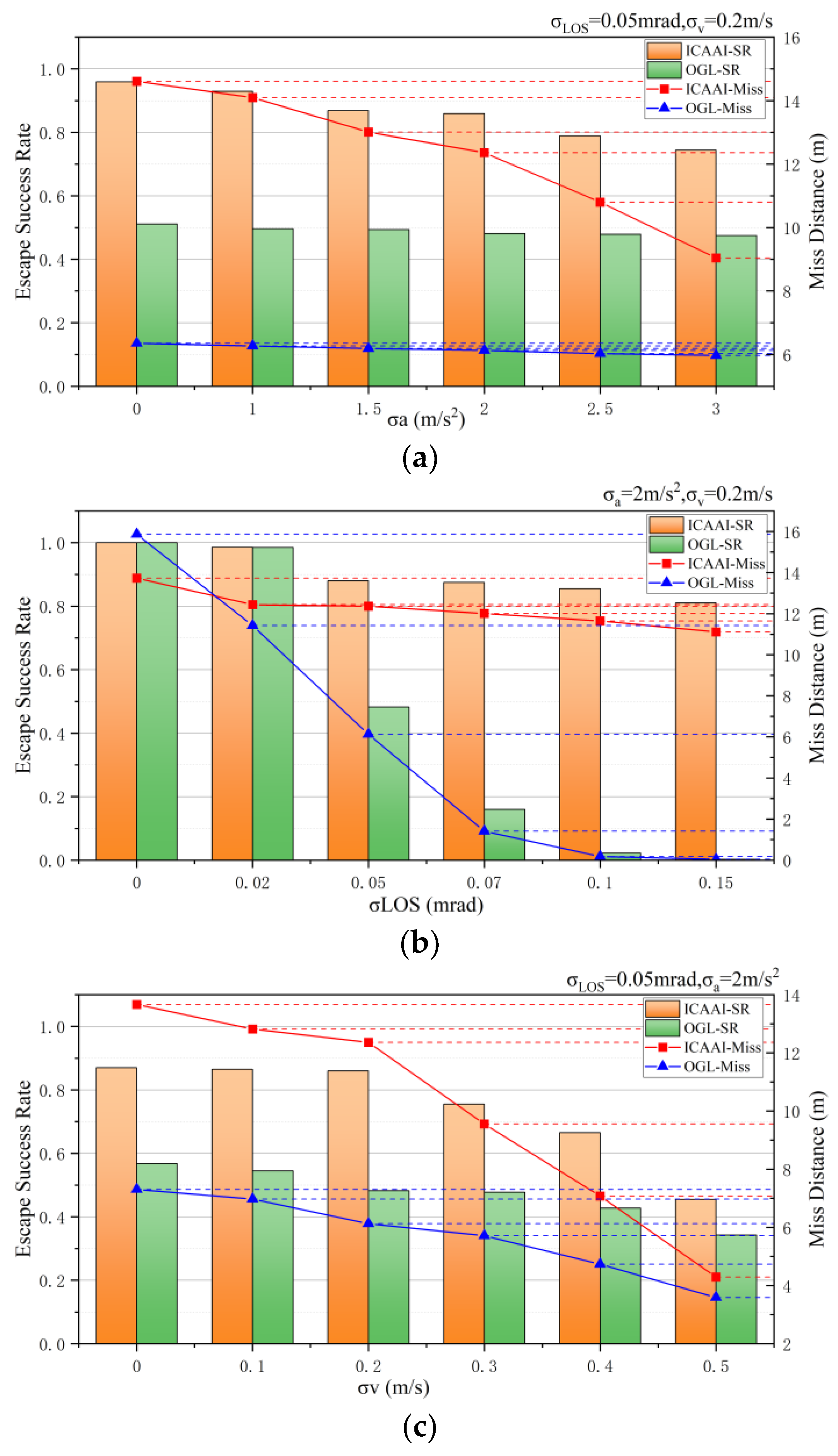
4.6. Experiment 4: Robustness of the RL-Based Guidance Method

In addition to the unperturbed, fully observable game, the following noisy, partially observable game studies have been analyzed separately in this manuscript. The parameters used to describe the imperfect information model defined in Section 3 are shown in

Table 5. Parameters of the different imperfect information models.

Measurement Noise	Parameter	Case 1	Case 2	Case 3
LOS	${\sigma }_{LOS}\left(\mathrm{mrad}\right)$	0.05	0~0.2	0.05
Velocity	${\sigma }_v\left(\mathrm{m/s}\right)$	0.2	0.2	0~0.5
Acceleration	${\sigma }_a\left(\mathrm{m/s}\right)$	1~3	2	2

. The Monte Carlo simulation method is used to obtain the escape success rate and the miss distance of the target using the proposed ICAAI guidance and SOGL guidance under different noise conditions. The results of the Monte Carlo simulation are shown in Figure 13.

Based on the simulation results of Case 2, it was observed that the OGL method exhibited significant sensitivity to LOS noise. In scenarios without LOS noise, the escape success rate of the proposed ICAAI guidance matched that of the OGL guidance, and, in some cases, the OGL method even achieved a larger miss distance. However, as the LOS noise variance increased to 0.05 mrad, the success rate of the OGL method dropped to approximately 50%. Eventually, at a LOS noise variance of 0.15 mrad, the target was practically unable to escape using the SOGL method, while the ICAAI guidance still maintained an escape success rate of around 80%.

Analyzing the simulation results of Case 1 and Case 3, it was found that due to the presence of LOS noise, the target employing the OGL method exhibited reduced sensitivity to acceleration and velocity noise. Nevertheless, its escape capability remained weaker compared to that of the ICAAI guidance. This could be attributed to the policy network propagating observation information with different weights, leveraging the exploration mechanism of reinforcement learning (RL). Consequently, training the agent in a deterministic environment resulted in a robust guidance policy with strong noise-resistant ability.

5. Conclusions

In this research, we solved the cooperative active defense guidance problem for a target with active defense attempting to evade an interceptor. Based on deep reinforcement learning algorithms, a collaborative guidance strategy termed ICAAI was formulated to enhance active spacecraft defense. Monte Carlo simulations were conducted to empirically substantiate the real-time performance, convergence, adaptiveness, and robustness of the introduced guidance strategy. The conclusions are stated as follows:

(1)

In the presence of less prior knowledge and observation noise, the proposed ICAAI guidance strategy is effective in achieving a higher success rate of target evasion by guiding the target to coordinate maneuvers with defensive spacecraft.

(2)

Utilizing a heuristic continuous reward function and an adaptive progressive curriculum learning method, we devised the ESC training approach to effectively tackle issues of low convergence efficiency and training process instability in ICAAI.

(3)

The ICAAI guidance strategy outperforms the linear–quadratic optimal guidance law (LQOGL) [10] in real-time performance. This framework also achieved an impressive update frequency of ${10}^3$ Hz, demonstrating substantial potential for onboard applications.

(4)

Simulation results confirm ICAAI’s effectiveness in reducing the relative distance between interceptor and defender, enabling successful target evasion. In contrast to traditional OGL methods, our approach exhibits enhanced robustness in noisy environments, particularly in mitigating line-of-sight (LOS) noise.