Young Duality for Variational Inequalities and Nonparametric Method of Demand Analysis in Input–Output Models with Inputs Substitution: Application for Kazakhstan Economy

Abstract

The global macroeconomic shocks of the last decade entail the restructuring of national production networks and induce processes of input substitution. We suggest mathematical tools of Young duality for variational inequalities for studying these processes. Based on the tools we provide, a new mathematical model of a production network with several final consumers is created. The model is formulated as a pair of conjugated problems: a complementarity problem for optimal resource allocation with neoclassical production functions and the Young dual problem for equilibrium price indices on network products. The solution of these problems gives an equilibrium point in the space of network inter-industry flows and price indices on goods. Based on our previous results, we suggest an algorithm for model identification with an official economic statistic in the case of constant elasticity of substitution production functions. We give an explicit solution to the complementarity problems in this case and develop the algorithm of the inter-industry flows scenario projection. Since the algorithm needs the scenario projection of final sales structure as its input, we suggest a modified methodology that allows the calculation of scenario shifts in final consumer spending. To do this, we employ the generalized nonparametric method of demand analysis. As a result, we develop new technology for scenario calculation of a national input–output table, including shifts in final consumer spending. The technology takes into account a substitution of inputs in the network and is based on officially published national statistics data. The application of the methodology to study tax collection scenarios for Kazakhstan’s production network is demonstrated.

1. Introduction

The current period of deglobalization and various economic shocks are leading to structural changes in regional economies. Macroeconomic analysis of the consequences of major government decisions in the context of shocks is relevant from the perspective of efficiently restructuring production networks in new economic conditions. Such analysis should take into account the interests of all major agents in the network, including the economic interests of different groups of final consumers (households, government, etc.). In this article, we propose a framework that allows for the analysis of the evolution of regional production networks taking into account the interests of final consumers. Our framework is based on modifications we have developed in the field of input–output (IO) analysis that consider input substitution in the network [1] coupled with an evaluation of the preferences of final consumers in the economy, based on a nonparametric demand analysis method [2]. The synthesis of models enables macroeconomic analysis of the evolution of inter-industry flows and the interests of different groups of final consumers in the regional production network resulting from the implementation of government economic policy programs or shocks.

Input–output analysis is a powerful tool for analyzing the balance of regional economies and scenario forecasting of inter-industry linkages under shock conditions. Traditionally, analysis is based on the Leontief model which describes the balance of the production network under the assumption of constant coefficients of direct costs [3,4]. This approach and its modifications are well developed and have applications in various sectors of the economy [5,6,7].

The restructuring of supply chains under deglobalization leads to input substitution in production networks. Input substitution is difficult to consider within the Leontief model [8]. The constancy of direct cost coefficients does not assume substitution, and direct modifications to the model with input substitution are limited in their applicability and often difficult to identify [9,10].

A more general approach to analyzing equilibrium in open production networks is the formulation of the optimal resource allocation problem in the form of a variational inequality and its special case, the complementarity problem that takes into account input substitution in the network. This approach, combined with the special case of duality, Young duality theory, allows for the solution of more general problems of forecasting economic equilibrium in an open production network [1]. We studied specific cases of the model with production technologies with a constant elasticity of substitution (CES), developed a methodology for model identification based on IO statistics tables of an economy, and demonstrated its applications to modern production networks (for example, see [11]).

In terms of the generalized model equilibrium, inter-industry flows and equilibrium product price indices in the production network are calculated as the solution to the complementarity problem and its corresponding Young dual problem, depending on the scenario-defined aggregate vector of final consumption and price indices for external resources. At the same time, the question remains open as to the correspondence of the competitive equilibrium found to the interests of different groups of final consumers. The employment of variational inequality representation allows us to consider a set of final consumers in the model. However, the projection of national production network structure with the developed model needs the input data of final consumption vectors of each final consumer for a projected year. These data are not usually included in official national macroeconomic forecasts. We suggest an algorithm for demand projection that is based on final consumer demand function calculation with the officially published time row of final sales flows and the corresponding time row of price indexes whose elements are the Young dual problem solutions for each year. The nonparametric method of trade statistics analysis [12,13] was used, which is based on Pareto’s theory of consumer demand [14], allows for the calculation of Konyus demand and price indices, and takes into account changes in consumption structure [2]. The calculation method is based on the well-known Floyd–Warshall algorithm [15,16] and is applicable to actual trade statistics data.

In this article, we propose a new methodology for analyzing and forecasting regional inter-industry balance taking into account the interests of final consumers in the production network. The methodology is based on the synthesis of a generalized inter-industry balance model based on variational inequalities and analysis of final demand using a generalized nonparametric method. It seems that this approach is new and has no analogues in the scientific literature.

We employ the complementarity problem theory and a special Young dual problem for equilibrium inter-industry cash flows and price calculation. Since in our applications we find an explicit solution to the problem, in this article we do not touch on general issues related to the existence and uniqueness of solutions to the variational inequalities. These problems may be points of further study. At the same time, the field is widely represented in the scientific literature for various problem statements. The solution and existence of economic equilibrium as corresponding variational inequality representation are studied in [17,18,19,20]. The existence problem of solutions for some kind of variational inequalities with monotone operators in nonreflexive Banach spaces are studied in [21]. Equilibrium problems and variational inequalities under generalized monotonicity assumptions on cost functions are discussed in [22]. The existence and uniqueness of solutions are proved for both scalar and vector problems in [22] as well.

The existing general numerical methods for calculation of an economic equilibrium employing the variational inequality technique, such as [23,24,25,26,27,28], rely on monotonicity. In contrast to these results, our technique for determining the inter-industry equilibrium point does not employ the monotonicity property. The technique is based on the calculation of an explicit solution of the variational inequality which corresponds to the initial nonlinear optimization problem as the solution of a special type of a dual variational inequality based on Young transform. The dual problem for equilibrium price indexes is reduced to solving the system of nonlinear algebraic equations. The obtained results allow us to present a clear algorithm of regional production network equilibrium scenario projection.

Among related research, it is worth noting the cycle of works on network economics by Nagurney [29,30], where the apparatus of game theory and variational inequalities is used to analyze equilibrium in supply chains with different topologies, with applications in food, labor, healthcare, etc. Note that in contrast to our results, the equilibrium is found in that work by fixed price assumption.

Another close cycle of research related to the analysis of competitive equilibrium of complex production networks belongs to Acemouglu, Carvalho with co-authors (see [31,32,33,34]). In these works, the propagation of shocks is analyzed using examples of production networks with different topologies and nonlinear production functions.

The difference and novelty of our approach is the use of Young duality theory, which allows for the construction of the Young dual optimization problem to find equilibrium prices in the production network. Moreover, in the case of CES class technologies, the solution to the problem of finding competitive equilibrium in the space of supply volumes and prices has a clear algorithm of solution, and variational inequality representation combined with the nonparametric method allows for analysis of the individual interests of final consumers. This result seems to be useful for government decision-making processes.

This paper is organized as follows.

Section 2.1 includes the generalization of the input–output (IO) balance optimization model with substitution of inputs for an open production network which we provide in [1]. We give the basic definitions and state the resource allocation problem in terms of a complementarity problem. We pose the corresponding Young dual problem for equilibrium prices.

Section 3 presents the key points for applications of the model in the case of constant elasticity of substitution (CES) production: the solution of the inverse identification problem and the scheme of the scenario input—output table evaluation. We have presented this technology in several articles. For example, see [11].

In Section 4, we present the new framework for production network cash flow forecasting, including final demand flows of groups of agents. Our approach is based on the synthesis of the IO balance model with CES technologies and the nonparametric method of demand analysis. We provide a summary of the results of the nonparametric method of demand analysis, which gives an algorithm of Konyus–Divisia indices (for price and volume) evaluation [2].

Section 5 focuses on the application of our framework. We use our previous results [11] where we identified the IO balance model with CES technologies for an actual high aggregated production network of Kazakhstan. We apply the synthesis of the obtained IO balance model of Kazakhstan and the nonparametric method to evaluate and analyze a Kazakhstan production network of 2022 and final consumer interests in a scenario of changes of budget expenditures secured by tax revenues.

The Conclusion highlights the main results and advantages of the developed framework for applications in government decision-making processes.

2. Variational Inequalities and Young Duality in Input–Output Models with Substitution of Inputs: Baseline Framework

Variational inequalities theory was first developed to deal with equilibrium problems and was widely extended as a useful tool for the study of optimization problems, operations research, and applications in many fields [30,35,36,37,38] In this section, we apply finite-dimensional variational inequalities and the special duality theory that we call Young duality [1,39] for the formalization of production networks with substitution of inputs.

2.1. Finite-Dimensional Variational Inequality: Basic Definitions and Facts

In this section, we give the base definitions and representations of rational behavior problems of economic agents in terms of variational inequality.

Following [40,41], the variational inequality is a pair $\left(A,f\right)$, where $A\subset R^n$, $f:A\to 2^{R^n}$. The vector $\widehat{x}\in A$ is a solution of the variational inequality $\left(A,f\right)$, if there exists $p\in f\left(\widehat{x}\right)$$〈p,\widehat{x}〉\ge 〈p,x〉$ for any $x\in A$.

Here and below, $〈y,x〉$ denotes the inner product of a pair of vectors y and x.

Let A be a convex subset of ${\mathbb{R}}^n$ and $F:{\mathbb{R}}^n\to \mathbb{R}$ be a concave function. Consider the convex programming problem

$$\underset{x\in A}{max}F\left(x\right)$$

(1)

Proposition 1 

([1]). For $\widehat{x}\in A$ to be a solution to the convex programming problem (1), it is necessary and sufficient that $\widehat{x}$ be a solution to the variational inequality $\left(A,\partial F\right)$. Here, $\partial F$ is a superdifferential of F.

Variational inequality is useful for modeling the rational behavior of economic agents. Consider a normal-form game $\Gamma =\left\{N,{\left\{X_i\right\}}_{i\in N},{\left\{u_i\left(x_i,x_{-i}\right)\right\}}_{i\in N}\right\},$

where $X_i$—convex compact set, $u_i\left(x_i,x_{-i}\right)$ is concave by $x_i\in X_i$ for any fixed strategies of other players $x_{-i}\in X_{-i}$. The set $X=X_1\times \dots \times X_n$.

Construct the multivalued mapping

$$G\left(x\right)={\partial }_{x_1}{u}_1\left(x_1,x_{-1}\right)\times \dots \times {\partial }_{x_n}{u}_n\left(x_n,x_{-n}\right).$$

Proposition 2 

([1]). The outcome $\widehat{x}$ of $\Gamma =\left\{N,{\left\{X_i\right\}}_{i\in N},{\left\{u_i\left(x_i,x_{-i}\right)\right\}}_{i\in N}\right\}$ is Nash equilibrium if and only if $\widehat{x}\in A$ is a solution of variational inequality $\left(X,G\right)$.

In the special case, when we operate with a convex cone as a feasible set, a variational inequality turns to a complementarity problem. The basic competitive equilibrium model for a system of agents is the Arrow–Debreu model [42]. Under the condition of equality of demand and supply of goods (Walras’ law in the narrow sense), the question of the existence of competitive equilibrium is reduced to the existence of a corresponding complementarity problem solution.

Proposition 3 

([1]). Let A be a convex cone. The vector $\widehat{x}\in A$ is a solution of the variational inequality $\left(A,f\right)$ if and only if there exists a linear functional $p\in \left(-A^{*}\right)\cap f\left(\widehat{x}\right)$ such that $〈p,\widehat{x}〉=0$, where $A^{*}$ is the conjugate cone to the cone A.

See [1] for detailed proofs of Propositions 1–3.

In a narrow sense, Walras’ law assumes strict equality between costs of demand and supply. Therefore, in the Arrow–Debreu model, the vector of equilibrium prices is determined up to multiplication by a positive factor.

The apparatus of variational inequalities can be applied to construct the vector of equilibrium prices in the case of Walras’ law in a broad sense (the cost of demand should not exceed the cost of supply at any non-zero prices). Let A be the set of supply vectors of final goods and services in the economy, and let $g\left(p\right)$ be a multivalued (in general) mapping that determines the total demand of consumers depending on the price vector p. Let

$$g^{-1}\left(x\right)=\left\{p\left|x\in g\left(p\right)\right.\right\}$$

be the inverse demand mapping. If $\widehat{x}\in A$ is a solution to the variational inequality $\left(A,g^{-1}\right)$, then (by definition) there exists $p\in g^{-1}\left(\widehat{x}\right)$ such that $〈p,\widehat{x}〉\ge 〈p,x〉$ for any $x\in A$. Then, p is the vector of equilibrium prices. The vector of equilibrium prices is analogous to Lagrange multipliers in optimization models. The traditional economic interpretation of Lagrange multipliers for resource balance constraints is their interpretation as prices for resources. This interpretation is based on the construction and analysis of the dual problem. In the next section, we construct such a problem for the resource allocation problem in an open production network cluster.

2.2. Model of Production Cluster as an Element of Production Network Resource Allocation Problem and Young Duality

This section summarizes propositions that we proved in the article [1].

Let us describe the total set of supply vectors for final goods and services based on the input–output balance model. Consider an open production network cluster with the following structure:

• m pure industries which produce goods $1,\dots ,m$;
• n production factors, which are inputs of industries but are not produced in the cluster;
• one aggregate final consumer with final consumption vector of cluster’s products $X^0=\left(X_1^0,\dots ,X_m^0\right)$;
• The final consumer buys products $X^0$ at prices $\widehat{p}=({\widehat{p}}_1,\dots ,{\widehat{p}}_m)>0$;
• $X^j=\left(X_1^j,\dots ,X_m^j\right)$ - intermediate inputs of industry j;
• $l^j=\left(l_{INT}^j,l_{EXT}^j\right)$ - external (for the cluster) inputs of industry j with primary resources (inputs) of the cluster’s industries $l_{INT}^j=\left(l_{1,INT}^j,\dots ,l_{n,INT}^j\right)$ and imported into the cluster resources $l_{EXT}^j=\left(l_{1,EXT}^j,\dots ,l_{k,EXT}^j\right)$ given by statistics price indexes $s=(s_{INT},s_{EXT})$;

  $$s_{INT}=\left(s_{1,INT},\dots ,s_{n,INT}\right),s_{EXT}=\left(s_{1,EXT},\dots ,s_{k,EXT}\right),$$
• $L_{INT}=\left(L_{1,INT},\dots ,L_{n,INT}\right)\ge 0$ is a total available volume of primary inputs for the network, i.e.,

  $$\sum _{j=1}^m{l}_{i,INT}^j\le L_{i,INT},i=1,\dots ,n,$$
• $L_{EXT}\left(L_{1,EXT},\dots ,L_{k,EXT}\right)\ge 0$ is a total available volume of external intermediate inputs of the cluster, i.e.,

  $$\sum _{j=1}^m{l}_{i,EXT}^j\le L_{i,EXT},i=1,\dots ,k,$$
• The output of each industry $j=1,\dots ,m$ is given by the neoclassical production function $F_j\left(X^j,l_{INT}^j,l_{EXT}^j\right)\in {\Phi }_{m+n+k}$, where ${\Phi }_{m+n+k}$ is the set of concave, monotonically nondecreasing, continuous, and positively homogeneous degree one functions on $R_{+}^{m+n+k}$, $F_j\left(0,0,0\right)=0$.

Note that

$$X^0\left(\widehat{p},s_{EXT}\right)=X^{int}\left(\widehat{p},s_{EXT}\right)+X^{exp}\left(\widehat{p},s_{EXT}\right),X^{int}\left(\widehat{p},s_{EXT}\right)>0,X^{exp}\left(\widehat{p},s_{EXT}\right)\ge 0.$$

where $X^{int}$ is a vector of internal final consumption of products and $X^{exp}$ is a vector of export of cluster’s products.

Let each technology use at least one type of primary input (labor, for ex.). The dual description of the production technology of the j-th industry is the cost function [43]

$$\begin{array}{c}{q}_j\left(\widehat{p},s_{INT},s_{EXT}\right)=\hfill \\ inf\left\{\frac{\widehat{p}{X}^j+s_{INT}{l}_{INT}^j+s_{EXT}{l}_{EXT}^j}{F_j\left(X^j,l_{INT}^j,l_{EXT}^j\right)}\left|X^j\ge 0,l_{INT}^j\ge 0,l_{EXT}^j\ge 0,F_j\left(X^j,l_{INT}^j,l_{EXT}^j\right)>0\right.\right\}.\hfill \end{array}$$

(2)

The cost function $q_j\left(\widehat{p},s_{INT},s_{EXT}\right)$ is called the Yang transform of the production function $F_j\left(X^j,l_{INT}^j,l_{EXT}^j\right)$. Let us assume that the group of industries of the cluster is productive, i.e., the strong inequalities

$$F_j\left({\widehat{X}}^j,{\widehat{l}}_{INT}^j,{\widehat{l}}_{EXT}^j\right)>\sum _{i=1}^m{\widehat{X}}_j^i,j=1,\dots ,m$$

hold for some values

$${\widehat{X}}^1\ge 0,\dots ,{\widehat{X}}^m\ge 0,{\widehat{l}}_{INT}^1,\dots ,{\widehat{l}}_{INT}^m,{\widehat{l}}_{EXT}^1,\dots ,{\widehat{l}}_{EXT}^m\ge 0.$$

Consider the following resource allocation problem

$$\underset{X_j^i}{max}〈\widehat{p},X^0〉$$

(3)

$$F_j\left(X^j,l_{EXT}^j,l_{INT}^j\right)\ge \sum _{i=0}^m{X}_j^i,j=1,\dots ,m$$

(4)

$$\sum _{j=1}^m{l}_{EXT}^j\le L_{EXT},\sum _{j=1}^m{l}_{INT}^j\le L_{INT}$$

(5)

$$X^0\ge 0,X^1\ge 0,\dots ,X^m\ge 0,l_{EXT}^1\ge 0,\dots ,l_{EXT}^m\ge 0,l_{INT}^1\ge 0,\dots ,l_{INT}^m\ge 0.$$

(6)

Denote the feasible set of final consumption vector $X^0$ as $\Gamma \left(L_{EXT},L_{INT}\right)$. Given vectors $\widehat{p},L_{EXT},L_{INT}$ the optimal solution of the task (3)–(6) is a functional $H\left(\widehat{p},L_{EXT},L_{INT}\right)$. Note that for the fixed price vector $\widehat{p}$, the functional $H\left(\widehat{p},L_{EXT},L_{INT}\right)$ is the support function of the set $\Gamma \left(L_{EXT},L_{INT}\right)$. Note that $H\left(\widehat{p},L_{EXT},L_{INT}\right)$ is convex in $\widehat{p}$ (as a support function) and concave in $L_{EXT},L_{INT}$ (as aggregate production function).

In [1], we proved the following proposition.

Proposition 4 

([1]). The set of vectors ${\tilde{X}}^0\ge 0,{\tilde{X}}^1\ge 0,\dots ,{\tilde{X}}^m\ge 0,{\tilde{l}}_{EXT}^1\ge 0,\dots ,{\tilde{l}}_{EXT}^m\ge 0,{\tilde{l}}_{INT}^1\ge 0,\dots ,{\tilde{l}}_{INT}^m\ge 0$ is a solution of the problem (3)–(6) if and only if there exist vectors $p\ge \widehat{p}$, $s_{EXT}\ge 0$, $s_{INT}\ge 0$ that imply

$$\begin{array}{c}\left({\tilde{X}}^j,{\tilde{l}}_{EXT}^j,{\tilde{l}}_{INT}^j\right)\in Argmax\left\{p_j{F}_j\left(X^j,l_{EXT}^j,l_{INT}^j\right)-\right.\\ \left.p{X}^j-s_{EXT}{l}_{EXT}^j-s_{INT}{l}_{INT}^j\left|X^j\ge 0,l_{EXT}^j\ge 0,l_{INT}^j\ge 0\right.\right\},j=1,\dots ,m,\end{array}$$

$$〈s_{EXT},l_{EXT}-\sum _{j=1}^m{\tilde{l}}_{EXT}^j〉=0,〈s_{INT},l_{INT}-\sum _{j=1}^m{\tilde{l}}_{INT}^j〉=0,〈p-\widehat{p},{\tilde{X}}^0〉=0.$$

Moreover,

$$\left(s_{EXT},s_{INT}\right)\in {\partial }_{L_{EXT},L_{INT}}H\left(\widehat{p},L_{EXT},L_{INT}\right),$$

and

$$q_j\left(p,s_{EXT},s_{INT}\right)\ge p_{j}j=1,\dots ,m.$$

In the case of $F_j\left({\tilde{X}}^j,{\tilde{l}}_{EXT}^j,{\tilde{l}}_{INT}^j\right)>0$, the following equality holds

$$q_j\left(p,s_{EXT},s_{INT}\right)=p_j.$$

Recall that ${\partial }_{L_{EXT},L_{INT}}H\left(\widehat{p},L_{EXT},L_{INT}\right)$ denotes superdifferential of $H\left(\widehat{p},L_{EXT},L_{INT}\right)$ with respect to $L_{EXT},L_{INT}$ at a fixed $\widehat{p}$.

In a closed economic system with administrative control of external links, total external inputs are restricted, i.e., values $L_{EXT}$ and $L_{INT}$ are fixed in the resource allocation problem (3)–(6).

Otherwise, in an open economic system, external inputs can be varied with given prices $s_{EXT}$, $s_{INT}$ such that

$$\left(s_{EXT},s_{INT}\right)\in {\partial }_{L_{EXT},L_{INT}}H\left(\widehat{p},L_{EXT},L_{INT}\right)$$

Remark 1 

([1]). $H\left(\widehat{p},L_{EXT},L_{INT}\right)$ is a non-zero, positively homogeneous first degree, concave, continuous, non-negative on the non-negative orthant function.

The dual description of an open cluster we give by the Young transform of the functional $H\left(\widehat{p},L_{EXT},L_{INT}\right)$ with respect to variables $L_{EXT},L_{INT}$ has the form

$$h\left(\widehat{p},s_{EXT},s_{INT}\right)=inf\left\{\frac{〈s_{EXT},L_{EXT}〉+〈s_{INT},L_{INT}〉}{H\left(\widehat{p},L_{EXT},L_{INT}\right)}\left|L_{EXT}\ge 0,L_{INT}\ge 0,H\left(\widehat{p},L_{EXT},L_{INT}\right)\ge 0\right.\right\}.$$

Remark 2 

([1]). The function $h\left(\widehat{p},s_{EXT},s_{INT}\right)$ is a non-zero, positively homogeneous first degree, concave, continuous, non-negative on the non-negative orthant function.

Note that the Young transform is an involution [11], i.e.,

$$H\left(\widehat{p},L_{EXT},L_{INT}\right)=inf\left\{\frac{〈s_{EXT},L_{EXT}〉+〈s_{INT},L_{INT}〉}{h\left(\widehat{p},s_{EXT},s_{INT}\right)}\left|s_{EXT}\ge 0,s_{INT}\ge 0,h\left(\widehat{p},s_{EXT},s_{INT}\right)>0\right.\right\}$$

.

The Young transform of the linear function $\langle \widehat{p},X^0\rangle$ is a fixed proportions function, i.e.,

$$\underset{1\le i\le m}{min}\frac{p_i}{{\widehat{p}}_i}.$$

Then, from [39] (Theorem 1), we obtain the following fact.

Proposition 5 

([1]). The following equality holds

$$h\left(\widehat{p},s_{EXT},s_{INT}\right)=\underset{p}{max}\left\{\underset{1\le i\le m}{min}\frac{p_i}{{\widehat{p}}_i}\left|q_j\left(p,s_{EXT},s_{INT}\right)\ge p_j\ge 0,j=1,\dots ,m\right.\right\}.$$

Remark 3. 

If the cluster output includes the product j, then the cost of j-th production $q_j\left(p,\pi ,s\right)$ does not exceed the price $p_j$ of j-th product. Therefore, the cluster of a production network selects its “production niche” in the feasible technology set I, i.e., it makes a decision regarding the subset $J\subseteq I$ of goods, which are produced by the cluster. By that, the remaining products $I\setminus J$ are imported from other clusters of the network.

Thus, we can define a “production niche” of a production cluster.

Definition 1 

([1]). The set $\left\{J,p\right\}$ is a “production niche” of a cluster J with equilibrium prices p, if $J\subset \{1,\dots ,m\},p\in int{\mathbb{R}}_{+}^J$ and there exist vectors of intermediates and primaries $\left\{{\tilde{X}}^j,{\tilde{l}}_{EXT}^j,{\tilde{l}}_{INT}^j\left|j\in J\right.\right\}$, which imply

$$\begin{array}{c}\left({\tilde{X}}^j,{\tilde{l}}_{EXT}^j,{\tilde{l}}_{INT}^j\right)\in Argmax\\ \left\{p_j{F}_j\left(X^j,l_{EXT}^j,l_{INT}^j\right)-\right.p{X}^j-s_{EXT}{l}_{EXT}^j-s_{INT}{l}_{INT}^j\left|X^j\ge 0,l_{EXT}^j\ge 0,l_{INT}^j\ge 0\right\},j\in J,\end{array}$$

$$X_j^0\left(p,s_{EXT}\right)=F_j\left({\tilde{X}}^j,{\tilde{l}}_{EXT}^j,{\tilde{l}}_{INT}^j\right)-\sum _{i=1}^m{\tilde{X}}_j^i>0,j\in J.$$

In [1], we proved the following theorem.

Theorem 1 

([1]). The set $\left\{J,p\right\}$ is a “production niche” of the cluster with equilibrium prices p if and only if

$$q_j\left(p,s_{EXT},s_{INT}\right)=p_j>0,ifj\in J;q_j\left(p,s_{EXT},s_{INT}\right)\ge p_j,ifj\notin J.$$

Theorem 1 implies that if $\left\{J,p\right\}$ is a “production niche” of the cluster J with equilibrium prices p, then the following equalities hold

$$\begin{array}{c}〈p,X^0\left(p,s_{EXT}\right)〉=\\ {\displaystyle \sum _{j\in J}}\left(p_j{F}_j\left(X^j,l_{EXT}^j,l_{INT}^j\right)-〈p,X^j〉\right)={\displaystyle \sum _{j\in J}}\left(〈s_{EXT},l_{EXT}^j〉+〈s_{INT},l_{INT}^j〉\right).\end{array}$$

Thus, the total cost of external inputs equals the total cost of final consumption of the cluster.

By analogue, the final consumption $X^0\left(p,s_{EXT}\right)$ is shared among the internal and external (exporting) parts

$$X^0\left(p,s_{EXT}\right)=X^{exp}\left(p,s_{EXT}\right)+X^{int}\left(p,s_{EXT}\right),$$

and the trade balance of the production cluster is as follows:

$$〈p,X^{exp}\left(p,s_{EXT}\right)〉-\sum _{j\in J}〈s_{EXT},l_{EXT}^j〉.$$

The assessment of savings and current capital outflow is as follows

$$\sum _{j\in J}〈s_{INT},l_{INT}^j〉-〈p,X^{int}\left(p,s_{EXT}\right)〉.$$

Note that by international trade, the trade balance is governed by national currency exchange rates.

2.3. Young Duality in Production Network with M Clusters

Let $F_j^{\alpha }\left(X^{j\alpha },l^{j\alpha }\right)\in \Phi$ be a production function of industry j of the cluster $\alpha$, with

• Intermediate inputs $X^{j\alpha }$ which are produced by the whole set of clusters of the production network;
• Primary inputs $l^{j\alpha }$, which are internal primaries for the cluster $\alpha$.

By analogy with the previous section, we assume that the system of clusters is productive.

The cost function of the j-th industry of the cluster $\alpha$ depends on the price index vector p for products as well as on primary input costs $s^{\alpha }$ of the cluster $\alpha$ and is given by the Young transform of $F_j^{\alpha }\left(X^{j\alpha },l^{j\alpha }\right)$

$$q_{j\alpha }\left(p,s^{\alpha }\right)=\underset{X^{j\alpha },l^{j\alpha }}{inf}\left\{\frac{〈p,X^{j\alpha }〉+〈s^{\alpha },l^{j\alpha }〉}{F_{j\alpha }\left(X^{j\alpha },l^{j\alpha }\right)}\left|X^{j\alpha }\ge 0,l^{j\alpha }\ge 0,\right.F_{j\alpha }\left(X^{j\alpha },l^{j\alpha }\right)>0\right\}.$$

Let us denote by $L^{\alpha }$ the total supply vector of available primary inputs of the cluster $\alpha$. Then, the feasible set $\Gamma \left(L^1,\dots ,L^M\right)$ of final demand vectors $X^0$ is defined by the following system of inequalities

$$\begin{array}{c}{\displaystyle \sum _{\alpha =1}^M}{F}_{j\alpha }\left(X^{j\alpha },l^{j\alpha }\right)\ge {\displaystyle \sum _{\alpha =1}^M}{\displaystyle \sum _{i=1}^n}{X}_j^{i\alpha }+X_j^0,j=1,\dots ,m\\ {\displaystyle \sum _{j=1}^n}{l}^{j\alpha }\le L^{\alpha }\alpha =1,\dots ,M,\\ X^0\ge 0;X_j^{i\alpha }\ge 0;l^{j\alpha }\ge 0j,i=1,\dots ,m,\alpha =1,\dots ,M.\end{array}$$

Let us denote by $H\left(\widehat{p},L^1,\dots ,L^M\right)$ the support function of the set $\Gamma \left(L^1,\dots ,L^M\right)$.

Then, the Young transform of $H\left(\widehat{p},L^1,\dots ,L^M\right)$ in accordance to variables $L^1,\dots ,L^M$ is as follows [1]

$$h\left(\widehat{p},s^1,\dots ,s^M\right)=\underset{p}{max}\underset{j}{min}\left\{\frac{p_j}{{\widehat{p}}_j}\left|\underset{1\le \alpha \le M}{min}{q}_{i\alpha }\left(p,s^{\alpha }\right)\ge p_i>0,i=1,\dots ,m\right.\right\}$$

Let us denote by $X^0\left(p\right)=\left(X_1^0\left(p\right),\dots ,X_m^0\left(p\right)\right)$ final demand functions in the production network with a system of clusters. Now, we define the equilibrium prices for the production network with open clusters.

Definition 2 

([1]). Consider the system of open production clusters $1,\dots ,M$ with primary input price index vectors $\left\{s^{\alpha }\left|\alpha =1,\dots ,M\right.\right\}$. The vector $p>0$ is an equilibrium price vector in a production network with a system of open clusters if there exist

$$\left\{\left({\tilde{X}}^{j\alpha },{\tilde{l}}^{j\alpha }\right)\left|j=1,..,m;\alpha =1,..,M\right.\right\}$$

such that

$$\left({\tilde{X}}^{j\alpha },{\tilde{l}}^{j\alpha }\right)\in \underset{X^{j\alpha }\ge 0,l^{j\alpha }\ge 0}{Argmax}\left\{p_j{F}_{j\alpha }\left(X^{j\alpha },l^{j\alpha }\right)-p{X}^{j\alpha }-s^{\alpha }{l}^{j\alpha }\right\},j=1,..,m;\alpha =1,..,M,$$

$$\sum _{\alpha =1}^M{F}_{j\alpha }\left({\tilde{X}}^{j\alpha },{\tilde{l}}^{j\alpha }\right)-\sum _{\alpha =1}^M\sum _{i=1}^n{\tilde{X}}_j^{i\alpha }=X_j^0\left(p\right)j=1,\dots ,m.$$

Corollary 1 

([1]). Given primary input price index vectors $\left\{s^{\alpha }\left|\alpha =1,\dots ,M\right.\right\}$ for production clusters, the vector $p>0$ is an equilibrium price vector in a production network with a system of open clusters if and only if it gives the solution to the following system

$$\underset{1\le \alpha \le M}{min}{q}_{i\alpha }\left(p,s^{\alpha }\right)=p_i,i=1,\dots ,m.$$

Thus, the output of the cluster $\beta \in 1,\dots ,M$ includes only products whose cost does not exceed their price of final demand. Therefore, the following set is the “production niche” of the cluster $\beta \in 1,\dots ,M$

$$J_{\beta }=\left\{i\left|q_{i\beta }\left(p,s^{\beta }\right)=p_i=\underset{1\le \alpha \le M}{min}{q}_{i\alpha }\left(p,s^{\alpha }\right)\right.\right\}$$

3. Applications of the Model: National Input–Output Table Projection

In this section, we give a summary of results for regional input–output (IO) data evaluation with the developed model. More detailed proofs can be found in [11].

3.1. The Case of Ces Technologies: Young Transform

Consider a local economy with an open production network and final demand with the whole set of final consumers in the economy, including export.

In the case of constant elasticity of substitution (CES) technologies, the model can be evaluated explicitly for the given statistics data of national input–output (IO) tables.

Production functions in the case of CES technologies with intermediate inputs vector $X^j$ and primaries (n products) input vector $l^j$ of the industry $j=1,\dots ,m$ have the form

$$F_j\left(X^j,l^j\right)={\left(\sum _{i=1}^m{\left(\frac{X_i^j}{w_i^j}\right)}^{-{\rho }_j}+\sum _{k=1}^n{\left(\frac{l_k^j}{w_{m+k}^j}\right)}^{-{\rho }_j}\right)}^{-\frac{1}{{\rho }_j}},j=1,\dots ,m,$$

(7)

where ${\rho }_j\in \left(-1,0\right)\cup \left(0,+\infty \right)$, $w_1^j>0,\dots ,w_{m+n}^j>0$, $j=0,\dots ,m$.

Note that the constant elasticity of substitution of industry j equals to

$${\sigma }_j=\frac{1}{1+{\rho }_j},j=1,\dots ,m.$$

The CES cost function of industry j is evaluated by Young transform of $F_j\left(X^j,l^j\right)$ as follows

$$q_j\left(p,s\right)={\left(\sum _{i=1}^m{\left(w_i^j{p}_i\right)}^{\frac{{\rho }_j}{1+{\rho }_j}}+\sum _{k=1}^n{\left(w_{m+k}^j{s}_k\right)}^{\frac{{\rho }_j}{1+{\rho }_j}}\right)}^{\frac{1+{\rho }_j}{{\rho }_j}},j=1,\dots ,m$$

(8)

3.2. Identification of the Model with CES Technologies: Evaluation of National IO Tables

As we showed in the previous section, the nonlinear IO balance model includes the problem of optimal resource allocation (3)–(6) and the Young dual problem and in a general case is posed in the form of variational inequality. Proposition 4 implies that the solution of the dual problem gives equilibrium prices for products of the network. At the same time, inter-industry flows in base year prices are evaluated as a solution of resource allocation problem.

The input data set for identification of the model comprises official national accounts statistics with IO Tables of an economy. The standard form of symmetric IO table Z of domestic products in current prices is shown in

Table 1. Symmetric Input–Output Table of domestic product flows.

		Intermediate consumption	Final consumption	Total output
Symmetric Input-Output Table of domestic products flows		Domestic Products	Housholds, Government, Gross capital formation (+change in inventories), Export
			$Z_1^0$	$Y_1$
		$Z_i^j$	$Z_2^0$	$Y_2$
			…
Domestic products		$i,j=1...m$	$Z_m^0$	$Y_m$
		I Quadrant	II Quadrant
Primary inputs	$\begin{array}{c}\\ \mathrm{Imported}\hfill \\ \\ \mathrm{intermediates}\hfill \end{array}$	$\begin{array}{c}\mathrm{III}\mathrm{Quadrant}\\ \\ Z_{m+1}^j\end{array}$
	$\begin{array}{c}\\ \mathrm{Gross}\hfill \\ \mathrm{Value}\hfill \\ \mathrm{Added}\hfill \end{array}$	$Z_{m+2}^j$ $j=1...m$
Total Output		$Y_1{Y}_2...Y_m$

.

The IO Table has the structure of three quadrants (I,II,III). Quadrant I includes inter-industry cash flows $Z_i^j\ge 0,i,j=1..m$ for the intermediates of industries. Quadrant II presents final consumption flows of the economy (households, government, export, etc.), which we aggregate into a single column vector $Z^0=\left(Z_1^0,..,Z_m^0\right)\ge 0$. Quadrant III includes cash flows $Z_{m+i}^j\ge 0$ from industries for n primary inputs. Note that $n=2$ in the Table 1), i.e., from two rows of primaries for applications: imported intermediate inputs $Z_{m+1}^j$ and gross value added (GVA) $Z_{m+2}^j$, $j=1..m$, which can be considered as the measure of labor employed.

Note that we operate with a production network with the total output of any industry being positive, i.e., $Y_j>0$, $j=1,\dots ,m$.

Remark 4. 

The symmetry of the IO Table Z implies

$$Y_j=\sum _{i=1}^{m+n}{Z}_i^j=\sum _{i=1}^m{Z}_j^i+Z_j^0>0,j=1..m,$$

(9)

$$\sum _{j=1}^m\sum _{i=1}^n{Z}_{m+i}^j=\sum _{i=1}^m{Z}_i^0.$$

(10)

Let us denote

$$a_{ij}=\frac{Z_i^j}{{\sum }_{k=1}^{m+n}{Z}_k^j},b_{kj}=\frac{Z_{m+k}^j}{{\sum }_{k=1}^{m+n}{Z}_k^j},i,j=1..m,k=1..n,$$

(11)

with the following obvious properties

$$\sum _{i=1}^m{a}_{ij}+\sum _{k=1}^n{b}_{kj}=1,\sum _{k=1}^n{b}_{kj}>0,i,j=1..m,k=1..n.$$

Let us denote $\left(m\times m\right)$ matrix A with entry $a_{ij}\ge 0$ and $\left(n\times m\right)$ matrix B with entry $b_{kj}\ge 0$. Note that A is a Leontief matrix with correctly Leontief inverse (here, E is $\left(m\times m\right)$-identity matrix)

$${\left(E-A\right)}^{-1}\ge 0,$$

(12)

Let us fix the base year with known statistics IO Table Z in the form of Table 1. In accordance with (11), we evaluate matrices $A,B$ and parameters of CES technologies (7) as follows

$$w_i^j={\left(a_{ij}\right)}^{\frac{1+{\rho }_j}{{\rho }_j}},w_{m+k}^j={\left(b_{kj}\right)}^{\frac{1+{\rho }_j}{{\rho }_j}},,i,j=1,..,m,k=1,\dots ,n,$$

(13)

In [11], we proved that the solution of the resource allocation problem with CES technologies (7) precisely repeats quadrants I and II of the statistics IO Table of the base year (see [11], Proposition 3) for any fixed values of ${\rho }_j$. This result coupled with solving the Young dual problem (see [11], Proposition 4) and IO table elements representation (see [11], p. 11) provides the following result.

Proposition 6. 

Given vectors of primary inputs price indexes $s=\left(s_1,\dots ,s_n\right)>0$ and total final consumption $Z^0={(Z_1^0,\dots ,Z_m^0)}^T\ge 0$ (in current prices) for a target year, the corresponding equilibrium state of the production network is evaluated as follows:

• Equilibrium price indexes $p_1,\dots ,p_m$ are the solution of the system

  $${\left(\sum _{i=1}^m{a}_{ij}{\left(p_i\right)}^{\frac{{\rho }_j}{1+{\rho }_j}}+\sum _{k=1}^n{b}_{kj}{\left(s_k\right)}^{\frac{{\rho }_j}{1+{\rho }_j}}\right)}^{\frac{1+{\rho }_j}{{\rho }_j}}=p_j,j=1,\dots ,m;$$

  (14)
• Quadrants I and III for a target IO table Z (see Table 1) take the form

  $$\begin{array}{c}{Z}_i^j={\left(\frac{p_i}{p_j}\right)}^{\frac{{\rho }_j}{1+{\rho }_j}}{a}_i^j{Y}_j={\lambda }_{ij}{Y}_j,i,j=1,\dots ,m,\hfill \\ Z_{m+k}^j={\left(\frac{s_k}{p_j}\right)}^{\frac{{\rho }_j}{1+{\rho }_j}}{b}_k^j{Y}_j,k=1,\dots ,n,j=1,\dots ,m;\end{array}$$

  (15)
• Total Output $Y=(Y_1,\dots ,Y_m)$ is evaluated from the balance linear system

  $$Y={\left(E-\Lambda \right)}^{-1}{Z}^0,\Lambda =∥{\lambda }_{ij}∥,{\lambda }_{ij}=a_{ij}{\left(\frac{p_i}{p_j}\right)}^{\frac{{\rho }_j}{1+{\rho }_j}},i,j=1,\dots ,m.$$

  (16)

In Proposition 6, elasticity parameters ${\rho }_j$ are generally indefinite at this stage. However, given official statistics IO Tables for a range of years, we can calibrate the model by Proposition 6 and evaluate ${\rho }_j$, $j=1,\dots ,m$ with some criteria, which give the best model evaluations of macroeconomic values of the network (see [11]). If the elasticity parameters are evaluated ${\rho }_j$, then on the basis of Proposition 6 we obtain a useful tool for IO Table scenario projection.

In [11,43], we applied the developed model for evaluation of a number of regional production networks.

4. Nonparametric Method in Demand Analysis: An Approach to Analysis of Interests of Individual Consumer Groups by Io Model with Ces Technologies

The developed model-based approach to the IO Table scenario projection allows us to project equilibrium inter-industry flows and equilibrium prices in the network by the given scenario conditions of total final consumption of industry products and price indexes on primary inputs. However, there exist a number of groups of final consumers which have generally different interests. The developed IO model by itself cannot explain to what extent the interests of final consumer groups will be satisfied at the new equilibrium prices. In this section, we suggest a new approach to the solution of this problem that is based on the synthesis of our model and the nonparametric method of demand analysis. As a result, we obtain the tool for scenario IO Table projection with the detailed quadrant III scenario evaluation (see Table 1).

We present the application of this tool in Section 5 for analysis of Kazakhstan’s production network.

4.1. Nonparametric Method of Demand Analysis

The approach to evaluation of demand and price indices, which takes into account the change of consumer preferences, is based on Pareto’s theory of demand [44]. According to this theory, a representative economic agent chooses a consumption basket by maximizing the utility function with budget constraint. If we know the demand function, then the problem of recovering the corresponding utility function is related to the integrability problem of demand functions. This question is studied by revealed preference theory [45]. The results of revealed preference theory allow us to test whether given trade statistics (i.e., observations of prices and consumption for a group of goods in a finite time period) is consistent with Pareto demand theory. Let us denote by ${\Phi }_0$ the class of non-negative on $R_{+}^m$, positive on $int{R}_{+}^m$, continuous, concave, and positively homogeneous of degree one utility functions. Then, the criterion for trade statistics to be consistent with Pareto theory with an utility function $F^0\in {\Phi }_0$, which is a homothetic axiom of revealed preference [13,46].

We say that the trade statistics is rationalizable by a utility function $F^0$ if the trade statistics is consistent with Pareto demand theory. In this case, we can construct so-called Konyus–Divisia consumption and price indexes [2], which take into account the change of consumer’s basket structure and give generalization to well-known Laspeyres and Paasche indices with a fixed structure of the basket. Moreover, Konyus–Divisia consumption and price indices are related through Young transform [2].

Let $P\left(X\right)=(P_1\left(X\right),\dots ,P_m\left(X\right))$ be an inverse demand function which describes behavior of the consumer’s group. The function $P\left(X\right)$ reflects the relationship between consumption of products $X=(X_1,\dots ,X_m)$ and corresponding prices. We suggest that functions $P_1\left(X\right),\dots ,P_m\left(X\right)$ are continuous on $R_{+}^m$. The initial data for Konyus–Divisia indices evaluation are trade statistics ${\left\{P_t,X_t\right\}}_{t=0}^T$ which give the values of inverse demand function in a finite number of points ${\left\{X_t\right\}}_{t=0}^T$ for a considered group of products. Testing the hypothesis of rationalizability of trade statistics and the algorithm for calculating Konyus–Divizia indices are based on the following theorem.

Theorem 2 

([13,46]). Given trade statistics ${\left\{P_t,X_t\right\}}_{t=0}^T$ the following statements are equivalent:

1. 

Trade statistics is rationalizable in class ${\Phi }_0$, i.e., there exists the utility function $F^0\left(X\right)\in {\Phi }_0$ with property

$$X_t\in Argmax\left\{F^0\left(X\right)\right|\langle P_t,X\rangle \le \langle P_t,X_t\rangle ,X\ge 0\},t=0,\dots ,T;$$

(17)

2. 

Trade statistics satisfies Homothetic Axiom of Revealed Preference (HARP), which means that for all ordered time sub-series $\left\{t_1,\dots ,t_k\right\}\in \{0,1,\dots ,T\}$, the following inequality holds

$$\langle P_{t_1},X_{t_2}\rangle ·\langle P_{t_2},X_{t_3}\rangle ·\dots ·\langle P_{t_{k-1}},X_{t_k}\rangle ·\langle P_{t_k},X_{t_1}\rangle \ge \langle P_{t_1},X_{t_1}\rangle ·\dots ·\langle P_{t_k},X_{t_k}\rangle ;$$

3. 

The system of linear inequalities

$${\lambda }_t\langle P_t,X_t\rangle \le {\lambda }_{\tau }\langle P_{\tau },X_t\rangle ,t,\tau =0,\dots ,T$$

(18)

has a positive solution ${\lambda }_0>0,{\lambda }_1>0,\dots ,{\lambda }_T>0$;

4. 

The function

$$F^0\left(X\right)=\underset{t=0,\dots ,T}{min}{\lambda }_t\langle P_t,X\rangle ,$$

(19)

where ${\lambda }_t>0$, $t=0,\dots ,T$ satisfy (18) rationalizes the trade statistics.

Positive solution of the system (18) could be evaluated by Floyd–Warshall algorithm [2,15,16].

Then, time series of Konyus–Divisia consumption indices are evaluated as [2]

$$F^0\left(X_t\right)={\lambda }_t\langle P_t,X_t\rangle ,t=0,\dots ,T,$$

(20)

and time series of Konyus–Divisia price indices are evaluated as [2]

$$Q\left(P_t\right)=\frac{1}{{\lambda }_t},t=0,\dots ,T$$

(21)

This approach to the evaluation of consumption and price indices is called the nonparametric approach (see [2,47]).

In general, the conditions of rationalizability of trade statistics may be violated. The reason for this may be, for example, errors that arise by the formation of statistics time series. The issue of an indicator that measures the degree of rationalization of trade statistics was considered in [2,12,47].

As a result, the generalized nonparametric method was developed [2], which is based on the inclusion of an additional parameter $w>1$ in the system (18), which measures the level of rationalization of trade statistics. In this case, the system (18) takes the form

$${\lambda }_t\langle P_t,X_t\rangle \le w{\lambda }_{\tau }\langle P_{\tau },X_t\rangle ,t,\tau =0,\dots ,T$$

(22)

The minimal value of $w_{min}>1$, which implies the consistency of the system of inequalities (22), is called irrationality index. Positive solution of the system (22) implies the time series of generalized Konyus–Divisia demand index (20) and generalized Konyus–Divisia price index (21).

4.2. Framework Concept for Analysis of Interests of Final Consumers in Network Economy

National account systems share the following main groups as part of final consumption (see quadrant II in the Table 1): households, government, export, and gross capital formation. Note that IO statistics include the full quadrant II, i.e., it contains consumption vectors in current prices of each final consumer.

Given the initial national IO statistics for a range of years, the synthesis of the IO model with CES technologies and the generalized nonparametric approach allows us to suggest a framework for scenario analysis of the interests of groups of final consumers.

For projection of consumption vectors of different final consumers with the framework, we need to set the scenario conditions, which include the following projection data:

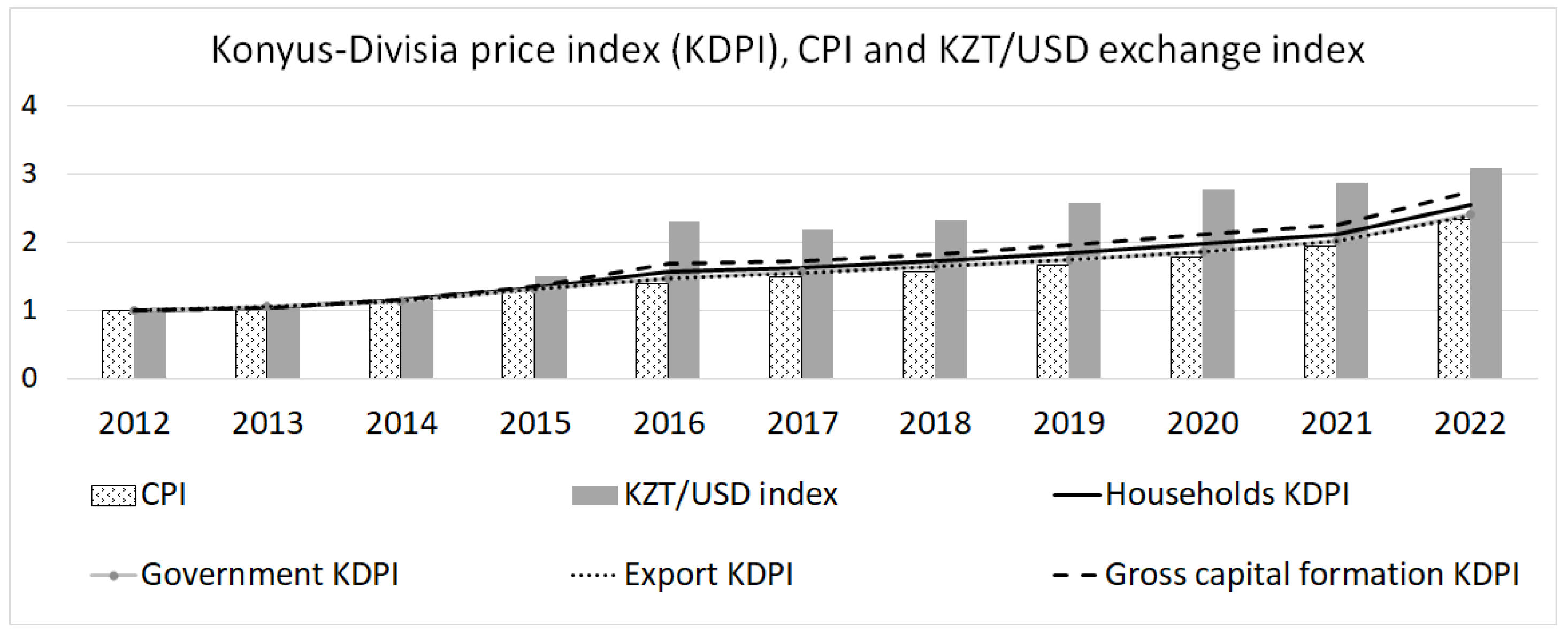
• Price indices of primary inputs: currency exchange rate $s_1$ for imported intermediates and consumer price index (CPI) $s_2$ for gross value added;
• Total final consumption values $A^{\pi }={\displaystyle \sum _{i=1}^m}{Z}_i^{0,\pi }+Z_{imp}^{0,\pi }$ for each final consumer $\pi$, where $Z_{imp}^{0,\pi }$ denotes the total final demand on imported products of agent $\pi$.

We denote this set of scenario conditions for a projected period by $SData$.

As a result of the framework scenario evaluation, we calculate equilibrium prices of products and IO Table Z for a projected year with detailed quadrant II and additional row of final consumption of imported products, i.e., we evaluate vectors $Z^{0,\pi }=\left(Z_1^{0,\pi },\dots ,Z_m^{0,\pi },Z_{imp}^{0,\pi }\right)$ and for each final consumer $\pi$. Then, the vector of total domestic final consumption for a projected year $Z^0=(Z_1^0,\dots ,Z_m^0)$ is the sum of vectors $\left(Z_1^{0,\pi },\dots ,Z_m^{0,\pi }\right)$ by $\pi$.

In applications, we aggregate the initial IO structure to several large production complexes (up to 10). The aggregation principles are based on the analysis of economy features and depend on the objectives of the study. High-level aggregation guarantees more stable model calibration results in case of statistics errors and is useful for many tasks of macroeconomic analysis. However, the methodology can be generalized to the case of a detailed input–output balance.

The framework algorithm includes two stages.

Stage I. Identification.

Step 1. Based on studying the structure of the national production network, aggregate the initial statistics IO Tables for a given range of years $\mathbf{T}=\{0,\dots ,T\}$ to m large industrial complexes.

Step 2. Form the initial data base $IData$ for model identification: aggregated annual IO Tables $Z\left(t\right)$, $t\in \mathbf{T}$, average annual price indices of primary inputs: currency exchange rate $s_1\left(t\right)$ for imported products and consumer price index (CPI) $s_2\left(t\right)$ for gross value added, $t\in \mathbf{T}$.

Step 3. Given $IData$ fix the base year $t_0\in \mathbf{T}$ with a given IO Table $Z\left(t_0\right)$ and identify the IO balance model with CES technologies (7) (see Section 3.2), i.e.,

• Calculate matrices $A,B$ by (11) with IO Table $Z\left(t_0\right)$,
• Calibrate the model by evaluating ${\rho }_j$, $j=1,\dots ,m$ (7) with $IData$.

As a result, the IO model with CES technologies is ready for scenario IO Table projection given primary price indices $s_1,s_2$ and a vector of total final consumption $Z^0$ for a projected year (Proposition 6).

Step 4. Given statistics of price indices of primaries $s_1,s_2$ for the period $\mathbf{T}$ ($Ibase$) we evaluate equilibrium price indices $p\left(t\right)=(p_1\left(t\right),\dots ,p_m\left(t\right))$, $t\in \mathbf{T}$ for domestic products $1,\dots ,m$ of the network by the solution of (14).

Step 5. For each final consumer $\pi$ from the quadrant II of IO Table $Z\left(t\right)$ (households, government, etc.), we form the annual final consumption vector

$$X_{\pi }^0\left(t\right)=\left(\frac{Z_1^{0,\pi }\left(t\right)}{p_1\left(t\right)},\dots ,\frac{Z_m^{0,\pi }\left(t\right)}{p_m\left(t\right)},\frac{Z_{imp}^{0,\pi }\left(t\right)}{s_1\left(t\right)}\right),t\in \mathbf{T}$$

as data $IData$.

Step 6. Denote $P\left(t\right)=(p\left(t\right),s_1\left(t\right))$. Given trade statistics $\left\{P\left(t\right),X_{\pi }^0\left(t\right)\right\}$ for each final consumer $\pi$, we apply the generalized non parametric method, i.e., we evaluate

(1)

Irrationality index $w_{min}>1$ and ${\left\{{\lambda }_t\right\}}_{t\in \mathbf{T}}$ by solving the system (22),

(2)

Demand function $F_{\pi }^0\left(X\right)$ by (19),

(3)

Konyus–Divisia consumption and price indices time series by (20) and (21) correspondingly.

Stage II. Scenario evaluation

Step 1. Set scenario conditions $SData$ for a projected year.

Step 2. Evaluate equilibrium price indices for projected year $p=(p_1,\dots ,p_m)>0$ of products $1,\dots ,m$ by solution of (14)).

Step 3. Given equilibrium price indices $P=(p_1,\dots ,p_m,s_1)>0$ and demand function $F_{\pi }^0\left(X\right)$ evaluate demand vector $Z^{0,\pi }=\left(Z_1^{0,\pi },\dots ,Z_m^{0,\pi },Z_{imp}^{0,\pi }\right)$ of each final consumer $\pi$ for the projected year by solution of the problem (17) with budget constraint $A^{\pi }$:

$$\begin{array}{c}\underset{X}{max}{F}_{\pi }^0\left(X\right)\\ \langle P,X\rangle \le A^{\pi }.\end{array}$$

(23)

If $X^{*}$ is a solution of the problem (23) then

$$Z_i^{0,\pi }=p_i{X}_i^{*},i=1,\dots ,m,Z_{imp}^{0,\pi }=s_1{X}_{m+1}^{*}.$$

(24)

We calculate the scenario projection of Konyus–Divisia consumption index as $F_{\pi }^0\left(X^{*}\right)$. We calculate the scenario projection of Konyus–Divisia price index as $\frac{A_{\pi }}{F_{\pi }^0\left(X^{*}\right)}$.

Step 4. Given total final consumption of each domestic product $Z_j^0={\displaystyle \sum _{\pi }}{Z}_j^{0,\pi }$, $j=1,\dots ,m$ (i.e., quadrant II of IO Table Z), we evaluate the quadrants I, III of IO Table Z for projected year by (15).

5. Applications: Scenario Evaluations of Final Consumption Structure of Kazakhstan Economy

In paper [11], we identified the IO model with CES technologies by the IO statistics 2012–2020 of Kazakhstan, having 2013 as the base year. Aggregation principles of IO Table reflected the heterogeneity of the Kazakhstan production network in relation to export–import flows. We aggregated economy sectors into four large industrial complexes: manufacturing, exporting, infrastructure, and services [11]. The comparison of calculated macroeconomic indices with statistics from 2013–2020 demonstrated high accuracy of model-based evaluations [11].

In this section, we present the result of two-stage framework scenario calculations (Section 4.2) of a four-sector IO Table of Kazakhstan, based on the results of [11]. The modified framework allows us to evaluate not only the quadrants I, III of IO Table Z, but also detailed aspects of industrial complexes and final consumer quadrant II. That is the novelty of our approach.

For evaluations, we use the official Kazakhstan statistics [48,49,50]. Given the initial base $IData$ (Stage I, Step II), we use the IO model-based results of [11] to execute steps 3–6 of the Stage I (Section 4.2). We evaluate the irrationality index $w_{min}>1$ for each final consumer of the Kazakhstan production network 2012–2020: households, government, export, and gross capital formation (Step 6). In

Table 2. Irrationality indices.

	Consumer	Irrationality Index
1	Households	1.00051
2	Government	1.00017
3	Export	1.00063
4	Gross capital formation	1.00245

, we present calculated values of irrationality index of each final consumer. All irrationality indices are close to $1.0$, so the trade statistics of each final consumer is rationalizable. In accordance with Stage I (Step 6), we evaluate demand functions $F_{\pi }^0\left(X\right)$ of each final consumer $\pi$ as well as Konyus–Divisia consumption and price indices time series 2012–2021. For 2022, the IO Table is not published yet, so we form the base scenario conditions 2022 $SDataB$ by actual Kazakhstan statistics [49,50,51]. We shoe the statistics for 2022 of total final consumption values $A^{\pi }$ in Appendix A,

Table A1. Kazakhstan 2021 and 2022 GDP by final use, million KZT [51].

	${\mathit{A}}^{\mathit{\pi }}$	2021	2022
Household final consumption	$A^1$	42,419,295.9	49,724,894.8
Government final consumption	$A^2$	9,461,635.3	11,680,972.2
Gross capital formation	$A^4$	22,275,240.5	25,030,635.8
Export	$A^3$	28,245,396.0	43,354,558.7

. We apply Stage II of the framework to evaluate the indices for the base scenario 2022. In Figure 1 and Figure 2, we show the results of Konyus–Divisia indices evaluation 2013–2021 by trade statistics and base scenario evaluation 2022 compared to 2012. The comparison of results to consumer price index (CPI) and exchange rate (KZT/USD) statistics 2012–2022 confirms the adequacy of framework-based evaluations (Figure 1). Note that evaluation of statistics show the inflation growth in 2022.

As we see in Figure 2, the framework-based evaluation of Konyus–Divisia index reflects the main features of dynamic agents’ final demand, which are connected to macroeconomic shocks. For example, the fall of household and export spending and the increase in government spending during the 2020 COVID pandemic year as well as recovery of export in 2021, 2022. The household demand fall in 2022 reflects a negative Konyus–Divisia price index dynamic (see Figure 1). At the same time, we can see a slow change of KDDI which indicates capital investment stagnation.

We show the result of evaluation of total outputs 2021, 2022 (2022—base scenario) of aggregate complexes as well as statistics 202in Figure 3. We show an evaluation of IO Table 2022 for base scenario in Appendix A,

Table A3. IO Table 2022. Evaluation. (tln. KZT).

	Manufacturing	Exporting	Infrastructure	Service	Total Intermediates	Households Final Consumption	Government Final Consumtpion	Gross Capital Formation	Export	Total Final Consumption	Total Demand
Manufacturing	0.47	1.02	0.41	2.01	3.90	3.97	0.00	0.57	0.67	5.21	9.11
Exporting	2.35	14.68	1.73	4.79	23.55	7.82	0.18	5.47	36.30	49.76	73.31
Infrastructure	0.37	4.38	1.43	2.88	9.06	5.86	0.63	0.71	2.87	10.07	19.12
Service	0.39	5.85	2.39	9.52	18.16	23.76	10.87	9.99	0.49	45.11	63.27
Import	0.98	4.66	1.79	4.67	12.09	6.82	0.00	8.30	0.00	15.11	27.20
GVA	4.55	42.72	11.38	39.41
Total output	9.11	73.31	19.12	63.27

.

Evaluation of final consumer demand for 2022 shows essential shifts in the consumption structure of households, export, and gross capital formation (see

Table 3. Demand structure 2022 evaluation (in comparable prices), compared to 2021. Base scenario.

	Households	Government	Export	Gross Capital Formation
Manufacturing	−1.0%	4.6%	−42.7%	−32.2%
Exporting	1.8%	4.6%	33.2%	−3.4%
Infrastructure	37.0%	4.6%	33.0%	7.0%
Service	−18.0%	4.6%	−50.6%	−1.1%
Import	11.7%	-	-	33.5%

) At the same time, we see the uniform growth of government spending 2022, because due to calculations, 2021 has the closest to the optimal structure of government spending in the period 2012–2021. A decrease in the final demand of households, export, and gross capital formation in manufacturing products with an increase in the final consumption of imports threatens the growing import dependence of Kazakhstan’s economy.

Scenario evaluations for 2022 within the framework aimed to evaluate the responses of production network as well as final consumption structure to tax collection shifts. We consider two groups of scenario conditions $SData$ that we interpret as “high taxes” and “low taxes”. The both scenarios differs from the base scenario $SDataB$ 2022 by budget constraints values $A^{\pi }$ only

• “High taxes”, $A^{\pi }$ formation scenario: increase by 1 tln KZT of government spending (budget constraints) while decreasing household and export spending (budget constraints) by 0.5 tln KZT each compared to base scenario 2022;
• “Low taxes”, $A^{\pi }$ formation scenario: increase by 1 tln KZT of households spending while decreasing government spending by 1 tln KZT compared to base scenario 2022.

With the developed framework, we evaluate the “high taxes” and “low taxes” scenario for IO Table 2022 and compare the results with the base scenario IO Table 2022. In Figure 4, we show the propagation of scenario shift of tax collection trough the production network of Kazakhstan. Note that the service complex only demonstrates an opposite economic response to tax shift among the four large industrial complexes of Kazakhstan. At the same time, the exporting sector has the most negative shift in the “high taxes” scenario, while manufacturing has the most positive shift in the "low taxes" scenario.

In Figure 5, we show evaluated shifts of the total final consumption structure for 2022 to 2021 for the considered scenarios. The evaluation confirms the risk of higher import dependence and the heterogeneity of Kazakhstan’s economy. At the same time, the growth of export earnings ensures the fulfillment of the international trade balance.

We present an evaluation of the “high taxes” and “low taxes” scenario demand structure for 2022 compared to 2021 (in compatible prices) in Appendix A,

Table A4. Low-taxes scenario demand structure 2022 evaluation, compared to 2021.

	Households	Government	Export	Gross Capital Formation
Manufacturing	1.0%	−4.3%	−42.7%	−32.2%
Exporting	3.9%	−4.3%	33.2%	−3.4%
Infrastructure	39.8%	−4.3%	33.0%	7.0%
Service	−16.3%	−4.3%	−50.6%	−1.1%
Import	14.0%	-	-	33.5%

and

Table A5. High-taxes scenario demand structure 2022 evaluation, compared to 2021.

	Households	Government	Export	Gross Capital Formation
Manufacturing	−2.1%	13.6%	−43.4%	−32.2%
Exporting	0.7%	13.6%	31.6%	−3.4%
Infrastructure	35.5%	13.6%	31.3%	7.0%
Service	−18.8%	13.6%	−51.2%	−1.1%
Import	10.6%	-	-	33.5%

.

6. Conclusions

The paper provides the following main results.

• A new IO framework with CES technologies for scenario analysis and forecasting of national IO Tables with substitution of inputs is developed.
• The framework is based on synthesis of two technologies:

  (1)

  Variational inequality theory and Young duality for evaluating equilibrium prices and equilibrium inter-industry flows in production network;

  (2)

  Generalized nonparametric method of demand analysis for evaluation of demand functions of final consumers and scenario projection of final demand structure.

• The clear methodology of the solution of the inverse problem of framework identification is developed, which is based on officially published national statistics data.
• The framework-based algorithm for scenario evaluations is provided.
• The results of applying the algorithm to national IO Tables with the full three-quadrant structure are constructed: inter-industry cash flows (quadrant I), final demand for products of industries of major final consumers (quadrant II), and industry cash flows for intermediate consumption of primary inputs (quadrant III).
• Application of the framework for analysis and scenario projection to the production network of Kazakhstan’s economy is considered. The results show the appropriate accuracy of the model evaluations in comparison to the official statistical data. The model calculations show that the isolated growth of tax collection negatively affects the real sector indicators of the economy. At the same time, the isolated reduction of tax collection activates production. This suggests that tax reforms should be accompanied by measures to support production.
• It should be noted that the algorithm application based on the model is limited by parameter identification opportunity. Several-year IO Tables with a similar set of products should be available from official statistics for elasticity of substitution and demand functions of final consumer identification.

We plan to develop our research both in terms of practical applications and in the direction of obtaining theoretical results on the existence and uniqueness of a solution of variational inequalities that arise when describing an equilibrium in complex production networks. The theory of monotone operators could be useful for the study of such problems.

The results obtained in this article confirm that the developed IO framework with CES technologies provides a useful tool for real-time scenario analysis and forecast of inter-industry cash-flows, taking into account the interests of final consumers in national production networks. The developed technology can be used as part of macroeconomic decision support systems for planning sustainable production and economic development.