On the Theory of Methane Hydrate Decomposition in a One-Dimensional Model in Porous Sediments: Numerical Study
Abstract
1. Introduction
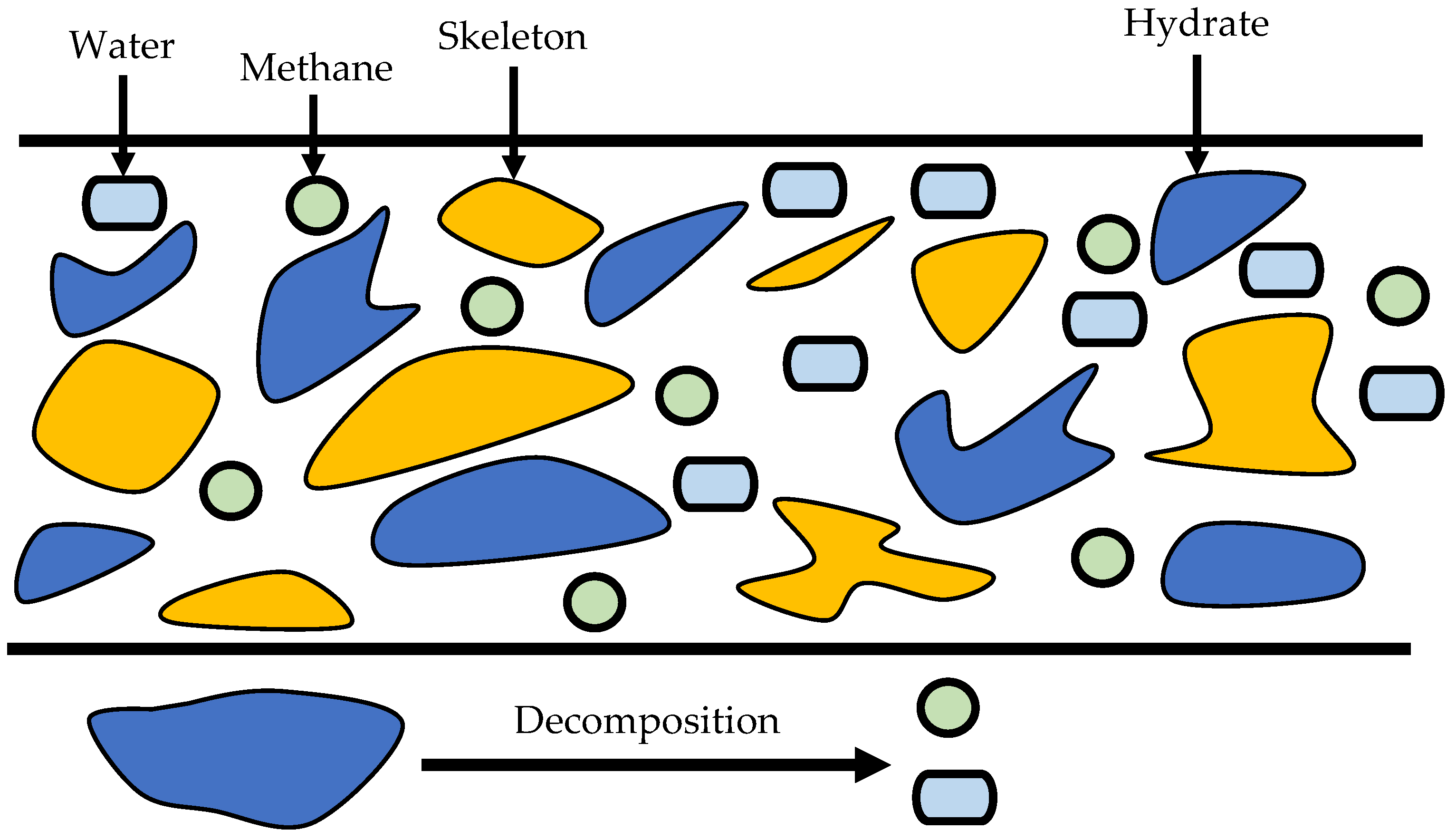
2. Description of the Physical Approach
- The gas hydrates in the numerical simulation are measured in SI units, without taking into account the composition of the salt.
- The behavior of multiphase fluid flow in uniform porous media is described by Darcy’s law, and hydrate is stagnant in porous media.
- Gravity and capillary forces are not taken into account.
- The thermal conductivity that is supposed to be included in the total heat transfer equation as compared to convection is negligible, which means that the thermal conductivities of the energy equations are neglected.
- The current model discusses the states of filtering flow of a fluid through a porous medium in the case of incompressible fluids by another fluid, by the same fluid, and in the case of an ideal gas.
- In the case of heat and mass transfer, the influence of diffusion and dispersion was ignored, and during the decomposition process, there is no ice phase.
- During hydrate decomposition, the hydrate-bearing sediments were considered stiff and not distorted.
3. Theoretical Analysis and Mathematical Model
Hydrate Decomposition in A Three-Phase Porous Medium
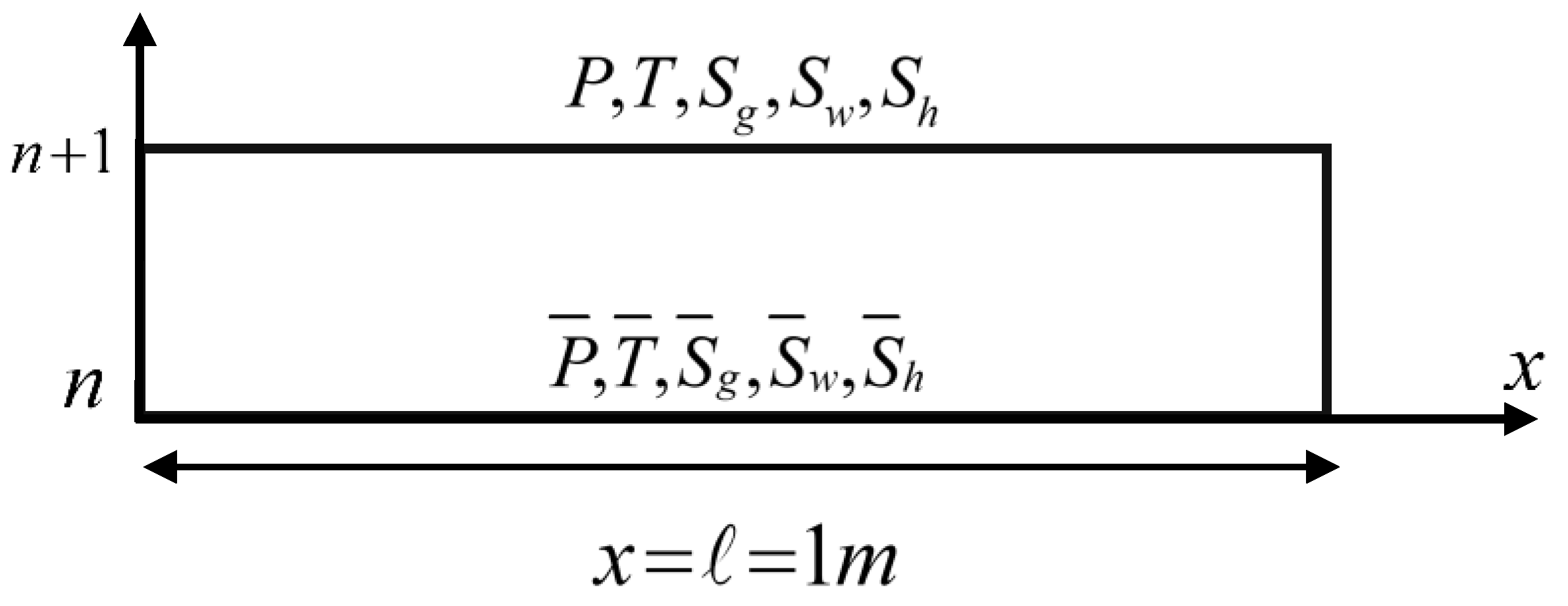
4. Discretization and Linearization of the Governing Equations
- Three-phase flow (gas, liquid, hydrate).
- Two-phase flow (gas, liquid).
- Two-phase flow (gas, hydrate).
- Two-phase flow (liquid, hydrate).
5. Thermodynamic Equilibrium of Hydrate Decomposition in a Three-Phase Porous Medium
6. Thermodynamic Equilibrium of Hydrate Decomposition in a Two-Phase Porous Medium
- Case 2: ,
- Case 3: ,
- Case 4: .
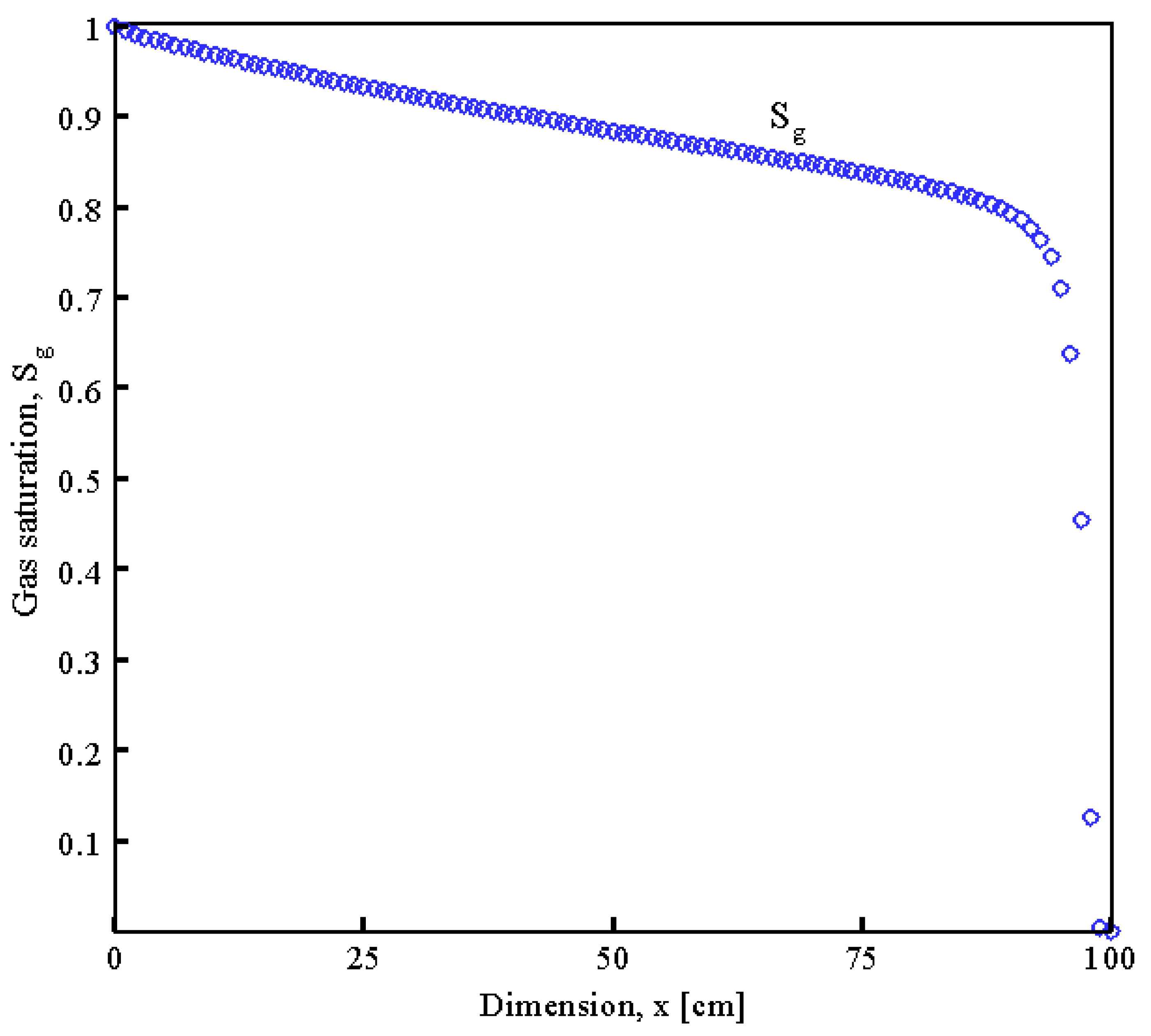
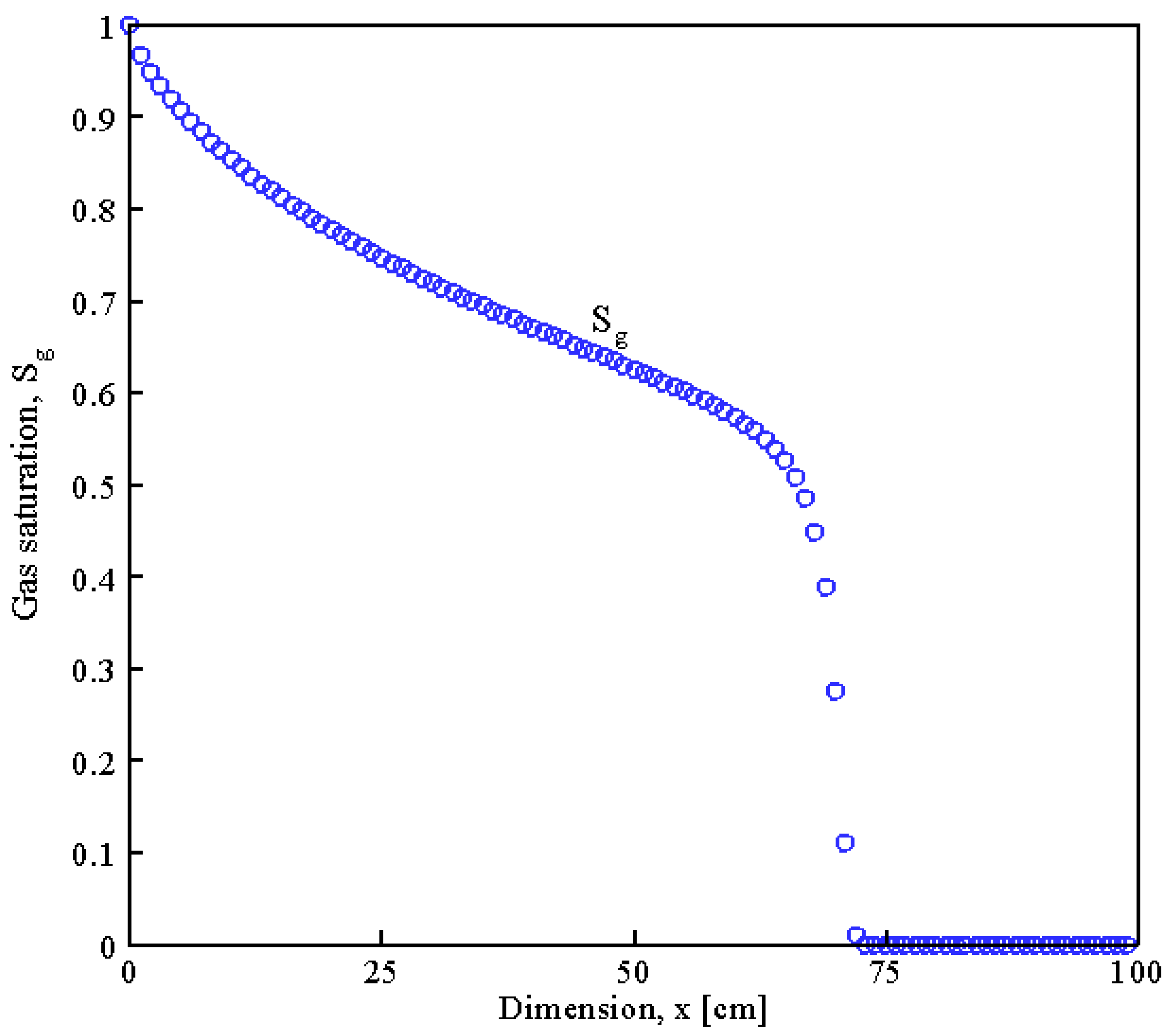
7. Conclusions
- The spatial coordinate is divided into finite intervals.
- In addition, the initial values and physical parameters used in our numerical calculations of the proposed model are illustrated in Table 1.
- The Newton–Raphson method was employed to determine the essential variables such as pressure, temperature, and the rate of saturation of pores with hydrate and water in the spatial distribution over different values of time.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Sloan, E.D. Clathrate Hydrates of Natural Gas, 2nd ed.; Marcel Dekker Inc: New York, NY, USA, 1998. [Google Scholar]
- Max, M.D.; Dillon, W.P. Oceanic methane hydrate: Character of the Blake Ridge hydrate stability zone and potential for methane extraction. J. Pet. Geol. 1998, 21, 343–358. [Google Scholar] [CrossRef]
- Ruan, X.; Song, Y.; Zhao, J.; Liang, H.; Yang, M.; Li, Y. Numerical simulation of methane production from hydrates induced by different depressurizing approaches. Energies 2012, 5, 438–458. [Google Scholar] [CrossRef]
- Malagar, B.R.C.; Lijith, K.P.; Singh, D.N. Singh. Formation & dissociation of methane gas hydrates in sediments: A critical review. J. Nat. Gas Sci. Eng. 2019, 65, 168–184. [Google Scholar]
- Gao, Y.; Yang, M.; Zheng, J.N.; Chen, B. Production characteristics of two class water-excess methane hydrate deposits during depressurization. Fuel 2018, 232, 99–107. [Google Scholar] [CrossRef]
- Misyura, S.Y. The influence of porosity and structural parameters on different kinds of gas hydrate dissociation. Sci. Rep. 2016, 6, 30324. [Google Scholar] [CrossRef]
- Ye, H.; Wu, X.; Li, D. Numerical Simulation of Natural Gas Hydrate Exploitation in Complex Structure Wells: Productivity Improvement Analysis. Mathematics 2021, 9, 2184. [Google Scholar] [CrossRef]
- Mao, P.; Wu, N.; Ning, F.; Hu, G.; Sun, J.; Chen, Q.; Guo, Y.; Bu, Q.; Wan, Y. Behaviors of gas and water production from hydrate induced by depressurization with different types of wells. Nat. Gas Ind. 2020, 40, 168–176. [Google Scholar]
- Gaidukova, O.; Misyura, S.; Strizhak, P. Key Areas of Gas Hydrates Study: Review. Energies 2022, 15, 1799. [Google Scholar] [CrossRef]
- You, K.; Flemings, P.B. Methane Hydrate Formation and Evolution During Sedimentation. J. Geophys. Res. Solid Earth 2021, 126, e2020JB02123. [Google Scholar] [CrossRef]
- Kumar, A.; Maini, B.; Bishnoi, P.R.; Clarke, M.; Zatsepina, O.; Srinivasan, S. Experimental determination of permeability in the presence of hydrates and its effect on the dissociation characteristics of gas hydrates in porous media. J. Pet. Sci. Eng. 2010, 70, 114–122. [Google Scholar] [CrossRef]
- Xu, Q.; Liu, C.; Liu, Q.; Zhu, Y.; Zhou, H.; Guo, L. Interfacial characteristics of steam jet condensation in subcooled water pipe flow—An experimental and numerical study. Chem. Eng. Sci. 2022, 251, 117457. [Google Scholar] [CrossRef]
- Xu, Q.; Zhu, Y.; Zhou, H.; She, Y.; Guo, L. Flow characteristic of steam jet condensed into a water pipe flow—A numerical study. Appl. Therm. Eng. 2022, 205, 118034. [Google Scholar] [CrossRef]
- Konno, Y.; Oyama, H.; Nagao, J.; Masuda, Y.; Kurihara, M. Numerical analysis of the dissociation experiment of naturally occurring gas hydrate in sediment cores obtained at the Eastern Nankai Trough, Japan. Energy Fuels 2010, 24, 6353–6358. [Google Scholar] [CrossRef]
- Makogon, Y.F. Hydrates of Natural Gas, 1st ed.; Penn Well Publishing Company: Tulsa, OK, USA, 1997. [Google Scholar]
- Khataniar, S.; Kamath, V.A.; Omenihu, S.D.; Patil, S.H.; Dandekar, A.Y. Modelling and economic analysis of gas production from hydrates by depressurization method. Can. J. Chem. Eng. 2002, 80, 135–143. [Google Scholar] [CrossRef]
- Pooladi-Darvish, M.; Zatsepina, O.; Hong, H.F. Behaviour of Gas Production from Type III Hydrate Reservoirs. In Proceedings of the 6th International Conference on Gas Hydrates, Vancouver, BC, Canada, 6–10 July 2008. [Google Scholar]
- Musakaev, N.G.; Khasanov, M.K.; Borodin, S.L. The mathematical model of the gas hydrate deposit development in permafrost. Int. J. Heat Mass Transf. 2018, 118, 455–461. [Google Scholar] [CrossRef]
- Gamwo, I.K.; Liu, Y. Mathematical modeling and numerical simulation of methane production in a hydrate reservoir. Ind. Eng. Chem. Res. 2010, 49, 5231–5245. [Google Scholar] [CrossRef]
- Zhao, J.; Shi, D.; Zhao, Y. Mathematical model and simulation of Gas Hydrate reservoir decomposition by depressurization. Oil Gas Sci. Technol. Rev. IFP Energ. Nouv. 2012, 67, 379–385. [Google Scholar] [CrossRef]
- Khasanov, M.K.; Musakaev, N.G.; Stolpovsky, M.V.; Kildibaeva, S.R. Mathematical model of decomposition of methane hydrate during the injection of liquid Carbon dioxide into a reservoir saturated with methane and its hydrate. Mathematics 2020, 8, 1482. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, L.; Lv, Q.; Yang, M.; Ling, Z.; Zhao, J. Assessment of gas production from natural gas hydrate using depressurization, thermal stimulation and combined methods. RSC Adv. 2016, 6, 47357. [Google Scholar] [CrossRef]
- Jin, Y.; Yang, D.; Li, S.; Pang, W. Hydrate dissociation conditioned to depressurization below the quadruple point and salinity addition. Fuel 2019, 225, 115758. [Google Scholar] [CrossRef]
- Wan, Q.-C.; Si, H.; Li, B.; Li, G. Heat transfer analysis of methane hydrate dissociation by depressurization and thermal stimulation. Int. J. Heat Mass Transf. 2018, 127, 206–217. [Google Scholar] [CrossRef]
- Fitzgerald, G.C.; Castaldi, M.J. Thermal stimulation-based methane production from hydrate bearing quartz sediment. Ind. Eng. Chem. Res. 2013, 52, 6571–6581. [Google Scholar] [CrossRef]
- Fan, S.; Zhang, Y.; Tian, G.; Liang, D.; Li, D. Natural Gas Hydrate Dissociation by Presence of Ethylene Glycol. Energy Fuels 2006, 20, 324–326. [Google Scholar] [CrossRef]
- Yamamoto, K.; Nagakubo, S. Review of Energy Efficiency of the Gas Production Technologies from Gas Hydrate-Bearing Sediments. Front. Energy Res. 2021, 9, 741715. [Google Scholar] [CrossRef]
- Goel, N. In situ methane hydrate dissociation with carbon dioxide sequestration: Current knowledge and issues. J. Pet. Sci. Eng. 2006, 51, 169–184. [Google Scholar] [CrossRef]
- Bao, J.; Chen, Z.; Xian, C. Investigations of CO2 storage capacity and flow behavior in shale formation. J. Pet. Sci. Eng. 2022, 208, 109659. [Google Scholar]
- Omidi, M.; Shahsavand, A.; Share Mohammadi, H. Modeling and simulation of hydrate thermal dissociation around gas production pipe from suboceanic sediment. J. Nat. Gas Sci. Eng. 2016, 32, 48–58. [Google Scholar] [CrossRef]
- Kwon, T.-H.; Cho, G.-C. Gas hydrate dissociation in sediments: Pressure-temperature evolution. Geochem. Geophys. Geosystems 2008, 9, Q03019. [Google Scholar] [CrossRef]
- Poveshchenko, Y.; Rahimly, P.; Rahimly, O.; Podryga, V.; Gasilova, I. A Numerical Approach to Study the Thermal Influence on Gas Hydrates by Physical Process Splitting. Int. J. Numer. Anal. Mod. 2020, 17, 404–433. [Google Scholar]
- Rempel, A.W.; Buffett, B.A. Mathematical models of gas hydrate accumulation, in Gas Hydrates: Relevance to World Margin Stability and Climate Change. Geol. Soc. Spec. 1998, 137, 63–74. [Google Scholar] [CrossRef]
- Xu, W.; Ruppel, C. Predicting the occurrence, distribution, and evolution of methane gas hydrate in porous marine sediments. J. Geophys. Res. 1999, 104, 5081–5095. [Google Scholar] [CrossRef]
- Rahimly, P.I.; Poveshchenko, Y.A.; Rahimly, O.R.; Podryga, V.O.; Kazakevich, G.I.; Gasilova, I.V. The Use of Splitting with Respect to Physical Processes for Modeling the Dissociation of Gas Hydrates. Math. Model. Comput. Simul. 2018, 10, 69–78. [Google Scholar] [CrossRef]
- Chen, X.; Espinoza, D.N.; Luo, J.S.; Tisato, N.; Flemings, P.B. Pore-scale evidence of ion exclusion during methane hydrate growth and evolution of hydrate pore-habit in sandy sediments. Mar. Pet. Geol. 2020, 117, 104340. [Google Scholar] [CrossRef]
- Deusner, C.; Bigalke, N.; Kossel, E.; Haeckel, M. Methane production from gas hydrate deposits through injection of supercritical CO2. Energies 2012, 5, 2112–2140. [Google Scholar] [CrossRef]
- Ji, C.; Ahmadi, G.; Smith, D.H. Natural gas production from hydrate decomposition by depressurization. Chem. Eng. Sci. 2001, 56, 5801–5814. [Google Scholar] [CrossRef]
- Ji, C.; Ahmadi, G.; Smith, D.H. Constant rate natural gas production from a well in a hydrate reservoir. Energy Convers. Manag. 2003, 44, 2403–2423. [Google Scholar] [CrossRef]
- Yousif, M.H.; Abass, H.H.; Selim, M.S.; Sloan, E.D. Experimental and theoretical investigation of methane gas hydrate dissociation in porous media. SPE Reserv. Eng. 1991, 6, 69–76. [Google Scholar]
- Moridis, G.J. Numerical studies of gas production from class 2 and class 3 hydrate accumulations at the mallik site, Mackenzie Delta, Canada. SPE Res. Eval. Eng. 2004, 7, 175–183. [Google Scholar] [CrossRef]
- Corey, A.T. The interrelation between gas and oil relative permeabilities. Prod. Mon. 1954, 19, 38–41. [Google Scholar]
- Shagapov, V.S.; Khasanov, M.K. Regimes of methane recovery from gas hydrate on injection of “warm” carbon dioxide into a porous medium. High Temp. 2017, 55, 737–745. [Google Scholar] [CrossRef]
- Shagapov, V.S.; Khasanov, M.K.; Musakaev, N.G.; Duong, N.H. Theoretical research of the gas hydrate deposits development using the injection of carbon dioxide. Int. J. Heat Mass Transf. 2017, 107, 347–357. [Google Scholar] [CrossRef]
- Shagapov, V.S.; Musakaev, N.G.; Khasanov, M.K. Injection of liquid carbon dioxide into a reservoir partially saturated with methane hydrate. J. Appl. Mech. Tech. Phys. 2016, 57, 1083–1092. [Google Scholar] [CrossRef]
- Khasanov, M.K.; Shagapov, V.S. Methane Gas Hydrate Decomposition in a Porous Medium Upon Injection of a Warm Carbon Dioxide Gas. J. Eng. Phys. Thermophys. 2016, 89, 1123–1133. [Google Scholar] [CrossRef]
- Khasanov, M.K.; Stolpovsky, M.V.; Gimaltdinov, I.K. Mathematical model for carbon dioxide injection into porous medium saturated with methane and gas hydrate. Int. J. Heat Mass Transf. 2018, 127, 21–28. [Google Scholar] [CrossRef]
- Khasanov, M.K.; Stolpovsky, M.V.; Gimaltdinov, I.K. Mathematical model of injection of liquid carbon dioxide in a reservoir saturated with methane and its hydrate. Int. J. Heat Mass Transf. 2019, 132, 529–538. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, C.; Zhang, K.; Zhang, L.; Yao, J.; Sun, H.; Yang, Y. Pore-scale investigation of methane hydrate dissociation using the lattice Boltzmann method. Water Resour. Res. 2019, 55, 8422–8444. [Google Scholar] [CrossRef]
- Eduardo Lozano, E.; Aslam, T.D. Implicit fast sweeping method for hyperbolic systems of conservation laws. J. Comput. Phys. 2021, 430, 110039. [Google Scholar] [CrossRef]
- Zuev, A.I. On an algorithm for solution of nonlinear systems by the sweep method. Trudy Mat. Inst. Steklov. 1966, 74, 152–155. [Google Scholar]
- Bulygin, A.D. Algorithm of the Parallel Sweep Method for Numerical Solution of the Gross–Pitaevskii Equation with Highest Nonlinearities. Supercomput. Front. Innov. 2018, 5, 115–118. [Google Scholar]
- Galperin, B. Large Eddy Simulation of Complex Engineering and Geophysical Flows; Cambridge University Press: London, UK, 1993. [Google Scholar]
- Chivers, I.D.; Sleightholme, J. Introduction to Programming with Fortran; Springer-Verlag London Limited: London, UK, 2006. [Google Scholar]
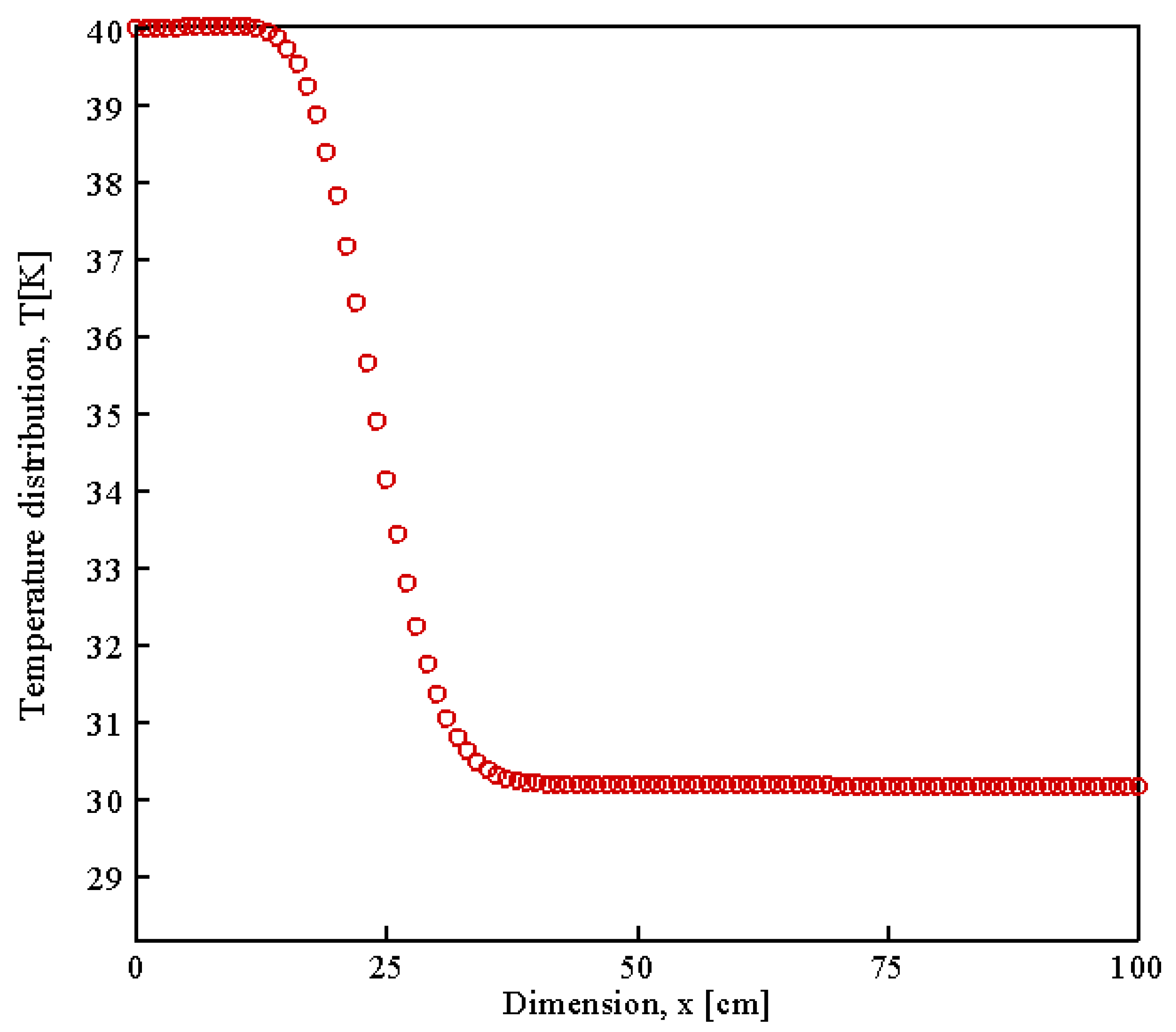
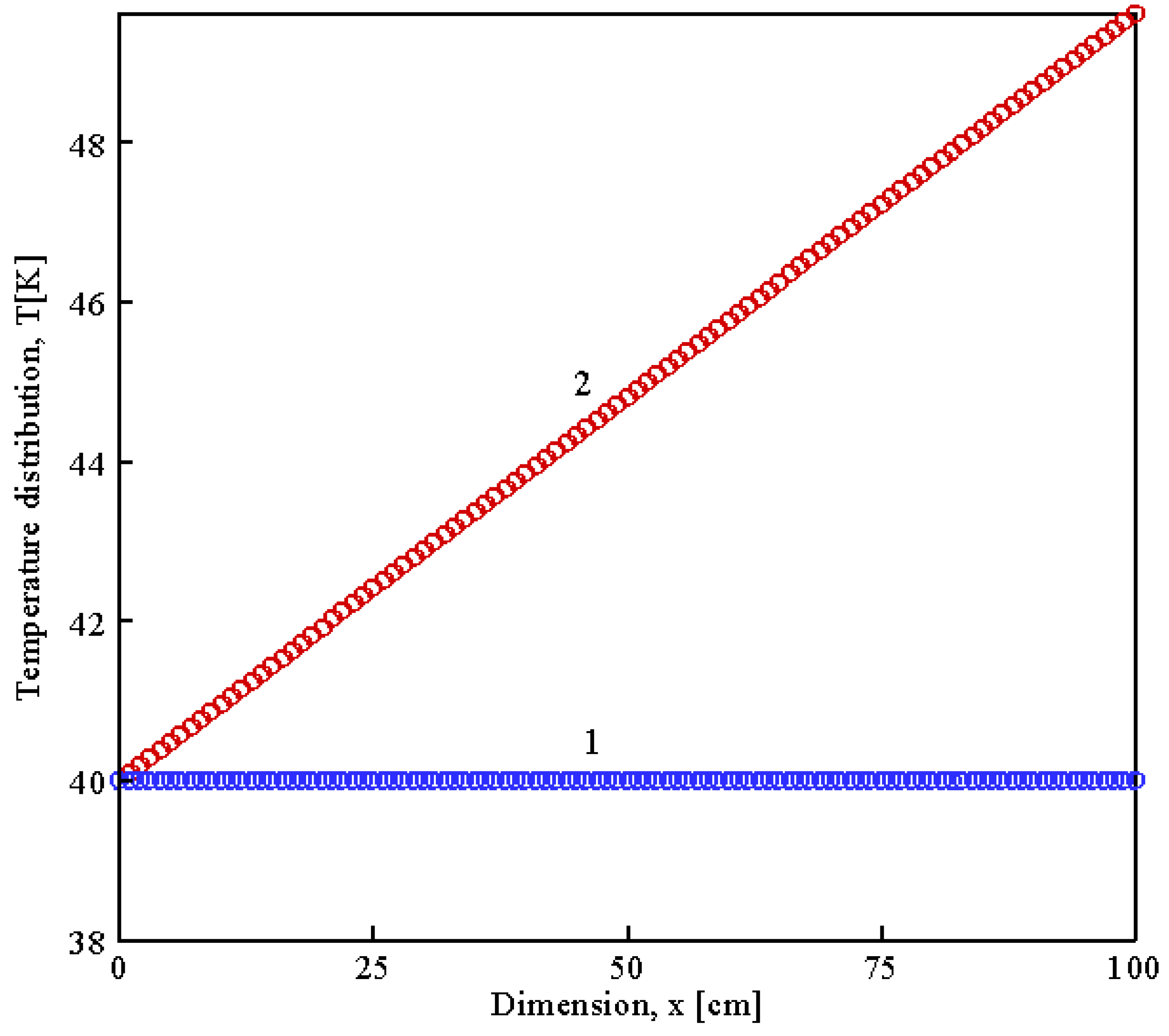
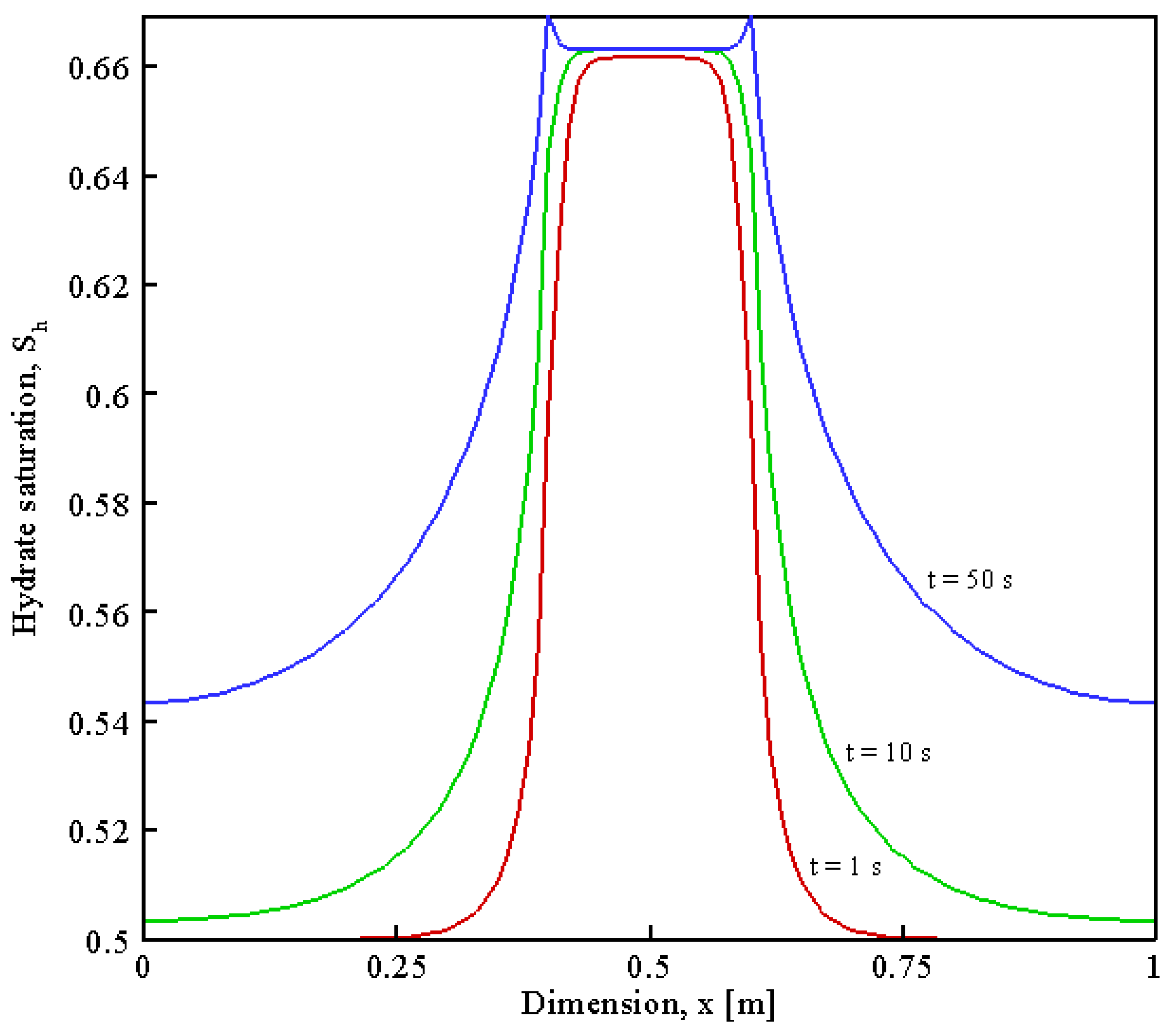
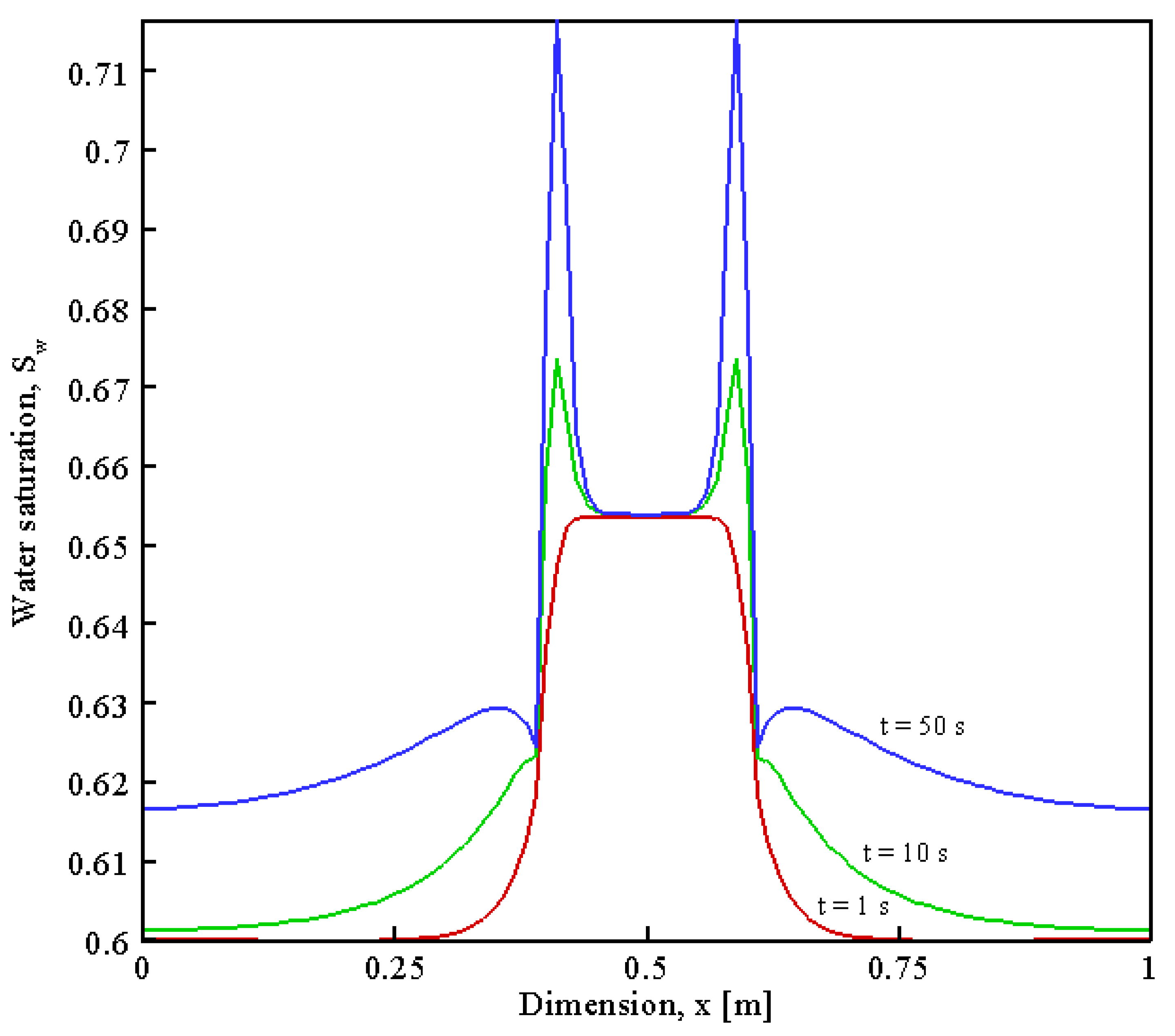


| Parameter | Value | Unit | Description |
|---|---|---|---|
| 2 | Initial pressure | ||
| Heat capacity of gas | |||
| Heat capacity of liquid | |||
| Heat capacity of skeleton | |||
| Porosity | |||
| - | Initial saturation of the gas | ||
| - | Initial saturation of the liquid | ||
| - | Initial saturation of the hydrate | ||
| Density of liquid | |||
| Density of hydrate | |||
| Density of skeleton | |||
| Gas constant | |||
| Adiabatic exponent | |||
| Viscosity of the gas | |||
| Viscosity of the liquid | |||
| The mass fraction of methane in the hydrate | |||
| The latent heat of phase transition | |||
| Source of characteristics in the downhole area | |||
| - | - | The hydration number | |
| Superscripts | |||
| Initial | |||
| Three phase equilibrium | |||
| Gas | |||
| Liquid | |||
| Hydrate | |||
| Abbreviations | |||
| Methane hydrates | |||
| Finite difference method | |||
| Hydrate-bearing sediments | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abu-Nab, A.K.; Koldoba, A.V.; Koldoba, E.V.; Poveshchenko, Y.A.; Podryga, V.O.; Rahimly, P.I.; Bakeer, A.E. On the Theory of Methane Hydrate Decomposition in a One-Dimensional Model in Porous Sediments: Numerical Study. Mathematics 2023, 11, 341. https://doi.org/10.3390/math11020341
Abu-Nab AK, Koldoba AV, Koldoba EV, Poveshchenko YA, Podryga VO, Rahimly PI, Bakeer AE. On the Theory of Methane Hydrate Decomposition in a One-Dimensional Model in Porous Sediments: Numerical Study. Mathematics. 2023; 11(2):341. https://doi.org/10.3390/math11020341
Chicago/Turabian StyleAbu-Nab, Ahmed K., Alexander V. Koldoba, Elena V. Koldoba, Yury A. Poveshchenko, Viktoriia O. Podryga, Parvin I. Rahimly, and Ahmed E. Bakeer. 2023. "On the Theory of Methane Hydrate Decomposition in a One-Dimensional Model in Porous Sediments: Numerical Study" Mathematics 11, no. 2: 341. https://doi.org/10.3390/math11020341
APA StyleAbu-Nab, A. K., Koldoba, A. V., Koldoba, E. V., Poveshchenko, Y. A., Podryga, V. O., Rahimly, P. I., & Bakeer, A. E. (2023). On the Theory of Methane Hydrate Decomposition in a One-Dimensional Model in Porous Sediments: Numerical Study. Mathematics, 11(2), 341. https://doi.org/10.3390/math11020341







