Improving the Performance of RODNet for MMW Radar Target Detection in Dense Pedestrian Scene
Abstract
:1. Introduction
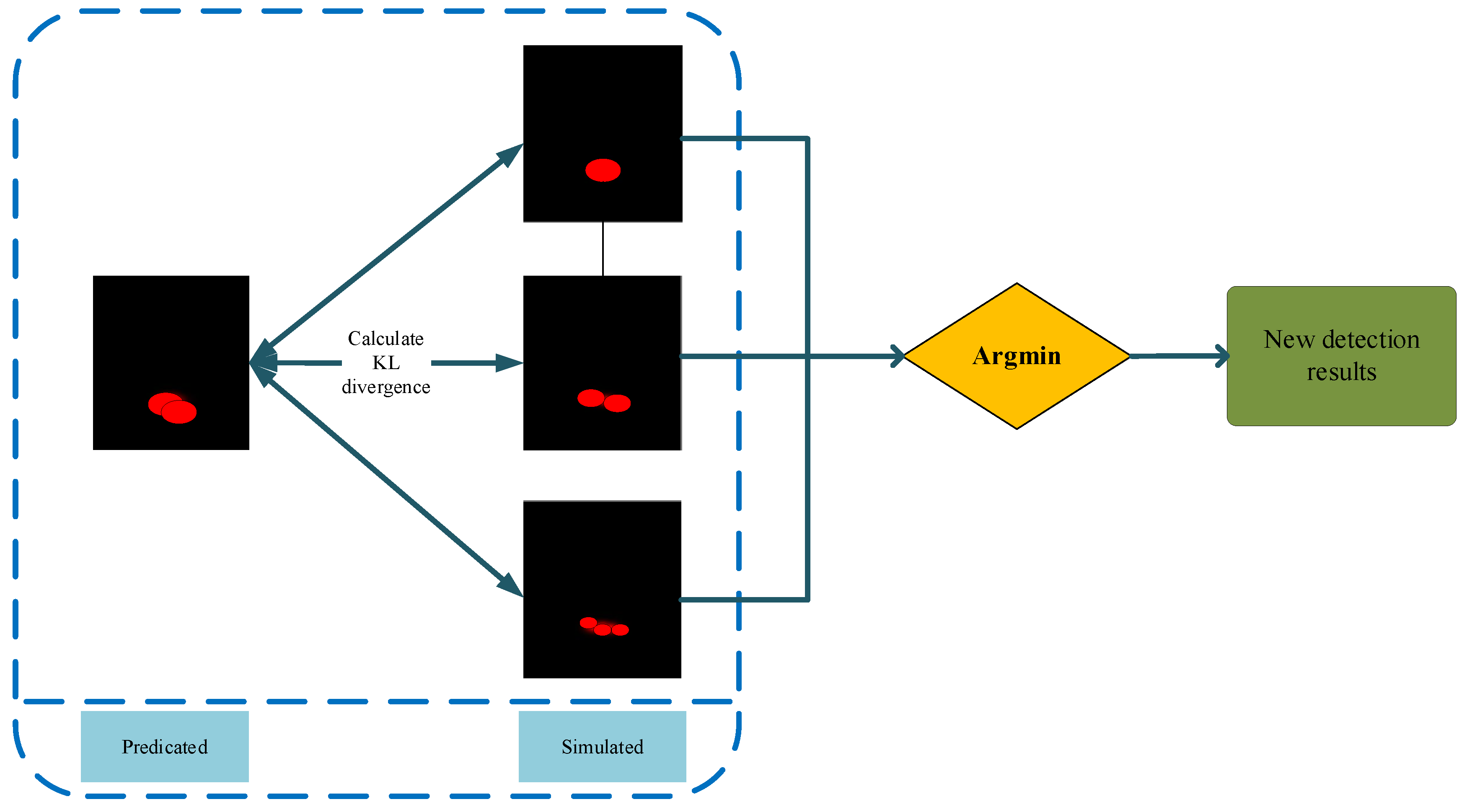
- Based on the actual data, we analyze the characteristics of ConfMap predicated by RODNet and the limitations of the OLS target-location detection method. The relationship among ConfMap value distribution, occupied grid spatial distribution, and target number is analyzed.
- GMM-TN, a target-state likelihood model with ConfMap value for observation is introduced for simulating the conditional ConfMap value and occupied grid spatial distribution with target number as condition.
- The KL distance measure between the predicated ConfMap of RODNet and the simulated ConfMap under the condition of the given target number is derived, and the maximum posteriori target number estimation is constructed. The CRUW dataset is used to verify the improved missed detection and false alarm of the method.
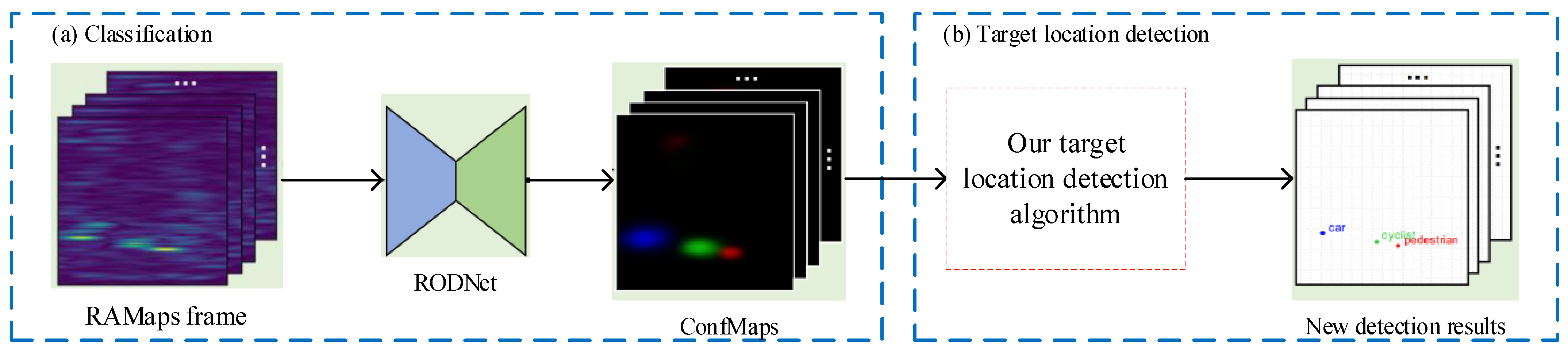
2. RODNet ConfMap Characteristics and Limitations
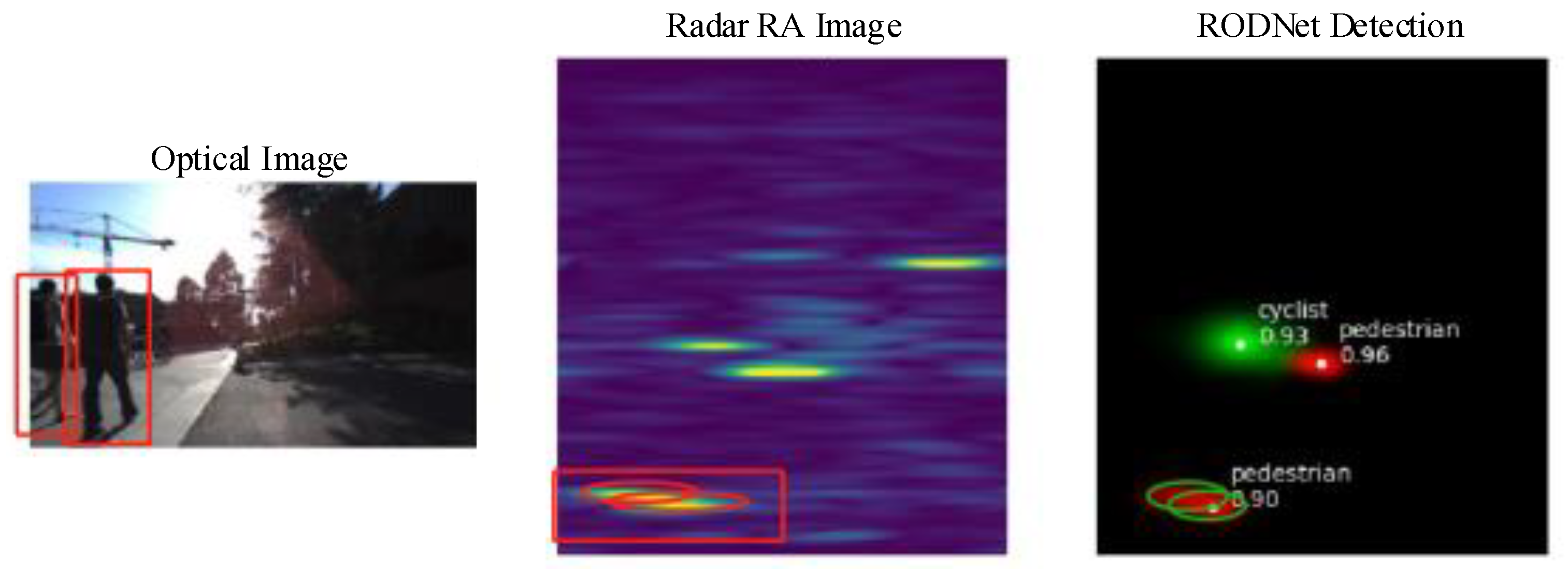
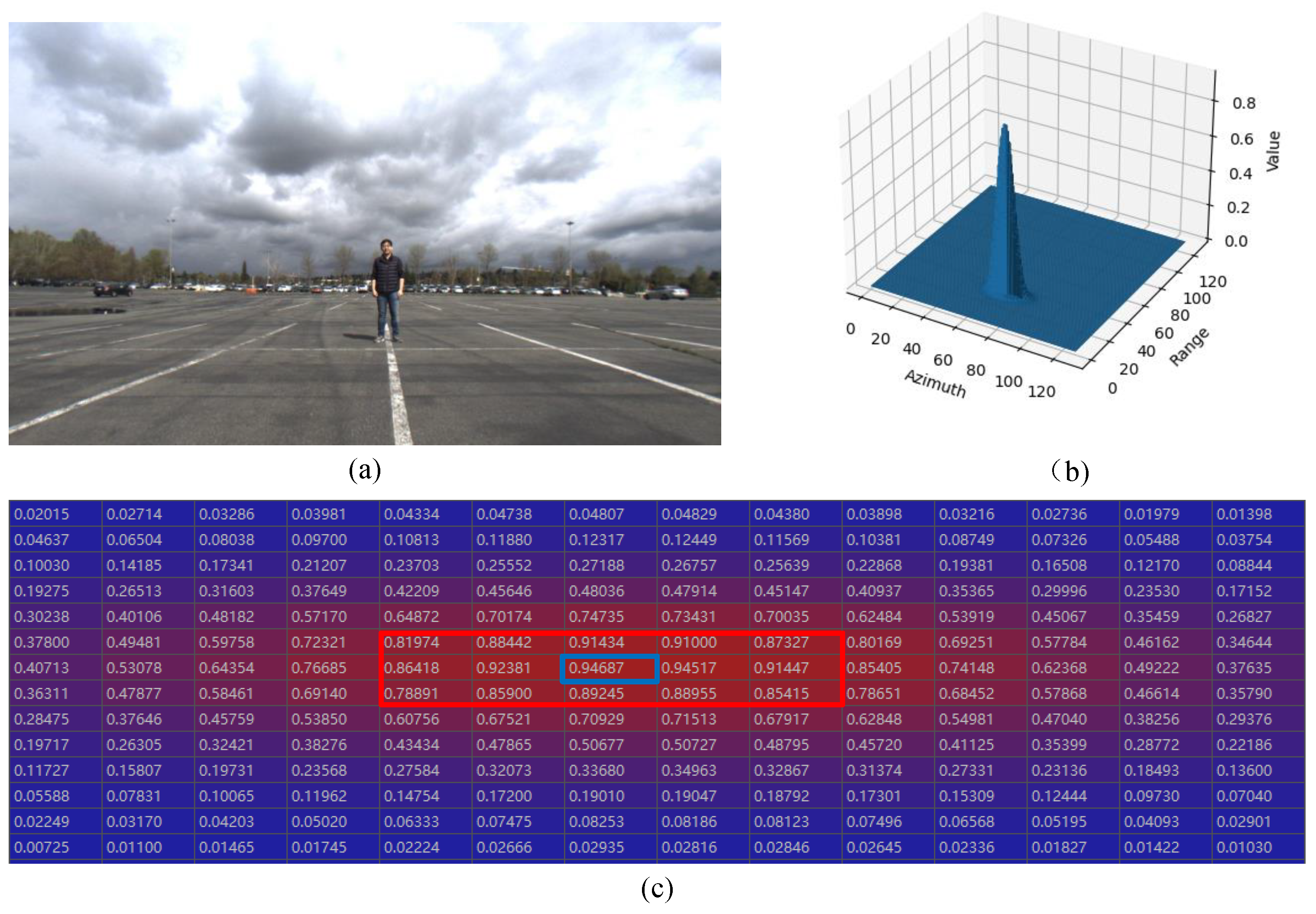
2.1. ConfMap Characteristic Analysis
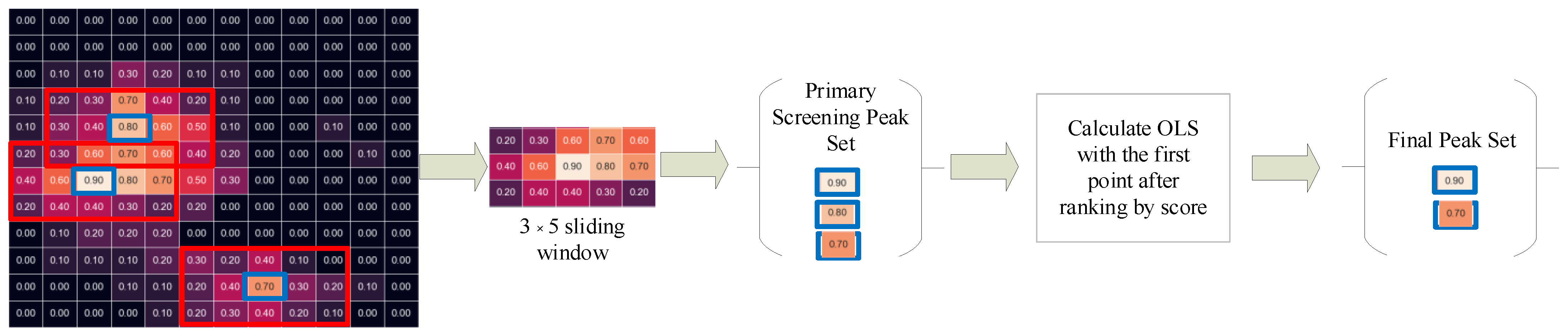
2.2. Object-Location Similarity (OLS) Limitation Analysis
- Point target hypothesis;
- No point target overlap will occur in ConfMap;
- The value distribution of ConfMap is related to the corresponding probability distribution of point target location and class;
- Considering the above assumptions, there are several typical cases, which can be analyzed as below.
- Case (1): Single target in ConfMap
- Case (2): No overlapped multiple targets in ConfMap
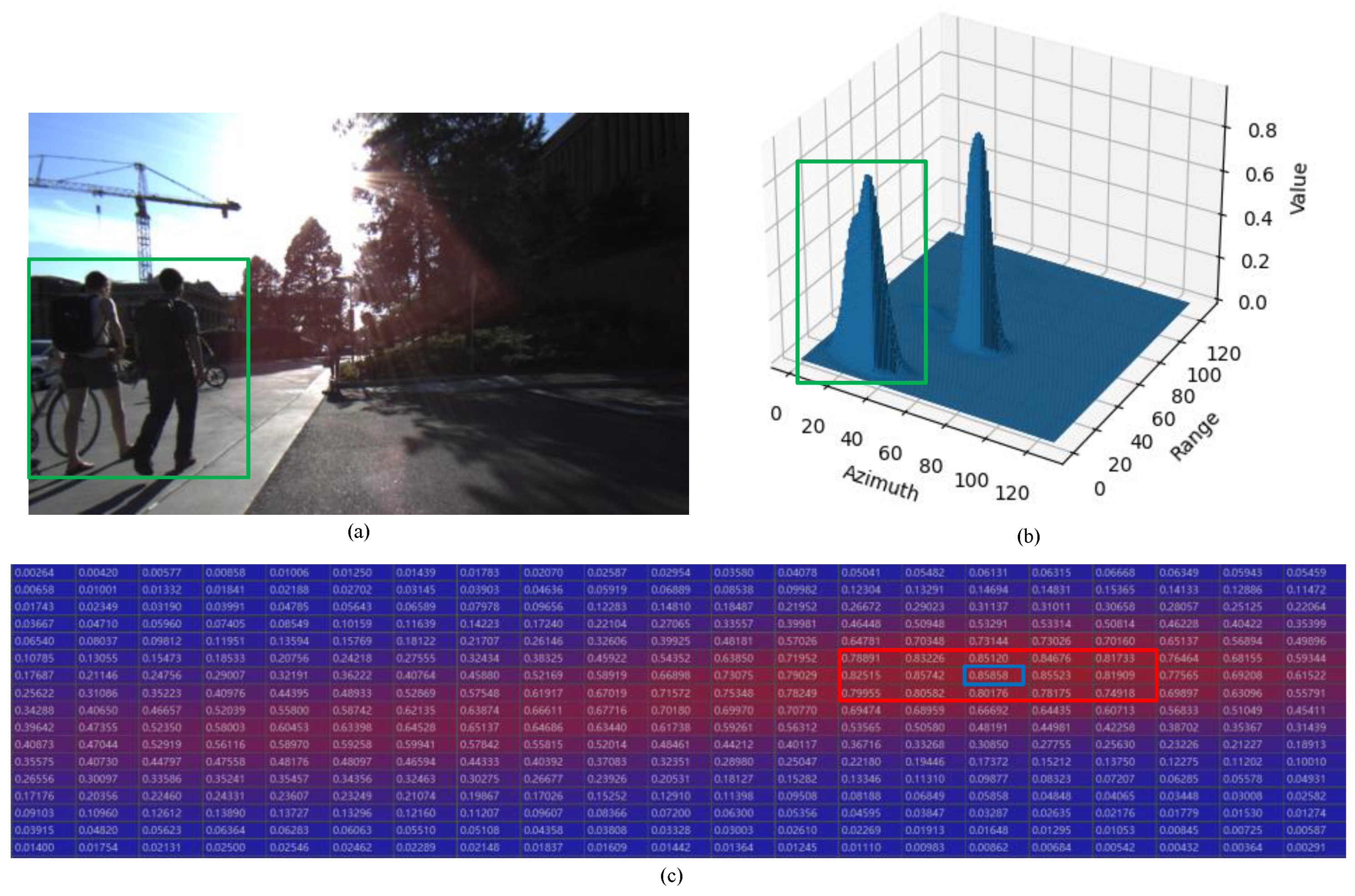
- Case (3): Type 1 overlapped multiple targets in ConfMap
- Case (4): Type 2 overlapped multiple targets in ConfMap
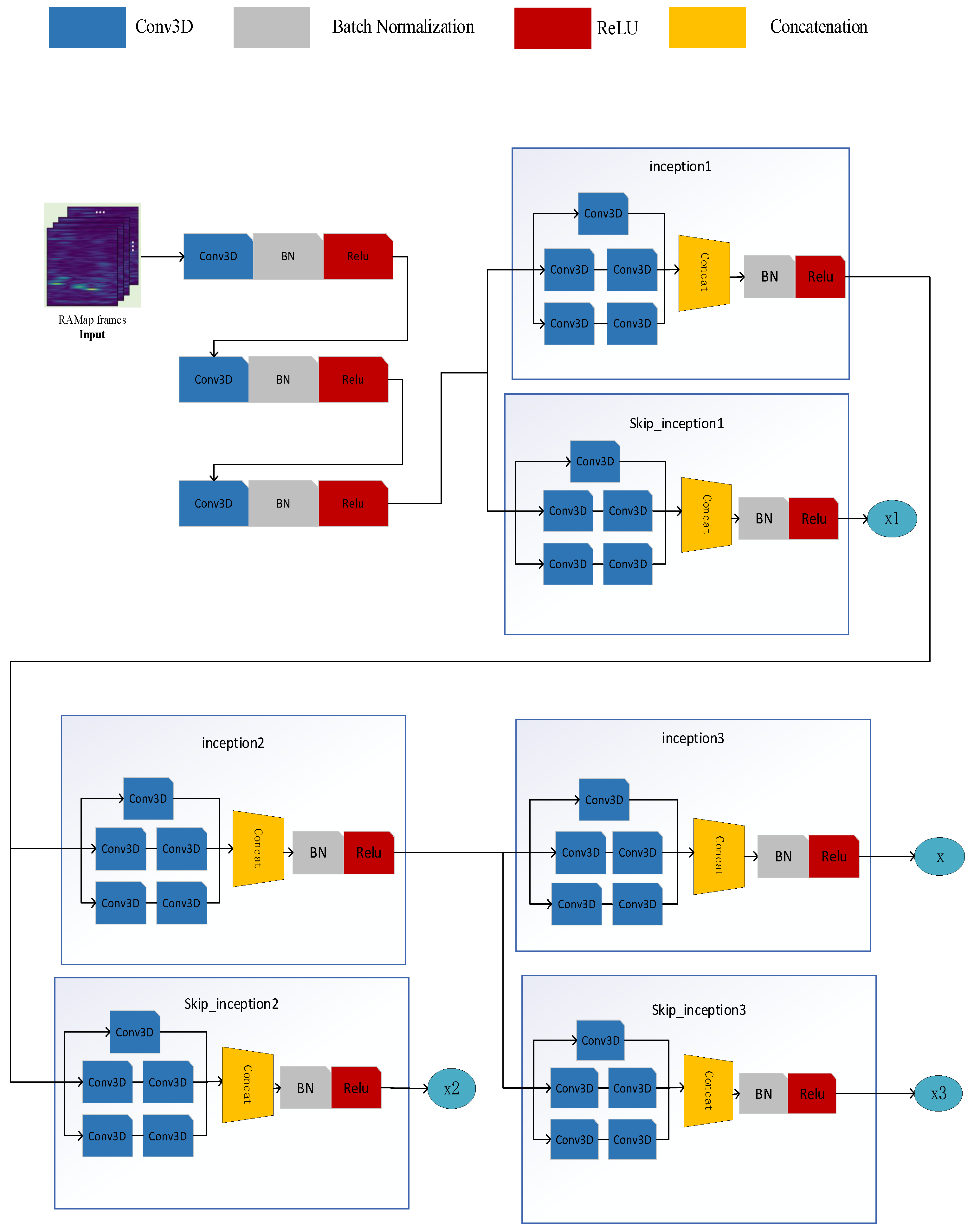
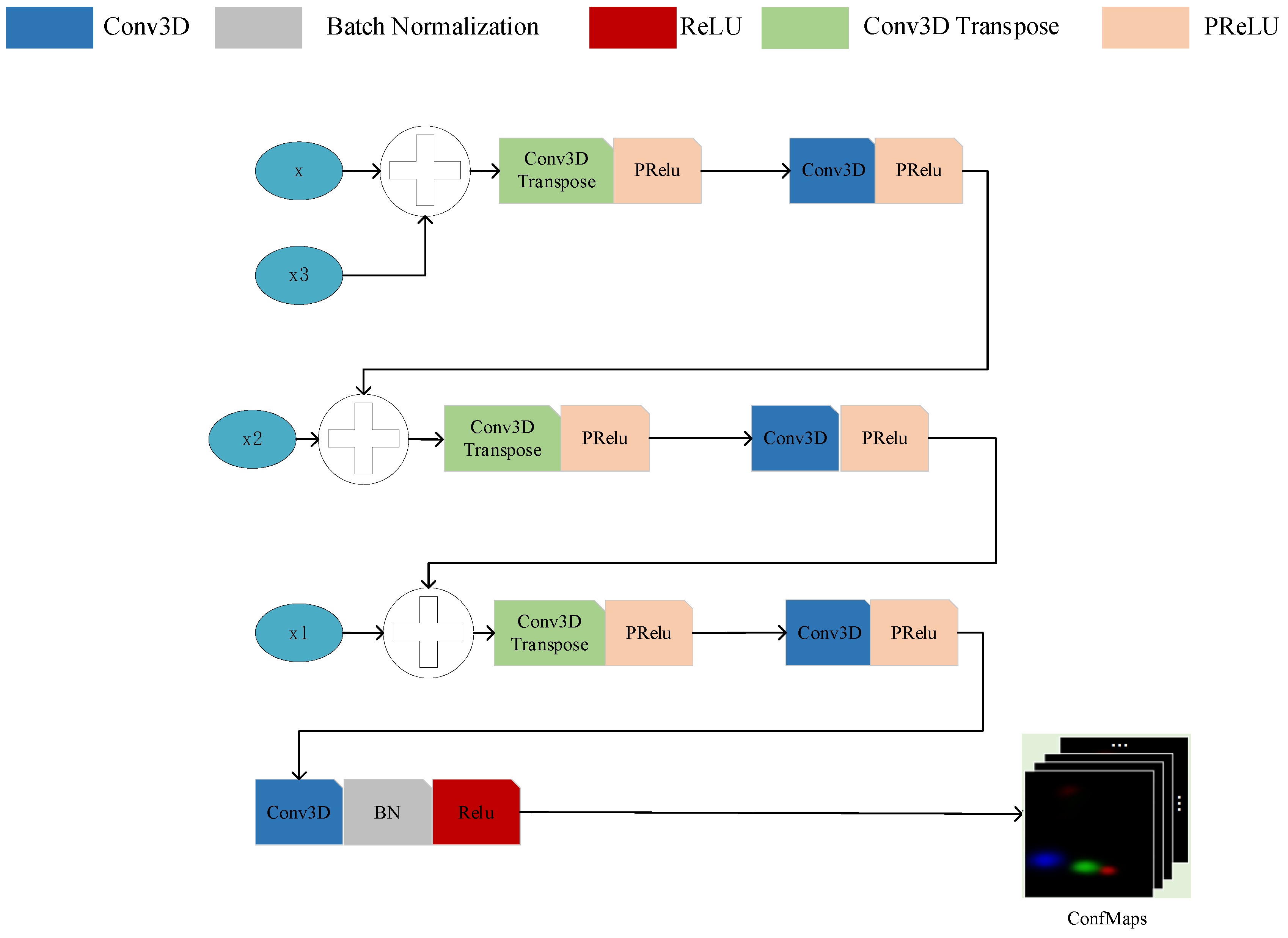
3. Dense Target-Location Detection Method Based on Maximum Likelihood Estimation
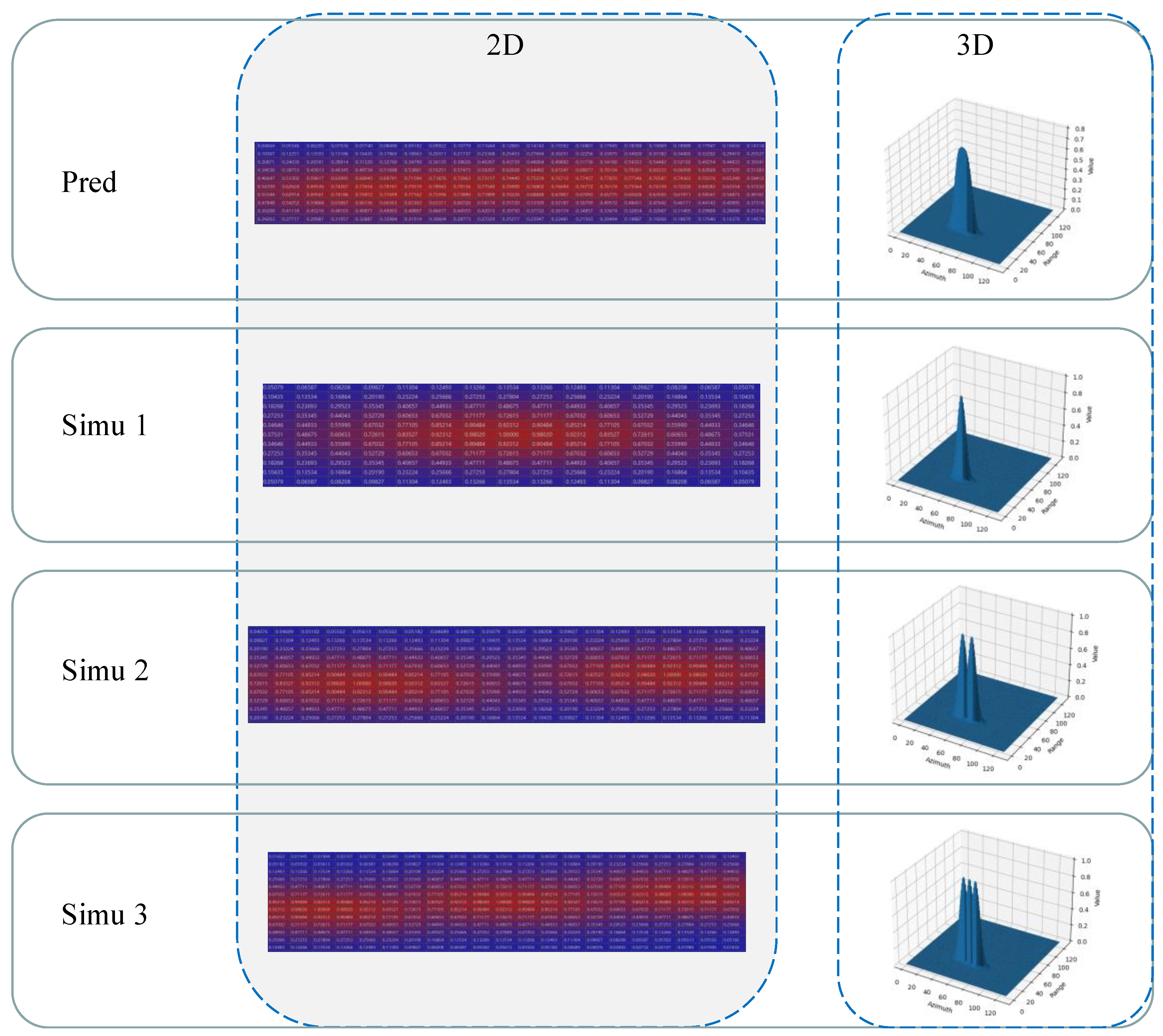
3.1. Gaussian Mixture Model with Target Number
- Point target hypothesis;
- Point target overlap may occur in ConfMap;
- Both the value distribution and occupied grid spatial distribution of ConfMap are related to the corresponding probability distribution of point target location and class.
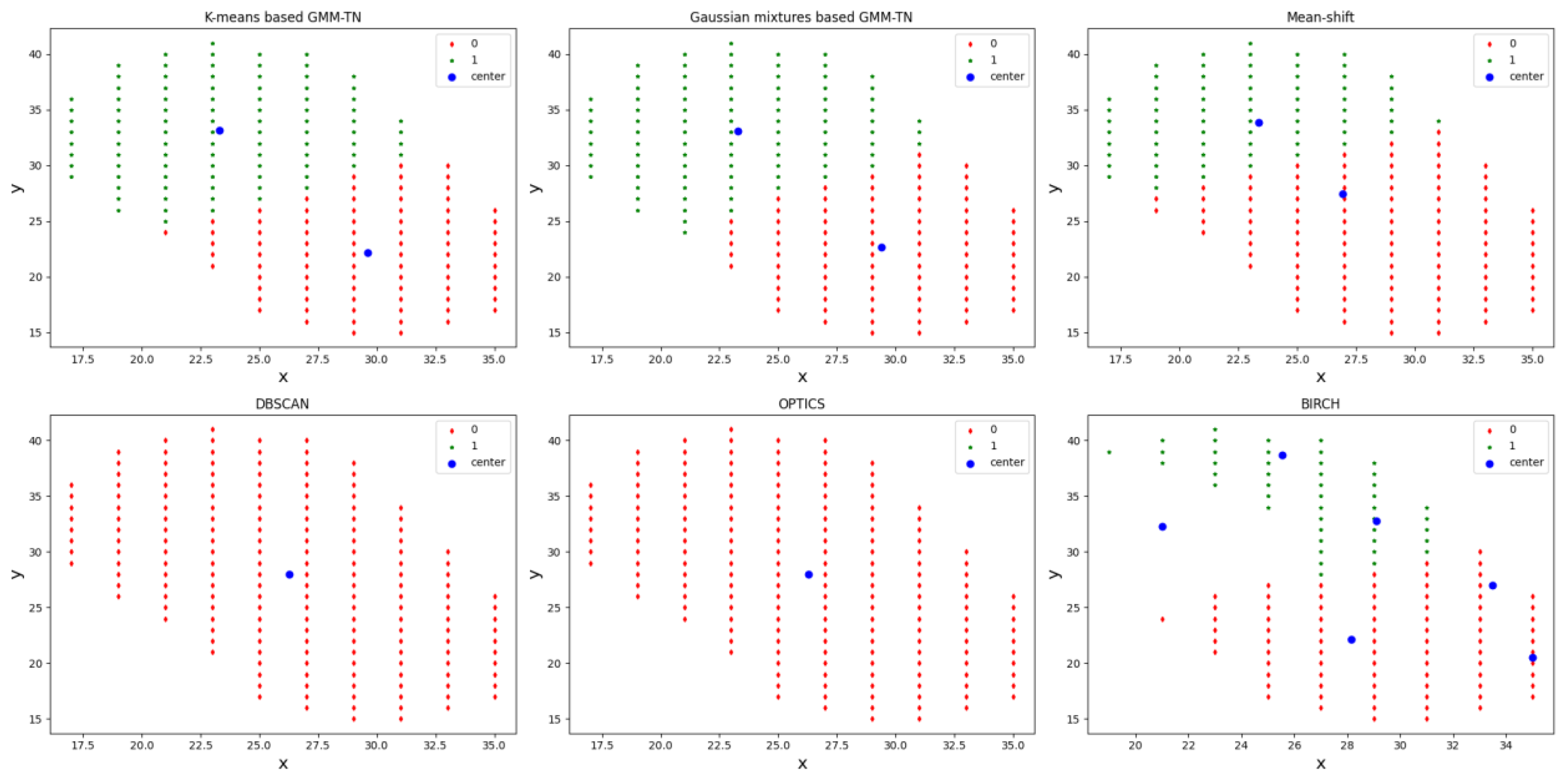
3.2. Target Number Estimation Method
- (1)
- Sort the scores of the results;
- (2)
- Calculate the distance between each coordinate and the highest score coordinate in turn;
- (3)
- If the threshold is exceeded, the grid coordinate is saved to another list; otherwise, the coordinates and the surrounding area greater than 0.3 enter our algorithm;
- (4)
- Loop steps (2) and (3) until the last one is over and repeat steps (2) and (3) in the ‘another list’.
4. Experiments and Analysis
4.1. Experimental Data and Processing Steps
4.2. Typical Sample Results and Analysis
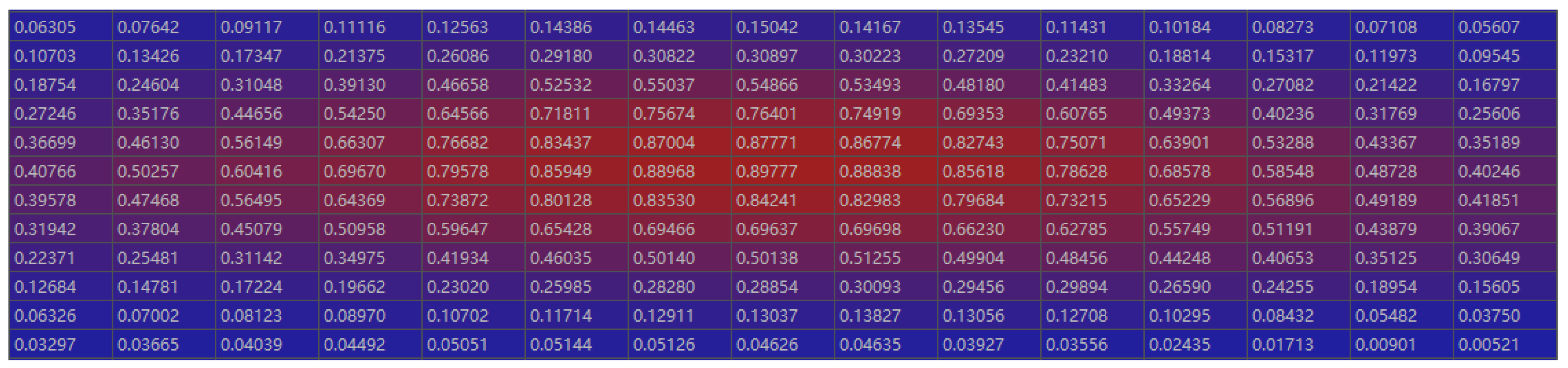
4.2.1. GMM-TN Model Based ConfMap Simulation Results
4.2.2. Target Number Estimation Compared with the Other Clustering Methods
4.2.3. Detection Results Comparison for Dense and Non-Dense Pedestrian Scenes
4.3. Statistical Evaluation of Large Amounts of Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronyms | Full Name |
| MMW | Millimeter-wave |
| RA | Range–azimuth |
| CNNs | Convolutional Neural Networks |
| OLS | Object-Location Similarity |
| GMM-TN | Gaussian Mixture Model with target number |
| KL divergence | Kullback–Leibler divergence |
| AP | Average Precision |
| AR | Average Recall |
| CFAR Detection | Constant False Alarm Rate Detection |
| FFT | Fast Fourier Transform |
| TDC | Temporal deformable convolution |
| MIMO | Multiple-Input Multiple-Output |
| DCN | Deformable convolution network |
| ConfMap | Confidence Map |
| IoU | Intersection over union |
| HG | Hourglass |
| 2DMLKL | Two-dimensional symmetric KL divergence |
| 1DMLKL | One-dimensional symmetric KL divergence |
| CRUW [40] | Camera-Radar of the University of Washington |
| DP scene | Dense Pedestrian scene |
| NDP scene | Non-Dense Pedestrian scene |
| CRF | Camera-radar fusion |
| TNA | Target Number Accuracy |
References
- de Ponte Müller, F. Survey on ranging sensors and cooperative techniques for relative positioning of vehicles. Sensors 2017, 17, 271. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yoneda, K.; Suganuma, N.; Yanase, R.; Aldibaja, M. Automated driving recognition technologies for adverse weather conditions. Iatss Res. 2019, 43, 253–262. [Google Scholar] [CrossRef]
- Schneider, M. Automotive radar-status and trends. In Proceedings of the German Microwave Conference, Ulm, Germany, 5–7 April 2005; pp. 144–147. [Google Scholar]
- Nabati, R.; Qi, H. CenterFusion: Center-based Radar and Camera Fusion for 3D Object Detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 5–9 January 2021; pp. 1527–1536. [Google Scholar]
- Richards, M.A. Fundamentals of Radar Signal Processing; Tata McGraw-Hill Education: New Delhi, India, 2005. [Google Scholar]
- Gao, X.; Xing, G.; Roy, S.; Liu, H. Experiments with mmwave automotive radar test-bed. In Proceedings of the 2019 53rd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 3–6 November 2019. [Google Scholar]
- Chen, X.; Ma, H.; Wan, J.; Li, B.; Xia, T. Multi-view 3d object detection network for autonomous driving. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1907–1915. [Google Scholar]
- Du, X.; Ang, M.H.; Karaman, S.; Rus, D. A general pipeline for 3d detection of vehicles. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 3194–3200. [Google Scholar]
- Liang, M.; Yang, B.; Wang, S.; Urtasun, R. Deep continuous fusion for multi-sensor 3d object detection. In Proceedings of the European Conference on Computer Vision (ECCV), Lecture Notes in Computer Science, Munich, Germany, 8–14 September 2018; Springer: Cham, Switzerland, 2018; Volume 11220, pp. 641–656. [Google Scholar]
- Ku, J.; Mozifian, M.; Lee, J.; Harakeh, A.; Waslander, S.L. Joint 3d proposal generation and object detection from view aggregation. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1–8. [Google Scholar]
- Qi, C.; Liu, W.; Wu, C.; Su, H.; Guibas, L. Frustum PointNets for 3D Object Detection from RGB-D Data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 918–927. [Google Scholar]
- Fukushima, K. A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybern. 1980, 36, 193–202. [Google Scholar] [CrossRef] [PubMed]
- Waibel, A.; Hanazawa, T.; Hinton, G.; Shikano, K.; Lang, K.J. Phoneme recognition using time-delay neural networks. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 328–339. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Danzer, A.; Griebel, T.; Bach, M.; Dietmayer, K. 2d car detection in radar data with pointnets. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 61–66. [Google Scholar]
- Wang, L.; Tang, J.; Liao, Q. A study on radar target detection based on deep neural networks. IEEE Sens. Lett. 2019, 3, 1–4. [Google Scholar] [CrossRef]
- Nabati, R.; Qi, H. Rrpn: Radar region proposal network for object detection in autonomous vehicles. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 3093–3097. [Google Scholar]
- John, V.; Nithilan, M.; Mita, S.; Tehrani, H.; Sudheesh, R.; Lalu, P. So-net: Joint semantic segmentation and obstacle detection using deep fusion of monocular camera and radar. In Proceedings of the Pacific-Rim Symposium on Image and Video Technology, Image and Video Technology, PSIVT 2019, Sydney, Australia, 18–22 September 2019; Springer: Cham, Switzerland, 2020; Volume 11994, pp. 138–148. [Google Scholar]
- Yu, J.; Hao, X.; Gao, X.; Sun, Q.; Liu, Y.; Chang, P.; Zhang, Z.; Gao, F.; Shuang, F. Radar Object Detection Using Data Merging, Enhancement and Fusion. In Proceedings of the 2021 International Conference on Multimedia Retrieval (ICMR ’21), Taipei, Taiwan, 21 August 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 566–572. [Google Scholar]
- Sun, P.; Niu, X.; Sun, P.; Xu, K. Squeeze-and-Excitation network-Based Radar Object Detection With Weighted Location Fusion. In Proceedings of the 2021 International Conference on Multimedia Retrieval (ICMR ’21), Taipei, Taiwan, 21 August 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 545–552. [Google Scholar]
- Zheng, Z.; Yue, X.; Keutzer, K.; Vincentelli, A.S. Scene-aware Learning Network for Radar Object Detection. In Proceedings of the 2021 International Conference on Multimedia Retrieval (ICMR ’21), Taipei, Taiwan, 21 August 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 573–579. [Google Scholar]
- Ju, B.; Yang, W.; Jia, J.; Ye, X.; Chen, Q.; Tan, X.; Sun, H.; Shi, Y.; Ding, E. DANet: Dimension Apart Network for Radar Object Detection. In Proceedings of the 2021 International Conference on Multimedia Retrieval (ICMR ’21), Taipei, Taiwan, 21 August 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 533–539. [Google Scholar]
- Hsu, C.-C.; Lee, C.; Chen, L.; Hung, M.-K.; Lin, Y.-L.; Wang, X.-Y. Efficient-ROD: Efficient Radar Object Detection based on Densely Connected Residual Network. In Proceedings of the 2021 International Conference on Multimedia Retrieval (ICMR ’21), Taipei, Taiwan, 21 August 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 526–532. [Google Scholar]
- Gao, X.; Xing, G.; Roy, S.; Liu, H. RAMP-CNN: A Novel Neural Network for Enhanced Automotive Radar Object Recognition. IEEE Sens. J. 2021, 21, 5119–5132. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, Z.; Gao, X.; Hwang, J.-N.; Xing, G.; Liu, H. RODNet: Object Detection under Severe Conditions Using Vision-Radio Cross-Modal Supervision. arXiv 2020, arXiv:2003.01816. [Google Scholar]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- Guo, W.; Wang, J.; Wang, S. Deep multimodal representation learning: A survey. IEEE Access 2019, 7, 63373–63394. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Urmson, C.; Anhalt, J.; Bagnell, D.; Baker, C.; Bittner, R.; Clark, M.; Dolan, J.; Duggins, D.; Galatali, T.; Geyer, C. Autonomous driving in urban environments: Boss and the urban challenge. J. Field Robot. 2008, 25, 425–466. [Google Scholar] [CrossRef]
- Van Brummelen, J.; O’Brien, M.; Gruyer, D.; Najjaran, H. Autonomous vehicle perception: The technology of today and tomorrow. Transp. Res. Part C Emerg. Technol. 2018, 89, 384–406. [Google Scholar] [CrossRef]
- Giacalone, J.-P.; Bourgeois, L.; Ancora, A. Challenges in aggregation of heterogeneous sensors for Autonomous Driving Systems. In Proceedings of the 2019 IEEE Sensors Applications Symposium (SAS), Sophia Antipolis, France, 11–13 March 2019; pp. 1–5. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 52, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Rashinkar, P.; Krushnasamy, V. An overview of data fusion techniques. In Proceedings of the 2017 International Conference on Innovative Mechanisms for Industry Applications (ICIMIA), Bangalore, India, 21–23 February 2017; pp. 694–697. [Google Scholar]
- Fung, M.L.; Chen, M.Z.; Chen, Y.H. Sensor fusion: A review of methods and applications. In Proceedings of the 2017 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 3853–3860. [Google Scholar]
- Fayyad, J.; Jaradat, M.A.; Gruyer, D.; Najjaran, H. Deep learning sensor fusion for autonomous vehicle perception and localization: A review. Sensors 2020, 20, 4220. [Google Scholar] [CrossRef] [PubMed]
- Bombini, L.; Cerri, P.; Medici, P.; Alessandretti, G. Radar-vision fusion for vehicle detection. In Proceedings of the International Workshop on Intelligent Transportation, Hamburg, Germany, 14–15 May 2006; pp. 65–70. [Google Scholar]
- Newell, A.; Yang, K.; Deng, J. Stacked hourglass networks for human pose estimation. In Proceedings of the European Conference on Computer Vision, Venice, Italy, 22–29 October 2017; Springer: Berlin/Heidelberg, Germany, 2016; pp. 483–499. [Google Scholar]
- MacQueen, J. Some methods for classification and analysis of multivariate observation. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Los Angelas, CA, USA, 18–21 July 1965; University of California: Los Angeles, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, Oregon, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Wang, Y.; Wang, G.; Hsu, H.M.; Liu, H.; Hwang, J.N. Rethinking of Radar’s Role: A Camera-Radar Dataset and Systematic Annotator via Coordinate Alignment. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L. Pytorch: An imperative style, high-performance deep learning library. arXiv 2019, arXiv:1912.01703. [Google Scholar]
- Comaniciu, D.; Meer, P. Mean Shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef] [Green Version]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. DBSCAN revisited, revisited: Why and how you should (still) use DBSCAN. ACM Trans. Database Syst. 2017, 42, 19. [Google Scholar] [CrossRef]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.P.; Sander, J. OPTICS: Ordering points to identify the clustering structure. ACM Sigmod Rec. 1999, 28, 49–60. [Google Scholar] [CrossRef]
- Schubert, E.; Gertz, M. Improving the Cluster Structure Extracted from OPTICS Plots. In Proceedings of the LWDA 2018: Conference “Lernen, Wissen, Daten, Analysen”, Mannheim, Germany, 22–24 August 2018; pp. 318–329. [Google Scholar]
- Tian, Z.; Ramakrishnan, R. Miron Livny: BIRCH: An Efficient Data Clustering Method for Very Large Databases. ACM Sigmod Rec. 1999, 25, 103–114. [Google Scholar]
- Angelov, A.; Robertson, A.; Murray-Smith, R.; Fioranelli, F. Practical classification of different moving targets using automotive radar and deep neural networks. IET Radar Sonar Navig. 2018, 12, 1082–1089. [Google Scholar] [CrossRef]








| Methods | AP | AR |
|---|---|---|
| Decision Tree [6] | 4.70 | 44.26 |
| CFAR+ResNet [47] | 40.49 | 60.56 |
| CFAR+VGG-16 [6] | 40.73 | 72.88 |
| RODNet [25] | 85.98 | 87.86 |
| Scene | Evaluation Index | RODNet | ROD-2DMLKL | ROD-1DMLKL |
|---|---|---|---|---|
| Dense pedestrian | AP | 55.70% | 80.62% | 84.59% |
| AR | 52.27% | 83.33% | 88.28% | |
| Non-dense pedestrian | AP | 93.43% | 87.98% | 92.68% |
| AR | 94.72% | 88.47% | 93.32% |
| Scene | Evaluation Index | RODNet | ROD-2DMLKL | ROD-1DMLKL |
|---|---|---|---|---|
| Dense pedestrian | TNA | 52.63% | 89.73% | 96.21% |
| Non-dense pedestrian | 89.70% | 90.62% | 95.59% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, Z.; Wang, Y.; Xie, G.; Lin, Y.; Shen, W.; Jiang, W. Improving the Performance of RODNet for MMW Radar Target Detection in Dense Pedestrian Scene. Mathematics 2023, 11, 361. https://doi.org/10.3390/math11020361
Li Y, Li Z, Wang Y, Xie G, Lin Y, Shen W, Jiang W. Improving the Performance of RODNet for MMW Radar Target Detection in Dense Pedestrian Scene. Mathematics. 2023; 11(2):361. https://doi.org/10.3390/math11020361
Chicago/Turabian StyleLi, Yang, Zhuang Li, Yanping Wang, Guangda Xie, Yun Lin, Wenjie Shen, and Wen Jiang. 2023. "Improving the Performance of RODNet for MMW Radar Target Detection in Dense Pedestrian Scene" Mathematics 11, no. 2: 361. https://doi.org/10.3390/math11020361
APA StyleLi, Y., Li, Z., Wang, Y., Xie, G., Lin, Y., Shen, W., & Jiang, W. (2023). Improving the Performance of RODNet for MMW Radar Target Detection in Dense Pedestrian Scene. Mathematics, 11(2), 361. https://doi.org/10.3390/math11020361







