Mathematical Modeling and Thermal Control of a 1.5 kW Reversible Solid Oxide Stack for 24/7 Hydrogen Plants
Abstract
:1. Introduction
- Development of a practical control-oriented model for a reversible solid oxide stack prototype considering a linear degradation model.
- Validation of the proposed model with experimental data under different scenarios and the introduction of an offline algorithm to identify the unknown model parameters.
- Present the mathematical structure and the main considerations of the balance of plant agents and the controllers implemented for the optimal functioning of the system.
- Analyze the thermal effects of the controlled plant under different conditions.
2. Mathematical Model
2.1. Fluid Dynamics: Manifolds Mass Flow
2.2. Fluid Dynamics: Stack Mass Flow
2.3. Electrochemical Model
2.3.1. Nernst Voltage
2.3.2. Ohmic Losses
2.3.3. Activation Losses
2.3.4. Concentration Losses
2.4. Thermodynamics
2.5. Stack Degradation: A Linear Approach
3. Balance of Plant Agents
3.1. Heat Exchangers
3.2. Boiler
3.3. Condenser
4. Control-Oriented Model and Control Definition
Controllers for Thermal Safety
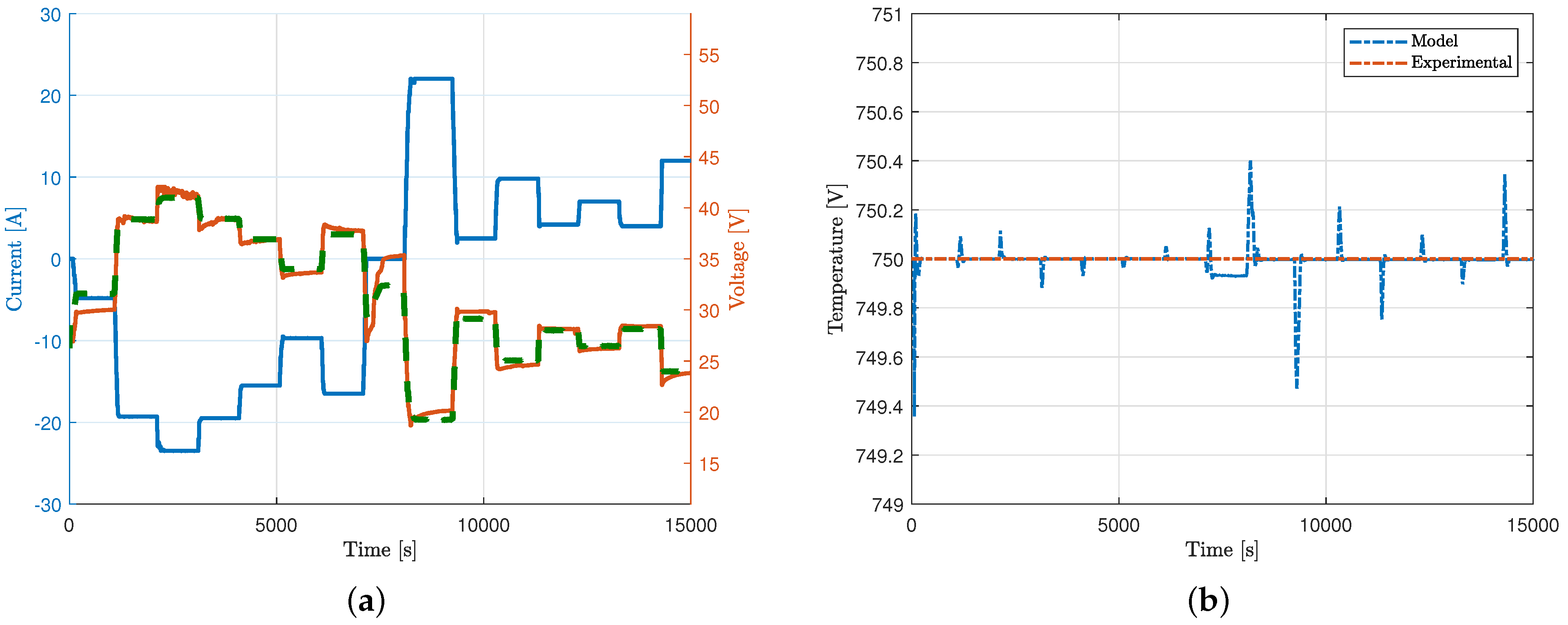
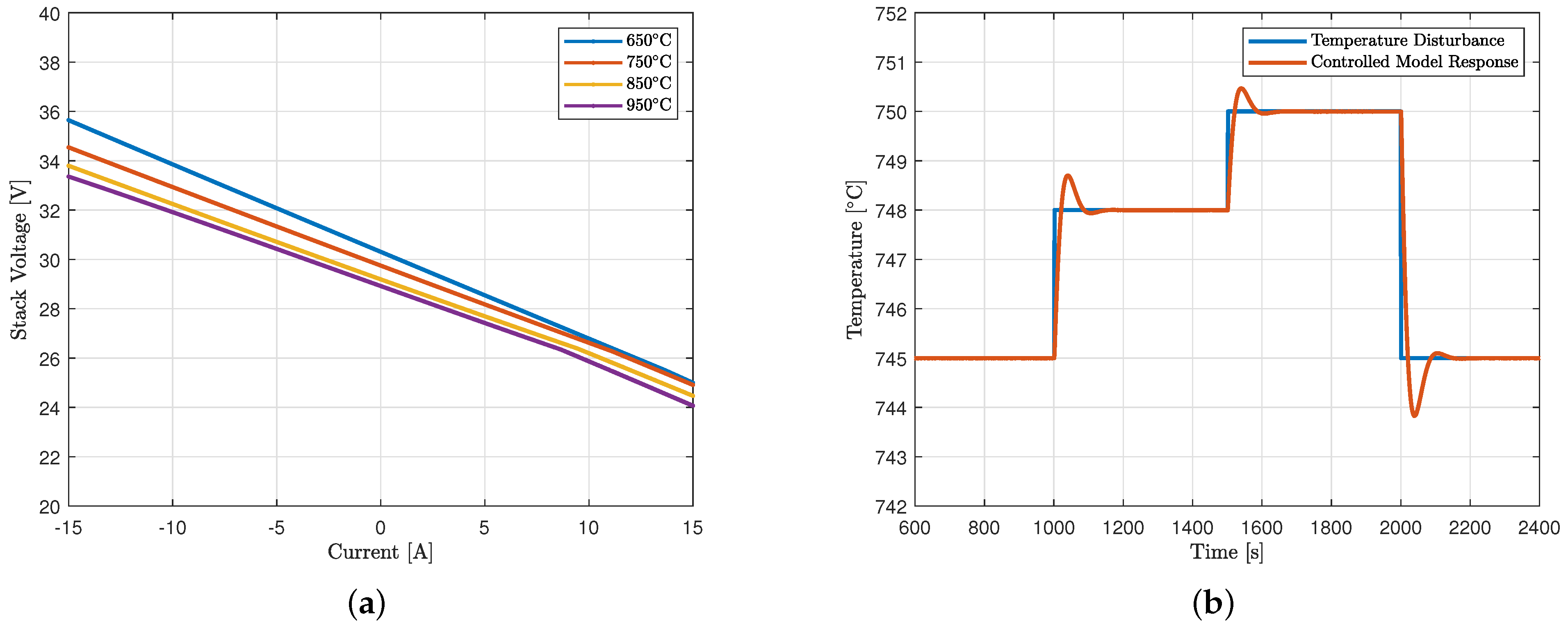
5. Results and Analysis
5.1. Parameter Estimation
5.2. Polarization Curves
5.3. Dynamic Response
5.4. Thermal Effects Analysis
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Estimated Parameter | Symbol | Value | Units |
|---|---|---|---|
| Stack Area | 63 | cm2 | |
| Stack Mass | 5.5 | kg | |
| Faraday Constant | F | 96,487 | C/mol |
| Number of Cells | 30 | - | |
| Oven Power | 2.75 | kW | |
| Oven Losses Constant | 0.7 | ||
| Universal Gas Constant | R | ||
| Air Gas Constant | |||
| H2 Molar Mass | g/mol | ||
| H2O Molar Mass | g/mol | ||
| O2 Molar Mass | g/mol | ||
| N2 Molar Mass | g/mol | ||
| Inlet Manifold Valve Constant | |||
| Outlet Manifold Valve Constant | |||
| Anode Valve Constant | |||
| Cathode Valve Constant | |||
| Electrolyte Thickness (8YSZ) | 10 | ||
| O2 Effective Diffusion Coefficient | |||
| H2O Effective Diffusion Coefficient | |||
| H2 Effective Diffusion Coefficient | |||
| Hydrogen Lowest Heating Value | 246,870 | ||
| Ionic Conductivity Pre-exponential Factor | 466 | s | |
| Electrolyte Activation Energy | J/mol |
| Estimated Parameter | Symbol | Value | Units |
|---|---|---|---|
| Cathode Phenomenological Coefficient | |||
| Anode Phenomenological Coefficient | |||
| Cathode Activation Energy | J/mol | ||
| Anode Activation Energy | J/mol | ||
| Contact Resistance | 0.3 |
References
- Marra, D.; Pianese, C.; Polverino, P.; Sorrentino, M. Models for Solid Oxide Fuel Cell Systems: Exploitation of Models Hierarchy for Industrial Design of Control and Diagnosis Strategies; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Gómez, S.Y.; Hotza, D. Current developments in reversible solid oxide fuel cells. Renew. Sustain. Energy Rev. 2016, 61, 155–174. [Google Scholar] [CrossRef]
- Subotić, V.; Thaller, T.; Königshofer, B.; Menzler, N.H.; Bucher, E.; Egger, A.; Hochenauer, C. Performance assessment of industrial-sized solid oxide cells operated in a reversible mode: Detailed numerical and experimental study. Int. J. Hydrog. Energy 2020, 45, 29166–29185. [Google Scholar] [CrossRef]
- Pukrushpan, J.T.; Peng, H.; Stefanopoulou, A.G. Control-oriented modeling and analysis for automotive fuel cell systems. J. Dyn. Sys. Meas. Control 2004, 126, 14–25. [Google Scholar] [CrossRef]
- Bao, C.; Ouyang, M.; Yi, B. Modeling and control of air stream and hydrogen flow with recirculation in a PEM fuel cell system—I. Control-oriented modeling. Int. J. Hydrog. Energy 2006, 31, 1879–1896. [Google Scholar] [CrossRef]
- Solsona, M.; Kunusch, C.; Ocampo-Martinez, C. Control-oriented model of a membrane humidifier for fuel cell applications. Energy Convers. Manag. 2017, 137, 121–129. [Google Scholar] [CrossRef]
- Zhang, X.; Li, J.; Li, G.; Feng, Z. Development of a control-oriented model for the solid oxide fuel cell. J. Power Sources 2006, 160, 258–267. [Google Scholar] [CrossRef]
- Xing, Y.; Costa-Castello, R.; Na, J.; Renaudineau, H. Control-oriented modelling and analysis of a solid oxide fuel cell system. Int. J. Hydrog. Energy 2020, 45, 20659–20672. [Google Scholar] [CrossRef]
- Motylinski, K.; Kupecki, J.; Numan, B.; Hajimolana, Y.S.; Venkataraman, V. Dynamic modelling of reversible solid oxide cells for grid stabilization applications. Energy Convers. Manag. 2021, 228, 113674. [Google Scholar] [CrossRef]
- Liu, G.; Zhao, W.; Li, Z.; Xia, Z.; Jiang, C.; Kupecki, J.; Pang, S.; Deng, Z.; Li, X. Modeling and control-oriented thermal safety analysis for mode switching process of reversible solid oxide cell system. Energy Convers. Manag. 2022, 255, 115318. [Google Scholar] [CrossRef]
- Frank, M.; Deja, R.; Peters, R.; Blum, L.; Stolten, D. Bypassing renewable variability with a reversible solid oxide cell plant. Appl. Energy 2018, 217, 101–112. [Google Scholar] [CrossRef]
- Ma, R.; Gao, F.; Breaz, E.; Huangfu, Y.; Briois, P. Multidimensional reversible solid oxide fuel cell modeling for embedded applications. IEEE Trans. Energy Convers. 2017, 33, 692–701. [Google Scholar] [CrossRef]
- Iora, P.; Chiesa, P. High efficiency process for the production of pure oxygen based on solid oxide fuel cell–solid oxide electrolyzer technology. J. Power Sources 2009, 190, 408–416. [Google Scholar] [CrossRef]
- Hauck, M.; Herrmann, S.; Spliethoff, H. Simulation of a reversible SOFC with Aspen Plus. Int. J. Hydrog. Energy 2017, 42, 10329–10340. [Google Scholar] [CrossRef]
- Kazempoor, P.; Braun, R. Model validation and performance analysis of regenerative solid oxide cells for energy storage applications: Reversible operation. Int. J. Hydrog. Energy 2014, 39, 5955–5971. [Google Scholar] [CrossRef]
- Ni, M.; Leung, M.K.; Leung, D.Y. A modeling study on concentration overpotentials of a reversible solid oxide fuel cell. J. Power Sources 2006, 163, 460–466. [Google Scholar] [CrossRef]
- Luo, Y.; Shi, Y.; Zheng, Y.; Cai, N. Reversible solid oxide fuel cell for natural gas/renewable hybrid power generation systems. J. Power Sources 2017, 340, 60–70. [Google Scholar] [CrossRef]
- Botta, G.; Romeo, M.; Fernandes, A.; Trabucchi, S.; Aravind, P. Dynamic modeling of reversible solid oxide cell stack and control strategy development. Energy Convers. Manag. 2019, 185, 636–653. [Google Scholar] [CrossRef]
- Zhu, J.; Lin, Z. Degradations of the electrochemical performance of solid oxide fuel cell induced by material microstructure evolutions. Appl. Energy 2018, 231, 22–28. [Google Scholar] [CrossRef]
- Naeini, M.; Cotton, J.S.; Adams II, T.A. Data-Driven Modeling of Long-Term Performance Degradation in Solid Oxide Electrolyzer Cell System. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2022; Volume 49, pp. 847–852. [Google Scholar]
- Yang, C.; Guo, R.; Jing, X.; Li, P.; Yuan, J.; Wu, Y. Degradation mechanism and modeling study on reversible solid oxide cell in dual-mode—A review. Int. J. Hydrog. Energy 2022, 47, 37895–37928. [Google Scholar] [CrossRef]
- Khan, M.; Xu, X.; Knibbe, R.; Zhu, Z. Air electrodes and related degradation mechanisms in solid oxide electrolysis and reversible solid oxide cells. Renew. Sustain. Energy Rev. 2021, 143, 110918. [Google Scholar] [CrossRef]
- Zhang, X.; O’Brien, J.E.; O’Brien, R.C.; Housley, G.K. Durability evaluation of reversible solid oxide cells. J. Power Sources 2013, 242, 566–574. [Google Scholar] [CrossRef]
- Knibbe, R.; Traulsen, M.L.; Hauch, A.; Ebbesen, S.D.; Mogensen, M. Solid oxide electrolysis cells: Degradation at high current densities. J. Electrochem. Soc. 2010, 157, B1209. [Google Scholar] [CrossRef]
- Tietz, F.; Sebold, D.; Brisse, A.; Schefold, J. Degradation phenomena in a solid oxide electrolysis cell after 9000 h of operation. J. Power Sources 2013, 223, 129–135. [Google Scholar] [CrossRef]
- Blum, L.; Batfalsky, P.; De Haart, L.; Malzbender, J.; Menzler, N.H.; Peters, R.; Quadakkers, W.J.; Remmel, J.; Tietz, F.; Stolten, D. Overview on the Jülich SOFC development status. ECS Trans. 2013, 57, 23. [Google Scholar] [CrossRef]
- Gazzarri, J.; Kesler, O. Short-stack modeling of degradation in solid oxide fuel cells: Part I. Contact degradation. J. Power Sources 2008, 176, 138–154. [Google Scholar] [CrossRef]
- Navasa, M.; Graves, C.; Chatzichristodoulou, C.; Skafte, T.L.; Sundén, B.; Frandsen, H.L. A three dimensional multiphysics model of a solid oxide electrochemical cell: A tool for understanding degradation. Int. J. Hydrog. Energy 2018, 43, 11913–11931. [Google Scholar] [CrossRef]
- Rizvandi, O.B.; Miao, X.Y.; Frandsen, H.L. Multiscale modeling of degradation of full solid oxide fuel cell stacks. Int. J. Hydrog. Energy 2021, 46, 27709–27730. [Google Scholar] [CrossRef]
- Naeini, M.; Lai, H.; Cotton, J.S.; Adams, T.A. A Mathematical Model for Prediction of Long-Term Degradation Effects in Solid Oxide Fuel Cells. Ind. Eng. Chem. Res. 2021, 60, 1326–1340. [Google Scholar] [CrossRef]
- Naeini, M.; Cotton, J.S.; Adams, T.A. An eco-technoeconomic analysis of hydrogen production using solid oxide electrolysis cells that accounts for long-term degradation. Front. Energy Res. 2022, 10, 1015465. [Google Scholar] [CrossRef]
- Saarinen, V.; Pennanen, J.; Kotisaari, M.; Thomann, O.; Himanen, O.; Iorio, S.D.; Hanoux, P.; Aicart, J.; Couturier, K.; Sun, X.; et al. Design, manufacturing, and operation of movable 2× 10 kW size rSOC system. Fuel Cells 2021, 21, 477–487. [Google Scholar] [CrossRef]
- Akikur, R.; Saidur, R.; Ping, H.; Ullah, K. Performance analysis of a co-generation system using solar energy and SOFC technology. Energy Convers. Manag. 2014, 79, 415–430. [Google Scholar] [CrossRef]
- Mottaghizadeh, P.; Santhanam, S.; Heddrich, M.P.; Friedrich, K.A.; Rinaldi, F. Process modeling of a reversible solid oxide cell (r-SOC) energy storage system utilizing commercially available SOC reactor. Energy Convers. Manag. 2017, 142, 477–493. [Google Scholar] [CrossRef]
- Pukrushpan, J.T.; Stefanopoulou, A.G.; Peng, H. Control of Fuel Cell Power Systems: Principles, Modeling, Analysis and Feedback Design; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Weber, A.; Ivers-Tiffée, E. Materials and concepts for solid oxide fuel cells (SOFCs) in stationary and mobile applications. J. Power Sources 2004, 127, 273–283. [Google Scholar] [CrossRef]
- Noren, D.; Hoffman, M.A. Clarifying the Butler–Volmer equation and related approximations for calculating activation losses in solid oxide fuel cell models. J. Power Sources 2005, 152, 175–181. [Google Scholar] [CrossRef]
- Costamagna, P.; Honegger, K. Modeling of solid oxide heat exchanger integrated stacks and simulation at high fuel utilization. J. Electrochem. Soc. 1998, 145, 3995. [Google Scholar] [CrossRef]
- Chan, S.; Khor, K.; Xia, Z. A complete polarization model of a solid oxide fuel cell and its sensitivity to the change of cell component thickness. J. Power Sources 2001, 93, 130–140. [Google Scholar] [CrossRef]
- Wendel, C.H.; Gao, Z.; Barnett, S.A.; Braun, R.J. Modeling and experimental performance of an intermediate temperature reversible solid oxide cell for high-efficiency, distributed-scale electrical energy storage. J. Power Sources 2015, 283, 329–342. [Google Scholar] [CrossRef]
- Fukunaga, H.; Ihara, M.; Sakaki, K.; Yamada, K. The relationship between overpotential and the three phase boundary length. Solid State Ionics 1996, 86, 1179–1185. [Google Scholar] [CrossRef]
- Li, G.; Xiao, G.; Guan, C.; Hong, C.; Yuan, B.; Li, T.; Wang, J.Q. Assessment of thermodynamic performance of a 20 kW high-temperature electrolysis system using advanced exergy analysis. Fuel Cells 2021, 21, 550–565. [Google Scholar] [CrossRef]
- Hernández-Pacheco, E.; Singh, D.; Hutton, P.N.; Patel, N.; Mann, M.D. A macro-level model for determining the performance characteristics of solid oxide fuel cells. J. Power Sources 2004, 138, 174–186. [Google Scholar] [CrossRef]
- Bird, R.B. Transport phenomena. Appl. Mech. Rev. 2002, 55, R1–R4. [Google Scholar] [CrossRef]
- Bernadet, L.; Gousseau, G.; Chatroux, A.; Laurencin, J.; Mauvy, F.; Reytier, M. Influence of pressure on solid oxide electrolysis cells investigated by experimental and modeling approach. Int. J. Hydrog. Energy 2015, 40, 12918–12928. [Google Scholar] [CrossRef]
- Wonsyld, K.; Bech, L.; Nielsen, J.U.; Pedersen, C.F. Operational robustness studies of solid oxide electrolysis stacks. J. Energy Power Eng. 2015, 9, 128–140. [Google Scholar] [CrossRef]
- Mai, A.; Iwanschitz, B.; Schuler, J.A.; Denzler, R.; Nerlich, V.; Schuler, A. Hexis’ SOFC System Galileo 1000 N–Lab and Field Test Experiences. ECS Trans. 2013, 57, 73. [Google Scholar] [CrossRef]
- Yin, J.; Jensen, M.K. Analytic model for transient heat exchanger response. Int. J. Heat Mass Transf. 2003, 46, 3255–3264. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
del Pozo Gonzalez, H.; Torrell, M.; Bernadet, L.; Bianchi, F.D.; Trilla, L.; Tarancón, A.; Domínguez-García, J.L. Mathematical Modeling and Thermal Control of a 1.5 kW Reversible Solid Oxide Stack for 24/7 Hydrogen Plants. Mathematics 2023, 11, 366. https://doi.org/10.3390/math11020366
del Pozo Gonzalez H, Torrell M, Bernadet L, Bianchi FD, Trilla L, Tarancón A, Domínguez-García JL. Mathematical Modeling and Thermal Control of a 1.5 kW Reversible Solid Oxide Stack for 24/7 Hydrogen Plants. Mathematics. 2023; 11(2):366. https://doi.org/10.3390/math11020366
Chicago/Turabian Styledel Pozo Gonzalez, Hector, Marc Torrell, Lucile Bernadet, Fernando D. Bianchi, Lluís Trilla, Albert Tarancón, and Jose Luis Domínguez-García. 2023. "Mathematical Modeling and Thermal Control of a 1.5 kW Reversible Solid Oxide Stack for 24/7 Hydrogen Plants" Mathematics 11, no. 2: 366. https://doi.org/10.3390/math11020366
APA Styledel Pozo Gonzalez, H., Torrell, M., Bernadet, L., Bianchi, F. D., Trilla, L., Tarancón, A., & Domínguez-García, J. L. (2023). Mathematical Modeling and Thermal Control of a 1.5 kW Reversible Solid Oxide Stack for 24/7 Hydrogen Plants. Mathematics, 11(2), 366. https://doi.org/10.3390/math11020366







