A Game-Theory-Based Approach to Modeling Lane-Changing Interactions on Highway On-Ramps: Considering the Bounded Rationality of Drivers
Abstract
:1. Introduction
2. Literature Review
2.1. Rule-Based Models
2.2. Utility-Theory-Based Models
2.3. Game-Theory-Based Models
3. Methodology
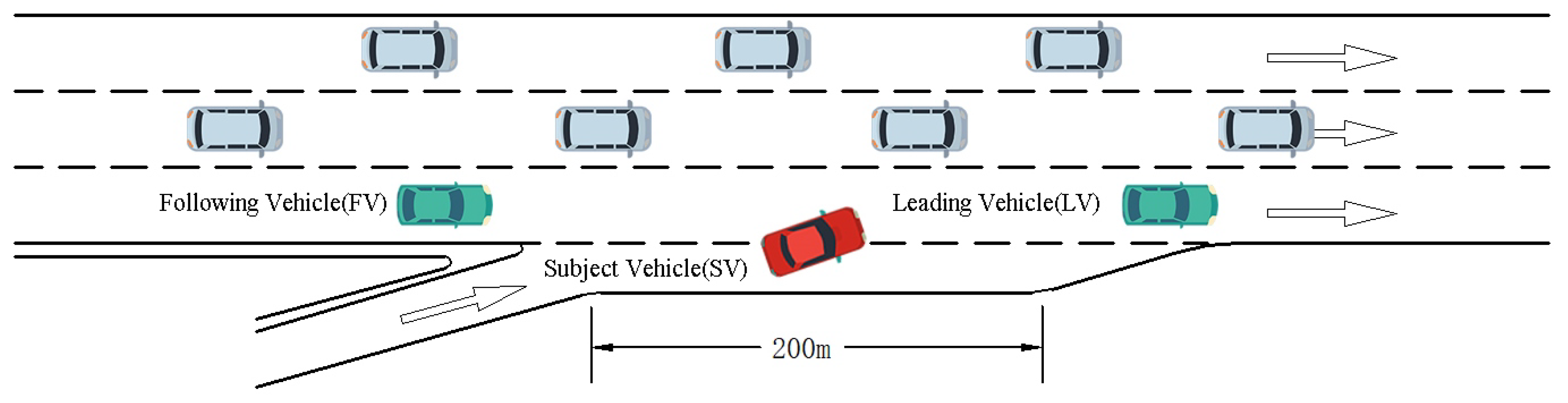
3.1. Game Definition
3.2. Payoff Formulation
3.2.1. Payoffs for the FV
3.2.2. Payoffs for the SV
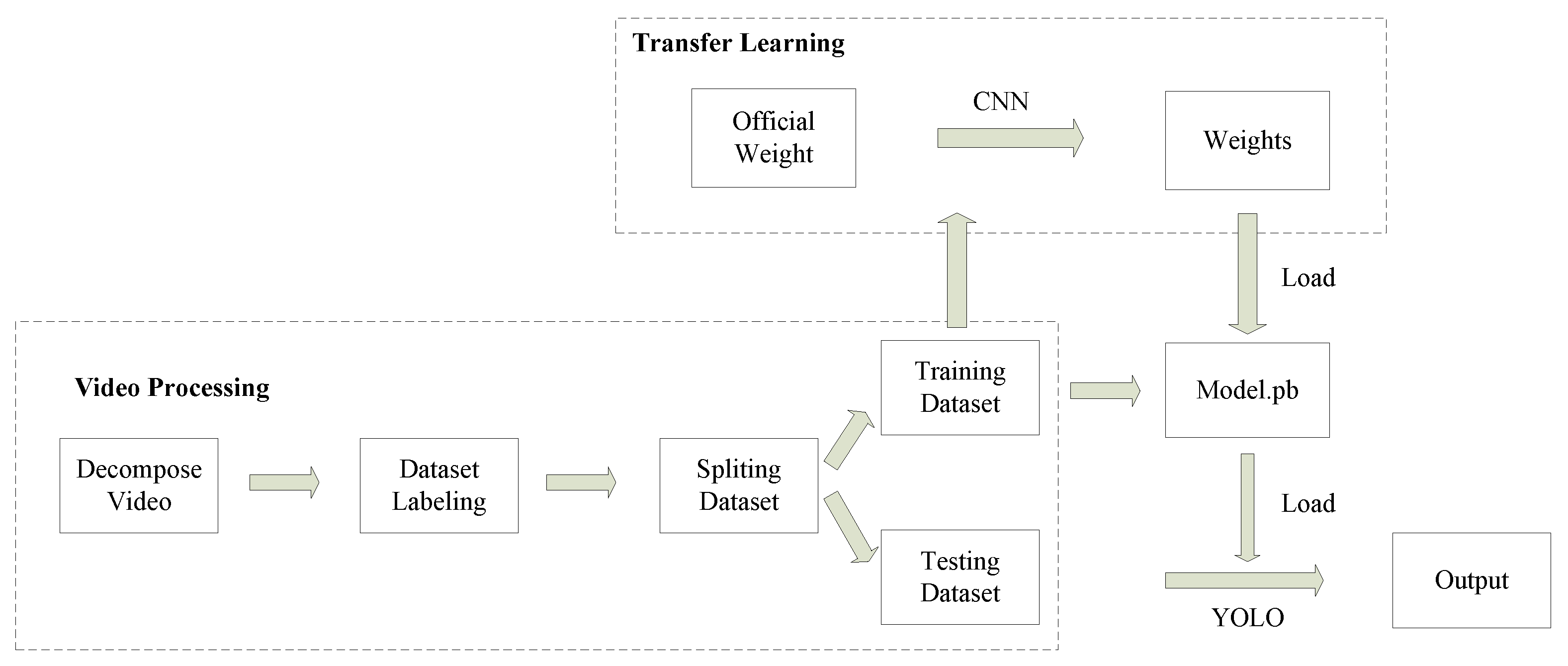
4. Data Sources and Processing
4.1. Data Description
4.1.1. NGSIM Data
4.1.2. Data Collected from the UAV Aerial Survey
4.2. Merging and Non-Merging Identification
- Our study mainly focused on car drivers’ merging and yielding behaviors, so other types of vehicles (i.e., trucks and motorcycles) were removed.
- Ali [1] pointed out that a balance between merging and waiting events is necessary because it will impact the calibration and validation results. A reasonable decision-making horizon should be selected to avoid the dominance of non-merging events. This study empirically extracted the drivers’ strategy based on a 2 s interval.
- The merging process was split into three phases, as in [25], which were the lane-keeping (LK) decision horizon, lane-changing (LC) decision horizon, and LC duration. The point at which the SV passed the lane boundary was regarded as the LC point.
- The collected data were inconsistent in their time periods. A short time period could only partially represent part of the process of vehicle merging; some of the driving behaviors during lane-changing were ignored. Too long of a time period caused an imbalance of merging and non-merging events and amplified the noise in the vehicle trajectory, which was detrimental to the subsequent model training and testing. Therefore, the first 5S data before the LC point were used to identify the merging and non-merging behaviors.
4.3. Decisions of Players in Typical Scenarios
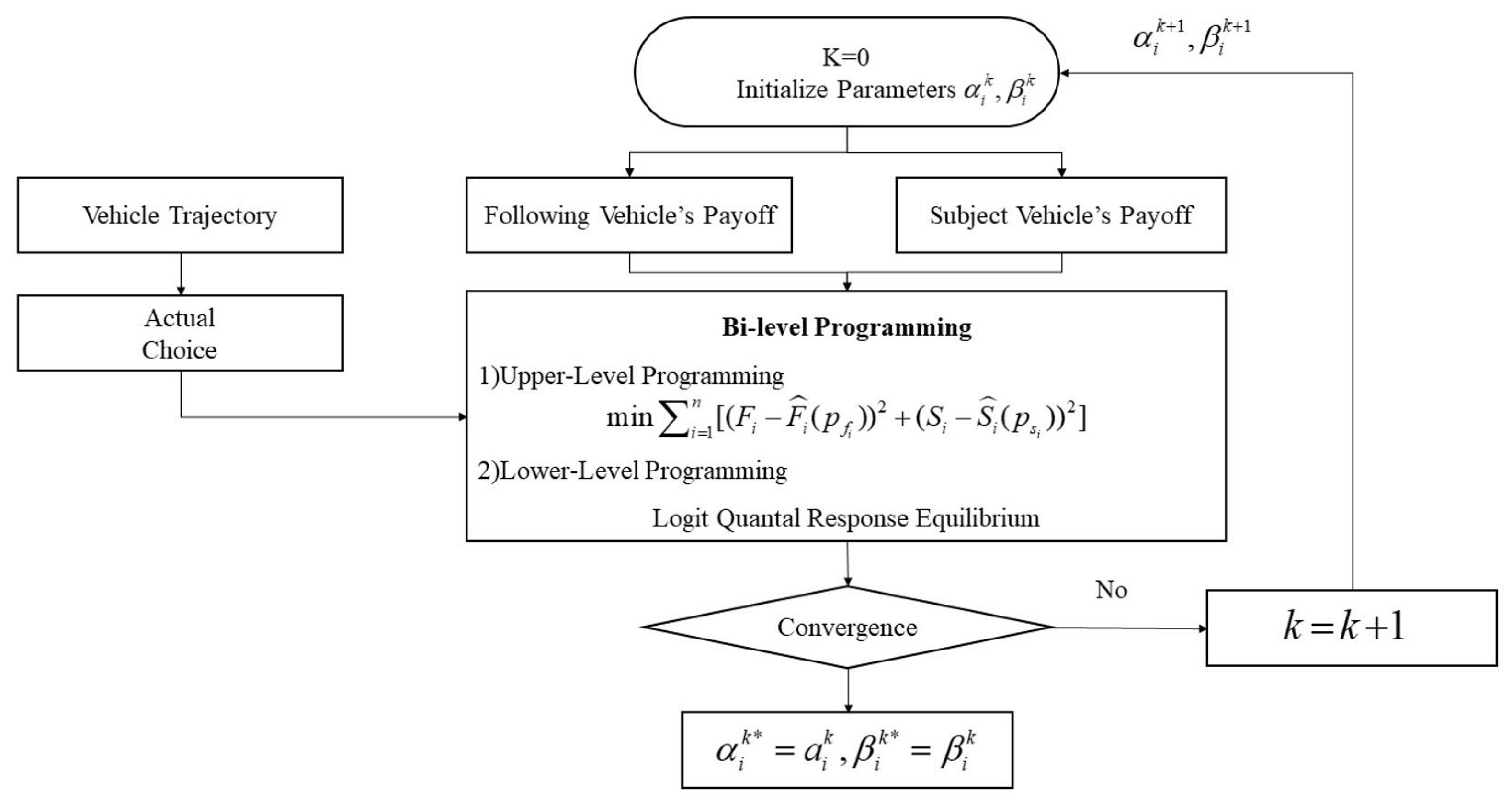
5. Model Calibration and Validation
5.1. Model Calibration
5.2. Model Validation
6. Discussion and Conclusions
6.1. Discussion
6.2. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ali, Y.; Zheng, Z.; Haque, M.M.; Wang, M. A game theory-based approach for modelling mandatory lane-changing behaviour in a connected environment. Transp. Res. Part C Emerg. Technol. 2019, 106, 220–242. [Google Scholar] [CrossRef]
- Xia, Y.; Qu, Z.; Sun, Z.; Li, Z. A Human-Like Model to Understand Surrounding Vehicles’ Lane Changing Intentions for Autonomous Driving. IEEE Trans. Veh. Technol. 2021, 70, 4178–4189. [Google Scholar] [CrossRef]
- Li, K.; Wang, X.; Xu, Y.; Wang, J. Lane changing intention recognition based on speech recognition models. Transp. Res. Part C Emerg. Technol. 2016, 69, 497–514. [Google Scholar] [CrossRef]
- Wang, J.; Gao, C.; Zhu, Z.; Yan, X. Multi-lane changing model with coupling driving intention and inclination. Promet-Traffic Transp. 2017, 29, 185–192. [Google Scholar] [CrossRef] [Green Version]
- Wei, C.; Hui, F.; Yang, Z.; Jia, S.; Khattak, A.J. Fine-grained highway autonomous vehicle lane-changing trajectory prediction based on a heuristic attention-aided encoder-decoder model. Transp. Res. Part C Emerg. Technol. 2022, 140, 103706. [Google Scholar] [CrossRef]
- Zhang, Y.; Zou, Y.; Tang, J.; Liang, J. Long-term prediction for high-resolution lane-changing data using temporal convolution network. Transp. B Transp. Dyn. 2022, 10, 849–863. [Google Scholar] [CrossRef]
- Yu, H.; Tseng, H.E.; Langari, R. A human-like game theory-based controller for automatic lane changing. Transp. Res. Part C Emerg. Technol. 2018, 88, 140–158. [Google Scholar] [CrossRef]
- Tajdari, F.; Roncoli, C.; Papageorgiou, M. Feedback-Based Ramp Metering and Lane-Changing Control With Connected and Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 939–951. [Google Scholar] [CrossRef]
- Wang, M.; Hoogendoorn, S.P.; Daamen, W.; van Arem, B.; Happee, R. Game theoretic approach for predictive lane-changing and car-following control. Transp. Res. Part C Emerg. Technol. 2015, 58, 73–92. [Google Scholar] [CrossRef]
- Arbis, D.; Dixit, V.V. Game theoretic model for lane changing: Incorporating conflict risks. Accid. Anal. Prev. 2019, 125, 158–164. [Google Scholar] [CrossRef]
- Administration, F.H. Interstate 80 Freeway Dataset; Federal Highway Administration, US Department of Transportation: Washington, DC, USA, 2006. [Google Scholar]
- Jin, C.J.; Knoop, V.L.; Li, D.; Meng, L.Y.; Wang, H. Discretionary lane-changing behavior: Empirical validation for one realistic rule-based model. Transp. A Transp. Sci. 2019, 15, 244–262. [Google Scholar] [CrossRef] [Green Version]
- Gipps, P. A model for the structure of lane-changing decisions. Transp. Res. Part B Methodol. 1986, 20, 403–414. [Google Scholar] [CrossRef]
- Yang, Q.; Koutsopoulos, H.N. A Microscopic Traffic Simulator for evaluation of dynamic traffic management systems. Transp. Res. Part C Emerg. Technol. 1996, 4, 113–129. [Google Scholar] [CrossRef]
- Hidas, P. Modelling vehicle interactions in microscopic simulation of merging and weaving. Transp. Res. Part C Emerg. Technol. 2005, 13, 37–62. [Google Scholar] [CrossRef]
- Wang, G.; Hu, J.; Li, Z.; Li, L. Cooperative lane changing via deep reinforcement learning. arXiv 2019, arXiv:1906.08662. [Google Scholar] [CrossRef]
- Amini, E.; Omidvar, A.; Elefteriadou, L. Optimizing operations at freeway weaves with connected and automated vehicles. Transp. Res. Part C Emerg. Technol. 2021, 126, 103072. [Google Scholar] [CrossRef]
- Ahmed, K.I. Modeling Drivers’ Acceleration and Lane Changing Behavior. Doctoral Dissertation, Massachusetts Institute of Technology, Cambridge, MA, USA, 1999. [Google Scholar]
- Toledo, T.; Koutsopoulos, H.N.; Ben-Akiva, M.E. Modeling integrated lane-changing behavior. Transp. Res. Rec. 2003, 1857, 30–38. [Google Scholar] [CrossRef] [Green Version]
- Kita, H. A merging–giveway interaction model of cars in a merging section: A game theoretic analysis. Transp. Res. Part A Policy Pract. 1999, 33, 305–312. [Google Scholar] [CrossRef]
- Liu, H.X.; Xin, W.; Adam, Z.; Ban, J. A game theoretical approach for modelling merging and yielding behaviour at freeway on-ramp sections. Transp. Traffic Theory 2007, 3, 197–211. [Google Scholar]
- Talebpour, A.; Mahmassani, H.S.; Hamdar, S.H. Modeling Lane-Changing Behavior in a Connected Environment: A Game Theory Approach. Transp. Res. Procedia 2015, 7, 420–440. [Google Scholar] [CrossRef] [Green Version]
- Kang, K.; Rakha, H.A. Game Theoretical Approach to Model Decision Making for Merging Maneuvers at Freeway On-Ramps. Transp. Res. Rec. 2017, 2623, 19–28. [Google Scholar] [CrossRef]
- Ali, Y.; Zheng, Z.; Haque, M.M.; Yildirimoglu, M.; Washington, S. CLACD: A complete LAne-Changing decision modeling framework for the connected and traditional environments. Transp. Res. Part C Emerg. Technol. 2021, 128, 103162. [Google Scholar] [CrossRef]
- Shao, H.; Zhang, M.; Feng, T.; Dong, Y. A Discretionary Lane-Changing Decision-Making Mechanism Incorporating Drivers’ Heterogeneity: A Signalling Game-Based Approach; Wiley-Blackwell: Hoboken, NJ, USA, 2020. [Google Scholar]
- Lin, D.; Li, L.; Jabari, S.E. Pay to change lanes: A cooperative lane-changing strategy for connected/automated driving. Transp. Res. Part C Emerg. Technol. 2019, 105, 550–564. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Zhang, S. Lane change behavior with uncertainty and fuzziness for human driving vehicles and its simulation in mixed traffic. Phys. A Stat. Mech. Its Appl. 2022, 606, 128–130. [Google Scholar] [CrossRef]
- Yu, Y.; Luo, X.; Sy, Q.; Peng, W. A dynamic lane-changing decision and trajectory planning model of autonomous vehicles under mixed autonomous vehicle and human-driven vehicle environment. Phys. A Stat. Mech. Its Appl. 2022, 609, 128–361. [Google Scholar] [CrossRef]
- Li, J.; Chen, D.; Zhang, M. Equilibrium modeling of mixed autonomy traffic flow based on game theory. Transp. Res. Part B Meth. 2022, 166, 110–127. [Google Scholar] [CrossRef]
- Kesting, A.; Treiber, M.; Helbing, D. General Lane-Changing Model MOBIL for Car-Following Models. Transp. Res. Rec. 2007, 1999, 86–94. [Google Scholar] [CrossRef] [Green Version]
- Kang, K.; Rakha, H.A. A repeated game freeway lane changing model. Sensors 2020, 20, 1554. [Google Scholar] [CrossRef] [Green Version]
- Shen, S.; Zhou, H.; Huang, L.; Fan, E.; Keli, H.U.; Cao, Q. Quantal Response Equilibrium-Based Method for Preventing WSNs Malware Infection. Chin. J. Sens. Actuators 2017, 30, 1589–1595. [Google Scholar] [CrossRef]
- Wolshon, B.; Pande, A. Traffic Engineering Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Montanino, M.; Punzo, V. Trajectory data reconstruction and simulation-based validation against macroscopic traffic patterns. Transp. Res. Part B Methodol. 2015, 80, 82–106. [Google Scholar] [CrossRef]
- Dong, S.; Zhou, Y.; Chen, T.; Li, S.; Gao, Q.; Ran, B. An integrated Empirical Mode Decomposition and Butterworth filter based vehicle trajectory reconstruction method. Phys. A Stat. Mech. Its Appl. 2021, 583, 126295. [Google Scholar] [CrossRef]
- Coifman, B.; Li, L. A critical evaluation of the Next Generation Simulation (NGSIM) vehicle trajectory dataset. Transp. Res. Part B Methodol. 2017, 105, 362–377. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef]
- Veeramani, B.; Raymond, J.W.; Chanda, P. DeepSort: Deep convolutional networks for sorting haploid maize seeds. BMC Bioinform. 2018, 19, 289. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rafati Fard, M.; Shariat Mohaymany, A.; Shahri, M. A new methodology for vehicle trajectory reconstruction based on wavelet analysis. Transp. Res. Part C Emerg. Technol. 2017, 74, 150–167. [Google Scholar] [CrossRef]
- Ozaki, H. Reaction and anticipation in the car-following behavior. In Proceedings of the 12th International Symposium on Theory of Traffic Flow and Transportation, Berkeley, CA, USA, 21–23 July 1992; pp. 349–366. [Google Scholar]
- McKelvey, R.D.; Palfrey, T.R. Quantal Response Equilibria for Normal Form Games. Games Econ. Behav. 1995, 10, 6–38. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Fricker, J.D. Incorporating conflict risks in pedestrian-motorist interactions: A game theoretical approach. Accid. Anal. Prev. 2021, 159, 106254. [Google Scholar] [CrossRef]
- Sun, J.; Zheng, Z.; Sun, J. Stability analysis methods and their applicability to car-following models in conventional and connected environments. Transp. Res. Part B Methodol. 2018, 109, 212–237. [Google Scholar] [CrossRef]


| Player 2: SV | |||
|---|---|---|---|
| Actions | Merge | Wait | |
| Player 1: FV | Accelerate/Block | ||
| Do Nothing | |||
| Decelerate/Yield | |||
| Players | Player 2: SV | |||
|---|---|---|---|---|
| Payoff for FV | Player 1: FV | Actions | Merge () | Wait () |
| Accelerate () | ||||
| Do nothing () | ||||
| Decelerate () | ||||
| Payoff for SV | Player 1: FV | Actions | Merge () | Wait () |
| Accelerate () | ||||
| Do nothing () | ||||
| Decelerate () | ||||
| SV | FV | Total | ||||
|---|---|---|---|---|---|---|
| Merge | Wait | Accelerate/Block | Do Nothing | Decelerate/Yield | ||
| NGSIM data | 198 | 231 | 46 | 331 | 52 | 429 |
| UAV data | 34 | 48 | 12 | 64 | 10 | 86 |
| FV | SV | ||||
|---|---|---|---|---|---|
| NGSIM | 0.11 | 0.72 | 0.16 | 0.53 | 0.47 |
| UAV survey | 0.25 | 0.62 | 0.13 | 0.56 | 0.43 |
| Strategy | Players | Parameter | NGSIM | UAV Survey | Parameter | NGSIM | UAV Survey |
|---|---|---|---|---|---|---|---|
| Accelerate and Merge | FV | −2.14 | 2.84 | 2.44 | 5.40 | ||
| Decelerate and Merge | 2.80 | −1.31 | 5.90 | 1.96 | |||
| Do nothing and Merge | 0.66 | 3.10 | −0.30 | −1.31 | |||
| Accelerate and Wait | −1.70 | 1.35 | 4.24 | 3.43 | |||
| Decelerate and Wait | 5.95 | 0.36 | 3.12 | 4.82 | |||
| Do nothing and Wait | 2.81 | 1.78 | 5.92 | −1.37 | |||
| Accelerate and Merge | SV | 3.40 | 2.74 | −1.18 | 0.05 | ||
| Decelerate and Merge | 3.35 | 1.61 | −1.29 | 3.09 | |||
| Do nothing and Merge | 3.78 | 1.57 | 1.57 | 4.92 | |||
| Accelerate and Wait | 1.56 | 0.99 | −2.13 | 4.70 | |||
| Decelerate and Wait | 0.48 | 2.38 | 5.30 | 2.13 | |||
| Do nothing and Wait | 3.98 | −2.90 | −1.39 | −1.03 |
| NGSIM I-80 | UAV Aerial Survey | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N | TP | FP | DR (%) | FAR (%) | N | TP | FP | DR (%) | FAR (%) | |
| Merge | 63 | 54 | 9 | 86 | 14 | 14 | 13 | 1 | 93 | 7 |
| Wait | 66 | 50 | 16 | 76 | 24 | 12 | 9 | 3 | 75 | 25 |
| Overall | 129 | 104 | 25 | 81 | 22 | 26 | 22 | 5 | 85 | 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Ren, G.; Cao, Q.; Song, J.; Liu, Y.; Dong, C. A Game-Theory-Based Approach to Modeling Lane-Changing Interactions on Highway On-Ramps: Considering the Bounded Rationality of Drivers. Mathematics 2023, 11, 402. https://doi.org/10.3390/math11020402
Chen W, Ren G, Cao Q, Song J, Liu Y, Dong C. A Game-Theory-Based Approach to Modeling Lane-Changing Interactions on Highway On-Ramps: Considering the Bounded Rationality of Drivers. Mathematics. 2023; 11(2):402. https://doi.org/10.3390/math11020402
Chicago/Turabian StyleChen, Weihan, Gang Ren, Qi Cao, Jianhua Song, Yikun Liu, and Changyin Dong. 2023. "A Game-Theory-Based Approach to Modeling Lane-Changing Interactions on Highway On-Ramps: Considering the Bounded Rationality of Drivers" Mathematics 11, no. 2: 402. https://doi.org/10.3390/math11020402
APA StyleChen, W., Ren, G., Cao, Q., Song, J., Liu, Y., & Dong, C. (2023). A Game-Theory-Based Approach to Modeling Lane-Changing Interactions on Highway On-Ramps: Considering the Bounded Rationality of Drivers. Mathematics, 11(2), 402. https://doi.org/10.3390/math11020402








