Numerical Study of Thermo-Electric Conversion for TEG Mounted Wavy Walled Triangular Vented Cavity Considering Nanofluid with Different-Shaped Nanoparticles
Abstract
1. Introduction
2. Mathematical Model
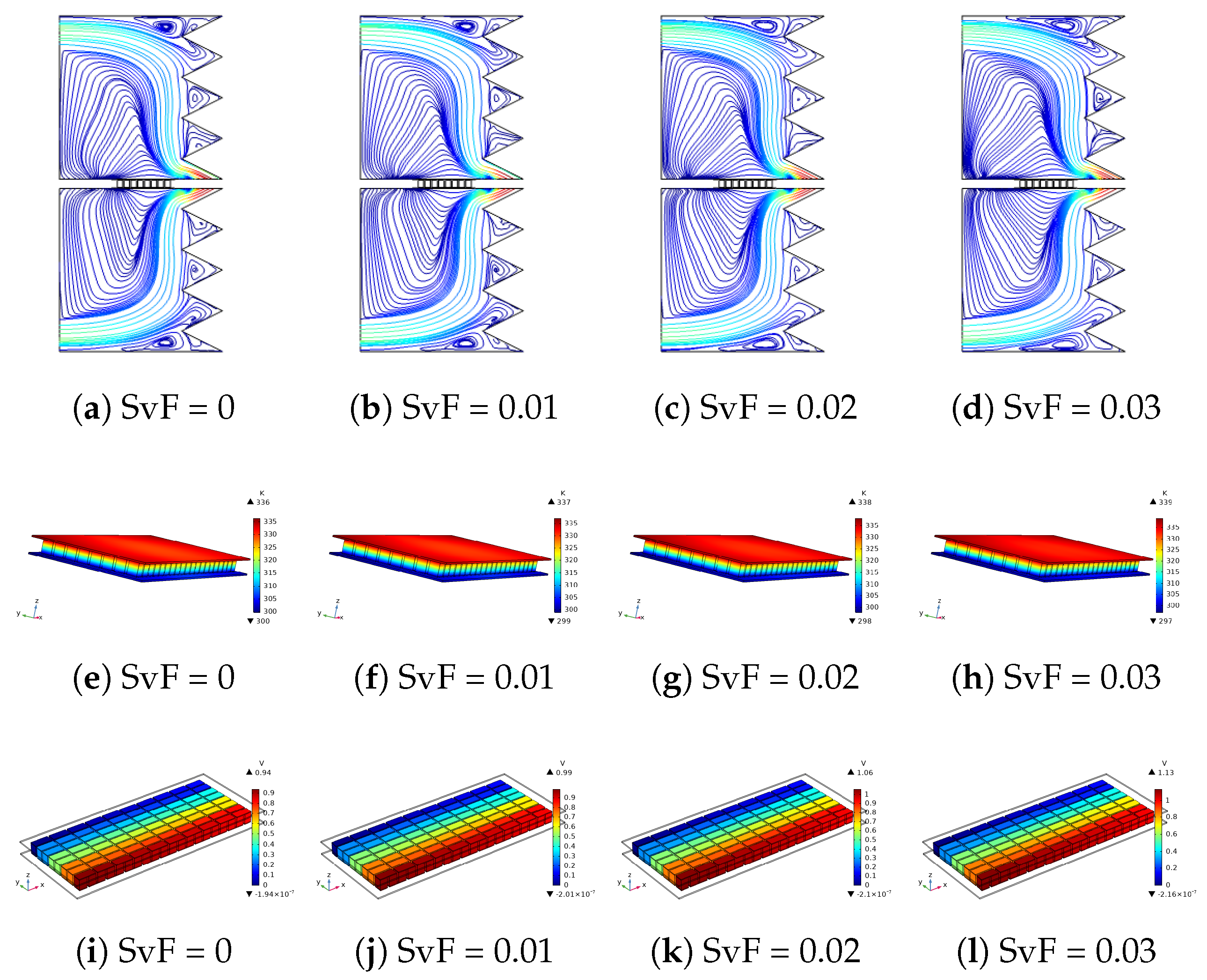
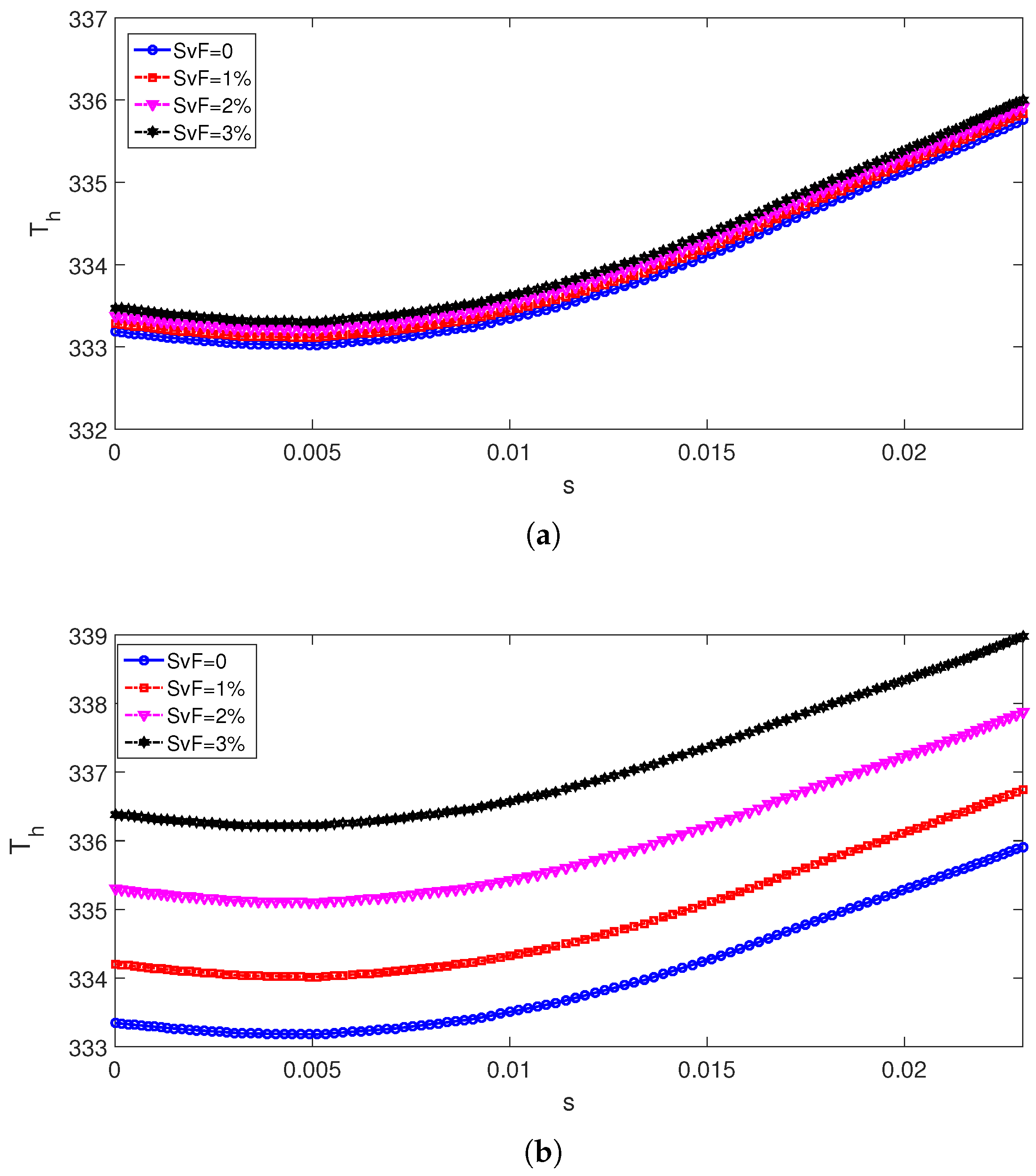
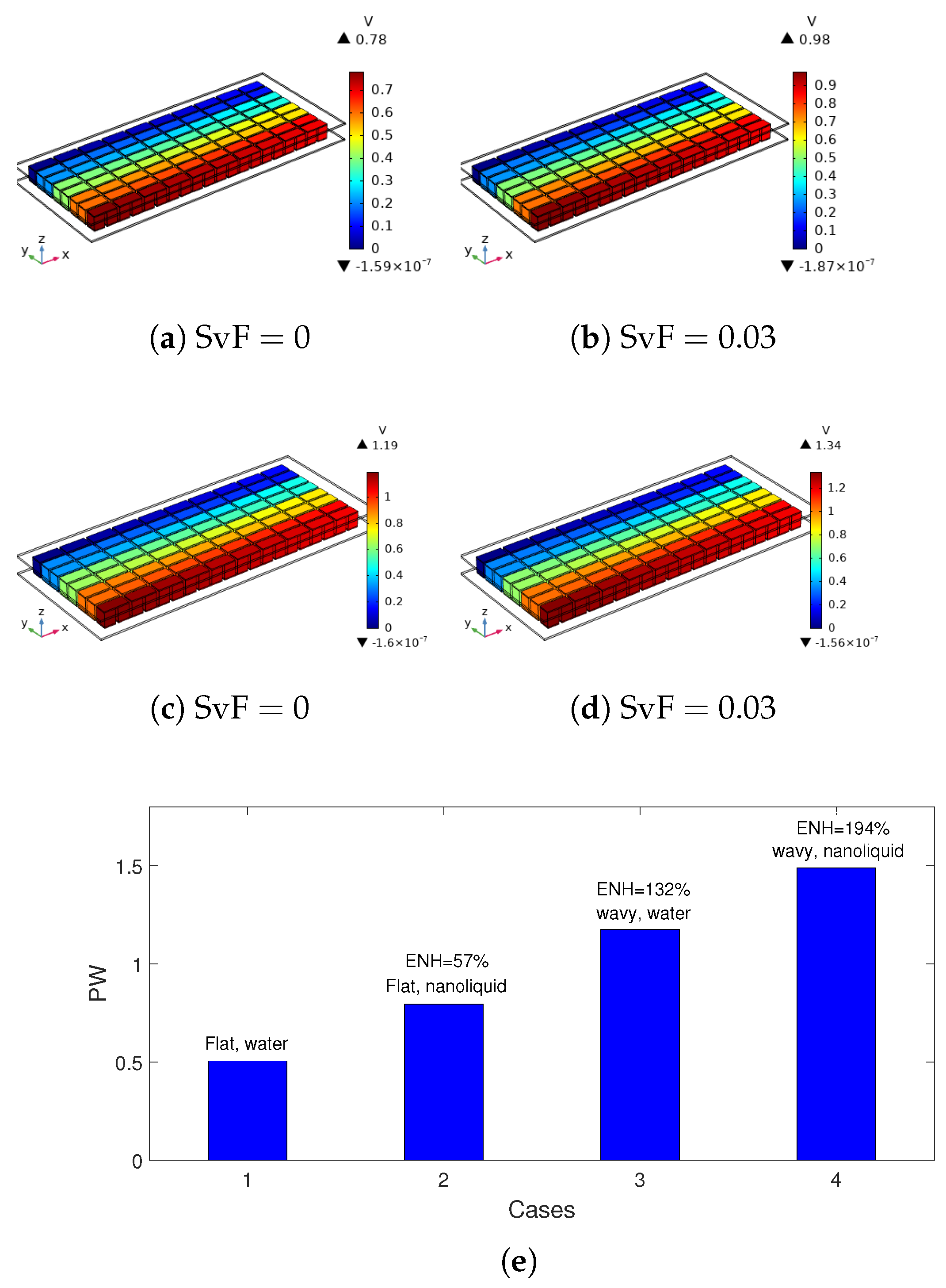
3. Results and Discussion
4. Conclusions
- Impacts of wave amplitude on the flow field and conversion performance is significant as compared to the wave number of the VCs.
- The rise of TEG power is in the range of 9.44–25.5% when varying the wave number, while it is in the range of 74.48–92.4% when varying the amplitude of the triangular wave.
- When NFs with the highest and lowest amount of NPs are compared, TEG power rises by about 50.7% for NF-cylinder while it is 4% for NF-spherical. Higher powers are obtained by using cylindrical NPs as compared to spherical ones in the HT fluid.
- The results show that simultaneously using differently shaped NPs and the wavy form of the cavity has significant impacts on the overall performance improvements. As compared to the flat-walled VC case using only pure fluid, introducing a wavy form of the wall and including cylindrical NPs in the base fluid, up to a 194% rise of generated power is obtained.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| h | heat transfer coefficient |
| H | cavity height |
| k | thermal conductivity |
| n | unit normal vector |
| N | wave number |
| Nu | Nusselt number |
| p | pressure |
| Pr | Prandtl number |
| Re | Reynolds number |
| T | temperature |
| u, v, w | x-y-z velocity components |
| w, w | inlet-outlet port size |
| x, y, z | Cartesian coordinates |
| x | wave amplitude |
| ZT | figure of merit |
| Greek Characters | |
| thermal diffusivity | |
| dynamic viscosity | |
| kinematic viscosity | |
| density of the fluid | |
| electrical conductivity | |
| solid volume fraction | |
| Subscripts | |
| c | cold wall |
| h | hot wall |
| m | average |
| nf | nanofluid |
| Abbreviations | |
| FEM | finite element method |
| VC | vented cavity |
| TEG | thermoelectric generator |
References
- Patil, D.S.; Arakerimath, R.R.; Walke, P.V. Thermoelectric materials and heat exchangers for power generation—A review. Renew. Sustain. Energy Rev. 2018, 95, 1–22. [Google Scholar] [CrossRef]
- Karthick, K.; Suresh, S.; Hussain, M.M.M.D.; Ali, H.M.; Kumar, C.S.S. Evaluation of solar thermal system configurations for thermoelectric generator applications: A critical review. Sol. Energy 2019, 188, 111–142. [Google Scholar] [CrossRef]
- Champier, D. Thermoelectric generators: A review of applications. Energy Convers. Manag. 2017, 140, 167–181. [Google Scholar] [CrossRef]
- Gelbstein, Y. Pb1−x SnxTe alloys: Application considerations. J. Electron. Mater. 2011, 40, 533–536. [Google Scholar] [CrossRef]
- Gelbstein, Y.; Davidow, J.; Leshem, E.; Pinshow, O.; Moisa, S. Significant lattice thermal conductivity reduction following phase separation of the highly efficient GexPb1−xTe thermoelectric alloys. Phys. Status Solidi (b) 2014, 251, 1431–1437. [Google Scholar] [CrossRef]
- Ahmed, S.E. Caputo fractional convective flow in an inclined wavy vented cavity filled with a porous medium using Al2O3-Cu hybrid nanofluids. Int. Commun. Heat Mass Transf. 2020, 116, 104690. [Google Scholar] [CrossRef]
- Akdag, U.; Akcay, S.; Demiral, D. Heat transfer enhancement with laminar pulsating nanofluid flow in a wavy channel. Int. Commun. Heat Mass Transf. 2014, 59, 17–23. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Oztop, H.F. Forced convection and thermal predictions of pulsating nanofluid flow over a backward facing step with a corrugated bottom wall. Int. J. Heat Mass Transf. 2017, 110, 231–247. [Google Scholar] [CrossRef]
- Shehzad, N.; Zeeshan, A.; Ellahi, R.; Vafai, K. Convective heat transfer of nanofluid in a wavy channel: Buongiorno’s mathematical model. J. Mol. Liq. 2016, 222, 446–455. [Google Scholar] [CrossRef]
- Wang, C.C.; Chen, C.K. Forced convection in a wavy-wall channel. Int. J. Heat Mass Transf. 2002, 45, 2587–2595. [Google Scholar] [CrossRef]
- Miroshnichenko, I.V.; Sheremet, M.A.; Pop, I.; Ishak, A. Convective heat transfer of micropolar fluid in a horizontal wavy channel under the local heating. Int. J. Mech. Sci. 2017, 128, 541–549. [Google Scholar] [CrossRef]
- Ahmed, M.; Shuaib, N.; Yusoff, M.Z. Numerical investigations on the heat transfer enhancement in a wavy channel using nanofluid. Int. J. Heat Mass Transf. 2012, 55, 5891–5898. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Oztop, H.F. Corrugated conductive partition effects on MHD free convection of CNT-water nanofluid in a cavity. Int. J. Heat Mass Transf. 2019, 129, 265–277. [Google Scholar] [CrossRef]
- Pehlivan, H.; Taymaz, I.; İslamoğlu, Y. Experimental study of forced convective heat transfer in a different arranged corrugated channel. Int. Commun. Heat Mass Transf. 2013, 46, 106–111. [Google Scholar] [CrossRef]
- Tokgoz, N.; Tunay, T.; Sahin, B. Effect of corrugated channel phase shifts on flow structures and heat transfer rate. Exp. Therm. Fluid Sci. 2018, 99, 374–391. [Google Scholar] [CrossRef]
- Rashidi, S.; Akbarzadeh, M.; Masoodi, R.; Languri, E. Thermal-hydraulic and entropy generation analysis for turbulent flow inside a corrugated channel. Int. J. Heat Mass Transf. 2017, 109, 812–823. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Analysis of hybrid nanofluid and surface corrugation in the laminar convective flow through an encapsulated PCM filled vertical cylinder and POD-based modeling. Int. J. Heat Mass Transf. 2021, 178, 121623. [Google Scholar] [CrossRef]
- Kurtulmuş, N.; Sahin, B. A review of hydrodynamics and heat transfer through corrugated channels. Int. Commun. Heat Mass Transf. 2019, 108, 104307. [Google Scholar] [CrossRef]
- Saeidi, S.; Khodadadi, J. Forced convection in a square cavity with inlet and outlet ports. Int. J. Heat Mass Transf. 2006, 49, 1896–1906. [Google Scholar] [CrossRef]
- Angirasa, D. Mixed convection in a vented enclosure with an isothermal vertical surface. Fluid Dyn. Res. 2000, 26, 219–233. [Google Scholar] [CrossRef]
- Ismael, M.A.; Jasim, H.F. Role of the fluid-structure interaction in mixed convection in a vented cavity. Int. J. Mech. Sci. 2018, 135, 190–202. [Google Scholar] [CrossRef]
- Saeidi, S.; Khodadadi, J. Transient flow and heat transfer leading to periodic state in a cavity with inlet and outlet ports due to incoming flow oscillation. Int. J. Heat Mass Transf. 2007, 50, 530–538. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Numerical investigation and dynamical analysis of mixed convection in a vented cavity with pulsating flow. Comput. Fluids 2014, 91, 57–67. [Google Scholar] [CrossRef]
- Zahmatkesh, I.; Sheremet, M.; Yang, L.; Heris, S.Z.; Sharifpur, M.; Meyer, J.P.; Ghalambaz, M.; Wongwises, S.; Jing, D.; Mahian, O. Effect of nanoparticle shape on the performance of thermal systems utilizing nanofluids: A critical review. J. Mol. Liq. 2021, 321, 114430. [Google Scholar] [CrossRef]
- Sajid, M.U.; Ali, H.M. Recent advances in application of nanofluids in heat transfer devices: A critical review. Renew. Sustain. Energy Rev. 2019, 103, 556–592. [Google Scholar] [CrossRef]
- Mahian, O.; Kianifar, A.; Heris, S.Z.; Wen, D.; Sahin, A.Z.; Wongwises, S. Nanofluids effects on the evaporation rate in a solar still equipped with a heat exchanger. Nano Energy 2017, 36, 134–155. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K. A review on the applications of nanofluids in solar energy field. Renew. Energy 2018, 123, 398–406. [Google Scholar] [CrossRef]
- Arshad, W.; Ali, H.M. Graphene nanoplatelets nanofluids thermal and hydrodynamic performance on integral fin heat sink. Int. J. Heat Mass Transf. 2017, 107, 995–1001. [Google Scholar] [CrossRef]
- Mahbubul, I.; Khan, M.M.A.; Ibrahim, N.I.; Ali, H.M.; Al-Sulaiman, F.A.; Saidur, R. Carbon nanotube nanofluid in enhancing the efficiency of evacuated tube solar collector. Renew. Energy 2018, 121, 36–44. [Google Scholar] [CrossRef]
- Xiong, Q.; Bozorg, M.V.; Doranehgard, M.H.; Hong, K.; Lorenzini, G. A CFD investigation of the effect of non-Newtonian behavior of Cu-water nanofluids on their heat transfer and flow friction characteristics. J. Therm. Anal. Calorim. 2020, 139, 2601–2621. [Google Scholar] [CrossRef]
- Wang, L.; Huang, C.; Yang, X.; Chai, Z.; Shi, B. Effects of temperature-dependent properties on natural convection of power-law nanofluids in rectangular cavities with sinusoidal temperature distribution. Int. J. Heat Mass Transf. 2019, 128, 688–699. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. A study of heat transfer in power law nanofluid. Therm. Sci. 2016, 20, 2015–2026. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Chamkha, A.J. Magnetohydrodynamics mixed convection in a power law nanofluid-filled triangular cavity with an opening using Tiwari and Das’ nanofluid model. J. Therm. Anal. Calorim. 2019, 135, 419–436. [Google Scholar] [CrossRef]
- ul Haq, M.R.; Hussain, M.; Bibi, N.; Shigidi, I.M.; Pashameah, R.A.; Alzahrani, E.; El-Shorbagy, M.; Safaei, M.R. Energy transport analysis of the magnetized forced flow of power-law nanofluid over a horizontal wall. J. Magn. Magn. Mater. 2022, 560, 169681. [Google Scholar] [CrossRef]
- Qeays, I.A.; Yahya, S.M.; Asjad, M.; Khan, Z.A. Multi-performance optimization of nanofluid cooled hybrid photovoltaic thermal system using fuzzy integrated methodology. J. Clean. Prod. 2020, 256, 120451. [Google Scholar] [CrossRef]
- Karana, D.R.; Sahoo, R.R. Effect on TEG performance for waste heat recovery of automobiles using MgO and ZnO nanofluid coolants. Case Stud. Therm. Eng. 2018, 12, 358–364. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Performance assessment of a thermoelectric module by using rotating circular cylinders and nanofluids in the channel flow for renewable energy applications. J. Clean. Prod. 2021, 279, 123426. [Google Scholar] [CrossRef]
- Rajaee, F.; Rad, M.A.V.; Kasaeian, A.; Mahian, O.; Yan, W.M. Experimental analysis of a photovoltaic/thermoelectric generator using cobalt oxide nanofluid and phase change material heat sink. Energy Convers. Manag. 2020, 212, 112780. [Google Scholar] [CrossRef]
- Nnanna, A.G.A.; Rutherford, W.; Elomar, W.; Sankowski, B. Assessment of thermoelectric module with nanofluid heat exchanger. Appl. Therm. Eng. 2009, 29, 491–500. [Google Scholar] [CrossRef]
- Nazari, S.; Safarzadeh, H.; Bahiraei, M. Experimental and analytical investigations of productivity, energy and exergy efficiency of a single slope solar still enhanced with thermoelectric channel and nanofluid. Renew. Energy 2019, 135, 729–744. [Google Scholar] [CrossRef]
- Ahammed, N.; Asirvatham, L.G.; Wongwises, S. Thermoelectric cooling of electronic devices with nanofluid in a multiport minichannel heat exchanger. Exp. Therm. Fluid Sci. 2016, 74, 81–90. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Identification of pulsating flow effects with CNT nanoparticles on the performance enhancements of thermoelectric generator (TEG) module in renewable energy applications. Renew. Energy 2020, 162, 1076–1086. [Google Scholar] [CrossRef]
- Ferrouillat, S.; Bontemps, A.; Poncelet, O.; Soriano, O.; Gruss, J.A. Influence of nanoparticle shape factor on convective heat transfer and energetic performance of water-based SiO2 and ZnO nanofluids. Appl. Therm. Eng. 2013, 51, 839–851. [Google Scholar] [CrossRef]
- Liu, F.; Cai, Y.; Wang, L.; Zhao, J. Effects of nanoparticle shapes on laminar forced convective heat transfer in curved ducts using two-phase model. Int. J. Heat Mass Transf. 2018, 116, 292–305. [Google Scholar] [CrossRef]
- Benkhedda, M.; Boufendi, T.; Tayebi, T.; Chamkha, A.J. Convective heat transfer performance of hybrid nanofluid in a horizontal pipe considering nanoparticles shapes effect. J. Therm. Anal. Calorim. 2020, 140, 411–425. [Google Scholar] [CrossRef]
- Abderrahmane, A.; Hatami, M.; Medebber, M.; Haroun, S.; Ahmed, S.E.; Mohammed, S. Non-Newtonian nanofluid natural convective heat transfer in an inclined Half-annulus porous enclosure using FEM. Alex. Eng. J. 2022, 61, 5441–5453. [Google Scholar] [CrossRef]
- Kolsi, L.; Selimefendigil, F.; Said, L.B.; Mesloub, A.; Alresheedi, F. Forced Convection of Non-Newtonian Nanofluid Flow over a Backward Facing Step with Simultaneous Effects of Using Double Rotating Cylinders and Inclined Magnetic Field. Mathematics 2021, 9, 3002. [Google Scholar] [CrossRef]
- Alsabery, A.; Chamkha, A.; Saleh, H.; Hashim, I. Transient natural convective heat transfer in a trapezoidal cavity filled with non-Newtonian nanofluid with sinusoidal boundary conditions on both sidewalls. Powder Technol. 2017, 308, 214–234. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F.; Kolsi, L.; Omri, M. Performance analysis of thermoelectric generator mounted chaotic channel by using non-Newtonian nanofluid and modeling with efficient computational methods. Alex. Eng. J. 2022, 61, 3527–3549. [Google Scholar] [CrossRef]
- Khedher, N.B.; Selimefendigil, F.; Kolsi, L.; Aich, W.; Ben Said, L.; Boukholda, I. Performance Optimization of a Thermoelectric Device by Using a Shear Thinning Nanofluid and Rotating Cylinder in a Cavity with Ventilation Ports. Mathematics 2022, 10, 1075. [Google Scholar] [CrossRef]
- Kim, C.N. Development of a numerical method for the performance analysis of thermoelectric generators with thermal and electric contact resistance. Appl. Therm. Eng. 2018, 1305, 408–417. [Google Scholar] [CrossRef]
- Timofeeva, E.V.; Routbort, J.L.; Singh, D. Particle shape effects on thermophysical properties of alumina nanofluids. J. Appl. Phys. 2009, 106, 014304. [Google Scholar] [CrossRef]
- Vajjha, R.S.; Das, D.K. Experimental determination of thermal conductivity of three nanofluids and development of new correlations. Int. J. Heat Mass Transf. 2009, 52, 4675–4682. [Google Scholar] [CrossRef]
- Lewis, R.W.; Nithiarasu, P.; Seetharamu, K.N. Fundamentals of the Finite Element Method for Heat and Fluid Flow; John Wiley & Sons: West Sussex, UK, 2004. [Google Scholar]
- Heinrich, J.C.; Pepper, D.W. Intermediate Finite Element Method: Fluid Flow and Heat Transfer Applications; Routledge: New York, NY, USA, 2017. [Google Scholar]
- Reddy, J.N.; Gartling, D.K. The Finite Element Method in Heat Transfer and Fluid Dynamics; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Sourtiji, E.; Gorji-Bandpy, M.; Ganji, D.; Hosseinizadeh, S. Numerical analysis of mixed convection heat transfer of Al2O3-water nanofluid in a ventilated cavity considering different positions of the outlet port. Powder Technol. 2014, 262, 71–81. [Google Scholar] [CrossRef]

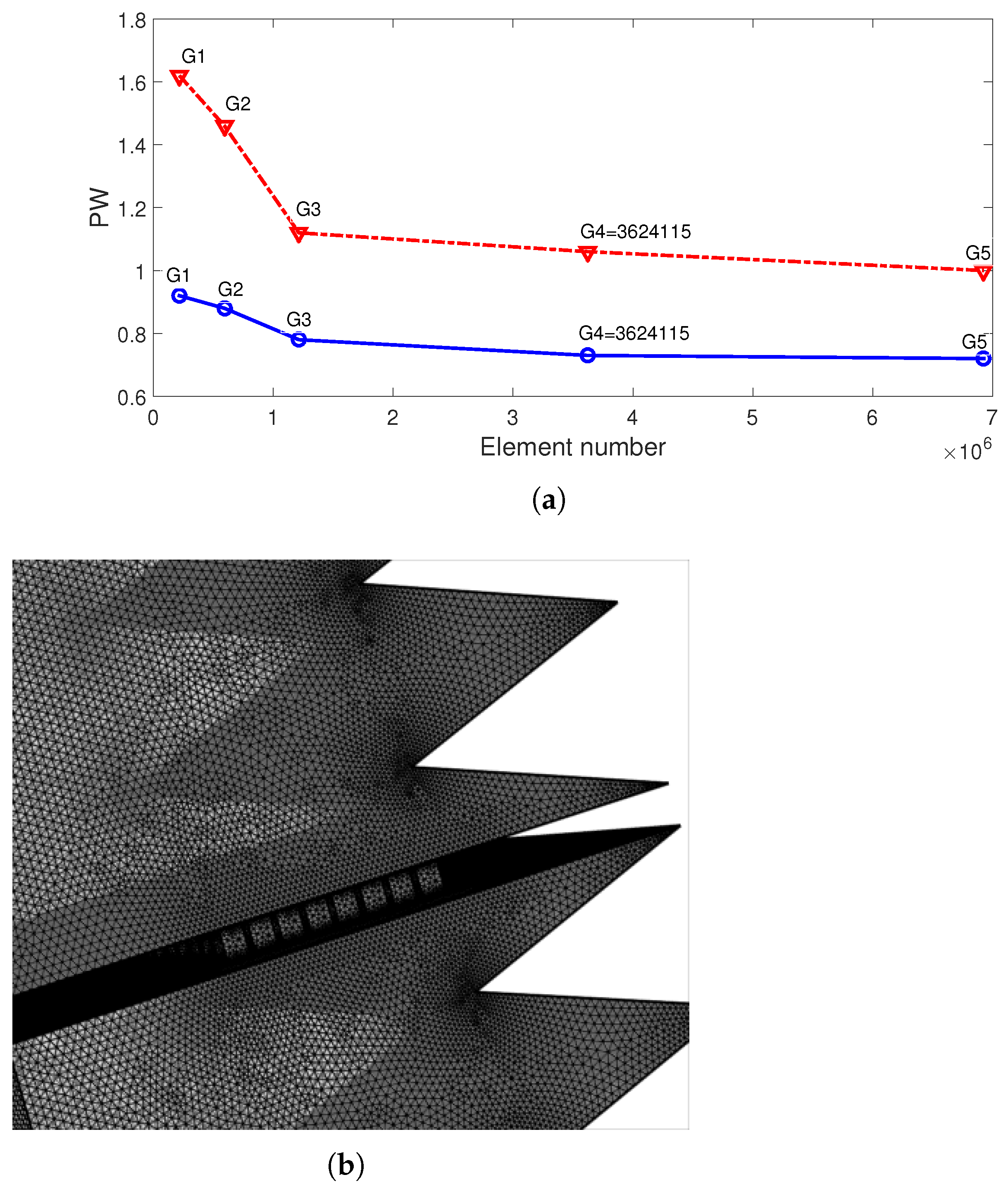


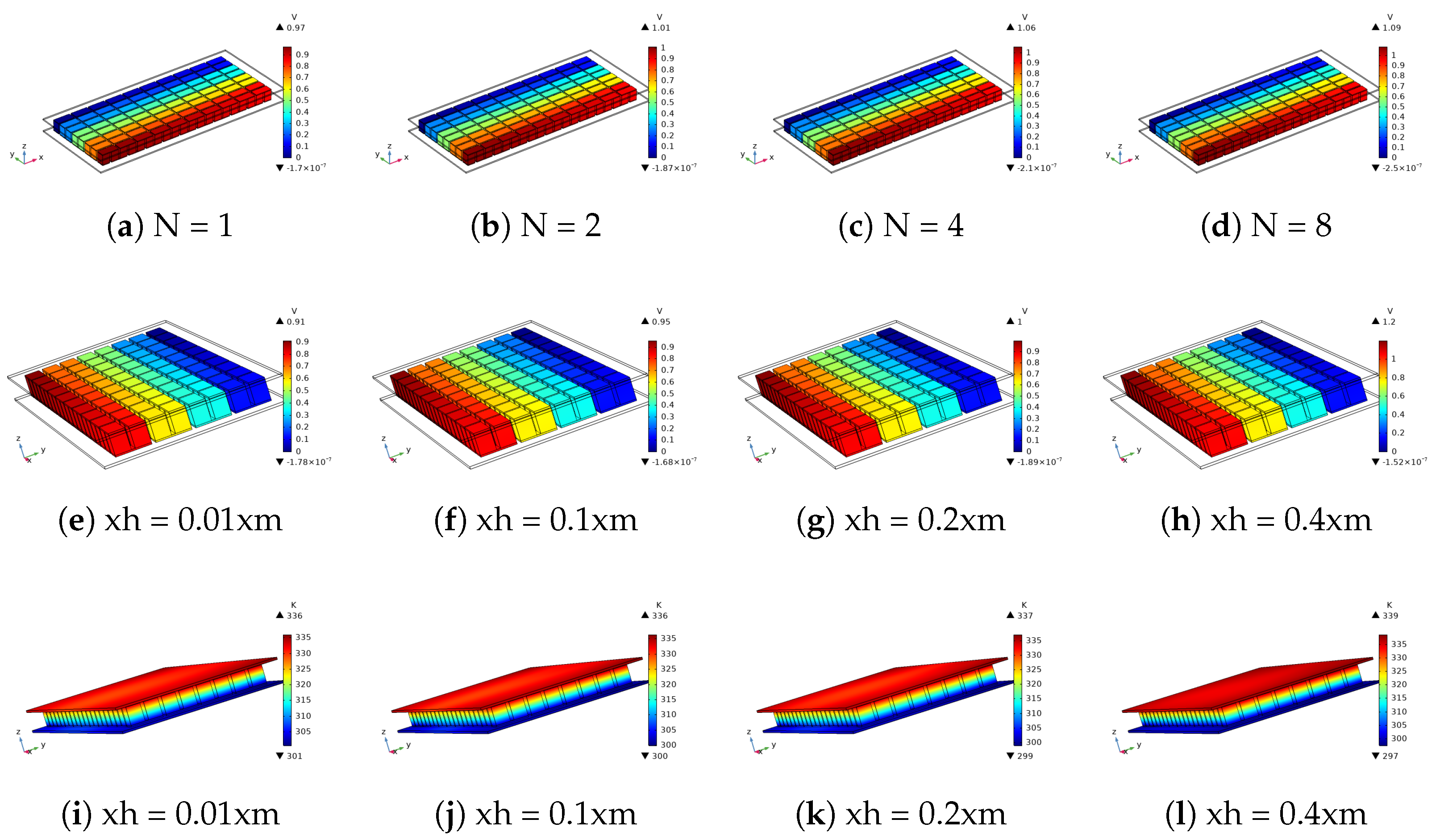
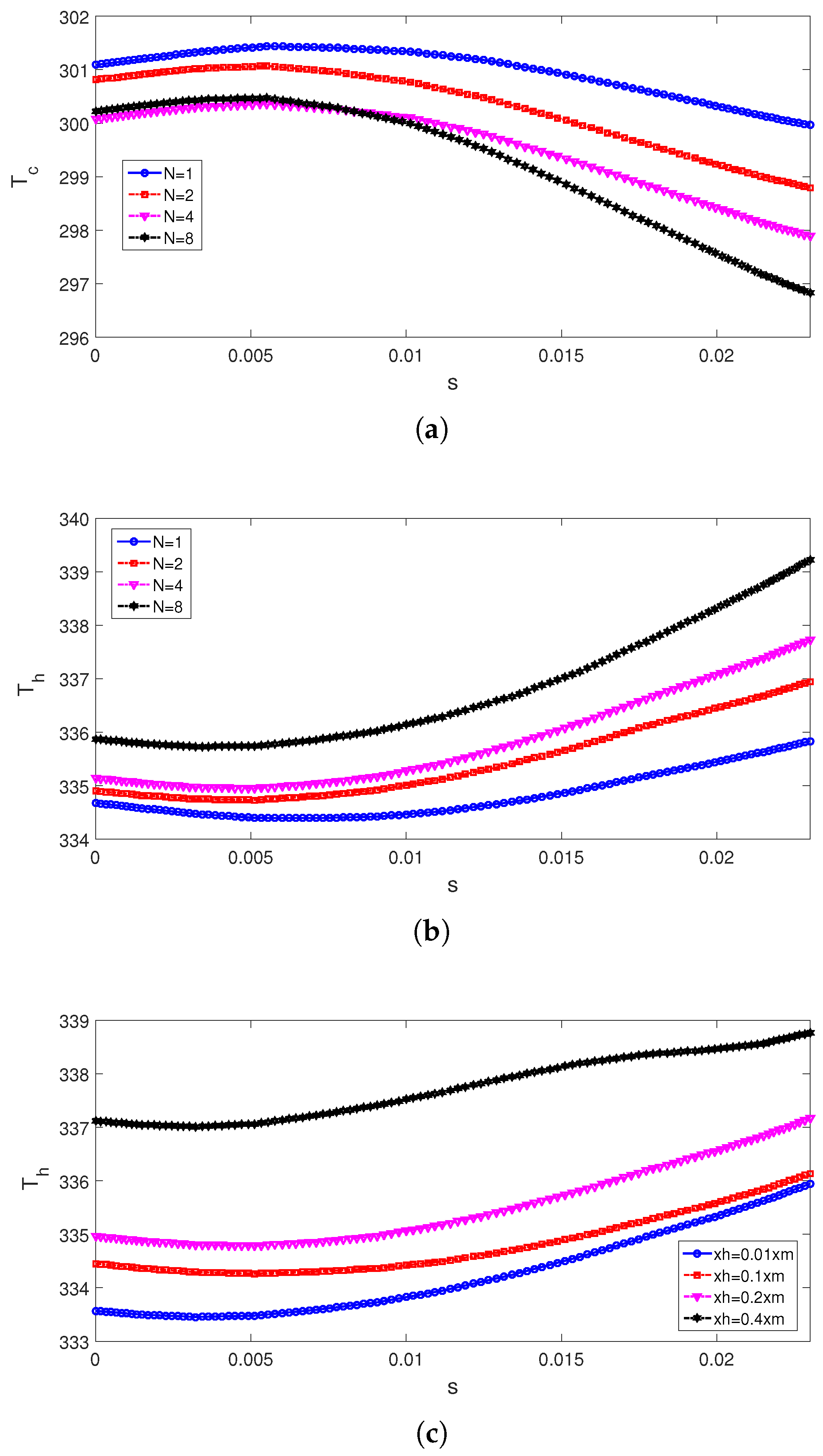
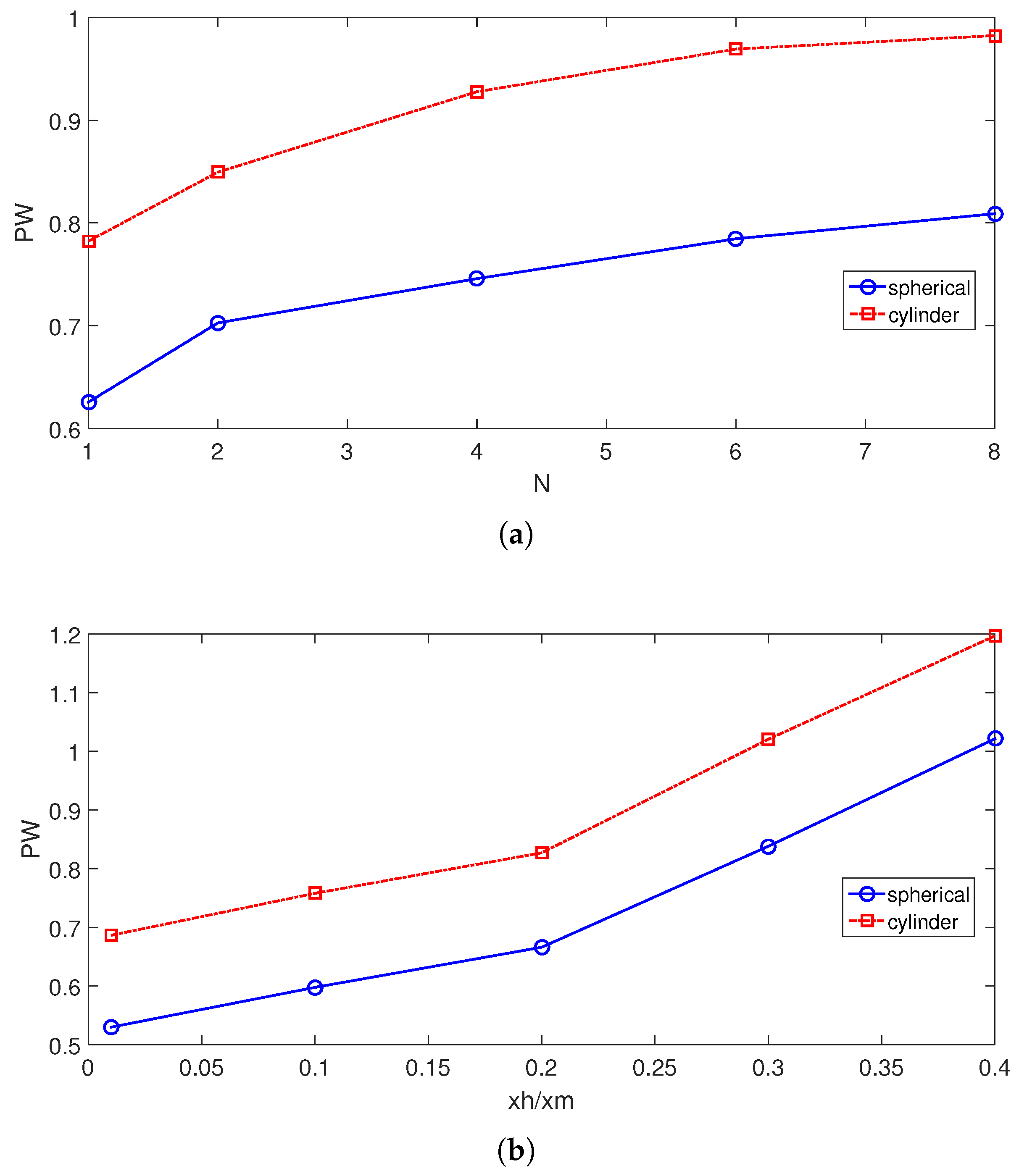

| Symbol | P Type Leg (BiTe) | N Type Leg (BiTe) | Electrode (Copper) | Ceramic (Alumina) | |
|---|---|---|---|---|---|
| Thermal conductivity | k (W/m K) | 1.6 | 1.6 | 400 | 27 |
| Electric conductivity | (S/m) | - | |||
| Seebeck coefficient | (V/K) | - | |||
| Heat capacity | C (J/kg K) | 154 | 154 | 385 | 900 |
| Density | (kg/m) | 7700 | 7700 | 8960 | 3900 |
| Property | Symbol | Water | AlO |
|---|---|---|---|
| Density (kg/m) | 997 | 3970 | |
| Specific heat (J/kg K) | c | 4179 | 765 |
| Viscosity (mPa.s) | 0.895 | - | |
| Thermal conductivity (W/m K) | k | 0.613 | 40 |
| Shape | C | A | A |
|---|---|---|---|
| Blade | 2.74 | 14.6 | 123.3 |
| Cylinder | 3.95 | 13.5 | 904.4 |
| Bricks | 3.37 | 1.9 | 471.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selimefendigil, F.; Omri, M.; Aich, W.; Besbes, H.; Ben Khedher, N.; Alshammari, B.M.; Kolsi, L. Numerical Study of Thermo-Electric Conversion for TEG Mounted Wavy Walled Triangular Vented Cavity Considering Nanofluid with Different-Shaped Nanoparticles. Mathematics 2023, 11, 483. https://doi.org/10.3390/math11020483
Selimefendigil F, Omri M, Aich W, Besbes H, Ben Khedher N, Alshammari BM, Kolsi L. Numerical Study of Thermo-Electric Conversion for TEG Mounted Wavy Walled Triangular Vented Cavity Considering Nanofluid with Different-Shaped Nanoparticles. Mathematics. 2023; 11(2):483. https://doi.org/10.3390/math11020483
Chicago/Turabian StyleSelimefendigil, Fatih, Mohamed Omri, Walid Aich, Hatem Besbes, Nidhal Ben Khedher, Badr M. Alshammari, and Lioua Kolsi. 2023. "Numerical Study of Thermo-Electric Conversion for TEG Mounted Wavy Walled Triangular Vented Cavity Considering Nanofluid with Different-Shaped Nanoparticles" Mathematics 11, no. 2: 483. https://doi.org/10.3390/math11020483
APA StyleSelimefendigil, F., Omri, M., Aich, W., Besbes, H., Ben Khedher, N., Alshammari, B. M., & Kolsi, L. (2023). Numerical Study of Thermo-Electric Conversion for TEG Mounted Wavy Walled Triangular Vented Cavity Considering Nanofluid with Different-Shaped Nanoparticles. Mathematics, 11(2), 483. https://doi.org/10.3390/math11020483









