The Roots of the Reliability Polynomials of Circular Consecutive-k-out-of-n:F Systems
Abstract
:1. Introduction
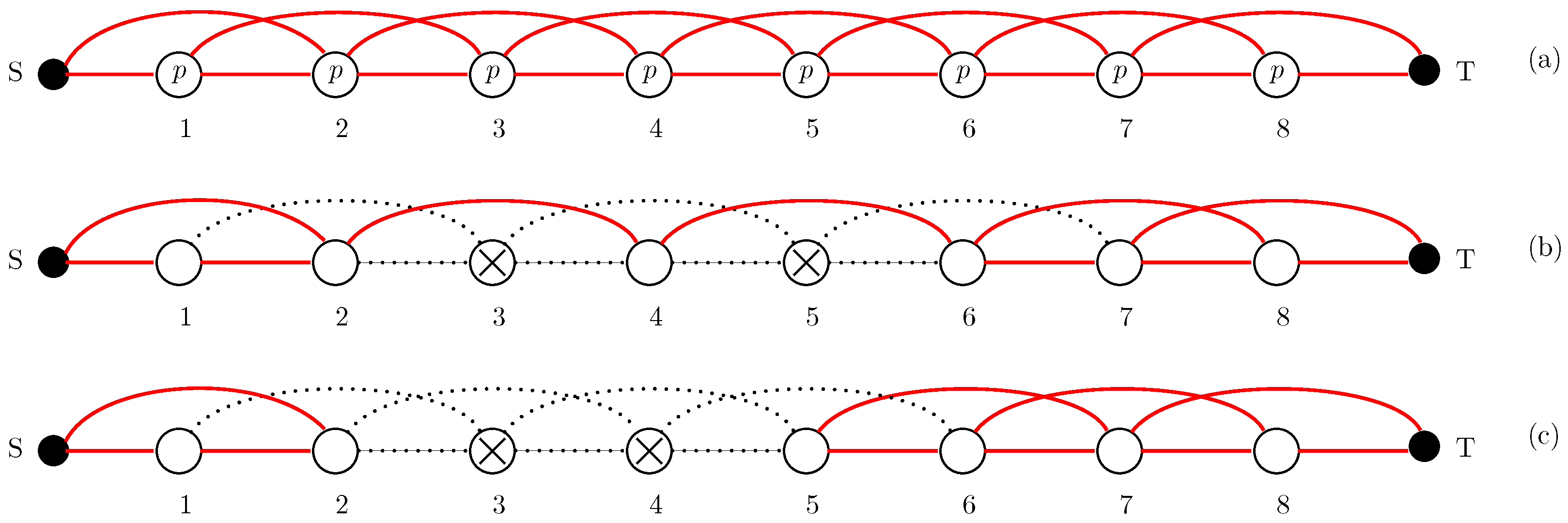
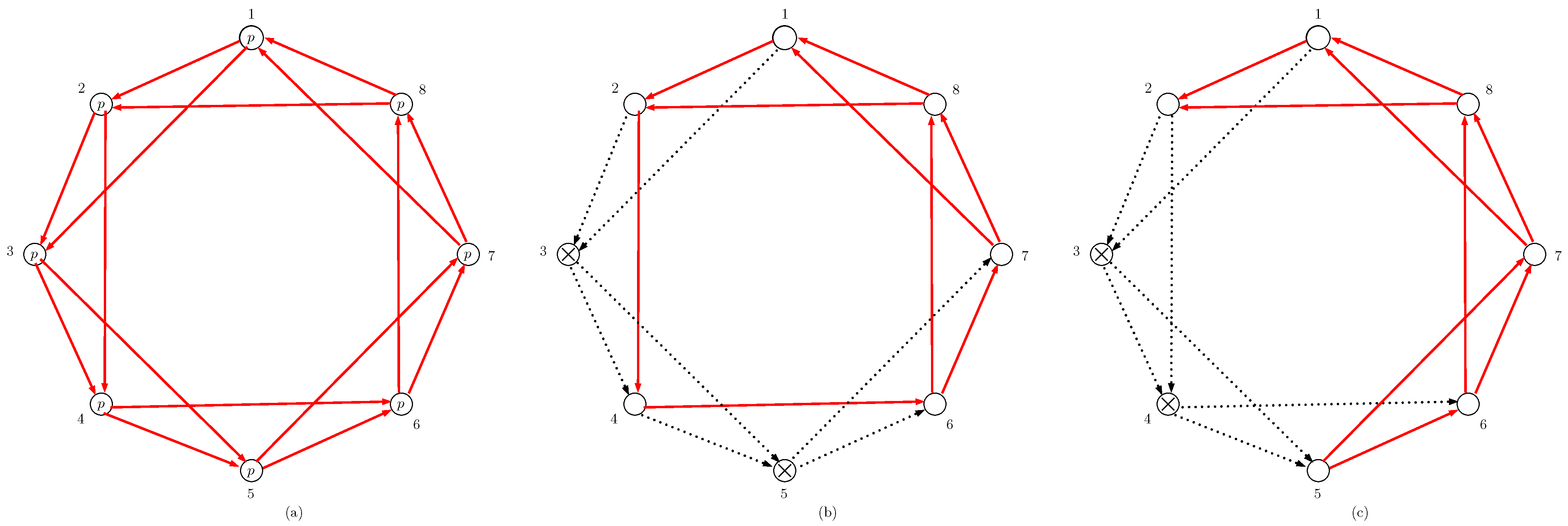
2. The Circular Consecutive--out-of-:F Systems Have Unbounded Roots
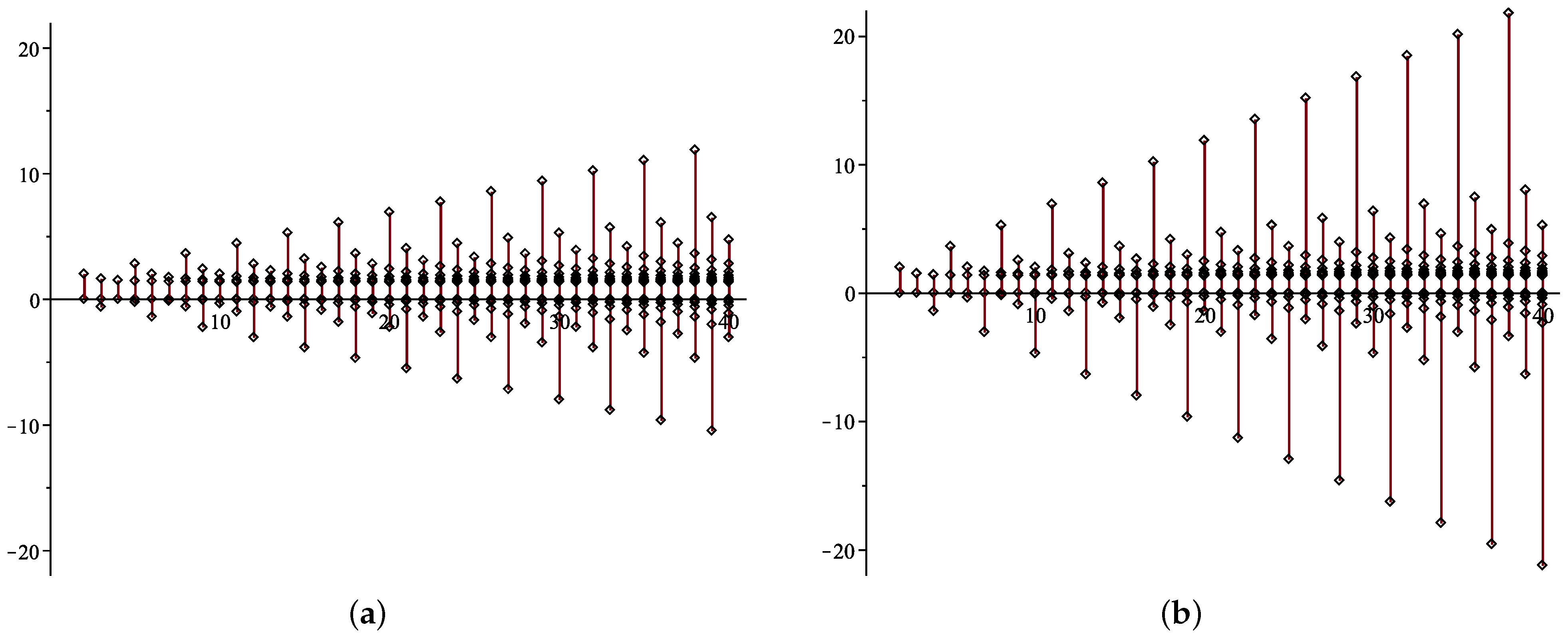
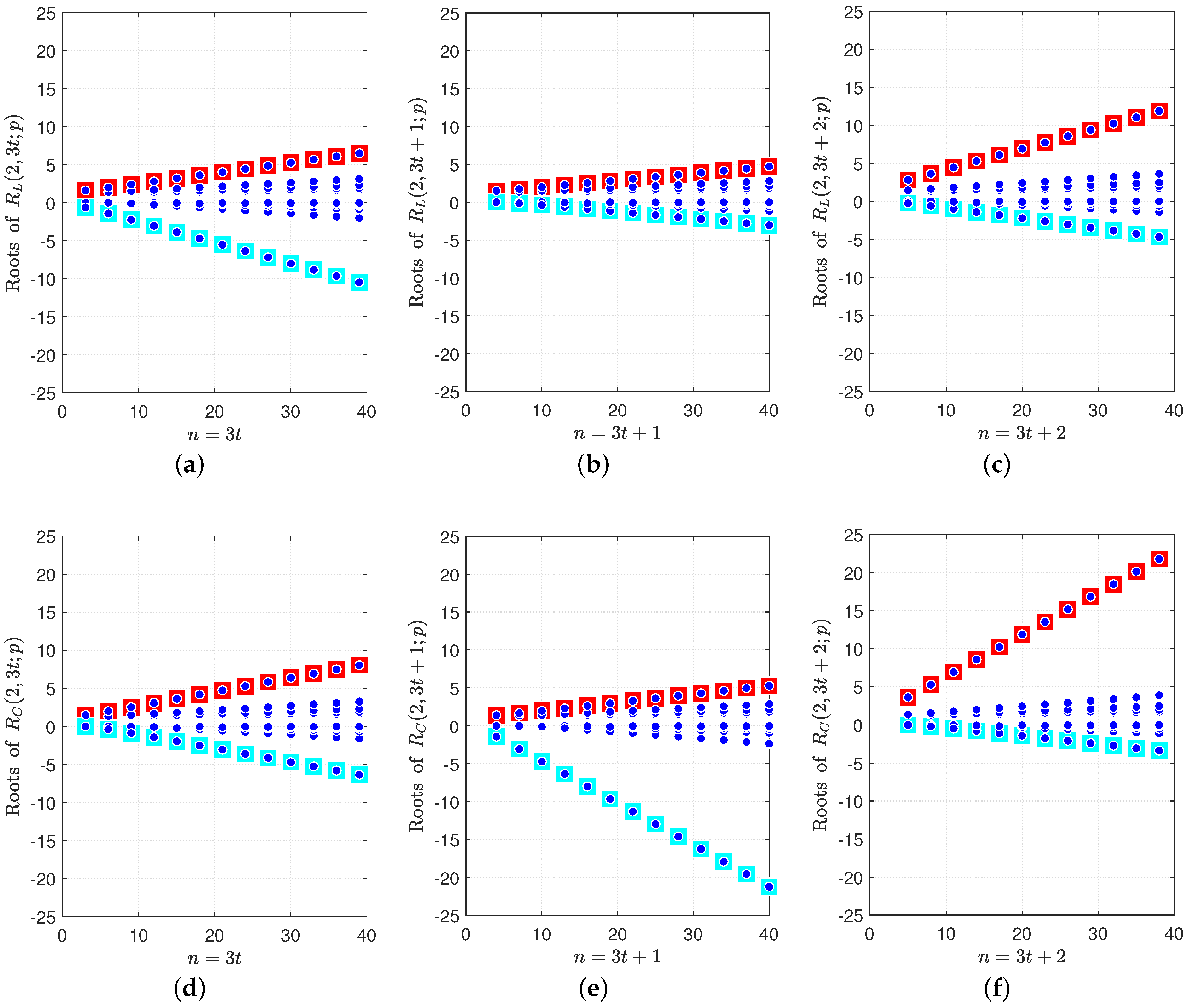
3. The Roots of Consecutive-2-out-of-:F Systems
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kontoleon, J.M. Reliability determination of a r-succesive-out-of-n:F system. IEEE Trans. Reliab. 1980, R-29, 437. [Google Scholar] [CrossRef]
- Chiang, D.T.; Niu, S. Reliability of consecutive-k-out-of-n:F system. IEEE Trans. Reliab. 1981, R-30, 87–89. [Google Scholar] [CrossRef]
- Derman, C.; Lieberman, G.J.; Ross, S.M. On the consecutive-k-out-of-n:F system. IEEE Trans. Reliab. 1982, R-31, 57–63. [Google Scholar] [CrossRef]
- Chang, G.J.; Cui, L.; Hwang, F.K. Reliabilities of Consecutive-k Systems; Springer: New York, NY, USA, 2000. [Google Scholar]
- Kuo, W.; Zuo, M.J. Optimal Reliability Modeling: Principles and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Chao, M.T.; Fu, J.C.; Koutras, M.V. Survey of reliability studies of consecutive-k-out-of-n:F & related systems. IEEE Trans. Reliab. 1995, 44, 120–127. [Google Scholar]
- Triantafyllou, I.S.; Koutras, M.K. Reliability properties of (n,f,k) systems. IEEE Trans. Reliab. 2014, 63, 357–366. [Google Scholar] [CrossRef]
- Beiu, V.; Dăuş, L. Reliability bounds for two dimensional consecutive systems. Nano Comm. Netw. 2015, 6, 145–152. [Google Scholar] [CrossRef]
- Dăuş, L.; Beiu, V. Lower and upper reliability bounds for consecutive-k-out-of-n:F systems. IEEE Trans. Reliab. 2015, 64, 1128–1135. [Google Scholar] [CrossRef]
- Mohammadi, F.; Sáenz-de-Cabezón, E.; Wynn, H.P. Efficient multicut enumeration of k-out-of-n:F and consecutive k-out-of-n:F systems. Pattern Recog. Lett. 2018, 102, 82–88. [Google Scholar] [CrossRef]
- Dafnis, S.D.; Makri, F.S.; Philippou, A.N. The reliability of a generalized consecutive system. Appl. Math. Comput. 2019, 359, 186–193. [Google Scholar] [CrossRef]
- Radwan, T. New bounds for all types of multi-state consecutive k-out-of-r-from-n: F system reliability. IEEE Access 2019, 7, 172562–172570. [Google Scholar] [CrossRef]
- Drăgoi, V.F.; Cowel, S.R.; Beiu, V. Tight Bounds on the coefficients of consecutive k-out-of-n:F systems. In Intelligent Methods in Computing, Communications and Control, Proceedings of the International Conference Computers Communications and Control (ICCCC 2020), Oradea, Romania, 11–15 May 2020; Springer: Cham, Switzerland, 2021; pp. 35–44. [Google Scholar]
- Triantafyllou, I.S. On the consecutive k1 and k2-out-of-n reliability systems. Mathematics 2020, 8, 630. [Google Scholar] [CrossRef]
- Xiao, H.; Zhang, Y.; Xiang, Y.; Peng, R. Optimal design of a linear sliding window system with consideration of performance sharing. Reliab. Eng. Sys. Saf. 2020, 198, 106900. [Google Scholar] [CrossRef]
- Eryilmaz, S. Age-based preventive maintenance for coherent systems with applications to consecutive-k-out-of-n and related systems. Reliab. Eng. Sys. Saf. 2020, 204, 107143. [Google Scholar] [CrossRef]
- Zhao, F.; Peng, R.; Zhang, N. Inspection policy optimization for a k-out-of-n/Cl(k′,n′;F) system considering failure dependence: A case study. Reliab. Eng. Sys. Saf. 2023, 237, 109331. [Google Scholar] [CrossRef]
- Beiu, A.C.; Beiu, R.M.; Beiu, V. Optimal design of linear consecutive systems. In Proceedings of the ACM International Conference Nanoscale Computing and Communication NANOCOM 2022, Barcelona, Spain, 5–7 October 2022; p. 24. [Google Scholar]
- Philippou, A.N. Distributions and Fibonacci polynomials of order k, longest runs and reliability of consecutive-k-out-of-n:F systems. In Fibonacci Numbers and Their Applications; Philippou, A.N., Bergum, G.E., Horadam, A.F., Eds.; Reidel: Dordrecht, The Netherlands, 1986; pp. 203–227. [Google Scholar]
- Hoggatt, V.E.; Bicknell, M. Generalized Fibonacci polynomials. Fibonacci Q. 1973, 11, 457–465. [Google Scholar]
- Charalambides, C.A. Lucas numbers and polynomials of order k and the length of the longest circular success run. Fibonacci Q. 1991, 29, 290–297. [Google Scholar]
- Brown, J.I.; Colbourn, C.J. Roots of the reliability polynomial. SIAM J. Discr. Math. 1992, 5, 571–585. [Google Scholar] [CrossRef]
- Brown, J.I.; Colbourn, C.J.; Cox, D.; Graves, C.; Mol, L. Network reliability: Heading out on the highway. Networks 2021, 77, 146–160. [Google Scholar] [CrossRef]
- Comtet, L. Advanced Combinatorics; Reidel: Dordrecht, The Netherlands; Boston, MA, USA, 1974. [Google Scholar]
- Brenti, F.; Royle, G.F.; Wagner, D.G. Location of zeros of chromatic and related polynomials of graphs. Canad. J. Math. 1994, 46, 55–80. [Google Scholar] [CrossRef]
- Brown, J.I.; Mol, L. On the roots of all-terminal reliability polynomials. Discr. Math. 2017, 340, 1287–1299. [Google Scholar] [CrossRef]
- DeGagné, C.D.C. Network Reliability, Simplicial Complexes, and Polynomial Roots. Ph.D. Thesis, Dalhousie University, Halifax, NS, Canada, 2020. [Google Scholar]
- Brown, J.I.; DeGagné, C.D.C. Roots of two-terminal reliability polynomials. Networks 2021, 78, 153–163. [Google Scholar] [CrossRef]
- Dăuş, L.; Drăgoi, V.F.; Jianu, M.; Bucerzan, D.; Beiu, V. On the roots of certain reliability polynomials. In Intelligent Methods in Computing, Communications and Control, Proceedings of the International Conference Computers Communications and Control (ICCCC 2022), Oradea, Romania, 16–20 May 2022; Springer: Cham, Switzerland, 2023; pp. 401–414. [Google Scholar]
- Jianu, M. On the roots of a family of polynomials. Fractal Fract. 2023, 7, 339. [Google Scholar] [CrossRef]
- Jackson, B. A zero-free interval for chromatic polynomials of graphs. Comb. Probab. Comput. 1993, 2, 325–336. [Google Scholar] [CrossRef]
- Thomassen, C. The zero-free intervals for chromatic polynomials of graphs. Comb. Probab. Comput. 1997, 6, 497–506. [Google Scholar] [CrossRef]
- Cameron, P.J.; Morgan, K. Algebraic properties of chromatic roots. Electron. J. Comb. 2017, 24, 1–21. [Google Scholar] [CrossRef]
- Sokal, A.D. Chromatic roots are dense in the whole complex plane. Comb. Probab. Comput. 2004, 13, 221–261. [Google Scholar] [CrossRef]
- Brown, J.I.; Wagner, D.G. On the imaginary parts of chromatic roots. J. Graph. Theor. 2020, 93, 299–311. [Google Scholar] [CrossRef]
- Gutman, I.; Harary, F. Generalizations of the matching polynomial. Util. Math. 1983, 24, 97–106. [Google Scholar]
- Brown, J.I.; Hickman, C.A.; Nowakowski, R.J. On the location of roots of independence polynomials. J. Algebr. Comb. 2004, 19, 273–282. [Google Scholar] [CrossRef]
- Brown, J.I.; Cameron, B. A note on purely imaginary independence roots. Discr. Math. 2020, 343, 112113. [Google Scholar] [CrossRef]
- Brown, J.I.; Cameron, B. Maximum modulus of independence roots of graphs and trees. Graph. Combinator. 2020, 36, 877–894. [Google Scholar] [CrossRef]
- Beraha, S.; Kahane, J.; Weiss, N.J. Limits of zeroes of recursively defined families of polynomials. In Studies in Foundations and Combinatorics; Rota, G.C., Ed.; Academic Press: New York, NY, USA, 1978; pp. 213–232. [Google Scholar]
- Jianu, M.; Dăuş, L.; Drăgoi, V.F.; Beiu, V. Reliability polynomials of consecutive-k-out-of-n:F systems have unbounded roots. Networks 2023, 82, 222–228. [Google Scholar] [CrossRef]
- Du, D.Z.; Hwang, F.K. A direct algorithm for computing reliability of a consecutive-k cycle. IEEE Trans. Reliab. 1988, R-37, 70–72. [Google Scholar] [CrossRef]
- Hoggatt, V.E.; Bicknell-Johnson, M. Convolution arrays for Jacobsthal and Fibonacci polynomials. Fibonacci Q. 1978, 16, 385–402. [Google Scholar]
- Koshy, T. Fibonacci and Lucas Numbers with Applications; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Tereszkiewicz, A.; Wawreniuk, I. Generalized Jacobsthal polynomials and special points for them. Appl. Math. Comput. 2015, 268, 806–814. [Google Scholar] [CrossRef]
| Fibonacci Polynomials | Jacobsthal Polynomials | |
|---|---|---|
| Lucas Polynomials | Jacobsthal–Lucas Polynomials | |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jianu, M.; Dăuş, L.; Drăgoi, V.-F.; Beiu, V. The Roots of the Reliability Polynomials of Circular Consecutive-k-out-of-n:F Systems. Mathematics 2023, 11, 4252. https://doi.org/10.3390/math11204252
Jianu M, Dăuş L, Drăgoi V-F, Beiu V. The Roots of the Reliability Polynomials of Circular Consecutive-k-out-of-n:F Systems. Mathematics. 2023; 11(20):4252. https://doi.org/10.3390/math11204252
Chicago/Turabian StyleJianu, Marilena, Leonard Dăuş, Vlad-Florin Drăgoi, and Valeriu Beiu. 2023. "The Roots of the Reliability Polynomials of Circular Consecutive-k-out-of-n:F Systems" Mathematics 11, no. 20: 4252. https://doi.org/10.3390/math11204252





