An Isogeometric Over-Deterministic Method (IG-ODM) to Determine Elastic Stress Intensity Factor (SIF) and T-Stress
Abstract
:1. Introduction
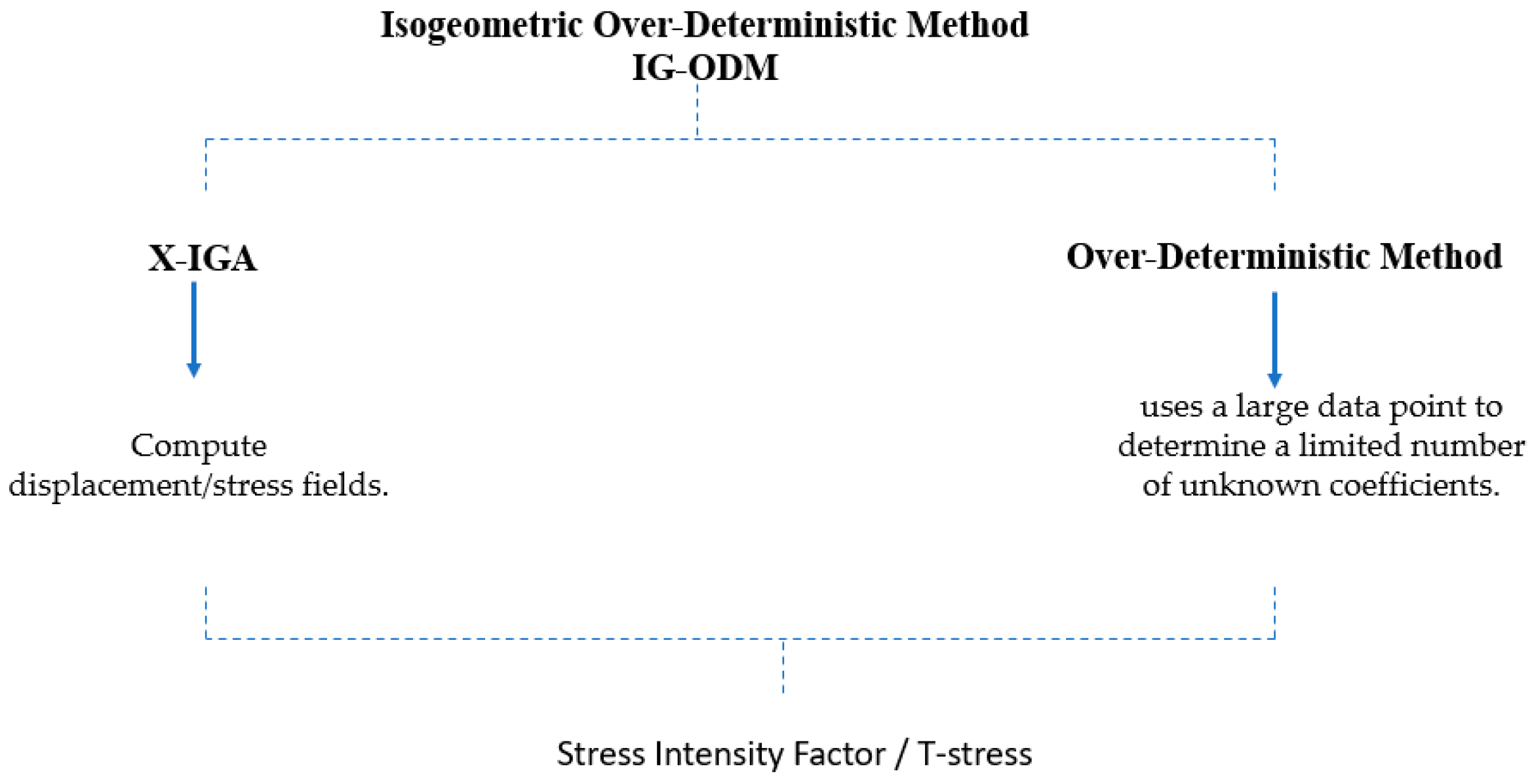
2. Models and Method
2.1. Extended Iso-Geometric Analysis (IGA)
- Partition of unity: ;
- The continuity of the basic functions is , where p is the polynomial degree and m is the multiplicity of the knot;
- The support of is included in ;
- The first derivative of a B-spline basis function.
- Knot insertion is the h-refinement; this refinement changes the basic functions defined on a node vector, to a new basis :
- Degree elevation entails raising the polynomial order of the basic functions, and well nodes are added to the edge. The added values are values that already exist in the initial node vector, they are the p-refinement.
2.2. Iso-Geometric Over-Deterministic Method
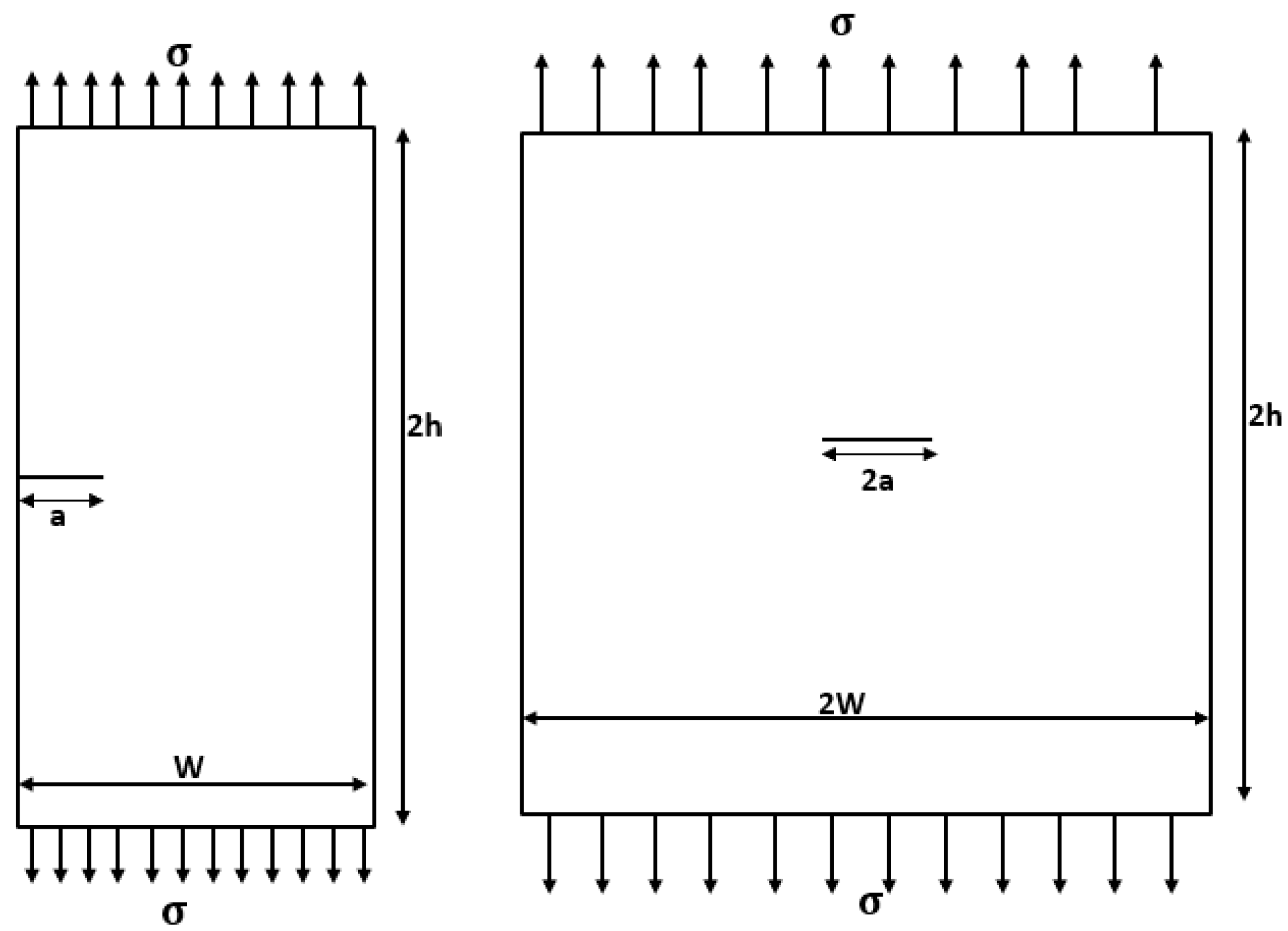
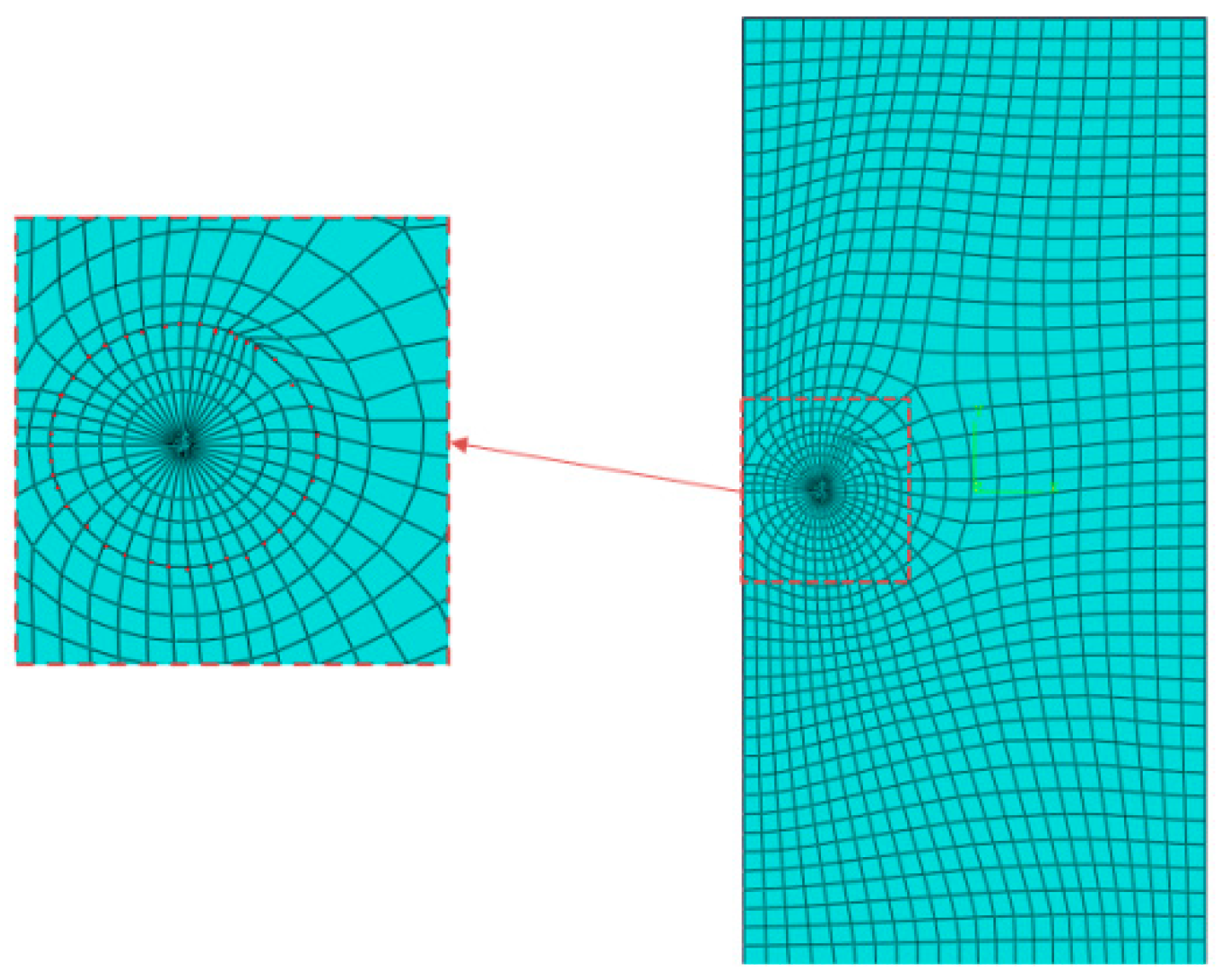
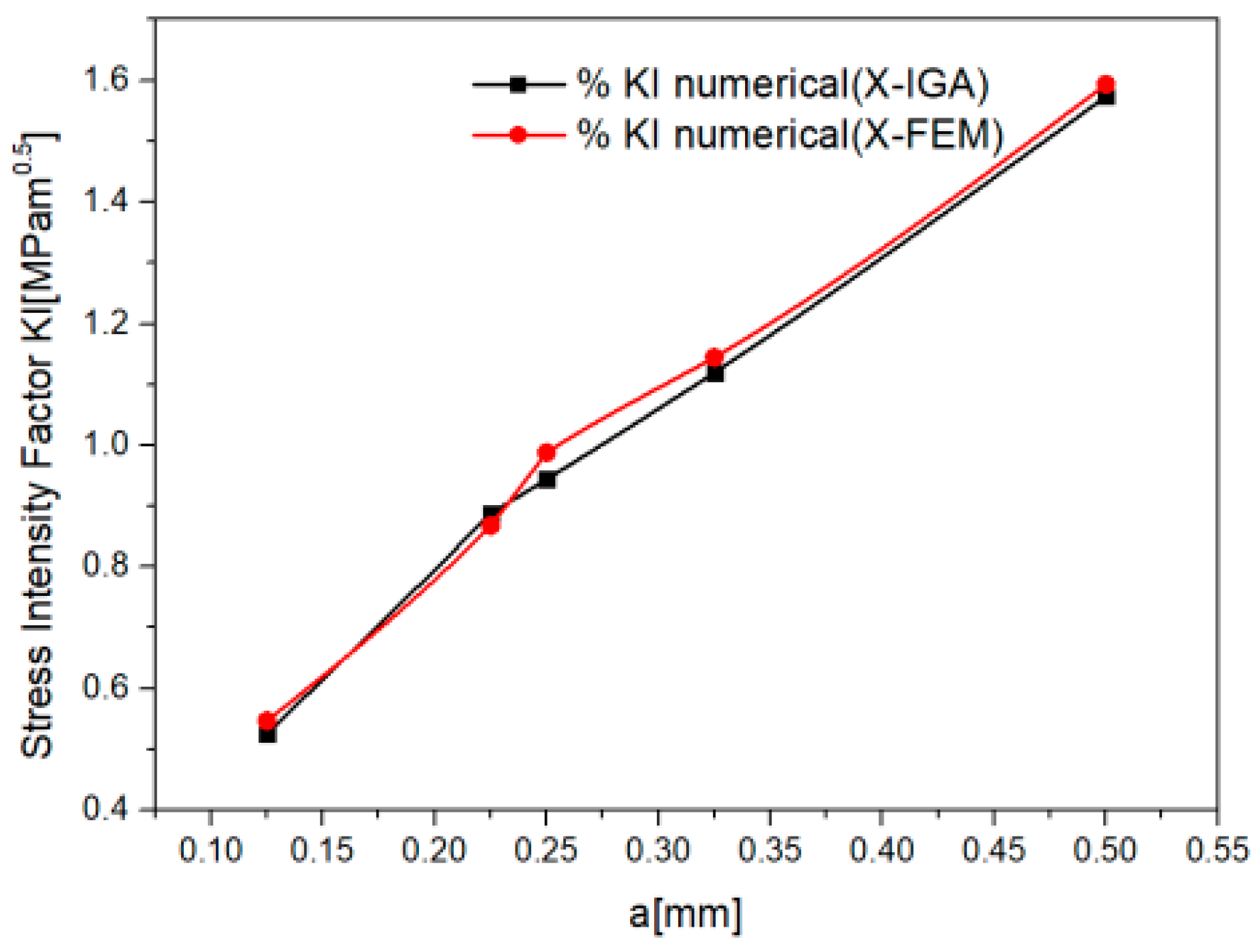
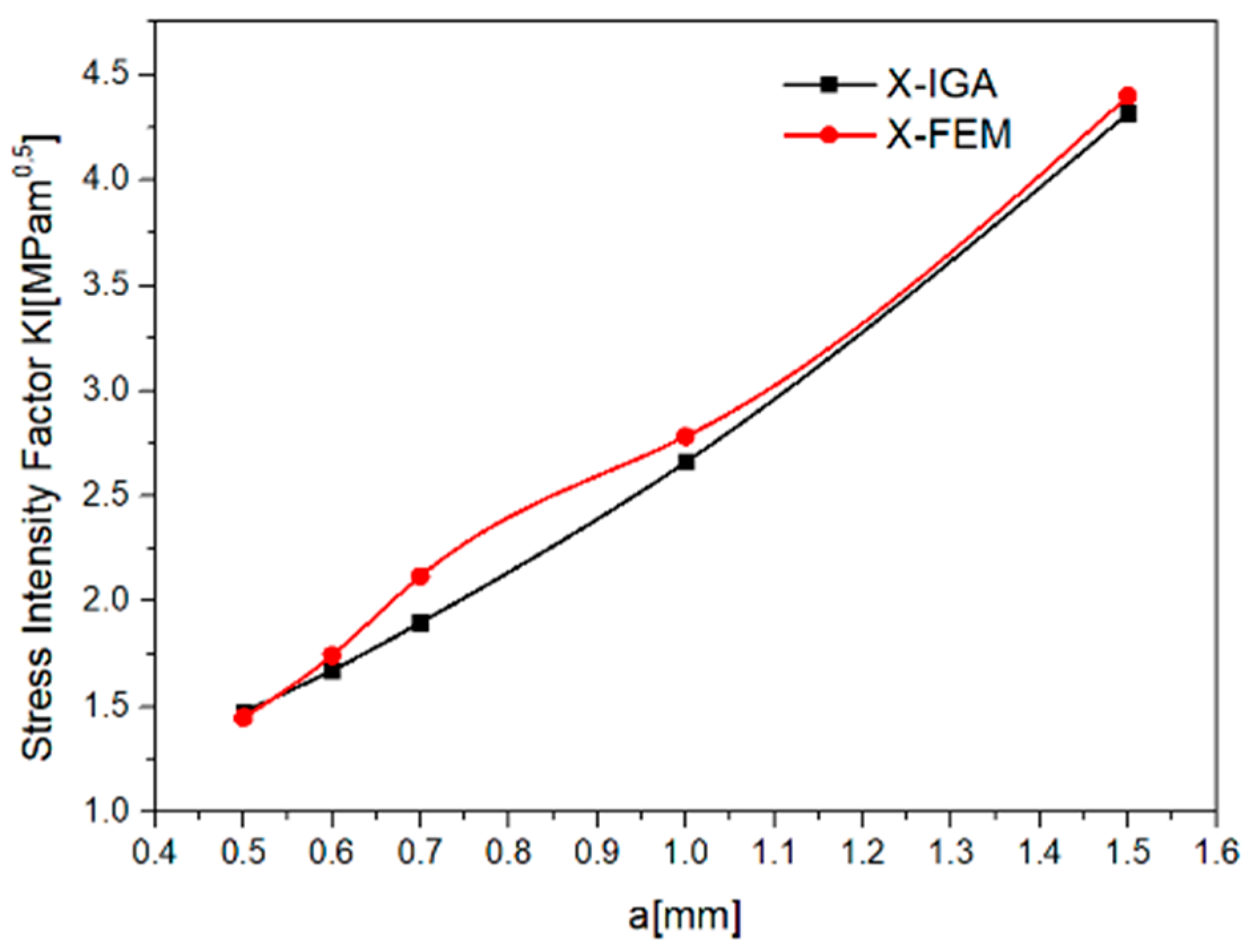
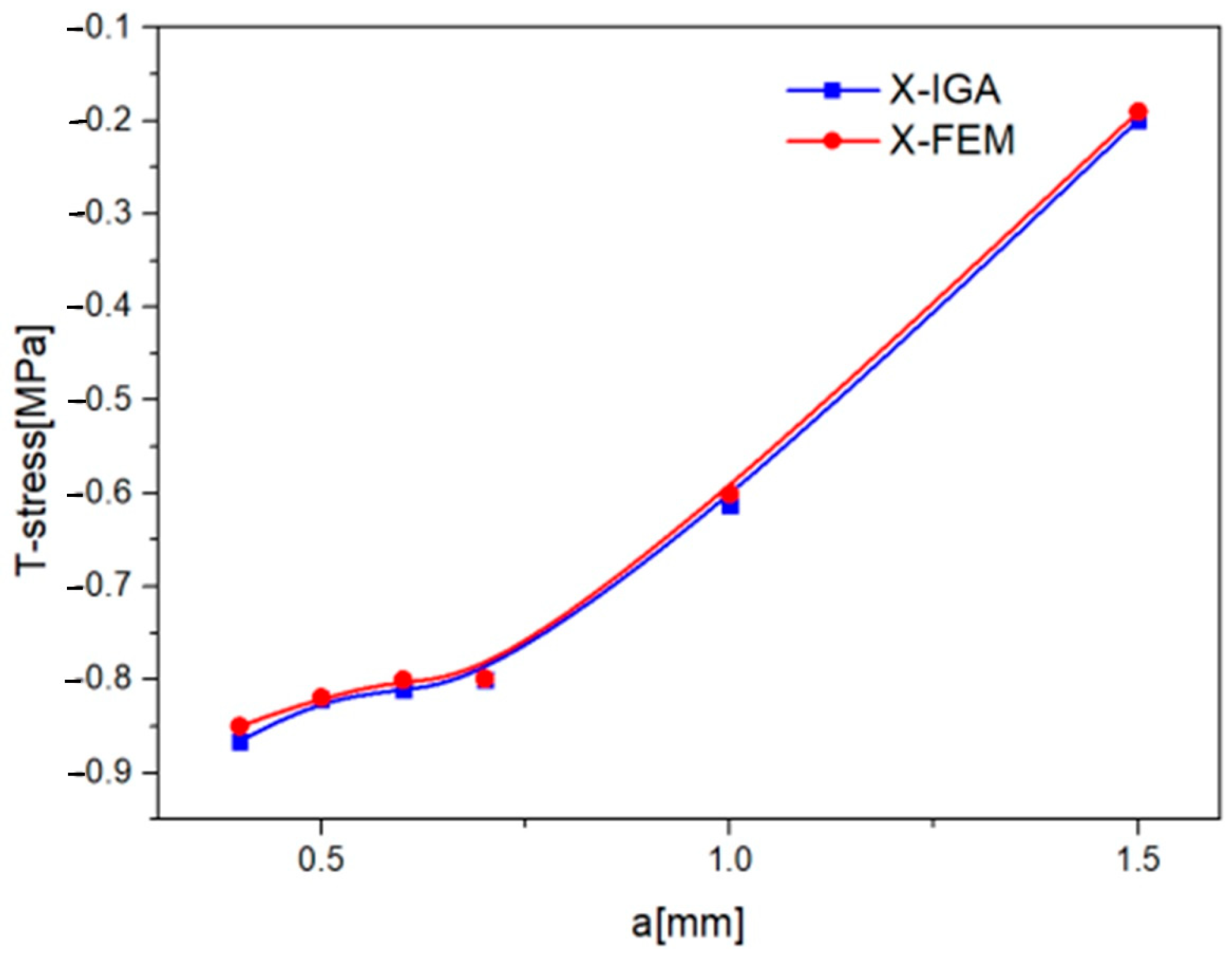
3. Results
4. Discussion and Conclusions
- The T-stress is introduced to enrich SIF, in a better presentation of the crack.
- The SIF and T-stress are determined using IG-ODM, which is an efficient method for computing fracture parameters.
- The IG-ODM approach proves to be more efficient when the displacement field is accurately determined, utilizing a more precise numerical method such as X-IGA.
- IGA, as a technology, allows for interaction with CAD systems, leading to improved solution accuracy and reduced computational costs.
- In order to obtain accurate results using IG-ODM, it is essential that the number of crack parameters exceeds the number of nodal displacements determined by X-IGA.
- Because of the relatively significant numerical errors that exist in nodes that are very near to the fracture tip, it is better to obtain the essential data from nodes that are further away from the crack tip, and it is preferable to select nodes from a particular ring.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cotterell, B. Notes on the paths and stability of cracks. Int. J. Fract. 1966, 2, 526–533. [Google Scholar] [CrossRef]
- Nejati, M.; Ghouli, S.; Ayatollahi, M.R. Crack tip asymptotic fields in anisotropic planes: Importance of higher order terms. Appl. Math. Model. 2021, 91, 837–862. [Google Scholar] [CrossRef]
- Matvienko, Y.G. The effect of crack-tip constraint in some problems of fracture mechanics. Eng. Fail. Anal. 2020, 110, 104413. [Google Scholar] [CrossRef]
- Jayadevan, K.R.; Narasimhan, R.; Ramamurthy, T.S.; Dattaguru, B. Effect of T-stress and loading rate on crack initiation in rate sensitive plastic materials. Int. J. Solids Struct. 2002, 39, 1757–1775. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Hashemi, R. Computation of stress intensity factors (KI, KII) and T-stress for cracks reinforced by composite patching. Compos. Struct. 2007, 78, 602–609. [Google Scholar] [CrossRef]
- Sherry, A.H.; France, C.C.; Goldthorpe, M.R. Compendium of t-stress solutions for two and three dimensional cracked geometries. Fatigue Fract. Eng. Mater. Struct. 1995, 18, 141–155. [Google Scholar] [CrossRef]
- Shahani, A.R.; Tabatabaei, S.A. Effect of T-stress on the fracture of a four point bend specimen. Mater. Des. 2009, 30, 2630–2635. [Google Scholar] [CrossRef]
- Fayed, A.S. Numerical Analysis of Crack Initiation Direction in Quasi-brittle Materials: Effect of T-Stress. Arab. J. Sci. Eng. 2019, 44, 7667–7676. [Google Scholar] [CrossRef]
- Miao, X.T.; Zhou, C.Y.; Lv, F.; He, X.H. Three-dimensional finite element analyses of T-stress for different experimental specimens. Theor. Appl. Fract. Mech. 2017, 91, 116–125. [Google Scholar] [CrossRef]
- Yakoubi, K.; Montassir, S.; Moustabchir, H.; Elkhalfi, A.; Pruncu, C.I.; Arbaoui, J.; Umar Farooq, M. An Extended Finite Element Method (XFEM) Study on the Elastic T-Stress Evaluations for a Notch in a Pipe Steel Exposed to Internal Pressure. Mathematics 2021, 9, 507. [Google Scholar] [CrossRef]
- Yang, B.; Ravi-Chandar, K. Evaluation of elastic T-stress by the stress difference method. Eng. Fract. Mech. 1999, 64, 589–605. [Google Scholar] [CrossRef]
- Hou, C.; Wang, Z.; Jin, X.; Ji, X.; Fan, X. Determination of SIFs and T-stress using an over-deterministic method based on stress fields: Static and dynamic. Eng. Fract. Mech. 2021, 242, 107455. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Nejati, M. An over-deterministic method for calculation of coefficients of crack tip asymptotic field from finite element analysis: Calculating coefficients of crack tip asymptotic field from FE analysis. Fatigue Fract. Eng. Mater. Struct. 2011, 34, 159–176. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, K. Crack tip asymptotic field coefficients analyses based on extended finite element method using over-deterministic displacement field fitting method. Theor. Appl. Fract. Mech. 2021, 113, 102971. [Google Scholar] [CrossRef]
- Cuong-Le, T.; Nguyen, K.D.; Nguyen-Trong, N.; Khatir, S.; Nguyen-Xuan, H.; Abdel-Wahab, M. A three-dimensional solution for free vibration and buckling of annular plate, conical, cylinder and cylindrical shell of FG porous-cellular materials using IGA. Compos. Struct. 2021, 259, 113216. [Google Scholar] [CrossRef]
- Shafei, E.; Faroughi, S.; Rabczuk, T. Nonlinear transient vibration of viscoelastic plates: A NURBS-based isogeometric HSDT approach. Comput. Math. Appl. 2021, 84, 1–15. [Google Scholar] [CrossRef]
- Hinz, J.; Jaeschke, A.; Möller, M.; Vuik, C. The role of PDE-based parameterization techniques in gradient-based IGA shape optimization applications. Comput. Methods Appl. Mech. Eng. 2021, 378, 113685. [Google Scholar] [CrossRef]
- Hou, W.; Jiang, K.; Zhu, X.; Shen, Y.; Hu, P. Extended isogeometric analysis using B++ splines for strong discontinuous problems. Comput. Methods Appl. Mech. Eng. 2021, 381, 113779. [Google Scholar] [CrossRef]
- Fathi, F.; de Borst, R. Geometrically nonlinear extended isogeometric analysis for cohesive fracture with applications to delamination in composites. Finite Elem. Anal. Des. 2021, 191, 103527. [Google Scholar] [CrossRef]
- Ghorashi, G.; Valizadeh, N.; Mohammadi, S. Extended isogeometric analysis for simulation of stationary and propagating cracks. Int. J. Numer. Methods Eng. 2012, 89, 1069–1101. [Google Scholar] [CrossRef]
- Yadav, A.; Godara, R.K.; Bhardwaj, G. A review on XIGA method for computational fracture mechanics applications. Eng. Fract. Mech. 2020, 230, 107001. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Bordas, S.P.A.; Rabczuk, T. Isogeometric analysis: An overview and computer implementation aspects. Math. Comput. Simul. 2015, 117, 89–116. [Google Scholar] [CrossRef]
- Montassir, S.; Yakoubi, K.; Moustabchir, H.; Elkhalfi, A.; Rajak, D.K.; Pruncu, C.I. Analysis of Crack Behaviour in Pipeline System Using FAD Diagram Based on Numerical Simulation under XFEM. Appl. Sci. 2020, 10, 6129. [Google Scholar] [CrossRef]
- Williams, M.L. On the Stress Distribution at the Base of a Stationary Crack. (10 June 2021)ASME. J. Appl. Mech. 1957, 24, 109–114. [Google Scholar] [CrossRef]
- Sanford, R.J. Application of the least-squares method to photoelastic analysis: Two global methods for determining certain key parameters from full-field fringe patterns based on the method of least squares are presented. Exp. Mech. 1980, 20, 192–197. [Google Scholar] [CrossRef]
- Xiao, Q.Z.; Karihaloo, B.L.; Liu, X.Y. Direct determination of SIF and higher order terms of mixed mode cracks by a hybrid crack element. Int. J. Fract. 2004, 125, 207–225. [Google Scholar] [CrossRef]
- Bui, Q.; Zheng, X.; Gu, S. Static and dynamic fracture analysis in elastic solids using a multiscale extended isogeometric analysis. Eng. Fract. Mech. 2019, 207, 109–130. [Google Scholar] [CrossRef]
- Nguyen-Thanh, N.; Valizadeh, N.; Nguyen, M.N.; Nguyen-Xuan, H.; Zhuang, X.; Areias, P.; Zih, Y.; Bazilevsg, L.; De Lorenzisa, T.; Rabczuk, T. An extended isogeometric thin shell analysis based on Kirchhoff–Love theory. Comput. Methods Appl. Mech. Eng. 2015, 284, 265–291. [Google Scholar] [CrossRef]
- El Fakkoussi, S.; Moustabchir, H.; Elkhalfi, A.; Pruncu, C.I. Application of the Extended Isogeometric Analysis (X-IGA) to Evaluate a Pipeline Structure Containing an External Crack. J. Eng. 2018, 2018, 4125765. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Nejati, M.; Ghouli, S. The finite element over-deterministic method to calculate the coefficients of crack tip asymptotic fields in anisotropic planes. Eng. Fract. Mech. 2020, 231, 106982. [Google Scholar] [CrossRef]
- Lai, W.; Yu, T.; Bui, T.Q.; Wang, Z.; Curiel-Sosa, J.L.; Das, R.; Hirose, S. 3-D elasto-plastic large deformations: IGA simulation by Bézier extraction of NURBS. Adv. Eng. Softw. 2017, 108, 68–82. [Google Scholar] [CrossRef]
- Montassir, S.; Moustabchir, H.; Elkhalfi, A.; Scutaru, M.L.; Vlase, S. Fracture Modelling of a Cracked Pressurized Cylindrical Structure by Using Extended Iso-Geometric Analysis (X-IGA). Mathematics 2021, 9, 2990. [Google Scholar] [CrossRef]
- Kapoor, H.; Kapania, R.K. Geometrically nonlinear NURBS isogeometric finite element analysis of laminated composite plates. Compos. Struct. 2012, 94, 3434–3447. [Google Scholar] [CrossRef]
- Cotterell, A. Slightly curved or kinked cracks. Int. J. Fract. 1980, 16, 155–169. [Google Scholar] [CrossRef]
- Codarcea-Munteanu, L.; Marin, M.; Vlase, S. The study of vibrations in the context of porous micropolar media thermoelasticity and the absence of energy dissipation. J. Comput. Appl. Mech. 2023, 54, 437–454. [Google Scholar] [CrossRef]
- Kim, J.-H.; Paulino, G.H. T-stress, mixed-mode stress intensity factors, and crack initiation angles in functionally graded materials: A unified approach using the interaction integral method. Comput. Methods Appl. Mech. Eng. 2003, 192, 1463–1494. [Google Scholar] [CrossRef]
- Shah, P.D.; Tan, C.L.; Wang, X. T-stress solutions for two-dimensional crack problems in anisotropic elasticity using the boundary element method. Fatigue Fract. Eng. Mater. Struct. 2006, 29, 343–356. [Google Scholar] [CrossRef]
- Sladek, J.; Sladek, V. Evaluation of the Elastic T-stress in Three-dimensional Crack Problems Using an Integral Formula. Int. J. Fract. 2000, 101, 47–52. [Google Scholar] [CrossRef]
- Wang, X. Elastic T-stress solutions for semi-elliptical surface cracks in finite thickness plates. Eng. Fract. Mech. 2003, 70, 731–756. [Google Scholar] [CrossRef]
- Koubaiti, O.; Elkhalfi, A.; El-Mekkaoui, J.; Mastorakis, N. Solving the problem of constraints due to Dirichlet boundary conditions in the context of the mini element method. Int. J. Mech. 2020, 14, 12–22. [Google Scholar]
- El Ouadefli, L.; El Moutea, O.; El Akkad, A.; Elkhalfi, A.; Vlase, S.; Scutaru, M.L. Mixed Isogeometric Analysis of the Brinkman Equation. Mathematics 2023, 11, 2750. [Google Scholar] [CrossRef]
- El Ouadefli, L.A.; El Akkad, S.A.; El Moutea, O.; Moustabchir, H.; Elkhalfi, A.; Scutaru, L.M.; Muntean, R. Numerical simulation for Brinkman system with varied permeability tensor. Mathematics 2022, 10, 3242. [Google Scholar] [CrossRef]

| ,] | T-Stress [MPa] | |||
|---|---|---|---|---|
| IG-ODM | 1.8884 | --- | −1.1037 | --- |
| Ref. [13] | 1.9252 | 1.911% | −1.1044 | 0.06% |
| Ref. [26] | 1.923 | 1.799% | −1.1116 | 0.64% |
| ,] | T-Stress [MPa] | |||
|---|---|---|---|---|
| IG-ODM | 2.6631 | −0.6129 | --- | |
| Abaqus Contour Integral | 2.657 | 0.2% | −0.6008 | 2% |
| Ref. [13] | 2.6560 | 0.267% | −0.6028 | 1.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yakoubi, K.; Elkhalfi, A.; Moustabchir, H.; El Akkad, A.; Scutaru, M.L.; Vlase, S. An Isogeometric Over-Deterministic Method (IG-ODM) to Determine Elastic Stress Intensity Factor (SIF) and T-Stress. Mathematics 2023, 11, 4293. https://doi.org/10.3390/math11204293
Yakoubi K, Elkhalfi A, Moustabchir H, El Akkad A, Scutaru ML, Vlase S. An Isogeometric Over-Deterministic Method (IG-ODM) to Determine Elastic Stress Intensity Factor (SIF) and T-Stress. Mathematics. 2023; 11(20):4293. https://doi.org/10.3390/math11204293
Chicago/Turabian StyleYakoubi, Khadija, Ahmed Elkhalfi, Hassane Moustabchir, Abdeslam El Akkad, Maria Luminita Scutaru, and Sorin Vlase. 2023. "An Isogeometric Over-Deterministic Method (IG-ODM) to Determine Elastic Stress Intensity Factor (SIF) and T-Stress" Mathematics 11, no. 20: 4293. https://doi.org/10.3390/math11204293
APA StyleYakoubi, K., Elkhalfi, A., Moustabchir, H., El Akkad, A., Scutaru, M. L., & Vlase, S. (2023). An Isogeometric Over-Deterministic Method (IG-ODM) to Determine Elastic Stress Intensity Factor (SIF) and T-Stress. Mathematics, 11(20), 4293. https://doi.org/10.3390/math11204293








