Adaptive Sliding Mode Attitude Tracking Control for Rigid Spacecraft Considering the Unwinding Problem
Abstract
:1. Introduction
2. Attitude Tracking Control Problem Formulation of Spacecraft
2.1. Attitude Kinematics and Dynamics for a Rigid Spacecraft
2.2. Attitude Error Kinematics and Dynamics for a Rigid Spacecraft
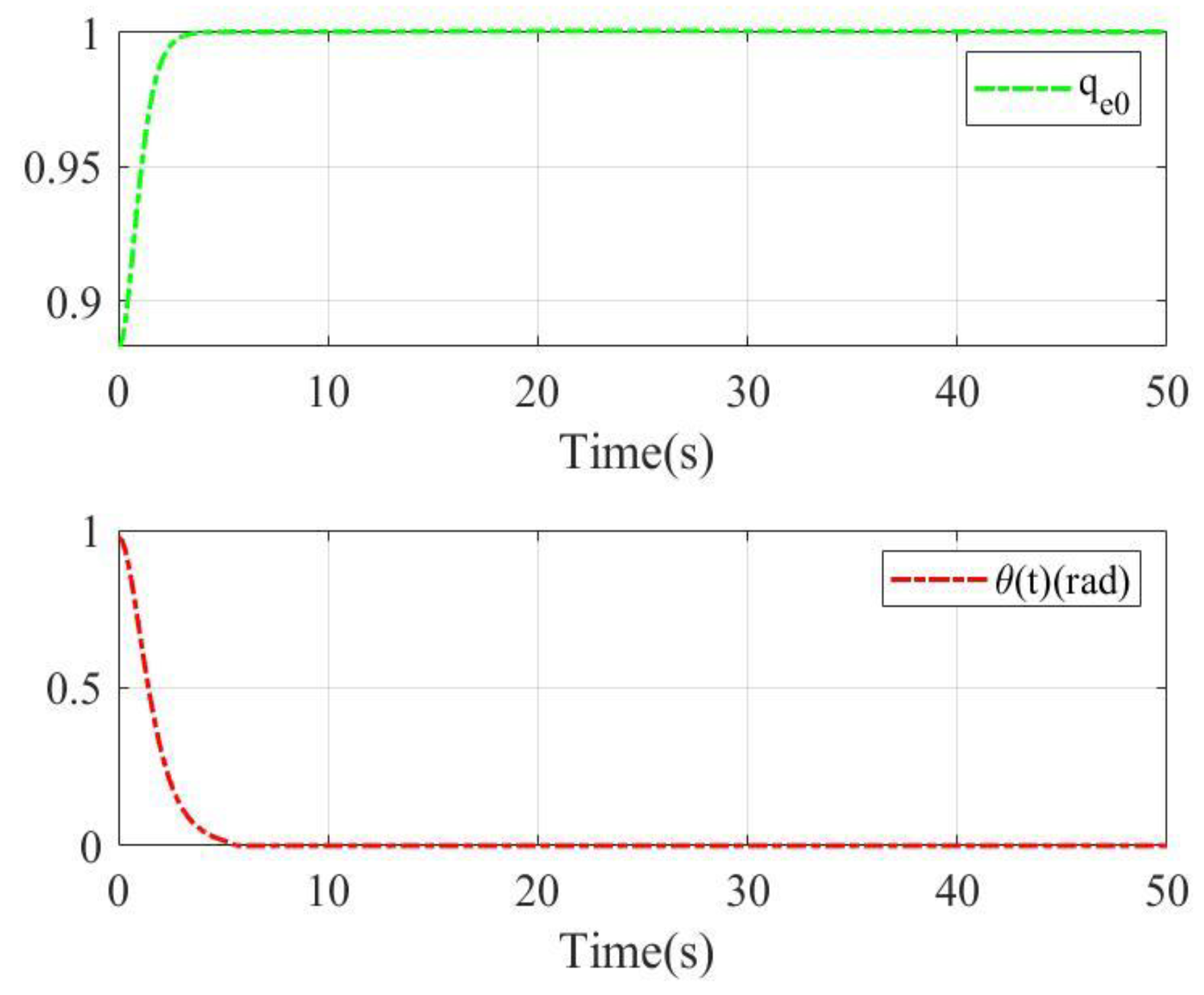
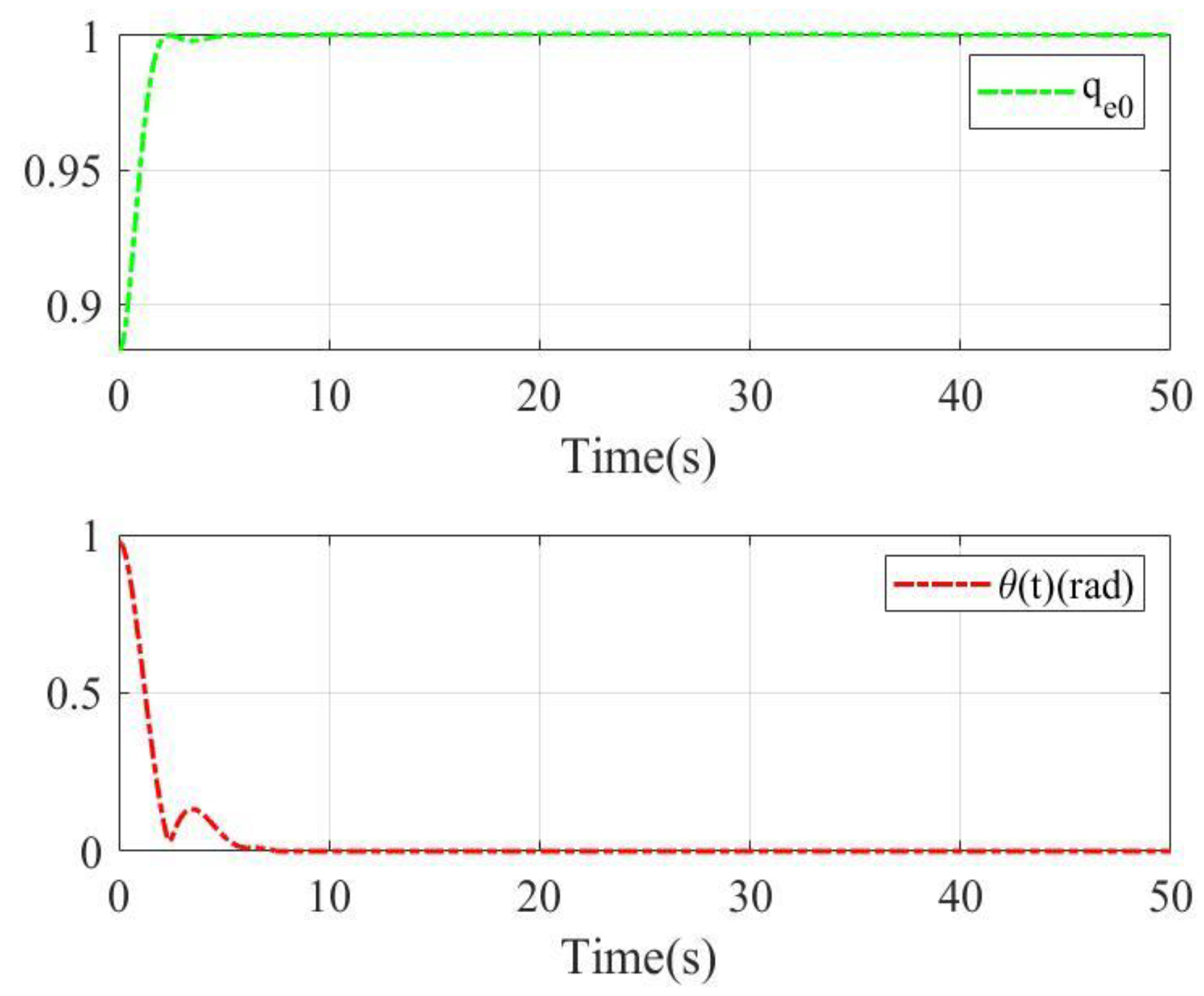
2.3. The Unwinding Phenomenon
2.4. Control Objective
3. Controller Design
3.1. Sliding Mode Surface Design
3.2. Anti-Unwinding Adaptive Sliding Mode Attitude Tracking Control Law Design and Convergence Analysis
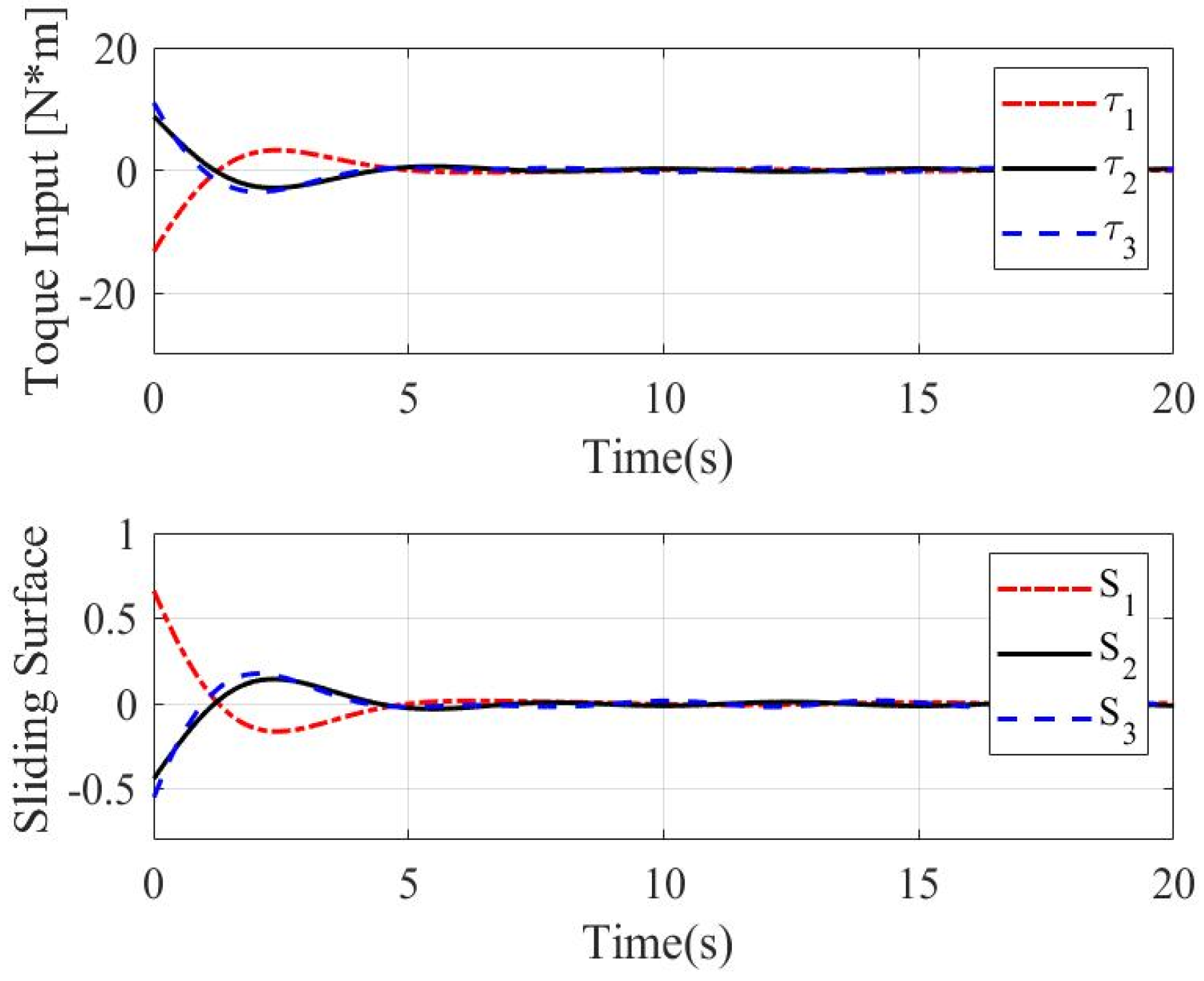
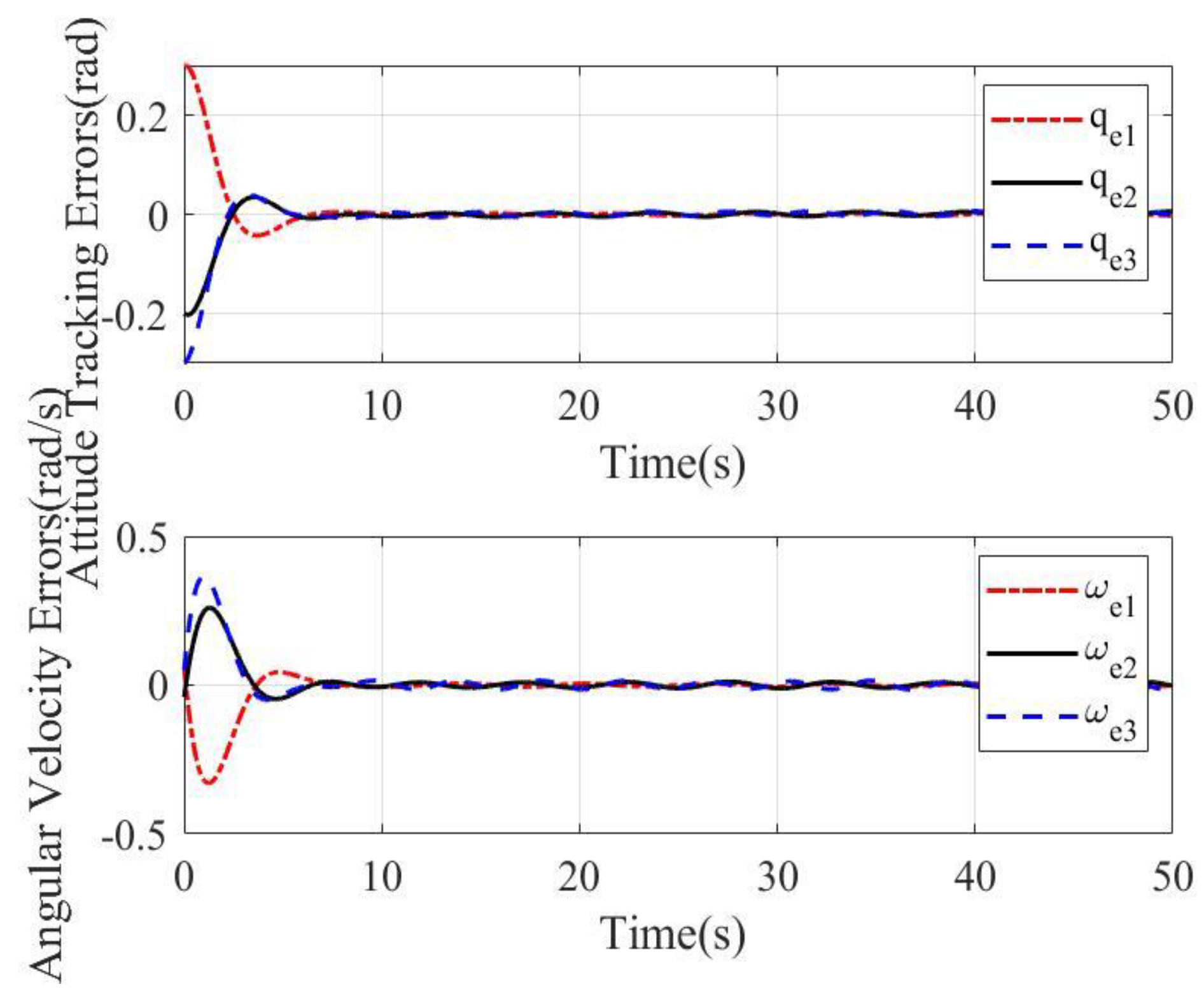
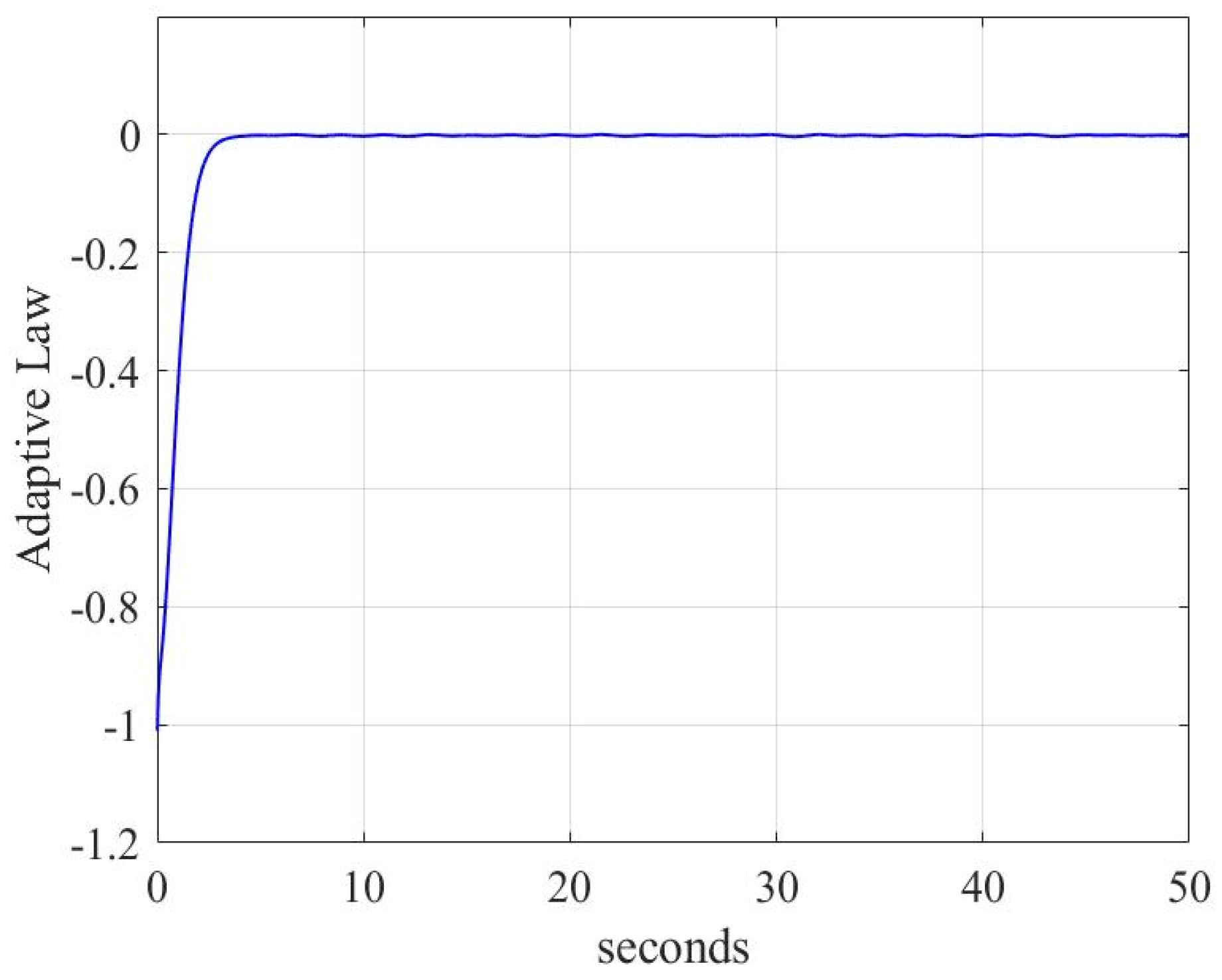
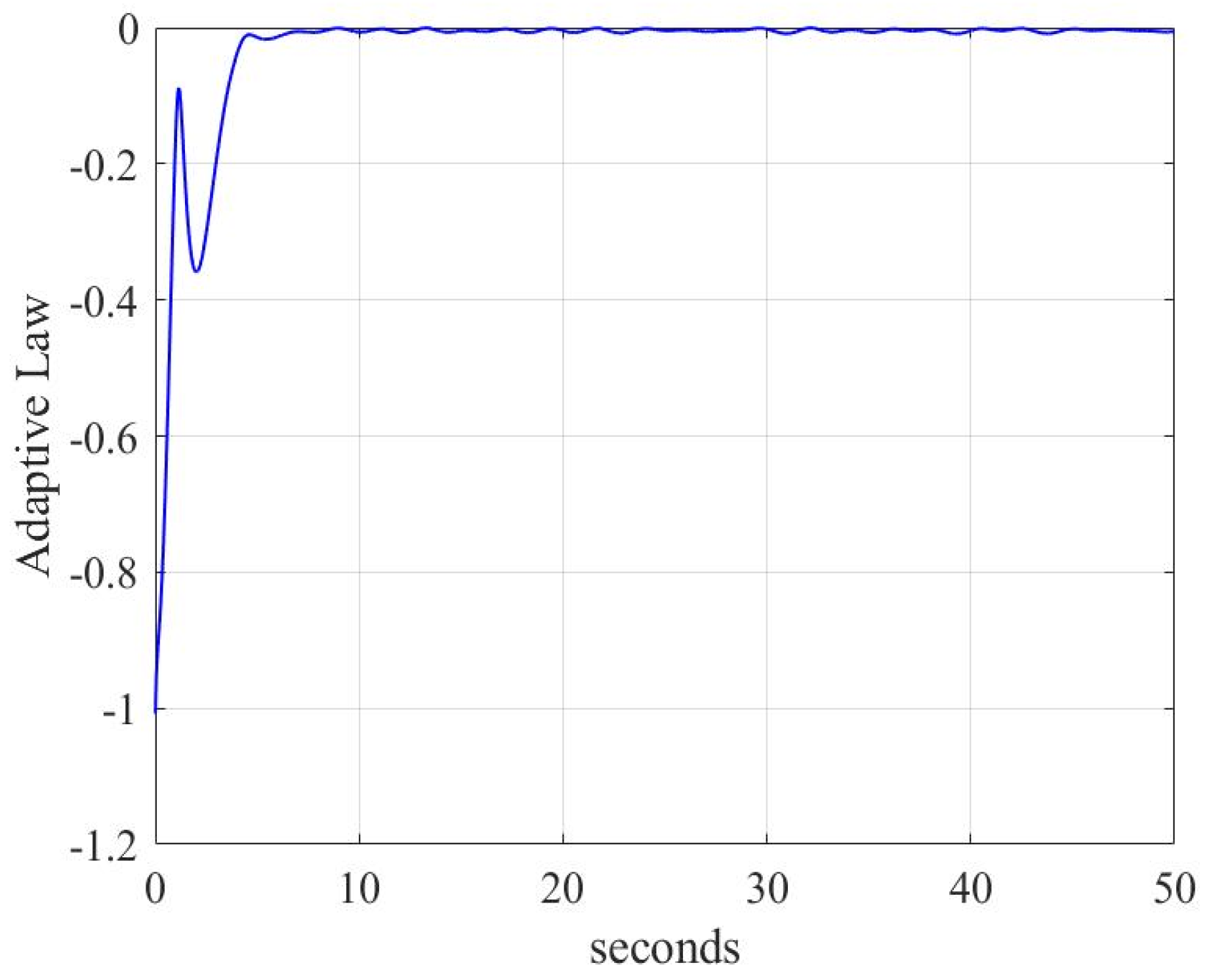
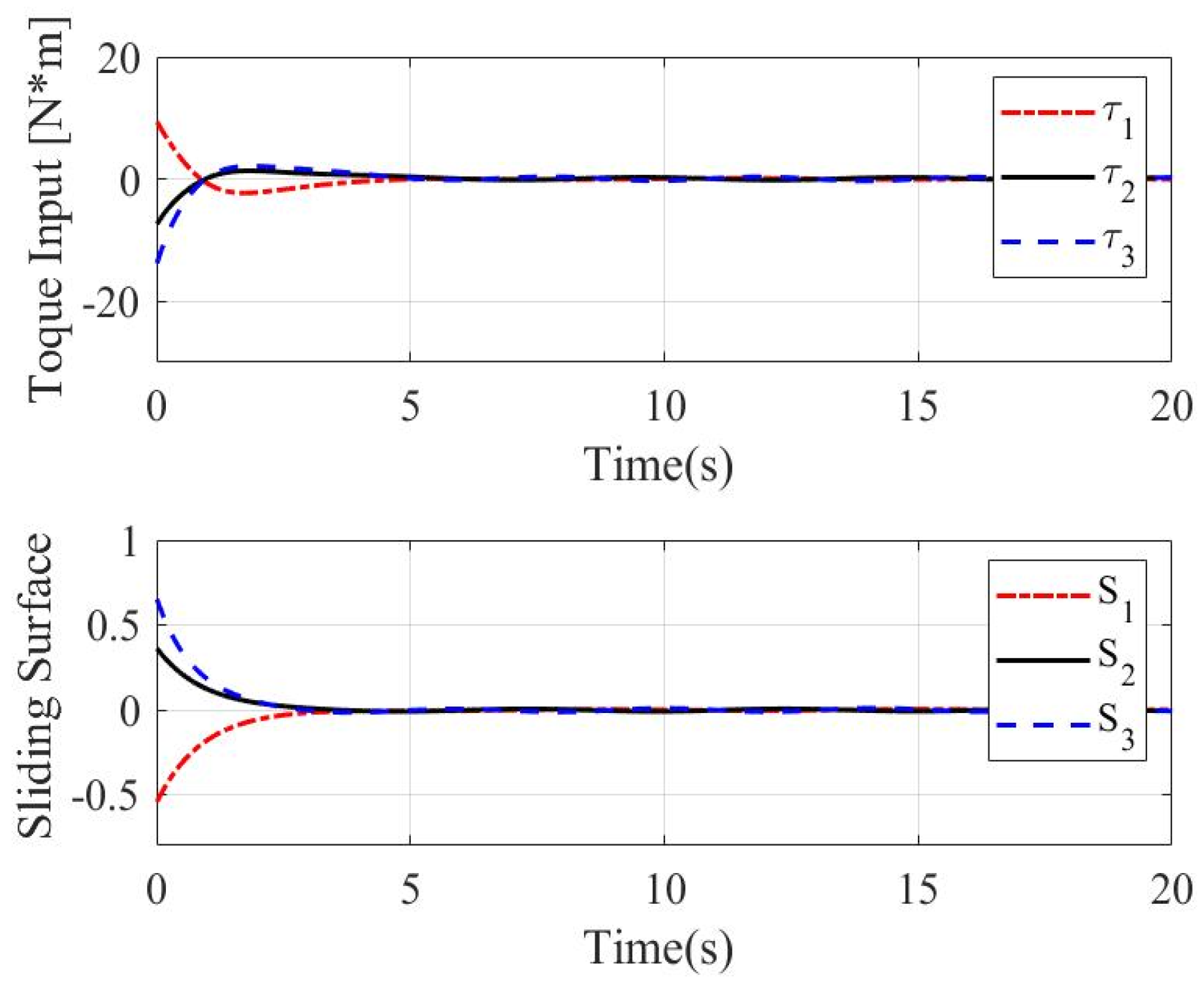
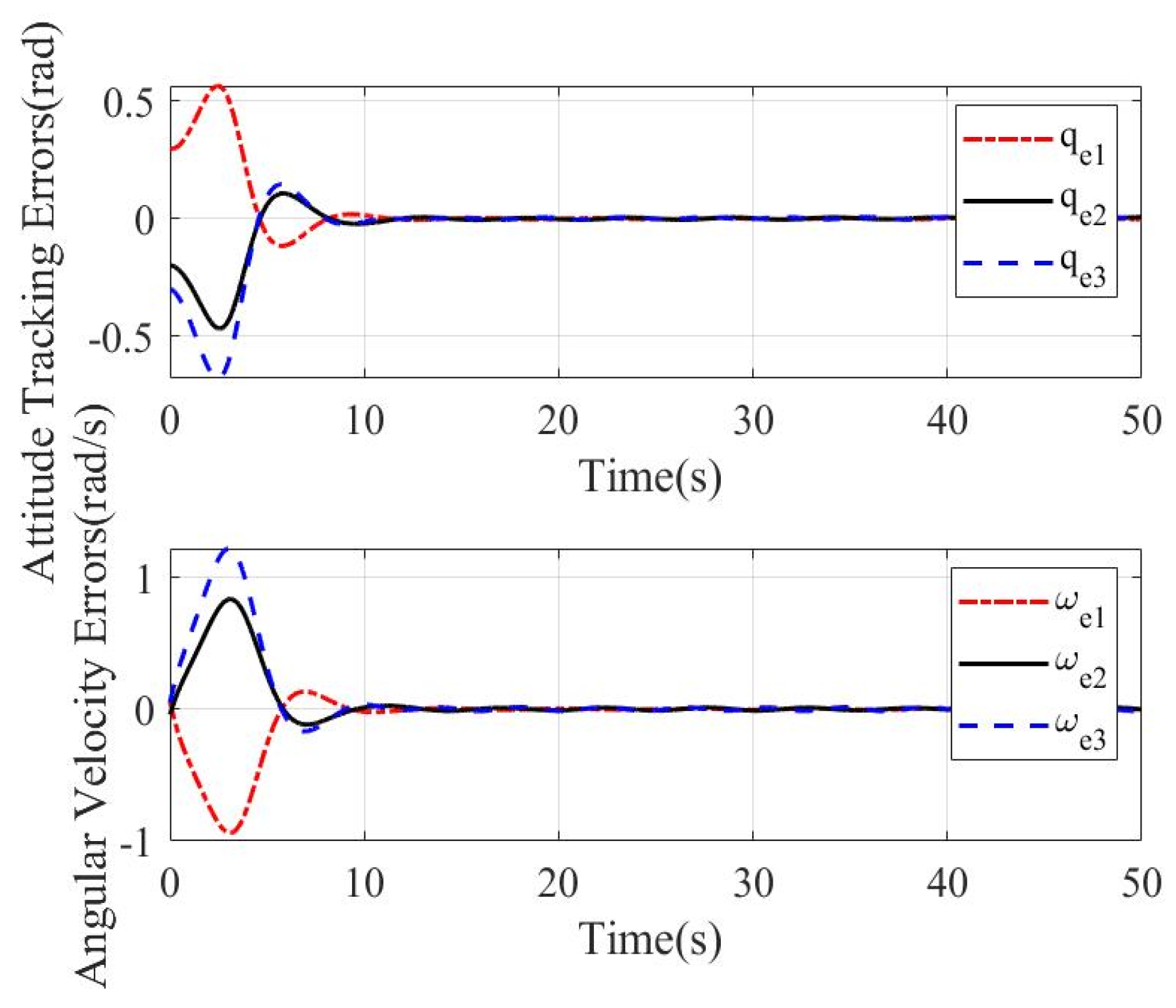
4. Simulation Results
4.1. Case 1
4.2. Case 2
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, C.; Ye, D.; Shi, K.; Sun, Z. Robust high-precision attitude control for flexible spacecraft with improved mixed H2/H∞ control strategy under poles assignment constraint. Acta Astronaut. 2017, 136, 166–175. [Google Scholar] [CrossRef]
- Sun, L.; Huo, W.; Jiao, Z. Adaptive backstepping control of spacecraft rendezvous and proximity operations with input saturation and full-state constraint. IEEE Tran. Ind. Electron. 2017, 64, 480–492. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, J. Attitude tracking and disturbance rejection of rigid spacecraft by adaptive control. IEEE Trans. Autom. Control 2009, 54, 600–605. [Google Scholar] [CrossRef]
- Gao, Z.; Han, B.; Qian, M.; Lin, J. Active fault tolerant control for flexible spacecraft with sensor faults based on adaptive integral sliding mode. J. Nanjing Inst. Meteorol. 2018, 10, 146–152. [Google Scholar]
- Li, Q.; Yuan, J.; Wang, H. Sliding mode control for autonomous spacecraft rendezvous with collision avoidance. Acta Astronaut. 2018, 151, 743–751. [Google Scholar] [CrossRef]
- Sun, L.; Huo, W.; Jiao, Z. Disturbance observer-based robust relative pose control for spacecraft rendezvous and proximity operations under input saturation. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1605–1617. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; Wang, L. Disturbance observer based attitude control for flexible spacecraft with input magnitude and rate constraints. Aerosp. Sci. Technol. 2018, 72, 486–492. [Google Scholar] [CrossRef]
- Xia, K.; Huo, W. Disturbance observer based fault-tolerant control for cooperative spacecraft rendezvous and docking with input saturation. Nonlinear Dyn. 2017, 88, 2735–2745. [Google Scholar] [CrossRef]
- Cai, W.C.; Liao, X.H.; Song, Y.D. Indirect robust adaptive fault-tolerant control for attitude tracking of spacecraft. J. Guid. Control. Dyn. 2008, 31, 1456–1463. [Google Scholar] [CrossRef]
- Hu, Q.L.; Ma, G.F. Control of three-axis stabilized flexible spacecraft using variable structure strategies subject to input nonlinearities. J. Vib. Control 2006, 12, 659–681. [Google Scholar] [CrossRef]
- Huo, B.Y.; Xia, Y.Q.; Yin, L.J.; Fu, M.Y. Fuzzy Adaptive Fault-Tolerant Output Feedback Attitude-Tracking Control of Rigid Spacecraft. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 8. [Google Scholar] [CrossRef]
- Lu, K.F.; Xia, Y.Q. Adaptive attitude tracking control for rigid spacecraft with finite-time convergence. Automatica 2013, 49, 3591–3599. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Han, F. On nonsingular terminal sliding-mode control of nonlinear systems. Automatica 2013, 49, 1715–1722. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S.; Ren, H. Finite time fault tolerant control for robot manipulators using time delay estimation and continuous nonsingular fast terminal sliding mode control. IEEE Trans. Cybern. 2017, 47, 1681–1693. [Google Scholar] [CrossRef] [PubMed]
- Bhat, S.P.; Bernstein, D.S. A topological obstruction to continuous global stabilization of rotational motion and the unwinding phenomenon. Syst. Control Lett. 2000, 39, 63–70. [Google Scholar] [CrossRef]
- Xia, Y.Q.; Fu, M.Y. Compound Control Methodology for Flight Vehicles; Springer: Berlin, Germany, 2013. [Google Scholar]
- Huo, B.Y.; Xia, Y.Q.; Lu, K.; Fu, M.Y. Adaptive fuzzy finite-time fault-tolerant attitude control of rigid spacecraft. J. Frankl. Inst.-Eng. Appl. Math. 2015, 352, 4225–4246. [Google Scholar] [CrossRef]
- Lee, D. Fault-tolerant finite-time controller for attitude tracking of rigid spacecraft using intermediate quaternion. IEEE Trans. Aerosp. Electron. Syst. 2020, 57, 540–553. [Google Scholar] [CrossRef]
- Hu, Q.L.; Li, L. Anti-unwinding attitude control of spacecraft considering input saturation and angular velocity constraint. Actaeronautica Astronaut. Sin. 2015, 36, 1259–1266. [Google Scholar]
- Kristiansen, R.; Nicklasson, P.; Gravdahl, J. Satellite attitude control by quaternion-based backstepping. IEEE Trans. Control Syst. Technol. 2009, 17, 227–232. [Google Scholar] [CrossRef]
- Dong, R.Q.; Wu, A.G.; Zhang, Y. Anti-unwinding sliding mode attitude maneuver control for rigid spacecraft. IEEE Trans. Autom. Control 2022, 67, 978–985. [Google Scholar] [CrossRef]
- Chen, Y.P.; Lo, S.C. Sliding-mode controller design for spacecraft attitude tracking maneuvers. IEEE Trans. Aerosp. Electron. Syst. 1993, 29, 1328–1333. [Google Scholar] [CrossRef]
- Quoc, V.T.; Brian, D.O.A.; Hyo, S.A. Pose localization of leader–follower networks with direction measurements. Automatica 2020, 120, 109125. [Google Scholar]
- Mouaad, B.; Abdelhamid, T. Bearing-Based Distributed Pose Estimation for Multi-Agent Networks. IEEE Control. Syst. Lett. 2023, 7, 2617–2622. [Google Scholar]
- Shuster, M.D. A survey of attitude representations. Navigation 1993, 8, 439–517. [Google Scholar]
- Zhu, Z.; Xia, Y.Q.; Fu, M.Y. Adaptive sliding mode control for attitude stabilization with actuator saturation. IEEE Trans. Industr. Electron. 2011, 58, 4898–4907. [Google Scholar] [CrossRef]
- Liao, Y.; Yang, Y.J.; Wen, Y.L. Deformation Module Spaceeraft Attitude Control Techniques; National Defense Industry Press: Beijing, China, 2020. [Google Scholar]
- Khalil, H. Nonlinear Systems; Prentice-Hall Press: Englewood Cliffs, NJ, USA, 2002. [Google Scholar]
- Xiao, B.; Hu, Q.L.; Zhang, Y.; Huo, X. Fault-tolerant tracking control of spacecraft with attitude-only measurement under actuator failures. J. Guid. Control Dyn. 2014, 37, 838–849. [Google Scholar] [CrossRef]
- Xu, B.; Huang, X.; Wang, D.; Sun, F. Dynamic surface control of constrained hypersonic flight models with parameter estimation and actuator compensation. Asian J. Control 2014, 16, 162–174. [Google Scholar] [CrossRef]
- Lu, K.F.; Xia, Y.Q.; Fu, M.Y. Controller design for rigid spacecraft attitude tracking with actuator saturation. Inf. Sci. 2013, 220, 343–366. [Google Scholar] [CrossRef]




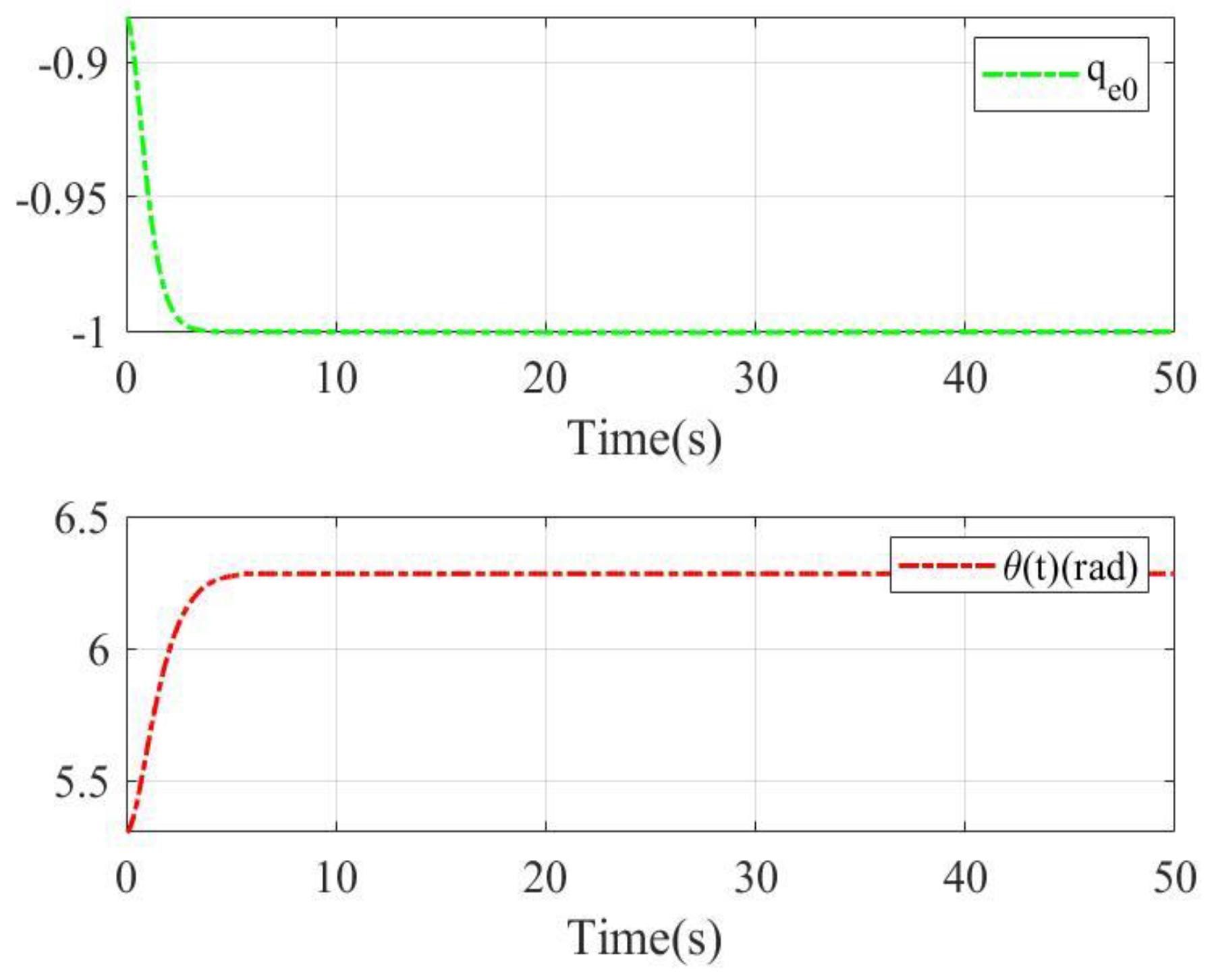

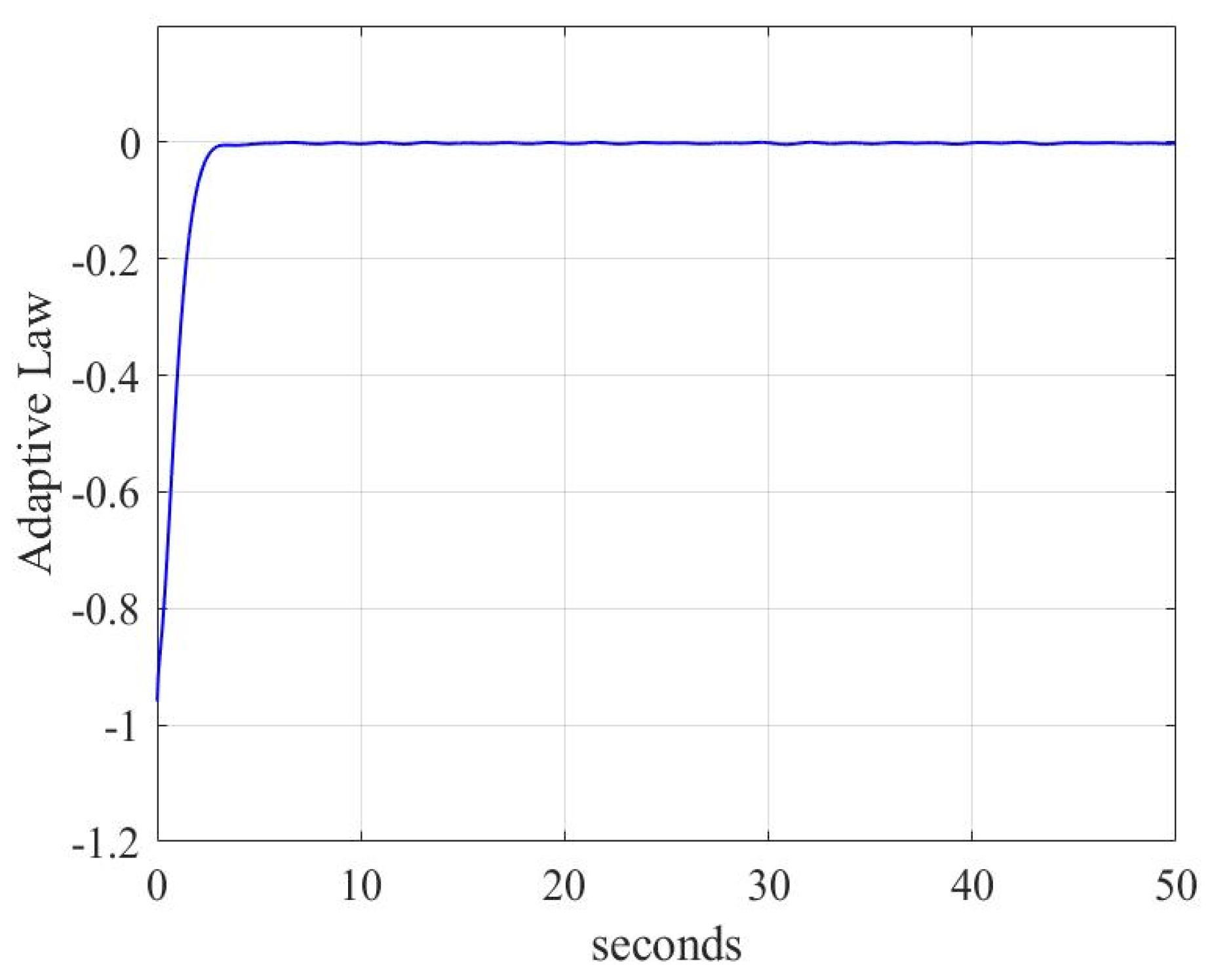

| Variables | Values |
|---|---|
0 |
| Variables | Values |
|---|---|
| 2 | |
| 0.1 | |
| 20 | |
| 0.01 | |
| 100 |
| Case | |
|---|---|
| 1 | |
| 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huo, B.; Du, M.; Yan, Z. Adaptive Sliding Mode Attitude Tracking Control for Rigid Spacecraft Considering the Unwinding Problem. Mathematics 2023, 11, 4372. https://doi.org/10.3390/math11204372
Huo B, Du M, Yan Z. Adaptive Sliding Mode Attitude Tracking Control for Rigid Spacecraft Considering the Unwinding Problem. Mathematics. 2023; 11(20):4372. https://doi.org/10.3390/math11204372
Chicago/Turabian StyleHuo, Baoyu, Mingjun Du, and Zhiguo Yan. 2023. "Adaptive Sliding Mode Attitude Tracking Control for Rigid Spacecraft Considering the Unwinding Problem" Mathematics 11, no. 20: 4372. https://doi.org/10.3390/math11204372
APA StyleHuo, B., Du, M., & Yan, Z. (2023). Adaptive Sliding Mode Attitude Tracking Control for Rigid Spacecraft Considering the Unwinding Problem. Mathematics, 11(20), 4372. https://doi.org/10.3390/math11204372






