Fully Nonlinear Evolution of Free-Surface Waves with Constant Vorticity under Horizontal Electric Fields
Abstract
:1. Introduction
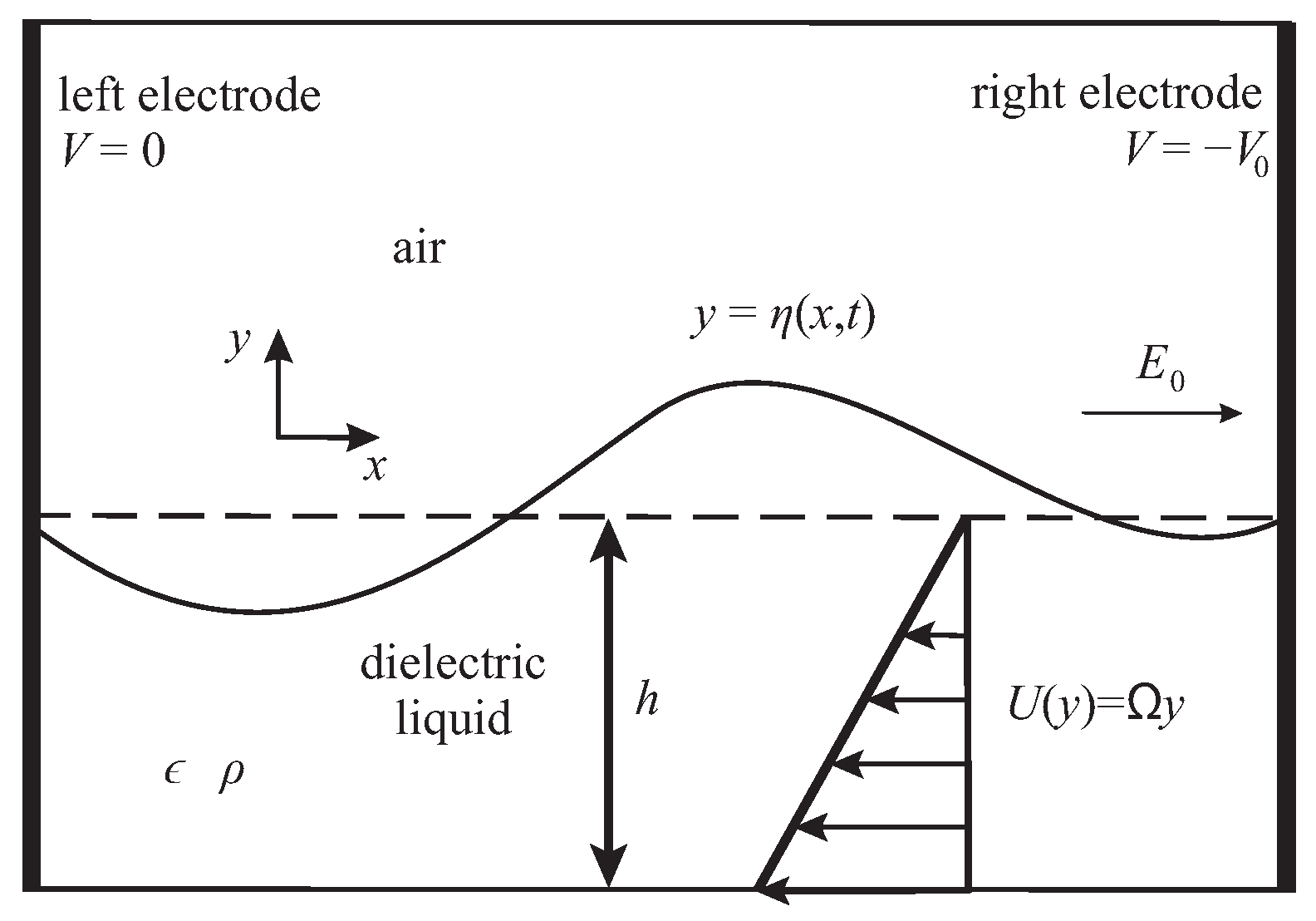
2. Mathematical Formulation
2.1. Dynamic Equations
2.2. Equations in Conformal Variables
3. Results
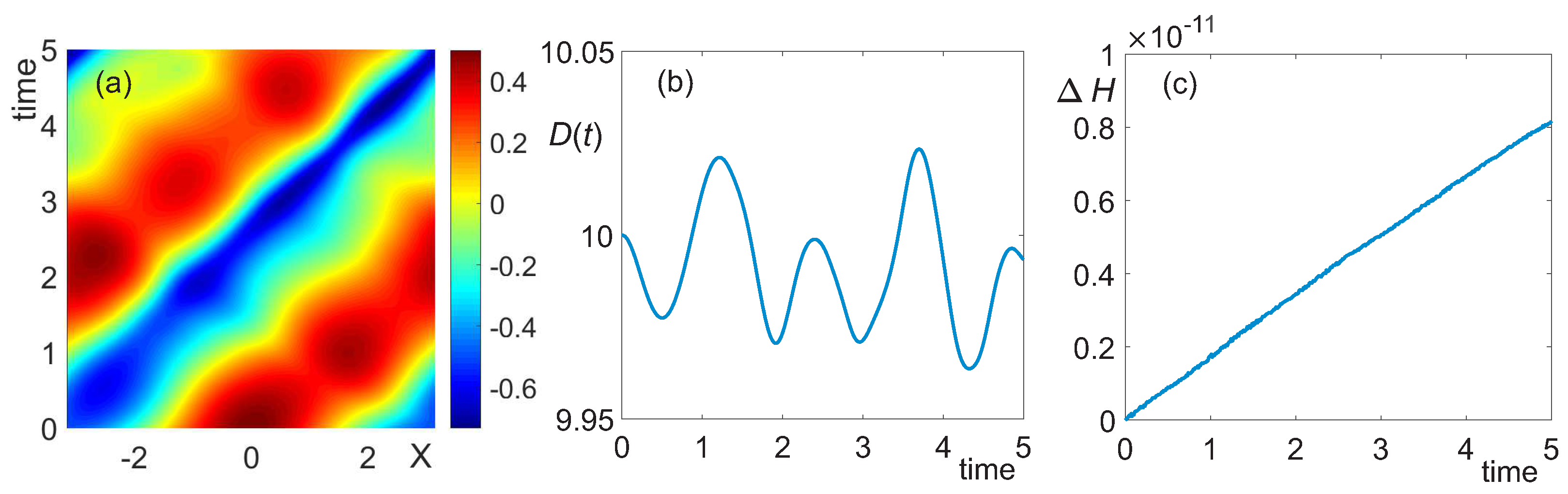
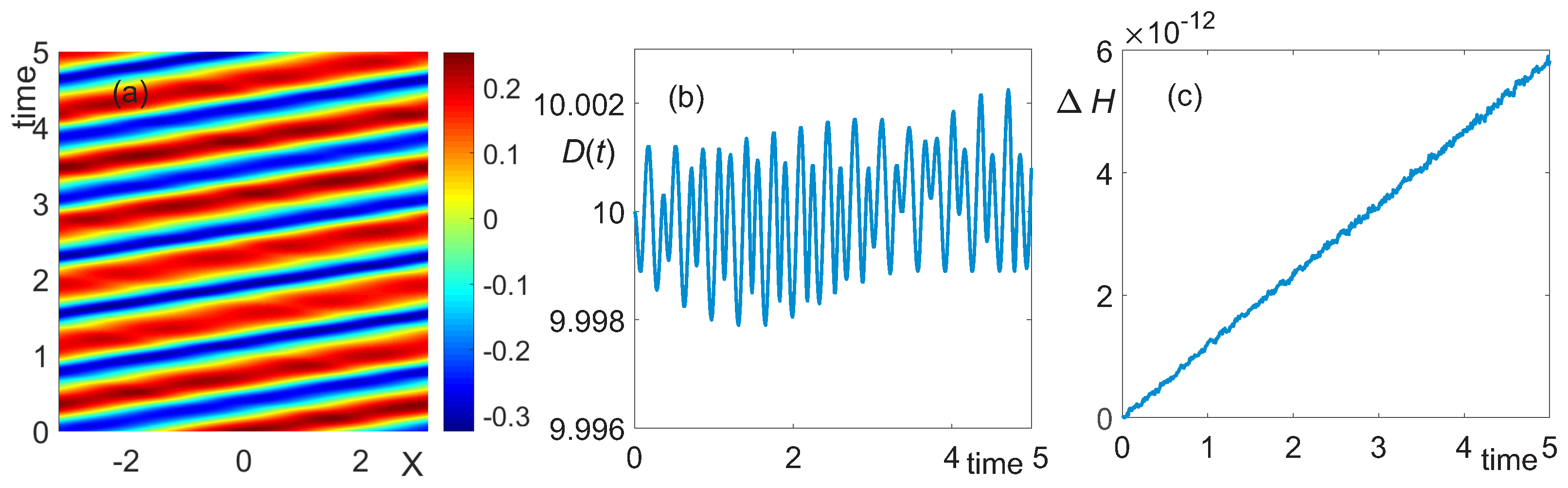
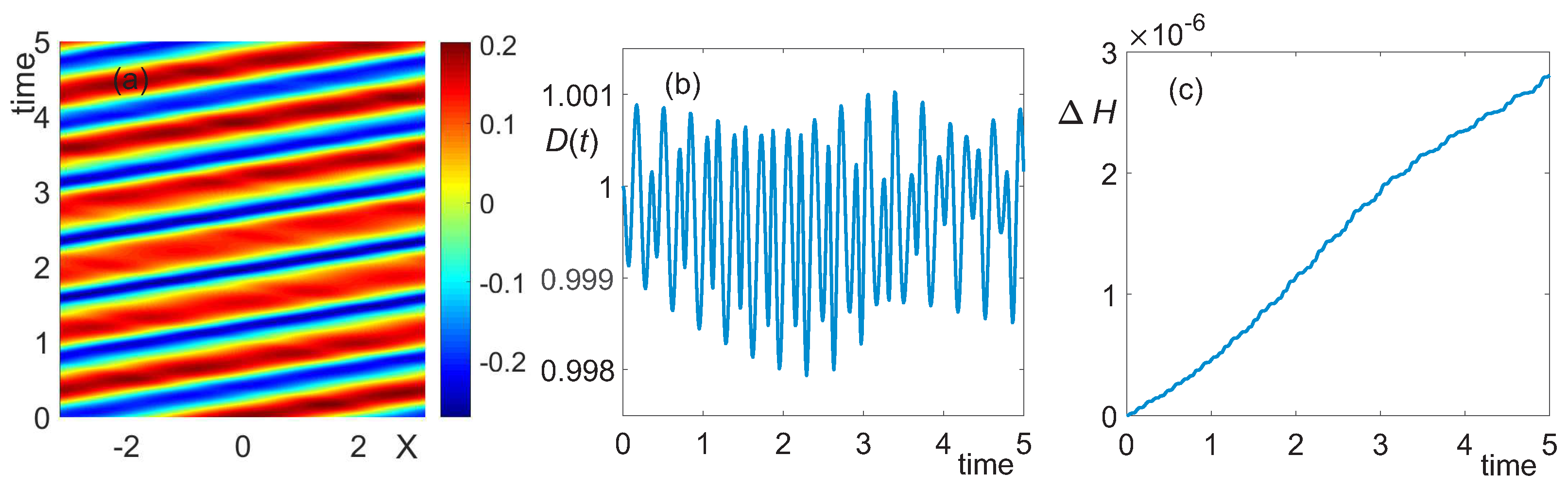
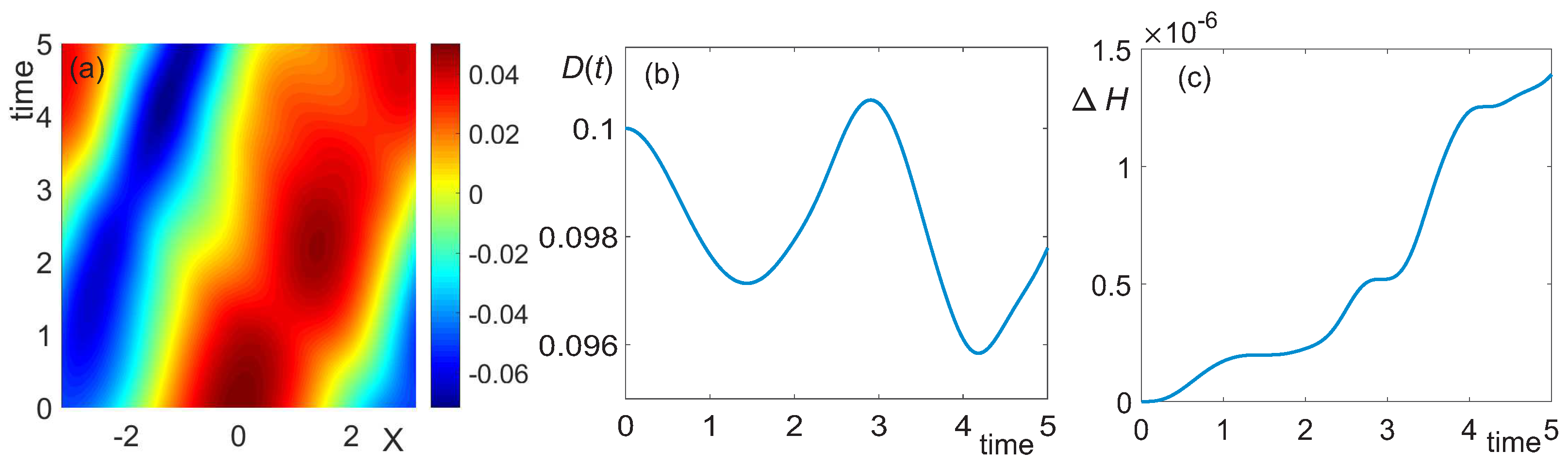
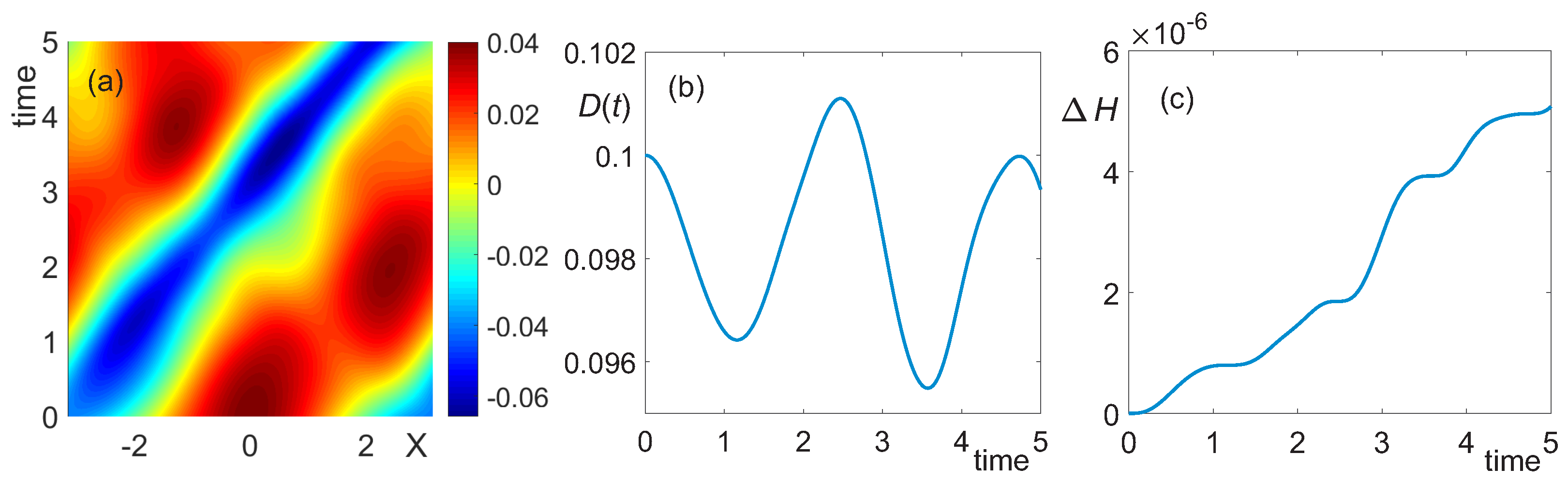
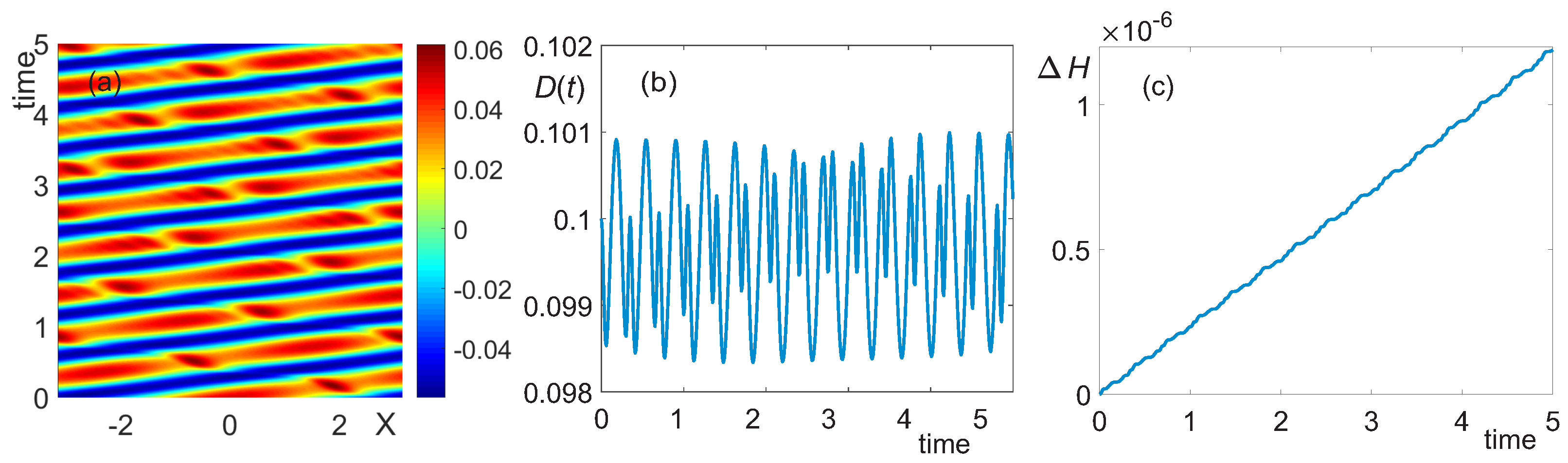
3.1. Deep Water, h = 10
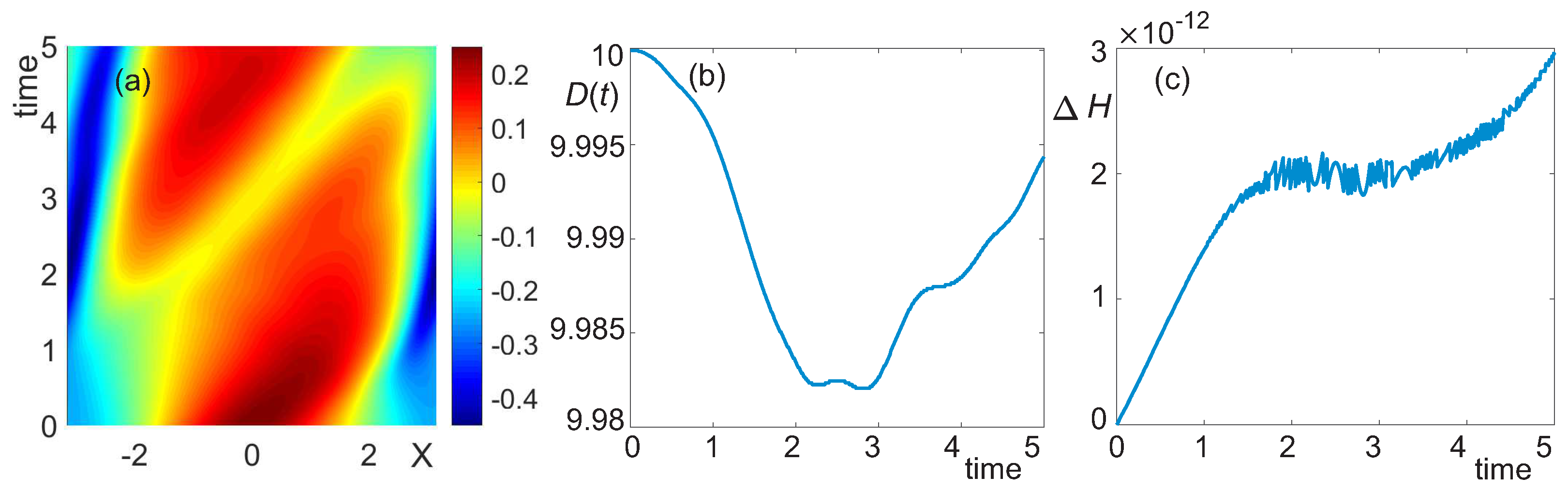
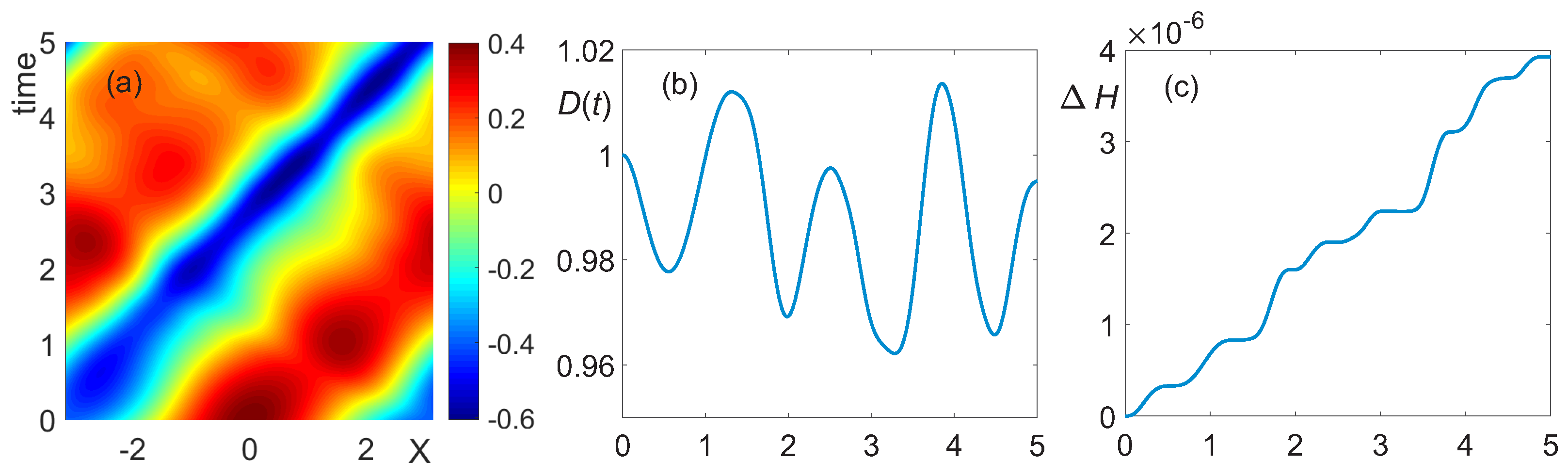
3.2. Intermediate Depth,
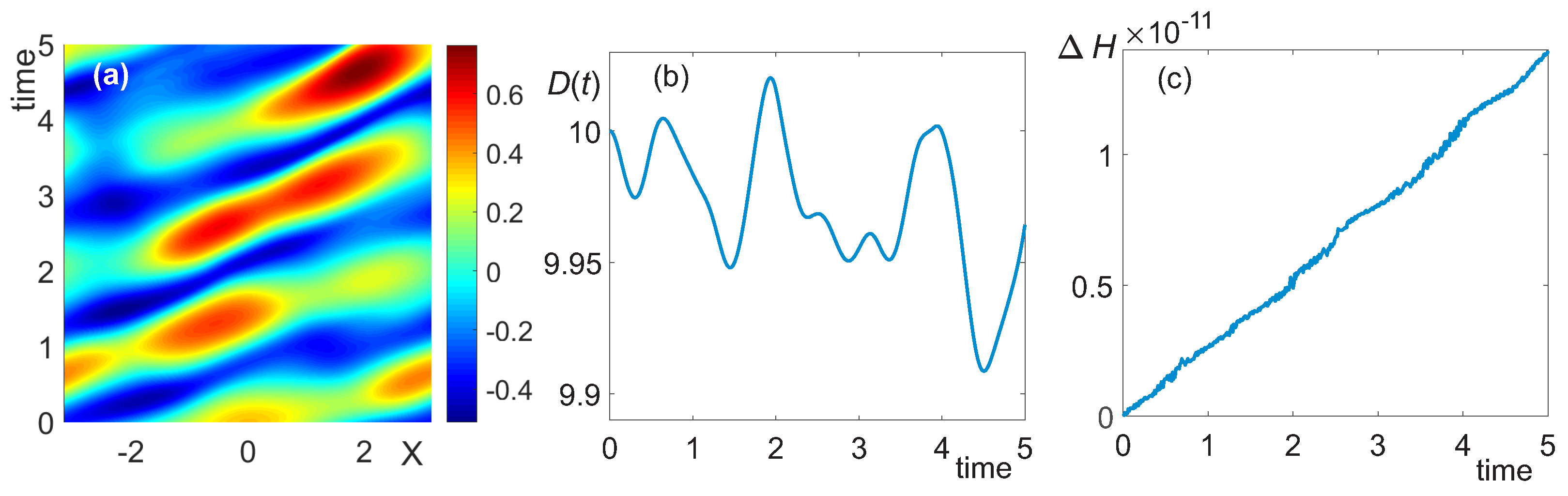
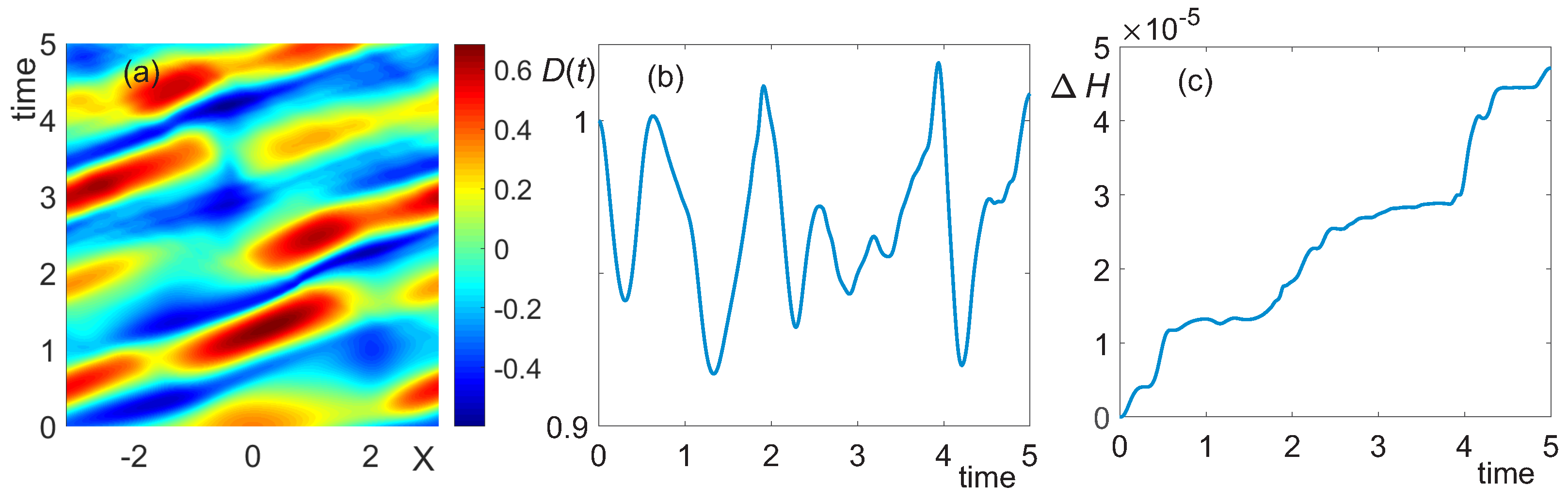
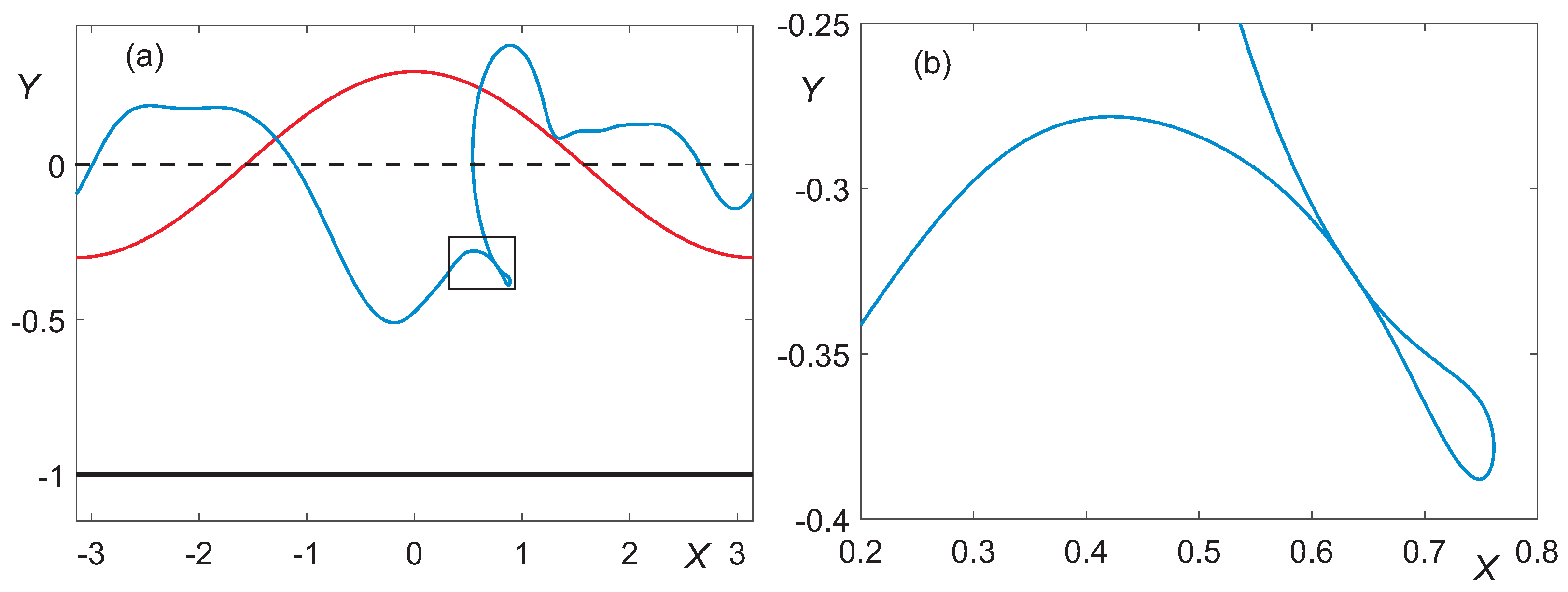
3.3. Shallow Water,
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Papageorgiou, D.T. Film flows in the presence of electric fields. Annu. Rev. Fluid Mech. 2019, 51, 155–187. [Google Scholar] [CrossRef]
- Melcher, J.R. Electrohydrodynamic and magnetohydrodynamic surface waves and instabilities. Phys. Fluids 1961, 4, 1348. [Google Scholar] [CrossRef]
- Guo, W.; Zhang, Q.; He, D. On the nonlinear behaviour of the Rayleigh–Taylor instability with a tangential electric field for inviscid and perfect dielectric fluids. J. Fluid Mech. 2023, 958, A36. [Google Scholar] [CrossRef]
- Deng, X.D.; Wang, P.; Shi, B.L.; Fu, Q.F.; Jia, B.Q. Temporal instability of a viscous liquid film on an oscillating plane in the presence of static electric field. AIP Adv. 2023, 13, 045019. [Google Scholar] [CrossRef]
- Zhilenko, D.Y.; Krivonosova, O.E. Suppression of the instability of rotating flows. Tech. Phys. Lett. 2022, 48, 156–160. [Google Scholar] [CrossRef]
- Li, D.; Li, Y.; Li, Z.; Wang, Y. Theory analyses and applications of magnetic fluids in sealing. Friction 2023, 11, 1771–1793. [Google Scholar] [CrossRef]
- Zubarev, N.M. Nonlinear waves on the surface of a dielectric liquid in a strong tangential electric field. Phys. Lett. A 2004, 333, 284–288. [Google Scholar] [CrossRef]
- Zubarev, N.M. Nonlinear waves on the surface of a dielectric liquid in a horizontal electric field in 3D geometry: Exact solutions. JETP Lett. 2009, 89, 271–274. [Google Scholar] [CrossRef]
- Zubarev, N.M. Formation of root singularities on the free surface of a conducting fluid in an electric field. Phys. Lett. A 1998, 243, 128–131. [Google Scholar] [CrossRef]
- Zubarev, N.M. Exact solutions of the equations of motion of liquid helium with a charged free surface. J. Exp. Theor. Phys. 2002, 94, 534–554. [Google Scholar] [CrossRef]
- Galtier, S. Turbulence in space plasmas and beyond. J. Phys. A Math. Theor. 2018, 51, 293001. [Google Scholar] [CrossRef]
- Boyer, F.; Falcon, E. Wave turbulence on the surface of a ferrofluid in a magnetic field. Phys. Rev. Lett. 2008, 101, 244502. [Google Scholar] [CrossRef]
- Dorbolo, S.; Falcon, E. Wave turbulence on the surface of a ferrofluid in a horizontal magnetic field. Phys. Rev. E 2011, 83, 046303. [Google Scholar] [CrossRef]
- Ricard, G.; Falcon, E. Transition from wave turbulence to acousticlike shock-wave regime. Phys. Rev. Fluids 2023, 8, 014804. [Google Scholar] [CrossRef]
- Kochurin, E.A. Wave turbulence of a liquid surface in an external tangential electric field. JETP Lett. 2019, 109, 303–308. [Google Scholar] [CrossRef]
- Kochurin, E.; Ricard, G.; Zubarev, N.; Falcon, E. Three-dimensional direct numerical simulation of free-surface magnetohydrodynamic wave turbulence. Phys. Rev. E 2022, 105, L063101. [Google Scholar] [CrossRef] [PubMed]
- Dmitriev, I.A.; Kochurin, E.A.; Zubarev, N.M. Numerical study of free-surface electro-hydrodynamic wave turbulence. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 1408–1413. [Google Scholar] [CrossRef]
- Crapper, G.D. An exact solution for progressive capillary waves of arbitrary amplitude. J. Fluid Mech. 1957, 2, 532–540. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. The instabilities of gravity waves of finite amplitude in deep water I. Superharmonics. Proc. R. Soc. Lond. 1978, 360, 471–488. [Google Scholar] [CrossRef]
- Tiron, R.; Choi, W. Linear stability of finite-amplitude capillary waves on water of infinite depth. J. Fluid Mech. 2012, 696, 402–422. [Google Scholar] [CrossRef]
- Vanden-Broeck, J.-M. New families of steep solitary in water of finite depth with constant vorticity. Eur. J. Mech. B Fluids 1995, 14, 761–774. [Google Scholar]
- Choi, W. Nonlinear surface waves interacting with a linear shear current. Math. Comput. Simul. 2009, 80, 29–36. [Google Scholar] [CrossRef]
- Gao, T.; Milewski, P.A.; Wang, Z. Capillary-gravity solitary waves on water of finite depth interacting with a linear shear current. Stud. Appl. Math. 2021, 147, 1036–1057. [Google Scholar] [CrossRef]
- Murashige, S.; Choi, W. Parasitic Capillary Waves on Small-Amplitude Gravity Waves with a Linear Shear Current. J. Mar. Sci. Eng. 2021, 9, 1217. [Google Scholar] [CrossRef]
- Hur, V.M.; Wheeler, M.H. Exact free surfaces in constant vorticity flows. J. Fluid Mech. 2020, 896, R1. [Google Scholar] [CrossRef]
- Lokharu, E. On the amplitude and the flow force constant of steady water waves. J. Fluid Mech. 2021, 921, A2. [Google Scholar] [CrossRef]
- Lokharu, E.; Wahlèn, E.; Weber, J. On the Amplitude of Steady Water Waves with Favorable Constant Vorticity. J. Math. Fluid. Mech. 2023, 25, 58. [Google Scholar] [CrossRef]
- Hunt, M.J.; Dutykh, D. Free surface flows in electrohydrodynamics with a constant vorticity distribution. Water Waves 2021, 3, 297–317. [Google Scholar] [CrossRef]
- Flamarion, M.V.; Gao, T.; Ribeiro-Jr, R.; Doak, A. Flow structure beneath periodic waves with constant vorticity under normal electric fields. Phys. Fluids 2022, 34, 127119. [Google Scholar] [CrossRef]
- Ovsjannikov, L.V. To the shallow water theory foundation. Arch. Mech. 1974, 26, 6. [Google Scholar]
- Dyachenko, A.I.; Kuznetsov, E.A.; Spector, M.; Zakharov, V.E. Analytical description of the free surface dynamics of an ideal fluid (canonical formalism and conformal mapping). Phys. Lett. A 1996, 221, 736. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Dyachenko, A.I.; Vasilyev, O.A. New method for numerical simulation of a nonstationary potential flow of incompressible fluid with a free surface. Eur. J. Mech. B Fluids 2002, 21, 283. [Google Scholar] [CrossRef]
- Ruban, V.P. Waves over curved bottom: The method of composite conformal mapping. J. Exp. Theor. Phys. 2020, 130, 797–808. [Google Scholar] [CrossRef]
- Ruban, V.P. Water waves over a time-dependent bottom: Exact description for 2D potential flows. Phys. Lett. A 2005, 340, 194–200. [Google Scholar] [CrossRef]
- Korotkevich, A.O.; Prokofiev, A.; Zakharov, V.E. On the dissipation rate of ocean waves due to white capping. JETP Lett. 2019, 109, 309–315. [Google Scholar] [CrossRef]
- Dyachenko, S.; Newell, A.C. Whitecapping. Stud. Appl. Math. 2016, 137, 199–213. [Google Scholar] [CrossRef]
- Nachbin, A. Water wave models using conformal coordinates. Physica D 2023, 445, 133646. [Google Scholar] [CrossRef]
- Dyachenko, S.A.; Semenova, A. Canonical conformal variables based method for stability of Stokes waves. Stud. Appl. Math. 2023, 150, 705–715. [Google Scholar] [CrossRef]
- Kochurin, E.A. Formation of regions with high energy and pressure gradients at the free surface of liquid dielectric in a tangential electric field. J. Appl. Mech. Tech. Phys. 2018, 59, 79–85. [Google Scholar] [CrossRef]
- Gao, T.; Milewski, P.A.; Papageorgiou, D.T.; Vanden-Broeck, J.M. Dynamics of fully nonlinear capillary–gravity solitary waves under normal electric fields. J. Eng. Math. 2018, 108, 107–122. [Google Scholar] [CrossRef]
- Gao, T.; Doak, A.; Vanden-Broeck, J.M.; Wang, Z. Capillary–gravity waves on a dielectric fluid of finite depth under normal electric field. Eur. J. Mech. B Fluids 2019, 77, 98–107. [Google Scholar] [CrossRef]
- Gao, T.; Wang, Z.; Vanden-Broeck, J.M. Nonlinear wave interactions on the surface of a conducting fluid under vertical electric fields. Phyica D 2023, 446, 133651. [Google Scholar] [CrossRef]
- Doak, A.; Gao, T.; Vanden-Broeck, J.M. Global bifurcation of capillary-gravity dark solitary waves on the surface of a conducting fluid under normal electric fields. Q. J. Mech. Appl. Math. 2022, 75, 215–234. [Google Scholar] [CrossRef]
- Kochurin, E.; Ricard, G.; Zubarev, N.; Falcon, E. Numerical simulation of collinear capillary-wave turbulence. JETP Lett. 2020, 112, 757–763. [Google Scholar] [CrossRef]
- Ricard, G.; Falcon, E. Experimental quasi-1D capillary-wave turbulence. Europhys. Lett. 2021, 135, 64001. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flamarion, M.V.; Kochurin, E.; Ribeiro-Jr, R. Fully Nonlinear Evolution of Free-Surface Waves with Constant Vorticity under Horizontal Electric Fields. Mathematics 2023, 11, 4467. https://doi.org/10.3390/math11214467
Flamarion MV, Kochurin E, Ribeiro-Jr R. Fully Nonlinear Evolution of Free-Surface Waves with Constant Vorticity under Horizontal Electric Fields. Mathematics. 2023; 11(21):4467. https://doi.org/10.3390/math11214467
Chicago/Turabian StyleFlamarion, M. V., E. Kochurin, and R. Ribeiro-Jr. 2023. "Fully Nonlinear Evolution of Free-Surface Waves with Constant Vorticity under Horizontal Electric Fields" Mathematics 11, no. 21: 4467. https://doi.org/10.3390/math11214467
APA StyleFlamarion, M. V., Kochurin, E., & Ribeiro-Jr, R. (2023). Fully Nonlinear Evolution of Free-Surface Waves with Constant Vorticity under Horizontal Electric Fields. Mathematics, 11(21), 4467. https://doi.org/10.3390/math11214467





