A Study of Traveling Wave Structures and Numerical Investigations into the Coupled Nonlinear Schrödinger Equation Using Advanced Mathematical Techniques
Abstract
:1. Introduction
2. Improved Modified Extended Tanh-Function Technique
Application of the Method
3. Generalized Tanh Method
Application of the Method
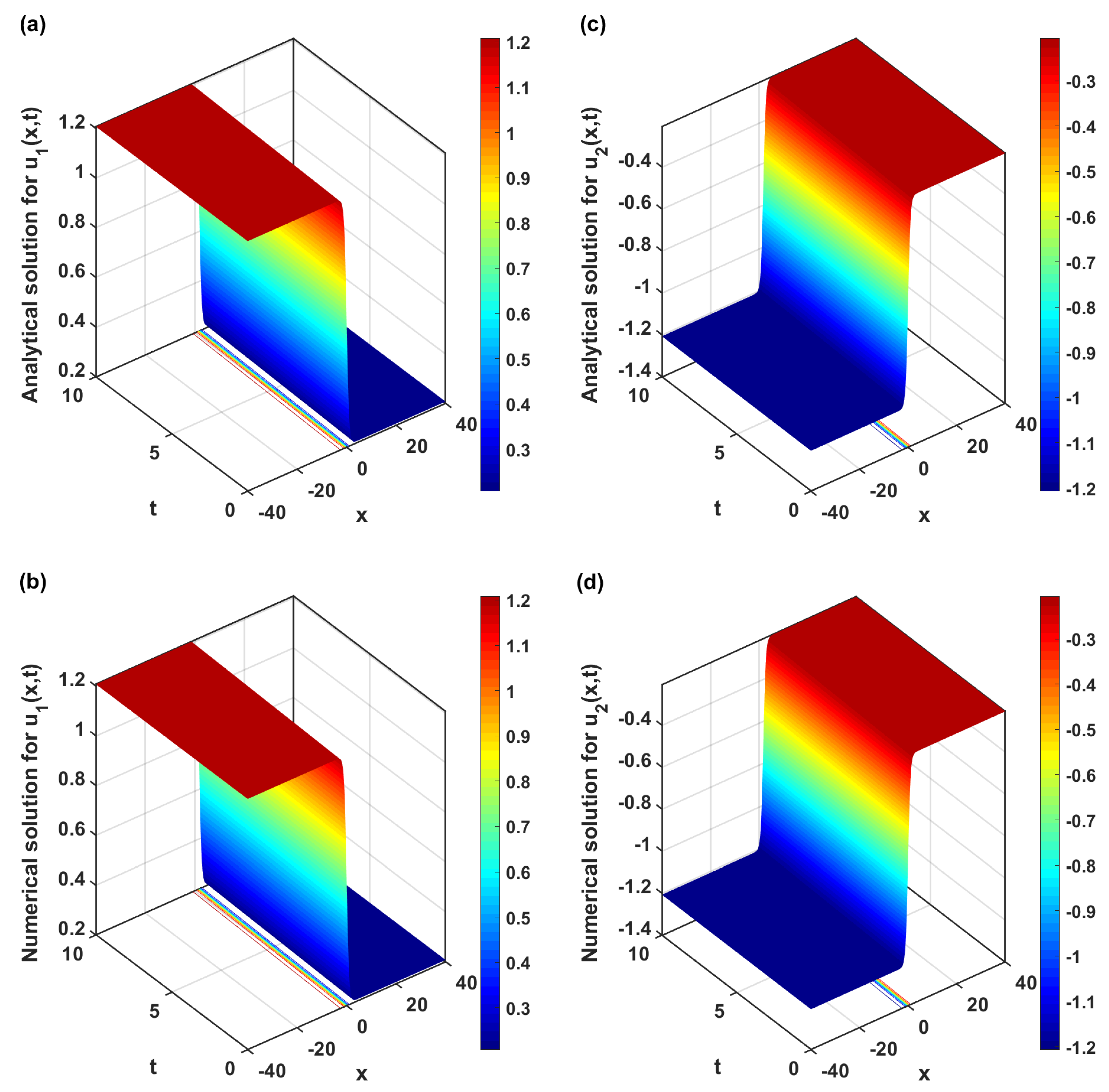
4. Numerical Solution
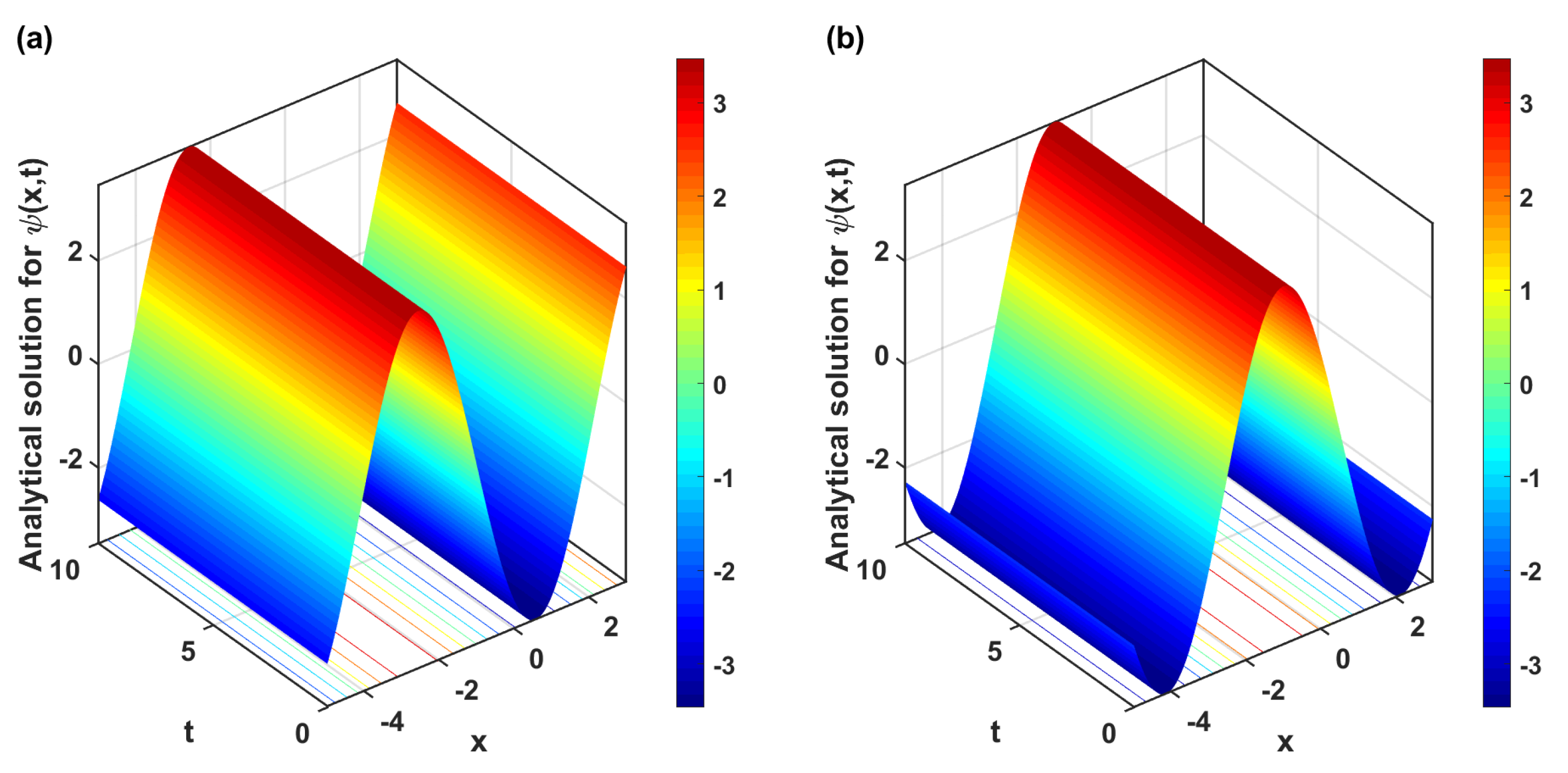
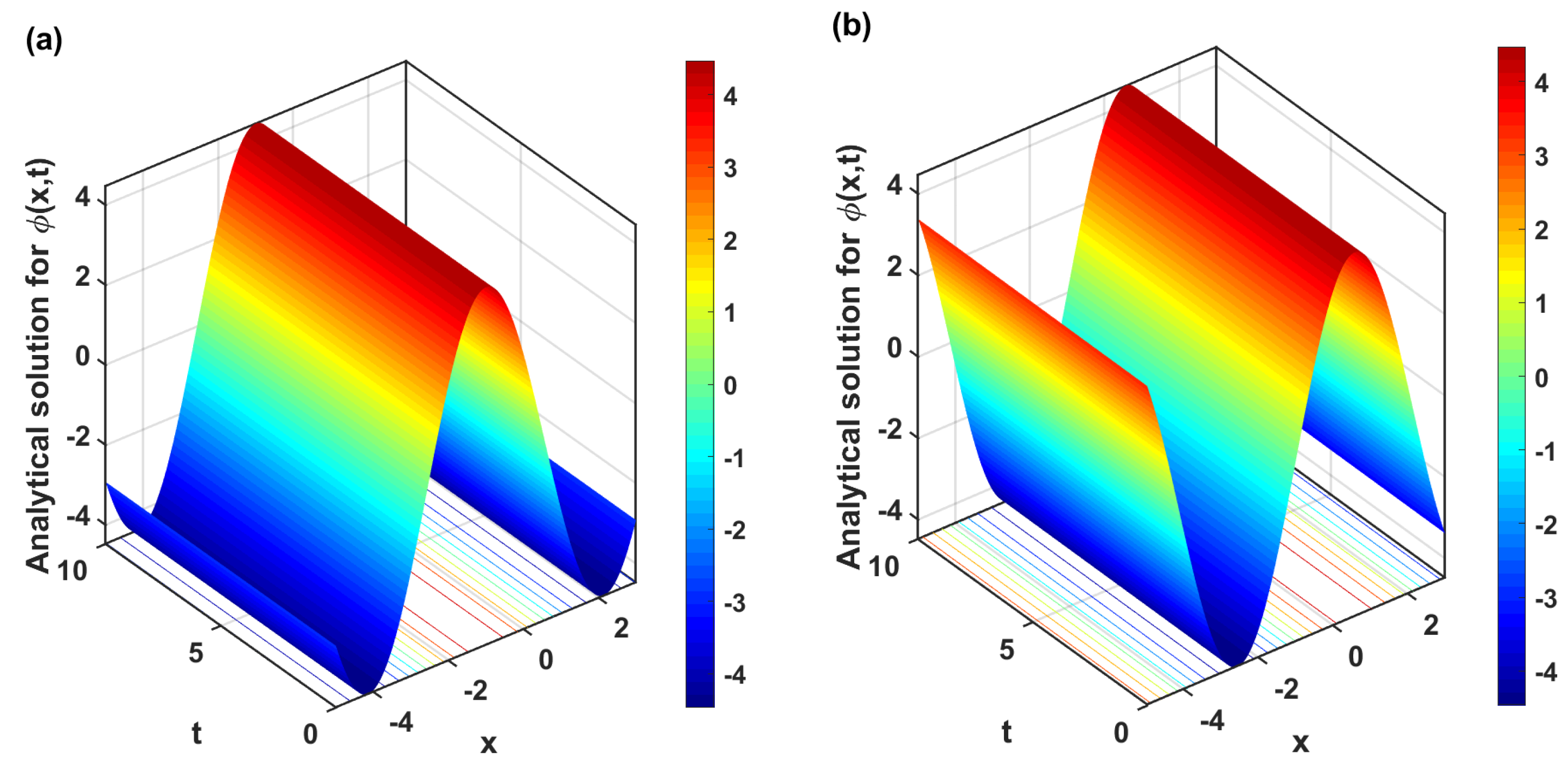
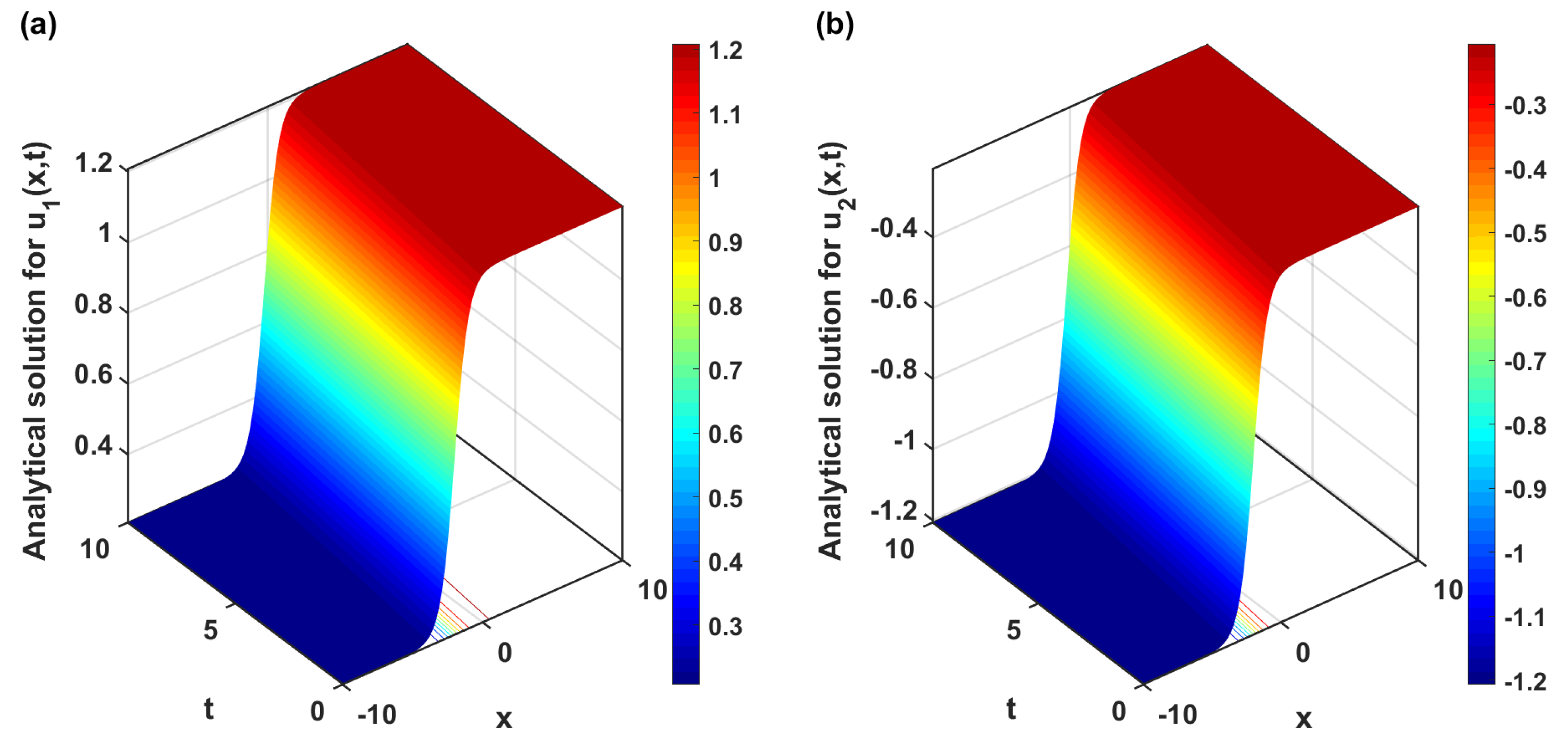
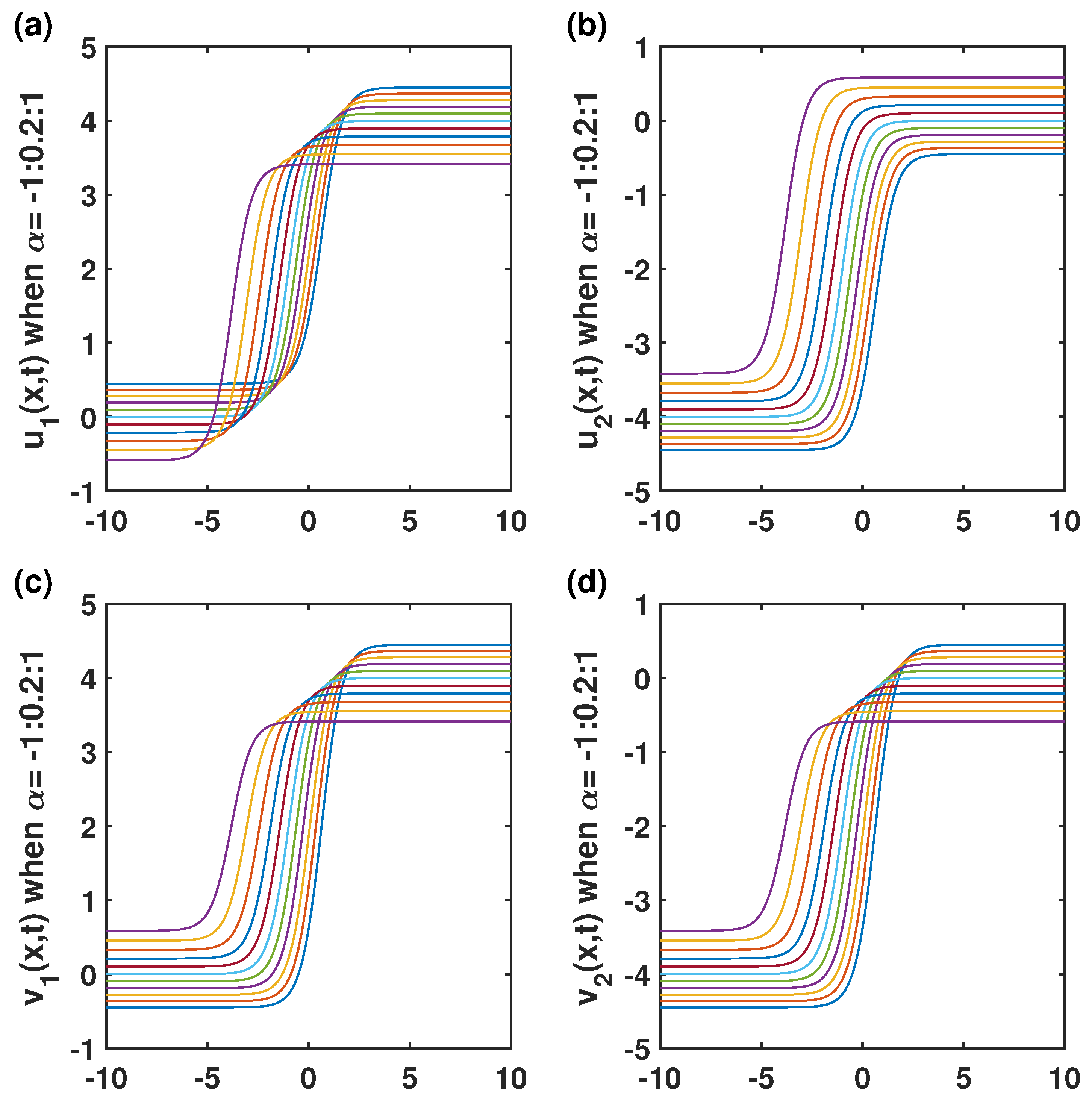
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Malik, S.; Hashemi, M.S.; Kumar, S.; Rezazadeh, H.; Mahmoud, W.; Osman, M.S. Application of new Kudryashov method to various nonlinear partial differential equations. Opt. Quantum Electron. 2023, 55, 8. [Google Scholar] [CrossRef]
- Kumar, S.; Nisar, K.S.; Niwas, M. On the dynamics of exact solutions to a (3 + 1)-dimensional YTSF equation emerging in shallow sea waves: Lie symmetry analysis and generalized Kudryashov method. Results Phys. 2023, 48, 106432. [Google Scholar] [CrossRef]
- Almatrafi, M.B.; Alharbi, A. New Soliton Wave Solutions to a Nonlinear Equation Arising in Plasma Physics. Cmes-Comput. Model. Eng. Sci. 2023, 137, 827–841. [Google Scholar] [CrossRef]
- Alharbi, A.; Almatrafi, M.B.; Abdelrahman, M.A. Constructions of the Travelling Wave Solutions to the MRLW Equation and Their Stability and Accuracy Arising in Plasma Physics. Int. J. Appl. Comput. Math. 2023, 9, 46. [Google Scholar] [CrossRef]
- Djilali, M.; Hakem, A.L.I. (G′/G)-Expansion Method To Seek Traveling Wave Solutions For Some Fractional Nonlinear PDES Arising in Ntural Sciences. Adv. Theory Nonlinear Anal. Its Appl. 2023, 7, 303–318. [Google Scholar] [CrossRef]
- Dai, C.; Zhang, J. Jacobian elliptic function method for nonlinear differential-difference equations. Chaos Solitons Fractals 2006, 27, 1042–1047. [Google Scholar] [CrossRef]
- Wei, C.C.; Tian, B.; Yang, D.Y.; Liu, S.H. Jacobian-elliptic-function and rogue-periodic-wave solutions of a high-order nonlinear Schrödinger equation in an inhomogeneous optical fiber. Chin. J. Phys. 2023, 81, 354–361. [Google Scholar] [CrossRef]
- Abdulla, S.O.; Abdulazeez, S.T.; Modanli, M. Comparison of third-order fractional partial differential equation based on the fractional operators using the explicit finite difference method. Alex. Eng. J. 2023, 70, 37–44. [Google Scholar] [CrossRef]
- Yokuş, A.; Kaya, D. Comparison exact and numerical simulation of the traveling wave solution in nonlinear dynamics. Int. J. Mod. Phys. 2020, 34, 2050282. [Google Scholar] [CrossRef]
- Ahmad, H.; Khan, T.A.; Stanimirovic, P.S.; Shatanawi, W.; Botmart, T. New approach on conventional solutions to nonlinear partial differential equations describing physical phenomena. Results Phys. 2022, 41, 105936. [Google Scholar] [CrossRef]
- Ali, H.; Kamrujjaman, M. Numerical solutions of nonlinear parabolic equations with Robin condition: Galerkin approach. TWMS J. Appl. Eng. Math. 2022, 12, 851–863. [Google Scholar]
- Alharbi, A.R. Numerical solutions to two-dimensional fourth order parabolic thin film equations using the Parabolic Monge-Ampere method. AIMS Math. 2023, 8, 16463–16478. [Google Scholar] [CrossRef]
- Alharbi, A.R. Numerical investigation for the GRLW equation using Parabolic Monge Ampere Equation. Comput. Sci. 2020, 15, 443–462. [Google Scholar]
- Budd, C.J.; Williams, J.F. Moving mesh generation using the parabolic Monge–Ampère equation. SIAM J. Sci. Comput. 2009, 31, 3438–3465. [Google Scholar] [CrossRef]
- Alharbi, A.; Naire, S. An adaptive moving mesh method for thin film flow equations with surface tension. J. Comput. Appl. Math. 2017, 319, 365–384. [Google Scholar] [CrossRef]
- DiPietro, K.L.; Lindsay, A.E. Monge—Ampére simulation of fourth order PDEs in two dimensions with application to elastic-electrostatic contact problems. J. Comput. Phys. 2017, 349, 328–350. [Google Scholar] [CrossRef]
- Rashidinia, J.; Mohammadi, R. Tension spline approach for the numerical solution of nonlinear Klein–Gordon equation. Comput. Phys. Commun. 2010, 181, 78–91. [Google Scholar] [CrossRef]
- Nikan, O.; Molavi-Arabshai, S.M.; Jafari, H. Numerical simulation of the nonlinear fractional regularized long-wave model arising in ion acoustic plasma waves. Discret. Contin. Dyn. Syst. S 2021, 14, 3685. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z.; Rasoulizadeh, M.N. Soliton wave solutions of nonlinear mathematical models in elastic rods and bistable surfaces. Eng. Anal. Bound. Elem. 2022, 143, 14–27. [Google Scholar] [CrossRef]
- Qiu, Y.; Tian, B.; Xian, D.; Xian, L. New exact solutions of nontraveling wave and local excitation of dynamic behavior for GGKdV equation. Results Phys. 2023, 49, 106463. [Google Scholar] [CrossRef]
- Lotfy, K.; El-Bary, A.A.; Hassan, W.; Alharbi, A.R.; Almatrafi, M.B. Electromagnetic and Thomson effects during photothermal transport process of a rotator semiconductor medium under hydrostatic initial stress. Results Phys. 2020, 16, 102983. [Google Scholar] [CrossRef]
- Alharbi, A. Traveling-wave and numerical solutions to a Novikov-Veselov system via the modified mathematical methods. AIMS Math. 2023, 8, 1230–1250. [Google Scholar] [CrossRef]
- Abdelrahman, M.A.; Sohaly, M.A.; Alharbi, A. The new exact solutions for the deterministic and stochastic (2+ 1)-dimensional equations in natural sciences. J. Taibah Univ. Sci. 2019, 13, 834–843. [Google Scholar] [CrossRef]
- Abdelrahman, M.A.; Alharbi, A. Analytical and numerical investigations of the modified Camassa—Holm equation. Pramana 2021, 95, 117. [Google Scholar] [CrossRef]
- Khuri, S.A. A complex tanh-function method applied to nonlinear equations of Schrödinger type. Chaos Solitons Fractals 2004, 20, 1037–1040. [Google Scholar] [CrossRef]
- Ismail, M.S.; Taha, T.R. Numerical simulation of coupled nonlinear Schrödinger equation. Math. Comput. Simul. 2001, 56, 547–562. [Google Scholar] [CrossRef]
- Sonnier, W.J.; Christov, C.I. Strong coupling of Schrödinger equations: Conservative scheme approach. Math. Comput. Simul. 2005, 69, 514–525. [Google Scholar] [CrossRef]
- Sun, Z.Z.; Zhao, D.D. On the L∞ convergence of a difference scheme for coupled nonlinear Schrödinger equations. Comput. Math. Appl. 2010, 59, 3286–3300. [Google Scholar] [CrossRef]
- Gu, J.; Akbulut, A.; Kaplan, M.; Kaabar, M.K.A.; Yue, X.-G. A novel investigation of exact solutions of the coupled nonlinear Schrodinger equations arising in ocean engineering, plasma waves, and nonlinear optics. J. Ocean. Eng. Sci. 2022; In Press. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Cheemaa, N. Propagation of nonlinear complex waves for the coupled nonlinear Schrödinger Equations in two core optical fibers. Phys. Stat. Mech. Its Appl. 2019, 529, 121330. [Google Scholar] [CrossRef]
- Elwakil, S.A.; El-Labany, S.K.; Zahran, M.A.; Sabry, R. Modified extended tanh-function method for solving nonlinear partial differential equations. Phys. Lett. A 2002, 299, 179–188. [Google Scholar] [CrossRef]
- Fan, E.; Hona, Y.C. Generalized tanh method extended to special types of nonlinear equations. Z. Für Naturforschung 2002, 57, 101375. [Google Scholar] [CrossRef]
- Yang, Z.; Hon, B.Y.C. An Improved Modified Extended tanh-Function Method. Z. Für Naturforschung 2006, 61, 103–115. [Google Scholar] [CrossRef]
- Brown, P.N.; Hindmarsh, A.C.; Petzold, L.R. Using Krylov methods in the solution of large-scale differential-algebraic systems. SIAM J. Sci. Comput. 1994, 15, 1467–1488. [Google Scholar] [CrossRef]


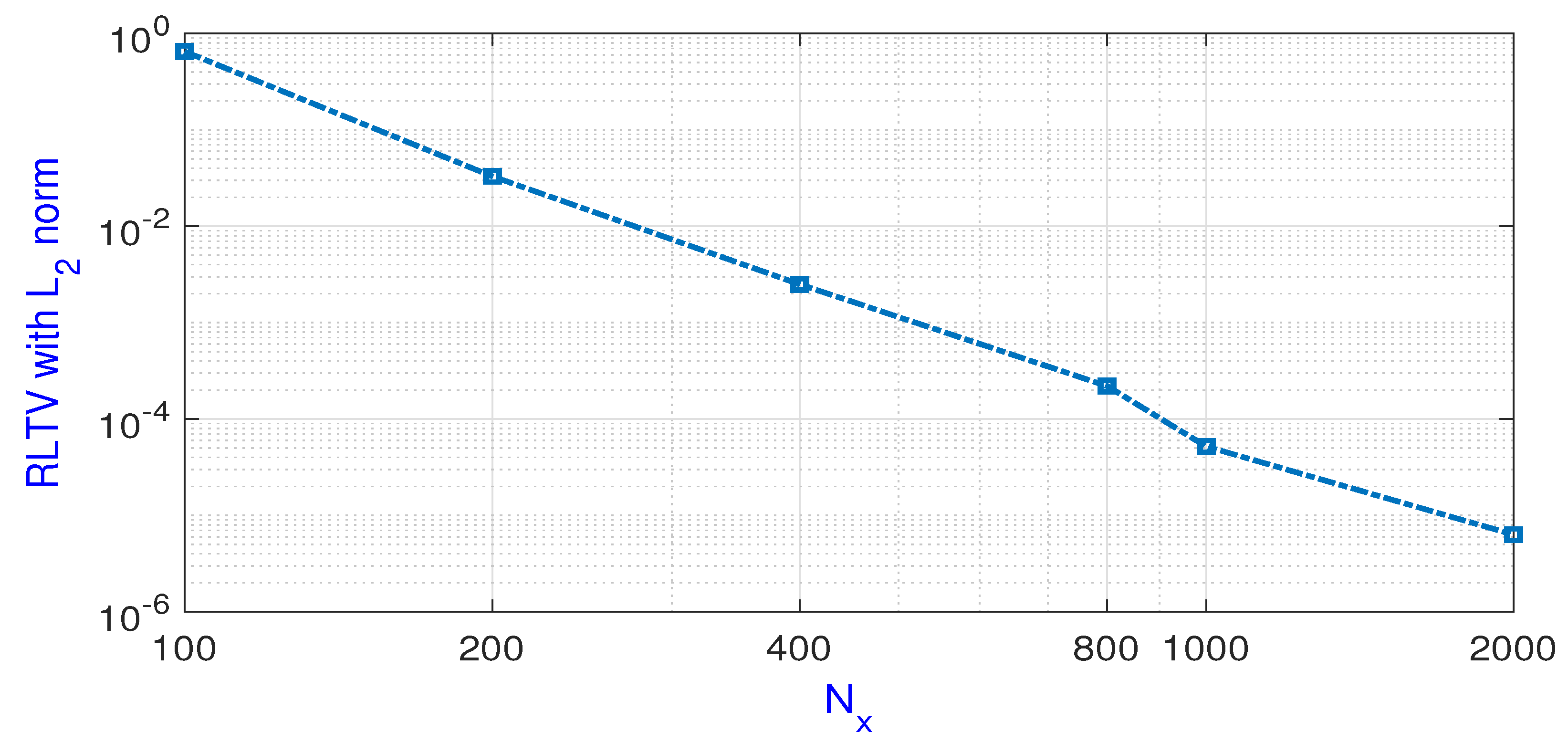
| The Relative Error | CPU | |
|---|---|---|
| 200 | s | |
| 400 | s | |
| 800 | s | |
| 1000 | s | |
| 2000 | s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alharbi, T.G.; Alharbi, A. A Study of Traveling Wave Structures and Numerical Investigations into the Coupled Nonlinear Schrödinger Equation Using Advanced Mathematical Techniques. Mathematics 2023, 11, 4597. https://doi.org/10.3390/math11224597
Alharbi TG, Alharbi A. A Study of Traveling Wave Structures and Numerical Investigations into the Coupled Nonlinear Schrödinger Equation Using Advanced Mathematical Techniques. Mathematics. 2023; 11(22):4597. https://doi.org/10.3390/math11224597
Chicago/Turabian StyleAlharbi, Taghread Ghannam, and Abdulghani Alharbi. 2023. "A Study of Traveling Wave Structures and Numerical Investigations into the Coupled Nonlinear Schrödinger Equation Using Advanced Mathematical Techniques" Mathematics 11, no. 22: 4597. https://doi.org/10.3390/math11224597
APA StyleAlharbi, T. G., & Alharbi, A. (2023). A Study of Traveling Wave Structures and Numerical Investigations into the Coupled Nonlinear Schrödinger Equation Using Advanced Mathematical Techniques. Mathematics, 11(22), 4597. https://doi.org/10.3390/math11224597





