Analysis of Decision-Making in a Green Supply Chain under Different Carbon Tax Policies
Abstract
:1. Introduction
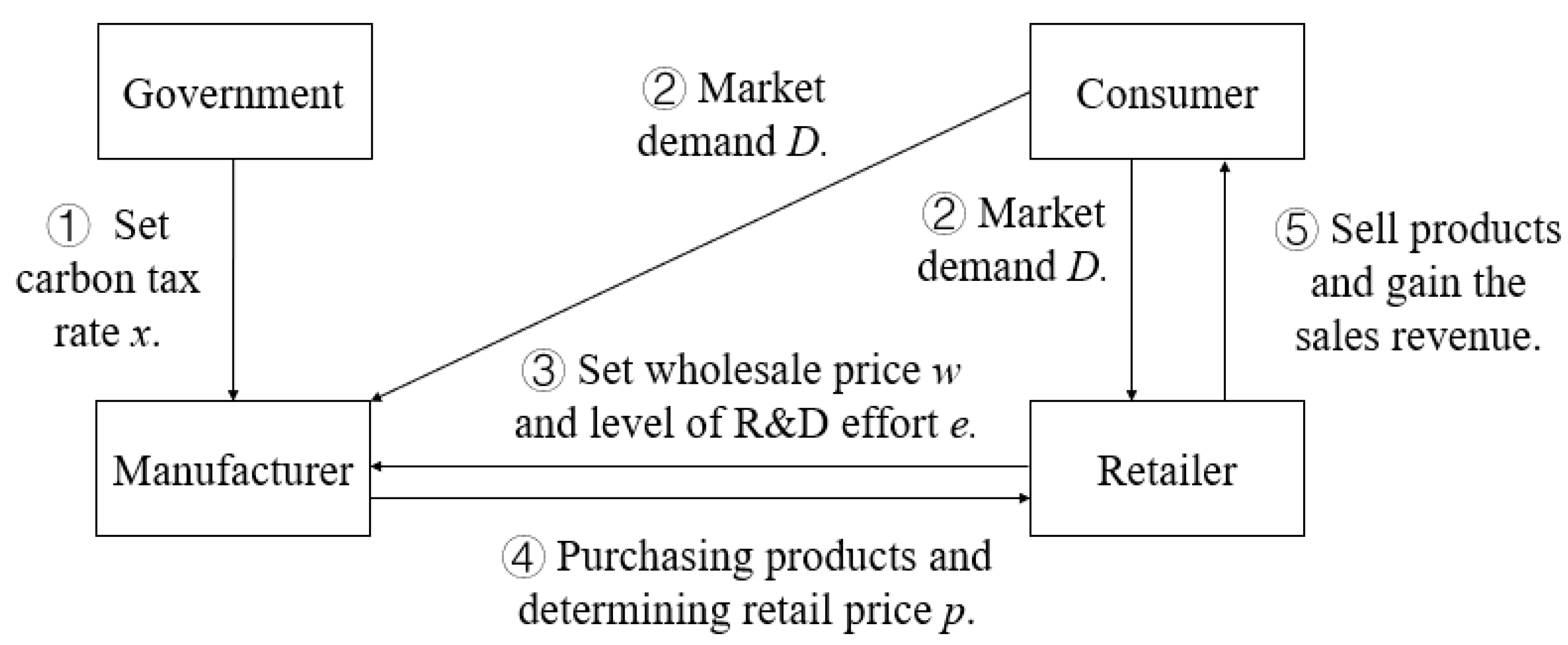
2. Problem Description and Assumptions
3. Model
3.1. The Model with a Uniform Carbon Tax
3.2. The Model with a Non-Uniform Carbon Tax
4. Numerical Analysis
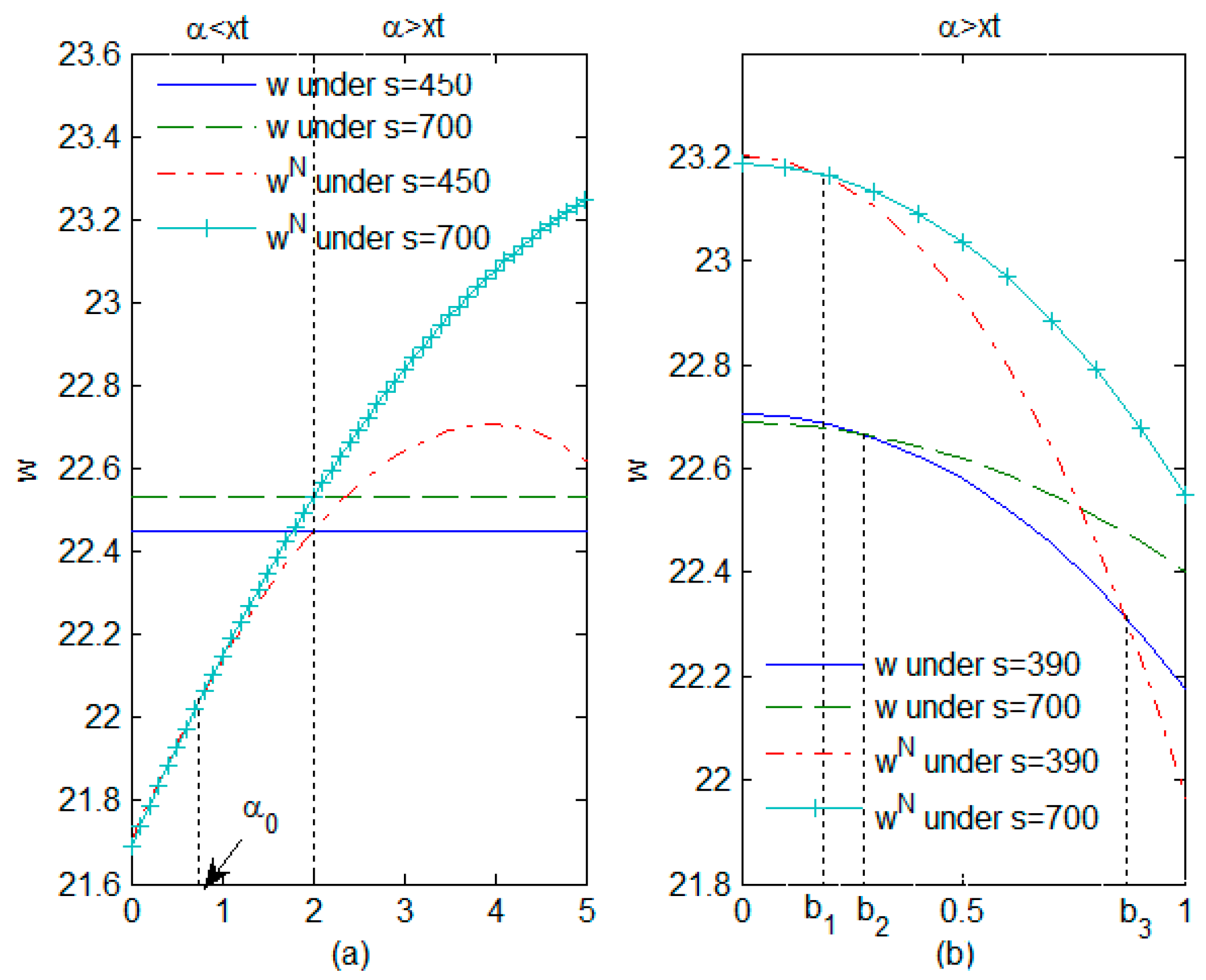
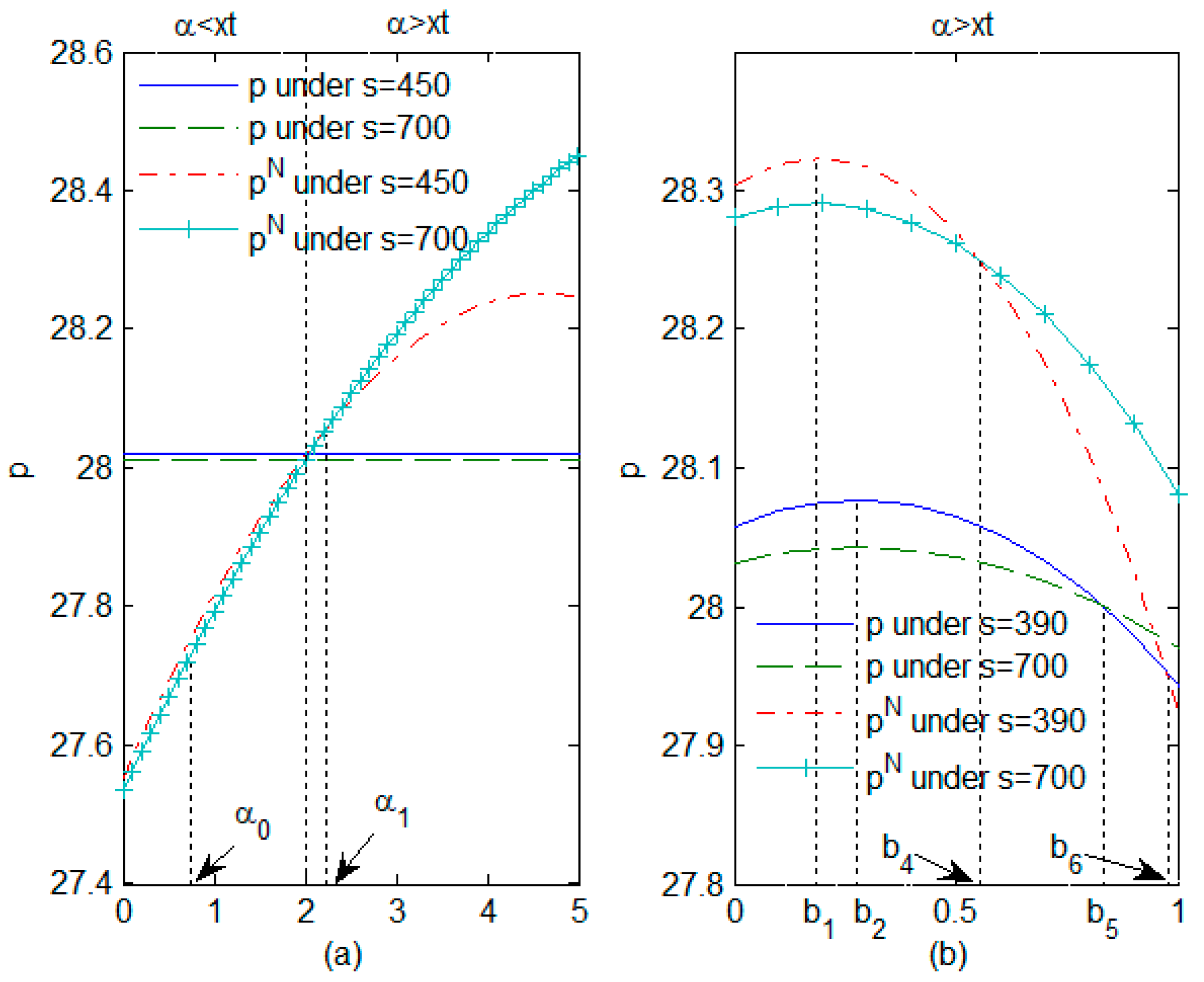
4.1. Impact of Carbon Tax per Unit of Product and Rate of Reduction in Carbon Emissions on Decision Variables
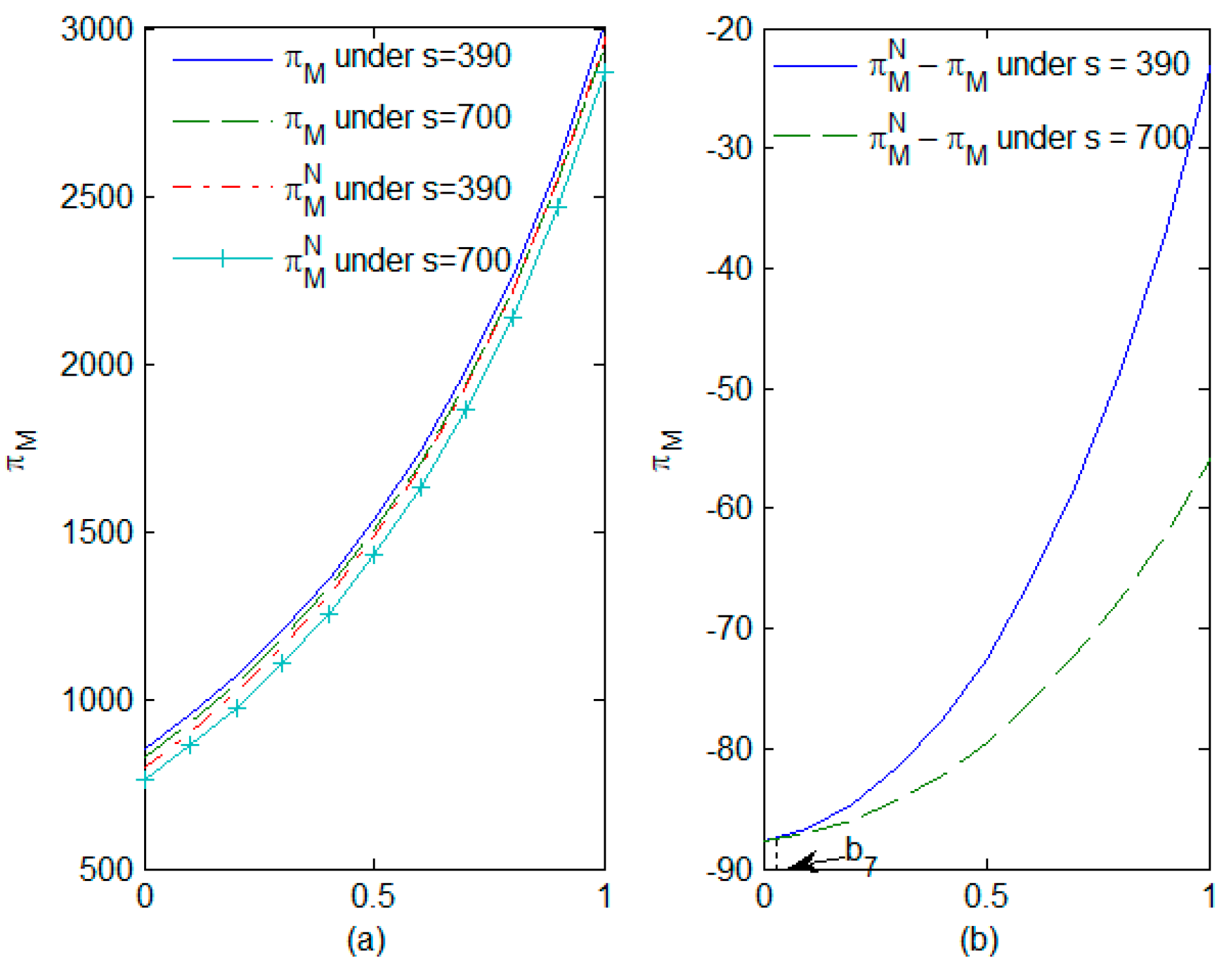
4.2. Impact of the Proportion of the Population with Green Preferences and the Rate of Reduction in Carbon Emissions on Expected Profits
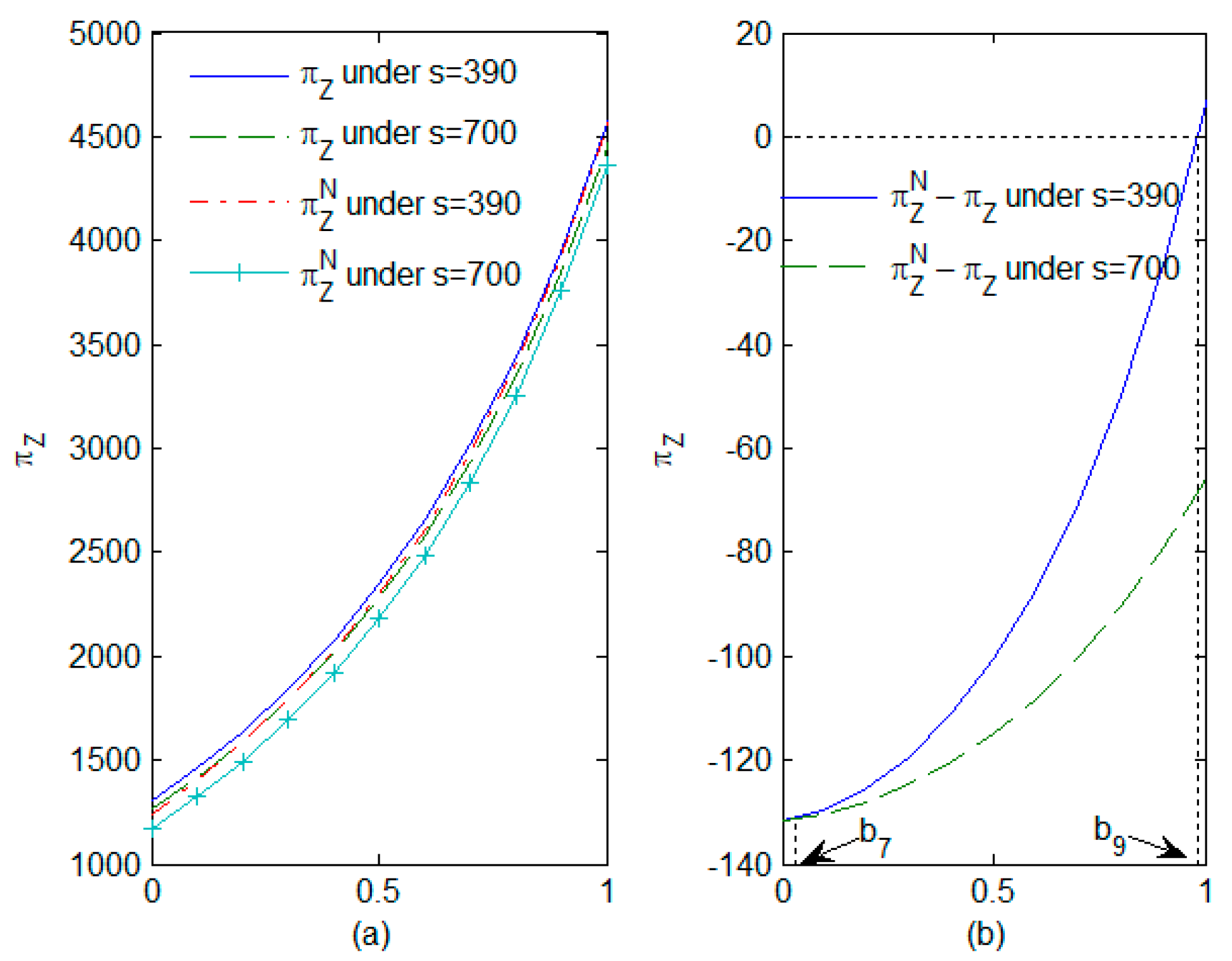
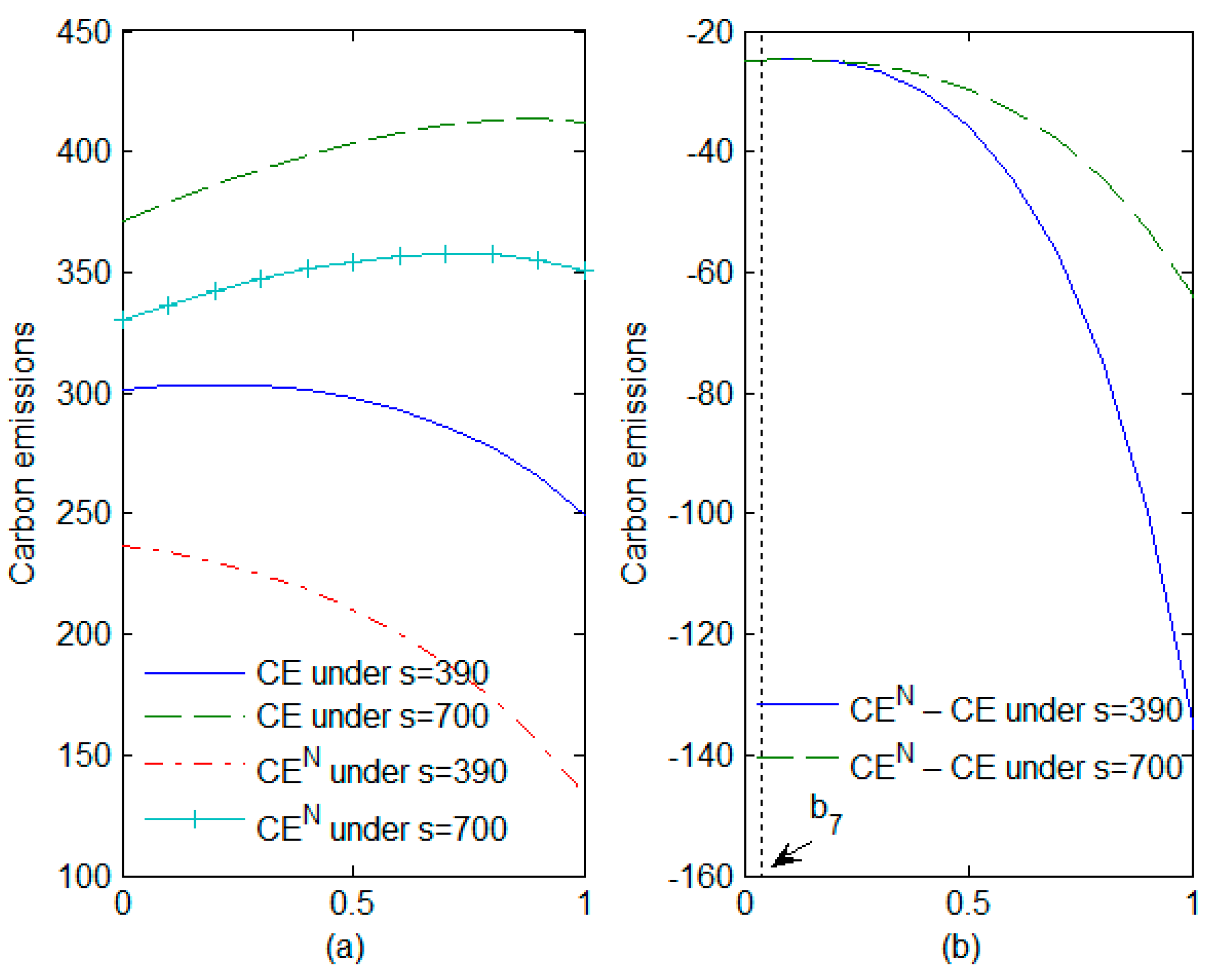
4.3. Impact of the Proportion of the Population with Green Preferences and the Rate of Reduction in Carbon Emissions on Carbon Emissions
5. Case Study
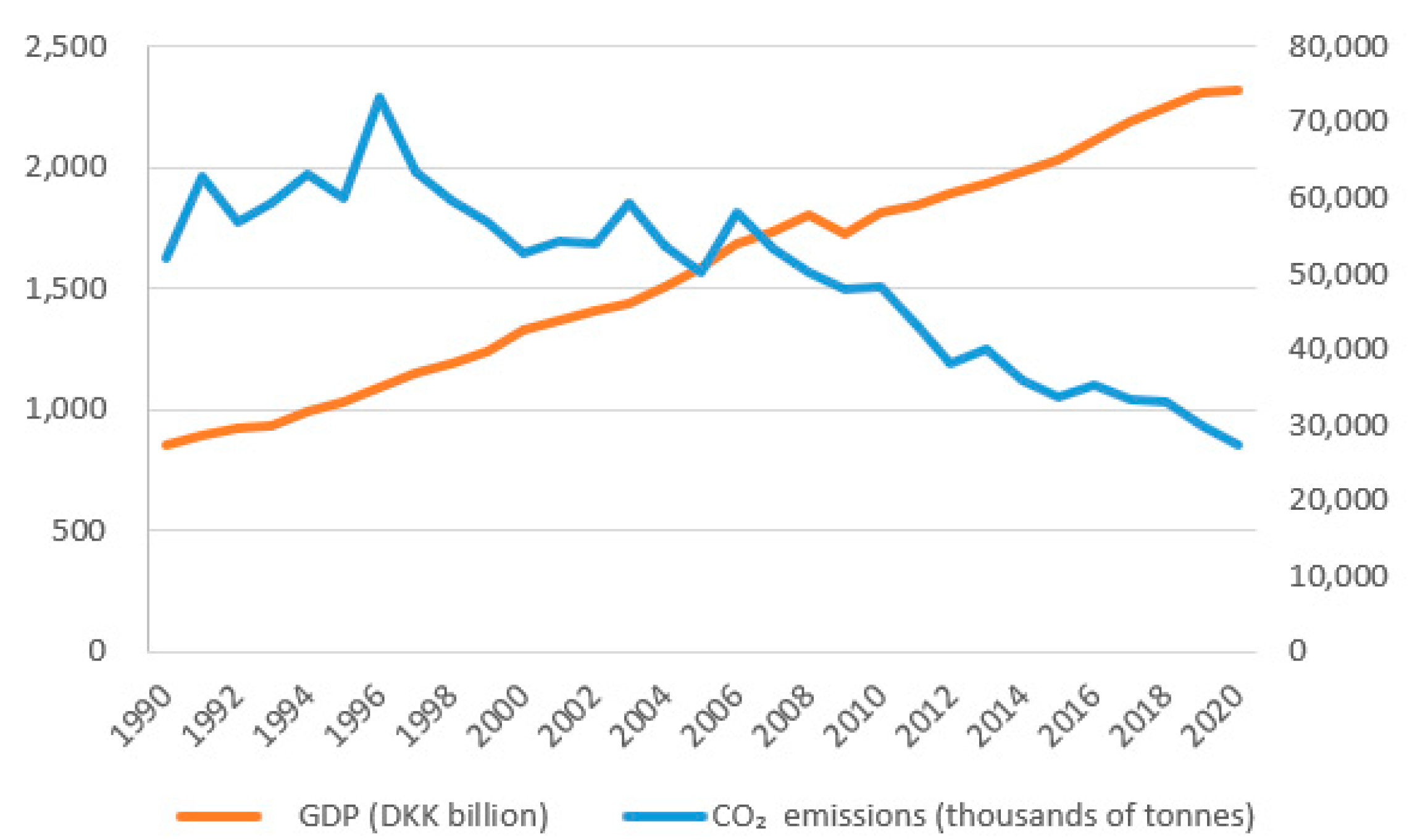
5.1. Implementation Background
5.2. Implementation Plan
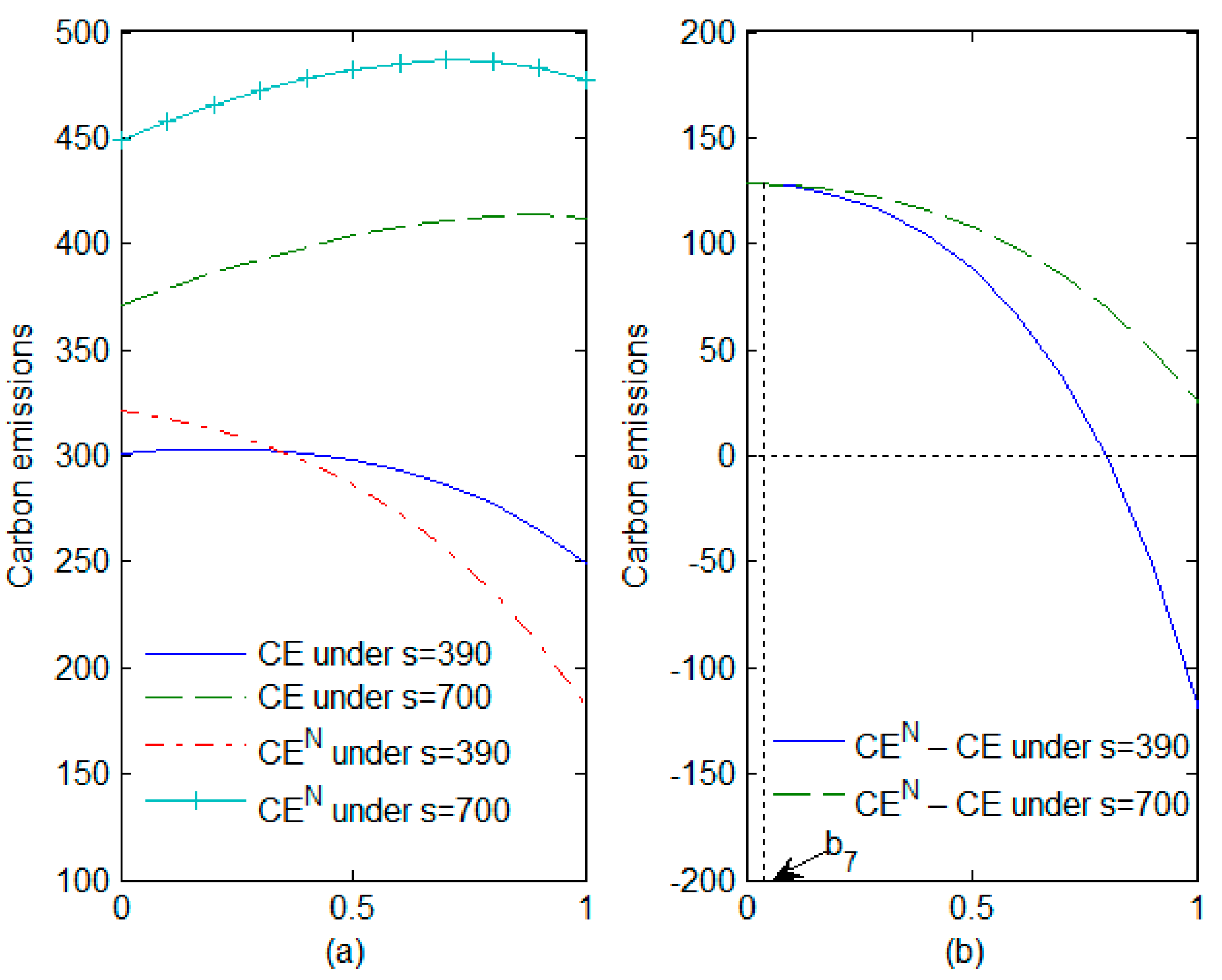
5.3. Implementation Effect
6. Conclusions
- (1)
- Carbon tax policies significantly influence supply-chain decisions by affecting the carbon tax per unit of product. Regardless of whether the carbon tax policy is uniform or non-uniform, an increase in the carbon tax per unit of product leads to a higher level of R&D effort. However, wholesale and retail prices exhibit an inverted U-shaped relationship with the carbon tax per unit of product. An increase in R&D costs and in the proportion of green-preferring consumers will raise wholesale prices but can reduce retail prices under certain conditions. The gains derived from green innovation result in a reduction in both wholesale and retail prices. Furthermore, an increase in the carbon tax per unit of product correspondingly contributes to a decrease in wholesale and retail prices when the benefits of green innovation are sufficiently high.
- (2)
- Consumers’ green preferences positively impact the expected profits of supply chains and have an inverted U-shaped relationship with carbon emissions. In situations in which the proportion of consumers with green preference is relatively high, a high carbon tax per unit of product can result in increased profits for the retailer and even reduce the profits of the supply chain. Conversely, when the proportion of consumers with green preferences is relatively low, policies involving a high carbon tax per unit of product might inadvertently lead to an increase in carbon emissions, particularly in scenarios characterized by low R&D costs. Meanwhile, manufacturers with high R&D costs at the same level of green preference have higher carbon emissions.
- (3)
- A high carbon tax per unit of product will always reduce the manufacturer’s profits, but in the case of high R&D returns and low innovation costs, the retailer’s profit may increase as well. When the gain in profits for a retailer is greater than the loss in profits for a manufacturer, the overall profits of the supply chain will increase with the carbon tax per unit of product. Additionally, when the benefits associated with green innovation are relatively low, a high carbon tax per unit of product can contribute to increased carbon emissions, particularly in situations in which the carbon emissions per unit of product are relatively high.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
Appendix E
Appendix F
- (1)
- Combining Equations (8) and (18), we can get when ,
- (2)
- Combining Equations (9) and (19), we find that whenwhereandWhen ,.
- (3)
- Combining Equations (10) and (20), we find that whenwhereandWhen , .
- (4)
- Combining Equations (13) and (21), we obtain when .
- (5)
- Combining Equations (14) and (22), we find that when
Appendix G
- (1)
- Combining Equations (8) and (18), we find that when
- (2)
- Combining Equations (9) and (19), we find that when
- (3)
- Combining Equations(10) and (20), we find that when
- (4)
- Combining Equations (13) and Equation (21), we obtain when .
- (5)
- Combining Equations (14) and Equation (22), we find that when
Appendix H
- (1)
- Combining Equations (8) and (18), we obtain that
- (2)
- Combining Equations (9) and (19), we find that when
- (3)
- Combining Equations (10) and (20), we find that when
- (4)
- Combining Equations (13) and (21), we obtain when .
- (5)
- Combining Equations (14) and (22), we f that when
- (1)
- Combining Equations (8) and (18), we find that
- (2)
- Combining Equations (9) and (19), we obtain find when
- (3)
- Combining Equations (10) and (20), we find that when
- (4)
- Combining Equations (13) and (21), we obtain when .
- (5)
- Combining Equations (14) and (22), we find that when
References
- Mitra, S.; Datta, P.P. Adoption of green supply chain management practices and their impact on performance: An exploratory study of Indian manufacturing firms. Int. J. Prod. Res. 2014, 52, 2085–2107. [Google Scholar] [CrossRef]
- Wen, X.; Cheng, H.; Cai, J.; Lu, C. Govrnment subside policies and effect analysis in green supply chain. Chin. J. Manag. 2018, 15, 625–632. [Google Scholar]
- Liu, G.; Yang, T.; Zhang, X. Pricing of green supply chain and decisions on product green degree considering green preference and sales effort. J. Beijing Jiaotong Univ. (Soc. Sci. Ed.) 2019, 18, 115–126. [Google Scholar] [CrossRef]
- Fussler, C.; James, P. Driving Eco-Innovation: A Breakthrough Discipline for Innovation and Sustainability; Pitman Publishing: London, UK; Washington, DC, USA, 1996; pp. 68–74. ISBN 978-0-273-62207-9. [Google Scholar]
- Wang, W.; Zhang, R. Research on financing strategies for green product suppliers under government subsidies—Green credit VS prepayment. J. Syst. Manag. 2023, accepted. [Google Scholar]
- Liu, S.; Zhang, Y. Greenhouse gas emissions reduction: A theoretical framework and global solution. Econ. Res. J. 2009, 44, 4–13. [Google Scholar]
- Zhang, J.; Wang, K.; Zhang, Y. Carbon emission abatement performance of carbon emissions trading scheme—Based on the intermediary effect of low-carbon technology innovation. Soft Sci. 2022, 36, 102–108. [Google Scholar] [CrossRef]
- Zhou, D.; Cai, X.; Zhang, D.; Zhang, Y. Carbon tax policy simulation based on CGE model: A case study of Guangdong province. Clim. Change Res. 2020, 16, 516–525. [Google Scholar]
- Ghosh, D.; Shah, J. Supply chain analysis under green sensitive consumer demand and cost sharing contract. Int. J. Prod. Econ. 2015, 164, 319–329. [Google Scholar] [CrossRef]
- Li, B.; Zhu, M.; Jiang, Y.; Li, Z. Pricing policies of a competitive dual-channel green supply chain. J. Clean. Prod. 2016, 112, 2029–2042. [Google Scholar] [CrossRef]
- Gao, J.; Han, H.; Hou, L. Decision-making in closed-loop supply chain with dominant retailer considering products’ green degree and sales effort. Manag. Rev. 2015, 27, 187–196. [Google Scholar] [CrossRef]
- Zhang, C.-T.; Liu, L.-P. Research on coordination mechanism in three-level green supply chain under non-cooperative game. Appl. Math. Model. 2013, 37, 3369–3379. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, J.; Liu, J. Decision analysis of a dual channel green supply chain considering the fairness concern. Ind. Eng. Manag. 2020, 25, 9–19. [Google Scholar] [CrossRef]
- Jiang, S.; Li, S.; Wang, H. Pricing decision of green supply chain considering risk aversion. Syst. Eng. 2016, 34, 94–100. [Google Scholar]
- Liu, P.; Yi, S. Pricing policies of green supply chain considering targeted advertising and product green degree in the big data environment. J. Clean. Prod. 2017, 164, 1614–1622. [Google Scholar] [CrossRef]
- Liu, S.S.; Hua, G.; Ma, B.J.; Cheng, T.C.E. Competition between green and non-green products in the blockchain era. Int. J. Prod. Econ. 2023, 264, 108970. [Google Scholar] [CrossRef]
- Yang, S.; Xiao, D. Channel choice and coordination of two-stage low-carbon supply chain. Soft Sci. 2017, 31, 92–98. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, F.; Zhou, Z. Study on joint contract coordination to promote green product demand under the retailer-dominance. J. Ind. Eng. Eng. Manag. 2020, 34, 194–204. [Google Scholar] [CrossRef]
- Lin, D. Accelerability vs. scalability: R&D investment under financial constraints and competition. Manag. Sci. 2023, 69, 4078–4107. [Google Scholar] [CrossRef]
- Zhu, W.; He, Y. Green product design in supply chains under competition. Eur. J. Oper. Res. 2017, 258, 165–180. [Google Scholar] [CrossRef]
- Benjaafar, S.; Li, Y.; Daskin, M. Carbon footprint and the management of supply chains: Insights from simple models. IEEE Trans. Autom. Sci. Eng. 2013, 10, 99–116. [Google Scholar] [CrossRef]
- Yang, H.; Luo, J. Emission reduction in a supply chain with carbon tax policy. Syst. Eng.-Theory Pract. 2016, 36, 3092–3102. [Google Scholar]
- Ma, Q.; Song, H.; Chen, G. Research on product pricing and production decision-making under the supply chain environment considering the carbon-trading mechanism. Chin. J. Manag. Sci. 2014, 22, 37–46. [Google Scholar] [CrossRef]
- Cao, X.; Wu, X. The Collaborative strategy for carbon reduction technology innovation on dual-channel supply chain under the carbon tax policy. J. Cent. China Norm. Univ. (Nat. Sci.) 2020, 54, 898–909. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhang, P.; Guo, N. Impact of carbon tax and consumers’ environmental awareness on carbon emissions in supply chains. Syst. Eng.-Theory Pract. 2014, 34, 2245–2252. [Google Scholar]
- Xu, C.; Wang, C.; Huang, R. Impacts of horizontal integration on social welfare under the interaction of carbon tax and green subsidies. Int. J. Prod. Econ. 2020, 222, 107506. [Google Scholar] [CrossRef]
- Yu, W.; Wang, Y.; Feng, W.; Bao, L.; Han, R. Low carbon strategy analysis with two competing supply chain considering carbon taxation. Comput. Ind. Eng. 2022, 169, 108203. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, F.; Zhou, Z. Pricing decisions and social welfare in a supply chain with multiple competing retailers and carbon tax policy. J. Clean. Prod. 2018, 190, 752–777. [Google Scholar] [CrossRef]
- Jaber, M.Y.; Glock, C.H.; El Saadany, A.M.A. Supply chain coordination with emissions reduction incentives. Int. J. Prod. Res. 2013, 51, 69–82. [Google Scholar] [CrossRef]
- Diao, X.; Zeng, Z.; Sun, C. Research on coordination of supply chain with two products based on mix carbon policy. Chin. J. Manag. Sci. 2021, 29, 149–159. [Google Scholar] [CrossRef]
- Ghosh, A. Optimization of a production-inventory model under two different carbon policies and proposal of a hybrid carbon policy under random demand. Int. J. Sustain. Eng. 2021, 14, 280–292. [Google Scholar] [CrossRef]
- Zhao, L.; Jin, S.; Jiang, H. Investigation of complex dynamics and chaos control of the duopoly supply chain under the mixed carbon policy. Chaos Solitons Fractals 2022, 164, 112492. [Google Scholar] [CrossRef]
- Zhu, C.; Ma, J.; Li, J. Joint emission reduction decisions and Its optimization under hybrid carbon regulations. J. Syst. Manag. 2023, accepted. [Google Scholar]
- Zhu, C.; Ma, J. Optimal decisions in two-echelon supply chain under hybrid carbon regulations: The perspective of inner carbon trading. Comput. Ind. Eng. 2022, 173, 108699. [Google Scholar] [CrossRef]
- Li, X.; Han, R. Impact of government policy on supply chain enterprises decisions under the low-carbon economy. Sci. Technol. Manag. Res. 2016, 36, 240–245. [Google Scholar]
- Chen, W.; Hu, Z.-H. Using evolutionary game theory to study governments and manufacturers’ behavioral strategies under various carbon taxes and subsidies. J. Clean. Prod. 2018, 201, 123–141. [Google Scholar] [CrossRef]
- Guo, J.; Huang, R. A carbon tax or a subsidy? Policy choice when a green firm competes with a high carbon emitter. Environ. Sci. Pollut. Res. 2022, 29, 12845–12852. [Google Scholar] [CrossRef]
- Meng, W. Comparation of subsidy and cooperation policy based on emission reduction R & D. Syst. Eng. 2010, 28, 123–126. [Google Scholar]
- Vaughan, D.; Skerritt, D.J.; Duckworth, J.; Sumaila, U.R.; Duffy, M. Revisiting Fuel Tax Concessions (FTCs): The economic implications of fuel subsidies for the commercial fishing fleet of the United Kingdom. Mar. Policy 2023, 155, 105763. [Google Scholar] [CrossRef]
- Qiu, R.; Xu, J.; Xie, H.; Zeng, Z.; Lv, C. Carbon tax incentive policy towards air passenger transport carbon emissions reduction. Transp. Res. Part D: Transp. Environ. 2020, 85, 102441. [Google Scholar] [CrossRef]
- Zhang, W.; Lee, H.-H. Investment strategies for sourcing a new technology in the presence of a mature technology. Manag. Sci. 2022, 68, 4631–4644. [Google Scholar] [CrossRef]
- He, Y.; Chen, Z.; Liao, N. The impact mechanism of government subsidy approach on manufacturer’s decision—Making in green supply chain. Chin. J. Manag. Sci. 2022, 30, 87–98. [Google Scholar] [CrossRef]
- Deng, L.; Liu, Z. One-period pricing strategy of ‘Money Doctors’ under cumulative prospect theory. Port. Econ. J. 2017, 16, 113–144. [Google Scholar] [CrossRef]


| Symbol | Definition |
|---|---|
| Parameters | |
| c | Unit production cost |
| D | Total market demand |
| a | Potential market demand |
| d | Influence of sales price on demand |
| λ | Influence of R&D effort on demand |
| s | Cost parameter for R&D effort |
| x | Carbon tax rates |
| t | Carbon emissions per unit of product |
| b | Carbon-emission reduction rate |
| θ | Proportion of population with a green preference for consumers |
| τ | Level of preference of green-preference consumers |
| u | Influence of green-preference level on price sensitivity |
| m | Proportion of fossil energy with high carbon content |
| n | Proportion of carbon emissions from production |
| z | Carbon tax on carbon emissions from production |
| Profit of firms (j = M, R) | |
| Decision variables | |
| w | The product’s wholesale price |
| e | Level of R&D effort |
| p | The product’s sales price |
| Carbon Tax Policy | Year | Status of Implementation |
|---|---|---|
| General energy tax | 1977 | The general energy tax initially targeted petroleum products and electricity. The energy tax was imposed on coal in 1982. Subsequently, in 1997, natural gas was also included under the energy-tax framework. In 2013, the electricity tax was abolished. |
| Carbon dioxide tax | 1992 | The carbon dioxide tax is levied on the energy consumed by different sectors. The current tax system is designed to differentiate rates based on the carbon dioxide content of various fuels. The intention is to ensure that the price of the tax for different types of energy is approximately equivalent to a tax of DKK 100 per ton of carbon dioxide emitted. |
| Sulfur dioxide tax | 1996 | There are two tax methods available to taxable enterprises. The first method is a product tax, which is levied based on the sulfur content of the taxable fuel. The tax rate for the product tax is set at DKK 20 per kilogram of sulfur. The second method is an emissions tax, which is imposed based on the actual emissions of sulfur dioxide. The tax rate for the emissions tax is DKK 10 per kilogram of sulfur dioxide emitted. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, L.; Tan, J.; Dai, J. Analysis of Decision-Making in a Green Supply Chain under Different Carbon Tax Policies. Mathematics 2023, 11, 4631. https://doi.org/10.3390/math11224631
Deng L, Tan J, Dai J. Analysis of Decision-Making in a Green Supply Chain under Different Carbon Tax Policies. Mathematics. 2023; 11(22):4631. https://doi.org/10.3390/math11224631
Chicago/Turabian StyleDeng, Liurui, Jie Tan, and Jiawu Dai. 2023. "Analysis of Decision-Making in a Green Supply Chain under Different Carbon Tax Policies" Mathematics 11, no. 22: 4631. https://doi.org/10.3390/math11224631
APA StyleDeng, L., Tan, J., & Dai, J. (2023). Analysis of Decision-Making in a Green Supply Chain under Different Carbon Tax Policies. Mathematics, 11(22), 4631. https://doi.org/10.3390/math11224631




