nmPLS-Net: Segmenting Pulmonary Lobes Using nmODE
Abstract
:1. Introduction
- The main contribution of this study is the combination of nmODE with convolutional neural networks in the task of pulmonary lobe segmentation. This combination leverages nmODE’s high nonlinearity and memory capabilities better to identify global pulmonary features and the relationships between these features;
- This study employs a novel fissure-enhanced associative learning approach to make the model focus on detail identification near pulmonary fissures;
- This study conducted experiments on two datasets, and our network achieved competitive overall segmentation results, significantly outperforming previous works in segmenting the right middle pulmonary lobe.
2. Related Works
2.1. Medical Image Processing
2.2. Neural Ordinary Differential Equations
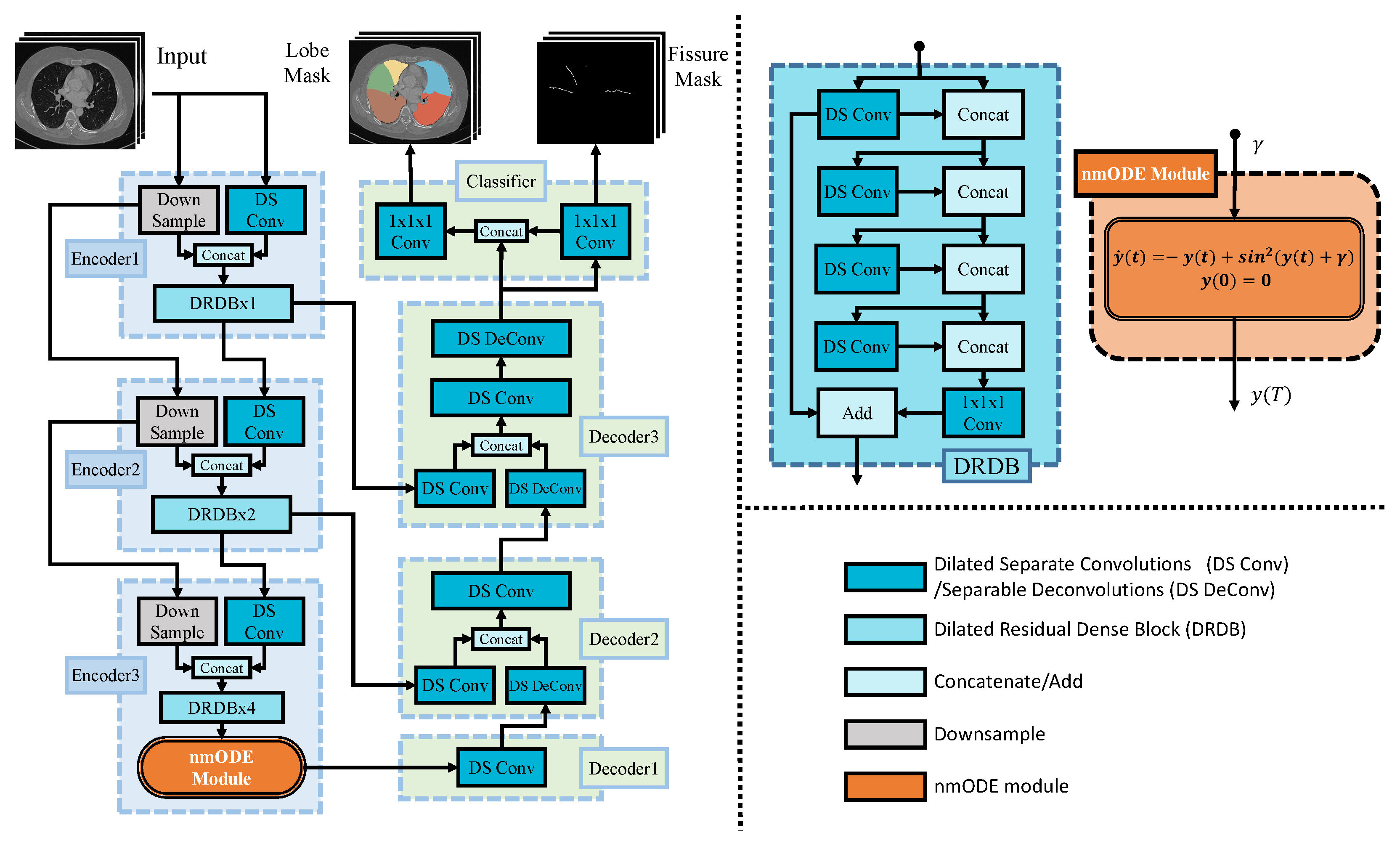
3. Methods
3.1. Problem Formulation
3.2. Model
3.3. Neural Memory Ordinary Differential Equation (nmODE)
3.4. Fissure-Enhanced Associative Learning
| Algorithm 1 Pulmonary Fissure Label Generation Algorithm |
|
3.5. Loss Functions
4. Experiments
4.1. Experimental Settings
4.2. Quantitative Experiment Results
4.3. Ablation Experiment
4.4. Qualitative Analysis
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yi, Z. nmODE: Neural memory ordinary differential equation. Artif. Intell. Rev. 2023, 56, 14403–14438. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings, Part III 18, Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Shoaib, M.A.; Lai, K.W.; Chuah, J.H.; Hum, Y.C.; Ali, R.; Dhanalakshmi, S.; Wang, H.; Wu, X. Comparative studies of deep learning segmentation models for left ventricle segmentation. Front. Public Health 2022, 10, 981019. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Chuah, J.H.; Lai, K.W.; Chow, C.O.; Gochoo, M.; Dhanalakshmi, S.; Wang, N.; Bao, W.; Wu, X. Conventional machine learning and deep learning in Alzheimer’s disease diagnosis using neuroimaging: A review. Front. Comput. Neurosci. 2023, 17, 1038636. [Google Scholar] [CrossRef] [PubMed]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Virtual, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Liu, Z.; Hu, H.; Lin, Y.; Yao, Z.; Xie, Z.; Wei, Y.; Ning, J.; Cao, Y.; Zhang, Z.; Dong, L.; et al. Swin transformer v2: Scaling up capacity and resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 12009–12019. [Google Scholar]
- Chen, J.; Lu, Y.; Yu, Q.; Luo, X.; Adeli, E.; Wang, Y.; Lu, L.; Yuille, A.L.; Zhou, Y. Transunet: Transformers make strong encoders for medical image segmentation. arXiv 2021, arXiv:2102.04306. [Google Scholar]
- Shen, J.; Lu, S.; Qu, R.; Zhao, H.; Zhang, L.; Chang, A.; Zhang, Y.; Fu, W.; Zhang, Z. A boundary-guided transformer for measuring distance from rectal tumor to anal verge on magnetic resonance images. Patterns 2023, 4, 100711. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, Y.; Wang, Y.; Hou, F.; Yuan, J.; Tian, J.; Zhang, Y.; Shi, Z.; Fan, J.; He, Z. A survey of visual transformers. arXiv 2023, arXiv:2111.06091. [Google Scholar] [CrossRef] [PubMed]
- Milletari, F.; Navab, N.; Ahmadi, S.A. V-net: Fully convolutional neural networks for volumetric medical image segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 565–571. [Google Scholar]
- Imran, A.A.Z.; Hatamizadeh, A.; Ananth, S.P.; Ding, X.; Terzopoulos, D.; Tajbakhsh, N. Automatic segmentation of pulmonary lobes using a progressive dense V-network. In Proceedings of the International Workshop on Deep Learning in Medical Image Analysis, Granada, Spain, 20 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 282–290. [Google Scholar]
- Ferreira, F.T.; Sousa, P.; Galdran, A.; Sousa, M.R.; Campilho, A. End-to-end supervised lung lobe segmentation. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–8. [Google Scholar]
- Tang, H.; Zhang, C.; Xie, X. Automatic pulmonary lobe segmentation using deep learning. In Proceedings of the 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), Venice, Italy, 8–11 April 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1225–1228. [Google Scholar]
- Lee, H.; Matin, T.; Gleeson, F.; Grau, V. Efficient 3D fully convolutional networks for pulmonary lobe segmentation in CT images. arXiv 2019, arXiv:1909.07474. [Google Scholar]
- Xie, W.; Jacobs, C.; Charbonnier, J.P.; Van Ginneken, B. Relational modeling for robust and efficient pulmonary lobe segmentation in CT scans. IEEE Trans. Med Imaging 2020, 39, 2664–2675. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.; Xu, X.; Feng, J.; Huang, H.; Zuo, X.; Xu, G.; Ma, G.; Chen, B.; Wu, J.; Huang, Y.; et al. Learnable interpolation and extrapolation network for fuzzy pulmonary lobe segmentation. IET Image Process. 2023, 17, 3258–3270. [Google Scholar] [CrossRef]
- Liu, J.; Wang, C.; Guo, J.; Shao, J.; Xu, X.; Liu, X.; Li, H.; Li, W.; Yi, Z. RPLS-Net: Pulmonary lobe segmentation based on 3D fully convolutional networks and multi-task learning. Int. J. Comput. Assist. Radiol. Surg. 2021, 16, 895–904. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NA, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Haber, E.; Ruthotto, L. Stable architectures for deep neural networks. Inverse Probl. 2017, 34, 014004. [Google Scholar] [CrossRef]
- Chen, R.T.Q.; Rubanova, Y.; Bettencourt, J.; Duvenaud, D.K. Neural Ordinary Differential Equations. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; Volume 31. [Google Scholar]
- Dupont, E.; Doucet, A.; Teh, Y.W. Augmented Neural ODEs. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Chen, R.T.Q.; Amos, B.; Nickel, M. Learning Neural Event Functions for Ordinary Differential Equations. In Proceedings of the International Conference on Learning Representations, Virtual Event, 3–7 May 2021. [Google Scholar]
- Zhang, T.; Yao, Z.; Gholami, A.; Gonzalez, J.E.; Keutzer, K.; Mahoney, M.W.; Biros, G. ANODEV2: A coupled neural ODE framework. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- Poucet, B.; Save, E. Attractors in memory. Science 2005, 308, 799–800. [Google Scholar] [CrossRef]
- Wills, T.J.; Lever, C.; Cacucci, F.; Burgess, N.; O’Keefe, J. Attractor dynamics in the hippocampal representation of the local environment. Science 2005, 308, 873–876. [Google Scholar] [CrossRef] [PubMed]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]




| (a) Comparison between the target method and previous state-of-art work training on the base dataset. | |||||||
| Model | Metric | RU | RM | RL | LU | LL | AVG |
| PLS-Net | DC | ||||||
| ASSD | |||||||
| Precision | |||||||
| Recall | |||||||
| Jaccard Index | |||||||
| RPLS-Net | DC | ||||||
| ASSD | |||||||
| Precision | |||||||
| Recall | |||||||
| Jaccard Index | |||||||
| nmPLS-Net | DC | ||||||
| ASSD | |||||||
| Precision | |||||||
| Recall | |||||||
| Jaccard Index | |||||||
| (b) Comparison between the target method and previous state-of-art work training on the LUNA16 dataset. | |||||||
| Model | Metric | RU | RM | RL | LU | LL | AVG |
| PLS-Net | DC | ||||||
| ASSD | |||||||
| Precision | |||||||
| Recall | |||||||
| Jaccard Index | |||||||
| RPLS-Net | DC | ||||||
| ASSD | |||||||
| Precision | |||||||
| Recall | |||||||
| Jaccard Index | |||||||
| nmPLS-Net | DC | ||||||
| ASSD | |||||||
| Precision | |||||||
| Recall | |||||||
| Jaccard Index | |||||||
| Model | Metric | RU | RM | RL | LU | LL | AVG |
|---|---|---|---|---|---|---|---|
| PLS-Net | DC | ||||||
| ASSD | |||||||
| Precision | |||||||
| Recall | |||||||
| Jaccard Index | |||||||
| RPLS-Net | DC | ||||||
| ASSD | |||||||
| Precision | |||||||
| Recall | |||||||
| Jaccard Index | |||||||
| nmPLS-Net | DC | ||||||
| ASSD | |||||||
| Precision | |||||||
| Recall | |||||||
| Jaccard Index |
| nmODE | FEAL | Metric | RU | RM | RL | LU | LL | AVG |
|---|---|---|---|---|---|---|---|---|
| DC | ||||||||
| ASSD | ||||||||
| Precision | ||||||||
| Recall | ||||||||
| Jaccard Index | ||||||||
| DC | ||||||||
| ASSD | ||||||||
| ✓ | Precision | |||||||
| Recall | ||||||||
| Jaccard Index | ||||||||
| DC | ||||||||
| ASSD | ||||||||
| ✓ | Precision | |||||||
| Recall | ||||||||
| Jaccard Index | ||||||||
| DC | ||||||||
| ASSD | ||||||||
| ✓ | ✓ | Precision | ||||||
| Recall | ||||||||
| Jaccard Index |
| Metric | (CE, Focal) | (Dice, Focal) | (CE+Dice, Focal) | (Dice+Focal, Dice) | (Dice+Focal, CE) | (CE+Focal, Focal) | (Dice+Focal, Focal) |
|---|---|---|---|---|---|---|---|
| mDC | |||||||
| mASSD | |||||||
| mPrecision | |||||||
| mRecall | |||||||
| mJaccard-Index |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, P.; Niu, H.; Yi, Z.; Xu, X. nmPLS-Net: Segmenting Pulmonary Lobes Using nmODE. Mathematics 2023, 11, 4675. https://doi.org/10.3390/math11224675
Dong P, Niu H, Yi Z, Xu X. nmPLS-Net: Segmenting Pulmonary Lobes Using nmODE. Mathematics. 2023; 11(22):4675. https://doi.org/10.3390/math11224675
Chicago/Turabian StyleDong, Peizhi, Hao Niu, Zhang Yi, and Xiuyuan Xu. 2023. "nmPLS-Net: Segmenting Pulmonary Lobes Using nmODE" Mathematics 11, no. 22: 4675. https://doi.org/10.3390/math11224675
APA StyleDong, P., Niu, H., Yi, Z., & Xu, X. (2023). nmPLS-Net: Segmenting Pulmonary Lobes Using nmODE. Mathematics, 11(22), 4675. https://doi.org/10.3390/math11224675






