Abstract
The goal of this paper is to build some approximate closed-form solutions for a class of dynamical systems involving a Hamilton–Poisson part. The chaotic behaviors are neglected. These solutions are obtained by means of a new version of the optimal parametric iteration method (OPIM), namely, the modified optimal parametric iteration method (mOPIM). The effect of the physical parameters is investigated. The Hamilton–Poisson part of the dynamical systems is reduced to a second-order nonlinear differential equation, which is analytically solved by the mOPIM procedure. A comparison between the approximate analytical solution obtained with mOPIM, the analytical solution obtained with the iterative method, and the corresponding numerical solution is presented. The mOPIM technique has more advantages, such as the convergence control (in the sense that the residual functions are smaller than 1), the efficiency, the writing of the solutions in an effective form, and the nonexistence of small parameters. The accuracy of the analytical and corresponding numerical results is illustrated by graphical and tabular representations. The same procedure could be successfully applied to more dynamical systems.
Keywords:
modified optimal parametric iteration method; periodical orbits; dynamical system; Hamilton–Poisson realization MSC:
37B65; 37C79; 65H20; 37J06; 37J35; 65L99
1. Introduction
Many nonlinear phenomena that appear in engineering, chemistry, physics, economics, and biology can be modeled by the nonlinear dynamical systems of the form , , where such that the system admits a Hamilton–Poisson structure (e.g., is a Hamilton–Poisson system) and is an additive term. There are two functionally independent constants of motion, (the Hamiltonian function) and (the Casimir function).
In the last decade, the dynamical properties have been examined by several researchers as bifurcation route, Poincar map, frequency spectrum, amplitude modulation, topological horseshoe, the existence of heteroclinic orbit or homoclinic orbit, equilibria, Lyapunov exponent spectrum, a dissipative system, phase portraits, bifurcation diagrams, and Hopf bifurcation. These properties characterize the chaotic behaviors of the dynamical system. Li et al. [1] studied a three-dimensional autonomous chaotic system that is found to possess two nonhyperbolic equilibria. Pham et al. [2] introduced a new system with an infinite number of equilibrium points. Wang et al. [3] presented a watermark encryption algorithm for a new memristive chaotic system. Zhang et al. [4] proposed a numerical scheme for the study of the dislocated projective synchronization (DPS) between the fractional-order and the integer-order chaotic systems. Tong [5] investigated the chaotic attractor for a three-dimensional (3D) chaotic system that possess invariable Lyapunov exponent spectra and controllable signal amplitude. He et al. [6] introduced a new four-dimensional chaotic system with coexisting attractors having three quadratic nonlinearities and only one unstable fixed point. Singh et al. [7] reported a new 4D dissipative chaotic system studying the coexistence of asymmetric hidden chaotic attractors with a curve of equilibria. Sun et al. [8] proposed a novel kind of compound–combination antisynchronization scheme among five chaotic systems. Cicek et al. [9] implemented in practical applications a new three-dimensional continuous time chaotic system by an electronic circuit design. Lai et al. [10] numerically investigated a new 3D autonomous chaotic system with coexisting attractors. Varan et al. [11] implemented a synchronization circuit model of a third-degree Malasoma system with chaotic flow. Su [12] investigated the horseshoe chaos using the topological horseshoe theory, taking into account a three-dimensional (3D) autonomous chaotic system. Zhou et al. [13] introduced and analyzed theoretically the basic dynamical properties of a three-dimensional chaotic system. The result shows the chaotic attractor by the realization of a circuit experiment. Akgul et al. [14] explored a three-dimensional chaotic system with cubic nonlinearities. They applied the electronic circuit implementation for real environment application. Pham et al. [15] introduced a three-dimensional chaotic system displaying both hidden attractors with infinite equilibria and hidden attractors without equilibrium. Zhang [16] investigated a method for generating complex grid multiwing chaotic attractors. Kacar [17] developed a four-dimensional chaotic system and implemented an analogue circuit and microcontroller. Tuna et al. [18] presented numerical, analog, and digital circuit modelings by using a 3D chaotic system with a single equilibrium point. Naderi et al. [19] explored the exponential synchronization of the chaotic system without a linear term and its application in secure communication by using the exponential stability theorem and showing the ability and effectiveness of the proposed method by numerical simulation. Li et al. [20] studied complicated dynamical behaviors of a three-dimensional chaotic system with quadratic nonlinearities.
Recently, Liu et al. [21] developed a new multiwing chaotic system that has an excellent effect on image encryption. Hu et al. [22] designed a circuit implementation to verify the physical feasibility of an asymmetric memristor-based chaotic system with only one equilibrium point. Sun et al. [23] studied a color image encryption scheme base on a 5D memristive chaotic system. Wang et al. [24] explored the problem in image encryption on the basis of a chaotic system with time delay. Guo et al. [25] proposed a multivortex hyperchaotic system, emphasizing its application to image encryption and outstanding anticropping and antinoise performance. Yildirim et al. [26] used the particle swarm optimization (PSO) and ant colony optimization (ACO) to optimize the initial conditions of a continuous-time chaotic system. Ding et al. [27] proposed a cryptosystem and its application in image encryption. Lai et al. [28] proposed a four-dimensional multiscroll chaotic system with application to image encryption. Lu et al. [29] proposed an encryption algorithm for 3D medical models.
Recently, Karimov et al. [30] implemented an analog circuit and proposed a novel technique for reconstructing ordinary differential equations (ODEs) describing the circuit from data. This technique is shown for a well-studied Rssler chaotic system. Karimov et al. [31] studied the synchronization between a circuit modeling the Rssler chaotic system and a computer model by using adaptive generalized synchronization.
Beyond chaotic behaviors, some systems could have nonlinear singularities. Such systems are investigated using the topological degree theory and the qualitative analysis of a Poincar map with action angle variables [32]. Cheng et al. [33] established the existence of homoclinic solutions for a differential inclusion system involving the -Laplacian by using a variational principle. Fonda et al. [34] proved the existence and multiplicity results for periodic solutions of Hamiltonian systems using the Poincar–Birkhoff fixed point theorem.
Many nonlinear differential problems from applied engineering are analytically solved by some methods, namely, the multiple scales technique [35], the optimal iteration parametrization method (OIPM) [36], the optimal homotopy asymptotic method (OHAM) [37,38,39], and the optimal homotopy perturbation method (OHPM) [40,41,42].
The structure of this paper is as follows: In Section 2, we present in detail some dynamical systems involving a Hamilton–Poisson part. The steps of the mOPIM technique are the subject of Section 3. Section 4 presents the semianalytical solutions obtained by the mOPIM method. Section 5 provides the numerical results and emphasizes the validation of the method. The conclusions and perspectives are highlighted in Section 6.
2. A Class of Dynamical Systems Involving a Hamilton–Poisson Part
The T system analyzed in [43] describes the stability of the chaotic behavior by an integrable deformation. This system has the following form:
with a chaotic behavior for some positive values, , , [44].
A Hamilton–Poisson part of the system (1) is
The functionally independent constants of motion of the system (2) are
Remark 1.
Considering the initial conditions:
the phase curves of dynamics (1) are the intersections of the following surfaces:
2.1. Closed-Form Solutions of the T System Involving a Hamilton–Poisson Part
For the system (2), there are following cases:
- (i)
- In the case , the transformations
The third equation from Equation (2) yields
From the first Equation (2), we obtain
- (ii)
- For , the closed-form solutions can be written as
Equation (2) yields
The following nonlinear problem gives the unknown function :
with .
2.2. Other 3D Dynamical Systems Involving a Hamilton–Poisson Part
- (i)
- A three-dimensional autonomous chaotic system with three multipliers presented in [45] ishaving a Hamilton–Poisson part, namely,with and .The closed-form solutions of the system (14) could be written aswhere , for .is an unknown smooth function, a solution of the nonlinear problem:If , then the closed-form solutions arewhere , is an unknown smooth function, a solution of the nonlinear problem (16), with the initial conditions
- (ii)
- The Qi chaotic system [46] has the formThe analysis of energy exchange was examined by transforming into a Kolmogorov-type system. It is shown that this system possesses four forms of energy, by decomposing the vector field of this chaotic system into four forms of torque: inertial, internal, dissipative, and external.The chaotic system presented in [47] isThe system can have hyperchaotic behaviors. A physically realizable system is shown by a circuit implementation of the chaotic system.The hyperchaotic system described in [48] isA circuit experiment was implemented, proving rich dynamics, and can exhibit periodic, quasi-periodic, chaos, and hyperchaos behavior.The last three chaotic systems have the same Hamilton–Poisson part, namely,with and .The proposed closed-form solutions of the system (22) arewhere , for , is an unknown smooth function, a solution of the nonlinear problem (16), being a particular case of the system (14) with .
- (iii)
- The chaotic system with hyperbolic sine nonlinearity [49]has a Hamilton–Poisson part, namely,with and .The closed-form solutions of the system (25) could bewhere , for , is an unknown smooth function, a solution of the nonlinear problem (16) (taking ) with the initial conditionsIf , then the closed-form solutions arewhere , is an unknown smooth function, a solution of the nonlinear problem (16), with the initial conditions
- (iv)
- The chaotic system explored in [50] has the formwith the Hamilton–Poisson part:with and .The closed-form solutions of the system (31) arewhere , for , is an unknown smooth function, a solution of the nonlinear problem (16) (taking b = m = d = 1) with the initial conditionsIf , then the closed-form solutions arewhere , is an unknown smooth function, a solution of the nonlinear problem (16) (taking b = m = d = 1), with the initial conditions
- (v)
- A hyperchaotic system [51] explores the phase portraits, Lyapunov exponents, bifurcation diagram, and Poincar map:The Hamilton–Poisson part iswith and .An electronic circuit was designed. This system generates multiwing nonequilibrium attractors.The closed-form solutions of the system (37) could bewhere , is an unknown smooth function, a solution to the nonlinear problem
- (vi)
- A three-dimensional autonomous chaotic system with only one positive term was explored in [52]:with a Hamilton–Poisson part, namely,with and .The closed-form solutions of the system (41) could be written aswhere , is an unknown smooth function, a solution of the nonlinear problem
- (vii)
- An autonomous chaotic system with cubic nonlinearity was presented in [53]:with the Hamilton–Poisson part, namely,with and .The closed-form solutions of the system (45) arewhere , for , is an unknown smooth function, a solution of the nonlinear problem:If , then the closed-form solutions arewhere , is an unknown smooth function, a solution of the nonlinear problem (47), with the initial conditions
- (viii)
- A three-dimensional chaotic system with a large scope was illustrated in [54]:with the Hamilton–Poisson partwith and .The closed-form solutions of the system (51) could bewhere , for , is an unknown smooth function, a solution of the nonlinear problem:If , then the closed-form solutions arewhere , is an unknown smooth function, a solution of the nonlinear problem (53), with the initial conditions
In the present paper, a modified version of the OPIM technique, namely, the modified optimal parametric iteration method (mOPIM), is proposed to obtain the approximate closed-form solutions of the system (2) subject to the initial conditions given by Equation (4).
3. The Basic Idea of the mOPIM Technique
Let the second-order nonlinear differential equation be
subject to the initial conditions
where is a linear operator, a nonlinear operator, a boundary operator, g a known function, u an unknown smooth function depending on the independent variable t, and .
Marinca et al. [36] proposed the following iterative scheme, namely, optimal parametric iteration method (OPIM), defined by
where , , and are auxiliary continuous functions; (obtained from Taylor series expansion of the nonlinear operator ); is the (n + 1)-th-order approximate solution of Equations (56) and (57), denoted by ; and is the initial approximation, a solution of the linear differential problem:
The real constants , , are are unknown convergence-control parameters and can be optimally computed.
Remark 2.
- (1)
- In the case of nonlinear oscillators, the integration of Equation (58) produces secular terms of the form , , , , , , and so on. The presence of has the advantage of avoiding the secular terms that appear through integration with the OPIM method, and that makes the oscillation amplitude tend toward infinity (physically, the resonance phenomenon occurs).
- (2)
- The OPIM method was successfully applied in the case of ODEs with boundary conditions (see Ref) [55], such as
- (a)
- Thin film flow of a fourth-grade fluid down a vertical cylinderwhere . The linear operator is chosen as .
- (b)
- Thermal radiation on MHD flow over a stretching porous sheetThe initial guess is chosen as and , with .
- (c)
- The oscillator with cubic and harmonic restoring forceThe linear operator is chosen as .
- (d)
- The Thomas–Fermi equationThe linear operator is chosen as , and the nonlinear operator yields .
- (e)
- Lotka–Volterra model with three speciesThe initial approximations are chosen as , , and or , , and , and so on.
Next, we propose a modified version of the OPIM procedure, namely, the modified optimal parametric iteration method (mOPIM), in the following form:
where the new auxiliary continuous function is a nonzero function and , , and have the same signification. The unknown real parameters , , , and are optimally computed at least.
The -order approximate solution of Equation (65) is well determined if the convergence-control parameters are known.
If is the initial approximation of Equation (59), the nonlinear operators , , , and that appear in Equation (65) have the form
where is a positive integer, and and are known functions that depend on .
Using the linearly independent functions , we introduce some types of approximate solutions of Equation (56).
Definition 1.
Functions of the mOPIM sequences are called mOPIM functions of Equation (56).
The mOPIM sequences with the property
are called convergent to the solution of Equation (56), where .
Definition 2.
The mOPIM functions satisfying the conditions
are called ε-approximate mOPIM solutions of Equation (56).
Definition 3.
The mOPIM functions satisfying the conditions
are called weak ε-approximate mOPIM solutions of Equation (56) on the real interval .
The existence of weak -approximate mOPIM solutions is built by the theorem presented above.
Theorem 1.
Equation (56) admits a sequence of weak ε-approximate mOPIM solutions.
Proof.
It is similar to the theorem from [56]. □
4. Approximate Analytic Solutions via mOPIM
This section emphasizes the applicability of the mOPIM procedure for the nonlinear differential problems given by Equations (8) and (9) using only one iteration. This problem could be written in the form of Equation (56), taking the following operators ():
Taking into consideration the linear operator given by Equation (71), the initial approximation , the solution of Equation (59) is
with , .
Using Equation (71), a simple computation yields the following expressions:
Returning to Equation (65), there are a lot of possibilities to choose the following auxiliary functions:
or and so on.
By the integration of Equation (65) and using the expressions given by Equations (71)–(75), the first-order approximate solution could be obtained:
with the unknown real parameters , , , , and , depending on the parameters , , , , , , , , , , , , , , and , and can be optimally identified.
Analogously, for the value , the expression is a linear combination between the elementary functions 1, , , , , , , , and .
Then the first-order approximate solution obtained from Equation (65) is a linear combination between the elementary functions 1, , , , , , , , and .
For an arbitrary integer number , inductively, the expression is a linear combination between the elementary functions 1, and , for . Therefore, the the first-order approximate solution will be of the form
where the unknown convergence-control parameters , , , , and for could be optimally computed.
Using the same procedure, the approximate closed-form solutions of the nonlinear problems presented in Section 2.2 could be obtained by means of the mOPIM method.
5. Numerical Results and Discussions
This section illustrates the validation of the applied method by a comparison between the obtained analytic results and the corresponding numerical ones. Additionally, the corresponding absolute errors are graphically and tabularly presented.
The unknown convergence-control parameters , , , , , and for from Equation (77) are optimally computed for some values of the index number and are exposed in Appendix A.
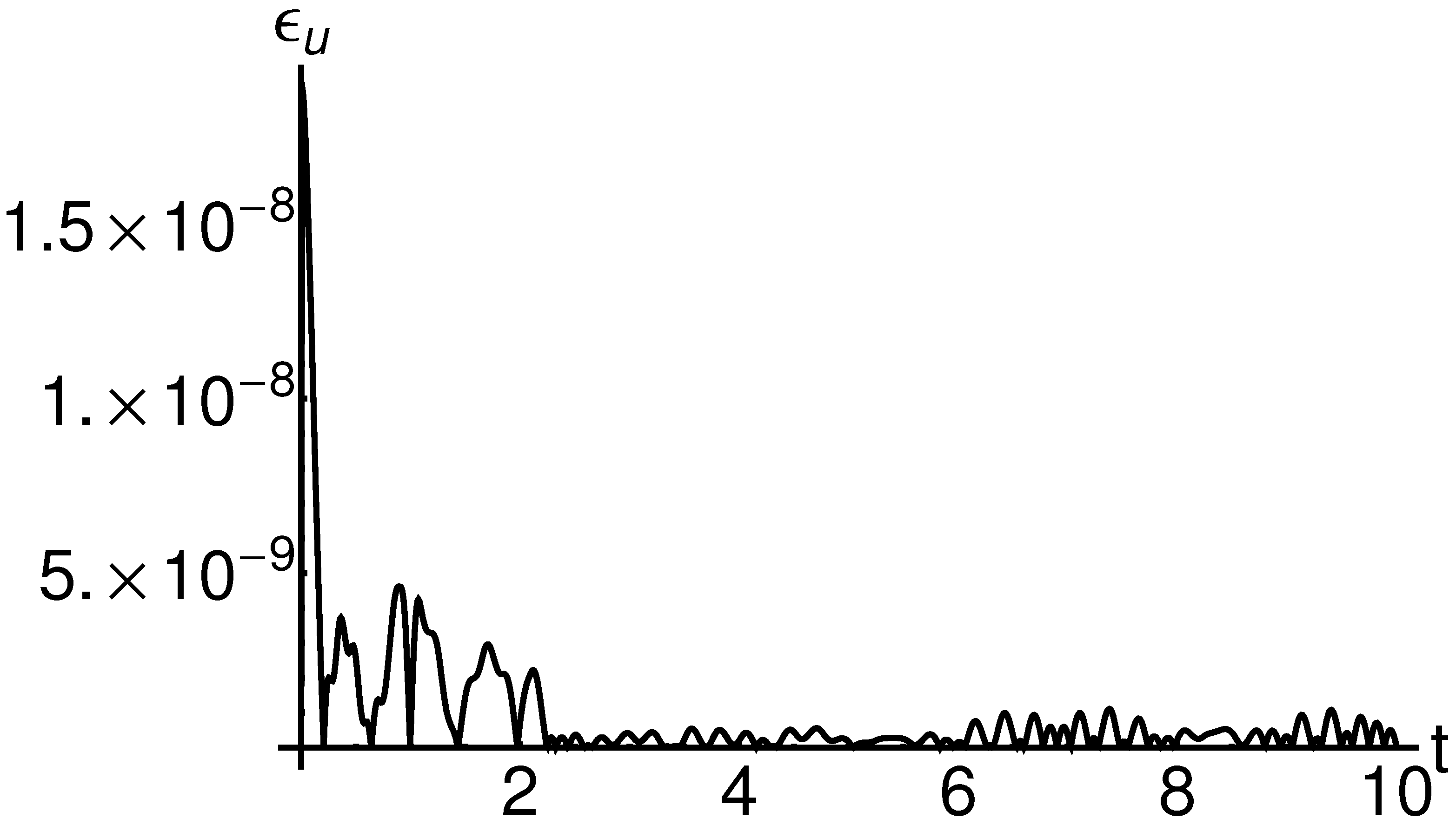
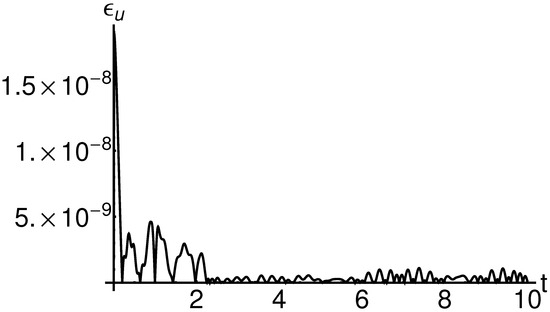
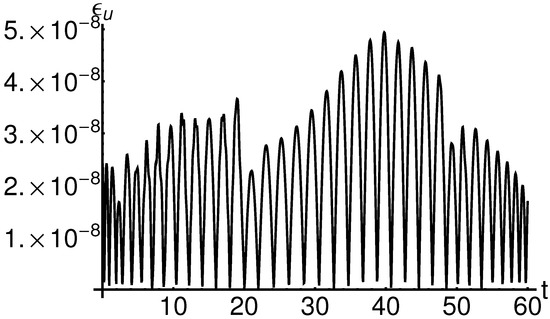
From Table 1 and Table 2, it is easy to see that a good agreement between the obtained analytic results and the corresponding numerical ones is revealed for . For this value of in Figure 1, the variation of absolute error is depicted.


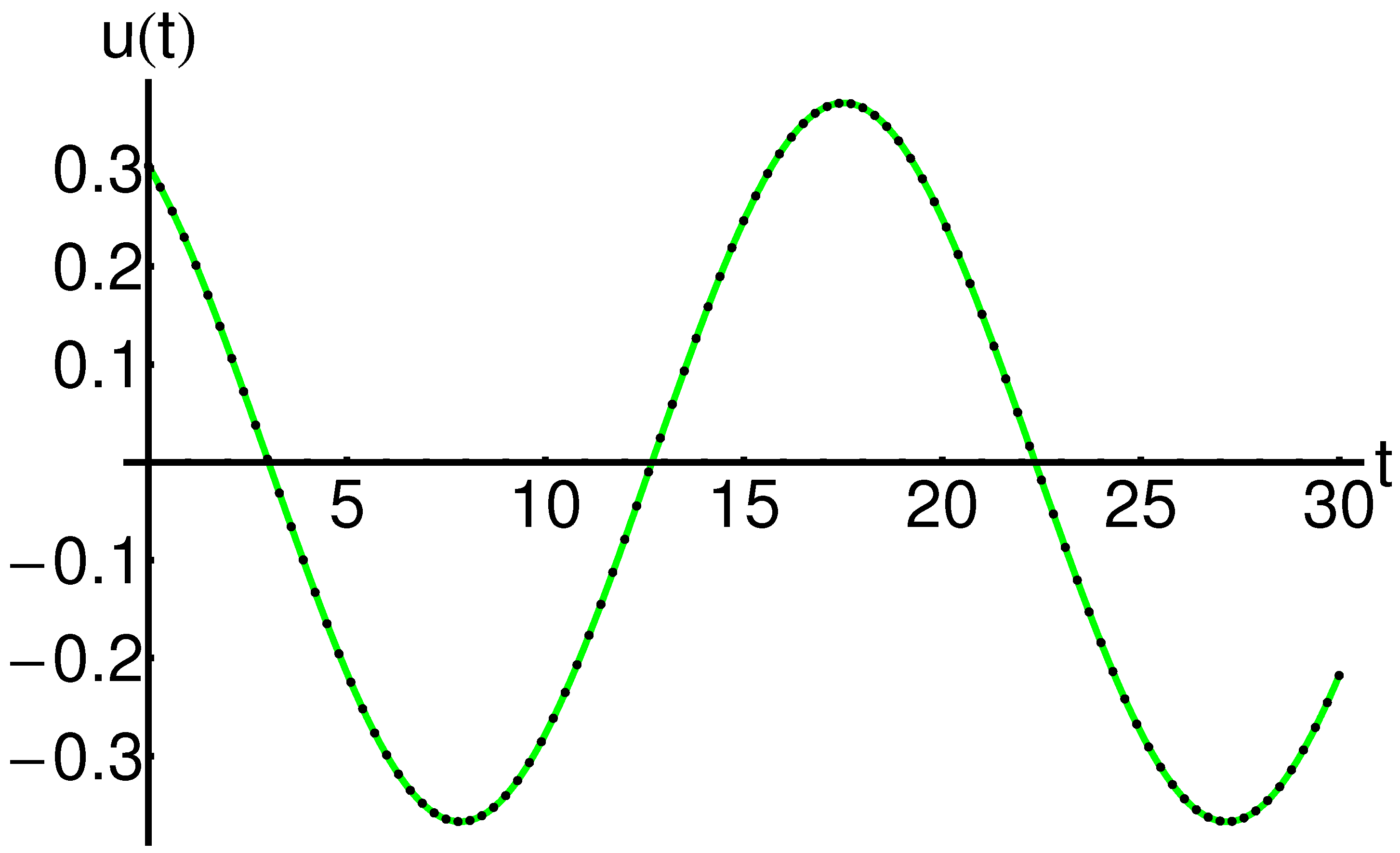
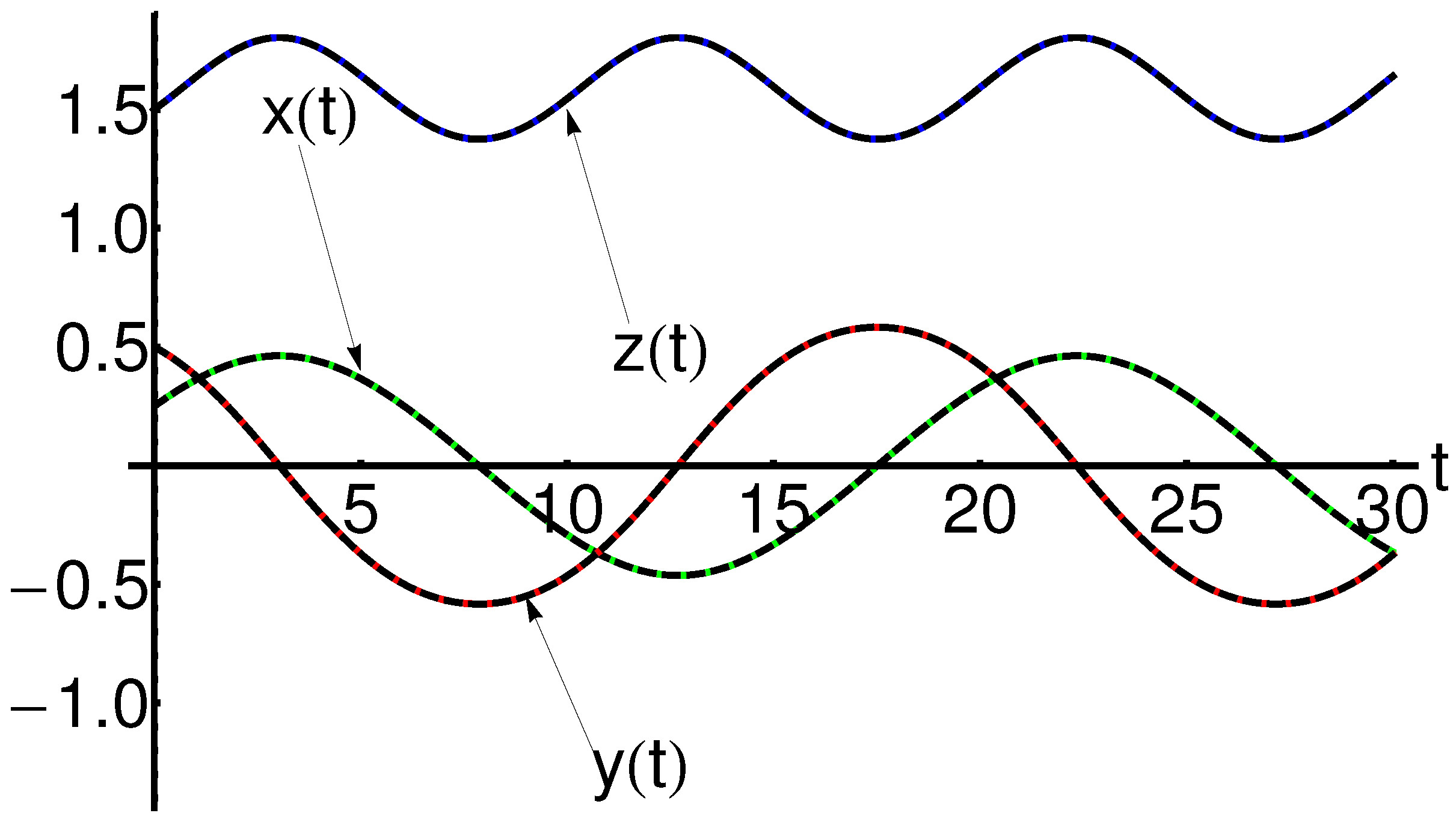
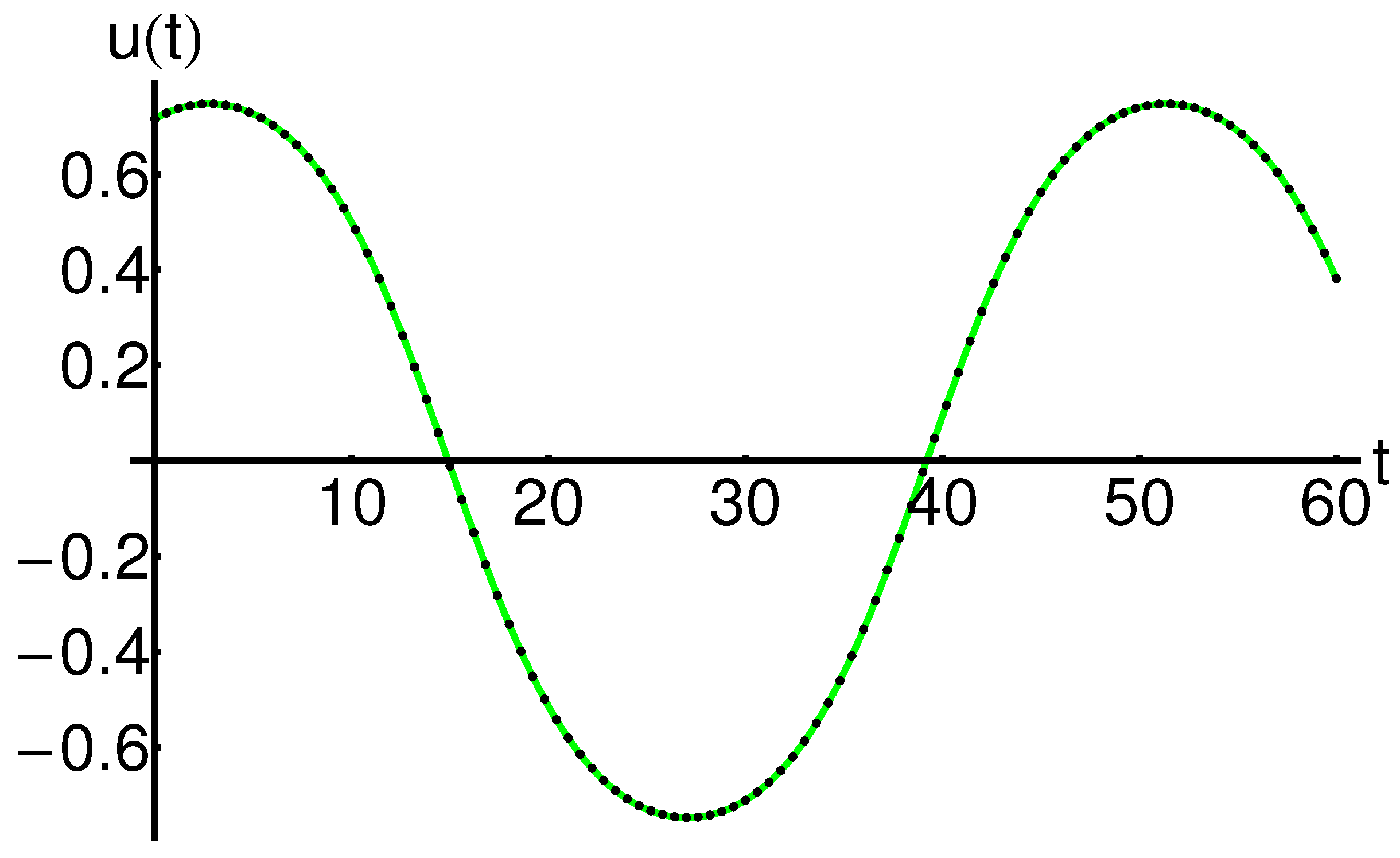
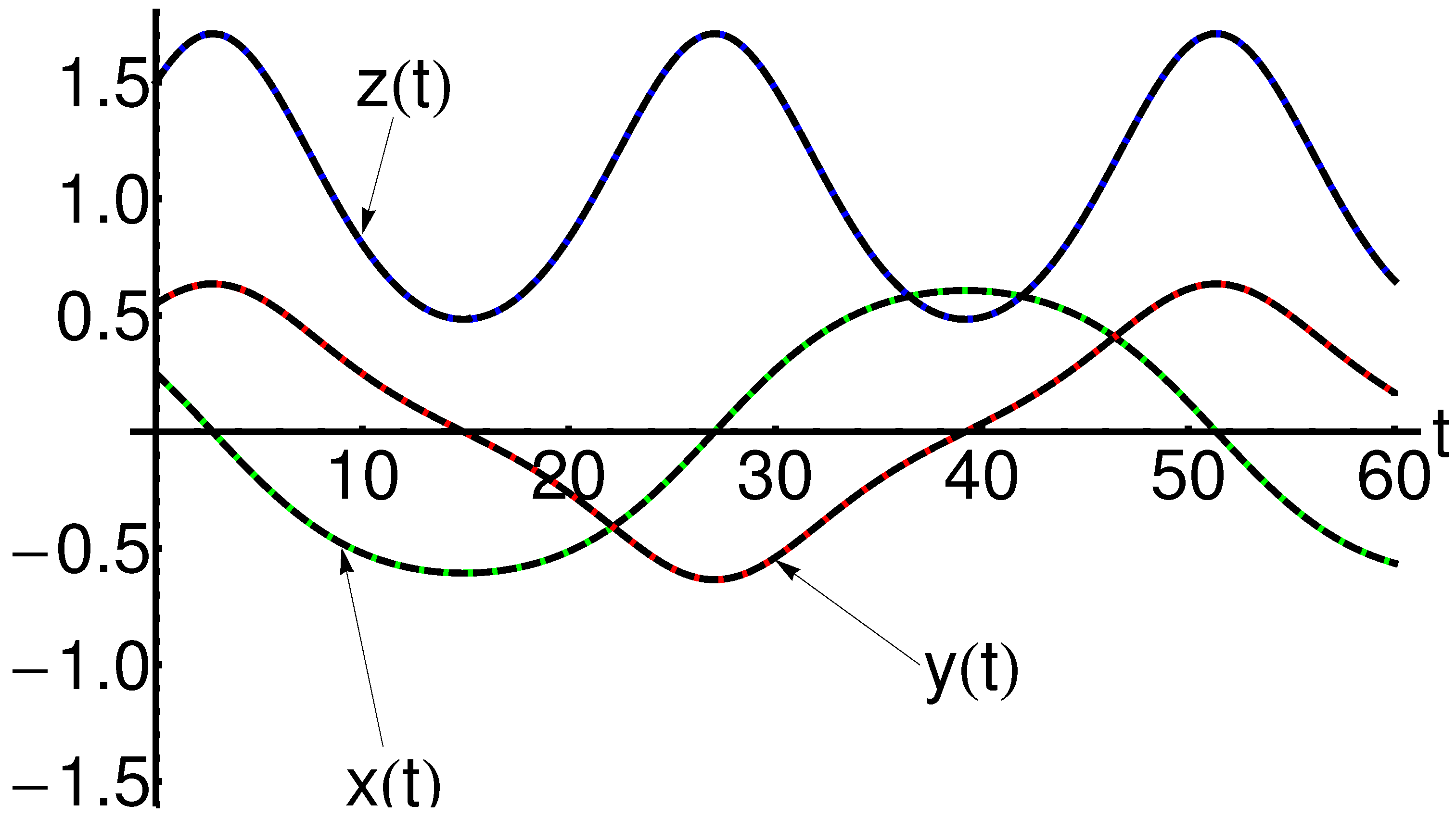
A comparison between the approximate analytic solution of Equations (8) and (9) given by Equation (77) and the corresponding numerical solution for is highlighted in Table 3 and Table 4 and qualitatively represented in Figure 2 and Figure 3. Similarly, for , the comparative solutions are exposed in Table 5 and Table 6, respectively, in Figure 4, Figure 5 and Figure 6.


Table 4.
The approximate analytic solution (7) and the corresponding numerical solution for , the initial conditions , , , and (absolute errors: ).
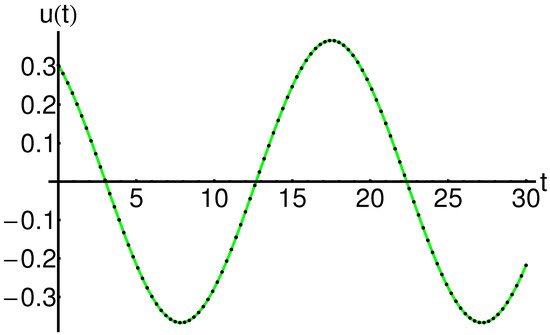
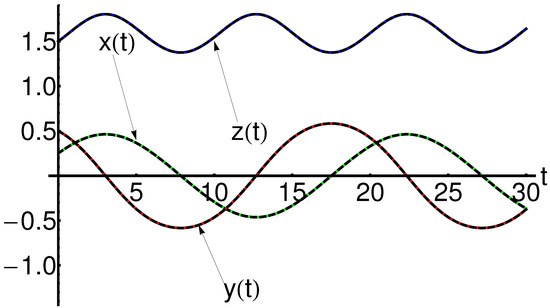


Table 6.
The approximate analytic solution (10) and the corresponding numerical solution for , the initial conditions , , , and (absolute errors: ).
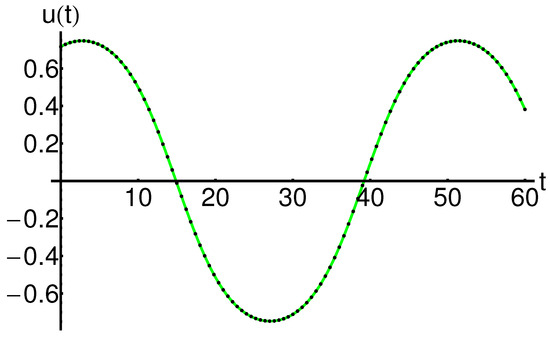
For the first dynamical system described in Section 2.2, the obtained solutions by the mOPIM technique and the corresponding numerical results are presented in detail by the comparison in Table 7, Table 8, Table 9, Table 10, Table 11 and Table 12.


Table 8.
The approximate analytic solution (15) and the corresponding numerical solution for , , and , the initial conditions , , , and (absolute errors: ).


Table 10.
The approximate analytic solution (26) and the corresponding numerical solution for the initial conditions , , , and (absolute errors: ).


Table 12.
The approximate analytic solution (32) and the corresponding numerical solution for the initial conditions , , , and (absolute errors: ).
mOPIM Solutions versus Iterative Solutions
To emphasize the advantages of the presented method, the iterative solutions are obtained by the iterative method [57].
If the system (2) is integrated over the interval , it results in
The iterative procedure leads to
The solutions of Equation (2), using the iterative algorithm, can be written as
The iterative solutions , after six iterations and considering the initial conditions, , , and (presented in Table 13), and the physical constant , taking into account the algorithm (79), become

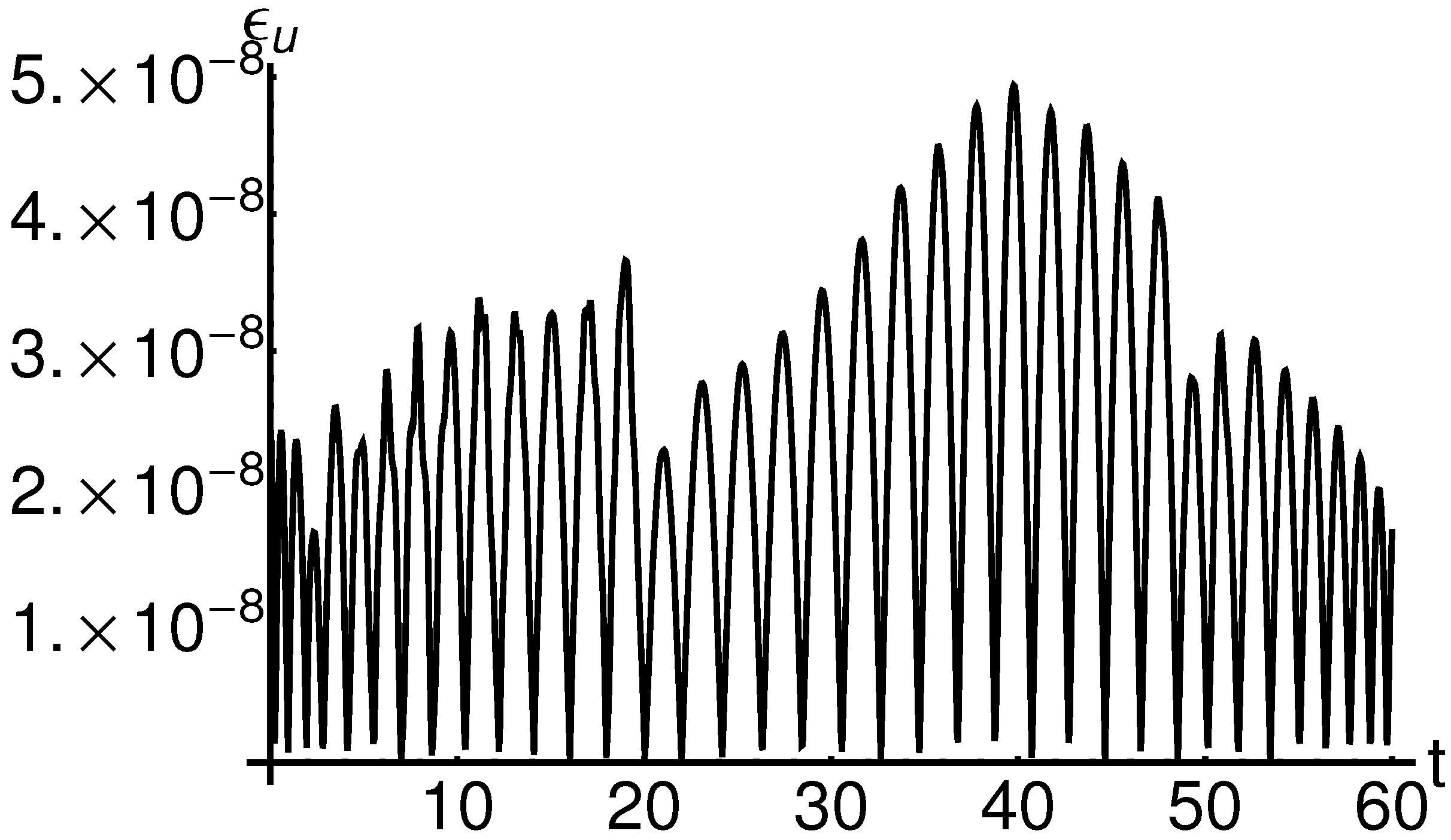
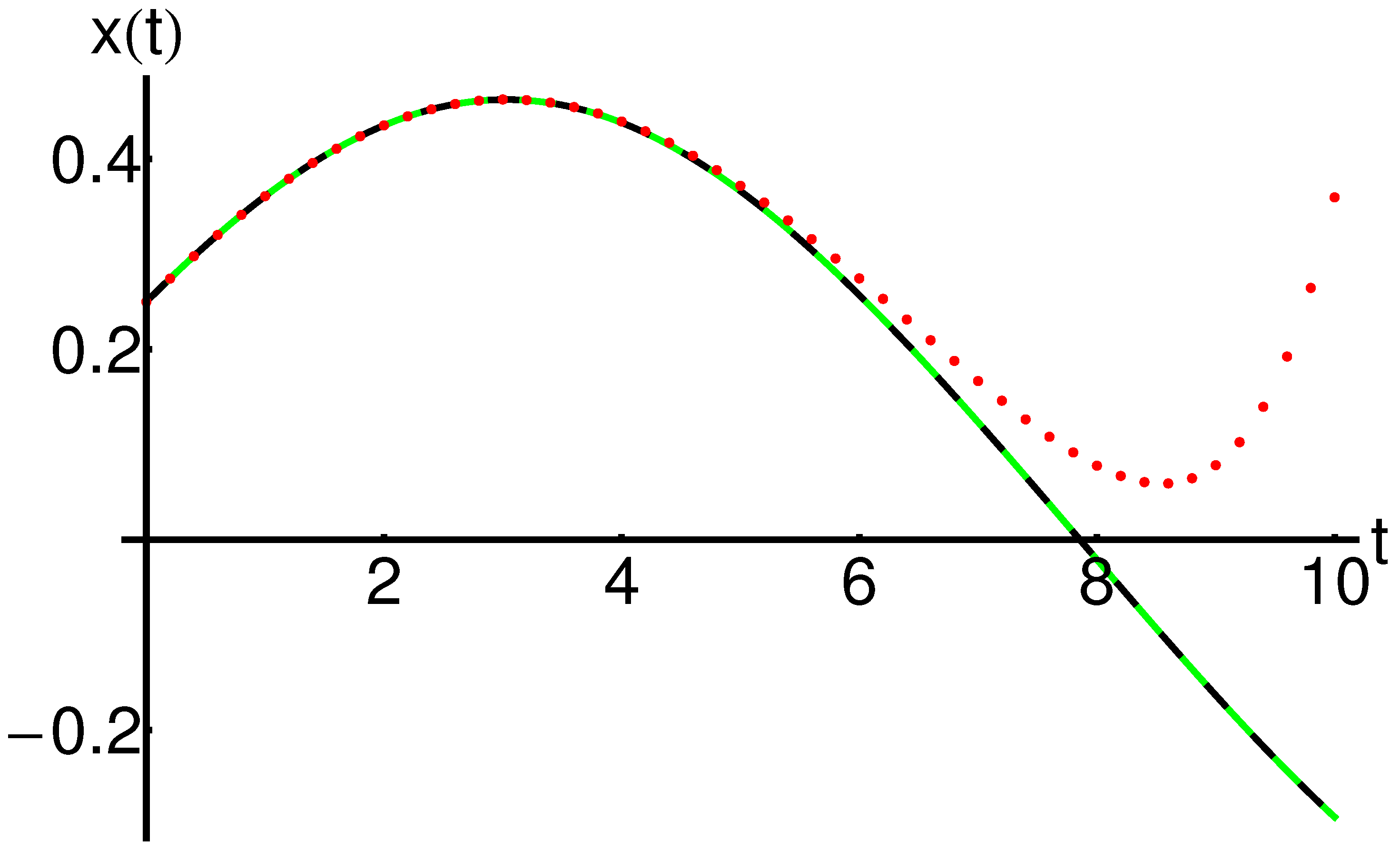
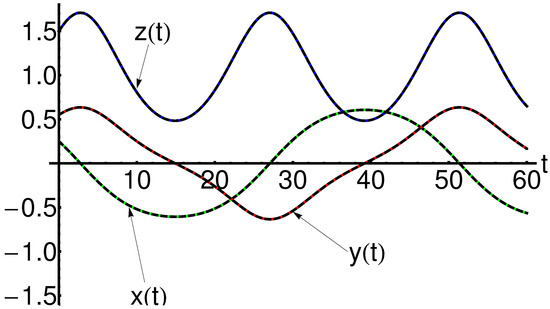
In Figure 7 and Table 13, respectively, is presented a parallel between the mOPIM solutions and the corresponding iterative solutions given in Equation (80). This comparative analysis highlights the efficiency and the accuracy of the modified mOPIM method using only one iteration.
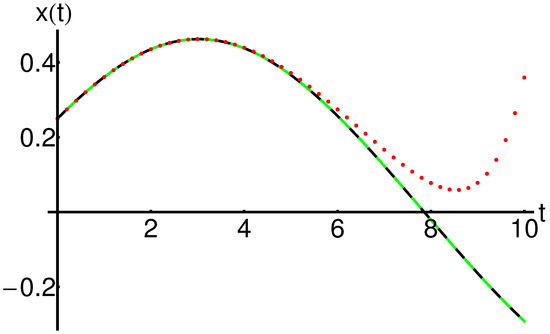
Figure 7.
Profile of the approximate analytical solution of Equation (2) given by Equation (A5), the iterative solution given by Equation (80), and the corresponding numerical solution: mOPIM solution (dashed line), iterative solution (dotted line), and numerical solution (solid line), respectively.
The precision and efficiency of the mOPIM method (using just one iteration) against the iterative method are described in [57] (using six iterations), arising from the presented comparison.
6. Conclusions
A new analytical approach, namely, the modified optimal parametric iteration method (mOPIM), for solving second-order nonlinear differential equations is developed using only one iteration.
In this way, the closed-form analytical approximate solutions are built for a class of nonlinear dynamical systems that possess a Hamilton–Poisson structure.
The obtained results are validated by graphically comparing them with the corresponding numerical solutions. The corresponding absolute errors are tabulated.
A comparison between the approximate analytical solution obtained with mOPIM, the analytical solution obtained with the iterative method, and the corresponding numerical solution highlights the advantages of the mOPIM method.
These comparisons prove the precision of the applied method in the sense that the semianalytical solutions are approaching the exact solution; e.g., the residual functions are much smaller than 1.
The achieved results have high potential, especially given the strong alignment demonstrated between the analytical and numerical outcomes, and they encourage the study of other dynamical systems with similar properties.
The possibility of a comparison between our results and some experiments based on the dynamical systems having a Hamilton–Poisson structure could be the subject of a future work.
Author Contributions
Conceptualization, N.P.; data curation, R.-D.E. and N.P.; formal analysis, N.P.; investigation, R.-D.E.; methodology, R.-D.E.; software, R.-D.E.; supervision, N.P.; validation, R.-D.E. and N.P.; visualization, R.-D.E. and N.P.; writing—original draft, R.-D.E. and N.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, C.-L.; Xiong, J.-B. A simple chaotic system with non-hyperbolic equilibria. Optik 2017, 128, 42–49. [Google Scholar] [CrossRef]
- Pham, V.-T.; Jafari, S.; Volos, C. A novel chaotic system with heart-shaped equilibrium and its circuital implementation. Optik 2017, 131, 343–349. [Google Scholar] [CrossRef]
- Wang, B.; Zoub, F.C.; Zhang, Y. New memritive chaotic system and the application in digital watermark. Optik 2018, 172, 873–878. [Google Scholar] [CrossRef]
- Zhang, X.-Q.; Xiao, J.; Zhang, Q. Dislocated projective synchronization between fractional-order chaotic systems and integer-order chaotic systems. Optik 2017, 130, 1139–1150. [Google Scholar] [CrossRef]
- Tong, Y.-N. Dynamics of a three-dimensional chaotic system. Optik 2015, 126, 5563–5565. [Google Scholar] [CrossRef]
- He, Y.; Xu, H.-M. Yet another four-dimensional chaotic system with multiple coexisting attractors. Optik 2017, 132, 24–31. [Google Scholar] [CrossRef]
- Singh, J.P.; Roy, B.K. Coexistence of asymmetric hidden chaotic attractors in a new simple 4-D chaotic system with curve of equilibria. Optik 2017, 145, 209–217. [Google Scholar] [CrossRef]
- Sun, J.; Shen, Y. Compound–combination anti–synchronization of five simplest memristor chaotic systems. Optik 2016, 127, 9192–9200. [Google Scholar] [CrossRef]
- Cicek, S.; Ferikoglu, A.; Pehlivan, I. A new 3D chaotic system: Dynamical analysis, electronic circuit design, active control synchronization and chaotic masking communication application. Optik 2016, 127, 4024–4030. [Google Scholar] [CrossRef]
- Lai, Q.; Chen, S. Research on a new 3D autonomous chaotic system with coexisting attractors. Optik 2016, 127, 3000–3004. [Google Scholar] [CrossRef]
- Varana, M.; Yalcin, F.; Uyaroglu, Y. Synchronizations and secure communication applications of a third degree Malasoma system with chaotic flow. Optik 2016, 127, 11086–11093. [Google Scholar] [CrossRef]
- Su, K. Dynamic analysis of a chaotic system. Optik 2015, 126, 4880–4886. [Google Scholar] [CrossRef]
- Zhou, W.J.; Wang, Z.P.; Wu, M.W.; Zheng, W.H.; Weng, J.F. Dynamics analysis and circuit implementation of a new three-dimensional chaotic system. Optik 2015, 126, 765–768. [Google Scholar] [CrossRef]
- Akgul, A.; Hussain, S.; Pehlivan, I. A new three-dimensional chaotic system, its dynamical analysis and electronic circuit applications. Optik 2016, 127, 7062–7071. [Google Scholar] [CrossRef]
- Pham, V.-T.; Jafari, S.; Volos, C.; Gotthans, T.; Wang, X.; Hoang, D.V. A chaotic system with rounded square equilibrium and with no-equilibrium. Optik 2017, 130, 365–371. [Google Scholar] [CrossRef]
- Zhang, C. Theoretical design and circuit realization of complex grid multi-wing chaotic system. Optik 2016, 127, 4584–4589. [Google Scholar] [CrossRef]
- Kacar, S. Analog circuit and microcontroller based RNG application of a new easy realizable 4D chaotic system. Optik 2016, 127, 9551–9561. [Google Scholar] [CrossRef]
- Tuna, M.; Fidan, C.B. Electronic circuit design, implementation and FPGA-based realization of a new 3D chaotic system with single equilibrium point. Optik 2016, 127, 11786–11799. [Google Scholar] [CrossRef]
- Naderi, B.; Kheiri, H. Exponential synchronization of chaotic system and application in secure communication. Optik 2016, 127, 2407–2412. [Google Scholar] [CrossRef]
- Li, C.; Li, H.; Tong, Y. Analysis of a novel three-dimensional chaotic system. Optik 2013, 124, 1516–1522. [Google Scholar] [CrossRef]
- Liu, S.; An, X.; Wang, Y.; Shi, Q. Design of a new multi-wing chaotic system and its application in color image encryption. Optik 2023, 290, 171334. [Google Scholar] [CrossRef]
- Hu, C.; Tian, Z.; Wang, Q.; Zhang, X.; Liang, B.; Jian, C.; Wu, X. A memristor-based VB2 chaotic system: Dynamical analysis, circuit implementation, and image encryption. Optik 2022, 269, 169878. [Google Scholar] [CrossRef]
- Sun, B.; Zhang, C.; Peng, Q.; Du, B. Color image encryption algorithm based on 5D memristive chaotic system and group scrambling. Optik 2023, 287, 171132. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, B.F.; Liu, X.W. An image encryption approach on the basis of a time delay chaotic system. Optik 2021, 225, 165737. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, J.; Xie, Q.; Hou, J. Multi-vortex hyperchaotic systems based on memristors and their application to image encryption. Optik 2023, 287, 171119. [Google Scholar] [CrossRef]
- Yildirim, G.; Tanyildizi, E. An innovative approach based on optimization for the determination of initial conditions of continuous-time chaotic system as a random number generator. Chaos Solitons Fractals 2023, 172, 113548. [Google Scholar] [CrossRef]
- Ding, D.; Wang, W.; Yang, Z.; Hu, Y.; Wang, J.; Wang, M.; Niu, Y.; Zhu, H. An n-dimensional modulo chaotic system with expected Lyapunov exponents and its application in image encryption. Chaos Solitons Fractals 2023, 174, 113841. [Google Scholar] [CrossRef]
- Lai, Q.; Chen, Z. Grid-scroll memristive chaotic system with application to image encryption. Chaos Solitons Fractals 2023, 170, 113341. [Google Scholar] [CrossRef]
- Lu, Y.; Gong, M.; Gan, Z.; Chai, X.; Cao, L.; Wang, B. Exploiting one-dimensional improved Chebyshev chaotic system and partitioned diffusion based on the divide-and-conquer principle for 3D medical model encryption. Chaos Solitons Fractals 2023, 171, 113449. [Google Scholar] [CrossRef]
- Karimov, A.I.; Rybin, V.G.; Kopets, E.E.; Karimov, T.I.; Nepomuceno, E.; Butusov, D. Identifying empirical equations of chaotic circuit from data. Nonlinear Dyn. 2023, 111, 871–886. [Google Scholar] [CrossRef]
- Karimov, A.; Tutueva, A.; Karimov, T.; Druzhina, O.; Butusov, D. Adaptive generalized synchronization between circuit and computer implementations of the Rössler system. Appl. Sci. 2021, 11, 81. [Google Scholar] [CrossRef]
- Liang, Z.; Li, S.; Li, X. Periodic and quasi-periodic solutions of a four-dimensional singular differential system describing the motion of vortices. Adv. Nonlinear Anal. 2023, 12, 20220287. [Google Scholar] [CrossRef]
- Cheng, J.; Chen, P.; Zhang, L. Homoclinic solutions for a differential inclusion system involving the p(t)-Laplacian. Adv. Nonlinear Anal. 2023, 12, 20220272. [Google Scholar] [CrossRef]
- Fonda, A.; Garrione, M.; Gidoni, P. Periodic perturbations of Hamiltonian systems. Adv. Nonlinear Anal. 2016, 5, 367–382. [Google Scholar] [CrossRef]
- Amer, T.S.; Bek, M.A.; Hassan, S.S.; Elbendary, S. The stability analysis for the motion of a nonlinear damped vibrating dynamical system with three-degrees-of-freedom. Results Phys. 2021, 28, 104561. [Google Scholar] [CrossRef]
- Marinca, V.; Draganescu, G.E. Construction of approximate periodic solutions to a modified van der Pol oscillator. Nonlinear Anal. Real World Appl. 2010, 11, 4355–4362. [Google Scholar] [CrossRef]
- Herisanu, N.; Marinca, V. Accurate analytical solutions to oscillators with discontinuities and fractional-power restoring force by means of the optimal homotopy asymptotic method. Comput. Math. Appl. 2010, 60, 1607–1615. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N. The Optimal Homotopy Asymptotic Method—Engineering Applications; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Marinca, V.; Herisanu, N. An application of the optimal homotopy asymptotic method to Blasius problem. Rom. J. Tech. Sci. Appl. Mech. 2015, 60, 206–215. [Google Scholar]
- Marinca, V.; Herisanu, N. Nonlinear dynamic analysis of an electrical machine rotor-bearing system by the optimal homotopy perturbation method. Comput. Math. Appl. 2011, 61, 2019–2024. [Google Scholar] [CrossRef]
- Marinca, V.; Ene, R.D.; Marinca, B. Optimal Homotopy Perturbation Method for nonlinear problems with applications. Appl. Math. Comput. 2022, 21, 123–136. [Google Scholar]
- Ene, R.D.; Pop, N. Semi-Analytical Closed-Form Solutions for the Rikitake-Type System through the Optimal Homotopy Perturbation Method. Mathematics 2023, 11, 3078. [Google Scholar] [CrossRef]
- Lazureanu, C.; Caplescu, C. Stabilization of the T system by an integrable deformation. ITM Web Conf. 2020, 34, 03009. [Google Scholar] [CrossRef]
- Tigan, G. Analysis of a dynamical system deriven from the Lorenz system. Sci. Bull. Politeh. Univ. Timis. 2005, 50, 61–72. [Google Scholar]
- Gholamin, P.; Sheikhani, A.H.R. A new three-dimensional chaotic system: Dynamical properties and simulation. Chin. J. Phys. 2017, 55, 1300–1309. [Google Scholar] [CrossRef]
- Qi, G.; Zhang, J. Energy cycle and bound of Qi chaotic system. Chaos Solitons Fractals 2017, 99, 7–15. [Google Scholar] [CrossRef]
- Liu, J. A four-wing and double-wing 3D chaotic system based on sign function. Optik 2014, 125, 7089–7095. [Google Scholar] [CrossRef]
- Li, C.-L.; Xiong, J.-B.; Wen, L. A new hyperchaotic system and its generalized synchronization. Optik 2014, 125, 575–579. [Google Scholar] [CrossRef]
- Wang, Z.; Volos, C.; Kingni, S.T.; Azar, A.T.; Pham, V.-T. Four-wing attractors in a novel chaotic system with hyperbolic sine nonlinearity. Optik 2017, 131, 1071–1078. [Google Scholar] [CrossRef]
- Lu, J.; Chen, G.; Cheng, D. A new chaotic system and beyond: The generalized Lorenz-like system. Int. J. Bifurc. Chaos 2004, 14, 1507–1537. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, J.; Cang, S.; Wange, Z.; Chen, Z. Simplified hyper-chaotic systems generating multi-wingnon-equilibrium attractors. Optik 2016, 127, 2424–2431. [Google Scholar] [CrossRef]
- Denga, K.; Yu, S. Estimating ultimate bound and finding topological horseshoe for a new chaotic system. Optik 2014, 125, 6044–6048. [Google Scholar] [CrossRef]
- Zhang, M.; Han, Q. Dynamic analysis of an autonomous chaotic system with cubic nonlinearity. Optik 2016, 127, 4315–4319. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, W. A new three-dimensional chaotic system with wide range of parameters. Optik 2013, 124, 5528–5532. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N. Nonlinear Dynamical Systems in Engineering; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Ene, R.D.; Pop, N.; Lapadat, M.; Dungan, L. Approximate Closed-Form Solutions for the Maxwell-Bloch Equations via the Optimal Homotopy Asymptotic Method. Mathematics 2022, 10, 4118. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Jafari, H. An iterative method for solving nonlinear functional equations. J. Math. Anal. Appl. 2006, 316, 753–763. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).