Subgradient Extra-Gradient Algorithm for Pseudomonotone Equilibrium Problems and Fixed-Point Problems of Bregman Relatively Nonexpansive Mappings

Abstract

In this article, we introduce a new subgradient extra-gradient algorithm to find the common element of a set of fixed points of a Bregman relatively nonexpansive mapping and the solution set of an equilibrium problem involving a Pseudomonotone and Bregman–Lipschitz-type bifunction in reflexive Banach spaces. The advantage of the algorithm is that it is run without prior knowledge of the Bregman–Lipschitz coefficients. Finally, two numerical experiments are reported to illustrate the efficiency of the proposed algorithm.

1. Introduction

Let X be a reflexive real Banach space and C be a closed, convex and nonempty subset of $X.$ We denote the dual space of X by $X^{\ast }.$ The minimization problem for a function $f:C\to \mathbb{R}$ is defined as

$$\begin{array}{c}\hfill \mathrm{Find}{x}^{\ast }\in C\mathrm{such}\mathrm{that}f\left(x^{\ast }\right)\le f\left(y\right),\forall y\in C.\end{array}$$

(1)

In this case, $x^{\ast }$ is called a minimizer of f, and ${\mathrm{Argmin}}_{y\in C}f\left(y\right)$ denotes the set of minimizers of f. Minimization problems are very useful in optimization theory as well as convex and nonlinear analysis. An important generalization of Problem (1) for a bifunction $f:C\times C\to \mathbb{R}$ is the following equilibrium problem (EP), defined as

$$\begin{array}{c}\hfill \mathrm{Find}{x}^{\ast }\in C\mathrm{such}\mathrm{that}f(x^{\ast },y)\ge 0,\forall y\in C.\end{array}$$

(2)

We denote by $\mathrm{EP}\left(f\right)$ the solutions set of (2). Many interesting and demanding problems in nonlinear analysis, such as complementarity, the fixed point, Nash equilibria, optimization, the saddle point and variational inequality problems, can be reformulated as equilibrium problems (cf. [1,2,3,4]). Some authors have obtained results regarding the existence and stability of solutions of (EP) (cf.  [5,6]).

However, equilibrium problems in finite as well as infinite dimensional spaces were studied by [7,8,9,10]. Dadashi et al. [11] studied the subgradient extra-gradient method for Pseudomonotone equilibrium problems.

Recently, several authors have combined equilibrium problems with fixed-point problems. They have presented algorithms to solve them in Hilbert spaces [9,12]. Also, some authors have presented several methods for solving fixed-point problems in metric spaces, see [13,14,15].

One of the most popular methods used to solve equilibrium problems is the extra-gradient method. Authors have considered the extra-gradient method for monotone and Pseudomonotone equilibrium problems [4,16,17,18,19,20,21].

In [8], Reich and Sabach studied equilibrium problems and fixed-point problems in Banach spaces. In their paper, they presented two algorithms to find the common fixed points of many finite, firmly nonexpansive Bregman operators. Very recently, inspired by the extra-gradient method, Yang and Liu [22] presented an algorithm, which is called the subgradient extra-gradient method, to find a common solution to equilibrium problems and the fixed point of a quasinonexpansive mapping without the knowledge of the Lipschitz-type constants of the bifunction in Hilbert spaces. The algorithm is as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{y}_n=\mathrm{argmin}\{{\lambda }_{n}f(x_n,y)+\frac{1}{2}{\parallel x_n-y\parallel }^2:y\in C\},\hfill \\ z_n=\mathrm{argmin}\{{\lambda }_{n}f(y_n,y)+\frac{1}{2}{\parallel x_n-y\parallel }^2:y\in T_n\},\hfill \\ t_n={\alpha }_n{x}_0+(1-{\alpha }_n)z_n,\hfill \\ x_{n+1}={\beta }_n{z}_n+(1-{\beta }_n)S{t}_n,\hfill \end{array}\right.\end{array}$$

where $\mu \in (0,1)$, ${\lambda }_0>0$ and $x_0\in H$ is arbitrary. Also,

$$T_n=\{v\in H:⟨x_n-{\lambda }_n{w}_n-y_n,v-y_n⟩⩽0\},$$

$w_n\in {\partial }_{2}f(x_n,y_n)$ such that $x_n-{\lambda }_n{w}_n-y_n\in N_C\left(y_n\right)$ and

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\lambda }_{n+1}=\left\{\begin{array}{cc}min\left\{\frac{\mu (\parallel z_n-y_n{\parallel }^2+\parallel y_n-x_n{\parallel }^2)}{f(x_n,z_n)-f(x_n,y_n)-f(y_n,z_n)},{\lambda }_n\right\},\hfill & iff(x_n,z_n)-f(x_n,y_n)-f(y_n,z_n)>0,\hfill \\ {\lambda }_n,\hfill & otherwise,\hfill \end{array}\right.\end{array}\end{array}$$

in addition, the sequences $\left\{{\alpha }_n\right\}$ and $\left\{{\beta }_n\right\}$ satisfy the conditions

(i)

$\left\{{\alpha }_n\right\}\subset [0,1]$ and ${\sum }_{n=0}^{\infty }{\alpha }_n=\infty ,$

(ii)

${lim\; sup}_{n\to \infty }{\beta }_n\le 0,$ or ${\sum }_{n=0}^{\infty }\left|{\alpha }_n{\beta }_n\right|<\infty .$

Inspired by the above work, in the present paper, we introduce a new subgradient extra-gradient algorithm to find the common element of a set of fixed points of a Bregman relatively nonexpansive mapping and the solution set of an equilibrium problem involving a Pseudomonotone and Bregman–Lipschitz-type bifunction in reflexive Banach spaces.

This paper is organized as follows: In Section 2, we recall some definitions and preliminary results. Section 3 deals with our algorithm and the relevant convergence analysis. Finally, in Section 4, we illustrate the proposed subgradient extra-gradient method by considering two numerical experiments.

2. Materials and Methods

In this section, we recall some definitions and preliminaries. Suppose that $f:X\to (-\infty ,\infty ]$ is a convex, proper and lower semicontinuous function. We denote by $\mathrm{Argmin}$ the set of minimizers of f. If $\mathrm{Argmin}f$ is a singleton, its unique element is denoted by ${\mathrm{argmin}}_{x\in X}$$f\left(x\right).$ Additionally, we denote by $\mathrm{dom}f$ the domain of f; that is, the set $\{x\in X:f(x)<\infty \}.$ Let $x\in \mathrm{int}\mathrm{dom}f$. Given the proper, convex and lower semicontinuous function $f:X\to (-\infty ,\infty ]$, its subdifferential at some $x\in X$ is defined as

$$\partial f\left(x\right)=\{\xi \in X^{\ast }:f\left(x\right)+⟨y-x,\xi ⟩\le f\left(y\right),\forall y\in X\}.$$

Concerning this definition, we have

(i)

$\partial f\left(x\right)$ is empty when $f\left(x\right)=\infty$,

(ii)

$\partial f\left(x\right)$ is not in general empty when $x\in \mathrm{dom}f$,

(iii)

$\partial f\left(x\right)$ is nonempty when $x\in \mathrm{int}\mathrm{dom}f$; precisely, $\mathrm{int}\mathrm{dom}f\subset \mathrm{dom}(\partial f)$.

It will be useful to stress these facts in the present exposition. The function $f^{\ast }:X^{\ast }\to (-\infty ,\infty ]$ defined by

$$f^{\ast }\left(\xi \right)=sup\{⟨x,\xi ⟩-f\left(x\right):x\in X\},$$

is called the Fenchel conjugate of $f.$ It can be shown that $\xi \in \partial f\left(x\right)$ is equivalent to

$$\begin{array}{c}\hfill f\left(x\right)+f^{\ast }\left(\xi \right)=⟨x,\xi ⟩.\end{array}$$

(3)

We can show that $f^{\ast }$ is a proper, convex and lower semicontinuous function. The function f is called cofinite if $\mathrm{dom}{f}^{\ast }=X^{\ast }.$ Let $f:X\to (-\infty ,+\infty ]$ be a convex function. Given $x\in \mathrm{int}\mathrm{dom}f$ and $y\in X,$ the right-hand derivative of f at x in the direction y is given by

$${\displaystyle f^{\circ }(x,y):=\underset{t\downarrow 0}{lim}\frac{f(x+ty)-f\left(x\right)}{t}.}$$

(4)

A function f is called Gâteaux differentiable at $x\in \mathrm{int}\mathrm{dom}f$ if the limit as $t\to 0$ in (4) exists for each $y.$ The function f is said to be Gâteaux differentiable if it is Gâteaux differentiable at each $x\in \mathrm{int}\mathrm{dom}f.$ In this case, the gradient of f at x is the linear function $\nabla f\left(x\right),$ which is defined by $⟨y,\nabla f\left(x\right)⟩:=f^{\circ }(x,y)$ for all $y\in X$. We say that f is Fréchet differentiable at x if it is Gâteaux differentiable and the limit as $t\to 0$ in (4) is attained uniformly for every $y\in X$ with $\parallel y\parallel =1$. Also, we say that f is uniformly Fréchet differentiable on a bounded subset E of X if the limit is attained uniformly for $x\in E$ and $\parallel y\parallel =1$.

The function $f:X\to (-\infty ,+\infty )$ is called Legendre if it satisfies the following two conditions:

• (L1) $\mathrm{int}\mathrm{dom}f\ne \varnothing$ and subdifferential $\partial f$ is single valued on its domain,
• (L2) $\mathrm{int}\mathrm{dom}{f}^{\ast }\ne \varnothing$ and $\partial f^{\ast }$ is single valued on its domain.

Since X is reflexive, we always have ${(\partial f)}^{-1}=\partial f^{\ast }$ (see [23], p. 83). This fact, combined with Conditions (L1) and (L2), implies the following equalities which will be very useful in the sequel:

$$\begin{array}{cc}\hfill \nabla f=& {(\nabla f^{\ast })}^{-1},\hfill \\ \hfill \mathrm{ran}\nabla f=& \mathrm{dom}\nabla f^{\ast }=\mathrm{int}\mathrm{dom}{f}^{\ast },\hfill \\ \hfill \mathrm{ran}\nabla f^{\ast }=& \mathrm{dom}\nabla f=\mathrm{int}\mathrm{dom}f.\hfill \end{array}$$

Also, Conditions (L1) and (L2), in conjunction with Theorem 5.4 of  [24], imply that the functions f and $f^{\ast }$ are strictly convex on the interior of their respective domains and f is Legendre if and only if $f^{\ast }$ is Legendre. Several interesting examples of Legendre functions are presented in [24]. Among them are the functions $\frac{1}{p}{\parallel ·\parallel }^p$ with $p\in (1,\infty )$, where the Banach space X is smooth and strictly convex.

Given a Gâteaux differentiable convex function $f:X\to \mathbb{R},$ the Bregman distance with respect to f is defined as

$$D_f(x,y):=f\left(x\right)-f\left(y\right)-⟨\nabla f\left(y\right),x-y⟩,x,y\in E.$$

Note that $D_f:\mathrm{dom}f\times \mathrm{int}\mathrm{dom}f\to [0,+\infty ]$ is not a distance in the usual sense of the term. In general, $D_f$ is not symmetric and does not satisfy the triangle inequality. Clearly, $D_f(x,x)=0$, but $D_f(y,x)=0$ may not imply $x=y.$ In our case, when f is Legendre, this indeed holds (see [24], Theorem 7.3(vi)). However, $D_f$ satisfies the three-point identity

$$D_f(x,y)+D_f(y,z)-D_f(x,z)=⟨x-y,\nabla f\left(z\right)-\nabla f\left(y\right)⟩,$$

and four-point identity

$$D_f(x,y)+D_f(w,z)-D_f(x,z)-D_f(w,y)=⟨x-w,\nabla f\left(z\right)-\nabla f\left(y\right)⟩,$$

for any $x,w\in \mathrm{dom}f$ and $y,z\in \mathrm{int}\mathrm{dom}f.$

More information regarding Bregman functions and distances can be found in [4,24,25,26,27,28,29,30,31]. A function $f:X\to (-\infty ,+\infty ]$ is called totally convex at a point $x\in \mathrm{int}\mathrm{dom}f$ if its modulus of total convexity at x, that is, the function ${\upsilon }_f(x,·):[0,+\infty )\to [0,\infty ],$ defined by

$${\upsilon }_f(x,t):=inf\{D_f(y,x):y\in \mathrm{dom}f,\parallel y-x\parallel =t\},$$

is positive whenever $t>0.$ This notion was first introduced by Butnariu and Iusem in [28]. Let E be a nonempty subset of X. The modulus of the total convexity of f on E is defined by

$${\upsilon }_f(E,t)=inf\{{\upsilon }_f(x,t):x\in E\cap \mathrm{int}\mathrm{dom}f\}.$$

A function f is called totally convex on bounded subsets if ${\upsilon }_f(E,t)$ is positive for any nonempty and bounded subset E and for any $t>0.$ We will need the following lemmas in the proof of our results.

Lemma 1 

([32]). If $f:X\to \mathbb{R}$ is uniformly Fréchet differentiable and bounded on bounded subsets of X, then $\nabla f$ is uniformly continuous on bounded subsets of X from the strong topology of X to the strong topology of $X^{\ast }.$

The function f is called sequentially consistent (see [33]) if, for any two sequences $\left\{x_n\right\}\subset \mathrm{dom}f$ and $\left\{y_n\right\}\subset \mathrm{int}\mathrm{dom}f$, such that $\left\{x_n\right\}$ is bounded,

$$\underset{n\to \infty }{lim}{D}_f(y_n,x_n)=0,$$

and this implies that

$$\underset{n\to \infty }{lim}\parallel y_n-x_n\parallel =0.$$

Lemma 2 

([28]). If $\mathrm{dom}f$ contains at least two points, then the function f is totally convex on bounded sets if and only if the function f is sequentially consistent.

Lemma 3 

([34]). Let $f:X\to \mathbb{R}$ be a Legendre function such that $\nabla f^{\ast }$ is bounded on bounded subsets of $\mathrm{int}\mathrm{dom}{f}^{\ast }$. Let $x_0\in X$. If  $\left\{D_f(x_0,x_n)\right\}$ is bounded, then the sequence $\left\{x_n\right\}$ is bounded too.

Let f be a function and C be a closed, convex and nonempty subset of $\mathrm{int}\mathrm{dom}f.$

The Bregman projection (see [35]) concerning f of $x\in \mathrm{int}\mathrm{dom}f$ onto C is defined as the necessarily unique vector ${\overleftarrow{\mathrm{Proj}}}_C^f\left(x\right)\in C$, which satisfies

$$D_f({\overleftarrow{\mathrm{Proj}}}_C^f\left(x\right),x)=inf\{D_f(y,x):y\in C\}.$$

The Bregman projection concerning totally convex and Gâteaux differentiable functions has a variational characterization ([33], Corollary 4.4, p. 23).

Lemma 4. 

Let f be Gâteaux differentiable and totally convex on $\mathrm{int}$ $\mathrm{dom}$f. Let C be a closed, convex and nonempty subset of $\mathrm{int}\mathrm{dom}f$ and $x\in \mathrm{int}\mathrm{dom}f.$ Then, the following statements are equivalent:

(i) 

The vector $\widehat{x}\in C$ is the Bregman projection of x onto C concerning $f.$

(ii) 

The vector $\widehat{x}\in C$ is the unique solution of the variational inequality

$$⟨z-y,\nabla f\left(x\right)-\nabla f\left(z\right)⟩\ge 0,\forall y\in C.$$

(iii) 

The vector $\widehat{x}\in C$ is the unique solution of the inequality

$$D_f(y,z)+D_f(z,x)\le D_f(y,x),\forall y\in C.$$

With an admissible function $f:X\to (-\infty ,+\infty ],$ we associate the bifunction $V_f:X\times X^{\ast }\to [0,+\infty ]$ (see [36,37]) defined by

$$V_f(x,x^{\ast })=f\left(x\right)-⟨x,x^{\ast }⟩+f^{\ast }\left(x^{\ast }\right),\forall x\in X,x^{\ast }\in X^{\ast }.$$

Recall some properties of the bifunction $V_f.$ For all $x\in X$ and $x^{\ast }\in X^{\ast },$ we have

$$\begin{array}{c}\hfill V_f(x,x^{\ast })=D_f(x,\nabla f^{\ast }\left(x^{\ast }\right)),\end{array}$$

(5)

Also, for all $x\in X$ and $x^{\ast },y^{\ast }\in X^{\ast }$ (see [38]), we have

$$\begin{array}{c}\hfill V_f(x,x^{\ast })+⟨\nabla f^{\ast }\left(x^{\ast }\right)-x,y^{\ast }⟩\le V_f(x,x^{\ast }+y^{\ast }),\end{array}$$

(6)

Let $f:X\to (-\infty ,+\infty ]$ be a proper, lower semicontinuous function. Then, $f^{\ast }:X^{\ast }\to (-\infty ,+\infty ]$ is a proper, convex and weak${}^{\ast }$ lower semicontinuous function (see [39]). Therefore, $V_f$ is convex concerning the second variable. Hence, we have

$$\begin{array}{c}\hfill D_f\left(z,\nabla f^{\ast }\left(\sum _{i=1}^N{t}_i\nabla f\left(x_i\right)\right)\right)\le \sum _{i=1}^N{t}_i{D}_f(z,x_i),\forall z\in X,\end{array}$$

(7)

where ${\left\{x_i\right\}}_{i=1}^N\subset X$ and ${\left\{t_i\right\}}_{i=1}^N\subset (0,1)$ with ${\sum }_{i=1}^N{t}_i=1.$

Let B be the closed unit ball and S be the unit sphere of a Banach space X. Let $rB:=\{z\in X:\parallel z\parallel \le r\}$ for all $r>0$ and $f:X\to \mathbb{R}$ be a function. We say that f is uniformly convex on bounded subsets (see [40]) if ${\rho }_r\left(t\right)>0$ for all $r,t>0$, where ${\rho }_r:[0,\infty )\to [0,\infty ]$ is the gauge of the uniform convexity of f and is defined by

$${\rho }_r\left(t\right)=\underset{x,y\in rB,\parallel x-y\parallel =t,\alpha \in (0,1)}{inf}\frac{\alpha f\left(x\right)+(1-\alpha )f\left(y\right)-f(\alpha x+(1-\alpha \left)y\right)}{\alpha (1-\alpha )},\forall t\ge 0.$$

Lemma 5 

([41]). Let $f:X\to \mathbb{R}$ be a uniformly convex function on bounded subsets of X and $r>0$ be a constant. Then,

$$f\left(\sum _{k=0}^n{\alpha }_k{x}_k\right)\le \sum _{k=0}^n{\alpha }_{k}f\left(x_k\right)-{\alpha }_i{\alpha }_j{\rho }_r\left(\parallel x_i-x_j\parallel \right),$$

for all $i,j\in \{0,1,2,...,n\}$, $x_k\in rB$, ${\alpha }_k\in (0,1)$ and $k=0,1,2,...,n$ with ${\displaystyle \sum _{k=0}^n{\alpha }_k=1,}$ where ${\rho }_r$ is the gauge of the uniform convexity of f.

The function f is also said to be uniformly smooth on bounded subsets (see [40]) if

$$\underset{t\downarrow 0}{lim}\frac{{\sigma }_r\left(t\right)}{t}=0\mathrm{for}\mathrm{all}r>0,$$

where ${\sigma }_r:[0,\infty )\to [0,\infty ]$ is defined by

$${\sigma }_r\left(t\right)=\underset{x\in rB,y\in S,\alpha \in (0,1)}{sup}\frac{\alpha f(x+(1-\alpha \left)ty\right)+(1-\alpha )f(x-\alpha ty)-f\left(x\right)}{\alpha (1-\alpha )},$$

for all $t\ge 0.$ A function f is said to be super coercive if

$$\underset{\parallel x\parallel \to \infty }{lim}\frac{f\left(x\right)}{\parallel x\parallel }=+\infty .$$

Theorem 1 

([40]). Let $f:X\to \mathbb{R}$ be a super coercive convex function. Then, the following are equivalent:

(i) 

f is uniformly smooth on bounded

subsets of X and bounded on bounded subsets.

(ii) 

f is Fréchet differentiable and $\nabla f$ is uniformly

norm-to-norm continuous on bounded subsets of X.

(iii) 

$\mathrm{dom}$$f^{\ast }=X^{\ast },$$f^{\ast }$ is super coercive and uniformly convex on bounded subsets of $X^{\ast }$.

Theorem 2 

([40]). Suppose that $f:X\to \mathbb{R}$ is a convex function which is bounded on bounded subsets of X; then, the following are equivalent:

(i) 

f is super coercive and uniformly convex on bounded subsets of X.

(ii) 

$\mathrm{dom}$$f^{\ast }=X^{\ast },$$f^{\ast }$ is bounded on bounded subsets and

uniformly smooth on bounded subsets of $X^{\ast }$.

(iii) 

$\mathrm{dom}$$f^{\ast }=X^{\ast },$$f^{\ast }$ is Fréchet differentiable and $\nabla f^{\ast }$ is uniformly norm-to-norm continuous on bounded subsets of $X^{\ast }$.

Theorem 3 

([42]). Suppose that $f:X\to (-\infty ,+\infty ]$ is a Legendre function. The function f is totally convex on bounded subsets if and only if f is uniformly convex on bounded subsets.

Lemma 6 

([43]). Let C be a nonempty convex subset of X and $f:C\to \mathbb{R}$ be a convex and subdifferentiable function on C. Then, f attains its minimum at $x\in C$ if and only if $0\in \partial f\left(x\right)+N_C\left(x\right)$, where $N_C\left(x\right)$ is the normal cone of C at x; that is,

$$N_C\left(x\right):=\{x^{\ast }\in X^{\ast }:⟨x-z,x^{\ast }⟩\ge 0,\forall z\in C\}.$$

Lemma 7 

([44]). Let f and g be two convex functions on X such that there is a point $x_0\in \mathrm{dom}f\cap \mathrm{dom}g$ where f is continuous. Then,

$$\partial (f+g)\left(x\right)=\partial f\left(x\right)+\partial g\left(x\right),\forall x\in X.$$

Let C be a closed convex subset of X. A function $g:X\times X\to (-\infty ,+\infty ],$ such that $g(x,x)=0$ for all $x\in C$, is called a bifunction.

Throughout this paper, we consider bifunctions with the following properties:

• $B1.$g is monotone on C, that is

$$g(x,y)+g(y,x)\le 0,\forall x,y\in C.$$

• $B2.$g is Pseudomonotone on C; that is,

$$g(x,y)\ge 0\Rightarrow g(y,x)\le 0,\forall x,y\in C.$$

• $B3.$g is Bregman $\gamma$- strongly Pseudomonotone on C if there exists a constant $\gamma \ge 0$ such that

$$g(x,y)\ge 0\Rightarrow g(y,x)\le -\gamma D_f(y,x),\forall x,y\in C.$$

• $B4.$g is Bregman–Lipschitz-type continuous on C; that is, there exist two positive constants $c_1,c_2$ such that

$$g(x,y)+g(y,z)\ge g(x,z)-c_1{D}_f(y,x)-c_2{D}_f(z,y),\forall x,y,z\in C,$$

the constants $c_1,c_2$ are called Bregman–Lipschitz coefficients with respect to f (See [19]).

Lemma 8 

([19]). Let C be a nonempty closed convex subset of a reflexive Banach space X and $f:X\to \mathbb{R}$ be a Legendre and super coercive function. Suppose that $g:X\times X\to \mathbb{R}$ is a bifunction satisfying $B1-B4$. For the arbitrary sequences $\left\{x_n\right\}\subset C$ and $\left\{{\lambda }_n\right\}\subset (0,+\infty ),$ let $\left\{w_n\right\}$ and $\left\{z_n\right\}$ be sequences generated by

$$\left\{\begin{array}{c}{w}_n=\mathrm{argmin}\{{\lambda }_{n}g(x_n,y)+D_f(y,x_n):y\in C\},\hfill \\ z_n=\mathrm{argmin}\{{\lambda }_{n}g(w_n,y)+D_f(y,x_n):y\in C\}.\hfill \end{array}\right.$$

Then, we have

$$D_f(x^{\ast },z_n)\le D_f(x^{\ast },x_n)-(1-{\lambda }_n{c}_1)D_f(w_n,x_n)-(1-{\lambda }_n{c}_2)D_f(z_n,w_n),\forall x^{\ast }\in EP\left(g\right).$$

Let $S:X\to X$ be a mapping; the set of the fixed points of S is

$$F\left(S\right)=\{x\in X:S(x)=x\}.$$

A point $p\in X$ is called an asymptotic fixed point of S if X contains a sequence $\left\{x_n\right\}$ with $x_n\rightharpoonup p$ such that $\parallel S{x}_n-x_n\parallel \to 0$. The set of asymptotic fixed points of S is denoted by $\widehat{F}\left(S\right)$. The term “symptotic fixed point” was coined and used by Reich [45].

Definition 1. 

Let $S:X\to X$ be a mapping with $F\left(S\right)\ne \varnothing$. Then,

(i) 

S is called Bregman quasinonexpansive if $D_f(y,Sx)\le D_f(y,x)$ for all $x\in X,y\in F\left(S\right)$.

(ii) 

S is called Bregman relatively nonexpansive if S is Bregman quasinonexpansive and $F\left(S\right)=\widehat{F}\left(S\right)$.

Bregman quasinonexpansive mappings were studied by Butnariu et al. [46]. Here, we assume that the bifunction g satisfies the following conditions:

• $A1.$g is Pseudomonotone on C.
• $A2.$g is Bregman–Lipschitz-type continuous on C.
• $A3.$$g(x,·)$ is convex, lower semicontinuous and subdifferentiable on X for every fixed $x\in X$.
• $A4.$g is jointly weakly continuous on $X\times C$ in the sense that, if $x\in X,y\in C$ and $\left\{x_n\right\},\left\{y_n\right\}$ converge weakly to $x,y$, respectively, then $g(x_n,y_n)\to g(x,y)$ as $n\to \infty$.

Remark 1. 

If g satisfies $A1-A4$, then $\mathrm{EP}\left(g\right)$ is closed and convex (see [35]). If S is a Bregman quasinonexpansive mapping, then $F\left(S\right)$ is a closed convex subset of X ([33], Proposition 1).

Lemma 9 

([47]). Let $f:X\to (-\infty ,+\infty ]$ be uniformly Fréchet differentiable and totally convex on bounded subsets of X. Let C be a nonempty closed and convex subset of $\mathrm{int}$ $\mathrm{dom}f,$ $CB\left(C\right)$ denote the family of nonempty closed bounded subsets of C and $T:C\to CB\left(C\right)$ be a Bregman relatively nonexpansive mapping. Then, $F\left(T\right)$ is closed and convex.

Let $f:X\to (-\infty ,+\infty ]$ be a Gâteaux differentiable function and $x\in X$; recall that the proximal mapping of a proper convex and lower semicontinuous function $g:C\to (-\infty ,+\infty ]$ concerning f is defined by

$$Pro{x}_{g(·)}^f\left(x\right):=\mathrm{argmin}\left\{g\left(y\right)+D_f(y,x):y\in C\right\}.$$

(8)

Lemma 10 

([19]). Let $f:X\to (-\infty ,+\infty ]$ be a super coercive and Legendre function. Let $x\in \mathrm{int}\mathrm{dom}f,C\subset \mathrm{int}\mathrm{dom}f$ and $g:C\to (-\infty ,+\infty ]$ be a proper convex and lower semicontinuous function. Then, the following inequality holds:

$$g\left(y\right)-g\left({\mathrm{Prox}}_g^f\left(x\right)\right)+⟨{\mathrm{Prox}}_g^f\left(x\right)-y,\nabla f\left(x\right)-\nabla f\left({\mathrm{Prox}}_g^f\left(x\right)\right)⟩\ge 0,\forall y\in C.$$

(9)

Lemma 11 

([48]). Let $\left\{s_n\right\}$ be a sequence of non-negative real numbers satisfying the inequality

$$s_{n+1}\le (1-{\alpha }_n)s_n+{\alpha }_n{\beta }_n,\forall n\ge 0,$$

where $\left\{{\alpha }_n\right\}$ and $\left\{{\beta }_n\right\}$ satisfy the conditions

(i) 

$\left\{{\alpha }_n\right\}\subset [0,1]$ and ${\sum }_{n=0}^{\infty }{\alpha }_n=\infty ,$

(ii) 

${lim\; sup}_{n\to \infty }{\beta }_n\le 0,$ or ${\sum }_{n=0}^{\infty }\left|{\alpha }_n{\beta }_n\right|<\infty .$

Then, ${lim}_{n\to \infty }{s}_n=0.$

Lemma 12 

([49]). Let $\left\{a_n\right\}$ be a sequence of real numbers such that there exists a subsequence $\left\{n_i\right\}\subset \mathbb{N}$ such that $a_{n_i}<a_{n_i+1}$ for all $i\in \mathbb{N}.$ Then, there exists a subsequence $\left\{m_k\right\}\subset \mathbb{N}$ such that $m_k\to \infty$, and the following properties are satisfied by all (sufficiently large) numbers $k\in \mathbb{N}:$

$$a_{m_k}\le a_{m_k+1}and{a}_k\le a_{m_k+1}.$$

In fact, $m_k=max\{j\le k:a_j<a_{j+1}\}.$

3. Main Results

In this section, we assume that $f:X\to \mathbb{R}$ is a Legendre, super coercive and totally convex function on bounded subsets of X such that $\nabla f^{\ast }$ is bounded on bounded subsets of $\mathrm{int}\mathrm{dom}{f}^{\ast }$ and the bifunction $g:X\times X\to \mathbb{R}$ satisfies $A1-A4$. Now, we present the following Algorithm 1, and we prove a convergence theorem.

Algorithm 1 Subgradient extra-gradient algorithm

Choose ${\lambda }_0\in [\alpha ,\beta ]\subset (0,p)$, where $p=min\{\frac{1}{c_1},\frac{1}{c_2}\}$, $x_0\in X$ and $\mu \in (0,1).$ Set $n=0$ and go to Step 1. $Step1.$ Given the current iterate $x_n$, compute $$\begin{array}{c}\hfill y_n=\mathrm{argmin}\{{\lambda }_{n}g(x_n,y)+D_f(y,x_n):y\in C\}.\end{array}$$ $Step2.$ Choose $w_n\in {\partial }_{2}g(x_n,y_n)$ such that $\nabla f\left(x_n\right)-{\lambda }_n{w}_n-\nabla f\left(y_n\right)\in N_C\left(y_n\right)$ and compute $$\begin{array}{c}\hfill z_n=\mathrm{argmin}\{{\lambda }_{n}g(y_n,y)+D_f(y,x_n):y\in T_n\},\end{array}$$ where $$T_n=\{v\in X|⟨v-y_n,\nabla f\left(x_n\right)-{\lambda }_n{w}_n-\nabla f\left(y_n\right)⟩⩽0\}.$$ $Step3.$ Choose $\left\{{\alpha }_n\right\}$ and $\left\{{\beta }_n\right\}$ such that $${\displaystyle \left\{{\alpha }_n\right\}\subset (0,1),\sum _{n=0}^{\infty }{\alpha }_n=\infty ,\underset{n\to \infty }{lim}{\alpha }_n=0\mathrm{and}{\beta }_n\in [a,b]\subset (0,1),}$$ then compute $$\begin{array}{cc}\hfill t_n& =\nabla f^{\ast }\left({\alpha }_n\nabla f\left(x_0\right)+(1-{\alpha }_n)\nabla f\left(z_n\right)\right),\hfill \\ \hfill x_{n+1}& =\nabla f^{\ast }\left({\beta }_n\nabla f\left(z_n\right)+(1-{\beta }_n)\nabla f\left(S{t}_n\right)\right),\hfill \end{array}$$ $$\begin{array}{c}\hfill \begin{array}{c}\hfill {\lambda }_{n+1}=\left\{\begin{array}{cc}min\left\{\frac{\mu (D_f(z_n,y_n)+D_f(y_n,x_n))}{g(x_n,z_n)-g(x_n,y_n)-g(y_n,z_n)},{\lambda }_n\right\},\hfill & ifg(x_n,z_n)-g(x_n,y_n)-g(y_n,z_n)>0,\hfill \\ {\lambda }_n,\hfill & otherwise.\hfill \end{array}\right.\end{array}\end{array}$$ Set $n:=n+1$ and go back to Step 1.

The following lemmas will be useful in the proof of the main theorem.

Lemma 13. 

The sequence $\left\{{\lambda }_n\right\}$ generated by Algorithm 1 is bounded below with lower bound $min\left\{\frac{\mu }{max(c_1,c_2)},{\lambda }_0\right\}.$

Proof of Lemma 13. 

Since g satisfies the Bregman–Lipschitz-type condition with constants $c_1$ and $c_2$, for the case of $g(x_n,z_n)-g(x_n,y_n)-g(y_n,z_n)>0$, we have

$$\begin{array}{cc}\hfill g(x_n,z_n)-g(x_n,y_n)-g(y_n,z_n)& ⩽c_1{D}_f(z_n,y_n)+c_2{D}_f(y_n,x_n)\hfill \\ \hfill & ⩽max(c_1,c_2)(D_f(z_n,y_n)+D_f(y_n,x_n)).\hfill \end{array}$$

From the definition of ${\lambda }_n$, we see that this sequence is bounded from below. Indeed, if ${\lambda }_0⩽\frac{\mu }{max(c_1,c_2)}$, then $\left\{{\lambda }_n\right\}$ is bounded from below by ${\lambda }_0$; otherwise, $\left\{{\lambda }_n\right\}$ is bounded from below by $\frac{\mu }{max(c_1,c_2)}$. □

Remark 2. 

It is obvious that the sequence $\left\{{\lambda }_n\right\}$ is decreasing and the limit of $\left\{{\lambda }_n\right\}$ exists and we denote ${\displaystyle \underset{n\to +\infty }{lim}{\lambda }_n=\lambda }$. Clearly, $\lambda >0$. If ${\lambda }_0⩽\frac{\mu }{max(c_1,c_2)}$, then $\left\{{\lambda }_n\right\}$ is a constant sequence.

Lemma 14. 

The sequence $\left\{w_n\right\}$ generated by Algorithm 1 is well defined, and $C\subseteq T_n$.

Proof of Lemma 14. 

It follows from Lemmas 6 and 7 and the condition $A3$ that

$$y_n=\mathrm{argmin}\{{\lambda }_{n}g(x_n,y)+D_f(y,x_n):y\in C\},$$

if and only if

$$0\in {\lambda }_n{\partial }_{2}g(x_n,y_n)+{\nabla }_1{D}_f(y_n,x_n)+N_C\left(y_n\right).$$

There exists $w_n\in {\partial }_{2}g(x_n,y_n)$ and $w\in N_C\left(y_n\right)$ such that

$${\lambda }_n{w}_n+\nabla f\left(y_n\right)-\nabla f\left(x_n\right)+w=0.$$

Thus, we have

$$\begin{array}{cc}\hfill ⟨y-y_n,\nabla f\left(x_n\right)-\nabla f\left(y_n\right)⟩& =⟨y-y_n,w+{\lambda }_n{w}_n⟩\hfill \\ \hfill & =⟨y-y_n,w⟩+⟨y-y_n,{\lambda }_n{w}_n⟩\hfill \\ \hfill & ⩽⟨y-y_n,{\lambda }_n{w}_n⟩,\forall y\in C.\hfill \end{array}$$

This implies that $⟨y-y_n,\nabla f\left(x_n\right)-\nabla f\left(y_n\right)-{\lambda }_n{w}_n⟩⩽0$ for all $y\in C.$ Hence, $C\subseteq T_n$. □

Lemma 15. 

Suppose that $S:X\to X$ is a Bregman quasinonexpansive mapping. Let $\left\{x_n\right\},\left\{y_n\right\},\left\{z_n\right\}$ and $\left\{t_n\right\}$ be sequences generated by Algorithm 1 and $F\left(S\right)\cap \mathrm{EP}\left(g\right)\ne \varnothing$. Then, the sequences $\left\{x_n\right\},\left\{y_n\right\},\left\{z_n\right\}$ and $\left\{t_n\right\}$ are bounded.

Proof of Lemma 15. 

Since

$$z_n=\mathrm{argmin}\{{\lambda }_{n}g(y_n,y)+D_f(y,x_n):y\in T_n\}=Pro{x}_{{\lambda }_{n}g(y_n,.)}^f\left(x_n\right),$$

by Lemma 10, we have

$${\lambda }_n\left(g(y_n,z_n)-g(y_n,y)\right)⩽⟨z_n-y,\nabla f\left(x_n\right)-\nabla f\left(z_n\right)⟩,\forall y\in T_n.$$

(10)

Know that

$$F\left(S\right)\cap \mathrm{EP}\left(g\right)\subseteq C\subseteq T_n.$$

Assume that $u\in F\left(S\right)\cap \mathrm{EP}\left(g\right)$. Substituting $y=u$ into the last inequality, we have

$${\lambda }_n\left(g(y_n,z_n)-g(y_n,u)\right)⩽⟨z_n-u,\nabla f\left(x_n\right)-\nabla f\left(z_n\right)⟩.$$

(11)

From $u\in \mathrm{EP}\left(g\right)$, we obtain $g(u,y_n)⩾0$. Thus, $g(y_n,u)⩽0$ because of the Pseudomonotonicity of g. Hence, from (11) and ${\lambda }_n>0$, we obtain

$${\lambda }_{n}g(y_n,z_n)⩽⟨z_n-u,\nabla f\left(x_n\right)-\nabla f\left(z_n\right)⟩.$$

(12)

Since $w_n\in {\partial }_{2}g(x_n,y_n)$, we obtain

$$g(x_n,y)-g(x_n,y_n)⩾⟨y-y_n,w_n⟩,\mathrm{for}\mathrm{all}y\in X.$$

Substituting $y=z_n$ into the last inequality, we obtain that

$$g(x_n,z_n)-g(x_n,y_n)⩾⟨z_n-y_n,w_n⟩.$$

We have

$${\lambda }_n\left(g(x_n,z_n)-g(x_n,y_n)\right)⩾{\lambda }_n⟨z_n-y_n,w_n⟩.$$

(13)

From definition of $T_n$, we have

$$⟨z_n-y_n,\nabla f\left(x_n\right)-{\lambda }_n{w}_n-\nabla f\left(y_n\right)⟩⩽0,$$

we have

$$⟨z_n-y_n,\nabla f\left(x_n\right)-\nabla f\left(y_n\right)⟩⩽⟨z_n-y_n,{\lambda }_n{w}_n⟩.$$

(14)

Combining (12)–(14) with the three-point identity, we obtain that

$$\begin{array}{cc}\hfill {\lambda }_n\left(g(x_n,z_n)-g(x_n,y_n)-g(y_n,z_n)\right)& ⩾⟨u-z_n,\nabla f\left(x_n\right)-\nabla f\left(z_n\right)⟩+⟨z_n-y_n,{\lambda }_n{w}_n⟩\hfill \\ \hfill & ⩾⟨u-z_n,\nabla f\left(x_n\right)-\nabla f\left(z_n\right)⟩+⟨z_n-y_n,\nabla f\left(x_n\right)-\nabla f\left(y_n\right)⟩\hfill \\ \hfill & =D_f(u,z_n)-D_f(u,x_n)+D_f(z_n,y_n)+D_f(y_n,x_n).\hfill \end{array}$$

We have

$$\begin{array}{cc}\hfill D_f(u,z_n)& ⩽{\lambda }_n\left(g(x_n,z_n)-g(x_n,y_n)-g(y_n,z_n)\right)+D_f(u,x_n)\hfill \\ \hfill & -D_f(z_n,y_n)-D_f(y_n,x_n).\hfill \end{array}$$

We obtain

$$D_f(u,z_n)⩽\frac{\mu {\lambda }_n}{{\lambda }_{n+1}}\left(D_f(z_n,y_n)+D_f(y_n,x_n)\right)+D_f(u,x_n)-D_f(z_n,y_n)-D_f(y_n,x_n).$$

(15)

On the other hand

$$\underset{n\to +\infty }{lim}\frac{{\lambda }_n}{{\lambda }_{n+1}}\mu =\mu ,\mu \in (0,1).$$

(16)

There exists $N\in \mathbb{N}$ such that for all $n⩾N,$ we have $0<\frac{{\lambda }_n}{{\lambda }_{n+1}}\mu <1$. So, $D_f(u,z_n)$ $⩽D_f(u,x_n)$ for all $n⩾N.$ Therefore, we have

$$\begin{array}{cc}\hfill D_f(u,x_{n+1})& =D_f\left(u,\nabla f^{\ast }\left({\beta }_n\nabla f\left(z_n\right)+(1-{\beta }_n)\nabla f(S{t}_n\right)\right)\hfill \\ \hfill & ⩽{\beta }_n{D}_f(u,z_n)+(1-{\beta }_n)D_f(u,S{t}_n)\hfill \\ \hfill & ⩽{\beta }_n{D}_f(u,z_n)+(1-{\beta }_n)D_f(u,t_n)\hfill \\ \hfill & ={\beta }_n{D}_f(u,z_n)+(1-{\beta }_n)D_f\left(u,\nabla f^{\ast }\left({\alpha }_n\nabla f\left(x_0\right)+(1-{\alpha }_n)\nabla f\left(z_n\right)\right)\right)\hfill \\ \hfill & ⩽{\beta }_n{D}_f(u,z_n)+(1-{\beta }_n){\alpha }_n{D}_f(u,x_0)+(1-{\beta }_n)(1-{\alpha }_n)D_f(u,z_n)\hfill \\ \hfill & ⩽({\beta }_n+(1-{\beta }_n)(1-{\alpha }_n))D_f(u,x_n)+(1-{\beta }_n){\alpha }_n{D}_f(u,x_0)\hfill \\ \hfill & ⩽({\beta }_n+(1-{\beta }_n)(1-{\alpha }_n)+{\alpha }_n(1-{\beta }_n))max(D_f(u,x_n),D_f(u,x_0))\hfill \\ \hfill & ⩽max\left(D_f(u,x_n),D_f(u,x_0)\right)\hfill \\ \hfill & ⋮\hfill \\ \hfill & ⩽D_f(u,x_0).\hfill \end{array}$$

(17)

Therefore, the sequence $\left\{D_g(u,x_n)\right\}$ is bounded, and by Lemma 3, the sequence $\left\{x_n\right\}$ is bounded. We have $D_f(u,z_n)⩽D_f(u,x_n)$, which implies that $\left\{z_n\right\}$ is bounded. From (17) and using Lemma 8, we derive that

$$\begin{array}{cc}\hfill D_f(u,x_{n+1})& ⩽{\beta }_n{D}_f(u,z_n)+(1-{\beta }_n){\alpha }_n{D}_f(u,x_0)+(1-{\beta }_n)(1-{\alpha }_n)D_f(u,z_n)\hfill \\ \hfill & ⩽({\beta }_n+(1-{\beta }_n)(1-{\alpha }_n))D_f(u,z_n)+(1-{\beta }_n){\alpha }_n{D}_f(u,x_0)\hfill \\ \hfill & ⩽({\beta }_n+(1-{\beta }_n)(1-{\alpha }_n))\left(D_f(u,x_n)-(1-{\lambda }_n{c}_1)D_f(y_n,x_n)-(1-{\lambda }_n{c}_2)D_f(z_n,y_n)\right)+(1-{\beta }_n){\alpha }_n{D}_f(u,x_0)\hfill \\ \hfill & ⩽\left({\beta }_n+(1-{\beta }_n)(1-{\alpha }_n)\right)\left(D_f(u,x_n)-(1-{\lambda }_n{c}_1)D_f(y_n,x_n)\right)+(1-{\beta }_n){\alpha }_n{D}_f(u,x_0).\hfill \end{array}$$

We get that

$$\begin{array}{cc}\hfill & ({\beta }_n+(1-{\beta }_n)(1-{\alpha }_n))(1-{\lambda }_n{c}_1)D_f(y_n,x_n)\hfill \\ \hfill & ⩽({\beta }_n+(1-{\beta }_n)(1-{\alpha }_n))D_f(u,x_n)-D_f(u,x_{n+1})+(1-{\beta }_n){\alpha }_n{D}_f(u,x_0).\hfill \end{array}$$

Considering the limit supreme in the last inequality as $n\to \infty$, we obtain that ${\displaystyle \underset{n\to \infty }{lim}{D}_f(y_n,x_n)=0}$. Therefore, $\left\{y_n\right\}$ is bounded. Clearly, $\left\{t_n\right\}$ is bounded. □

Now, we are ready to prove our main theorem.

Theorem 4. 

Let S be a Bregman relatively nonexpansive mapping. Assume that $A_1-A_4$ are satisfied and $\Omega :=F\left(S\right)\cap \mathrm{EP}\left(g\right)\ne \varnothing$. Then, the sequence $\left\{x_n\right\}$ generated by Algorithm 1 converges strongly to ${\overleftarrow{\mathrm{Proj}}}_{\Omega }^f\left(x_0\right)$.

Proof of Theorem 4. 

By Remark 1 and Lemma 9, $\Omega$ is closed and convex. Assume that $x^{\ast }={\overleftarrow{\mathrm{Proj}}}_{\Omega }^f\left(x_0\right)$. By Lemma 4, we have

$$⟨z-x^{\ast },\nabla f\left(x_0\right)-\nabla f\left(x^{\ast }\right)⟩⩽0,\forall z\in \Omega .$$

(18)

From Lemma 8, we obtain $D_f(x^{\ast },z_n)⩽D_f(x^{\ast },x_n)$ for all $n⩾N$. Therefore,

$$\begin{array}{cc}\hfill D_f(x^{\ast },x_{n+1})& =D_f\left(x^{\ast },\nabla f^{\ast }\left({\beta }_n\nabla f\left(z_n\right)+(1-{\beta }_n)\nabla f(S{t}_n\right)\right)\hfill \\ \hfill & ⩽{\beta }_n{D}_f(x^{\ast },z_n)+(1-{\beta }_n)D_f(x^{\ast },S{t}_n)\hfill \\ \hfill & ⩽{\beta }_n{D}_f(x^{\ast },z_n)+(1-{\beta }_n)D_f(x^{\ast },t_n)\hfill \\ \hfill & ={\beta }_n{D}_f(x^{\ast },z_n)+(1-{\beta }_n)D_f(x^{\ast },\nabla f^{\ast }({\alpha }_n\nabla f\left(x_0\right)+(1-{\alpha }_n)\nabla f\left(z_n\right)))\hfill \\ \hfill & ⩽{\beta }_n{D}_f(x^{\ast },z_n)+(1-{\beta }_n){\alpha }_n{D}_f(x^{\ast },x_0)+(1-{\beta }_n)(1-{\alpha }_n)D_f(x^{\ast },z_n).\hfill \end{array}$$

(19)

We have

$$D_f(x^{\ast },x_{n+1})⩽\left({\beta }_n+(1-{\beta }_n)(1-{\alpha }_n)\right)D_f(x^{\ast },z_n)+(1-{\beta }_n){\alpha }_n{D}_f(x^{\ast },x_0).$$

(20)

From (15), we obtain

$$D_f(x^{\ast },z_n)⩽D_f(x^{\ast },x_n)-\left(1-\frac{\mu {\lambda }_n}{2{\lambda }_{n+1}}\right)\left(D_f(z_n,y_n)+D_f(y_n,x_n)\right).$$

(21)

Know that

$${\beta }_n+(1-{\beta }_n)(1-{\alpha }_n)=1-{\alpha }_n(1-{\beta }_n)<1.$$

From (20) and (21), we have

$$\begin{array}{cc}\hfill D_f(x^{\ast },x_{n+1})& ⩽D_f(x^{\ast },z_n)+(1-{\beta }_n){\alpha }_n{D}_f(x^{\ast },x_0)\hfill \\ \hfill & ⩽D_f(x^{\ast },x_n)-\left(1-\frac{\mu {\lambda }_n}{{\lambda }_{n+1}}\right)(D_f(z_n,y_n)+D_f(y_n,x_n))+(1-{\beta }_n){\alpha }_n{D}_f(x^{\ast },x_0).\hfill \end{array}$$

(22)

We divide the proof into two parts:

Case $1.$ In this case, we suppose that there exists $N_1\in \mathbb{N}$$(N_1⩾N)$, such that

$$D_f(x^{\ast },x_{n+1})⩽D_f(x^{\ast },x_n),$$

for all $n⩾N_1$. Then, the limit ${\displaystyle \underset{n\to \infty }{lim}{D}_f(x^{\ast },x_n)}$ exists. Let ${\displaystyle \underset{n\to \infty }{lim}{D}_f(x^{\ast },x_n)=l}$. By (22), we obtain

$$\left(1-\frac{\mu {\lambda }_n}{{\lambda }_{n+1}}\right)(D_f(z_n,y_n)+D_f(y_n,x_n))⩽D_f(x^{\ast },x_n)-D_f(x^{\ast },x_{n+1})+(1-{\beta }_n){\alpha }_n{D}_f(x^{\ast },x_0).$$

(23)

From (23), the fact that

$${\displaystyle \underset{n⟶\infty }{lim}\left(1-\frac{\mu {\lambda }_n}{{\lambda }_{n+1}}\right)=1-\mu >0\mathrm{and}\underset{n⟶\infty }{lim}{\alpha }_n=0,}$$

we obtain that

$${\displaystyle \left(1-\mu \right)\underset{n⟶\infty }{lim\; sup}(D_f(z_n,y_n)+D_f(y_n,x_n))⩽0.}$$

We have

$${\displaystyle \underset{n⟶\infty }{lim}{D}_f(z_n,y_n)=\underset{n⟶\infty }{lim}{D}_f(y_n,x_n)=0.}$$

From Lemma 2, we get that

$${\displaystyle \underset{n\to \infty }{lim}\parallel y_n-x_n\parallel =\underset{n\to \infty }{lim}\parallel z_n-y_n\parallel =0.}$$

(24)

Since $\left\{x_n\right\}$ is bounded, there exists a subsequence $\left\{x_{n_k}\right\}$ which converges weakly to some $z_0\in X$ and

$$\begin{array}{cc}\hfill {\displaystyle \underset{n⟶\infty }{lim\; sup}⟨x_n-x^{\ast },\nabla f\left(x_0\right)-\nabla f\left(x^{\ast }\right)⟩}& {\displaystyle =\underset{k⟶\infty }{lim}⟨x_{n_k}-x^{\ast },\nabla f\left(x_0\right)-\nabla f\left(x^{\ast }\right)⟩}\hfill \\ & =⟨z_0-x^{\ast },\nabla f\left(x_0\right)-\nabla f\left(x^{\ast }\right)⟩.\hfill \end{array}$$

(25)

From (24) and $x_{n_k}\rightharpoonup z_0$, we have $y_{n_k}\rightharpoonup z_0$ and $z_0\in C$. Since

$$y_{n_k}={\mathrm{Prox}}_{{\lambda }_{n_k}g(x_{n_k},·)}^f\left(x_{n_k}\right),$$

by Lemma 10 we deduce that

$${\lambda }_{n_k}\left(g(x_{n_k},y)-g(x_{n_k},y_{n_k})\right)⩾⟨y-y_{n_k},\nabla f\left(x_{n_k}\right)-\nabla f\left(y_{n_k}\right)⟩,\forall y\in C.$$

(26)

Considering the limit in the last inequality as $k\to \infty$ and using the assumptions $A4$, ${\displaystyle \underset{k⟶\infty }{lim}{\lambda }_{n_k}=\lambda >0}$, we obtain

$$\begin{array}{c}\hfill \lambda (g(z_0,y)-g(z_0,z_0))⩾⟨y-z_0,\nabla f\left(z_0\right)-\nabla f\left(z_0\right)⟩,\forall y\in C.\end{array}$$

Which implies that $g(z_0,y)\ge 0,$ for all $y\in C$. That is, $z_0\in \mathrm{EP}\left(g\right)$.

Next, we prove $z_0\in F\left(S\right)$. From $x_{n_k}\rightharpoonup z_0$ and (24), we obtain $z_{n_k}\rightharpoonup z_0$. Note that,

$${\displaystyle \underset{n⟶\infty }{lim}{\alpha }_n=0,}$$

therefore,

$$\begin{array}{cc}\hfill D(z_{n_k},t_{n_k})& =D\left(z_{n_k},\nabla f^{\ast }({\alpha }_{n_k}\nabla f\left(x_0\right)+(1-{\alpha }_{n_k})\nabla f\left(z_{n_k}\right))\right)\hfill \\ \hfill & \le {\alpha }_{n_k}D(z_{n_k},x_0)+(1-{\alpha }_{n_k})D(z_{n_k},z_{n_k})\hfill \\ \hfill & ={\alpha }_{n_k}D(z_{n_k},x_0).\hfill \end{array}$$

We obtain that

$${\displaystyle \underset{k⟶\infty }{lim}D(z_{n_k},t_{n_k})=0.}$$

We get that

$${\displaystyle \underset{k⟶\infty }{lim}\parallel z_{n_k}-t_{n_k}\parallel =0,}$$

(27)

and thus $t_{n_k}\rightharpoonup z_0$. Let

$$r=\underset{n}{sup}\{\parallel \nabla f\left(z_n\right)\parallel ,\parallel \nabla f\left(S{t}_n\right)\parallel \}.$$

The sequences $\left\{z_n\right\}$ and $\left\{S{t}_n\right\}$ are bounded and $\nabla f$ is bounded on bounded subsets of X, we have $r<\infty$. In view of Lemma 1 and Theorem 1, $\mathrm{dom}{f}^{\ast }=X^{\ast },$ $f^{\ast }$ is super coercive and uniformly convex on bounded subsets of $X^{\ast }$. Applying (5) and Lemma 5, we obtain

$$\begin{array}{cc}\hfill D_f\left(x^{\ast },x_{n_k+1}\right)=& D_f\left(x^{\ast },\nabla f^{\ast }\left({\beta }_{n_k}\nabla f\left(z_{n_k}\right)+\left(1-{\beta }_{n_k}\right)\nabla f\left(S{t}_{n_k}\right)\right)\right)\hfill \\ \hfill =& V_f\left(x^{\ast },{\beta }_{n_k}\nabla f\left(z_{n_k}\right)+\left(1-{\beta }_{n_k}\right)\nabla f\left(S{t}_{n_k}\right)\right)\hfill \\ \hfill =& f\left(x^{\ast }\right)+f^{\ast }\left({\beta }_{n_k}\nabla f\left(z_{n_k}\right)+\left(1-{\beta }_{n_k}\right)\nabla f\left(S{t}_{n_k}\right)\right)-⟨x^{\ast },{\beta }_{n_k}\nabla f\left(z_{n_k}\right)+\left(1-{\beta }_{n_k}\right)\nabla f\left(S{t}_{n_k}\right)⟩\hfill \\ \hfill \le & f\left(x^{\ast }\right)+{\beta }_{n_k}{f}^{\ast }\left(\nabla f\left(z_{n_k}\right)\right)+\left(1-{\beta }_{n_k}\right)f^{\ast }\left(\nabla f\left(S{t}_{n_k}\right)\right)-{\beta }_{n_k}\left(1-{\beta }_{n_k}\right){\rho }_r^{\ast }\left(\parallel \nabla f\left(z_{n_k}\right)-\nabla f\left(S{t}_{n_k}\right)\parallel \right)\hfill \\ \hfill & -⟨x^{\ast },{\beta }_{n_k}\nabla f\left(z_{n_k}\right)+\left(1-{\beta }_{n_k}\right)\nabla f\left(S{t}_{n_k}\right)⟩.\hfill \end{array}$$

T is a Bregman relatively nonexpansive mapping and

$$f\left(x\right)+f^{\ast }\left(x^{\ast }\right)=⟨x,x^{\ast }⟩$$

we have

$$\begin{array}{cc}\hfill D_f\left(x^{\ast },x_{n_k}\right)\le & f\left(x^{\ast }\right)+{\beta }_{n_k}⟨z_{n_k},\nabla f\left(z_{n_k}\right)⟩-{\beta }_{n_k}f\left(z_{n_k}\right)+\left(1-{\beta }_{n_k}\right)⟨S{t}_{n_k}),\nabla f\left(S{t}_{n_k}\right)⟩\hfill \\ \hfill & -\left(1-{\beta }_{n_k}\right)f\left(S{t}_{n_k}\right)-{\beta }_{n_k}\left(1-{\beta }_{n_k}\right){\rho }_r^{\ast }\left(\parallel \nabla f\left(z_{n_k}\right)-\nabla f\left(S{t}_{n_k}\right)\parallel \right)-{\beta }_{n_k}⟨x^{\ast },\nabla f\left(z_{n_k}\right)⟩-\left(1-{\beta }_{n_k}\right)⟨x^{\ast },\nabla f\left(S{t}_{n_k}\right)⟩\hfill \\ \hfill =& {\beta }_{n_k}{D}_f\left(x^{\ast },z_{n_k}\right)+\left(1-{\beta }_{n_k}\right)D_f\left(x^{\ast },S{t}_{n_k}\right)-{\beta }_{n_k}\left(1-{\beta }_{n_k}\right){\rho }_r^{\ast }\left(\parallel \nabla f\left(z_{n_k}\right)-\nabla f\left(S{t}_{n_k}\right)\parallel \right),\hfill \end{array}$$

therefore,

$$\begin{array}{cc}\hfill {\beta }_{n_k}\left(1-{\beta }_{n_k}\right){\rho }_r^{\ast }\left(\parallel \nabla f\left(z_{n_k}\right)-\nabla f\left(S{t}_{n_k}\right)\parallel \right)⩽& {\beta }_{n_k}{D}_f\left(x^{\ast },z_{n_k}\right)+\left(1-{\beta }_{n_k}\right)D_f\left(x^{\ast },S{t}_{n_k}\right)-D_f\left(x^{\ast },x_{n_k}\right)\hfill \\ \hfill ⩽& {\beta }_{n_k}{D}_f\left(x^{\ast },z_{n_k}\right)+\left(1-{\beta }_{n_k}\right)D_f\left(x^{\ast },t_{n_k}\right)-D_f\left(x^{\ast },x_{n_k}\right)\hfill \\ \hfill ⩽& \left(1-{\beta }_{n_k}\right)D_f\left(x^{\ast },\nabla f^{\ast }({\alpha }_{n_k}\nabla f\left(x_0\right)+(1-{\alpha }_{n_k})\nabla f\left(z_{n_k}\right)\right)+{\beta }_{n_k}{D}_f\left(x^{\ast },x_{n_k}\right)-D_f\left(x^{\ast },x_{n_k}\right)\hfill \\ \hfill ⩽& \left(1-{\beta }_{n_k}\right){\alpha }_{n_k}D(x^{\ast },x_0)+\left(1-{\beta }_{n_k}\right)(1-{\alpha }_{n_k})D(x^{\ast },z_{n_k})+{\beta }_{n_k}{D}_f\left(x^{\ast },x_{n_k}\right)-D_f\left(x^{\ast },x_{n_k}\right)\hfill \\ \hfill ⩽& \left(1-{\beta }_{n_k}\right){\alpha }_{n_k}D(x^{\ast },x_0)+\left(1-{\beta }_{n_k}\right)(1-{\alpha }_{n_k})D(x^{\ast },x_{n_k})+{\beta }_{n_k}{D}_f\left(x^{\ast },x_{n_k}\right)-D_f\left(x^{\ast },x_{n_k}\right).\hfill \end{array}$$

Passing the limit in the last inequality as $k\to \infty$, we obtain

$$\underset{k⟶\infty }{lim}{\rho }_r^{\ast }\left(\parallel \nabla f\left(z_{n_k}\right)-\nabla f\left(S{t}_{n_k}\right)\parallel \right)=0.$$

We prove that

$$\underset{k\to \infty }{lim}\parallel \nabla f\left({\overline{z}}_{n_k}\right)-\nabla f\left(S{t}_{n_k}\right)\parallel =0.$$

If this is not the case, there exists ${\epsilon }_0>0$ and a subsequence $\left\{n_{k_m}\right\}$ of $\left\{n_k\right\}$ such that

$$\parallel \nabla f\left(z_{n_{k_m}}\right)-\nabla f\left(z_{n_{k_m}}\right)\parallel \ge {\epsilon }_0.$$

Since ${\rho }^{\ast }$ is nondecreasing, we obtain

$${\rho }_r^{\ast }\left({\epsilon }_0\right)\le {\rho }_r^{\ast }\left(\parallel \nabla f\left(z_{n_{k_m}}\right)-\nabla f\left(z_{n_{k_m}}\right)\parallel \right)\mathrm{for}\mathrm{all}m\in \mathbb{N}.$$

Letting $m\to \infty$, we obtain ${\rho }_r^{\ast }\left({\epsilon }_0\right)\le 0.$ But this is a contradiction to the uniform convexity of $f^{\ast }$ on the bounded subsets of $X^{\ast }$. From Theorems 2 and 3, $\nabla f^{\ast }$ is uniformly continuous on the bounded subset of $X^{\ast }.$ Therefore, ${\displaystyle \underset{n\to \infty }{lim}\parallel z_{n_k}-S{t}_{n_k}\parallel =0}$. This, together with (27) and the triangle inequality, gives

$${\displaystyle \underset{n\to \infty }{lim}\parallel t_{n_k}-S{t}_{n_k}\parallel =0.}$$

The function f is uniformly continuous on the bounded subset of X ([50], Theorem 1.8), ${\displaystyle \underset{n\to \infty }{lim}[f\left(t_{n_k}\right)-f\left(S{t}_{n_k}\right)]=0,}$ and so, from the definition of the Bregman distance, we obtain

$${\displaystyle \underset{k⟶\infty }{lim}{D}_f(t_{n_k},S{t}_{n_k})=0.}$$

and thus $z_0$ is an asymptotic fixed point of Bregman relatively nonexpansive mapping S. Therefore, $z_0\in \widehat{F}\left(S\right)=F\left(S\right)$. Hence, $z_0\in \Omega$.

We now prove that ${\displaystyle \underset{n\to \infty }{lim}{D}_f(x^{\ast },x_n)=0}$. We have

$$\begin{array}{cc}\hfill D_f(x^{\ast },t_n)=& D_f\left(x^{\ast },\nabla f^{\ast }({\alpha }_n\nabla f\left(x_0\right)+(1-{\alpha }_n)\nabla f\left(z_n\right))\right)\hfill \\ \hfill =& V_f\left(x^{\ast },{\alpha }_n\nabla f\left(x_0\right)+(1-{\alpha }_n)\nabla f\left(z_n\right)\right)\hfill \\ \hfill \le & V_f\left(x^{\ast },{\alpha }_n\nabla f\left(x_0\right)+(1-{\alpha }_n)\nabla f\left(z_n\right)-{\alpha }_n(\nabla f\left(x_0\right)-\nabla f\left(x^{\ast }\right))\right)+{\alpha }_n⟨t_n-x^{\ast },\nabla f\left(x_0\right)-\nabla f\left(x^{\ast }\right)⟩\hfill \\ \hfill =& V_f(x^{\ast },(1-{\alpha }_n)\nabla f\left(z_n\right)+{\alpha }_n\nabla f\left(x^{\ast }\right))+{\alpha }_n⟨t_n-x^{\ast },\nabla f\left(x_0\right)-\nabla f\left(x^{\ast }\right)⟩\hfill \\ \hfill \le & (1-{\alpha }_n)D_f(x^{\ast },z_n)+{\alpha }_n{D}_f(x^{\ast },x^{\ast })+{\alpha }_n⟨t_n-x^{\ast },\nabla f\left(x_0\right)-\nabla f\left(x^{\ast }\right)⟩.\hfill \end{array}$$

We have

$$\begin{array}{cc}\hfill D_f(x^{\ast },x_{n+1})⩽& {\beta }_n{D}_f(x^{\ast },z_n)+(1-{\beta }_n)D_f(x^{\ast },t_n)\hfill \\ \hfill ⩽& {\beta }_n{D}_f(x^{\ast },z_n)+(1-{\beta }_n)\left((1-{\alpha }_n)D_f(x^{\ast },z_n)+{\alpha }_n⟨t_n-x^{\ast },\nabla f\left(x_0\right)-\nabla f\left(x^{\ast }\right)⟩\right)\hfill \\ \hfill =& \left({\beta }_n+(1-{\beta }_n)(1-{\alpha }_n)\right)D_f(x^{\ast },z_n)+{\alpha }_n(1-{\beta }_n)⟨t_n-x^{\ast },\nabla f\left(x_0\right)-\nabla f\left(x^{\ast }\right)⟩\hfill \\ \hfill =& \left(1-{\alpha }_n(1-{\beta }_n)\right)D_f(x^{\ast },z_n)+{\alpha }_n(1-{\beta }_n)⟨t_n-x^{\ast },\nabla f\left(x_0\right)-\nabla f\left(x^{\ast }\right)⟩\hfill \end{array}$$

(28)

From $t_n\rightharpoonup z_0$ and $z_0\in \Omega$, we obtain that

$${\displaystyle \underset{n\to \infty }{lim\; sup}⟨t_n-x^{\ast },\nabla f\left(x_0\right)-\nabla f\left(x^{\ast }\right)⟩=⟨z_0-x^{\ast },\nabla f\left(x_0\right)-\nabla f(x^{\ast }⟩⩽0.}$$

(29)

From Lemma 11 and (28), we deduce that

$${\displaystyle \underset{n\to \infty }{lim}{D}_f(x^{\ast },x_{n+1})=0.}$$

From Lemma 2, we have $\parallel x^{\ast }-x_{n+1}\parallel \to 0$. Since $x_{n_k}\rightharpoonup z_0$, we have $z_0=x^{\ast }.$

Case $2.$ There exists a subsequence $\left\{D_f(x^{\ast },x_{n_j})\right\}$ of $\left\{D_f(x^{\ast },x_n)\right\}$ such that

$$D_f(x^{\ast },x_{n_j})⩽D_f(x^{\ast },x_{n_j+1})\mathrm{for}\mathrm{all}j\in \mathbb{N}.$$

By Lemma 12, there exists an increasing sequence $\left\{m_k\right\}\subset \mathbb{N}$ such that ${\displaystyle \underset{k\to \infty }{lim}{m}_k=\infty }$, and the following inequalities hold for all $k\in \mathbb{N}$:

$$0⩽D_f(x^{\ast },x_{m_k})⩽D_f(x^{\ast },x_{m_{k+1}})\mathrm{and}{D}_f(x^{\ast },x_k)⩽D_f(x^{\ast },x_{m_{k+1}}).$$

(30)

From (22), we have

$$\left(1-\frac{\mu {\lambda }_n}{{\lambda }_{n+1}}\right)(D_f(z_n,y_n)+D_f(y_n,x_n))⩽D_f(x^{\ast },x_n)-D_f(x^{\ast },x_{n+1})+{\alpha }_n(1-{\beta }_n)D_f(x^{\ast },x_0).$$

Substituting $n=m_k$ into the last inequality, we obtain

$$\begin{array}{c}\hfill \left(1-\frac{\mu {\lambda }_{m_k}}{{\lambda }_{m_k+1}}\right)(D_f(z_{m_k},y_{m_k})+D_f(y_{m_k},x_{m_k}))⩽D_f(x^{\ast },x_{m_k})-D_f(x^{\ast },x_{m_k+1})+{\alpha }_{m_k}(1-{\beta }_{m_k})D_f(x^{\ast },x_0).\end{array}$$

From (20), we have

$${\displaystyle \underset{k\to \infty }{lim}1-\frac{\mu {\lambda }_{m_k}}{{\lambda }_{m_{k+1}}}=1-\mu >0\mathrm{and}\underset{k\to \infty }{lim}{\alpha }_{m_k}=0,}$$

we obtain

$${\displaystyle \underset{k\to \infty }{lim}{D}_f(z_{m_k},y_{m_k})=\underset{k\to \infty }{lim}{D}_f(y_{m_k},x_{m_k})=0.}$$

Using the same argument as in the proof of Case 1 and by (29), we obtain that

$${\displaystyle \underset{k\to \infty }{lim\; sup}⟨t_{m_k}-x^{\ast },\nabla f\left(x_0\right)-\nabla f\left(x^{\ast }\right)⟩⩽0.}$$

(31)

From (28) for all $m_k\ge N_1$, we have

$$\begin{array}{c}\hfill D_f(x^{\ast },x_{m_k+1})\le (1-{\alpha }_{m_k}(1-{\beta }_{m_k}))D_f(x^{\ast },x_{m_k})+{\alpha }_{m_k}(1-{\beta }_{m_k})⟨t_{m_k}-x^{\ast },\nabla f\left(x_0\right)-\nabla f\left(x^{\ast }\right)⟩.\end{array}$$

(32)

From (31) and Lemma 11, we derive that

$${\displaystyle \underset{k\to \infty }{lim}{D}_f(x^{\ast },x_{m_k+1})=0.}$$

On the other hand, we have

$$D_f(x^{\ast },x_k)⩽D_f(x^{\ast },x_{m_k+1}),$$

we have

$${\displaystyle \underset{k\to \infty }{lim}{D}_f(x^{\ast },x_k)=0.}$$

From Lemma 2, we obtain that ${\displaystyle \underset{k\to \infty }{lim}\parallel x^{\ast }-x_k\parallel =0}$. Therefore, $x_k⟶x^{\ast }$, which is the desired result. □

4. Application

In this section, we consider the particular equilibrium problem corresponding to the function g defined for every $x,y\in X$ by $g(x,y)=⟨y-x,Ax⟩$, with $A:X\to X^{\ast }$ being L-Lipschitz continuous; that is, there exists $L>0$ such that

$$\parallel Ax-Ay\parallel ⩽L\parallel x-y\parallel \mathrm{for}\mathrm{all}x,y\in X.$$

So, we obtain the classical variational inequality:

$$\begin{array}{c}\hfill \mathrm{Find}z\in C\mathrm{such}\mathrm{that}⟨y-z,Az⟩\ge 0,\forall y\in C.\end{array}$$

(33)

The set of solutions to this problem is denoted by $\mathrm{VI}(A,C).$ We have ([19], Lemma 4.1)

$$\begin{array}{cc}\hfill \mathrm{argmin}\{{\lambda }_{n}g(x_n,y)+D_f(y,x_n):y\in C\}& =\mathrm{argmin}\{{\lambda }_n⟨y-y_n,A{x}_n⟩+D_f(y,x_n):y\in C\}\hfill \\ & ={\overleftarrow{\mathrm{Proj}}}_C^f\left(\nabla f^{\ast }(\nabla f\left(x_n\right)-{\lambda }_{n}A{x}_n)\right).\hfill \end{array}$$

Therefore, we derive that

$$\begin{array}{c}\hfill \mathrm{argmin}\{{\lambda }_n⟨y-y_n,A{y}_n⟩+D_f(y,x_n):y\in T_n\}={\overleftarrow{\mathrm{Proj}}}_{T_n}^f(\nabla f^{\ast }(\nabla f\left(x_n\right)-{\lambda }_{n}A{y}_n).\end{array}$$

Let X be a real Banach space. The modulus of convexity ${\delta }_X:[0,2]\to [0,1]$ is defined by

$${\delta }_X\left(\epsilon \right)=inf\left\{1-\frac{\parallel x+y\parallel }{2}:\parallel x\parallel =\parallel y\parallel =1,\parallel x-y\parallel \ge \epsilon \right\}.$$

The space X is called uniformly convex if ${\delta }_X\left(\epsilon \right)>0$ for every $\epsilon \in (0,2]$, and is called p-uniformly convex if $p\ge 2$ and there exists $c_p>0$ such that ${\delta }_X\left(\epsilon \right)\ge c_p{\epsilon }^p$ for any $\epsilon \in (0,2]$.

The modulus of smoothness ${\rho }_X\left(t\right):[0,\infty )\to [0,\infty )$ is defined by

$${\rho }_X\left(t\right)=sup\left\{\frac{\parallel x+ty\parallel +\parallel x-ty\parallel }{2}-1:\parallel x\parallel =\parallel y\parallel =1\right\},$$

The space X is called uniformly smooth if

$${\displaystyle \underset{t\to 0}{lim}\frac{{\rho }_X\left(t\right)}{t}=0.}$$

For a p-uniformly convex space, the metric and Bregman distance have the following relation [51]:

$$t{\parallel x-y\parallel }^p\le D_{\frac{1}{p}{\parallel ·\parallel }^p}(x,y)\le ⟨x-y,J_X^p\left(x\right)-J_X^p\left(x\right)⟩,$$

(34)

where $t>0$ is a fixed number and the duality mapping $J_X^p\left(x\right):X\to 2^{X^{\ast }}$ is defined by

$$J_X^p\left(x\right)=\{f\in X^{\ast }:⟨x,f⟩={\parallel x\parallel }^p,\parallel f\parallel ={\parallel x\parallel }^{p-1}\},$$

for every $x\in X.$ We know that X is smooth if and only if $J_X^p$ is a single-valued mapping of X into $X^{\ast }.$ We also know that X is reflexive if and only if $J_X^p$ is surjective, and X is strictly convex if and only if $J_X^p$ is one-to-one. Therefore, if X is a smooth, strictly convex and reflexive Banach space, then $J_X^p$ is a single-valued bijection, and in this case, $J_X^p={\left(J_{X^{\ast }}^q\right)}^{-1}$, where $J_{X^{\ast }}^q$ is the duality mapping of $X^{\ast }.$

For $p=2,$ the duality mapping $J_X^p$ is called the normalized duality mapping and is denoted by $J.$ The function $\varphi :X^2\to \mathbb{R}$ is defined by

$$\varphi (y,x)={\Vert y\Vert }^2-2⟨y,Jx⟩+{\Vert x\Vert }^2,$$

for all $x,y\in X.$ The generalized projection ${\Pi }_C$ from X onto C is defined by

$${\Pi }_C\left(x\right)={\mathrm{argmin}}_{y\in C}\varphi (y,x)\forall x\in X,$$

where C is a nonempty closed and convex subset of $X.$

Let X be a uniformly smooth and uniformly convex Banach space and $f=\frac{1}{2}{\parallel ·\parallel }^2.$ Therefore,

$$\nabla f=J,D_{\frac{1}{2}{\parallel ·\parallel }^2}(x,y)=\frac{1}{2}\varphi (x,y)\mathrm{and}{\overleftarrow{\mathrm{Proj}}}_C^{\frac{1}{2}{\parallel ·\parallel }^2}={\Pi }_C.$$

If X is a Hilbert space, then

$$\nabla f=I,D_{\frac{1}{2}{\parallel ·\parallel }^2}(x,y)=\frac{1}{2}{\parallel x-y\parallel }^2\mathrm{and}{\overleftarrow{\mathrm{Proj}}}_C^{\frac{1}{2}{\parallel ·\parallel }^2}=P_C,$$

where $P_C$ is the metric projection.

Hence, we have the following corollary:

Corollary 1. 

Let X be a uniformly smooth and two-uniformly convex Banach space and C be a nonempty closed and convex subset of X. Let S be a Bregman relatively nonexpansive mapping and $g(x,y)=⟨y-x,Ax⟩$ for all $x,y\in X$. Let $A:X\to X^{\ast }$ be a monotone and Lipschitz-continuous mapping. Suppose that $\Omega =F\left(S\right)\cap \mathrm{VI}(A,C)\ne \varnothing ,$ ${\displaystyle \left\{{\alpha }_n\right\}\subset (0,1),\underset{n\to \infty }{lim}{\alpha }_n=0,\sum _{n=0}^{\infty }{\alpha }_n=\infty ,{\beta }_n\in [a,b]\subset (0,1),}$ and $\left\{{\lambda }_n\right\}$ is sequence defined in Algorithm 1. Then, the sequence $\left\{x_n\right\}$ generated by

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & {\lambda }_0,x_0\in X,\mu \in (0,1),\hfill \\ \hfill & y_n={\Pi }_C\left(J^{-1}(J\left(x_n\right)-{\lambda }_{n}A{x}_n\right),\hfill \\ \hfill & T_n=\{x\in X|⟨x-y_n,J\left(x_n\right)-{\lambda }_{n}A{x}_n-J\left(y_n\right)⟩⩽0\},\hfill \\ \hfill & z_n={\Pi }_C\left(J^{-1}(J\left(x_n\right)-{\lambda }_{n}A{y}_n\right),\hfill \\ \hfill & t_n=J^{-1}\left({\alpha }_{n}J\left(x_0\right)+(1-{\alpha }_n)J\left(z_n\right)\right),\hfill \\ \hfill & x_{n+1}=J^{-1}\left({\beta }_{n}J\left(z_n\right)+(1-{\beta }_n)J\left(S{t}_n\right)\right).\hfill \end{array}\right.\end{array}$$

converges strongly to $x^{\ast }={\Pi }_{\Omega }\left(x_0\right)$.

5. Numerical Experiment

In the following, two numerical experiments are considered to demonstrate the applicability of our main result.

Example 1. 

Let $X=\mathbb{R}$, $C=[0,1]$, $f=\frac{1}{2}{|·|}^2$ and $Sx=\frac{x}{2}sin\left(x\right)$, and we consider $x_0={10}^9>0$, ${\beta }_n=\frac{1}{2}$, ${\alpha }_n=\frac{1}{{10}^n+1}$ and ${\lambda }_0=\frac{1}{2}$ as well as $\mu =0.9$ and $\epsilon =0.001$. Define the bifunction g on $C\times C$ into $\mathbb{R}$ as follows:

$$g(x,y)=Bx(y-x),$$

where

$$\begin{array}{c}\hfill Bx=\left\{\begin{array}{cc}0,\hfill & x\le \epsilon ,\hfill \\ sin(x-\epsilon ),\hfill & \epsilon \le x.\hfill \end{array}\right.\end{array}$$

The bifunction g satisfies the conditions $A1,A3,A4$ and $A5$. Furthermore,

$$\begin{array}{cc}\hfill g(x,y)+g(y,z)-g(x,z)& =(y-z)(Bx-By)\hfill \\ \hfill & \ge -|y-z||x-y|\hfill \\ & \ge -\frac{{(y-z)}^2}{2}-\frac{{(x-y)}^2}{2}\hfill \\ & =-D_{\frac{1}{2}{\parallel ·\parallel }^2}(z,y)-D_{\frac{1}{2}{\parallel ·\parallel }^2}(y,x),\hfill \end{array}$$

which proves the condition $A2$ with $c_1=c_2=1.$ A simple computation shows that Algorithm 1 takes the following form:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & y_n=x_n-{\lambda }_{n}B{x}_n,\hfill \\ \hfill & T_n=X,\hfill \\ \hfill & z_n=x_n-{\lambda }_{n}B{y}_n,\hfill \\ \hfill & t_n={\alpha }_n{x}_0+(1-{\alpha }_n)z_n,\hfill \\ \hfill & x_{n+1}={\beta }_n{z}_n+(1-{\beta }_n)\frac{t_n}{2}sin\left(t_n\right),\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill {\lambda }_{n+1}=\left\{\begin{array}{cc}min\left\{\frac{\mu \left({(x_n-y_n)}^2+{(z_n-y_n)}^2\right)}{(z_n-y_n)(B{x}_n-B{y}_n)},{\lambda }_n\right\},\hfill & if(z_n-y_n)(B{x}_n-B{y}_n)\le 0,\hfill \\ {\lambda }_n,\hfill & otherwise.\hfill \end{array}\right.\end{array}$$

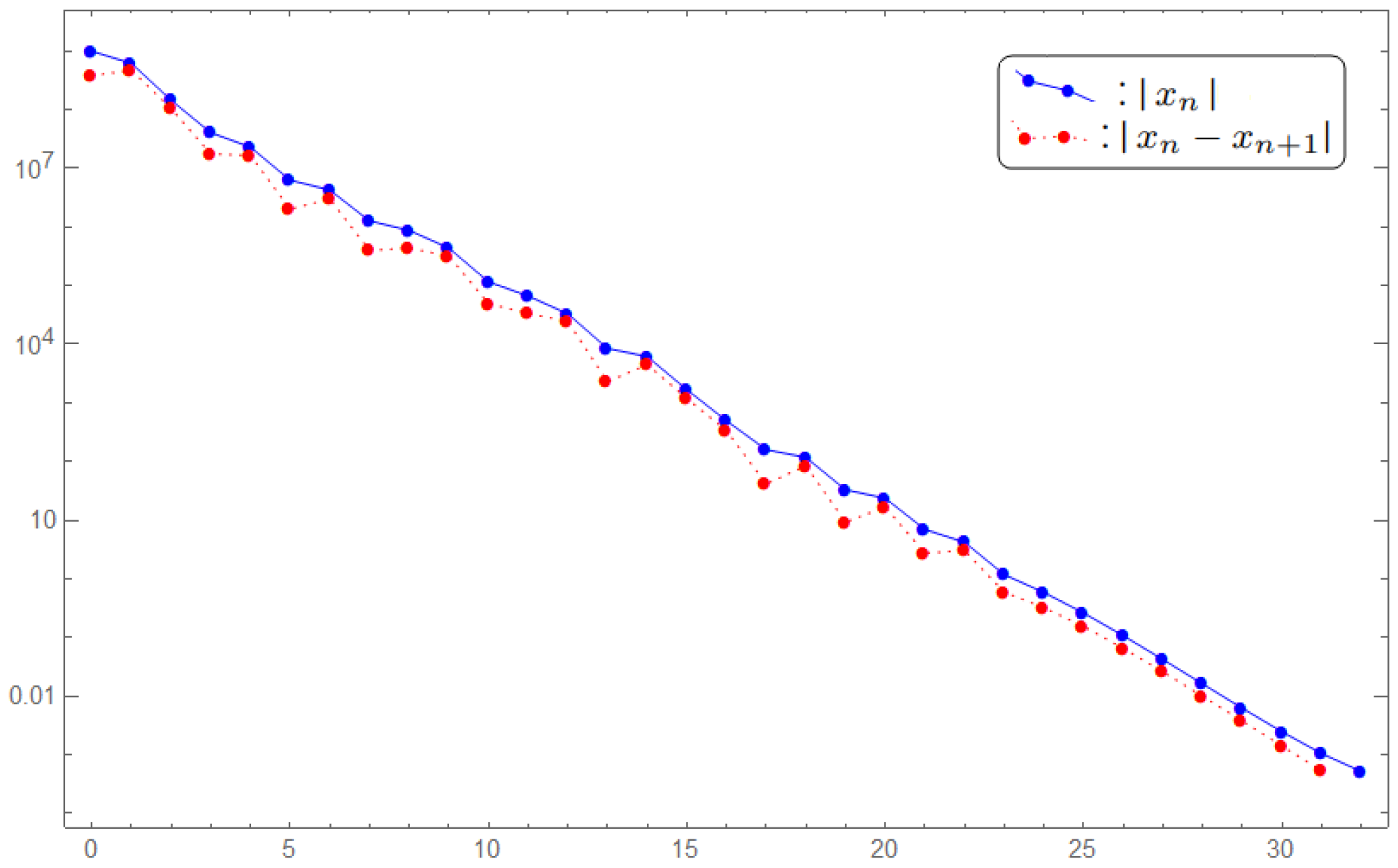
The decreasing values of $x_n$ and also the values of $|x_n-x_{n+1}|$ are shown in Figure 1; we see that the sequences $\left\{\right|x_n-x_{n+1}\left|\right\}$ and $\left\{\right|x_n\left|\right\}$ converge to zero.

Figure 1. The plotting of $|x_n|$ and $|x_{n-1}-x_n|$.

Now, another numerical example is given in an infinite dimensional space to show that our algorithm is efficient. We will use some notations that were introduced in [52].

Example 2. 

Suppose that $X=L^2\left([0,1]\right)$ with norm ${\parallel x\parallel }^2:={\int }_0^1{\left|x\left(t\right)\right|}^{2}dt$ and inner product $⟨x,y⟩:={\int }_0^{1}x\left(t\right)y\left(t\right)dt$ for all $x,y$ in $X.$ Let $C:=\{x\in X:\parallel x\parallel ⩽1\}$ be the unit ball. Define an operator $G:C\to X$ by

$$G\left(x\right)\left(t\right)={\int }_0^1\left(x\left(t\right)-F(t,s)h\left(x\right(s\left)\right)\right)ds+g\left(t\right),x\in C,t\in [0,1],$$

where

$$F(t,s)=\frac{2ts{e}^{t+s}}{e\sqrt{e^2-1}},h\left(x\right)=cosx,g\left(t\right)=\frac{2t{e}^t}{e\sqrt{e^2-1}}.$$

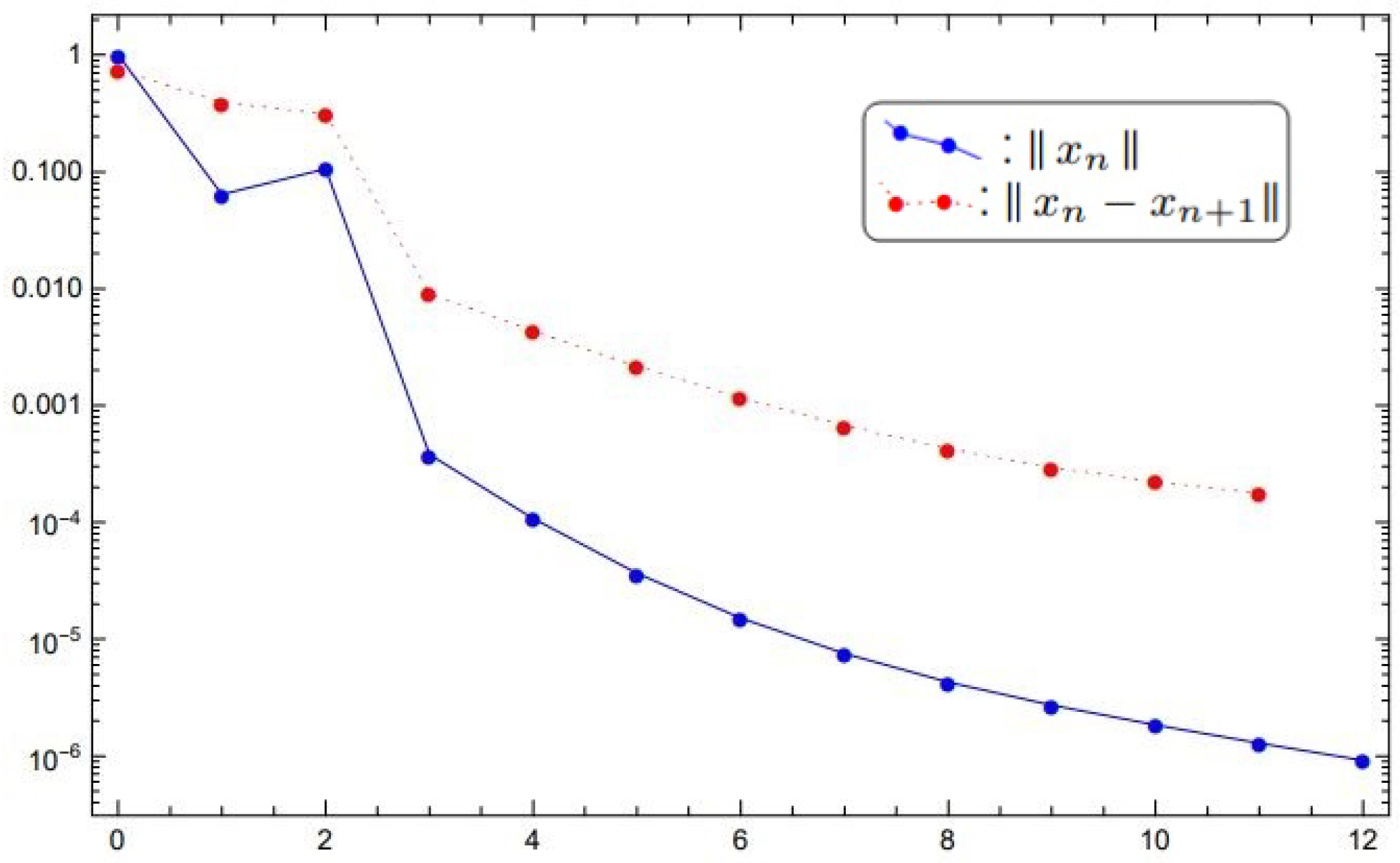
From [53], G is monotone (hence Pseudomonotone) and L-Lipschitz continuous with $c=2.$ The bifunction g is defined by $g(x,y)=⟨G\left(x\right),y-x⟩$, and $S:X\to X$ is defined by $S\left(x\right)=\frac{1}{2}\parallel x\parallel$ and $f\left(x\right)=\frac{1}{2}{\parallel x\parallel }^2.$ We consider $x_0=1$, ${\beta }_n=\frac{1}{2}$, ${\alpha }_n=\frac{1}{{10}^n+1}$ and ${\lambda }_0=\frac{1}{2}$ as well as $\epsilon ={10}^{-6}.$ The decreasing values of $\parallel x_n\parallel$ and also the values of $\parallel x_n-x_{n+1}\parallel$ are shown in Figure 2.

Figure 2. The plotting of $\Vert x_n\Vert$ and $\Vert x_{n-1}-x_n\Vert$.

6. Conclusions

The equilibrium problem encompasses, among its particular cases, convex optimization problems, variational inequalities, fixed-point problems, Nash equilibrium problems and other problems of interest in many applications. This paper proposes the subgradient extra-gradient algorithm to find a solution to an equilibrium problem involving a Pseudomonotone, which is also a fixed point of a Bregman relatively nonexpansive mapping in reflexive Banach spaces. We proved the strong convergence theorems for the proposed algorithm. Several experiments are reported to illustrate the numerical behavior of our algorithm.