1. Introduction
According to the definition of El-Ansary and Stern [
1], the power of a supply chain member is its ability to control the decision variables of other members of the supply chain. And the power differentials among supply chain members can be expressed indirectly through the game timing in supply chain games [
2,
3]. The first decisionmaker in the game influences the decisions of the later decisionmakers, thus creating its dominance. In this framework, a number of researchers have focused on the impact of dominance on supply chain performance [
4,
5,
6]. And most of these studies are based on a “single-supplier, single-retailer” supply chain structure (there is also a reasonable amount of literature that examines the structure of “one supplier and two retailers” or “two suppliers and one retailer”). With the general advancement of globalization and the rapid development of e-commerce, the “multiple-suppliers, multiple-retailers” model of multiple suppliers providing products to multiple retailers through online direct selling or offline wholesaling is very popular [
7]. The major difference between the above two models is that the latter introduces horizontal competition between suppliers (retailers). However, whether horizontal competition will break the profit advantage of the dominance is not very clear. In addition, much of the literature on the power structure of the supply chain is based on the reality that the rise of retail giants, such as Wal-Mart, continues to suppress suppliers in terms of wholesale prices, which may also affect consumer welfare. However, the shift of dominance from one party to another is a gradual process, and even Wal-Mart did not have dominance from the beginning of its operations. In reality, the non-dominant party may first undermine the dominant party’s power advantage in many ways. For example, Korpeoglu et al. [
8] suggested that a retailer can influence wholesale prices by changing the purchasing budget to exercise its own buyer’s power and obtain a higher level of profit. Geylani et al. [
9] developed a theoretical model to show how manufacturers strategically respond to dominant retailers. In these cases, the dominant party did not lose its dominance in terms of decision timing, but the non-dominant party undermined the dominant party’s power advantage through certain strategies. As the non-dominant party continues to grow, its power is further increased, resulting in equal status with the dominant party. For example, with the rapid development of Wal-Mart, Unilever gradually lost its dominant position in the supply chain, and the two formed an even situation. In current studies, modeling of the reality of this gradual decrease in dominance needs to be further explored.
Based on the above theories and motivations, we intend to extend the discussion of dominance advantage to “multiple-suppliers, multiple-retailers” supply systems and study the impact of the gradual weakening of suppliers’ dominance on the performance of supply chains and firms. The following questions are discussed through a comparative analysis of the equilibrium results under the three games:
In a “multiple-suppliers, multiple-retailers” supply system, does the party that prioritizes decisions still have a first-mover advantage?
Does competition between upstream suppliers (downstream retailers) affect the first-mover advantage? How?
Do fluctuations in market demand affect the first-mover advantage? How?
In a “multiple-suppliers, multiple-retailers” supply chain system, there is horizontal competition between suppliers (retailers) and vertical competition between suppliers and retailers. Suppliers (retailers) are substitutes, and there is no flow of goods in the horizontal competition. The study by Chen et al. [
10] showed that the power structure of the vertical supply chain has a more significant impact on the financial performance of individual firms or the entire supply chain than the horizontal supply chain. In order to simplify the model without compromising the purpose of the study, we assume that the market power between suppliers (retailers) is equal and thus adopt the Cournot game model. Although the Cournot game was first applied to competition in oligopolistic markets, researchers have also applied it to games between multiple horizontal competitors with equal market power. For example, Corbett and Karmarkar [
11] studied Cournot competition among multiple suppliers in a wholesale market. Roy et al. [
12] focused on the application of the Cournot game to business activities by finding strategic decisions and equilibrium solutions to the C&K-based Cournot game. Cabolis et al. [
13] studied the Cournot model of multiple oligopolies to capture the interplay between firms’ investment and merger decisions. Deo and Corbett [
14] studied the effect of the number of competitors on participants’ decisions in a Cournot game under output uncertainty. Of course, there can be power imbalances between the same levels, and the interested reader is referred to some recent literature, such as the studies by Chakraborty et al. (2021) [
15], Du et al. (2022) [
16], etc.
In the flow of goods, there is vertical competition between suppliers and retailers, which is reflected in their opposing interests in wholesale prices. Vertical competition in a supply chain can be represented by the Stackelberg game and the Nash game, depending on market power. In the Nash game, both parties have equal power and make decisions at the same time [
17,
18,
19]. And in the Stackelberg game, the market-dominant party has a first-mover advantage. Fang et al. have referred to vertical dominance as channel leadership [
20]. In recent years, there has been much literature on vertical competition in supply chains, which adopts the Stackelberg game to reflect the power difference between upstream and downstream of the supply chain. For example, Jin et al. [
21] studied the supply chain with suppliers as the dominant party, Pan Kewen et al. [
22] studied the supply chain with downstream retailers as the dominant party, and the studies by Xue et al. [
23] and Li et al. [
24] consider the case of different power structures. In terms of the impact of dominance on profit, similar findings were obtained: the dominant party has the right to prioritize decision-making and, therefore, has a first-mover advantage to obtain a higher level of profit. However, some researchers argue that whether a firm can benefit from dominance is also influenced by factors such as the demand function, demand uncertainty [
4,
5], the price sensitivity coefficient [
10,
25], and so on.
Based on the above research, this paper models the process of gradually decreasing the dominance of upstream suppliers and gradually increasing the power of downstream retailers in the “multiple-suppliers, multiple-retailers” supply chain, using the Cournot–Stackelberg game, the Market–Stackelberg game, and the Market–Nash game. (1) In the Cournot–Stackelberg game, the suppliers have dominance over the supply chain. A horizontal Cournot game is played between suppliers (retailers), and a supplier-dominated Stackelberg game is played between suppliers and retailers. In this game, the supplier has the strongest supply chain dominance, such as the four international major grain merchants, the United States ADM, Bunge, Cargill, and France’s Louis Dreyfus, which control 80% of the world’s grain trading volume with grain pricing power. (2) In the Market–Stackelberg game, the supplier still has dominance in the supply chain, but the retailer can undermine the supplier’s dominance advantage by deciding on purchasing budgets. Korpeoglu et al.’s [
8] research named it the Market game, and in this paper, in order to show both horizontal and vertical competition in supply chain systems, this game is referred to as the Market–Stackelberg game. The competition between some supermarket chains and strong brand suppliers is similar to this relationship: retailers such as Bravo, Home Depot, and Best Buy utilize their buyer power to obtain lower purchasing prices. (3) In the Market–Nash game, the power of supply chain members is balanced. All suppliers and retailers make decisions at the same time, and retailers still make purchasing budget decisions. Competition between general retail stores and non-branded suppliers is usually similar to this game, and it may also be the case between branded suppliers and retailers with comparable power. Further explanations of the three games can be found in the next section.
This paper also involves related research on market uncertainty. As early as the 1950s, Charnes et al. [
26] began to study uncertainty optimization. In recent years, more and more scholars have studied the uncertainty problem from the perspectives of information [
27], inventory [
28], paths [
29], and agricultural risk [
30] in the supply chain, using different demand functions to characterize market demand. With reference to Ailawadi’s [
31] view that the power structure and the timing of the game are affected by the way demand is modeled, this paper assumes that demand under the three games follows a random distribution to make the conclusions more general.
The papers of Shi et al., Wang et al., and Chen et al. are most similar to our study; they all studied the impact of dominance on supply chains based on a game-theoretic framework [
4,
5,
6]. The study by Shi et al. [
4] focused on a supply chain consisting of a retailer and a supplier under linear and isoelastic demand functions. They analyzed the Nash equilibrium of the three power structures: the supplier is absolutely dominant, the retailer is absolutely dominant, and the two have equal power. The results show that whether firms benefit from dominance depends on the form of the demand function: under linear demand, power-dominated firms are more profitable; under isoelastic demand, firms without dominance are more profitable. Wang et al. [
5] extended the research framework of Shi et al. [
4] but differed from their viewpoint of isoelastic demand counterparts. They adopted the retail margin percentage as the retailer’s decision variable in the retailer-dominated game in order to circumvent backward dominance. Chen et al. [
6] constructed a supply chain game model consisting of one supplier and two retailers in order to study the competition among retailers.
The difference between our paper and the aforementioned studies lies in the following aspects. (1) In terms of research objectives, we focus on the effects of market competition intensity and market volatility on the dominant power advantage of supply chains. (2) In terms of modeling, we construct a “multiple-suppliers, multiple-retailers” supply chain system with demand uncertainty and simulate the competitive intensity of the market through the change in the number of suppliers and retailers. We model the end-market uncertainty through a stochastic distribution in order to eliminate the influence of the form of the demand function (linear or nonlinear) on the results. We use three game models to represent the gradual weakening of suppliers’ dominance: absolute dominance, diminished dominance, and equal dominance. (3) It can be seen that the conclusions in this paper differ significantly from the above literature. Our research finds that the dominant advantage of a supply chain does not necessarily always exist—in a “multiple-suppliers, multiple-retailers” supply system, it is also affected by demand fluctuations and competition. Only when demand volatility in the consumer market is small do participants’ profits increase with their supply chain’s dominant power. However, when demand volatility is high, the profit advantage from the dominant power of the supply chain is no longer significant, and none of the supply chain members have incentives to strive for market dominance. In terms of competition, if the number of upstream suppliers is high, leading to intense competition, dominant power does not lead to more profits for either suppliers or retailers. If the number of downstream retailers increases, resulting in more demanders in the wholesale market, dominant power is more profitable, and both suppliers and retailers are willing to strive aggressively for dominant power.
The remainder of this essay is structured as follows: First, for the process of gradually decreasing the power of upstream sellers, the Cournot–Stackelberg game, the Market–Stackelberg game, and the Market–Nash game under demand uncertainty is built, and the game equilibrium is computed. Next, the impact of market demand fluctuations on the supply chain dominance is compared. Finally, a comparison of the impact of supply chain competition intensity (number of suppliers or retailers) is performed.
2. Problem Description
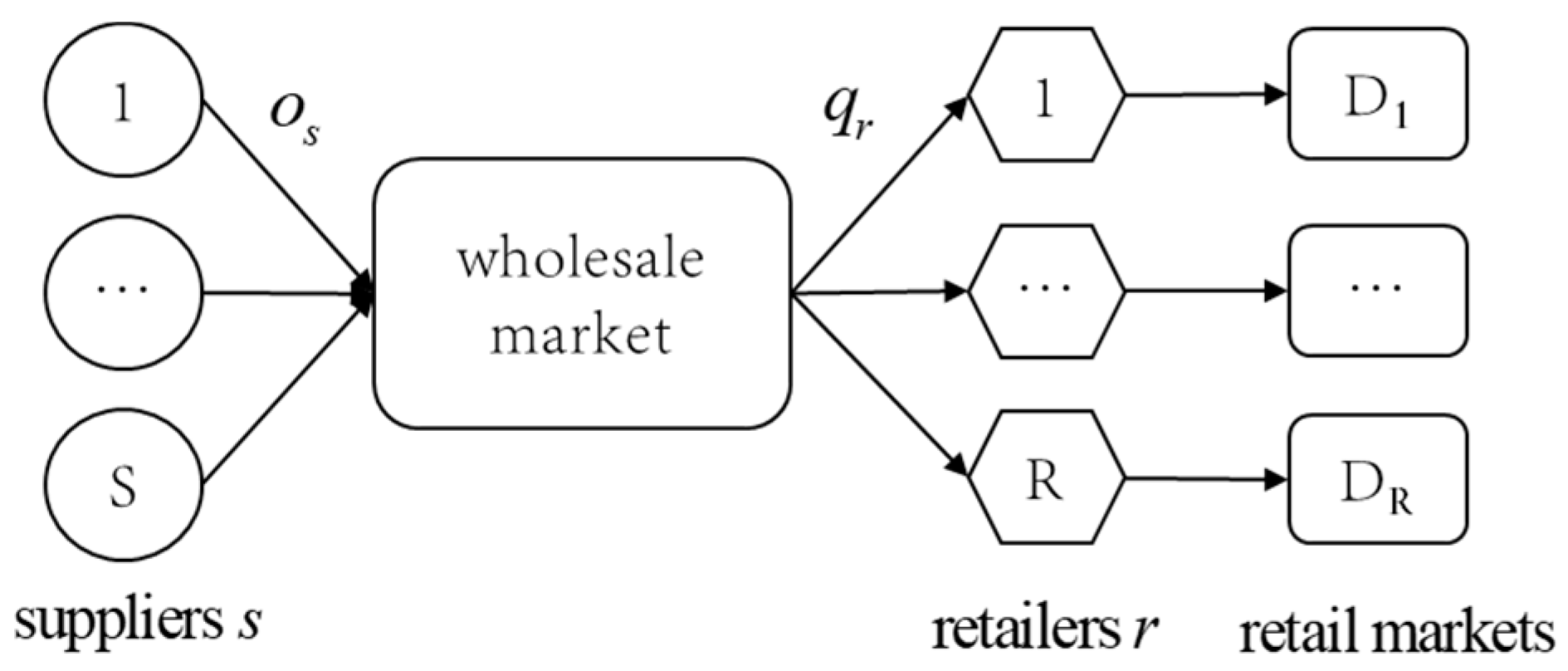
In this paper, we study the situation where multiple suppliers (
) supply multiple retailers (
) through the wholesale market under market uncertainty, as shown in
Figure 1. We assume that each retailer (
) faces its own independent end-market whose demand (
) is uncertain and follows a distribution with a cumulative distribution function
and a probability density function
. Note that the probability density function has an increasing generalized failure rate (IGFR), i.e., the demand function has the properties of the IGFR. This assumption stems from the reality that retailers in different cities or regions purchase products on the same wholesale market (online platform). All the horizontal competition mentioned in this paper is assumed to occur in the wholesale market: suppliers compete for demand, and the competitive pressure is reflected in selling; retailers compete for sources, and the competitive pressure is reflected in purchasing. At the same time, it is assumed that suppliers and retailers have complete information about each other and are both risk-neutral, pursuing their own profit maximization. For any retailer
, it procures an order quantity
from the wholesale market at the wholesale price
(then the total order quantity for all retailers is
) and sells the product at the retail price
.
For suppliers, the unit cost of production is
, the quantity that the supplier
sells to the wholesale market is
, and the total quantity produced is
, where
denotes the total quantity produced by all suppliers except supplier
. In the wholesale market, we assume a market-clearing condition, where all products provided by suppliers are purchased by retailers, i.e.,
.
and
denote the profits of supplier
and retailer
, respectively. Then, we have:
Then, the Cournot–Stackelberg, the Market–Stackelberg, and the Market–Nash games are used to simulate the game process of changing dominance between upstream suppliers and downstream retailers. The Sequence of events in these games is shown in
Figure 2, and the specific explanation will be discussed in the next section.
3. Modeling
In this paper, the superscript * denotes the best response function; the superscripts C, M, and N denote the Cournot–Stackelberg game, the Market–Stackelberg game, and the Cournot–Nash game models, respectively; and the subscripts s and r denote the supplier and the retailer, respectively.
3.1. A Cournot–Stackelberg Game Model Where the Seller Is Dominant
In the supplier-dominated Cournot–Stackelberg game, there is Cournot competition among suppliers and among retailers. However, suppliers have more market power and a first-mover advantage, so the Stackelberg game is played between suppliers and retailers. Their game timeline is shown in
Figure 2. In the first stage of decision-making, each supplier determines a production quantity by anticipating order quantities of retailers and its impact on wholesale price. Then, at the end of the first stage, the anticipated wholesale price is generated from market-clearing conditions. In the second stage, each retailer determines an order quantity by taking the wholesale price as given. Once production and purchases are determined separately, the market price can be determined according to the market clearing conditions. The decision-making goals of both retailers and suppliers are to maximize their expected profits. The expected profit functions of the supplier and the retailer are expressed as follows:
Nash equalization strategies are solved by backward induction, as shown in
Table 1. In the Nash equilibrium of this game, no supplier has an incentive to change his production quantity, and no retailer has an incentive to change her order quantity.
Proof. The retailer first determines the functional relationship between the ordering quantity and the wholesale price according to the principle of profit maximization, which can be obtained from the Equation for and the wholesale price . On the basis of market clearing, there is an equilibrium total production equal to the equilibrium total order quantity, i.e., , and there is . The supplier then determines the optimal production quantity based on the corresponding functional relationship between the retailer’s order quantity and the wholesale price. Substituting into Equation (3) and taking a first-order derivative of the wholesale price, the supplier’s optimal production quantity is obtained, and the optimal wholesale price is calculated as . The proof is complete. □
3.2. A Market–Stackelberg Game Model Where the Seller’s Dominance Erosion
The biggest difference between the Market–Stackelberg game and the Cournot–Stackelberg game is that the retailer, as a follower, changes the decision variable from purchasing quantity to purchasing budget. The purchasing budget information is then used to influence the supplier’s decision. The game timeline is shown in
Figure 2. In the first stage of decision-making, each supplier determines its production quantity by considering its impact on the wholesale price, and in the second stage, each retailer determines its procurement budget by considering its impact on the wholesale price. The wholesale price is determined according to the total procurement budget and the total production, while each retailer’s order quantity is determined by its procurement budget and the equilibrium wholesale price. Denote the procurement budget of the retailer
by
and denote the budget of all retailers by
, where
is the total purchasing budget of all retailers except the retailer
. Then, we can write the wholesale price
and retailer r’s order quantity
as follows:
At this point, the optimization problem for suppliers and retailers is:
The solution using backward induction leads to the equilibrium decisions of the members under the Market–Stackelberg game, as shown in
Table 1.
Proof. Firstly, from Equations (5) and (6), the derivation of
is obtained as
. Secondly, the expressions of
and
are substituted into the expected profit function of the retailer, and the optimal purchasing budget is obtained as
by making
. According to Equation (5), the expression of the wholesale price can be written as
. Then, the supplier, considering his own benefit maximization, performs the first-order derivation of the production quantity
, and the optimal production quantity is derived as
by making
. Finally, the equilibrium solution is substituted into the profit expression, and the profits of supplier
and retailer
can be obtained (see
Table 1). The proof is complete. □
3.3. A Market–Nash Game Model with Power Equilibrium between Sellers and Buyers
Unlike the previous two games, in a Market–Nash game, the retailer and the supplier make decisions on purchasing budget and production quantity at the same time, respectively (see
Figure 2). Therefore, no one has a first-mover advantage. To solve the Market–Nash problem, we only need to take the first-order derivatives of the objective functions (7) and (8) in the previous Market–Stackelberg model with respect to the purchasing budget
and the production quantity
, respectively. Then, make the first-order derivative solution equal to 0, i.e.,
and
, and solve the problem in conjunction with each other to obtain
and
. So, we obtain the optimal wholesale price
and the order quantity
.
3.4. Comparative Analysis of Game Equilibrium Solutions
In order to compare and analyze the differences in supply chain strategies under the three games, the above equilibrium solutions
,
, and
are substituted into the corresponding profit expressions to obtain the optimal profits for suppliers and retailers, as shown in
Table 1. For the sake of brevity, the Cournot–Stackelberg game, the Market–Stackelberg game model, and the Market–Nash game is abbreviated as the C–S game, M–S game, and M–N game, respectively.
Based on the above results, the following proposition is obtained:
Proposition 1. In a “multiple-suppliers, multiple-retailers” supply chain (), the retailer’s order quantity decision satisfies:
- (1)
The expressions for the retailer’s equilibrium order quantity under C–S, M–S, and M–N games are , , and , respectively;
- (2)
The retailer’s equilibrium order quantity in the M–S game is constantly smaller than that in the C–S game, i.e., ;
- (3)
Retailer’s order quantity is positively related to the number of suppliers under all three games, and, with the exception of the C–S game, order quantity is also positively related to the number of retailers.
Proof. Demand satisfies the generalized incremental failure rate (IGFR), i.e.,
is an increasing function, so we can obtain that:
According to the expressions of equilibrium order quantity
and
, it is clear that
(note that
refers to either
or
), i.e.,
Set , then we have . Perform a simple substitution, and then we obtain . Using inequalities (9) and (10), it is easy to observe that . Thus, is an increasing function on . And since , we have . Proposition 1-(2) is proved.
In the C–S and M–S games, the expressions of equilibrium order quantity are and , respectively. Since is an increasing function with respect to , then for the given parameters c and p, it is clear that a larger corresponds to a larger , i.e., is increasing with respect to . And according to the inverse function and implicit function derivation laws, holds in the M–N game. Therefore, in all three games, the retailers’ order quantity is positively related to the number of suppliers. Similarly, in the M–S and M–N games, according to the inverse function and implicit function derivation rule, we can get , . That is, the order quantity is also positively related to the number of retailers. In the C–S game, on the other hand, the equilibrium solution clearly shows that there is no relationship between the ordering quantity and the number of retailers. Propositions 1-(3) are proved. □
Since retailers face end markets with independent and identically distributed demand, their order quantity equals the amount of product flowing into the end market. From Propositions 1-(2), the dominant power of suppliers in the supply chain affects the products flowing into the end market. When retailers use a budget as a decision variable to constrain the dominance of suppliers, it reduces the total product inflow to the end market. Propositions 1-(3) show that when the supplier is absolutely dominant, changes in the number of retailers do not affect the equilibrium order quantity of each retailer. In contrast, when the supplier’s dominance becomes progressively weaker, an increase in the number of retailers stimulates each retailer to raise the equilibrium order quantity. This finding provides management insights for suppliers: when supplier dominance is weakened, they can buffer the negative impact of weakened power by aggressively exploring new markets to increase pressure on existing retailers and stimulate retailers to increase their order quantity.
Proposition 2. In a “multiple-suppliers, multiple-retailers” supply chain (), the supplier’s production quantity decision satisfies:
- (1)
Under the C–S, M–S, and M–N games, the supplier’s optimal production is , , and , respectively;
- (2)
The supplier’s production in the M–S game is constantly smaller than that in the C–S game, i.e., ;
- (3)
In all three games, a supplier’s production is positively related to the number of retailers and negatively related to the number of suppliers.
The proof is the same as the proof of Proposition 1, so the proof is omitted.
From Proposition 2, total output and total order quantity are equal due to the equilibrium of supply and demand in the wholesale market, so Proposition 2-(2) corresponds to Proposition 1-(2). They both show that the retailer’s use of budget decisions to weaken the supplier’s dominant power will reduce the total equilibrium output (total product inflow to the market). Proposition 2-(3) shows that regardless of whether the supplier has dominant power or not, he must increase output whenever he predicts an increase in the number of retailers and decrease output when he predicts an increase in suppliers.
Proposition 3. In a “multiple-suppliers, multiple-retailers” supply chain (), the wholesale price decision satisfies:
- (1)
Under the C–S, M–S, and M–N games, the optimal wholesale prices are , , and , respectively;
- (2)
The wholesale market price in the M–S game is constantly smaller than that in the C–S game, i.e., ;
- (3)
In contrast to the C–S and M–N games, the wholesale price in the M–S game is jointly determined by the supplier’s production decision and the retailer’s ordering decision.
Proof omitted.
A comparison of Proposition 3-(1) and Proposition 1-(1) shows that neither the retailer’s equilibrium order quantity nor the market equilibrium price is affected by the number of retailers in the C–S game. This is because retailers’ end markets are independent, and suppliers have no capacity constraints. Thus, despite an increase in the number of retailers, the supplier is always able to supply production that matches demand and thus cannot affect the wholesale price. Proposition 3-(2) shows that the wholesale market price in the M-S game is smaller than in the C–S game, indicating that the retailer can indeed benefit from using budget as a decision variable to obtain a lower wholesale price. The M–S game describes a common scenario in the marketplace: a retailer purchases products in the wholesale market and bargains with the supplier based on a limited budget, which reflects the retailer’s buyer power. However, it is not the case that an increase in retailer power necessarily affects the wholesale price in the M–N game. For example, the wholesale price is only related to the number of suppliers and the cost of production, despite the fact that the retailer acquires the same market power as the suppliers. Proposition 3 reveals this management insight: when the retailer has no market power at all, appropriate market power can achieve lower purchasing prices for it. And when the retailer has considerable power, it is difficult to use its power advantage to depress the purchasing price, and the effective way to reduce the purchasing price is to seek more sources of supply and encourage more suppliers to join the market.
Synthesizing Propositions 1, 2, and 3, it can be found that the relationship between equilibrium decision-making and power structure in a “multiple-suppliers, multiple-retailers” supply chain is different from in a “single-supplier, single-retailer” supply chain. In Shi et al.’s [
4] study of the impact of power structure on the “single-supplier, single-retailer” supply chain, they concluded that the wholesale price (order quantity) increases (decreases) with the power of the supplier and decreases (increases) with the power of the retailer. In a “multiple-suppliers, multiple-retailers” system, wholesale prices and order quantity do not behave in this absolutely monotonous manner as supplier or buyer power changes. In a “multiple-suppliers, multiple-retailers” system, the strength of the power structure’s influence on the equilibrium decision is heavily influenced by market volatility and competition intensity.
Based on the above analysis of the equilibrium solution, given the complexity of the model, we will next use numerical experiments to analyze the decisions and supply chain performance of the three games in the face of changes in external factors, such as demand fluctuations and competition intensity.