Bayesian Analysis of Unit Log-Logistic Distribution Using Non-Informative Priors
Abstract
:1. Introduction
2. Formulating Noninformative Priors: Preparation Steps
2.1. Jeffreys-Rule Prior
2.2. Useful Results in Establishing Reference and Matching Priors
3. Objective Priors for the Parameter
3.1. Reference Prior
3.2. Probability Matching Priors
3.3. Propriety of Posterior Distributions
4. Objective Priors for the Parameter
4.1. Reference Prior
4.2. Probability Matching Priors
4.3. Propriety of Posterior Distributions
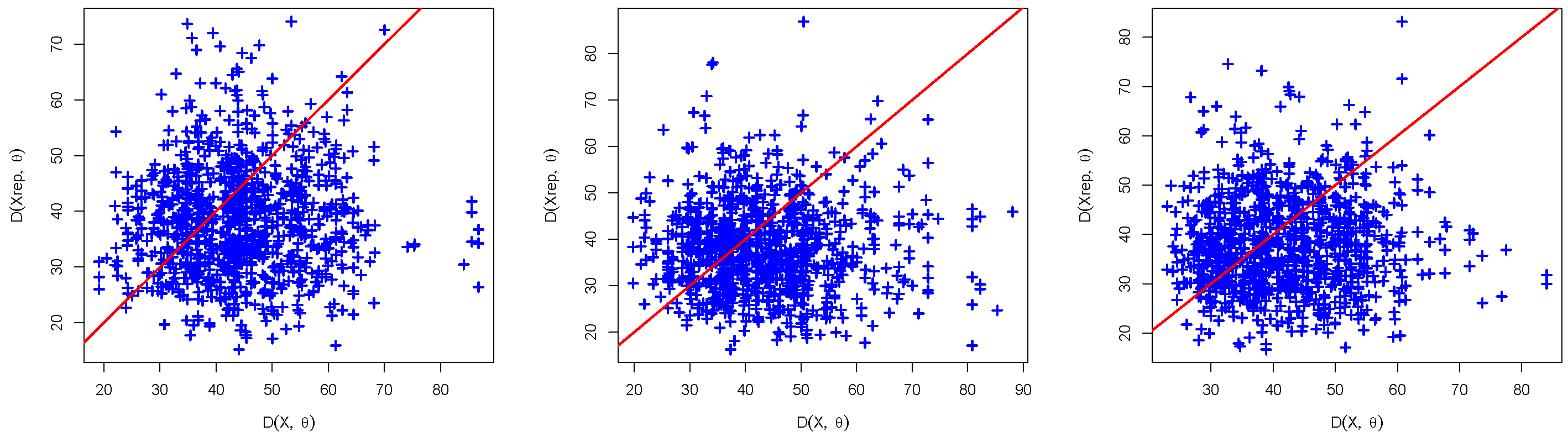
5. Posterior Predictive Assessment of the Model
- Input observed data .
- Sample from the posterior distribution, considering a specified prior and observed data under the specified prior, to obtain a posterior sample.
- For each generate new observations of the same size of the observed data using the UUL distribution; . This represents a predictive sample.
- Compute the discrepancy measures using the predictive and observed data, respectively and .
- Repeat steps 2–4 sufficiently large number of times K.
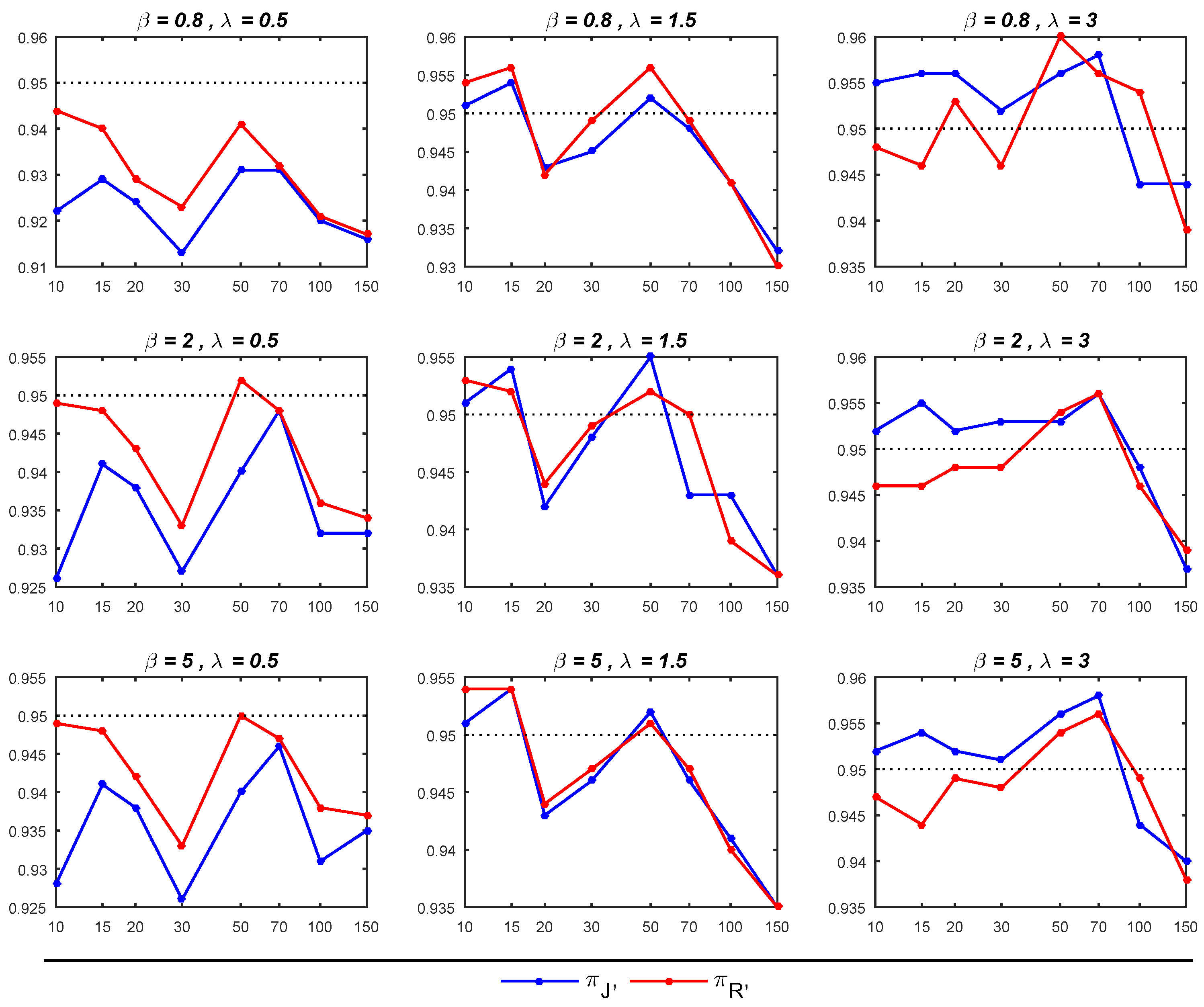
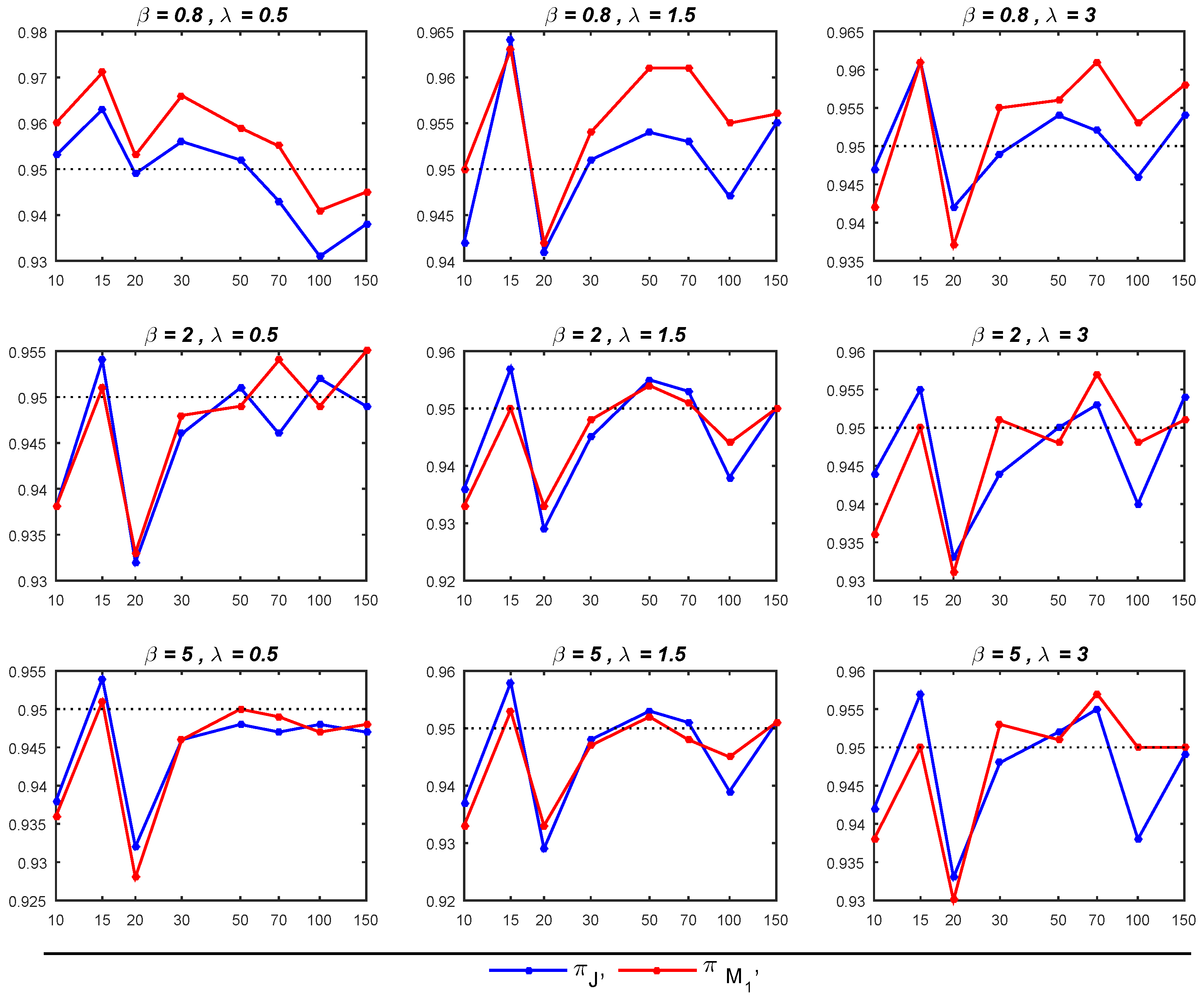
6. Simulation Study
- As expected, it is noticed that as the sample size increased, the performance of all estimators for and improved, leading to a reduction in MSEs.
- The Bayesian estimators for the parameter of interest, , under the prior tends to outperform its counterpart under the prior , particularly in terms of exhibiting smaller MSEs, especially for small sample sizes (when ). Moreover, in most cases with sample sizes up to 70, the 95% credible intervals under are close to the nominal level of 0.95, surpassing the corresponding intervals under . Nevertheless, when dealing with sample sizes exceeding 70, the 95% credible intervals for both priors tend to deviate from the nominal level of 0.95, though they generally remain above the 0.90 nominal level.
- The Bayesian estimator of exhibits better performance under , particularly when compared to , as it yields smaller MSEs. When both and are greater than 1, the 95% credible intervals derived from closely approximate the nominal level of 0.95, outperforming the corresponding intervals under . In other cases, the 95% credible intervals behave similarly for both priors. Moreover, for sample sizes exceeding 30, the 95% credible intervals not only approach the nominal level but also demonstrate greater stability.
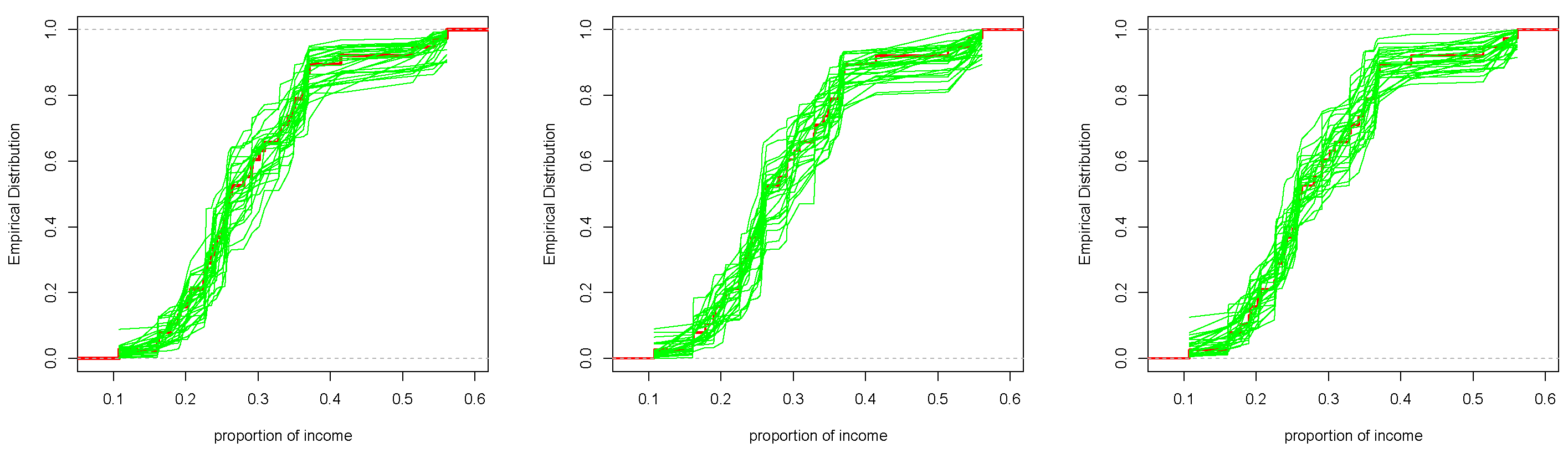
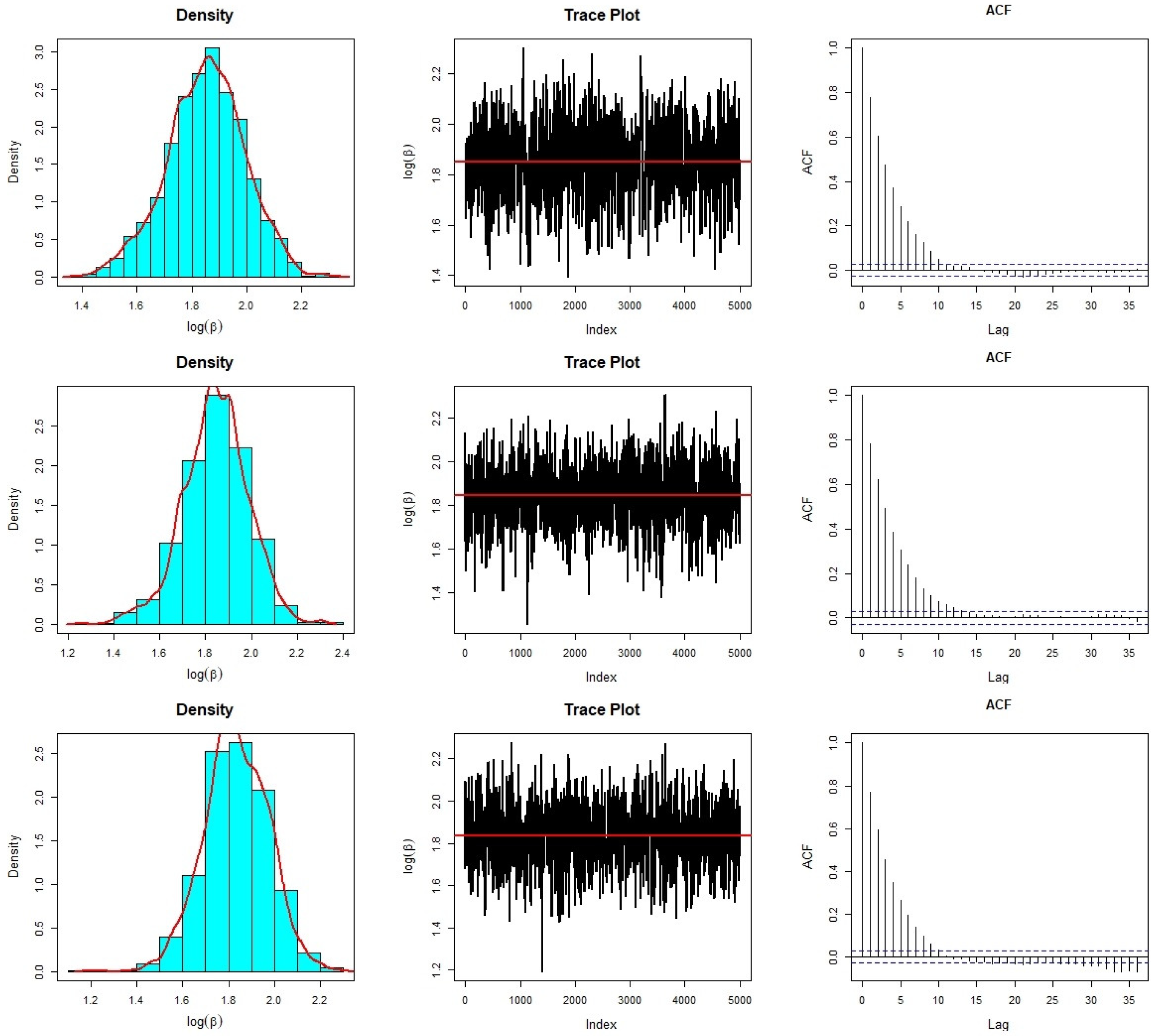
7. Real Data Analysis
8. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johnson, N.L. Systems of frequency curves generated by methods of translation. Biometrika 1949, 36, 149–176. [Google Scholar] [CrossRef] [PubMed]
- Kumaraswamy, P. A generalized probability density function for double-bounded random processes. J. Hydrol. 1980, 46, 79–88. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Mazucheli, J.; Menezes, A.F.B.; Alqallaf, F. The unit-inverse Gaussian distribution: A new alternative to two-parameter distributions on the unit interval. Commun. Stat. Theory Methods 2019, 48, 3423–3438. [Google Scholar] [CrossRef]
- Mazucheli, J.; Menezes, A.F.; Dey, S. Unit-Gompertz distribution with applications. Statistica 2019, 79, 25–43. [Google Scholar]
- Mazucheli, J.; Menezes, A.F.B.; Fernandes, L.B.; de Oliveira, R.P.; Ghitany, M.E. The unit-Weibull distribution as an alternative to the Kumaraswamy distribution for the modeling of quantiles conditional on covariates. J. Appl. Stat. 2020, 47, 954–974. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro-Reis, L.D. Unit log-logistic distribution and unit log-logistic regression model. J. Indian Soc. Probab. Stat. 2021, 22, 375–388. [Google Scholar] [CrossRef]
- Korkmaz, M.; Chesneau, C. On the unit Burr-XII distribution with the quantile regression modeling and applications. Comput. Appl. Math. 2021, 40, 29. [Google Scholar] [CrossRef]
- Korkmaz, M.C.; Korkmaz, Z.S. The unit log-log distribution: A new unit distribution with alternative quantile regression modeling and educational measurements applications. J. Appl. Stat. 2023, 50, 889–908. [Google Scholar] [CrossRef] [PubMed]
- Najwan Alsadat, N.; Elgarhy, M.; Karakaya, K.; Gemeay, A.M.; Chesneau, C.; Abd El-Raouf, M.M. Inverse Unit Teissier Distribution: Theory and Practical Examples. Axioms 2023, 12, 502. [Google Scholar] [CrossRef]
- Bernardo, J.M. Reference posterior distributions for Bayesian inference (C/R p128-147). J. R. Stat. Soc. Ser. 1979, 41, 113–128. [Google Scholar]
- Berger, J.O.; Bernardo, J.M. Ordered group reference priors with application to the multinomial problem. Biometrika 1992, 79, 25–37. [Google Scholar] [CrossRef]
- Berger, J.O.; Bernardo, J.M.; Sun, D.C. The formal definition of reference priors. Ann. Stat. 2009, 37, 905–938. [Google Scholar] [CrossRef]
- Welch, B.L.; Peers, H.W. On formulae for confidence points Based on integrals of weighted likelihoods. J. R. Stat. Soc. Ser. 1963, 25, 318–329. [Google Scholar] [CrossRef]
- Datta, G.S.; Sweeting, T.J. Probability matching priors. In Handbook of Statistics Vol. 25: Bayesian Thinking: Modeling and Computation; Dey, D.K., Rao, C.R., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 91–114. [Google Scholar]
- Datta, G.K.; Ghosh, M. On the invariance of noninformative priors. Ann. Stat. 1996, 24, 141–159. [Google Scholar] [CrossRef]
- Tibshirani, R. Noninformative priors for one parameter of many. Biometrika 1989, 76, 604–608. [Google Scholar] [CrossRef]
- Bernardo, J.M.; Smith, A.F.M. Bayesian Theory; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Guttman, J. The use of the concept of a future observation in goodness-of-fit problems. J. R. Stat. Soc. B 1967, 29, 83–100. [Google Scholar] [CrossRef]
- Meng, X.L. Posterior predictive p-values. Ann. Stat. 1994, 22, 1142–1160. [Google Scholar] [CrossRef]
- Gelman, A.; Meng, X.L.; Stern, H. Posterior Predictive Assessment of Model Fitness via Realized Discrepancies. Stat. Sin. 1996, 6, 733–760. [Google Scholar]
- Roberts, G.O.; Gelman, A.; Gilks, W.R. Weak convergence and optimal scaling of random walk Metropolis algorithms. Ann. Appl. Probab. 1997, 7, 110–120. [Google Scholar]



| Parameters | n | 10 | 15 | 20 | 30 | 50 | 70 | 100 | 150 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.8 | 0.5 | 0.5010 (0.922) | 0.3045 (0.929) | 0.2662 (0.924) | 0.1936 (0.913) | 0.1407 (0.931) | 0.1157 (0.931) | 0.0989 (0.920) | 0.0810 (0.916) | |
| 0.4712 (0.944) | 0.2988 (0.940) | 0.2653 (0.929) | 0.1925 (0.923) | 0.1406 (0.941) | 0.1158 (0.932) | 0.0987 (0.921) | 0.0807 (0.917) | |||
| 1.5 | 4.2766 (0.951) | 1.3487 (0.954) | 1.0293 (0.943) | 0.6621 (0.945) | 0.4591 (0.952) | 0.3675 (0.948) | 0.3039 (0.941) | 0.2401 (0.932) | ||
| 3.3626 (0.954) | 1.2351 (0.956) | 0.9639 (0.942) | 0.6330 (0.949) | 0.4472 (0.956) | 0.3602 (0.949) | 0.3002 (0.941) | 0.2379 (0.930) | |||
| 3 | 27.9630 (0.955) | 5.5104 (0.956) | 3.0399 (0.956) | 1.7268 (0.952) | 1.1224 (0.956) | 0.8870 (0.958) | 0.7118 (0.944) | 0.5448 (0.944) | ||
| 22.4203 (0.948) | 4.8432 (0.946) | 2.7289 (0.953) | 1.6036 (0.946) | 1.0762 (0.960) | 0.8572 (0.956) | 0.6976 (0.954) | 0.5365 (0.939) | |||
| 2 | 0.5 | 0.4969 (0.926) | 0.3014 (0.941) | 0.2624 (0.938) | 0.1908 (0.927) | 0.1387 (0.940) | 0.1138 (0.948) | 0.0976 (0.932) | 0.0791 (0.932) | |
| 0.4680 (0.949) | 0.2964 (0.948) | 0.2621 (0.943) | 0.1901 (0.933) | 0.1389 (0.952) | 0.1142 (0.948) | 0.0977 (0.936) | 0.0791 (0.934) | |||
| 1.5 | 4.2800 (0.951) | 1.3429 (0.954) | 1.0234 (0.942) | 0.6595 (0.948) | 0.4550 (0.955) | 0.3636 (0.943) | 0.2996 (0.943) | 0.2367 (0.936) | ||
| 3.3496 (0.953) | 1.2312 (0.952) | 0.9576 (0.944) | 0.6303 (0.949) | 0.4439 (0.952) | 0.3570 (0.950) | 0.2958 (0.939) | 0.2347 (0.936) | |||
| 3 | 27.8864 (0.952) | 5.5294 (0.955) | 3.0266 (0.952) | 1.7242 (0.953) | 1.1189 (0.953) | 0.8816 (0.956) | 0.7055 (0.948) | 0.5395 (0.937) | ||
| 22.4256 (0.946) | 4.8295 (0.946) | 2.7212 (0.948) | 1.6032 (0.948) | 1.0731 (0.954) | 0.8527 (0.956) | 0.6910 (0.946) | 0.5317 (0.939) | |||
| 5 | 0.5 | 0.4978 (0.928) | 0.3015 (0.941) | 0.2622 (0.938) | 0.1909 (0.926) | 0.1388 (0.940) | 0.1137 (0.946) | 0.0977 (0.931) | 0.0792 (0.935) | |
| 0.4679 (0.949) | 0.2964 (0.948) | 0.2623 (0.942) | 0.1901 (0.933) | 0.1389 (0.950) | 0.1141 (0.947) | 0.0977 (0.938) | 0.0790 (0.937) | |||
| 1.5 | 4.2751 (0.951) | 1.3456 (0.954) | 1.0226 (0.943) | 0.6600 (0.946) | 0.4549 (0.952) | 0.3634 (0.946) | 0.2995 (0.941) | 0.2366 (0.935) | ||
| 3.1325 (0.954) | 1.2329 (0.954) | 0.9577 (0.944) | 0.6298 (0.947) | 0.4438 (0.951) | 0.3572 (0.947) | 0.2959 (0.940) | 0.2347 (0.935) | |||
| 3 | 28.1580 (0.952) | 5.5408 (0.954) | 3.0291 (0.952) | 1.7246 (0.951) | 1.1180 (0.956) | 0.8829 (0.958) | 0.7051 (0.944) | 0.5401 (0.940) | ||
| 22.2549 (0.947) | 4.8106 (0.944) | 2.7228 (0.949) | 1.6020 (0.948) | 1.0726 (0.954) | 0.8531 (0.956) | 0.6911 (0.949) | 0.5313 (0.938) | |||
| Parameters | n | 10 | 15 | 20 | 30 | 50 | 70 | 100 | 150 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.8 | 0.5 | 0.3345 (0.953) | 0.2200 (0.963) | 0.1927 (0.949) | 0.1431 (0.956) | 0.1059 (0.952) | 0.0923 (0.943) | 0.0781 (0.931) | 0.0635 (0.938) | |
| 0.2864 (0.960) | 0.1954 (0.971) | 0.1747 (0.953) | 0.1325 (0.966) | 0.0996 (0.959) | 0.0875 (0.955) | 0.0749 (0.941) | 0.0612 (0.945) | |||
| 1.5 | 0.3309 (0.942) | 0.2160 (0.964) | 0.1871 (0.941) | 0.1374 (0.951) | 0.1007 (0.954) | 0.0854 (0.953) | 0.0710 (0.947) | 0.0558 (0.955) | ||
| 0.2868 (0.950) | 0.1953 (0.963) | 0.1721 (0.942) | 0.1290 (0.954) | 0.0960 (0.961) | 0.0820 (0.961) | 0.0691 (0.955) | 0.0546 (0.956) | |||
| 3 | 0.3320 (0.947) | 0.2162 (0.961) | 0.1869 (0.942) | 0.1366 (0.949) | 0.1003 (0.954) | 0.0849 (0.952) | 0.0705 (0.946) | 0.0550 (0.954) | ||
| 0.2881 (0.942) | 0.1960 (0.961) | 0.1721 (0.937) | 0.1290 (0.955) | 0.0962 (0.956) | 0.0822 (0.961) | 0.0689 (0.953) | 0.0540 (0.958) | |||
| 2 | 0.5 | 0.8321 (0.938) | 0.5430 (0.954) | 0.4664 (0.932) | 0.3411 (0.946) | 0.2524 (0.951) | 0.2130 (0.946) | 0.1772 (0.952) | 0.1376 (0.949) | |
| 0.7237 (0.938) | 0.4958 (0.951) | 0.4322 (0.933) | 0.3237 (0.948) | 0.2438 (0.949) | 0.2073 (0.954) | 0.1738 (0.949) | 0.1360 (0.955) | |||
| 1.5 | 0.8319 (0.936) | 0.5434 (0.957) | 0.4666 (0.929) | 0.3416 (0.945) | 0.2528 (0.955) | 0.2135 (0.953) | 0.1773 (0.938) | 0.1378 (0.950) | ||
| 0.7237 (0.933) | 0.4966 (0.950) | 0.4324 (0.933) | 0.3234 (0.948) | 0.2438 (0.954) | 0.2068 (0.951) | 0.1739 (0.944) | 0.1362 (0.950) | |||
| 3 | 0.8325 (0.944) | 0.5439 (0.955) | 0.4672 (0.933) | 0.3416 (0.944) | 0.2526 (0.950) | 0.2134 (0.953) | 0.1772 (0.940) | 0.1376 (0.954) | ||
| 0.7241 (0.936) | 0.4951 (0.950) | 0.4321 (0.931) | 0.3237 (0.951) | 0.2437 (0.948) | 0.2072 (0.957) | 0.1741 (0.948) | 0.1362 (0.951) | |||
| 5 | 0.5 | 2.0807 (0.938) | 1.3584 (0.954) | 1.1658 (0.932) | 0.8532 (0.946) | 0.6315 (0.948) | 0.5329 (0.947) | 0.4430 (0.948) | 0.3442 (0.947) | |
| 1.8091 (0.936) | 1.2402 (0.951) | 1.0807 (0.928) | 0.8095 (0.946) | 0.6096 (0.950) | 0.5186 (0.949) | 0.4349 (0.947) | 0.3405 (0.948) | |||
| 1.5 | 2.0793 (0.937) | 1.3584 (0.958) | 1.1661 (0.929) | 0.8541 (0.948) | 0.6322 (0.953) | 0.5337 (0.951) | 0.4430 (0.939) | 0.3444 (0.951) | ||
| 1.8112 (0.933) | 1.2414 (0.953) | 1.0812 (0.933) | 0.8089 (0.947) | 0.6095 (0.952) | 0.5177 (0.948) | 0.4344 (0.945) | 0.3408 (0.951) | |||
| 3 | 2.0818 (0.942) | 1.3599 (0.957) | 1.1684 (0.933) | 0.8533 (0.948) | 0.6312 (0.952) | 0.5338 (0.955) | 0.4432 (0.938) | 0.3442 (0.949) | ||
| 1.8108 (0.938) | 1.2371 (0.950) | 1.0798 (0.930) | 0.8088 (0.953) | 0.6095 (0.951) | 0.5182 (0.957) | 0.4351 (0.95) | 0.3403 (0.950) | |||
| Methods | Parameters | Estimates | SD | 95% CI |
|---|---|---|---|---|
| MLE | 6.4384 | 0.8800 | (4.7136, 8.1631) | |
| 0.2075 | 0.0749 | (0.0606, 0.3544) | ||
| Bayes estimates | - | - | - | 95% HPD CI |
| 6.4534 | 0.8772 | (4.8473, 8.2006) | ||
| 0.2165 | 0.0746 | (0.0905, 0.3667) | ||
| 6.3702 | 0.8753 | (4.7915, 8.0905) | ||
| 0.2256 | 0.0817 | (0.0946, 0.3969) | ||
| 6.3296 | 0.9024 | (4.6688, 8.0961) | ||
| 0.2234 | 0.0865 | (0.0872, 0.4043) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shakhatreh, M.K.; Aljarrah, M.A. Bayesian Analysis of Unit Log-Logistic Distribution Using Non-Informative Priors. Mathematics 2023, 11, 4947. https://doi.org/10.3390/math11244947
Shakhatreh MK, Aljarrah MA. Bayesian Analysis of Unit Log-Logistic Distribution Using Non-Informative Priors. Mathematics. 2023; 11(24):4947. https://doi.org/10.3390/math11244947
Chicago/Turabian StyleShakhatreh, Mohammed K., and Mohammad A. Aljarrah. 2023. "Bayesian Analysis of Unit Log-Logistic Distribution Using Non-Informative Priors" Mathematics 11, no. 24: 4947. https://doi.org/10.3390/math11244947
APA StyleShakhatreh, M. K., & Aljarrah, M. A. (2023). Bayesian Analysis of Unit Log-Logistic Distribution Using Non-Informative Priors. Mathematics, 11(24), 4947. https://doi.org/10.3390/math11244947






