Automated Settings of Overcurrent Relays Considering Transformer Phase Shift and Distributed Generators Using Gorilla Troops Optimizer

Abstract

The relative protective devices are cascaded in a proper sequence with a proper min/max coordination time margin (CTM) to minimize the outage area of the network in case of fault condition. This manuscript addresses a new methodology based on the gorilla troops optimizer (GTO) to produce the best automated settings for overcurrent relays. In the GTO, the exploration and exploitation phases are realized using five methodologies. Three of them are used in the exploration phase and the other two in the exploitation phase. In the exploration phase, all gorillas are considered as candidate solutions and the best one is considered as the silverback gorilla. Then again, the exploitation phase comprises two steps: (i) the first one is the follow of silverback gorilla, and (ii) the second one is the competition for adult females. The latter mentioned offers an added advantage to the GTO framework to move forward steadily to global minima and to avoid trapping into local minima. Two test cases under numerous scenarios are demonstrated comprising an isolated real distribution network with distributed generations for the Agiba Petroleum company which is in the Western Desert of Egypt. The relay coordination problem is adapted as an optimization problem subject to a set of predefined constraints which is solved using the GTO including fixed and varied inverse IEC curves, in which the practical constraints including transformer phase shift and other scenarios for min/max fault conditions are dealt with. In due course, this current effort aims at proving the best strategy for achieving the smoothest coordination of overcurrent relays (OCRs), with the least obtained value of CTMs for the studied cases being established via the automated relay settings. At last, it can be pointed out that the GTO successfully dealt with this problem and was able to produce competitive answers compared to other competitors.

1. Introduction

Overcurrent (OC) and earth fault (EF) protections along the power system network play a vital role among other types of protection units for various voltage levels [1,2]. Cascading the operating sequence of these relative units is needed to minimize the outage of the power system to secure its operations. In regard to the EF, it is a simple process to achieve the coordination, especially since there are few units to be cascaded and, in general, the definite time (DT) characteristic is enough for this study. The latter is alternatively called the coordination of discrimination to ensure the arrangements of the operations of the main and backup OC protection units and to allow specific time margins, which are known as a coordination time margin (CTM). This time margin is normally varying from 0.2 ms to 0.4 s, and it actually depends on the technology and generation of the OC relays (OCRs). More specifically, between digital relays, the CTM of 0.2 s may be used and for electromechanical relays, the CTM is something around 0.5 s [2,3,4].

Manual achievement of the coordination is tedious and requires a lot of time. Thus, the computerized alternative to this is essential. Even for the available tools, it is still difficult to tackle these drawbacks as the interfering of the engineers is still required. In the last decade, many efforts have been performed to automate such studies with minimal interferences from the engineers. Among these methods are: expert systems [3], linear programming [5,6,7], the simplex method [8,9], random search [10], and mixed-integer non-linear programing [11]. The deficiencies of these aforementioned methods have been proven when they are applied to larger systems. On the other hand, many researchers have proposed various optimization methodologies to deal with the same problem, aiming to generate automated relay settings such as the slime mold algorithm (SMA) [12], water cycle algorithm [13,14], whale optimization algorithm [15,16], firefly algorithm [17], adaptive fuzzy directional bat algorithm [18], genetic optimizer [19], moth-flame optimization [20], JAYA [21,22], Harris Hawks’ optimization [21,23], nature-inspired root tree algorithm [24], electromagnetic field optimization algorithm [25], and particle swarm optimization [26,27,28].

Further considerable efforts to accommodate microgrids and the involvement of distributed generators (DGs) in the coordination study have been reported, such as the methods for DGs-integrated distribution networks considering system dynamics [29,30], adaptive OC relay (OCR) coordination in grid-connected wind farms [31], adaptive OCR coordination scheme for windfarm-integrated power systems [32], optimum coordination of OCRs to enhance microgrid EF protection scheme [33], and optimal coordination of overcurrent relays in microgrids [34,35,36,37,38].

Further to the above, a comprehensive survey has been presented in [2,39], in which the readers are invited to go through such efforts. Extra heuristic-based optimizers are still being used by the esteemed researchers in order to improve the quality of the relay coordination outcome with the ultimate objective of generating an automated setting. Until this moment, many trials have been performed in the same manner. More recently, the gradient-based optimizer [40], various versions of differential evolution [41,42,43], stochastic fractal search algorithm [44], flower pollination for combination between arc-flash and coordination [45], harmony search algorithm [46], grey wolf optimizer [47], and so on [48,49,50,51,52,53,54,55,56], have been presented. Moreover, the practical coordination model is investigated in distribution networks penetrated with motors and transformers as declared in [57]. Adaptive protection coordination in distribution networks with DGs is deployed in [58], while the implementation of unsupervised learning techniques is exploited in [59] for the coordination of OCRs in microgrids.

Taking a closer look at the above-mentioned survey, numerous methods have been undertaken to attain the optimal settings for OC relays in traditional and smart grids as well, yet there is still room for improvement to include more constraints to attain industrial trust and meet the requirements. In the same context, and in line with the no-free-lunch theorem, the authors are motived to employ the gorilla troops-based optimization (GTO) method [60] to tackle this problem with the hope of having a competitive outcome compared to the existing results available in the literature. In GTO, the exploration and exploitation processes are realized using five methodologies. It can be confirmed that the GTO has been applied successfully to estimate the ungiven parameters of the single and double-diode models [61]. In this context, the deployment of GTO is exploited in [62] to solve the optimization problem of the integration of renewable-based DGs in power systems.

In this current effort, the GTO is used to produce the optimal settings in an automated manner of OCRs for two test cases under different intentional scenarios with the minimal interference of users, and in which new concepts for understanding the point at which to start the relay coordination for min/max fault scenarios are proposed. The first case is a 15-bus network with DGs which is widely used in the literature, and the second case is a real power network based in West Desert in Egypt for the Agiba petroleum company.

2. Optimization Problem Formulation

It is obviously known that the relation between the fault current passing through the relay ($I_f$) and the relay operating time ($t_{ri}$) is an inverse one as shown in (1).

$$t_{ri}=\frac{a}{{\left(\frac{I_f}{I_{pu}}\right)}^{ß}-1}. T_D$$

(1)

where: $I_{pu}$ is the relay current pickup, $T_D$ is the relay time dial setting, and $a$, and $ß$ are constants varying with the relay type characteristics (CCs) as presented in

Table 1. Constant values for various IEC standard curves.

Standard	$\mathit{T}\mathit{C}\mathit{C} \mathbf{Type}$	$\mathit{a}$	$\mathit{ß}$
IEC	NI	0.14	0.02
IEC	VI	13.50	1.00
IEC	EI	80.00	2.00
IEC	LI	120.00	1.00

. Figure 1 presents four standardized TCCs extracted from the IEC 60255-3 standard [1] plotted using a log-to-log scale.

The optimization process of OCRs in this paper threads through dedicated and ordered steps as follows:

• Preparing the model which includes the relay pairs definition, the level of fault currents, and the lower and upper boundaries of the decision variables.
• Constructing the fitness optimized function (FOF) that tends to minimize the total operating time (TOT) of the primary relays as disclosed in (2).

  $$FOF={\displaystyle \sum }_{i=1}^{N_P}{t}_{ri}$$

  (2)

  where: $N_P$ is the total number of the primary relays in the study case.
• Defining the lower and upper boundaries of independent and dependent constraints. The decision variables needed to be optimized represent the independent ones as demonstrated in (3)–(7).

  $$I_{pui,min} \le I_{pui} \le I_{pui,max}$$

  (3)

  $$I_{pui,min}\ge OLC\times I_{full load}$$

  (4)

  $$I_{pui,max}\le SF\times I_{f,min}$$

  (5)

  $$T_{Di,min} \le T_{Di} \le T_{Di,max}$$

  (6)

  $$TC{C}_{i,min} \le TC{C}_i \le TC{C}_{i,max}$$

  (7)

  where: $I_{pui,min}$, and $I_{pui,max}$ are the minimum and maximum values of the relay current pickup, respectively. In practice, $I_{pui,min}$ shall be greater than the equipment full load current ($I_{full load}$) by a certain value nominated as the over loading capacity ($OLC)$. On the other hand, $I_{pui,max}$ shall be lower than the minimum fault current ($I_{f,min})$ by a certain value called the sensitivity factor ($SF)$. Moreover, the relay time dial shall be bounded between minimum ($T_{Di,min})$ and maximum ($T_{Di,max})$ value besides the $TCC$, as is also the case in digital relays. $TC{C}_{i,min}, \mathrm{and} TC{C}_{i,max}$ are the lower and upper limits of the CCs’ type that have discrete values rather than other settings that have continuous values.
  The dependent constraints examined in this research lie in two types; the selectivity constraint and the minimum operating time constraint as dedicated in (8) and (9), respectively.

  $$CT{M}_{min,j} \le t_{bri}-t_{pri} \le CT{M}_{max,j}$$

  (8)

  $$t_{pri} \ge t_{min,i}$$

  (9)

  where: $t_{bri}$, and $t_{pri}$ are the operating time of the backup and primary relay, respectively, at the same fault point. $CT{M}_{min,j}$, and $CT{M}_{max,j}$ are the minimum and maximum values of CTM, respectively, while $t_{min,i}$ is the minimum possible operating time of the protection relay by activating its instantaneous CCs.
• Extracting the optimal values of the decision variables in addition to plotting the convergence trend of $FOF$.

3. Procedures of the GTO

The metaheuristic algorithms are more significant in solving many sophisticated engineering problems due to their simple implementation and are more superior than other heuristic techniques to crop global optimal solution. The metaheuristic techniques can be classified as: natural, swarm, physical, and human based. One of the new, nature-inspired algorithms which is inspired by the gorilla group trait is developed by [60] and is called GTO. In the GTO, the exploration and exploitation processes are implemented using five methodologies: three in the exploration phase and two in the exploitation phase. In the exploration phase, all gorillas are considered as nominee solutions and the best one is considered as the silverback gorilla. The three methodologies of the exploration phase can be summarized as: the resettlement to an unknown position when $rand<$ controlled the variable ($p$); then the transition to other different gorilla is decided if rand $rand\ge 0.5$; and lastly, the transition to a known position is selected when $rand<0.5$. These exploration processes can be depicted as:

$$GX\left(k+1\right)=\{\begin{array}{c}\left(HL-LL\right)\times r_1+LL rand<p\\ \left(r_2-C_1\right)\times X_r\left(k\right)+S\times C_2 rand\ge 0.5\\ X\left(k\right)-S\times \left[S\times \left(X\left(k\right)-G{X}_r\left(k\right)\right)+r_3\times \left(X\left(k\right)-G{X}_r\left(k\right)\right)\right] rand<0.5\end{array}$$

(10)

where: $GX\left(k+1\right)$ is the nominee location vector in the iteration of (k + 1) rank, $X\left(k\right)$ is the existing vector of the gorilla location, $r_1, r_2 and r_3$ and $rand$ are the updated random values between 0 and 1 in each iteration, $HL$, and $LL$ are the higher and lower values of desired understudying problem variables, respectively, $X_r$ is a randomly selected member of the gorilla group, $G{X}_r$ is the one vector of the random gorilla candidate’s updated location in each phase. The parameters $C_1, C_2 and S$ are calculated using:

$$C_1=1+\cos \left(2r_4\right)\left[1-\frac{it}{i{t}_{max}}\right]$$

(11)

$$S=C_1\times r_5$$

(12)

$$C_2=r_6\times X\left(k\right)$$

(13)

where: $r_4$ are updated random variables between 0 and 1, $it, i{t}_{max}$ are the current and maximum iteration, respectively, and $r_5$ is the random parameters between −1 and 1. The behavior of the gorilla silverback is emulated by (12) and $r_6$ is a random variable between $-C_1$ and $C_1$ in the problem dimension.

The exploitation phase consists of two methodologies, the first one is the following of the silverback gorilla when the variable $C_1\ge W$ and can be emulated by (14). However, the second one is the competition for adult females when $C_1<W$ and can be simulated by (15).

where: $W$ is a set point before the optimization process.

$$GX\left(k+1\right)=S\times {\left(\left|\frac{1}{N_G}\right|{\displaystyle \sum }_{m=1}^{N_G}G{X}_m\left(k\right)\right)}^{\frac{1}{2^S}}\times \left(X\left(k\right)-X_s\right)+X\left(k\right)$$

(14)

where: $X_s$ is the silverback gorilla location, which is the best solution, $G{X}_m\left(k\right)$ describes each nominee gorilla’s vector location in iteration k, and $N_G$ is the gross number of gorillas.

$$GX\left(m\right)=X_s-\left(2r_6-1\right) \left(Beta\times E\right) (X_s-X\left(k\right)$$

(15)

where: $r_6$ is a random value between 0 and 1, $Beta$ is a set parameter before optimization start and $E$ is the variable that simulates the violence on the solution dimension based on the value of the $rand$ variable.

The $X\left(k\right)$ is replaced by $GX\left(k\right)$ when the FOF value of $GX\left(k\right)$ is lower than one of $X\left(k\right)$.

The procedures of minimizing the FOF (i.e., the TOT of the primary relays) based on the GTO algorithm are depicted in Figure 2.

4. Study Cases and Results with Debates

The performance of the proposed GTO is evaluated in two various study cases with different topologies. The first one is the IEEE 15-bus system, which is deemed as a pure transmission network tackled many times before in the literature. The obtained results are compared to the latest powerful optimizers and manifest the superiority of the GTO over them for solving this highly constrained optimization problem. The second one is an isolated practical distribution network belonging to the Agiba petroleum company located in Egypt. 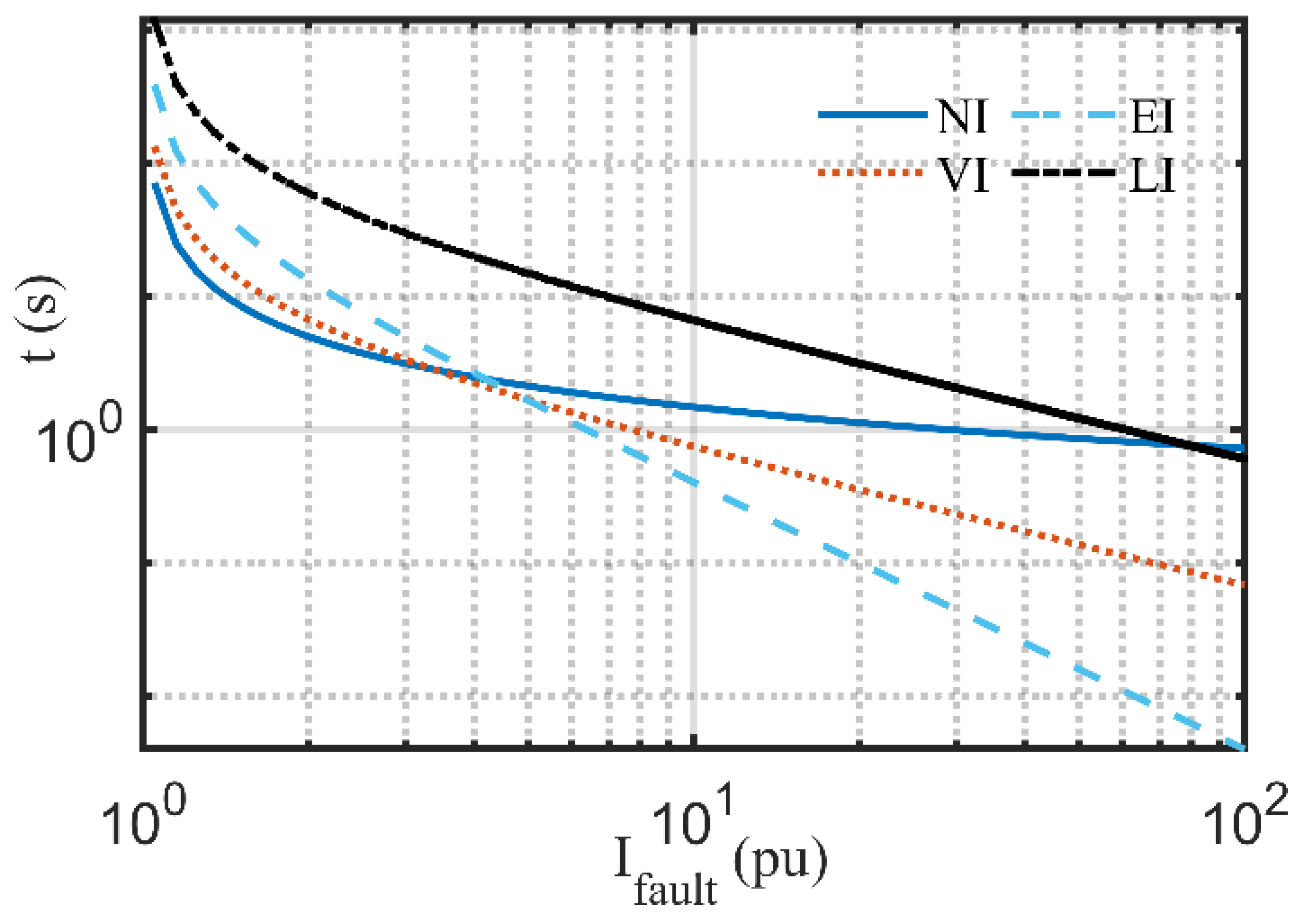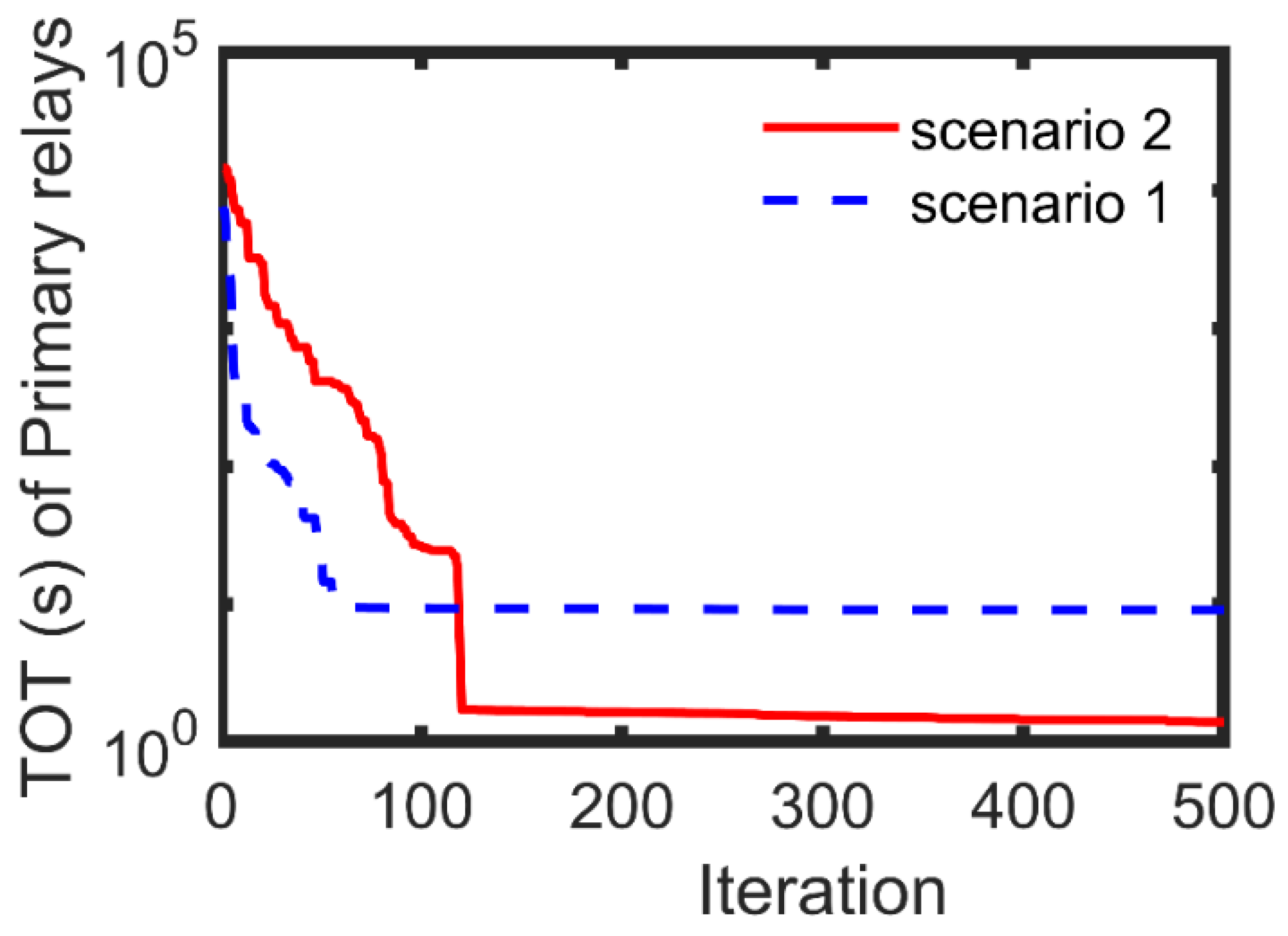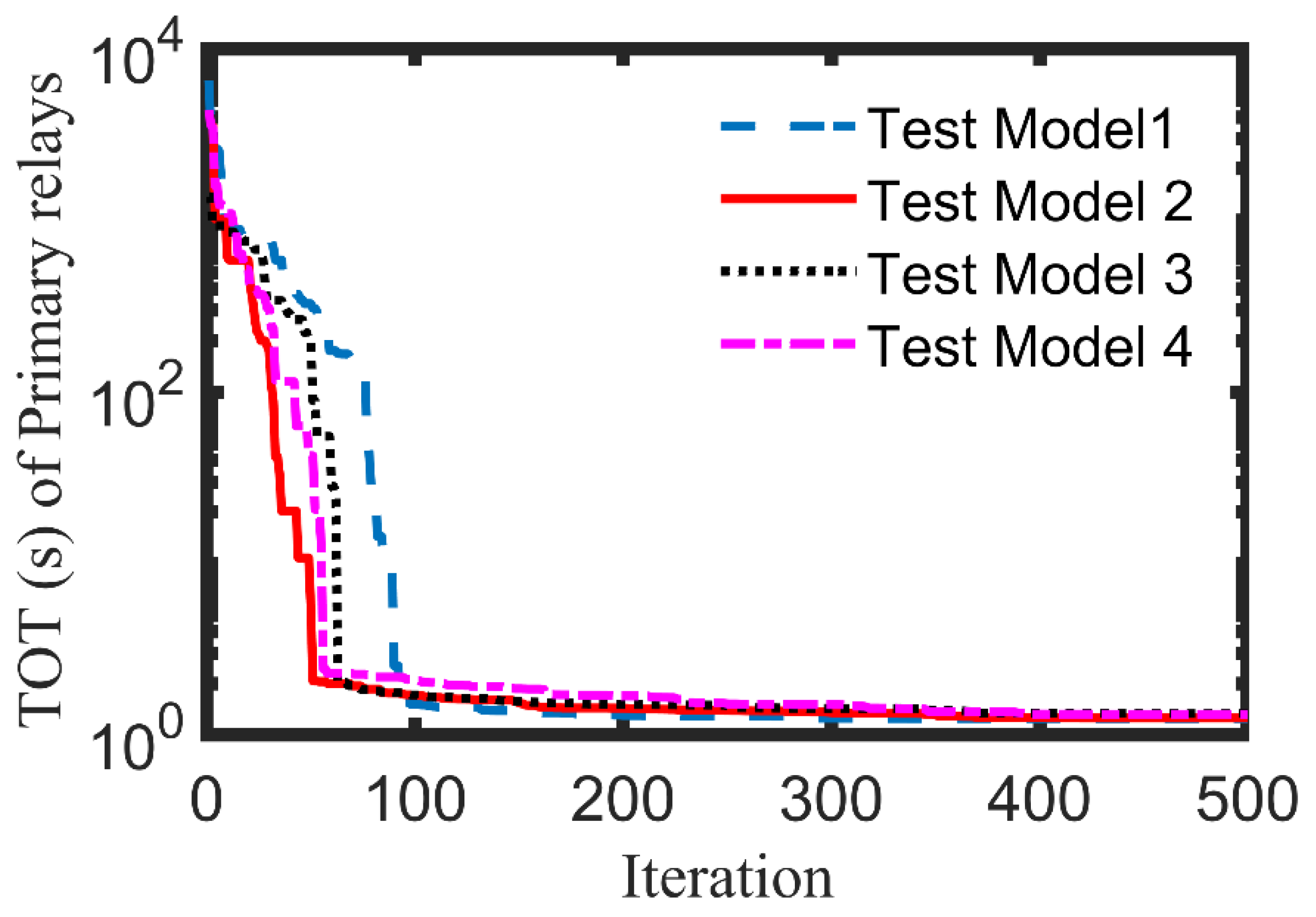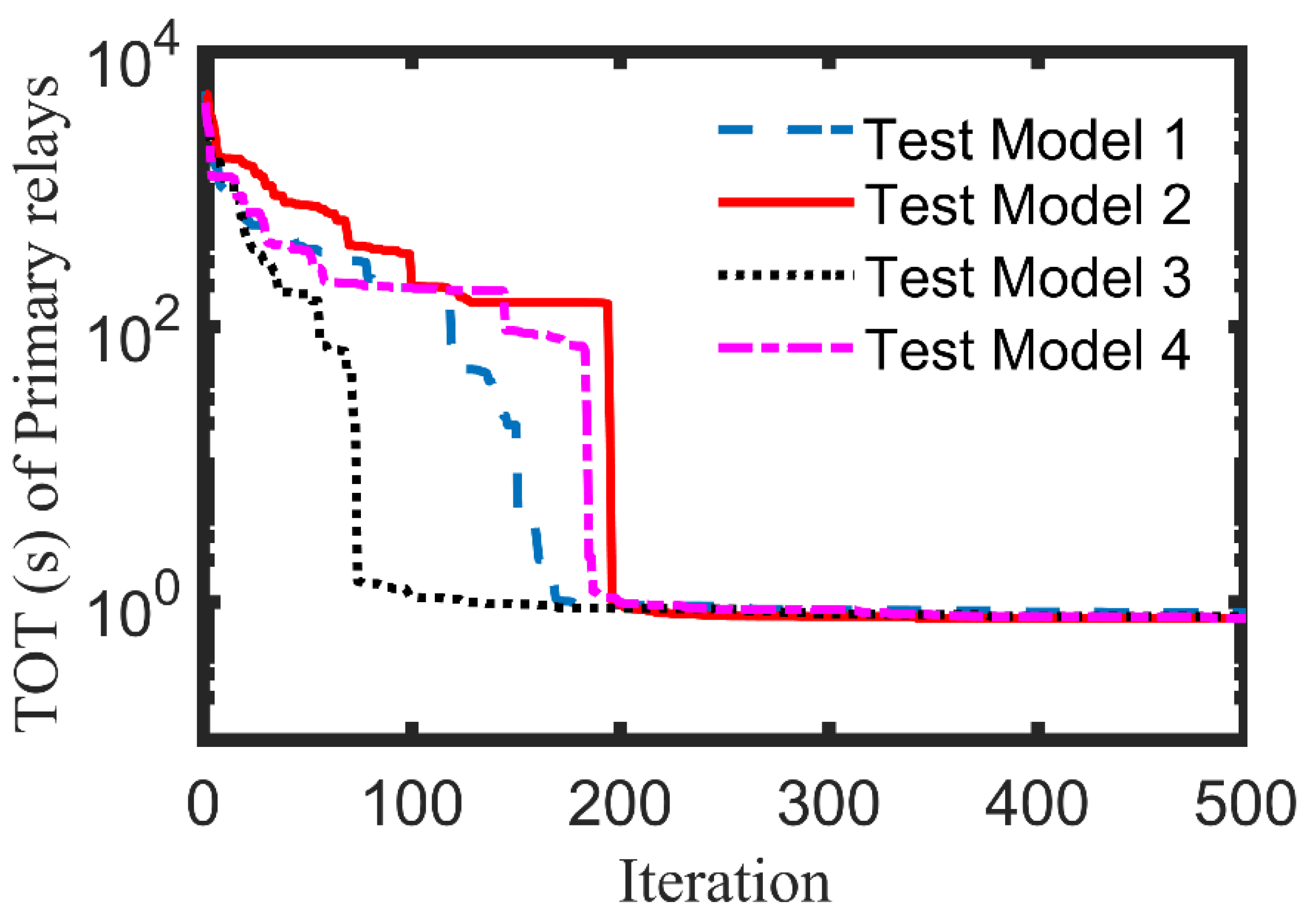Both networks are investigated using two scenarios; scenario one considers the fixed NI curve while scenario two optimizes the curve between the four standard IEC TCCs. Furthermore, the GTO control parameters are set as follows for better results: $p=0.000001$, $Beta=4$, $W=0.9$, $N_G=100$, and $i{t}_{max}=500$.

4.1. Study Case 1: The IEEE 15-Bus Network

Figure 3 depicts the single-line diagram (SLD) of the IEEE 15-bus network and its system data obtained can be found in [12,14,40,45].

To validate the GTO results, the following assumptions are considered for a fair comparison with other algorithms: (i) an OLC between 100% to 150% of the full load current with no considerations on the minimum fault current conditions, the (ii) $T_{Di,min}=0.05 \mathrm{s}$ for scenario one and 0.01 s for scenario two while $T_{Di,max}=1 \mathrm{s}$ for both scenarios, (iii) $CT{M}_{min,j}=0.2 \mathrm{s}$ and $CT{M}_{max,j}=0.4 \mathrm{s}$, and (iv) $TC{C}_{i,min}=1$ and $TC{C}_{i,max}=4$.

Table 2. Optimum DOCRs settings of the IEEE 15-bus using GTO.

Relay ID.	Scenario 1		Scenario 2
	${\mathit{I}}_{\mathit{p}} \left(\mathbf{A}\right)$	${\mathit{T}}_{\mathit{D}} \left(\mathbf{s}\right)$	${\mathit{I}}_{\mathit{p}} \left(\mathbf{A}\right)$	${\mathit{T}}_{\mathit{D}} \left(\mathbf{s}\right)$	Curve
R1	274.3358	0.0675	293.9991	0.0215	EI
R2	313.9608	0.0681	307.6176	0.0244	EI
R3	478.9256	0.0654	477.1756	0.0221	EI
R4	440.9214	0.0663	442.4978	0.0294	EI
R5	489.9721	0.0662	431.7093	0.0297	EI
R6	373.4484	0.0661	374.9995	0.0264	EI
R7	345.0252	0.0685	367.4998	0.0270	EI
R8	556.5137	0.0668	559.5983	0.0205	EI
R9	432.7932	0.0658	433.3580	0.0184	EI
R10	403.1725	0.0634	403.8370	0.0199	EI
R11	449.1812	0.0677	449.9982	0.0269	EI
R12	483.8421	0.0666	502.4489	0.0210	EI
R13	509.7451	0.0500	516.4943	0.0131	EI
R14	394.2057	0.0649	323.7574	0.0338	EI
R15	344.3698	0.0663	367.4998	0.0251	EI
R16	253.7067	0.0639	245.1271	0.0232	EI
R17	179.5477	0.0667	187.4989	0.0351	EI
R18	457.3094	0.0678	487.9445	0.0204	EI
R19	425.2535	0.0672	425.6398	0.0251	EI
R20	620.0474	0.0641	622.3204	0.0213	EI
R21	539.9664	0.0612	539.9992	0.0166	EI
R22	202.2495	0.0639	201.8658	0.0244	EI
R23	395.0120	0.0644	393.4877	0.0243	EI
R24	251.1717	0.0653	224.4215	0.0314	EI
R25	348.8178	0.0629	286.8513	0.0287	EI
R26	304.9423	0.0685	307.2427	0.0383	EI
R27	352.4827	0.0653	320.5883	0.0275	EI
R28	447.8116	0.0667	389.5427	0.0293	EI
R29	671.0048	0.0673	674.2527	0.0263	EI
R30	201.8216	0.0658	192.8832	0.0310	EI
R31	300.5795	0.0671	263.0405	0.0283	EI
R32	278.9333	0.0661	284.9837	0.0161	EI
R33	351.3740	0.0745	405.0106	0.0227	EI
R34	298.8261	0.0685	280.2785	0.0308	EI
R35	364.0380	0.0603	296.5395	0.0290	EI
R36	433.7195	0.0676	382.2169	0.0261	EI
R37	553.7038	0.0666	599.9994	0.0276	EI
R38	299.4094	0.0672	248.6752	0.0331	EI
R39	285.5946	0.0667	294.4203	0.0225	EI
R40	560.6371	0.0670	490.9930	0.0293	EI
R41	297.1019	0.0635	299.9973	0.0268	EI
R42	337.1191	0.0674	374.1360	0.0164	EI
TOT (s)	9.0775		1.3962

lists the optimized settings of DOCRs in the IEEE 15-bus network using the GTO for both scenarios. It is revealed that the GTO has been managed for selecting the EI curve for all relays in scenario two in the hope of achieving the best obtained FOF ever. The operating times of the primary/backup relays are recorded in

Table 3. Operating times of M/B relay pairs with their associated CTM values of the IEEE 15-bus based on GTO.

Relay Pairs		Scenario 1			Scenario 2			Relay Pairs		Scenario 1			Scenario 2
M	B	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)	M	B	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)
1	6	0.1783	0.3830	0.2047	0.0114	0.2154	0.2039	20	30	0.1742	0.3743	0.2002	0.0113	0.2162	0.2049
2	4	0.1730	0.3795	0.2065	0.0088	0.2320	0.2232	21	17	0.1519	0.3828	0.2309	0.0055	0.3053	0.2998
2	16	0.1730	0.4115	0.2385	0.0088	0.2271	0.2183	21	19	0.1519	0.3970	0.2451	0.0055	0.2135	0.2080
3	1	0.2115	0.4116	0.2000	0.0257	0.2319	0.2061	21	30	0.1519	0.3743	0.2224	0.0055	0.2162	0.2107
3	16	0.2115	0.4115	0.2000	0.0257	0.2271	0.2013	22	23	0.1930	0.4921	0.2991	0.0211	0.3744	0.3533
4	7	0.1976	0.4056	0.2080	0.0242	0.2655	0.2412	22	34	0.1930	0.4027	0.2097	0.0211	0.2242	0.2031
4	12	0.1976	0.4167	0.2191	0.0242	0.2249	0.2006	23	11	0.1744	0.3939	0.2195	0.0126	0.2212	0.2086
4	20	0.1976	0.4151	0.2175	0.0242	0.2287	0.2045	23	13	0.1744	0.4789	0.3046	0.0126	0.3325	0.3200
5	2	0.2375	0.4380	0.2005	0.0408	0.2440	0.2032	24	21	0.2021	0.4723	0.2702	0.0243	0.2634	0.2391
6	8	0.2318	0.4525	0.2207	0.0433	0.2467	0.2034	24	34	0.2021	0.4027	0.2006	0.0243	0.2242	0.2000
6	10	0.2318	0.4381	0.2063	0.0433	0.2474	0.2041	25	15	0.2295	0.4442	0.2148	0.0366	0.3377	0.3012
7	5	0.2377	0.4375	0.1998	0.0478	0.2506	0.2028	25	18	0.2295	0.4429	0.2134	0.0366	0.2582	0.2216
7	10	0.2377	0.4381	0.2004	0.0478	0.2474	0.1995	26	28	0.2325	0.4724	0.2399	0.0557	0.2799	0.2242
8	3	0.2147	0.4155	0.2008	0.0236	0.2237	0.2001	26	36	0.2325	0.4993	0.2668	0.0557	0.2809	0.2252
8	12	0.2147	0.4167	0.2020	0.0236	0.2249	0.2012	27	25	0.2580	0.4581	0.2001	0.0575	0.2573	0.1999
8	20	0.2147	0.4151	0.2005	0.0236	0.2287	0.2050	27	36	0.2580	0.4993	0.2413	0.0575	0.2809	0.2235
9	5	0.2357	0.4375	0.2018	0.0326	0.2506	0.2180	28	29	0.2654	0.4651	0.1997	0.0571	0.3316	0.2745
9	8	0.2357	0.4525	0.2168	0.0326	0.2467	0.2140	28	32	0.2654	0.5005	0.2352	0.0571	0.2589	0.2018
10	14	0.1993	0.4117	0.2124	0.0206	0.2224	0.2018	29	17	0.1821	0.3828	0.2007	0.0138	0.3053	0.2914
11	3	0.2042	0.4155	0.2113	0.0234	0.2237	0.2003	29	19	0.1821	0.3970	0.2149	0.0138	0.2135	0.1997
11	7	0.2042	0.4056	0.2014	0.0234	0.2655	0.2421	29	22	0.1821	0.3828	0.2007	0.0138	0.2139	0.2001
11	20	0.2042	0.4151	0.2109	0.0234	0.2287	0.2053	30	27	0.2096	0.4184	0.2089	0.0310	0.2318	0.2008
12	13	0.2112	0.4789	0.2677	0.0245	0.3325	0.3080	30	32	0.2096	0.5005	0.2910	0.0310	0.2589	0.2279
12	24	0.2112	0.4119	0.2007	0.0245	0.2452	0.2207	31	27	0.2037	0.4184	0.2147	0.0192	0.2318	0.2126
13	9	0.1809	0.5396	0.3587	0.0248	0.3331	0.3084	31	29	0.2037	0.4651	0.2614	0.0192	0.3316	0.3124
14	11	0.1804	0.3939	0.2134	0.0134	0.2212	0.2077	32	33	0.2263	0.4307	0.2044	0.0249	0.2510	0.2261
14	24	0.1804	0.4119	0.2315	0.0134	0.2452	0.2318	32	42	0.2263	0.4719	0.2456	0.0249	0.2697	0.2447
15	1	0.1729	0.4116	0.2387	0.0123	0.2319	0.2196	33	21	0.2720	0.4723	0.2003	0.0578	0.2634	0.2056
15	4	0.1729	0.3795	0.2065	0.0123	0.2320	0.2197	33	23	0.2720	0.4921	0.2201	0.0578	0.3744	0.3166
16	18	0.2014	0.4429	0.2415	0.0228	0.2582	0.2353	34	31	0.2698	0.4699	0.2001	0.0676	0.2674	0.1998
16	26	0.2014	0.4360	0.2345	0.0228	0.3996	0.3767	34	42	0.2698	0.4719	0.2021	0.0676	0.2697	0.2021
17	15	0.1944	0.4442	0.2499	0.0284	0.3377	0.3094	35	25	0.2369	0.4581	0.2212	0.0475	0.2573	0.2099
17	26	0.1944	0.4360	0.2416	0.0284	0.3996	0.3712	35	28	0.2369	0.4724	0.2355	0.0475	0.2799	0.2324
18	19	0.1581	0.3970	0.2389	0.0055	0.2135	0.2080	36	38	0.2291	0.4309	0.2018	0.0286	0.2285	0.1998
18	22	0.1581	0.3828	0.2247	0.0055	0.2139	0.2084	37	35	0.2564	0.4564	0.1999	0.0754	0.2759	0.2006
18	30	0.1581	0.3743	0.2162	0.0055	0.2162	0.2107	38	40	0.3000	0.5066	0.2066	0.0858	0.3276	0.2418
19	3	0.2053	0.4155	0.2102	0.0230	0.2237	0.2008	39	37	0.2847	0.4851	0.2005	0.0790	0.4681	0.3890
19	7	0.2053	0.4056	0.2002	0.0230	0.2655	0.2425	40	41	0.2676	0.4789	0.2113	0.0588	0.4148	0.3560
19	12	0.2053	0.4167	0.2114	0.0230	0.2249	0.2019	41	31	0.2304	0.4699	0.2395	0.0508	0.2674	0.2165
20	17	0.1742	0.3828	0.2087	0.0113	0.3053	0.2940	41	33	0.2304	0.4307	0.2003	0.0508	0.2510	0.2002
20	22	0.1742	0.3828	0.2087	0.0113	0.2139	0.2026	42	39	0.2022	0.4036	0.2014	0.0172	0.2174	0.2002

with no violations in the independent or dependent constraints. The entrenched fair comparison results in the obvious superiority of the GTO over other algorithms with various natures as announced in

Table 4. GTO TOT comparison with other algorithms of the IEEE 15-bus.

Scenario 1					Scenario 2
GTO	SMA [12]	EGWO [57]	MEFO [25]	MWCA [13]	GTO	SMA [12]	SFSA [44]	FPA [45]
9.0775	11.9761	12.2282	13.953	13.282	1.3962	2.4504	3.21	2.95

. The GTO achieves a TOT of 9.0775 s and 1.3962 s, attaining a 24.2% and a 43% reduction compared to SMA for scenarios one and two, respectively. Moreover, the FOF smooth convergence trend using the GTO for this highly penetrated DG network is shown in Figure 4.

4.2. Study Case Ⅱ: The Agiba Power Network

This network is an isolated practical one consisting of three DGs, five distribution transformers, five medium voltage motors, four MCCs, fourteen cables, and seventeen OCRs. The network SLD is designed using the Microsoft Visio platform as shown in Figure 5, while the system data regarding the equipment ratings and fault currents are announced in Appendix A (see

Table A1. Distributed Generator Data.

ID	${\mathit{S}}_{\mathit{r}\mathit{a}\mathit{t}\mathit{e}\mathit{d}} \left(\mathbf{kVA}\right)$	${\mathit{V}}_{\mathit{r}\mathit{a}\mathit{t}\mathit{e}\mathit{d}} \left(\mathbf{kV}\right)$	$\mathit{X}{\mathit{d}}^{″} (\mathit{\%})$	$\mathit{X}{\mathit{d}}^{\prime } (\mathit{\%})$	$\mathit{X}\mathit{d} (\mathit{\%})$	$\mathit{P}{\mathit{F}}_{\mathit{r}\mathit{a}\mathit{t}\mathit{e}\mathit{d}} (\%)$
DG1	3250	11	20.4	25.3	189	80
DG2	3250	11	20.4	25.3	189	80
DG3	3250	11	20.4	25.3	189	80

,

Table A2. Distribution Transformer Data.

ID	Voltage Ratio (kV)	${\mathit{S}}_{\mathit{r}\mathit{a}\mathit{t}\mathit{e}\mathit{d}} \left(\mathbf{kVA}\right)$	Impedance (%)	X/R	Vector Group
TR1	11/3.3	1600	6.13	5.76	Dy11
TR2	11/3.3	1600	5.12	5.76	Dy11
TR3	11/3.3	1600	6.13	5.76	Dy11
TR4	11/3.3	1600	6.13	5.76	Dy11
TR5	11/3.3	1600	6.37	5.76	Dy11

,

Table A3. Motor Data.

ID	Designation	${\mathit{V}}_{\mathit{r}\mathit{a}\mathit{t}\mathit{e}\mathit{d}} \left(\mathbf{kV}\right)$	${\mathit{P}}_{\mathit{r}\mathit{a}\mathit{t}\mathit{e}\mathit{d}} \left(\mathbf{kW}\right)$	${\mathit{I}}_{\mathit{r}\mathit{a}\mathit{t}\mathit{e}\mathit{d}} \left(\mathbf{A}\right)$	$\mathit{P}{\mathit{F}}_{\mathit{r}\mathit{a}\mathit{t}\mathit{e}\mathit{d}} (\%)$
MOPA	Oil Line Pump	3.3	490	101.4	90.5
MOPB	Oil Line Pump	3.3	490	101.4	90.5
MOPC	Oil Line Pump	3.3	490	101.4	90.5
MOPD	Oil Line Pump	3.3	610	123.4	92.29
WIP	Water Injection Pump	3.3	607	125.6	90.5

,

Table A4. Feeder Data.

ID	Length (m)	Area (mm2)	Conductor/Insulation
F_TR1	10	25	CU/XPLE
F_MCC-1	25	25	CU/XPLE
F_TR2	10	25	CU/XPLE
F_MCC-2	25	25	CU/XPLE
F_TR3	10	25	CU/XPLE
F_MCC-3	25	25	CU/XPLE
F_TR4	10	25	CU/XPLE
F_MCC-4	25	25	CU/XPLE
F_TR5	10	25	CU/XPLE
F_MOPA	15	35	CU/XPLE
F_MOPB	15	35	CU/XPLE
F_MOPC	15	35	CU/XPLE
F_MOPD	15	35	CU/XPLE
F_WIP	15	35	CU/XPLE

,

Table A5. MCC Data.

ID	${\mathit{V}}_{\mathit{r}\mathit{a}\mathit{t}\mathit{e}\mathit{d}} \left(\mathbf{kV}\right)$	$\mathit{P} \left(\mathbf{kW}\right)$	$\mathit{Q} \left(\mathbf{kVAr}\right)$	$\mathit{P}{\mathit{F}}_{\mathit{r}\mathit{a}\mathit{t}\mathit{e}\mathit{d}} (\%)$
MCC-1	11	177.8	77.2	91.73
MCC-2	11	90.8	39.2	91.81
MCC-3	11	355.7	154.6	91.71
MCC-4	11	177.8	77.2	91.73

,

Table A6. Full Load Current and Current Transformer Ratio.

Relay ID	${\mathit{I}}_{\mathit{f}\mathit{l}} \left(\mathbf{A}\right)$	CTR
R1	170.6	250/5
R2	170.6	250/5
R3	170.6	250/5
R4	83.98	100/5
R5	101.4	150/5
R6	10.17	25/5
R7	83.98	100/5
R8	125.6	150/5
R9	5.19	25/5
R10	83.98	100/5
R11	101.4	150/5
R12	20.36	50/5
R13	83.98	100/5
R14	101.4	150/5
R15	10.17	25/5
R16	83.98	100/5
R17	123.4	150/5

,

Table A7. Max-Fault Conditions (3 DGs are in service with Bus Coupler 1 and Bus Coupler 2 closed).

Relay Pair ID	Primary	Backup	3-Phase		2-Phase
			${\mathit{I}}_{\mathit{f}\mathit{p}} \left(\mathbf{A}\right)$	${\mathit{I}}_{\mathit{f}\mathit{b}} \left(\mathbf{A}\right)$	${\mathit{I}}_{\mathit{f}\mathit{p}} \left(\mathbf{A}\right)$	${\mathit{I}}_{\mathit{f}\mathit{b}} \left(\mathbf{A}\right)$
1	R5	R4	3244	973	2864	992
2	R4	R1	2810	937	2580	860
3	R4	R2	2810	937	2580	860
4	R4	R3	2810	937	2580	860
5	R6	R1	2810	937	2580	860
6	R6	R2	2810	937	2580	860
7	R6	R3	2810	937	2580	860
8	R8	R7	3786	1136	3350	1160
9	R7	R1	2810	937	2580	860
10	R7	R2	2810	937	2580	860
11	R7	R3	2810	937	2580	860
12	R9	R1	2810	937	2580	860
13	R9	R2	2810	937	2580	860
14	R9	R3	2810	937	2580	860
15	R11	R10	3244	973	2864	992
16	R10	R1	2810	937	2580	860
17	R10	R2	2810	937	2580	860
18	R10	R3	2810	937	2580	860
19	R12	R1	2810	937	2580	860
20	R12	R2	2810	937	2580	860
21	R12	R3	2810	937	2580	860
22	R14	R13	3244	973	2864	992
23	R13	R1	2810	937	2580	860
24	R13	R2	2810	937	2580	860
25	R13	R3	2810	937	2580	860
26	R15	R1	2810	937	2580	860
27	R15	R2	2810	937	2580	860
28	R15	R3	2810	937	2580	860
29	R17	R16	3167	950	2794	968
30	R16	R1	2810	937	2580	860
31	R16	R2	2810	937	2580	860
32	R16	R3	2810	937	2580	860

and

Table A8. Min-Fault Conditions (2 DGs are in service with Bus Coupler 1 and Bus Coupler 2 closed).

Relay Pair	Primary	Backup	3-Phase		2-Phase
			${\mathit{I}}_{\mathit{f}\mathit{p}} \left(\mathbf{A}\right)$	${\mathit{I}}_{\mathit{f}\mathit{b}} \left(\mathbf{A}\right)$	${\mathit{I}}_{\mathit{f}\mathit{p}} \left(\mathbf{A}\right)$	${\mathit{I}}_{\mathit{f}\mathit{b}} \left(\mathbf{A}\right)$
1	R5	R4	2505	751	2225	771
2	R4	R1	1669	835	1533	767
3	R4	R2	1669	835	1533	767
4	R6	R1	1669	835	1533	767
5	R6	R2	1669	835	1533	767
6	R8	R7	2879	864	2563	888
7	R7	R1	1669	835	1533	767
8	R7	R2	1669	835	1533	767
9	R9	R1	1669	835	1533	767
10	R9	R2	1669	835	1533	767
11	R11	R10	2505	751	2225	771
12	R10	R1	1669	835	1533	767
13	R10	R2	1669	835	1533	767
14	R12	R1	1669	835	1533	767
15	R12	R2	1669	835	1533	767
16	R14	R13	2505	751	2225	771
17	R13	R1	1669	835	1533	767
18	R13	R2	1669	835	1533	767
19	R15	R1	1669	835	1533	767
20	R15	R2	1669	835	1533	767
21	R17	R16	2452	736	2177	754
22	R16	R1	1669	835	1533	767
23	R16	R2	1669	835	1533	767

). The upcoming conditions are assumed during the optimization process which are summarized as follows:

• Transformer OCRs are fitted with the inrush inhibitor feature (2nd harmonic blocking) to transcend the inrush current during the energizing.
• Motors are started using Variable Frequency Drives (VFDs) which limit the starting current to one per unit.
• Equipment damage curves are not included in the study and considered as future works.
• Only phase OC protection coordination considering the transformers connection is performed.
• Bus coupler one and two are assumed to be closed.
• The maximum fault current condition is examined when the three DGs are in service.
• The minimum fault current condition is examined when only DG1 and DG2 are in service.

Since most of the distribution transformers are rated as the Dy11 vector group, a two-phase fault shall be theorized in addition to the three-phase fault. Figure 6 shows the two-phase fault currents distribution due to a two-phase fault (between b and c) at the star side, as it is clarified that the fault current at line C of the delta side is multiplied by two. Therefore, this network should be investigated using various test models of combinations between the three-phase and two-phase faults in addition to the maximum and minimum fault conditions. The following four test models are listed and a further analysis is performed to characterize each one.

• Test Model One: Maximum three-phase fault current condition;
• Test Model Two: Maximum general fault current condition;
• Test Model Three: Minimum two-phase fault current condition; and
• Test Model Four: Minimum general fault current condition.

The OCRs’ optimum settings tabulated in

Table 5. OCRs optimum settings of Agiba network using Test Model 1.

Relay ID.	Scenario 1		Scenario 2
	${\mathit{I}}_{\mathit{p}} \left(\mathbf{A}\right)$	${\mathit{T}}_{\mathit{D}} \left(\mathbf{s}\right)$	${\mathit{I}}_{\mathit{p}} \left(\mathbf{A}\right)$	${\mathit{T}}_{\mathit{D}} \left(\mathbf{s}\right)$	Curve
R1	331.6117	0.0644	340.3342	0.0470	VI
R2	330.5366	0.0604	341.1965	0.0314	EI
R3	331.2808	0.0627	341.0609	0.0304	EI
R4	167.7614	0.0639	135.9965	0.1137	VI
R5	199.1274	0.0205	152.1001	0.2837	EI
R6	20.3363	0.0370	15.2550	0.8794	VI
R7	156.3881	0.0723	150.7917	0.1205	VI
R8	226.3209	0.0207	248.9035	0.1443	EI
R9	10.1672	0.0425	10.3708	0.9998	VI
R10	164.7615	0.0646	167.8963	0.0889	VI
R11	152.1286	0.0226	202.3552	0.1596	EI
R12	40.5282	0.0316	37.4771	0.2736	VI
R13	167.2944	0.0639	167.9290	0.1754	EI
R14	196.5018	0.0206	202.7059	0.0556	VI
R15	15.2566	0.0503	19.4621	0.5316	VI
R16	163.7832	0.0639	160.8550	0.0909	VI
R17	243.5889	0.0188	238.0619	0.1101	EI
TOT (s)	1.2509		0.8368

and

Table 6. OCRs optimum settings of Agiba network using Test Model 2.

Relay ID.	Scenario 1		Scenario 2
	${\mathit{I}}_{\mathit{p}} \left(\mathbf{A}\right)$	${\mathit{T}}_{\mathit{D}} \left(\mathbf{s}\right)$	${\mathit{I}}_{\mathit{p}} \left(\mathbf{A}\right)$	${\mathit{T}}_{\mathit{D}} \left(\mathbf{s}\right)$	Curve
R1	300.7964	0.0688	341.1739	0.0300	EI
R2	303.7651	0.0674	341.1994	0.0276	EI
R3	290.8823	0.0688	341.0980	0.0287	EI
R4	154.0312	0.0678	167.8909	0.0909	VI
R5	164.0629	0.0220	201.7282	0.1612	EI
R6	16.5401	0.0387	20.3211	0.0572	LI
R7	146.5419	0.0755	136.0492	0.2656	EI
R8	251.0151	0.0200	188.4000	0.2519	EI
R9	10.2956	0.0424	10.3699	0.9998	VI
R10	167.5220	0.0647	166.6866	0.1765	EI
R11	152.1000	0.0226	152.1013	0.2835	EI
R12	40.0069	0.0317	40.6304	0.0284	LI
R13	151.1998	0.0685	138.6302	0.1137	VI
R14	152.1035	0.0226	167.4478	0.2337	EI
R15	17.9116	0.0381	20.3392	0.0572	LI
R16	125.9700	0.0745	167.6305	0.1751	EI
R17	185.1458	0.0209	185.1000	0.1923	EI
TOT (s)	1.2614		0.7607

are generated using the first two test models, respectively. The GTO accomplishes TOT of 1.2509 s and 0.8368 s for test model one while 1.2614 s and 0.7607 s for test model two using scenarios one and two, respectively. In addition, the M/B operating times and their associated CTM values are listed in

Table 7. Operating times of M/B relay pairs with their associated CTM values of the Agiba Network using Test Model 1.

M/B Relay Pair		Scenario 1			Scenario 2
M	B	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)
5	4	0.0501	0.2500	0.1999	0.0500	0.2494	0.1994
4	1	0.1543	0.4295	0.2753	0.0781	0.3620	0.2839
4	2	0.1543	0.4015	0.2472	0.0781	0.3841	0.3061
4	3	0.1543	0.4176	0.2634	0.0781	0.3708	0.2928
6	1	0.0501	0.4295	0.3794	0.0648	0.3620	0.2972
6	2	0.0501	0.4015	0.3514	0.0648	0.3841	0.3193
6	3	0.0501	0.4176	0.3676	0.0648	0.3708	0.3060
8	7	0.0499	0.2501	0.2002	0.0501	0.2490	0.1989
7	1	0.1701	0.4295	0.2594	0.0922	0.3620	0.2697
7	2	0.1701	0.4015	0.2313	0.0922	0.3841	0.2919
7	3	0.1701	0.4176	0.2475	0.0922	0.3708	0.2786
9	1	0.0500	0.4295	0.3795	0.0500	0.3620	0.3120
9	2	0.0500	0.4015	0.3515	0.0500	0.3841	0.3341
9	3	0.0500	0.4176	0.3677	0.0500	0.3708	0.3208
11	10	0.0501	0.2500	0.1999	0.0499	0.2502	0.2003
10	1	0.1549	0.4295	0.2746	0.0762	0.3620	0.2858
10	2	0.1549	0.4015	0.2466	0.0762	0.3841	0.3079
10	3	0.1549	0.4176	0.2628	0.0762	0.3708	0.2946
12	1	0.0500	0.4295	0.3795	0.0499	0.3620	0.3121
12	2	0.0500	0.4015	0.3515	0.0499	0.3841	0.3342
12	3	0.0500	0.4176	0.3676	0.0499	0.3708	0.3209
14	13	0.0501	0.2498	0.1997	0.0501	0.4308	0.3807
13	1	0.1542	0.4295	0.2753	0.0503	0.3620	0.3117
13	2	0.1542	0.4015	0.2473	0.0503	0.3841	0.3338
13	3	0.1542	0.4176	0.2634	0.0503	0.3708	0.3205
15	1	0.0641	0.4295	0.3654	0.0501	0.3620	0.3119
15	2	0.0641	0.4015	0.3374	0.0501	0.3841	0.3341
15	3	0.0641	0.4176	0.3536	0.0501	0.3708	0.3208
17	16	0.0500	0.2500	0.2000	0.0501	0.2502	0.2001
16	1	0.1529	0.4295	0.2766	0.0745	0.3620	0.2875
16	2	0.1529	0.4015	0.2486	0.0745	0.3841	0.3096
16	3	0.1529	0.4176	0.2647	0.0745	0.3708	0.2963

and

Table 8. Operating times of M/B relay pairs with their associated CTM values of the Agiba Network using Test Model 2.

M/B Relay Pair		Scenario 1			Scenario 2
M	B	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)
5	4	0.0500	0.2501	0.2000	0.2501	0.0501	0.2000
4	1	0.1587	0.4191	0.2603	0.3665	0.0780	0.2884
4	2	0.1587	0.4143	0.2556	0.3372	0.0780	0.2592
4	3	0.1587	0.4071	0.2484	0.3510	0.0780	0.2730
6	1	0.0501	0.4191	0.3690	0.3665	0.0500	0.3164
6	2	0.0501	0.4143	0.3642	0.3372	0.0500	0.2871
6	3	0.0501	0.4071	0.3570	0.3510	0.0500	0.3009
8	7	0.0503	0.2503	0.2000	0.2964	0.0500	0.2463
7	1	0.1737	0.4191	0.2453	0.3665	0.0499	0.3165
7	2	0.1737	0.4143	0.2406	0.3372	0.0499	0.2872
7	3	0.1737	0.4071	0.2333	0.3510	0.0499	0.3011
9	1	0.0500	0.4191	0.3691	0.3665	0.0500	0.3165
9	2	0.0500	0.4143	0.3643	0.3372	0.0500	0.2872
9	3	0.0500	0.4071	0.3571	0.3510	0.0500	0.3010
11	10	0.0501	0.2502	0.2001	0.4103	0.0500	0.3603
10	1	0.1562	0.4191	0.2629	0.3665	0.0499	0.3166
10	2	0.1562	0.4143	0.2582	0.3372	0.0499	0.2873
10	3	0.1562	0.4071	0.2509	0.3510	0.0499	0.3011
12	1	0.0500	0.4191	0.3691	0.3665	0.0500	0.3164
12	2	0.0500	0.4143	0.3643	0.3372	0.0500	0.2871
12	3	0.0500	0.4071	0.3571	0.3510	0.0500	0.3010
14	13	0.0500	0.2503	0.2003	0.2494	0.0499	0.1994
13	1	0.1594	0.4191	0.2596	0.3665	0.0797	0.2868
13	2	0.1594	0.4143	0.2549	0.3372	0.0797	0.2575
13	3	0.1594	0.4071	0.2476	0.3510	0.0797	0.2713
15	1	0.0501	0.4191	0.3690	0.3665	0.0500	0.3164
15	2	0.0501	0.4143	0.3643	0.3372	0.0500	0.2871
15	3	0.0501	0.4071	0.3570	0.3510	0.0500	0.3009
17	16	0.0501	0.2507	0.2005	0.4331	0.0527	0.3803
16	1	0.1629	0.4191	0.2562	0.3665	0.0500	0.3164
16	2	0.1629	0.4143	0.2515	0.3372	0.0500	0.2871
16	3	0.1629	0.4071	0.2442	0.3510	0.0500	0.3010

for the first two test models also. It can be observed that scenario two in test model two achieves the least possible TOT. In this context, the optimal settings for OCRs are also generated using the minimum fault current condition as announced in

Table 9. OCRs optimum settings of Agiba network using Test Model 3.

Relay ID.	Scenario 1		Scenario 2
	${\mathit{I}}_{\mathit{p}} \left(\mathbf{A}\right)$	${\mathit{T}}_{\mathit{D}} \left(\mathbf{s}\right)$	${\mathit{I}}_{\mathit{p}} \left(\mathbf{A}\right)$	${\mathit{T}}_{\mathit{D}} \left(\mathbf{s}\right)$	Curve
R1	319.6939	0.0505	311.2207	0.0208	EI
R2	341.1941	0.0491	340.4273	0.0181	EI
R4	165.7031	0.0558	154.7975	0.0744	EI
R5	200.7996	0.0176	196.5116	0.0795	EI
R6	15.2550	0.0345	16.0424	0.0394	LI
R7	125.9700	0.0712	131.2142	0.1403	EI
R8	188.4000	0.0192	217.2035	0.0864	EI
R9	7.7850	0.0398	10.3080	0.0616	LI
R10	161.5779	0.0567	151.4155	0.0779	EI
R11	152.1000	0.0197	183.5210	0.0412	VI
R12	30.5400	0.0291	30.5400	0.0249	LI
R13	125.9701	0.0659	146.6947	0.0832	EI
R14	152.1000	0.0197	171.1541	0.1047	EI
R15	15.2550	0.0345	20.0760	0.0314	LI
R16	163.2165	0.0555	125.9700	0.1105	EI
R17	201.7820	0.0174	234.5884	0.0532	EI
TOT (s)	1.3385		0.7875

and

Table 10. OCRs optimum settings of Agiba network using Test Model 4.

Relay ID.	Scenario 1		Scenario 2
	${\mathit{I}}_{\mathit{p}} \left(\mathbf{A}\right)$	${\mathit{T}}_{\mathit{D}} \left(\mathbf{s}\right)$	${\mathit{I}}_{\mathit{p}} \left(\mathbf{A}\right)$	${\mathit{T}}_{\mathit{D}} \left(\mathbf{s}\right)$	Curve
R1	300.9234	0.0570	341.1827	0.0197	EI
R2	302.8060	0.0529	341.1986	0.0307	VI
R4	167.5252	0.0544	125.9700	0.1075	EI
R5	152.1000	0.0197	199.3379	0.0774	EI
R6	15.2550	0.0345	16.4287	0.3422	VI
R7	125.9701	0.0703	126.0366	0.1436	EI
R8	188.4000	0.0193	188.4171	0.1158	EI
R9	7.7850	0.0398	7.7872	0.7265	VI
R10	125.9700	0.0653	167.3015	0.0599	EI
R11	152.1003	0.0201	153.7081	0.0501	VI
R12	40.6146	0.0269	40.7084	0.1364	VI
R13	167.7060	0.0544	167.9591	0.0594	EI
R14	202.7896	0.0176	152.1852	0.1332	EI
R15	20.2051	0.0323	15.2761	0.3681	VI
R16	166.9924	0.0538	165.3569	0.0588	EI
R17	185.1000	0.0181	221.1283	0.0328	VI
TOT (s)	1.3250		0.7589

, whereas the operating times are collected in

Table 11. Operating times of M/B relay pairs of the Agiba Network using Test Model 3.

M/B Relay Pair		Scenario 1			Scenario 2
M	B	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)
5	4	0.0499	0.2502	0.2002	0.0500	0.2499	0.1999
4	1	0.1717	0.4003	0.2286	0.0613	0.3273	0.2660
4	2	0.1717	0.4205	0.2488	0.0613	0.3554	0.2941
6	1	0.0500	0.4003	0.3503	0.0500	0.3273	0.2773
6	2	0.0500	0.4205	0.3705	0.0500	0.3554	0.3054
8	7	0.0502	0.2501	0.1999	0.0500	0.2505	0.2005
7	1	0.1944	0.4003	0.2060	0.0828	0.3273	0.2445
7	2	0.1944	0.4205	0.2262	0.0828	0.3554	0.2726
9	1	0.0500	0.4003	0.3503	0.0500	0.3273	0.2773
9	2	0.0500	0.4205	0.3705	0.0500	0.3554	0.3054
11	10	0.0500	0.2502	0.2002	0.0500	0.2499	0.1999
10	1	0.1726	0.4003	0.2278	0.0614	0.3273	0.2660
10	2	0.1726	0.4205	0.2480	0.0614	0.3554	0.2941
12	1	0.0500	0.4003	0.3503	0.0607	0.3273	0.2666
12	2	0.0500	0.4205	0.3705	0.0607	0.3554	0.2947
14	13	0.0500	0.2500	0.2000	0.0499	0.2500	0.2001
13	1	0.1800	0.4003	0.2204	0.0615	0.3273	0.2658
13	2	0.1800	0.4205	0.2406	0.0615	0.3554	0.2939
15	1	0.0501	0.4003	0.3503	0.0501	0.3273	0.2773
15	2	0.0501	0.4205	0.3705	0.0501	0.3554	0.3053
17	16	0.0499	0.2501	0.2002	0.0500	0.2538	0.2038
16	1	0.1697	0.4003	0.2307	0.0601	0.3273	0.2672
16	2	0.1697	0.4205	0.2509	0.0601	0.3554	0.2953

and

Table 12. Operating times of M/B relay pairs for Agiba Network using Test Model 4.

M/B Relay Pair		Scenario 1			Scenario 2
M	B	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)
5	4	0.0501	0.2502	0.2000	0.0501	0.2490	0.1989
4	1	0.1683	0.4224	0.2541	0.0585	0.3892	0.3307
4	2	0.1683	0.3945	0.2262	0.0585	0.3321	0.2736
6	1	0.0499	0.4224	0.3725	0.0500	0.3892	0.3391
6	2	0.0499	0.3945	0.3446	0.0500	0.3321	0.2821
8	7	0.0505	0.2508	0.2003	0.0503	0.2498	0.1994
7	1	0.1922	0.4224	0.2302	0.0782	0.3892	0.3110
7	2	0.1922	0.3945	0.2024	0.0782	0.3321	0.2539
9	1	0.0500	0.4224	0.3724	0.0501	0.3892	0.3391
9	2	0.0500	0.3945	0.3445	0.0501	0.3321	0.2820
11	10	0.0511	0.2514	0.2003	0.0502	0.2502	0.2000
10	1	0.1783	0.4224	0.2441	0.0578	0.3892	0.3314
10	2	0.1783	0.3945	0.2162	0.0578	0.3321	0.2744
12	1	0.0501	0.4224	0.3723	0.0502	0.3892	0.3389
12	2	0.0501	0.3945	0.3445	0.0502	0.3321	0.2819
14	13	0.0504	0.2502	0.1998	0.0501	0.2503	0.2002
13	1	0.1683	0.4224	0.2541	0.0578	0.3892	0.3314
13	2	0.1683	0.3945	0.2262	0.0578	0.3321	0.2743
15	1	0.0501	0.4224	0.3723	0.0500	0.3892	0.3391
15	2	0.0501	0.3945	0.3445	0.0500	0.3321	0.2821
17	16	0.0500	0.2503	0.2003	0.0501	0.2500	0.1999
16	1	0.1662	0.4224	0.2562	0.0554	0.3892	0.3338
16	2	0.1662	0.3945	0.2283	0.0554	0.3321	0.2767

, respectively, respectively. The output TOTs of test model three are 1.3385 s for scenario one and 0.7875 s for scenario two, while in test model four they are 1.325 s for scenario one and 0.7589 s for scenario two.

Figure 7 and Figure 8 depict the FOF convergence of the Agiba power network using scenarios one and two, respectively. Moreover, statistical measures are analyzed in

Table 13. Statistical measures of GTO performance in Agiba power network over 30 independent runs.

Test Model		Parametric Tests					Non-Parametric Tests	Elapsed Time (s)
		Min	Max	Mean	Median	SD	p-Value
Model 1	Scenario 1	1.2509	1.4947	1.3043	1.2839	0.0546	0	101.3520
	Scenario 2	0.8368	316.0821	41.4577	1.0940	91.2971	0.0106	96.4464
Model 2	Scenario 1	1.2614	1.5560	1.3321	1.3204	0.0612	0	89.0859
	Scenario 2	0.7607	51.9367	4.9727	1.0817	12.1945	0.0343	99.9674
Model 3	Scenario 1	1.3385	1.7845	1.4123	1.3814	0.1057	0.0003	78.1487
	Scenario 2	0.7875	261.3888	9.8377	1.1547	47.5108	0.1527	73.4870
Model 4	Scenario 1	1.3250	1.8892	1.3953	1.3587	0.1082	0.0007	78.1213
	Scenario 2	0.7589	109.7749	5.5243	1.2019	20.0733	0.1019	76.3707

to evaluate the GTO performance using parametric and non-parametric tests. The p-value is produced from the t-test using thirty independent runs and by being rounded to four decimals. It is worth to mention that the smaller the p-value, the stronger the evidence to reject the null hypothesis. Consequently, the output conclusions from the studied case with DGs considering the transformer phase shift are as follows:

• The GTO succeeds in obtaining the optimal solutions without any violations in practical isolated networks with DGs using various test models.
• The OCRs’ coordination using the minimum two-phase fault current guarantees the fast convergence rate. Therefore, it is the suitable choice in online applications.
• The output p-value is minimum in test models one and two, which assures that the attained results at each run are more correlated. Accordingly, the maximum fault current coordination using the fixed NI curve is the best suitable framework in the case of a radial DG network with distribution transformers.
• The distribution of the EF currents with their optimal coordination in the case of Dy11 transformers will be a future study.

Finally, these results demonstrate the efficacy of selecting the best suitable optimization test model in distribution networks. However, the validity of GTO results is examined over a well-known algorithm (WCA) that proves its superiority in all test models, as shown in

Table 14. GTO defense regarding the TOT in Agiba power network.

Test Model	Scenario	GTO	WCA
1	1	1.2509	1.6962
	2	0.8368	1.7862
2	1	1.2614	1.6556
	2	0.7607	1.4319
3	1	1.3385	1.7049
	2	0.7875	1.3996
4	1	1.3250	1.9487
	2	0.7589	1.4550

.

Moreover, further analysis is performed in each test model to manifest which of them will achieve the best smooth coordination between M/B relay pairs. This has been concluded by checking the coordination in the minimum fault condition when the opposite maximum fault condition is optimized and vice versa. The checked operating times and CTM values for the four test models are arranged in

Table 15. Coordination check of Test Model 1.

M/B Relay Pair		Scenario 1			Scenario 2
M	B	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)
5	4	0.0552	0.2940	0.2387	0.0840	0.3394	0.2554
4	1	0.1903	0.4837	0.2934	0.1362	0.4365	0.3004
4	2	0.1903	0.4520	0.2618	0.1362	0.5035	0.3673
6	1	0.0562	0.4837	0.4275	0.1095	0.4365	0.3270
6	2	0.0562	0.4520	0.3958	0.1095	0.5035	0.3940
8	7	0.0555	0.2911	0.2355	0.0869	0.3439	0.2570
7	1	0.2087	0.4837	0.2749	0.1616	0.4365	0.2750
7	2	0.2087	0.4520	0.2433	0.1616	0.5035	0.3419
9	1	0.0554	0.4837	0.4283	0.0844	0.4365	0.3521
9	2	0.0554	0.4520	0.3966	0.0844	0.5035	0.4191
11	10	0.0549	0.2936	0.2387	0.0839	0.3456	0.2617
10	1	0.1908	0.4837	0.2929	0.1342	0.4365	0.3023
10	2	0.1908	0.4520	0.2612	0.1342	0.5035	0.3693
12	1	0.0573	0.4837	0.4264	0.0848	0.4365	0.3517
12	2	0.0573	0.4520	0.3947	0.0848	0.5035	0.4187
14	13	0.0552	0.2934	0.2382	0.0661	0.7385	0.6724
13	1	0.1900	0.4837	0.2936	0.1435	0.4365	0.2930
13	2	0.1900	0.4520	0.2620	0.1435	0.5035	0.3600
15	1	0.0715	0.4837	0.4121	0.0847	0.4365	0.3519
15	2	0.0715	0.4520	0.3805	0.0847	0.5035	0.4188
17	16	0.0557	0.2932	0.2375	0.0838	0.3432	0.2594
16	1	0.1882	0.4837	0.2954	0.1309	0.4365	0.3057
16	2	0.1882	0.4520	0.2638	0.1309	0.5035	0.3726

,

Table 16. Coordination check of Test Model 2.

M/B Relay Pair		Scenario 1			Scenario 2
M	B	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)
5	4	0.0575	0.2949	0.2373	0.1069	0.3533	0.2464
4	1	0.2018	0.5097	0.3079	0.1509	0.5920	0.4411
4	2	0.2018	0.5047	0.3028	0.1509	0.5447	0.3938
6	1	0.0571	0.5097	0.4526	0.0922	0.5920	0.4998
6	2	0.0571	0.5047	0.4475	0.0922	0.5447	0.4525
8	7	0.0589	0.2926	0.2337	0.1095	0.5402	0.4308
7	1	0.2199	0.5097	0.2898	0.1687	0.5920	0.4233
7	2	0.2199	0.5047	0.2848	0.1687	0.5447	0.3761
9	1	0.0564	0.5097	0.4533	0.0919	0.5920	0.5001
9	2	0.0564	0.5047	0.4483	0.0919	0.5447	0.4528
11	10	0.0574	0.2974	0.2400	0.1065	0.7316	0.6252
10	1	0.2001	0.5097	0.3096	0.1689	0.5920	0.4231
10	2	0.2001	0.5047	0.3046	0.1689	0.5447	0.3758
12	1	0.0587	0.5097	0.4510	0.0928	0.5920	0.4992
12	2	0.0587	0.5047	0.4460	0.0928	0.5447	0.4520
14	13	0.0574	0.2944	0.2370	0.1065	0.3475	0.2410
13	1	0.2022	0.5097	0.3075	0.1526	0.5920	0.4394
13	2	0.2022	0.5047	0.3024	0.1526	0.5447	0.3921
15	1	0.0573	0.5097	0.4524	0.0923	0.5920	0.4997
15	2	0.0573	0.5047	0.4474	0.0923	0.5447	0.4524
17	16	0.0579	0.2903	0.2323	0.1120	0.7664	0.6544
16	1	0.2035	0.5097	0.3062	0.1695	0.5920	0.4225
16	2	0.2035	0.5047	0.3012	0.1695	0.5447	0.3752

,

Table 17. Coordination check of Test Model 3.

M/B Relay Pair		Scenario 1			Scenario 2
M	B	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)
5	4	0.0451	0.2144	0.1693	0.0301	0.1486	0.1185
4	1	0.1334	0.3537	0.2203	0.0176	0.2508	0.2331
4	2	0.1334	0.3683	0.2349	0.0176	0.2691	0.2514
6	1	0.0438	0.3537	0.3099	0.0268	0.2508	0.2240
6	2	0.0438	0.3683	0.3245	0.0268	0.2691	0.2423
8	7	0.0454	0.2195	0.1742	0.0292	0.1455	0.1163
7	1	0.1549	0.3537	0.1988	0.0238	0.2508	0.2269
7	2	0.1549	0.3683	0.2135	0.0238	0.2691	0.2452
9	1	0.0445	0.3537	0.3092	0.0268	0.2508	0.2239
9	2	0.0445	0.3683	0.3239	0.0268	0.2691	0.2422
11	10	0.0456	0.2148	0.1692	0.0381	0.1487	0.1106
10	1	0.1344	0.3537	0.2193	0.0176	0.2508	0.2331
10	2	0.1344	0.3683	0.2340	0.0176	0.2691	0.2514
12	1	0.0429	0.3537	0.3108	0.0324	0.2508	0.2184
12	2	0.0429	0.3683	0.3254	0.0324	0.2691	0.2367
14	13	0.0456	0.2190	0.1733	0.0300	0.1488	0.1188
13	1	0.1433	0.3537	0.2104	0.0177	0.2508	0.2331
13	2	0.1433	0.3683	0.2250	0.0177	0.2691	0.2514
15	1	0.0438	0.3537	0.3099	0.0267	0.2508	0.2240
15	2	0.0438	0.3683	0.3245	0.0267	0.2691	0.2423
17	16	0.0451	0.2144	0.1692	0.0302	0.1523	0.1221
16	1	0.1320	0.3537	0.2217	0.0173	0.2508	0.2335
16	2	0.1320	0.3683	0.2364	0.0173	0.2691	0.2517

,

Table 18. Coordination check of Test Model 4.

M/B Relay Pair		Scenario 1			Scenario 2
M	B	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)	${\mathit{t}}_{\mathit{M}} \left(\mathbf{s}\right)$	${\mathit{t}}_{\mathit{B}} \left(\mathbf{s}\right)$	CTM (s)
5	4	0.0437	0.2103	0.1666	0.0235	0.1410	0.1175
4	1	0.1313	0.3473	0.2160	0.0173	0.2409	0.2236
4	2	0.1313	0.3241	0.1929	0.0173	0.2373	0.2200
6	1	0.0439	0.3473	0.3034	0.0272	0.2409	0.2137
6	2	0.0439	0.3241	0.2802	0.0272	0.2373	0.2102
8	7	0.0437	0.2168	0.1731	0.0230	0.1372	0.1142
7	1	0.1536	0.3473	0.1937	0.0232	0.2409	0.2177
7	2	0.1536	0.3241	0.1705	0.0232	0.2373	0.2142
9	1	0.0446	0.3473	0.3027	0.0273	0.2409	0.2136
9	2	0.0446	0.3241	0.2795	0.0273	0.2373	0.2101
11	10	0.0446	0.2170	0.1724	0.0336	0.1403	0.1066
10	1	0.1427	0.3473	0.2046	0.0170	0.2409	0.2238
10	2	0.1427	0.3241	0.1814	0.0170	0.2373	0.2203
12	1	0.0426	0.3473	0.3047	0.0271	0.2409	0.2138
12	2	0.0426	0.3241	0.2815	0.0271	0.2373	0.2103
14	13	0.0432	0.2104	0.1672	0.0235	0.1402	0.1167
13	1	0.1313	0.3473	0.2160	0.0170	0.2409	0.2239
13	2	0.1313	0.3241	0.1928	0.0170	0.2373	0.2203
15	1	0.0436	0.3473	0.3037	0.0272	0.2409	0.2137
15	2	0.0436	0.3241	0.2805	0.0272	0.2373	0.2102
17	16	0.0434	0.2106	0.1672	0.0332	0.1414	0.1082
16	1	0.1297	0.3473	0.2176	0.0163	0.2409	0.2245
16	2	0.1297	0.3241	0.1945	0.0163	0.2373	0.2210

and

Table 19. CTM comparison of the various test models.

Test Model No	Scenario No	Sum of CTMs	Average of CTMs	Standard Deviation
1	1	7.1928	0.3127	0.0740
	2	8.0267	0.3490	0.0882
2	1	7.7956	0.3389	0.0868
	2	10.0687	0.4378	0.0929
3	1	5.6077	0.2438	0.0589
	2	4.8509	0.2109	0.0514
4	1	5.1629	0.2245	0.0531
	2	4.4683	0.1943	0.0443

. It can be notified that the best strategy for fulfilling the smoothest coordination is using test model four. That is because it achieves the minimum possible value of the summation of CTMs, average of CTMs, and standard deviation.

Eventually, this paper aims at proving the best strategy for achieving the smoothest coordination of OCRs in practical, isolated distribution networks. The conclusion is that using the general minimum fault condition is the best trend in this practical network., not only due to its achieving of the minimum TOT, but also because it preserves the smoothest coordination at the maximum fault points with the least obtained value of the CTM summation.

5. Conclusions

A new methodology based on GTO procedures have been proposed to produce the best settings of OCRs across two test cases under numerous scenarios in an automated manner, tests in which the practical constraints including the transformer phase shift and other scenarios for min/max fault conditions are considered with minimal interferences from protection engineers. The first case is a 15-bus network with DGs which is widely used in the literature to validate and signify the cropped results of GTOs when they are compared to others. The second test case is for an isolated real distribution network with DGs for the Agiba Petroleum company which is located in the West Desert of Egypt. The relay coordination problem is adapted as an optimization problem subject to a set of predefined constraints and is solved using the GTO including the fixed and varied inverse IEC curves. For this test case, the best strategy for achieving the smoothest coordination of OCRs in practical isolated distribution networks has been indicated considering the transformer phase shifting. The conclusion is that using the general minimum fault condition is the best trend in this practical network, not only due to achieving the minimum total operating time, but also since it preserves the smoothest coordination at the maximum fault points with the least obtained value of CTMs for the studied cases.