Broad Embedded Logistic Regression Classifier for Prediction of Air Pressure Systems Failure

Abstract

In recent years, the latest maintenance modelling techniques that adopt the data-based method, such as machine learning (ML), have brought about a broad range of useful applications. One of the major challenges in the automotive industry is the early detection of component failure for quick response, proper action, and minimizing maintenance costs. A vital component of an automobile system is an air pressure system (APS). Failure of APS without adequate and quick responses may lead to high maintenance costs, loss of lives, and component damages. This paper addresses classification problem where we detect whether a fault does or does not belong to APS. If a failure occurs in APS, it is classified as positive class; otherwise, it is classified as negative class. Hence, in this paper, we propose broad embedded logistic regression (BELR). The proposed BELR is applied to predict APS failure. It combines a broad learning system (BLS) and logistic regression (LogR) classifier as a fusion model. The proposed approach capitalizes on the strength of BLS and LogR for a better APS failure prediction. Additionally, we employ the BLS’s feature-mapped nodes for extracting features from the input data. Additionally, we use the enhancement nodes of the BLS to enhance the features from feature-mapped nodes. Hence, we have features that can assist LogR for better classification performances, even when the data is skewed to the positive class or negative class. Furthermore, to prevent the curse of dimensionality, a common problem with high-dimensional data sets, we utilize principal component analysis (PCA) to reduce the data dimension. We validate the proposed BELR using the APS data set and compare the results with the other robust machine learning classifiers. The commonly used evaluation metrics, namely Recall, Precision, an F1-score, to evaluate the model performance. From the results, we validate that performance of the proposed BELR.

1. Introduction

Air Processing System (APS) is a critical component in any brake system of heavy-duty vehicles. It plays an essential role in gauging brakes, controlling suspensions, shifting gears, etc. The effects of faulty APS are numerous. For instance, a faulty APS can cause improper functioning of gears, brakes, and suspension. These may lead to unpleasant/undesired situations such as total breakdown of the vehicles, which may lead to high maintenance costs and sometimes, in a critical situation, loss of life. To mitigate this side effect, the proper functioning of APS should be ensured; hence, its monitoring is vital. APS is said to be working properly when the APS supplies compressed air to its major components in an efficient, adequate, and timely manner.

Typically, in an automobile, the main components of APS are control units, circuit protection valves, and air dryers. A circuit-protection valve controls various circuits. Some of the circuits are a service brake circuit, a parking brake circuit, an auxiliary circuit, etc. It simply does this by activating them using different pre-set pressures. Furthermore, the air dryer removes excess moisture from the inlet air generated at the compressor. The control units dictate when to activate the compressor based on the pressure level in the APS. The control units consist of pressure sensors and temperature sensors.

APS failure detection is a key area of research [1,2]. It is a problem to detect whether an APS failure is the cause of a complete system breakdown or not. APS failures can result in huge maintenance costs and sometimes life-threatening situations. In recent years, machine learning-based techniques for APS failure detection are becoming increasingly popular. This is partly due to the large historical data set and the emergence of Industry 4.0 and the Industrial Internet of Things (IIoT). The core problems for APS failure detection/prediction are associated with:

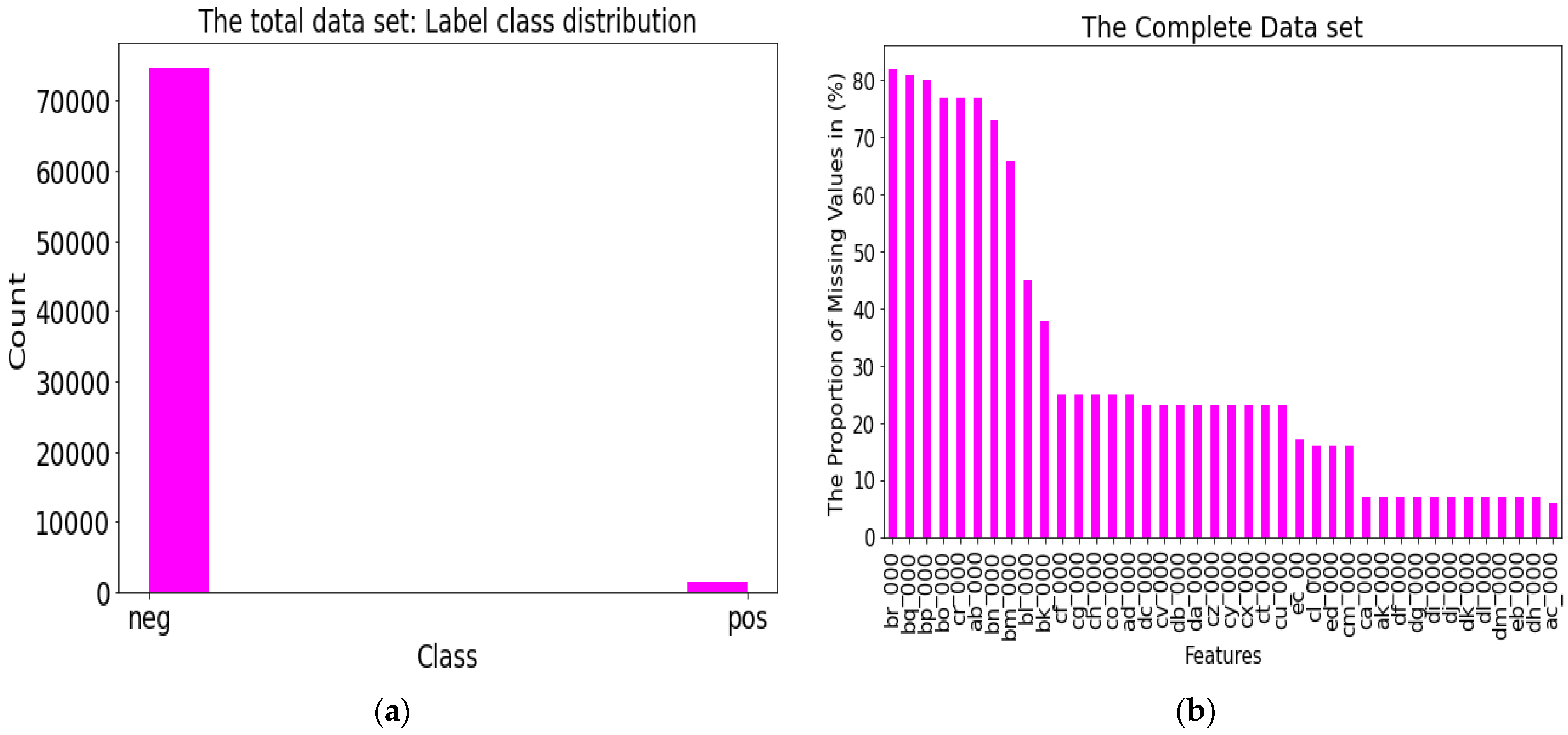
• High volume of missing values in the data.
• Strongly imbalanced distribution of classes.

Figure 1 presents the missing values and imbalanced class distribution for APS failure data sets. From the figures, we notice many missing values in the data set. Hence, to tackle the problem, we cannot use the commonly used deletion method, as the missing value are many and deletion methods will cause large chunks of the data to be deleted. This will leave no or fewer data to be explored or used for the machine learning task. It is obvious from Figure 1 that the number of negative class cases is far higher than the number of positive class cases. Hence, the data set is highly imbalanced.

The two problems, namely class imbalance and missing values, can affect the performance of any machine learning algorithm if proper care is not taken [3,4]. Many researchers have worked on various techniques for handling missing data in APS data sets [1,5]. The existing techniques combined the classical data imputation methods with the traditional machine learning methods. However, the impact of modern data imputation methods is not explored. This could improve the performance of the machine learning method significantly. Additionally, a using modern machine learning method such as flat structure neural networks can enhance performance when the data is skewed to the positive class or negative class.

Additionally, a deep neural network with traditional classifiers can be used for many classification tasks. For instance, in [6], a deep neural network is trained together with a classifier where highly efficient features are extracted from raw data by a deep neural network, and a classifier, logistic regression [7], is used for classification. However, using a deep neural network requires high computation resources, and it takes a long time to train. Instead of using deep structure, some researchers have investigated random vector functional-link neural networks (RVFLNN). Chen and Liu [8] proposed BLS based on the concept of RVFLNN and obtained a promising result in classification accuracy and learning speed. The BLS network [8,9] is different from the deep neural network in many aspects, and its structure can be constructed widely. Additionally, the BLS network adopted incremental learning, which has quick remodelling without needing to re-train the network from scratch, provided that the performance of the initial network is not acceptable. In essence, the BLS network can be trained quickly and has good generalization performance. Additionally, BLS is regarded as a universal approximator with sufficient nodes in the network.

This paper explores the strength of a broad learning system and logistic regression for APS failure prediction. The BLS network is a flat structure neural network. It has a feature-mapped layer and a feature-enhancement layer. In addition, another common issue in a typical real-life big data set is high dimension. The high dimensional data set can affect the machine learning algorithm’s performance. Additionally, it will increase the computational cost. To handle this, we explore principal component analysis (PCA) [10]. PCA is the widely used dimensionality reduction algorithm. Hence, to prevent the issue of the curse of dimensionally [11], we use PCA to reduce the dimension of the data set.

Furthermore, to the best of our knowledge, previous studies on APS failure detection have not investigated the performance of a flat structure neural network. A typical flat structure neural network example is a broad learning system. It has a broad layer structure where nodes are connected widely. More details of the network will be given in Section 3.

Generally, many machine learning models have difficulty handling imbalanced class distribution problems. However, the proposed approach can perform well under imbalanced class distribution problems. The proposed BELR does not require an additional or external method for imbalanced class distribution, as the feature-mapped nodes can extract features discriminative enough to enhance a classifier to separate classes from each other. The feature can be further enhanced by feature-enhancement nodes to uniquely classify each of the classes.

In summary, our method performance is reliable under challenging data sets such as the APS data set, which has an imbalance distribution problem. The idea of a missing mechanism is formalized in [12,13] where the study of missing data such as Missing at random (MAR), Missing not at random (MNAR), and Missing completely at random (MCAR) are presented in details. The data we employ in this paper have missing values across the feature set. A total of 169 features have missing values out of 170 features. Figure 2 shows the pattern of missing values in the data set across the features. From the Figure, the purple color represents the missing values, while the white or clear space represents where values exist in the data.

Additionally, the distribution of the data set and missing data is presented in [14]. In addition, Figure 2 shows the pattern of the missing values. From the idea in [12,13] and from the literature, the pattern of the missing values in the APS data set may be missing completely at random (MCAR). In our paper, the focus is not to categorize the pattern of the missing value in the APS data set. However, an appropriate method can be selected based on missing data mechanism in the data set. Thus, to prevent the destruction of the data set that could come from some missing value imputation method, we employ KNN imputer. In other words, we impute the missing value using the KNN technique [15]. Other methods such as imputation based on generative adversarial network (GAN) [14] could be explored. In [16], median imputation is explored for the problem of missing value. In this paper, we explore KNN imputation concept to tackle the problem of missing value. Figure 3 shows the pipeline of the proposed approach.

In summary, the contributions of this paper are summarized as follows:

• We propose broad embedded logistic regression (BELR). It is the fusion of broad learning system and logistic regression. We apply the proposed BELR to predict APS’s failure.
• We propose a hybrid objective function based on the classical logistic regression objective function.
• We impute the missing value using the KNN algorithm.
• We propose and explore feature-mapped nodes of the BLS to extract discriminative features from the input data and enhancement nodes for further separation of the two classes such that the skewed distribution data set cannot affect the performance of the proposed broad embedded logistic regression (BELR).
• We explore principal component analysis (PCA) for dimensionality reduction and combine BLS and logistic regression classifier for the prediction of air pressure failure detection.

The rest of the paper is presented as follows. Section 2 presents related work on APS failure prediction from the literature. In Section 3, we describe the broad learning system (BLS) and give the mathematical model of the BLS. Additionally, Logistic regression (LogR) is discussed. Section 4 presents the experiment where the APS data set is described, and the numerical results are presented. In addition, in Section 4, the performances of the comparison algorithms and results are discussed. Section 5 gives the conclusion.

2. Related Work

Diagnosis of transportation systems is a common task in the automotive industry. The problem is commonly handled using data analysis and machine learning methods. In this section, we focus on related works to APS failure prediction. Additionally, we present related work on the imbalanced classification problem from the literature.

2.1. APS Failure Prediction

First, standard machine learning approaches for APS failure prediction have been applied to the mentioned task. There are works on APS failure prediction. For instance, in [16,17], the failure of APS of heavy-duty vehicles is studied. In the paper, the weighted loss function is employed to improve the performance of the network architecture used. In addition, in [18], a fuzzy-based machine learning algorithm is utilized for air pressure failure prediction. The fuzzy-based algorithm was combined with a relaxed prediction horizon for better air-pressure failure-prediction performance. Furthermore, APS failure prediction was analyzed by [16,19] using various machine learning algorithms, namely Support vector machines (SVM), Multi-Layer Perception (MLP), and Naive Bayes. The author extracts a feature from the raw data set using the feature engineering method namely histogram. In addition, feature ranking was implemented in their feature-selection approach. In the work, the preprocessing method used for the missing value replacement is KNN imputation, where the nearest neighbour in each feature column replaces the missing value. The metric used in terms of cost is based on total misclassification by the algorithm. In the metric, $fp$ is set as a false positive, which predicts the failure wrongly, and $fn$ is set as a false negative, which is missing a failure. In their proposed approach, missing a failure has a cost of 500, while the cost of falsely predicting a failure is given by 10. In their approach, a mean cost of 0.6 was achieved. The mean cost is given by $\frac{1}{Numberoftestsample}\left(10\ast fp+500\ast fn\right)$.

Additionally, to consider imbalance class issues, in some works, weighted data classifiers are used for APS failure prediction [14], logistic regression (LogR), and SVM classifiers. In their method, class-specific weights were integrated into the classifier. The value of the weight for each class is chosen such that it is inversely proportional to the number of samples in a class. Other classical machine learning methods have been applied to the APS data set. For instance, the performance of many machine learning techniques on the APS data set was investigated in Refs. [20,21,22]. The problem is a binary classification task. In their approach, they resolve the class imbalance problem with the aid of SMOTE (Synthetic Minority Oversampling Technique) algorithm to balance the positive class and negative class examples. Additionally, the author performs feature engineering before applying the machine learning algorithm. Besides, a new method for predicting APS failure was proposed in Ref. [23]. The method maximizes Area Under the Curves (max AUC) by utilizing a linear decision boundary. It is specifically designed to handle imbalance class distribution in the data set.

From all the previous studies on APS failure prediction, most authors focus on exploring the classical machine learning algorithms such as SVM, KNN, NB, LogR, etc. In summary, to the best of our knowledge, no work on APS failure prediction has used the neural network or flat structure-based machine learning methods, namely extreme learning machine (ELM) [24,25,26] and broad learning system (BLS) [8,26,27,28,29]. However, ELM and BLS algorithms are popular among researchers, and they are widely used in many applications. This is partly because they are universal approximators; with sufficient hide nodes, they can estimate any functions. Additionally, they are fast and easy to implement. Hence, in this work, we proposed to combine a broad learning system (BLS) and logistic regression (LogR) to predict APS failure. The background details of BLS and LogR are given in the next sections.

2.2. Broad Learning System (BLS) and Logistic Regression (LogR)

2.2.1. Broad Learning System (BLS)

The concept of BLS [8] is a new technique. BLS and other variants [8,30,31] connect hidden nodes of a neural network broadly. As shown in Figure 4, the nodes are put together in a broad flat structure. A BLS network contains two hidden layers, namely the enhancement layer and feature-mapped layer.

The concept introduced in the BLS framework is promising. It is an efficient, simple learning algorithm. Due to the efficient feature-extraction capacity of the nodes in the feature-mapped layer and enhancement layer of the BLS, the original BLS and hybrid methods, where feature-mapped layer of BLS and other techniques are combined, have been used in many applications. However, much work has not been completed using neural network-based algorithms to predict APS failure in the case of APS failure. In view of the points and that BLS’s feature-mapped nodes and enhancement nodes can extract effective features from the input data, which can enhance the performance of a classifier, we combine BLS and logistic regression (LogR) to study APS failure prediction. Thus, we propose broad embedded logistic regression (BELR) for APS failure prediction.

2.2.2. Operation of BLS Networks

This subsection gives background knowledge on the operation of a BLS network. This paper proposed BLS for solving the air pressure system failure classification problem. In this paper, the classification problem is formulated as nonlinear logistic regression, where the input of a logistic regression algorithm is the feature from the BLS network. The final output is the sign of the predicted value or the probability of the predicted output. In other words, if the sign is positive, then the predicted value belongs to the positive class. Otherwise, the predicted class is negative. Let $x\hspace{0.17em}\in {ℝ}^D$ be the input data to the BLS network, where $D$ is the dimension of the input data, and $o\hspace{0.17em}\in ℝ$ be the output of a BLS network. In this section, for smooth and clear presentation, we present the input $x$ augmented with 1 as $\chi ={[x^{\mathrm{T}},1]}^{\mathrm{T}}$.

(a)

Feature-mapped nodes

The BLS network has two main layers, namely feature-mapped layer and enhancement layer. The feature-mapped layer is to extract features from input data. For the feature-mapped layer, there are n groups of the feature-mapped nodes. These $n$ groups are concatenated together to form one main feature extraction. The output of the main feature-extraction group is passed to the output layer, and another layer is called the enhancement layer. Each group from the $n$ groups is used to extract distinctive features. Each group has it on a specific number of nodes. For instance, in this paper, $f_i$ represents the $i$-th group of the feature-mapped nodes. Hence, for n groups of features-mapped nodes, the total number of features-mapped nodes is the following:

$$f={\displaystyle \sum }_{i=1}^n{f}_i$$

(1)

It should be noted that $f_i$ for $i=1,\dots n$ may not be equal. For each group of the feature-mapped node, which is the $i$-th group of features-mapped nodes, there is an associated learned projection matrix, and the $i$-th learned projection matrix is given by:

$${\Psi }_i=\left(\begin{array}{ccc}{\psi }_{i,1,1}& \cdots & {\psi }_{i,1,\left(D+1\right)}\\ ⋮& \ddots & ⋮\\ {\psi }_{i,f_i,1}& \cdots & {\psi }_{i,f_i,\left(D+1\right)}\end{array}\right)$$

(2)

where ${\Psi }_i\in {ℝ}^{f_i\times \left(D+1\right)}$. It is designed to generate features from the input data. The $i$-th group of mapped features $g_i$ are obtained by projecting the input data with the matrix ${\Psi }_i$. They are given by the following:

$$\begin{array}{rrr}\hfill {\mathfrak{g}}_i& \hfill =& \hfill {[g_{i,1},\cdots ,g_{i,f_i}]}^{\mathrm{T}}\\ \hfill & \hfill =& \hfill {\Psi }_i\chi \forall \hspace{0.17em}i=1,\cdots ,n,\end{array}$$

(3)

where $g_{i,u}$ is the $u$-th feature of the $u$-th group, where $i=1,\cdots ,n$, and $u=1,\cdots ,f_i$.

In the classical BLS, ${\Psi }_i$′s is constructed based on sparse optimization steps. There are many ways to achieve these steps. One way is to solve sparse optimization problems based on the alternating direction method of multipliers ADMM [32] algorithm. In Section 2.2.3-(a), we present the construction procedure of ${\Psi }_i$′s. In the classical BLS scheme, a linear operation is applied on ${\mathfrak{g}}_i$s. It should be noted that ${\mathfrak{g}}_i$s is not $\chi$ but features-extracted from $\chi$. Similarly, a nonlinear operation can be applied on ${\mathfrak{g}}_i$’s as well. In this paper, we apply a linear operation on ${\mathfrak{g}}_i$’s, that is, this paper follows the classical BLS framework. The outputs from the $n$ group of the feature-mapped nodes are gathered as

$$g={[{\mathfrak{g}}_1^{\mathrm{T}},\cdots ,{\mathfrak{g}}_n^{\mathrm{T}}]}^{\mathrm{T}}\in {ℝ}^f$$

(4)

Additionally, we let

$$q={[g^{\mathrm{T}},1]}^{\mathrm{T}}\in {ℝ}^{f+1}$$

(5)

for a smooth mathematical model presentation and as the augmented vector of $g$.

(b)

Enhancement nodes

Like the feature-mapped nodes, the enhancement nodes of the BLS network have $m$ groups of enhancement nodes. In the enhancement layer, the $j$-th group of enhancement nodes has $e_j$ nodes. The total number of enhancement nodes in the BLS network is given by

$$e={\displaystyle \sum }_{j=1}^m{e}_j$$

(6)

In addition, the output of $j$-th group of enhancement nodes is given by

$${\mathbf{ℌ}}_j={\left[{ℌ}_{j,1},\dots {ℌ}_{j,e_j}\right]}^T=\xi \left(W_{j}q\right)$$

(7)

where $j=1,\cdots ,m$ and $W_j$ is the weight that connects the output of feature-mapped nodes to the input of the enhancement nodes together. It should be known that, in the original BLS framework, $W_j$ is a randomly generated. The elements of $W_j$are denoted as

$$\begin{array}{rrr}\hfill W_j& \hfill =& \hfill \left(\begin{array}{ccc}{w}_{j,1,1}& \cdots & w_{j,1,f+1}\\ ⋮& \ddots & ⋮\\ w_{j,e_j,1}& \cdots & w_{j,e_j,f+1}\end{array}\right).\end{array}$$

(8)

It should be known that $\xi (\cdot )$ is the activation function for enhancement nodes. Each group of enhancement nodes can have its activation function. In the original BLS algorithm, the hyperbolic tangent is employed as the activation function for all the enhancement nodes. This paper uses hyperbolic tangent as the activation function for all enhancement nodes. We gather all the enhancement node outputs together as

$$\mathsf{\eta }={[{\mathfrak{h}}_1^{\mathrm{T}},\cdots ,{\mathfrak{h}}_m^{\mathrm{T}}]}^{\mathrm{T}}\in {ℝ}^e$$

(9)

(c)

Network Output

For a given input vector $x$, the output of the network is

$$o=\left[g^{\mathrm{T}}|{\mathsf{\eta }}^{\mathrm{T}}\right]\mathsf{\beta }$$

(10)

where $\mathsf{\beta }$ is the output weight vector. The number of elements in $\mathsf{\beta }$ is equal to $f+e$. Hence, its components are given by

$$\mathsf{\beta }={[{\beta }_1,\dots ,{\beta }_{f+e}]}^{\mathrm{T}}$$

(11)

2.2.3. Construction of Weight Matrices and Vectors

Given N training pairs ${\mathbb{D}}_{train}=\left\{\left(x_k,y_k\right):k=1,\dots ,N\right\}\}$, where $x_k={[x_{k,1},\cdots ,x_{k,D}]}^{\mathrm{T}}$ is a $D$ dimensional training input and $y_k$ is the corresponding target output as the training set. Consider that the training data matrix is formed by packing all the input $x_k$′s together. The augmented data matrix denoted as $X$ is given by

$$X=\left(\begin{array}{c}{x}_1^{\mathrm{T}}\\ ⋮\\ x_N^{\mathrm{T}}\end{array}|\begin{array}{c}1\\ ⋮\\ 1\end{array}\right)$$

(12)

(a)

Construction of the Projection Matrix ${\Psi }_i$

For each group of features-mapped nodes, one important thing in the framework of BLS is building the projection matrix ${\Psi }_i$. An important question then arises as follows: how to build the projection matrix? The approach presented here follows the procedures of [8,33]. In the BLS, a random matrix ${\mathcal{P}}_i\in {ℝ}^{\left(D+1\right)\times f_i}$ is generated first for each group of features-mapped nodes. Afterwards, we can obtain a random-projection data matrix $Q_i$, given by

$$Q_i=X{\mathcal{P}}_i$$

(13)

The projection matrix ${\Psi }_i$ is the result of the sparse approximation problem given by

$$\underset{{\Psi }_i}{\min }\left\{\parallel Q_i{\Psi }_i-X{\parallel }_F^2+\rho \parallel {\Psi }_i{\parallel }_1\right\}$$

(14)

where in (14), the term $\rho \parallel {\Psi }_i{\parallel }_1$ is to enforce the solution of (14) to be a sparse matrix. Additionally, $\rho$ is a regularization parameter for sparse regularization. In addition, $F$ is the popular Frobenius norm and $\parallel .{\parallel }_1$ is norm 1.

(b)

Construction of the Weight Matrices of the Enhancement Nodes

To some degree, the construction step of $W_j$′s is a bit straightforward. For instance, as detailed in [8,33,34], the traditional BLS algorithm and other variants randomly generate the weight matrices for each group of the enhancement nodes. Similarly, this paper follows the same procedure to generate $W_j$′s.

(c)

Construction of Output Weight Vector

This section gives the procedure to construct the output weight vector $\mathsf{\beta }$. Given the projection matrix ${\Psi }_i\prime s\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}\hspace{0.17em}i=1,\cdots ,n$ of the feature-mapped nodes, and the training data matrix $X$, the i-th training data feature matrix for all training samples is given by

$$\begin{array}{rrr}\hfill Z_i& \hfill =& \hfill \left(\begin{array}{c}{z}_{i,1}^{\mathrm{T}}\\ ⋮\\ z_{i,N}^{\mathrm{T}}\end{array}\right)=X{\Psi }_i^{\mathrm{T}}\end{array}$$

(15)

where $z_{i,k}={[z_{i,k,1},\cdots ,z_{i,k,f_i}]}^{\mathrm{T}}$, and

$$z_{i,k,u}={\displaystyle \sum }_{\iota =1}^D{\psi }_{i,u,\iota }{x}_{k,\iota }+{\psi }_{i,u,D+1}$$

(16)

Let $\mathcal{Z}$ be the collection of all training data feature matrices. Hence, we have

$$\mathcal{Z}=\left[Z_1,\cdots ,Z_n\right]$$

(17)

In this way, $\mathcal{Z}$ is an $N\times f$ matrix, denoted as

$$\mathcal{Z}=\left(\begin{array}{ccc}{\mathcal{Z}}_{1,1}& \cdots & {\mathcal{Z}}_{1,f}\\ ⋮& \ddots & ⋮\\ {\mathcal{Z}}_{N,1}& \cdots & {\mathcal{Z}}_{N,f}\end{array}\right)=\left(\begin{array}{c}{\mathcal{Z}}_1^{\mathrm{T}}\\ ⋮\\ {\mathcal{Z}}_N^{\mathrm{T}}\end{array}\right)$$

(18)

where the $k$-th row vector ${\mathcal{Z}}_k^{\mathrm{T}}$ of $\mathcal{Z}$ is the inputs of the enhancement nodes (the outputs of the feature-mapped nodes) for the $k$-th training input vector $x_k$. To handle input biases, we augment one vector into $\mathcal{Z}$, given by

$${\mathcal{Z}}^{\prime }=\left(\begin{array}{cc}{\mathcal{Z}}_1^{\mathrm{T}}& 1\\ ⋮& ⋮\\ {\mathcal{Z}}_N^{\mathrm{T}}& 1\end{array}\right)=\left(\begin{array}{c}{{\mathcal{Z}}^{\prime }}_1^{\mathrm{T}}\\ ⋮\\ {{\mathcal{Z}}^{\prime }}_N^{\mathrm{T}}\end{array}\right)$$

(19)

Furthermore, given $\mathcal{Z}$, the enhancement node outputs of the $j$-th enhancement group for all training data are given by

$$\begin{array}{rrr}\hfill H_j& \hfill =& \hfill \xi \left({\mathcal{Z}}^{\prime }{W}_j^{\mathrm{T}}\right)=\left(\begin{array}{c}{h}_{j,1}^{\mathrm{T}}\\ ⋮\\ h_{j,N}^{\mathrm{T}}\end{array}\right)\end{array}$$

(20)

for $j=1,\cdots ,m$, where

$$h_{j,k}={[h_{j,k,1},\cdots ,h_{j,k,e_j}]}^{\mathrm{T}}$$

(21)

and

$$h_{j,k,v}=\xi \left({\displaystyle \sum }_{\tau =1}^{f+1}{w}_{j,v,\tau }\mathcal{Z}{\prime }_{k,\tau }\right)$$

(22)

Packing all the enhancement node outputs together, we have

$$\begin{array}{rrr}\hfill \mathscr{H}& \hfill =& \hfill \left[H_1,\cdots ,H_m\right]\end{array}$$

(23)

where $\mathscr{H}$ is a $N\times \left({\displaystyle \sum }_{j=1}^m{e}_j\right)=N\times e$ matrix.

Define $\mathcal{A}=\left[\mathcal{Z}|\mathscr{H}\right]$. The output weight vector $\mathsf{\beta }$ can be calculated based on least square techniques:

$$arg\underset{\mathsf{\beta }}{\min }\Vert \mathcal{A}\mathsf{\beta }-y{\parallel }_{\rho }^{\rho }+\varrho \parallel \mathsf{\beta }{\parallel }_{\lambda }^{\lambda }$$

(24)

where $y={[y_1,\cdots ,y_N]}^{\mathrm{T}}$ is the collection of all training outputs. Equation (24) means that we can have different cost functions by setting different values of $\rho$, $\mathsf{\varrho }$, $\lambda$. It should be noted the value of $\rho$ and $\lambda$ are not necessarily the same. In this paper, to explore BLS for air pressure failure prediction, we reformulate the objective function (24) like that of logistic regression. In the next subsection, we give background details of logistic regression (LogR).

2.2.4. Logistic Regression

Logistic regression (LogR) is a widely used and popular probabilistic statistical classification technique. It is designed for binary classification problems. Logistic regression is detailed in [35]. The technique aims to maximize the likelihood function given by

$$J_{LogR}={\displaystyle \prod }_{k=1}^N{t}_k^{y_k}{\{1-t_k\}}^{1-y_k};t_k=\sigma \left(w^T{x}_k\right)$$

(25)

where $\sigma \left(z\right)=\frac{1}{1+{\exp }^{-z}}$ and $x_k$ is the $k$-th input vector. We can further modify (25) as a minimization problem. With manipulations, we turn (25) to a well-known cross-entropy error function (26). By taking the negative logarithm of the likelihood function (25), we arrive at

$$J\left(w\right)=-\log \left(J_{LogR}\right)=-{\displaystyle \sum }_{k=1}^N\{y_k\log \left(t_k\right)+\left(1-y_k\right)\log \left(1-t_k\right)\}$$

(26)

The gradient descent can be used to optimize the error function (25) to obtain an optimal output weight $w$.

3. The Proposed Technique

In the proposed approach, we capitalize on the strength of a broad learning system (BLS) and logistic regression (LogR). Figure 5 shows the structure of the fused BLS network with logistic regression classifier.

In Figure 5, input $X$ is passed to the feature-mapped layer, where the feature $Z^n$ is extracted and obtained. This feature is further enhanced to obtain an enhanced feature $H^m$. Both features are combined as $\mathcal{A}=\left[Z^n|H^m\right]$. The concatenated features are then passed to the logistic regression classifier for making the decision. The fusion of logistic regression and broad learning system, with the effectiveness of the feature-extraction layer and enhancement layer improves the performance of the network. For instance, when the feature nodes extract features from the input X, the enhancement nodes further enhance the features such that the distance between the positive class and negative class is widened. Hence, it able to separate between class even when the two classes are in balance.

In our approach, we incorporate the objective function of BLS (24) into the objective function of LogR (25). In other words, for the proposed broad embedded logistic regression model, we assume a non-linear relationship between the input of the logistic regression classifier and the output of logistic regression classifier. For easy notation and explanation, we let

$$\mathcal{A}=\left[{\mathcal{A}}_1,\cdots ,{\mathcal{A}}_{f+e}\right]=\left[\begin{array}{ccc}{a}_{1,1}& \dots & a_{1,f+e}\\ ⋮& \ddots & ⋮\\ a_{N,1}& \cdots & a_{N,f+e}\end{array}\right]$$

Additionally, the probability that $y_k=1$ is given by $p_k$. In other words, when the model predicts that $y_k=1$, the prediction probability is given by $p_k.$Hence, we formulate the relationship between feature $\mathcal{A}$ obtained from the BLS network and the output weight $\mathsf{\beta }={[{\beta }_1,\dots ,{\beta }_{f+e}]}^{\mathrm{T}}$. In addition, we add a bias term ${\beta }_0$ and ${\mathcal{A}}_0={\left[1,1,1\dots 1\right]}^T\mathrm{into}\mathrm{the}\mathrm{relationship}.$ Hence, for $k$-th input, we have

$$l_k=a_{k,0}{\beta }_0+{\displaystyle \sum }_{r=1}^{f+e}{\mathrm{a}}_{k,r}{\beta }_r={\log }_b\frac{p_k}{1-p_k}$$

(27)

where $l_k$ is the log-odds for the $k$-th. Furthermore, it should be noted that $b$ is an additional generalization, it is the base of the model.

For a more compact notation and to take the bias term into consideration, we specify the feature variables $\overline{\mathcal{A}}$and $\overline{\mathsf{\beta }}$ as $\left(f+e+1\right)$—dimensional vectors. They are given by

$$\begin{array}{rrr}\hfill & \hfill \overline{\mathcal{A}}=& \hfill \left[{\mathcal{A}}_0,{\mathcal{A}}_1,\cdots ,{\mathcal{A}}_{f+e+1}\right]\\ \hfill & \hfill \overline{\mathsf{\beta }}=& \hfill {[{\beta }_{0,}{\beta }_1,\dots ,{\beta }_{f+e+1}]}^{\mathrm{T}}\end{array}$$

(28)

where ${\mathcal{A}}_0={\left[a_{1,0},\dots a_{N,0}\right]}^T,{\mathcal{A}}_1={\left[a_{1,1},\dots a_{N,1}\right]}^T$,…, ${\mathcal{A}}_{f+e+1}={\left[a_{1,f+e+1},\dots a_{N,f+e+1}\right]}^T$.

Hence, we rewrite the logit, $l_k$ as

$$l_k={\displaystyle \sum }_{r=0}^{f+e}{\mathrm{a}}_{k,r}{\beta }_r={\log }_b\frac{p_k}{1-p_k}$$

(29)

Now, solving for the probability $p_k$ that the model predicts $y_k=1.$yields.

$$p_k=\frac{e^{l_k}}{1+e^{l_k}}=\sigma \left(l_k\right)$$

(30)

where b is substituted by $e$ and it is exponential function and where $\sigma (.)$ is the sigmoid function. With (30), we can easily compute the probability that $y_k=1$ for a given observation. The optimum $\mathsf{\beta }$ can be obtained by minimizing the negative log-likelihood of (30). Hence, the log-likelihood may be written as follows:

$$\begin{array}{rrr}\hfill J& \hfill =& \hfill {\displaystyle \sum _{k=1}^N}\{-y_k\log \left(p_k\right)-\left(1-y_k\right)\log \left(1-p_k\right)\}+\mathsf{\varrho }\parallel \mathsf{\beta }{\parallel }_{\lambda }^{\lambda }\\ \hfill & \hfill =& \hfill {\displaystyle \sum _{j=1}^N}\{-y_k\log \left({\sigma }_k\right)-\left(1-y_k\right)\log \left(1-{\sigma }_k\right)\}+\mathsf{\varrho }\parallel \mathsf{\beta }{\parallel }_{\lambda }^{\lambda }\end{array}$$

(31)

where

$${\sigma }_k=\frac{1}{1+ex{p}^{\left(l_k\right)}}=\frac{1}{1+ex{p}^{\left({{\displaystyle \sum }}_{r=0}^{f+e}{\mathrm{a}}_{k,r}{\beta }_r\right)}}$$

(32)

We employ gradient descent to optimize the proposed objective function (31). We name our proposed technique broad embedded logistic regression (BELR).

From (26) and (31), it should be noted that the traditional logistic regression can only manage the linear relationship between dependent variables and independent variables effectively. In other words, the classical logistic regression does not consider any possible nonlinear relationship between the dependent variable and independent variables. Unlike the classical logistic regression classifier, where the raw data are used as its input directly, in this paper, from (31), the output of the feature-mapped node and enhancement node of BLS is the input of the logistic regression classifier. In other words, enhanced features serve as the input of the logistic regression classifier. This improves the performance of the algorithm.

In addition, the objective function (31) of the proposed approach contains the regularizer $\mathsf{\varrho }\parallel \mathsf{\beta }{\parallel }_{\lambda }^{\lambda }$, where $\lambda$ can be chosen or set to different values to have different scenarios and to improve the performance of the network. For instance, for $\lambda =1$, the output weight of the proposed method will have a sparse solution. This setting can allow the network to automatically select a relevant feature from $\overline{\mathcal{A}}$, which may enhance the network performance. Similarly, if $\lambda$ is set to 2, the output weight will have dense values and the values will be small. This will prevent the network from overfitting. In this paper, our focus is not to have a sparse solution. Hence, in our experiment, we utilize $\lambda =2$.

4. Experiment and Settings

In this section, we compare the proposed BELR with other linear and non-linear algorithms, namely the original logistic regression (LogR), Random Forest classifier (RF), Gaussian Naive Bayes (GNB), K-nearest neighbour (KNN), and Support Vector Machine (SVM). We use four evaluation metrics in our comparison.

Table 1. The METRICS FOR THE MODELS comparison.

Evaluation Metrics	Equivalent Equation
Precision	$\frac{TP}{\left(TP+FP\right)}$
Recall	$\frac{TP}{\left(TP+FN\right)}$
F1-Score	$\frac{2\ast \left(Precision\ast Recall\right)}{\left(Precision+Recall\right)}$
Accuracy	$\mathrm{The}\mathrm{fraction}\mathrm{of}\mathrm{the}\mathrm{predictions}\mathrm{the}\mathrm{model}\mathrm{executed}\mathrm{correctly}\frac{TP+TN}{\left(TP+TN+FP+FN\right)}$

presents the evaluation metrics used to evaluate the performance of the comparison algorithms.

From the Table, False Positive (FP) is the number of examples which are predicted to be positive by the model but belong to the negative class. False Negative (FN) is the number of examples which are predicted to be negative by the model but belong to the positive class. True Positive (TP) is the number of examples which are predicted to be positive by the model and belong to the positive class.

Furthermore, for a fair comparison, in all the comparison algorithms, we use standard settings for all the parameters suggested in the scikit-learn machine learning package [36]. Additionally, we use APS data set [37,38]. This benchmark data set is commonly used to evaluate machine learning algorithms, specifically for APS failure prediction tasks. There are two problems with the data set. First, the data set contains a high number of missing values. Second, the data set has a high imbalance in class distribution.

In some papers, median imputation has been used to fill missing data. For instance, in [16], the median imputation technique was utilized to handle missing values. However, median imputation can cause destruction to the data. Hence, we employ a robust imputer, namely the KNN imputation method. Thus, we replace the missing values in each column using KNN. The data set used in this paper is quite challenging, as it has the issue of imbalanced class distribution. Our proposed BELR has a comparable good performance. This may be attributed to the ability of feature-mapped layer (nodes) to extract features from the input data and enhancement layer (nodes) for further enhancement of the feature such that the classes are separated from each other. Hence, this improves the performance of BELR under skew data set. This is validated when we compare the original logistic regression classifier and the proposed BELR.

After filling the missing data using KNN imputer, we use cross validation method to fit the comparison models. Furthermore, inside cross-validation, we extract features by using BLS on training set, then fit logistic regression on a feature from the training set, then used the test set to estimate quality metrics.

The total data points are split into 10-fold using stratified method of scikit-learn machine learning package and run each algorithm 10 times. For instance, in the first run we combine nine samples of the divided data as the training set and the remaining one sample for test set. We repeat this process 10 times using different set of data points as the training set and test set.

Table 2. Details of the data set and further details of the data set.

Total Number of Data Points	No Rows of Training Data	No Rows of Test Data
76,000	68,400	7600
Training Set		Test Set
Negative Case	Positive Case	Negative Case	Positive Case
67,162	123	7462	137

summarize the details of the data set used in the first run. In the experiment, we present the average performance of each compared algorithm.

From the table, the ratio of positive case to negative case in the training set is 0.001831, and for the test set, it is 0.018360. It should be noted that we have used stratified method of scikit-learn, a machine learning package, in our cross-validation methods. It takes into consideration the imbalance class of the data to split the data into 10-fold.

The Comparison of the Performance of the Compared Algorithms

In the subsection, we compare the proposed BELR and the original logistic regression (LogR), Random Forest classifier (RF), Gaussian Naive Bayes (GNB), K-nearest neighbour (KNN), and Support Vector Machine (SVM). The average performance in terms of the metrics listed in Table 1 is presented for the comparison algorithms. First, to prevent the effect of the curse of dimensionality, we use principal component analysis (PCA) to reduce the dimension and select an important feature from the input data. A total of 81 principal components are created after applying the PCA technique with a covariance value of 0.95. The initial dimension of input data is 170; however, after applying PCA, the dimension is reduced to 81, which is almost 50% of the feature variables compared to the initial feature variables. After applying PCA, we then apply comparison algorithms on the feature from PCA. We use 10-fold cross-validation concept. In the experiment, the total number of data point is 76,000. For each fold, there are 7600 data points after applying stratified cross-validation, ensuring that each fold has the same proportion of observations with a given categorical value. In the first run, we take one group (7600 data points) as the test set and the remaining nine groups (9 × 7600 data points) for training of the model. In the second run, we pick another 76,000 data points (a new group) as the test set and the remaining nine groups (9 × 7600 data points) to train the models. The process continues until we reach the 10th run or trial. The training set contains 67,162 negative cases and 123 positive cases. Similarly, the test set contains 7462 negative cases and 137 positive cases. Table 2 shows the details. From the experiment, the results obtained are presented in

Table 3. The performance of comparison algorithms under certain metrics.

Score (%)	GNB	LogR	RF	SVM	KNN	BELR
Precision	32.45	77.81	82.6	92.05	80.23	80.91
Sensitivity (Recall)	79.35	57.89	57.67	27.78	55.78	62.25
F1-Score	46.06	66.39	67.92	42.68	65.81	70.39
Accuracy	96.64	98.94	99.01	98.65	98.95	99.05

.

From Table 3, we notice that GNB has a recall of 79.35, and the performance looks better than the rest of the algorithms. However, GNB has a very poor performance in precision. It has a precision score of 32.45. In addition, it has a very poor performance in F1-score, with a score of 46.06.

For other algorithms, it is notice that SVM has a very good score in precision but a very poor score in recall. This resulted in a poor value of F1-score. However, LogR, RF, KNN, and the proposed BELR have good precision and recall scores from the Table. Their performances in terms of precision are relatively equal. The proposed BELR has the best average score in terms of Sensitivity (Recall). In addition, when we compared the performance of the compared algorithms in terms of average F1-score, the proposed BELR has the best F1-score, as shown in Table 3. Other scores for other evaluation metrics are presented in the Table. We use boxplot to present the average F1-score of all the compared algorithms. Figure 6 presents the average F1 score of the performance of the compared algorithms. It is noticed that the proposed BELR has a better F1 score from the box plot.

Overall, we notice that the performance of the proposed BELR is better than the other comparison algorithms under an imbalanced data set.

5. Conclusions

This paper proposes broad embedded logistic regression (BELR) for classification problems, specifically for APS failure prediction. In addition, its performance is studied under an exceedingly difficult data situation and an imbalanced class distribution problem. The feature-mapped nodes and enhancement nodes of the BLS are employed to handle imbalance data set due to the ability of the two types of nodes to generate/extract features that can uniquely separate two classes from each other. Hence, it improves the classification capacity of logistic regression classifier.

Furthermore, the APS data set has a problem of missing data, and in this paper we explore KNN imputation method to solve the problem of missing data using KNN_imputer from Sklearn. Sklearn is a machine learning package commonly used for processing data, building machine learning model. It should be noted that other missing data imputation methods such as generative adversarial network (GAN), etc., could be explored.

The performance of the proposed algorithm is better than other comparison algorithms, namely Gaussian Naive Bayes (GNB), Random Forest, K-nearest neighbor (KNN), Support Vector Machine (SVM), and Logistic Regression (LogR). The performance of the comparison algorithms is evaluated using popular and commonly used metrics in the literature, namely average F1-score, average Recall, average Precision, and average Accuracy. In terms of the F1-score, the performance of the proposed algorithm is the best among the comparison algorithms. The Table and the Figures presented in the experimental section validate that the proposed BELR performances are comparable with other algorithms.