DDSG-GAN: Generative Adversarial Network with Dual Discriminators and Single Generator for Black-Box Attacks

Abstract

As one of the top ten security threats faced by artificial intelligence, the adversarial attack has caused scholars to think deeply from theory to practice. However, in the black-box attack scenario, how to raise the visual quality of an adversarial example (AE) and perform a more efficient query should be further explored. This study aims to use the architecture of GAN combined with the model-stealing attack to train surrogate models and generate high-quality AE. This study proposes an image AE generation method based on the generative adversarial networks with dual discriminators and a single generator (DDSG-GAN) and designs the corresponding loss function for each model. The generator can generate adversarial perturbation, and two discriminators constrain the perturbation, respectively, to ensure the visual quality and attack effect of the generated AE. We extensively experiment on MNIST, CIFAR10, and Tiny-ImageNet datasets. The experimental results illustrate that our method can effectively use query feedback to generate an AE, which significantly reduces the number of queries on the target model and can implement effective attacks.

1. Introduction

With the emergence of deep neural networks, the security issues of artificial intelligence (AI) have become increasingly prominent. Because of the wide application of deep learning technology, the security of deep neural networks has also been increasingly questioned. The existence of an AE makes deep neural networks (DNN) cause disastrous consequences in many fields, such as the occurrence of traffic accidents in the field of automatic driving [1], malicious code successfully escaping detection [2], etc. AE is a major obstacle that various machine learning systems and even artificial intelligence (AI) must overcome. Its existence not only makes the output results of the model deviate greatly but can even make this deviation inevitable. This indicates that machine learning models rely on unreliable features to maximize performance. If the features are disturbed, it will lead to the misclassification of the model. For example, FGSM [3] enables a machine-learning model that classifies the original image as a panda with a probability of 57.7% but classifies its AE as a gibbon with a very high probability of 99.3%.

The vulnerability of DNN to AE has led to adversarial learning. On the one hand, studying an AE is to understand the mechanism of adversarial attacks to better develop corresponding defense technologies and construct more robust deep learning models. In addition, the existence of an AE reveals the serious security threat of DNN. Research on AE can provide a more comprehensive index for evaluating the robustness of DNN.

In adversarial attacks, because different models own different information access rights, the attackers need to consider different attack scenarios to design AE. Adversarial attacks contain two categories: white-box and black-box attacks.

In white-box attacks, adversaries can acquire the structure and parameter information of the target model. Therefore, they can use the target model’s gradient information to construct the AE. However, black-box attacks are more challenging to implement. In a black-box attack, the attackers can only interact with the target model through the input, which increases the difficulty of constructing AE. Still, it is more consistent with real-world attack scenarios.

Black-box attacks contain query-based and transfer-based attacks. Although the former can achieve a good attack effect, the query complexity is high, the query results are not fully utilized in the current attack methods, and masses of queries are easily resisted by defense mechanisms. The latter attack avoids the query to the target model. However, its attack effect is not ideal.

Combining transfer-based and query-based attacks, we design a generative adversary network (GAN) with dual discriminators and a single generator (DDSG-GAN) to generate an AE with better attack performance. We use the generator $G$ of the DDSG-GAN to generate the adversarial perturbation, and the trained discriminator $D_1$ can act as a surrogate model of the target model $T$. The discriminator $D_2$ is used to distinguish whether the input image is original. We experimentally evaluate our method on the MNIST [4], CIFAR10 [5], and Tiny-ImageNet [6] datasets and compare it with the state-of-the-art (SOTA) experimental results. The experiment results demonstrate that the proposed method has a high attack success rate and greatly reduces the number of queries to the target model. The generated AE with our proposed method has a higher visual quality. The main contributions are the following:

(1)

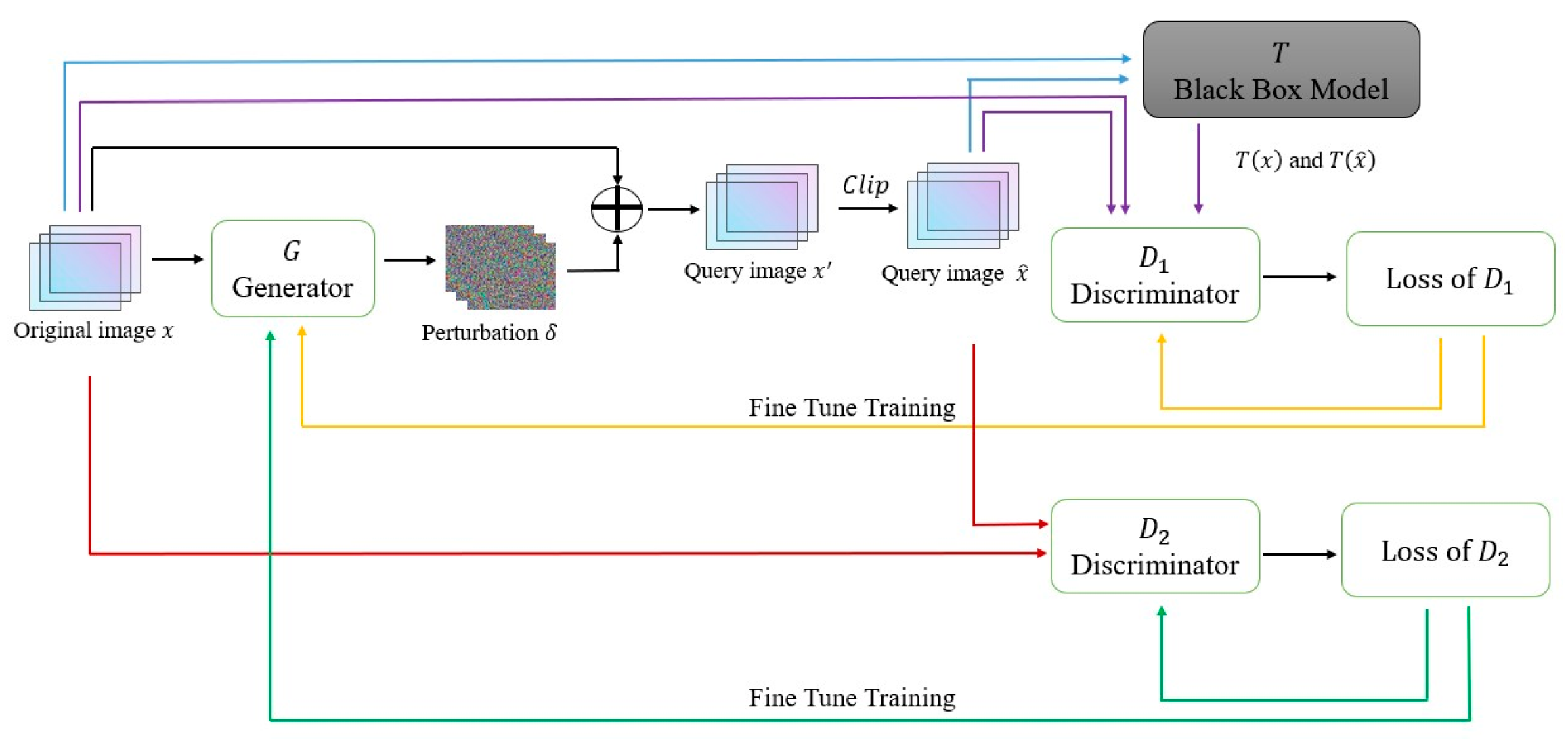
This study presents a novel image AE generation method based on the GANs of dual discriminators. The generator $G$ generates adversarial perturbation, and two discriminators constrain the generator in different aspects. The constraint of discriminator $D_1$ guarantees the success of the attack, and the constraint of discriminator $D_2$ ensures the visual quality of the generated AE.

(2)

This study designs a new method to train the surrogate model; we use original images and AEs to train our substitute model together. The training process contains two stages: pre-training and fine-tuning. To make the most of the query results of the AE, we put the query results of the AEs into the circular queue for the subsequent training, which greatly reduces the query requirement of the target model and makes efficient use of the query results.

(3)

This study introduces a clipping mechanism so that the generated AEs are within the $ϵ$ neighborhood of the original image.

The remainder of our paper is organized as follows. Section 2 introduces the related work of adversarial attacks. The proposed method of generating AE is described in Section 3. Section 4 demonstrates the effectiveness of the attack method through extensive experiments. Section 5 summarizes this paper.

2. Related Work

AEs can exist in many areas of artificial intelligence (AI), such as images, voice, text, and malware, and bring many potential risks to people’s lives. This study mainly focuses on adversarial attacks in image classification tasks. Adversarial attacks mainly contain white-box and black-box attacks. This section will summarize and review the relevant studies of adversarial attacks.

2.1. White-Box attack

In a white-box attack, the adversaries can acquire the structure and parameter information of the attacked target model, while in a black-box attack, the adversaries can only gain the prediction results of the target model about the input. The white-box attack has been developed earlier and is simpler to implement. At present, it can achieve a good attack effect.

White-box attacks mainly include three categories, which are summarized as follows:

(1) Optimize the objective function directly: Szegedy et al. [7] proposed directly optimizing the objective function with the box-constrained L-BFGS algorithm to generate adversarial perturbation. C&W [8] put forward three optimization-based attack methods after the defense distillation, successfully broke the defense distillation, and made the white-box attack reach a new height. Although the optimization-based methods can achieve a good attack effect, the optimization process takes a long time.

(2) Gradient-based attack method: FGSM [3] maintains that the existence of AEs is mainly due to the linear nature of the neural network and can add perturbations in the direction of the maximum gradient change of DNN to increase the classification loss of images. Due to FGSM being a one-step attack algorithm, the attack effect has yet to be improved. The success of FGSM has based on the hypothesis that the loss function is locally linear. If it is nonlinear, the attack’s success cannot be guaranteed. Based on this, Kurakin Alexey et al. [9] put forward I-FGSM, which obtains AEs through continuous iteration of the FGSM algorithm. Compared to FGSM, the I-FGSM can construct a more accurate perturbation, but from the performance of AEs in transfer attacks, I-FGSM is less effective than FGSM. Similar to the I-FGSM attack, the PGD [10] attack has more iterations and a better attack effect, whose disadvantage is its poor transfer attack ability.

(3) The attack method based on the generated neural network can train the neural network to generate AEs. Once the network training is completed, it can generate AEs in batches. For example, ATN [11] can convert an input image into AEs against the target model. It also has a strong attack capability, but the effect of a transfer attack is poor. AdvGAN [12] introduced the GANs into the method of generating AEs based on the generative neural network for the first time, and the trained AdvGAN network can convert random noise into AEs.

Other white-box attack algorithms, such as DeepFool [13], are based on the consideration of how to add the minimum perturbation to the original image. It is by reducing the distance between the image and the decision boundary of the target model to iteratively generate the minimum perturbation that can make the target model misclassified, which is relatively simple to implement and can achieve a good attack effect. One-pixel attack [14] is based on differential evolution. Each attack attempt to modify one pixel of data of an example achieves the result of model misclassification. This method has a good attack performance on less pixel information datasets, but for the datasets with a larger pixel space, the performance of the algorithm declined. The current white-box attack methods have been relatively mature and have achieved a good attack effect in MNIST, CIFAR10, ImageNet [6], and other datasets.

2.2. Black-Box attack

Compared with a white-box attack, a black-box attack is more difficult to implement. In the black-box attack setting, the adversary can only interact with the target model through input, which increases the difficulty of constructing the AEs. Black-box attacks are divided into query-based attacks and transfer-based attacks. Querying different target models will get different types of feedback results. According to the query results of the target model, query-based attacks can be divided into score-based attacks and decision-based attacks.

In the query-based attacks, by interacting with the target model, the Zero Order Optimization (ZOO) attack [15] uses the confidence score of the model’s feedback to estimate the target model’s gradient. Then, it uses the estimated gradient information to generate AEs. AutoZOOM [16] is the improved version of the ZOO attack, which introduces an autoencoder structure and greatly reduces the cost of useless pixel search. At the same time, AutoZOOM adopts a dynamic attack mechanism to further reduce the number of queries. After that, Bandits attack [17] uses the gradient prior information to improve the black-box attacks and introduces data-dependent and time-dependent priors to improve the query efficiency. However, the above methods are used for high-precision gradient estimation, so these inevitably require a lot of time and computing storage. Guo et al. put forward SimBA [18], which does not need to estimate the gradient of the target model and generates query samples by continuously greedily adding randomly sampled perturbation to the original image. According to the query results, it is decided to add or remove the perturbation on the target image. LeBA [19] combined transfer-based and query-based attacks to optimize SimBA further and achieve more efficient attacks.

With the outstanding performance of meta-learning in various classification tasks, Meta attacks [20] first combine adversarial attacks, and meta-learning First uses meta-learning to train a general Meta attack model. Then, it uses real attack information to fine-tune the Meta attack model, which greatly improves the query efficiency. The Simulator attack [21] further improves the attack model based on the Meta attack, which realizes the accurate simulation of any unknown target model. It improves the overall query efficiency of the model. However, because the model is relatively complex, there are comparatively high requirements for computer hardware configuration, and the training time is pretty long. Query-based black-box attacks can achieve a higher success rate. Still, this type of attack requires many query requirements and computing storage, and a large number of queries are easily resisted by the defense mechanism. Therefore, how to improve the efficiency of the query is the key to the current research.

Biggio et al. [22] found that the AEs generated against a certain machine learning model can be used to attack other models, which led researchers to think about transfer attacks. The goal of the transfer-based attack is that the AEs generated for one model can still attack other models. The core idea of the transfer-based black-box attack method [23,24] is to generate AEs on the source model and then transfer them to the target model. This method does not need to know the network structure and the parameters of the target model, nor does it need to query the target model. However, because there is a large distance between the source model and the target model, the attack effect is not satisfactory. The precondition for the realization of transfer-based attacks is the transfer ability of AE. Therefore, training a surrogate model that can highly simulate the target model will improve the AEs’ transferability. Therefore, the model-stealing attacks [25,26,27] are gradually applied to adversarial attacks. The model-stealing attacks obtain the labels of input data by querying the target model and then using the input and query results to train the black-box model’s surrogate model. The surrogate model trained by model stealing attacks can more accurately fit the target model and greatly improve the success rate of transfer attacks.

In recent research, many scholars have applied GANs [28] to the adversarial attack. Zhao et al. [29] built the semantic space of images on the architecture of GANs to obtain more natural AE. Xiao et al. [12] first introduced the idea of GANs in the attack algorithm based on neural networks to generate AE. They proposed a network architecture including a generator, discriminator, and target model. The trained generator can efficiently generate AEs for any input image, but it can only generate AEs for a single target class. Later, Zhou et al. [30] proposed a data-free surrogate model training based on GAN’s architecture to attack the target model. This method does not need a training data set but needs to combine a white-box attack algorithm, such as FGSM or PGD, to generate AE, and the training time is very long. Because it needs a lot of queries, this attack is easy to be avoided by the defense mechanism. In this paper, we focus on the black-box attack, based on the architecture of GANs, and combine it with the model-stealing attack to generate adversarial samples with a higher attack success rate and better visual quality.

3. Methodology

3.1. Preliminaries

3.1.1. Adversarial Examples and Adversarial Attack

Modifying the original images in a human-imperceptible way so that the modified images can be misclassified by the machine learning model, and the modified images are called AE. For a victim image classification model $T$, we use $\left(x,y\right)$ as the original image-label pair. The goal of the adversarial attack is to generate an AE $\widehat{x}$ so that target model $T$ can misclassify it. For the untargeted attack setting, it can be formulated as follows:

$$\begin{gathered} argmax T\left(x\right)=y, \mathrm{and} argmax T\left(\widehat{x}\right)\ne y, \\ s.t.\Vert \widehat{x}-x\Vert \le ϵ. \end{gathered}$$

(1)

For the targeted attack setting, it can be formulated as follows:

$$\begin{gathered} argmax T\left(x\right)=y, \mathrm{and} argmax T\left(\widehat{x}\right)\ne y, \\ s.t.\Vert \widehat{x}-x{\Vert }_p\le ϵ. \end{gathered}$$

(2)

where $\Vert ·{\Vert }_p$ denotes the $l_p$ norm, $t$ is the target class in the targeted attack, and $ϵ$ is the upper bound of the perturbation.

3.1.2. Attack Scenarios

In this paper, we consider the adversarial attack in the black-box scenario. Query-based black-box attacks can be divided into decision-based attacks and score-based attacks. In this paper, we focus on a decision-based attack scenario.

(1)

Score-based attacks. In this scenario, the attacker is unknown to any structure and parameter information of the target model, but for any input, the adversary can acquire the classification confidence.

(2)

Decision-based attacks. Similar to the attack scenario of score-based attacks, the adversary doesn’t know any structure and parameter information of the target model, but for any input, the attacker can acquire the classification label.

3.2. Model Architecture

In this section, we will introduce the method of generating AEs based on the dual discriminators and single generator of GAN (DDSG-GAN). This paper introduces the model architecture of GAN and designs a GAN with dual discriminators and a single generator to generate AEs. DDSG-GAN uses generator $G$ to generate adversarial perturbations and uses discriminators $D_1$ and $D_2$ to constrain the generated perturbations. Then, the trained discriminator $D_1$ can be used as a surrogate model of the target model $T$, and the overall structure of DDSG-GAN is shown in Figure 1. The input of Generator $G$ is the original image $x$, and the output is perturbation vector $\delta =G\left(x;{\theta }_g\right)$. Adding the perturbation vector to the original image and clipping it to obtain the query sample $\widehat{x}$. Input $x$ and $\widehat{x}$ into the target model $T$ to acquire the output $T\left(x\right)$ and $T\left(\widehat{x}\right)$. Discriminator $D_1$ uses image-output pairs $\left(x,T\left(x\right)\right)$ and $\left(\widehat{x},T\left(\widehat{x}\right)\right)$ for training, and Discriminator $D_2$ uses image-output pairs $\left(x,1\right)$ and $\left(\widehat{x},0\right)$ for training.

In DDSG-GAN, $T$ is the victim image classification black-box model. The generator $G$ will generate the perturbation vector $\delta$ of the input image $x$ and add $\delta$ to $x$. Then, through clip operation, we can get query sample $\widehat{x}$. The $T$’s query result is used to train discriminator $D_1$, and discriminator $D_2$ is used to identify whether the input is the original image. Both discriminators, $D_1$ and $D_2$, will constrain the generated perturbations.

In this training process, the generator and discriminator play a game relationship with each other. In each iteration, target model $T$ and discriminators $D_1$ and $D_2$ will calculate corresponding prediction results for each input. The discriminator $D_1$ fits the target model according to the output of the target model $T$. With the increasing of iterations, the fitting ability of the discriminator $D_1$ to $T$ is constantly enhanced so that the attack ability of generator $G$ to target model $T$ continues to increase. At the same time, the discriminator $D_2$ is increasingly capable of classifying true and fake samples so that generator $G$ will generate AEs closer to the original data distribution. This training process forms discriminators $D_1$ and $D_2$ with generator $G$ to keep playing games and making progress.

3.2.1. The Training of Discriminator $D_1$

The input of generator $G$ is the original image $x$, and the output is the perturbation vector $\delta =G\left(x;{\theta }_g\right)$ about the original image $x$. Add the generated perturbation vector to $x$ to get the query sample $x^{\prime }$. To ensure that the generated sample is within the $ϵ$ neighborhood of the original image, we clip $x^{\prime }$ or $\delta$ to get the final query sample $\widehat{x}$. In the $l_2$ norm attack,

$$\widehat{x}=Clip\left(x^{\prime },x\right)=\{\begin{array}{ll}x+\frac{ϵ}{\Vert x^{\prime }-{x\Vert }_p}·\left(x^{\prime }-x\right),& \Vert x^{\prime }-x{\Vert }_p\ge ϵ, \\ x^{\prime },& \Vert x^{\prime }-x{\Vert }_p<ϵ,\end{array}$$

(3)

where $\Vert x^{\prime }-x{\Vert }_p$ denotes the $l_p$ norm between $x$ and $x^{\prime }$, and $ϵ$ is the upper bound of the perturbation.

In the $l_{\infty }$ norm attack,

$${\delta }^{\prime }=clip\left(\delta ,{\alpha }_1,{\alpha }_2\right)=\{\begin{array}{l}{\alpha }_1, \delta <{\alpha }_1;\\ \delta , {\alpha }_1\le \delta \le {\alpha }_2,\\ {\alpha }_2, \delta >{\alpha }_2;\end{array}$$

(4)

where ${\alpha }_1$ and ${\alpha }_2$ are the upper bound and lower bound of clipping respectively. The final query sample $\widehat{x}=x+{\delta }^{\prime }$.

The adversarial attack’s goal is to make the target model misclassify the AE. It can be formulated as follows:

$$T\left(\widehat{x}\right)\ne y,$$

(5)

For the convenience of training, we convert (5) to maximize the following objective function:

$$\underset{\widehat{x}}{\max }L\left(T\left(\widehat{x}\right),y\right),$$

(6)

where $L\left(·,·\right)$ measures the difference between the output of target model $T$ and $y$.

In the process of solving the optimization problem (6), it is necessary to continuously query the target model $T$ to obtain $T\left(\widehat{x}\right)$. However, this will make the query calculation very large, which is easily avoided by the defense mechanism. In the cause of reducing the number of queries to the target model, we train the discriminator $D_1$ as a surrogate model for $T$ so that the query of $T$ can be transferred to $D_1$, which will greatly reduce the number of queries to the target model.

The training goal of the discriminator $D_1$ is to make it to be used as a surrogate model to simulate the function of model $T$. For the purpose of improving the fitting ability of $D_1$, we use the original image $x$ and the generated query sample $\widehat{x}$ to train $D_1$ together. The loss function for training the discriminator $D_1$ is as follows:

$$L_{D1}={\beta }_1\times d\left(D_1\left(x;{\theta }_{d1}\right),T\left(x\right)\right)+{\beta }_2\times d\left(D_1\left(\widehat{x};{\theta }_{d1}\right),T\left(\widehat{x}\right)\right),$$

(7)

where $T\left(x\right)$ and $T\left(\widehat{x}\right)$ are the query results obtained by inputting $x$ and $\widehat{x}$ into the target model $T,$ respectively, ${\theta }_{d1}$ is the parameters of model $D_1$, $D_1\left(\widehat{x};{\theta }_{d1}\right)$ is the predicting result of the discriminator $D_1$ about the query sample $\widehat{x}$, and $D_1\left(x;{\theta }_{d1}\right)$ is the predicting result of the discriminator $D_1$ about the original image $x$. ${\beta }_1$ and ${\beta }_2$ are the weight factors used to control the relative importance. In this paper, we set ${\beta }_1=2, {\beta }_2=1$.

For the decision-based black-box attack, the loss function of $D_1$ can be formulated as follows:

$$L_{D1}={\beta }_1\times CEL\left(D_1\left(x;{\theta }_{d1}\right),T\left(x\right)\right)+{\beta }_2\times CEL\left(D_1\left(\widehat{x};{\theta }_{d1}\right),T\left(\widehat{x}\right)\right),$$

(8)

where $CEL\left(a,b\right)$ denotes the cross-entropy function between $a$ and $b$.

For the score-based black-box attack, the adversary is obtained through query $T$ to get the classification probability for each class. So, we can convert the $T\left(x\right)$ obtained by the query into the corresponding label value and bring it into (8) to calculate the loss function of $D_1$ in this attack setting. Algorithm 1 presents the training procedure of $D_1$.

Algorithm 1	Training procedure of the Discriminator $D_1$
Input:	Training dataset $\left(x,T\left(x\right)\right)$ and $\left(x^{\prime },T\left(x^{\prime }\right)\right)$, where $x$ is the original image and $x^{\prime }$ is the sample after adding perturbation, target model $T$, the discriminator $D_1$ and its parameters ${\theta }_{d1}$, the generator $G$ and its parameters ${\theta }_g$; loss function $L\left(·,·\right)$ is defined in Equation (7).
Parameters:	Batch number $B$, learning rate ${\lambda }_1$, iterations $N$, weight factor ${\beta }_1$ and ${\beta }_2$, clipping upper bound ${\alpha }_1$ and lower bound ${\alpha }_2$.
Output:	The trained Discriminator $D_1$.
1:	for$epoch\leftarrow 1$ to $N$ do
2:	for $b\leftarrow 1$ to $B$ do
3:	$\delta =G\left(x;{\theta }_g\right)$
4:	if $norm=2$ do
5:	$x^{\prime }=x+\delta$
6:	$\widehat{x}=Clip\left(x^{\prime },x\right)$
7:	elif$\mathrm{norm}=\infty$do
8:	${\delta }^{\prime }=clip\left(\delta ,{\alpha }_1,{\alpha }_2\right)$
9:	$\widehat{x}=x+{\delta }^{\prime }$
10:	end if
11:	$\widehat{x}\leftarrow clip\left(\widehat{x},0,1\right)$
12:	$los{s}_{d1}={\beta }_1\times d\left(D_1\left(x;{\theta }_{d1}\right),T\left(x\right)\right)+{\beta }_2\times d\left(D_1\left(\widehat{x};{\theta }_{d1}\right),T\left(\widehat{x}\right)\right)$
13:	${\theta }_{d1}\leftarrow {\theta }_{d1}-{\lambda }_1\times {\nabla }_{{\theta }_{d1}}los{s}_{d1}$
14:	end for
15:	end for
16:	return $D_1$

3.2.2. The Training of Discriminator $D_2$

We train the discriminator $D_1$ as a surrogate model for $T$, so most of the queries on $T$ can be transferred to discriminator $D_1$. When the attack is successful, the AEs must be close to $x$, so discriminator $D_2$ can be set to distinguish whether the sample is sampled from the original images. If it is the original image, the label is 1. If it is the AE, the label is 0. The objective function for training the discriminator $D_2$ is:

$$L_{D2}=E_{x~P_{data}\left(x\right)}\left[\log \left(D_2\left(x;{\theta }_{d2}\right)\right)+\log \left(1-D_2\left(\widehat{x};{\theta }_{d2}\right)\right)\right],$$

(9)

where $P_{data}\left(x\right)$ is the data distribution of the original image $x$, $E$ denotes the calculation of the mean of the expression, ${\theta }_{d2}$ is the parameters of model $D_2$, $D_2\left(x;{\theta }_{d2}\right)$ is the predicting result of the discriminator $D_2$ about the original image $x$, and $D_2\left(\widehat{x};{\theta }_{d2}\right)$ is the predicting result of the discriminator $D_2$ about the query sample $\widehat{x}$.

The discriminator $D_2$ is used to judge whether the sample is true or fake and uses $D_2$ to train a good generator to fool $D_2$ so that the distribution of the generated AE can be closer to the original image. Algorithm 2 presents the training procedure of $D_2$.

Algorithm 2	Training procedure of the Discriminator $D_2$
Input:	Training dataset $\left(x,1\right)$ and $\left(\widehat{x},0\right)$, where $x$ is the original image and $\widehat{x}$ are the query samples, the discriminator $D_2$ and its parameters ${\theta }_{d2}$, loss function $L\left(·,·\right)$ is defined in Equation (9).
Parameters:	Batch number $B$, Learning rate ${\lambda }_2$, iterations $N$.
Output:	The trained Discriminator $D_2$.
1:	for$epoch\leftarrow 1$ to $N$ do
2:	for $b\leftarrow 1$ to $B$ do
3:	$los{s}_{d2}=E_{x~P_{data}\left(x\right)}\left[\log \left(D_2\left(x;{\theta }_{d2}\right)\right)+\log \left(1-D_2\left(\widehat{x};{\theta }_{d2}\right)\right)\right]$
4:	${\theta }_{d2}\leftarrow {\theta }_{d2}+{\lambda }_2\times {\nabla }_{{\theta }_{d2}}los{s}_{d2}$
5:	end for
6:	end for
7:	return $D_2$

3.2.3. The Training of Generator $G$

The input of generator $G$ is the original image $x$, and the output is the perturbation vector $\delta$ about $x$. On behalf of making the generated AE to fool the target model $T$, which needs to maximize the objective function (6). In this way, each update of generator $G$ needs to query $T$, and the parameter information of target model $T$ needs to be used in the backpropagation process, which does not conform to the scenario settings of black-box attacks. Therefore, we replace the target model $T$ with the discriminator $D_1$ and approximate (6) as follows (10):

$$\underset{\widehat{x}}{\max }L\left(D_1\left(\widehat{x};{\theta }_{d1}\right),y\right),$$

(10)

where $L\left(·,·\right)$ is the cross-entropy function. Since the output of $D_1$ has passed softmax, the denominator of (11) will not be 0, and (10) is equivalent to the following (11):

$$\underset{\widehat{x}}{\min }\frac{1}{L\left(D_1\left(\widehat{x};{\theta }_{d1}\right),y\right)},$$

(11)

generator $G$’s loss function regarding discriminator $D_1$ can be defined as follows (12):

$$L_{G\_D1}=\frac{1}{L\left(D_1\left(\widehat{x};{\theta }_{d1}\right),y\right)}.$$

(12)

While the attack is successful in ensuring that the generated AEs are closer to the distribution of the original image, the loss function of the generator $G$, with respect to the discriminator $D_2$, is defined as (13):

$$L_{G\_D2}=\log \left[1-D_2\left(\widehat{x};{\theta }_{d2}\right)\right].$$

(13)

To obtain a high attack success rate, it is necessary to continuously input $\widehat{x}$ into the target model $T$ and use the loss of output $T\left(\widehat{x}\right)$ with the ground truth (untargeted attack) or the target class (targeted attack) to optimize generator $G$. The objectivate loss function of the attack can be formulated as follows:

$$L_{att\_score}=\{\begin{array}{ll}{\widehat{y}}_T-{\widehat{y}}_t,& if untargeted attack, \\ {\widehat{y}}_t-{\widehat{y}}_T,& if targeted attack,\end{array}$$

(14)

where ${\widehat{y}}_t$ denotes the prediction probability of $T$ for the target class in the targeted attack or the prediction probability of $T$ for the real class in the untargeted attack, and ${\widehat{y}}_T$ denotes the maximum value among the predicted probabilities of other classes by $T$.

To reduce the number of queries and be more consistent with the black-box setting, we use discriminator $D_1$ instead of $T$ to optimize the training process. The objectivate loss function can be formulated as follows:

$$L_{att}=\{\begin{array}{ll}{\widehat{y}}_{D_1}-{\widehat{y}}_t,& if untargeted attack, \\ {\widehat{y}}_t-{\widehat{y}}_{D_1},& if targeted attack,\end{array}$$

(15)

where ${\widehat{y}}_t$ denotes the prediction probability of $D_1$ for the target class in the targeted attack or the prediction probability of $D_1$ for the real class in the untargeted attack, and ${\widehat{y}}_{D_1}$ denotes the maximum value among the predicted probabilities of other classes by $D_1$.

We train the generator $G$ by minimizing the following objectivate function:

$$L_G={\gamma }_1\times L_{G\_D1}+{\gamma }_2\times L_{G\_D2}+{\gamma }_3\times L_{att},$$

(16)

where ${\gamma }_i \left(i=1,2,3\right)$ is the weight factor of the three losses, which controls the relative importance of the three losses. $L_{G\_D1}$ makes the generated AE deceive discriminator $D_1$ step by step. $L_{G\_D2}$ makes generated AEs to be closer to the actual data distribution. $L_{att}$ is the attack loss, and its optimization produces a better attack effect. In this paper, the generator $G$ and discriminators $D_1$ and $D_2$ are obtained by solving the minimax function $\underset{G}{\min } \underset{D_1}{\min } \underset{D_2}{\max } L_G$.

3.2.4. Improved Model

We can find from the training of discriminator $D_1$ that every training update of $D_1$ needs to query $T$. To reduce the number of queries to $T$ while ensuring the fitting ability of $D_1$, we design a circular queue to limit the training of $D_1$. We divide the training process of $D_1$ into two stages: model pre-training and fine-tuning.

First, when the number of iterations $iter\le n$, setting ${\beta }_1=3,$ and ${\beta }_2=0$. We use $\left(x,T\left(x\right)\right)$ to train $D_1$ according to the Equation (7). When the number of iterations $iter>n$ and $iter mod m=0$, we add the query result $\left(\widehat{x},T\left(\widehat{x}\right)\right)$ of this iteration to circular queue $H$. So, when $iter>n$, setting ${\beta }_1=2$ and ${\beta }_2=1$ and when using $\left(x,T\left(x\right)\right)$, the query result $\left(\widehat{x},T\left(\widehat{x}\right)\right)$ is saved in the circular queue to fine-tuned $D_1$ according to the Equation (7).

In each iteration training, since we constantly use the query results of $T$ to train $D_1$, $D_1$ and $T$ are highly approximate. Therefore, the ultimate goal of generator $G$ can be converted to realize the discriminator $D_1$’s misclassification of AE. If the AE can successfully lead to $D_1$ misclassifying them, we can think that the AE can also successfully fool the target model $T$ with a high probability. Therefore, in the whole training process, we also trained a surrogate model that can highly simulate the target model while generating the adversarial perturbation, combining GANs and model-stealing attacks to improve the transferability of the AEs. Algorithm 3 presents the training procedure of the whole model.

Algorithm 3	Training procedure of the DDSG-GAN.
input:	Target model $T$, generator $G$ and it’s parameters ${\theta }_g$, discriminator $D_1$ and its parameters ${\theta }_{d1}$, discriminator $D_2$ and it’s parameters ${\theta }_{d2}$, original image–label pair $\left(x,y\right)$ the learning rate ${\eta }_g$, ${\eta }_{d1}$ and ${\eta }_{d2}$.
output:	The trained generator $G$.
1:	Initialize the model of $G$, $D_1$ and $D_2$.
2:	for$i\leftarrow 1$ to $N$ do
3:	for $j\leftarrow 1$ to $n_1$ do
4:	$\delta \leftarrow G\left(x;{\theta }_g\right)$
5:	if $norm=2$ do
6:	$x^{\prime }=x+\delta$
7:	$\widehat{x}\leftarrow Clip\left(x^{\prime },x\right)$
8:	elif $norm=\infty$ do
9:	${\delta }^{\prime }=clip\left(\delta ,{\alpha }_1,{\alpha }_2\right)$
10:	$\widehat{x}\leftarrow x+{\delta }^{\prime }$
11:	end if
12:	$\widehat{x}\leftarrow clip\left(\widehat{x},0,1\right)$    $⊳$ query example
13:	if $i>n$ and $i mod m=0$ do
14:	Input $\widehat{x}$ into the targeted model $T$ to get the query result
	Add $(\widehat{x};T\left(\widehat{x}\right))$ to the circular queue $H$
16:	end if
17:	if $i\le n$ do        $⊳$ pre-training of $D_1$
18:	$L_{D1}=d\left(D_1\left(x;{\theta }_{d1}\right),T\left(x\right)\right)$
19:	elif $i>n$ do        $⊳$ fine tuning of $D_1$
20:	$L_{D1}={\beta }_1\times d\left(D_1\left(x;{\theta }_{d1}\right),T\left(x\right)\right)+{\beta }_2\times d\left(D_1\left(\widehat{x};{\theta }_{d1}\right),T\left(\widehat{x}\right)\right)$ $⊳$$\left(\widehat{x};T\left(\widehat{x}\right)\right)$ is taken from the circular queue $H$
21:	end if
22:	${\theta }_{d1}\leftarrow {\theta }_{d1}-{\eta }_{d1}{\nabla }_{d1}{L}_{D1}\left({\theta }_{d1}\right)$
23:	end for
24:	for $j\leftarrow 1$ to $n_2$ do
25:	$L_{D2}=E_{x~P_{data\left(x\right)}}\left[\log \left(D_2\left(x;{\theta }_{d2}\right)\right)+\log \left(1-D_2\left(\widehat{x};{\theta }_{d2}\right)\right)\right]$
26:	${\theta }_{d2}\leftarrow {\theta }_{d2}+{\eta }_{d2}\times {\nabla }_{L_{D2}}\left({\theta }_{d2}\right)$
27:	end for
28:	for $j\leftarrow 1$ to $n_3$ do
29:	$L_G={\gamma }_1\times L_{G\_D1}+{\gamma }_2\times L_{G\_D2}+{\gamma }_3\times L_{att}$
30:	${\theta }_g\leftarrow {\theta }_g-{\eta }_g\times {\nabla }_{L_G}\left({\theta }_g\right)$
31:	end for
32:	end for
33:	return$G$

3.2.5. Generate Adversarial Examples

Firstly, according to algorithm 3, the adversary trains the generator $G$ for the target model $T$ under a specific attack setting. Secondly, we input the original image $x$ into the trained generator $G$ to obtain the corresponding perturbation vector $\delta$, and then add $\delta$ to the original sample to get the initial AE $x^{\prime }=x+\delta$. In order to ensure that the perturbation of the AE is within a small range, we perform the corresponding clipping operation on $x^{\prime }$ to obtain the AE $\widehat{x}$. If it is a $l_2$ norm attack, the clipping operation is performed according to the formula (3). If it is a $l_2$ norm attack, the clipping operation is performed according to the formula (4). Input the AE $\widehat{x}$ to the corresponding target $T$ model to attack.

Figure 2 shows the specific attack process of the MNIST dataset. As shown in Figure 2, after the training of DDSG-GAN, we input the original image $x$ into the trained generator to make AE $\widehat{x}$. Then, input $\widehat{x}$ into the corresponding target model to attack. The generator designed in this paper consists of an encoder and a decoder. The encoder is a 5-layer convolution network, and the decoder is a 3-layer convolution network. For different target models, DDSG-GAN will train different generators and get different attack results.

4. Experiment

4.1. Experiment Setting

In this section, we will introduce the specific details of the experiment, including datasets, target model architecture, method settings, and evaluation indicators.

Dataset: We evaluate the effectiveness of the proposed method through experimental results on MNIST, CIFAR10, and Tiny-ImageNet. For these datasets, we select images with the correct classification of the target model in their testing sets as their respective testing sets for evaluation. The number of selected images is 1000, 1000, and 1600, respectively.

Attack scenario: We use a decision-based attack in the black-box attack setting to evaluate the proposed method. The attackers can acquire the output results of the target model but cannot obtain any structure and parameter information about the target model.

Target model architecture: In the $l_{\infty }$ norm attack, for the MNIST dataset, we follow the advGAN [12] trained three image classification models for attack testing. Models A and B are from the paper [31], and model C is from the paper [8]. In the $l_{\infty }$ norm attack, we trained model D as the target model. The structure of these models is shown in

Table 1. MNIST classification model.

A	B	C	D
Conv(64,5,5) + Relu Conv(64,5,5) + Relu Dropout(0.25) FC(128) + Relu Dropout(0.5) FC + Softmax	Dropout (0.2) Conv(64,8,8) + Relu Conv(128,6,6) + Relu Conv(128,5,5) + Relu Dropout(0.5) FC + Softmax	Conv(32,3,3) + Relu Conv(32,3,) + Relu Conv(64,3,3) + Relu Conv(64,3,3) + Relu FC(200) + Relu Dropout (0.5) FC(200) + Relu FC + Softmax	Conv(128,3,3) + tanh Conv(64,3,3) + tanh FC(128) + Relu FC + Softmax

.

For the CIFAR10 dataset, we perform an $l_{\infty }$ norm attack. We also follow advGAN to train ResNet32 as the target model. In a Tiny-ImageNet dataset, we train the ResNet34 classification model as the target model, and perform $l_2$ norm attack.

DDSG-GAN model details: The DDSG-GAN model contains dual discriminators and a single generator. The generator consists of an encoder and a decoder. For MNIST and CIFAR10 data sets, we design the same generator structure. The encoder is a 5-layer convolutional network, and the decoder is a 3-layer convolutional network. Refer to Figure 2 for the specific generator structure. For the Tiny-ImageNet, we add a convolution layer in the encoder and generator, respectively. For the MNIST data set, the discriminator $D_1$ is a 4-layer convolutional neural network. The discriminator $D_1$ for the CIFAR10 data set is ResNet18 without pre-training. For the Tiny-ImageNet data set, there are two types of discriminators $D_1$, ResNet18 and ResNet50, which are pre-trained. We design the same discriminator $D_2$ for all data sets. The discriminator $D_2$ is a 2-classification network model composed of a 4-layer convolutional network, which is used to distinguish whether the sample is sampled from the original images.

Method setting: Multiple classification models are trained for MNIST, CIFAR10, and Tiny-ImageNet datasets. First, algorithm 3 is used to train the generator $G$. Then, the trained $G$ is used to generate the adversarial perturbation. Then, it is added to the original sample, and the AE is obtained by clipping operation. Finally, we use these AEs to attack classification models. In the targeted attack, the target class is set to $t=\left(y+1\right) mod C$, where $y$ is the ground truth, and $C$ is the total number of categories.

Evaluation indicators: (1) Attack success rate. In the untargeted attack, it is the proportion of the AE successfully divided into any other classes. In the targeted attack, it is the probability of classifying the image into a specific target class. (2) The magnitude of the perturbation. We conduct attack experiments under the $l_2$ and $l_{\infty }$ norm and set the corresponding perturbation threshold.

4.2. Experiments on MNIST

In this section, we use the $l_2$ and $l_{\infty }$ norms to perform targeted and untargeted attacks on MNIST, respectively.

Table 2. Experimental parameter setting of MNIST.

Name	${\mathit{l}}_{\mathit{\infty }} \mathbf{Norm}$	${\mathit{l}}_2\mathbf{Norm}$	Description
${\eta }_{d1}$	0.0001	0.0001	the learning rate for updating ${\theta }_{d1}$
${\eta }_{d2}$	0.0001	0.0001	the learning rate for updating ${\theta }_{d2}$
${\eta }_g$	0.001	0.001	the learning rate for updating ${\theta }_g$
$H$	20	10	query target model’s interval
$H^{’}s$ length	60,001	60,001	the maximum length of $H$
$n$	20	5	updating queue H’s interval
${\gamma }_1$	1	1	weight factor of ${\gamma }_1$ (15)
${\gamma }_2$	1	1	weight factor of ${\gamma }_2$ (15)
${\gamma }_3$	10 ($\mathrm{epoch}\le 20$)	1	weight factor of ${\gamma }_3$ (15)
	20 ($\mathrm{epoch}>20$)

shows the specific parameter settings. The untargeted attack aims to generate AEs that make the classification result of the target model different from the ground truth. The targeted attack aims to generate AEs that make the classification result of the target model in the specified category. The experimental results are shown in

Table 3. Training results of the surrogate model.

		Target Model A	Target Model B	Target Model C
Untargeted attack	Accuracy	99.33%	99.01%	99.16%
	Similarity	99.19%	99.04%	99.13%
Targeted attack	Accuracy	99.29%	99.12%	99.27%
	Similarity	99.19%	99.16%	99.22%

,

Table 4. Experimental results of untargeted attack under $l_{\infty }$ norm (ASR: the attack success rate).

Target Model	Accuracy	Method	ASR	ϵ
A	98.97%	Black-box (Surrogate Model [32] + FGSM)	69.4%	0.4
		Black-box (Surrogate Model [32] + PGD)	68.0%	0.4
		Black-box ($D_1$ as Surrogate Model + FGSM)	74.1%	0.3
		Black-box ($D_1$ as Surrogate Model + PGD)	90.2%	0.3
		DaST [30]	76.4%	0.3
		DDSG-GAN (Proposed)	100%	0.3
B	99.6%	Black-box (Surrogate Model [32]+ FGSM)	74.7%	0.4
		Black-box (Surrogate Model [32]+ PGD)	70.6%	0.4
		Black-box ($D_1$ as Surrogate Model + FGSM)	77.1%	0.3
		Black-box ($D_1$ as Surrogate Model + PGD)	82.8%	0.3
		DaST [30]	82.3%	0.3
		DDSG-GAN (Proposed)	99.9%	0.3
C	99.17%	Black-box (Surrogate Model [32]+ FGSM)	69.2%	0.4
		Black-box (Surrogate Model [32]+ PGD)	67.4%	0.4
		Black-box ($D_1$ as Surrogate Model + FGSM)	73.5%	0.3
		Black-box ($D_1$ as Surrogate Model + PGD)	91.3%	0.3
		DaST [30]	68.4%	0.3
		DDSG-GAN (Proposed)	100%	0.3

and

Table 5. Experimental results of targeted attack under $l_{\infty }$ norm.

Target Model	Accuracy	Method	ASR	ϵ
A	98.97%	Black-box (Surrogate Model [32]+ FGSM)	11.3%	0.4
		Black-box (Surrogate Model [32]+ PGD)	24.9%	0.4
		AdvGAN [12]	93.4%	0.3
		Black-box ($D_1$ as Surrogate Model + FGSM)	18.3%	0.3
		Black-box ($D_1$ as Surrogate Model + FGSM)	50.3%	0.3
		DaST [30]	28.7%	0.3
		DDGS-GAN (proposed)	98.0%	0.3
B	99.6%	Black-box (Surrogate Model [32]+ FGSM)	17.6%	0.4
		Black-box (Surrogate Model [32]+ PGD)	22.3%	0.4
		AdvGAN [12]	90.1%	0.3
		Black-box ($D_1$ as Surrogate Model + FGSM)	25.1%	0.3
		Black-box ($D_1$ as Surrogate Model + PGD)	53.9%	0.3
		DaST [30]	40.3%	0.3
		DDGS-GAN (proposed)	97.6%	0.3
C	99.17%	Black-box (Surrogate Model [32]+ FGSM)	11.0%	0.4
		Black-box (Surrogate Model [32]+ PGD)	29.3%	0.4
		AdvGAN [12]	94.02%	0.3
		Black-box ($D_1$ as Surrogate Model + FGSM)	18.0%	0.3
		Black-box ($D_1$ as Surrogate Model + PGD)	65.8%	0.3
		DaST [30]	25.6%	0.3
		DDGS-GAN (proposed)	94.6%	0.3

.

First, we attack the target models under $l_{\infty }$ norm. We train discriminator $D_1$ as a $T$’s surrogate model. We calculate the classification accuracy and similarity with the model $T$ (the proportion of the same number of output results of the surrogate model and that of the target model) against the MNSIT test set. The experimental results are shown in Table 3. The classification accuracy of several surrogate models and the similarity between them and the target model is close to above 99%, indicating that the surrogate model we trained can replace the target model’s function.

In the $l_{\infty }$ norm attack, we set the maximum perturbation threshold $ϵ=0.30$ to evaluate the proposed approach. We compare DDSG-GAN with surrogate model-based black-attack, DaST, and advGAN. The surrogate model is trained by two methods, respectively. The first is to train the surrogate model according to [32]. This method uses 150 images in the test set as the original training set $S_0$, which sets the Jacobian augmentation parameter $\lambda =1$, and runs 30 Jacobian augmentation iterations. The second is to use the trained discriminator $D_1$ as the surrogate model and combine FGSM and PGD for the black-box attacks. We set an upper bound on the number of queries to the target model in the DaST method. For MNIST data sets, the query of each image is set to 1000. Under this premise, the total query upper bound of the DaST method is $6\times {10}^7$.

For a surrogate model-based attack, we use the same DNN model as the surrogate model and attack the target model by combining FGSM and PGD attack algorithms. To make the surrogate model trained by the first method have a better attack effect, set $ϵ=0.40$, and the perturbation thresholds of other methods are set to $ϵ=0.30$. Table 4 shows that our proposed method (DDSG-GAN) achieves an attack success rate of nearly 100%, which is much higher than black-box attacks based on surrogate models and DaST. At the same time, we also calculated the average query numbers of the target model. For the target models A, B, and C, the query numbers of each image in the train set were 15, 20, and 28, respectively, which ensured a low query quantity. Because the target model is unknown, black-box attacks based on the surrogate model have a low success rate. If $D_1$ is the surrogate model, compared with the surrogate model trained by [32], if combined with the FGSM algorithm to attack, the attack success rate is increased by 3.8% (4.7%, 2.4%, 4.3%) on average. If combined with the PGD algorithm to attack, the attack success rate is increased by 19.4% (22.2%, 12.2%, 23.9%) on average, and the attack effect is significantly improved. It demonstrates that the surrogate model we trained can replace the target model to a large extent, and this method can also achieve a good attack effect.

Table 5 shows the result of the targeted attack under the $l_{\infty }$ norm, and we also compare it with the advGAN method. Compared with advGAN, the attack success rate of DDSG-GAN is 4.23% (6.5%, 7.5%, 0.58%) higher than advGAN on average, and three–four times higher than DaST. It also is much higher than the surrogate-model-based black-box attack. For target models A, B, and C, each image query numbers in the train set are 70, 75, and 109 times, respectively, also maintained at a low level. If $D_1$ is the surrogate model, compared with the surrogate model trained by [32], if combined with the FGSM algorithm to attack, the ASR is increased by 7.17% (7%, 7.5%, 7%) on average. If combined with the PGD algorithm to attack, the ASR is increased by 31.17% (25.4%, 31.6%, 36.5%) on average. The attack effect has also been significantly improved. In this attack setting, we visualize the generated AEs by DDSG-GAN on MNIST, which is shown in Figure 3. The top row shows the original samples of each class randomly selected from the training set. Other rows show the AEs generated by DDSG-GAN for the corresponding target model. The probability that each AE is classified into the target class is shown below the image.

We also carried out an untargeted attack under the $l_2$ norm, and the results are shown in

Table 6. Experimental results of untargeted attack under $l_2$ norm.

Attack Type	Method	ASR	ϵ	Agv. Queries
Untargeted attack	Bandits [17]	73%	1.99	2771
	Decision Boundary [33]	100%	1.85	13,630
	Opt-attack [34]	100%	1.85	12,925
	DDSG-GAN	90.6%	1.85	1431

. In the $l_2$ norm attack, DDSG-GAN achieved comparable ASR and perturbation size to other attack methods but reduced the number of queries.

4.3. Experiments on CIFAR10 and Tiny-ImageNet

We perform the untargeted and targeted attacks on CIFAR10 under $l_{\infty }$ norm. Different from the setting of experimental parameters of MNIST, we set $m=n=1$, ${\eta }_g=0.00001$, ${\eta }_{d1}=0.001$, and the maximum length of $H$ is set to 50,001. The target model of the attack is ResNet32, and its classification accuracy is 92.4%. In the targeted attack, the classification accuracy of the trained $D_1$ for the test set reaches 54.82%, and the similarity with the target model is 73.26%. The classification accuracy of the surrogate model trained by DaST is only 20.35%, and the accuracy of $D_1$ is 2.69 times higher. To verify the effectiveness of DDSG-GAN, we also compare it with DaST, advGAN, and the black-box attack based on the surrogate model on CIFAR10. The results are shown in

Table 7. Attack results under $l_{\infty }$ norm on CIFAR10.

Target Model/ Accuracy	Attack Type	Method	ASR	ϵ
ResNet-32/ 92.4%	Untargeted attack	Black-box (Surrogate Model [32]+ FGSM)	79.5%	0.4
		Black-box (Surrogate Model [32] + PGD)	20.7%	0.031
		Black-box ($D_1$ as Surrogate Model + FGSM)	84.4%	0.031
		Black-box ($D_1$ as Surrogate Model + PGD)	86.9%	0.031
		DaST [30]	68.0%	0.031
		DDSG-GAN (Proposed)	89.5%	0.031
	Targeted attack	Black-box (Surrogate Model [32]+ FGSM)	7.6%	0.4
		Black-box (Surrogate Model [32]+ PGD)	4.7%	0.031
		Black-box ($D_1$ as Surrogate Model + FGSM)	19.5%	0.031
		Black-box ($D_1$ as Surrogate Model + PGD)	16.9%	0.031
		AdvGAN [12]	78.47%	0.032
		DaST [30]	18.4%	0.031
		DDSG-GAN (Proposed)	79.4%	0.031

.

Under the setting of a targeted attack and untargeted attack, we have realized FGSM and PGD attacks based on the surrogate model. For FGSM, we set $ϵ=0.4$, as it is shown to be effective in [32]. For the other attack methods, we uniformly set the perturbation threshold to $ϵ=0.031$. We also set an upper bound on the number of queries to the target model in the DaST method on CIFAR10. We set the query of each image to 1000. Under this premise, the total query upper bound of the DaST method is $5\times {10}^7$. As can be seen from Table 7, DDSG-GAN has an obvious advantage over the other attack methods. Compared with advGAN, DDSG-GAN’s ARS in targeted attack is improved by 0.93%, and it is much higher than the black box attack based on the surrogate model and DaST. At the same time, the surrogate model we trained also achieved a good fitting effect. In the untargeted attack (targeted attack), if $D_1$ as the surrogate model combined with the FGSM algorithm to attack the target model, the ASR is 4.9% (10.9%) higher than the surrogate trained by [32], and the ASR combined with the PGD algorithm is increased by 10% (8.1%). The attack effect has obviously been improved. In the untargeted attack setting, visualization of AE generated by DDSG-GAN is shown in Figure 4. Figure 4a denotes original samples randomly selected from the training set. Figure 4b denotes AE generated by DDSG-GAN for the corresponding target model.

We perform an untargeted attack on Tiny-ImageNet under $l_2$ norm. Because the Tiny-ImageNet data set is large, only about 1/3 of the training set, that is, 32,000 pictures, are randomly selected for training in each iterative training. We set $m=n=1$, ${\eta }_g=0.001$, ${\eta }_{d1}={\eta }_{d2}=0.0001$, and $ϵ=4.6$. The maximum length of $H$ is set to 32,001. The pre-trained ResNet18 and ResNet50 are used as discriminators $D_1$. The classification accuracy of the trained $D_1$ for the test set is 52.3% and 45.8%, respectively. The results are shown in

Table 8. Attack results under $l_2$ norm on Tiny-ImageNet.

Attack Type	ϵ	${\mathit{D}}_1$	ASR
Untargeted attack	4.6	ResNet18	72.15%
		ResNet50	83.76%

. As can be seen from Table 8, the more complex the surrogate model, the better the attack effect. Therefore, in order to improve the attack effect, the complexity of the surrogate model can be appropriately increased.

4.4. Model Analysis

As can be seen from the above experimental results, compared with the black-box attack based on the surrogate model (under $l_{\infty }$ norm), DDSG-GAN has great advantages and a significantly higher attack success rate. In a black-box attack experiment based on the surrogate model, the surrogate model trained in this paper has a higher success rate of attack. In the $l_2$ norm attack, we can find that the query requirement of the target model is greatly reduced, and the success rate is kept at a high level. In addition, the attack effect of the model depends largely on the network architecture of the generator and the discriminator. When we use a fully connected neural network as the generator to perform algorithm 3, the ASR of the untargeted attack is only 80%. Therefore, designing a better network architecture helps improve the attack ability of the model.

5. Conclusions

Based on the structure of GAN, we design the architecture of generating AE with dual discriminators and a single generator and use the generator to generate the adversarial perturbation. Two discriminators constrain the generated perturbation, respectively. While ensuring the attack success rate and low image distortion, it also ensures a low query level. While training the generator, the discriminator $D_1$ gradually fits the target model, and, finally, it is trained as a surrogate model that can highly simulate the target model. In this way, $D_1$ combined with the white-box attack algorithm can carry out a black-box attack based on a surrogate model, and this attack method reaches a higher attack level, which shows that the surrogate model we trained has a good effect. When training the discriminator $D_1$, we added the structure of a circular queue to save the query results, which made efficient use of the query results and greatly reduced the query requirements. In future work, we will consider adding perturbation in key areas to ensure the attack effect and reduce unnecessary image distortion. At the same time, it is considered to select a broader data set, such as ImageNet, to improve the universality of the method.