Logarithm-Based Methods for Interpolating Quaternion Time Series

Abstract

In this paper, we discuss a modified quaternion interpolation method based on interpolations performed on the logarithmic form. This builds on prior work that demonstrated this approach maintains $C^2$ continuity for $\mathit{prescriptive}$ rotation. However, we develop and extend this method to $\mathit{descriptive}$ interpolation, i.e., interpolating an arbitrary quaternion time series. To accomplish this, we provide a robust method of taking the logarithm of a quaternion time series such that the variables $\theta$ and $\widehat{n}$ have a consistent and continuous axis-angle representation. We then demonstrate how logarithmic quaternion interpolation out-performs Renormalized Quaternion Bezier interpolation by orders of magnitude.

1. Introduction

Whether you are interested in modeling human kinetics [1], creating control strategies for satellites [2], or designing the next hit augmented reality app for smart phones [3], you need the most accurate understanding of the rotational measurements that inertial sensors will provide you. Simulating these complex engineering systems require sequential child/parent frame-of-reference transformations to keep track of position and rotations. A specific application of this is simulating airborne Light Detection and Ranging (LIDAR) sensors. A LIDAR sensor is comprised of a coordinated optical system of a pulsed laser and a fast framing detector that use time-of-flight measurements to estimate the range of an object near the ground (see Figure 1a). Utilizing this range along with the physical position and orientation of the aircraft, that point can then be geolocated. Over numerous optical scans to build up the signal, a 3D point cloud can be developed that estimates the physical dimensions of an entire ground scene spanning large distances.

To produce ground scene with high spatial resolution, significant care must be taken to track the angular and linear position, velocity, and accelerations of all of the components of the sensor, as well as systematic errors associated. As is detailed in Figure 1b, the Kinematically Linked Model Framework (KLMF) utilizes an incredibly complex sensor model to track all of these components to demonstrate the full propagation of all possible sources of error in the LIDAR sensor system [4]. Each component in the model framework is given its own coordinate system to track its position an orientation, which is allowed to vary in time. This system operates over huge orders of timing magnitude—a Geiger-mode LIDAR camera operates in the 10 s of kilohertz range [5] while GPS measurements occur only a few times per second [6]. Rotational velocity and linear acceleration are measured by an Inertial Measurement Unit (IMU), which generally outputs data in the 100–300 Hz range [7].

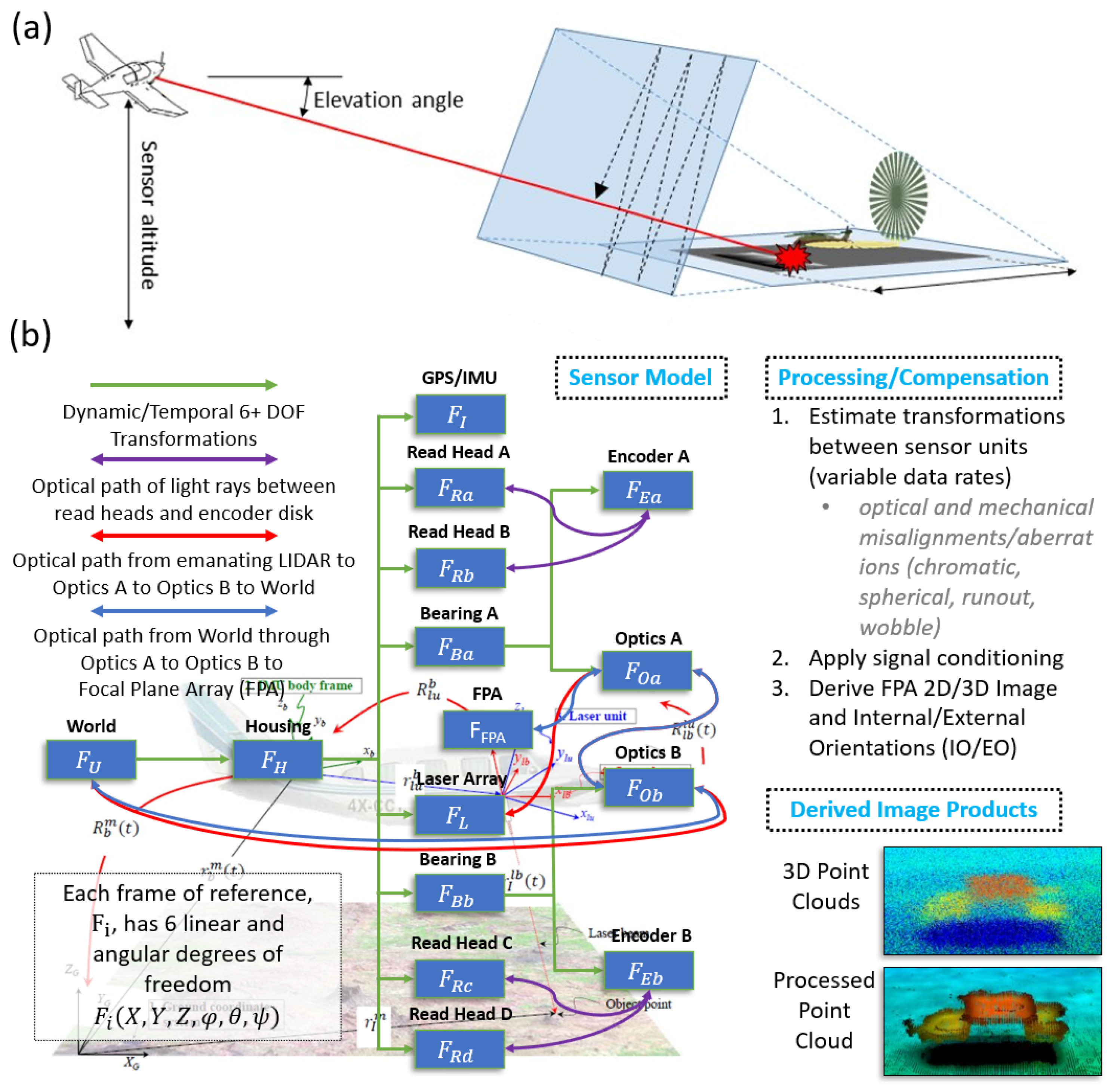
1.1. Relating Rotations across Parent/Child Pairs

A child’s orientation can be specified relative to its parent reference frame intuitively with Euler angles via composite rotations, $R\left(\{\varphi ,\theta ,\psi \}\right)$. If we chose a 313 convention, meaning a rotation around the z axis, the x axis, then the transformed $z^{\prime }$ axis, then the matrix is written as

$$\begin{array}{cc}\hfill {\overrightarrow{x}}^{\prime }& =R\left(\{\varphi ,\theta ,\psi \}\right){\overrightarrow{x}}_0\hfill \\ \hfill & =R_z\left(\varphi \right)R_x\left(\theta \right)R_z\left(\psi \right){\overrightarrow{x}}_0\hfill \end{array}$$

(1)

This means that the angular velocity of the child is a function of six variables—the three angles and their first derivatives. Further, the angular acceleration is a function of nine variables, all for just the behavior one child/parent relationship. So even simple systems of interconnected elements that each can rotate relative to each other can quickly become cumbersome to the point of intractable. Euler angles also can have inherent degeneracies due to a choice of angles that cause two of the rotation axes to become parallel (referred to as “Gimbal Lock” [8]).

1.2. A Brief Introduction to Quaternions

A robust alternative, then, is to perform rotations via “quaternions”. Very simply, a quaternion is a extension of complex numbers ( for a thorough introduction to quaternions and rotations, see [9]). If we define the basis elements $(i,j,k)$ to have the properties that $i^2=j^2=k^2=ijk=-1$, and that $i\ne j\ne k$, then a quaternion $\mathbf{q}$ is given by

$$\mathbf{q}=q_0+q_1\mathit{i}+q_2\mathit{j}+q_3\mathit{k}$$

(2)

where $q_i$ are real numbers. In this work, we will denote quaternions $\mathbf{q}$ in bold to distinguish them from vectors. A common way of writing a quaternion is as a composite of a “scaler” portion and “vector” portion. For a real scaler u and a real vector v, we can write $\mathbf{q}=[u,\overrightarrow{v}]$ where $u=q_0$ and $\overrightarrow{v}=\langle q_1,q_2,q_3\rangle$. This identifies u as the “scalar portion” of the quaternion, where $\overrightarrow{v}$ is the “vector portion”. If we have two arbitrary quaternions $\mathbf{q}=[u,\overrightarrow{v}]$ and $\mathbf{p}=[k,\overrightarrow{s}]$, the product of $\mathbf{q}$ and $\mathbf{p}$ is given by

$$\mathbf{q}\circ \mathbf{p}=[uk-\overrightarrow{v}·\overrightarrow{s},u\overrightarrow{s}+k\overrightarrow{v}+\overrightarrow{v}\times \overrightarrow{s}]$$

(3)

where ∘ is used to denote quaternion multiplication. In general, quaternion products do not commute. Taking the conjugate of a quaternion $\mathbf{q}$ involves merely negating the vector component, i.e., ${\mathbf{q}}^{*}=[u,-\overrightarrow{v}]$. The magnitude of a quaternion is given by the root sum square of the components, $\parallel \mathbf{q}\parallel =\mathbf{q}\circ {\mathbf{q}}^{*}=\sqrt{q_0^2+q_1^2+q_2^2+q_3^2}$. If $\parallel \mathbf{q}\parallel =1$, the $\mathbf{q}$ is a unit vector. For a choice of $\theta$ and $\widehat{n}$, any unit quaternion can be written as

$$\begin{array}{c}\mathbf{q}=\left[cos(\theta /2),sin(\theta /2)\widehat{n}\right]\end{array}$$

(4)

A candidate $(\theta ,\widehat{n})$ pair can be calculated as

$$\begin{array}{c}\theta =2arctan\left(\frac{\parallel \overrightarrow{v}\parallel }{u}\right)=2arctan\left(\frac{\sqrt{q_1^2+q_2^2+q_3^2}}{q_0}\right)\end{array}$$

(5)

$$\begin{array}{c}\widehat{n}=\frac{\langle q_1,q_2,q_3\rangle }{\sqrt{q_1^2+q_2^2+q_3^2}}\end{array}$$

(6)

We say “candidate” $(\theta ,\widehat{n})$ as it is not hard to prove that $\mathbf{q}(\theta ,\widehat{n})=\mathbf{q}(-\theta ,-\widehat{n})$. To perform a rotation, you first write a vector $\overrightarrow{x}$ as quaternion $\mathbf{x}=\left[0,\overrightarrow{x}\right]$ and then perform the rotation as

$${\mathbf{x}}^{\prime }=\mathbf{q}\circ \mathbf{x}\circ {\mathbf{q}}^{*}$$

(7)

More complex rotations are accomplished via sequential simple rotations, with a composited quaternion representing the sum total of all applied rotations. There is no need to keep track of the angles of each different rotation, merely the composite. This means that calculating the orientation of any given element in a large interconnected system is a matter of interpolation of the product of quaternion multiplication. For a rotating object, the angular velocity and angular acceleration are given by the relations

$$\begin{array}{c}\mathit{\omega }=\left[0,\overrightarrow{\omega }\right]=2\dot{\mathbf{q}}\circ {\mathbf{q}}^{*}\end{array}$$

(8)

$$\begin{array}{c}\mathit{\alpha }=\left[0,\overrightarrow{\alpha }\right]=2\ddot{\mathbf{q}}\circ {\mathbf{q}}^{*}\end{array}$$

(9)

Finally, if one looks at Equation (4), there is a resemblance to the Euler equation $expi\theta =cos\left(\theta \right)+isin\left(\theta \right)$. Inspired by this, the logarithm of a quaternion is defined as

$$log\left(\mathbf{q}(\theta ,\widehat{n})\right)=[0,\theta \widehat{n}]$$

(10)

Thus taking the logarithm of a quaternion is mathematically similar to moving into an axis-angle representation.

1.3. Slerp and Squad

In almost all cases either by design or necessity, we deal with discrete time series of quaternions $\left\{{\mathbf{q}}_i\right\}$. For simulating LIDAR, this comes from integrating the angular velocity as sampled by the IMU. This means we must first interpolate the quaternion functions and then perform differentiation. The simplest form of quaternion interpolation is Spherical Linear Interpolation (SLERP) [10], which involves a spherical blending between two elements of a time series (often referred to as “key frames”). For a time $t_i<t<t_{i+1}$, the interpolation is given by

$$\begin{array}{c}SLERP({\mathbf{q}}_i,{\mathbf{q}}_{i+1},h)=\frac{{\mathbf{q}}_{i}sin\left(\Omega (1-h)\right)+{\mathbf{q}}_{i+1}sin\left(\Omega h\right)}{sin\left(\Omega \right)}\end{array}$$

(11)

$$\begin{array}{c}h=\frac{t-t_i}{t_{i+1}-t_i}\end{array}$$

(12)

$$\begin{array}{c}\Omega =Angle\left({\mathbf{q}}_i\circ {\mathbf{q}}_{i+1}^{*}\right)\end{array}$$

(13)

where $Angle(·)$ is the minimum angle of the quaternion argument. This formulation ensures $C^0$ continuity, but will have discontinuities in the derivatives. Similar in kind, if the quaternions are evenly spaced, there is a Spherical and Quadrangle Interpolation (SQUAD) [11] that is formulated by

$$\begin{array}{c}SQUAD({\mathbf{q}}_i,{\mathbf{q}}_{i+1},{\mathbf{S}}_i,{\mathbf{S}}_{\mathbf{i}+\mathbf{1}},h)=SLERP\left(SLERP\left({\mathbf{q}}_i,{\mathbf{q}}_{i+1},h\right),SLERP\left({\mathbf{S}}_i,{\mathbf{S}}_{i+1},2h(1-h)\right)\right)\end{array}$$

(14)

$$\begin{array}{c}{\mathbf{S}}_{\mathbf{i}}={\mathbf{q}}_{i}exp\left(-\frac{ln\left({\mathbf{q}}_{\mathbf{i}}^{*}\circ {\mathbf{q}}_{i-1}\right)+ln\left({\mathbf{q}}_i^{*}\circ {\mathbf{q}}_{i+1}\right)}{4}\right)\end{array}$$

(15)

1.4. Renormalized Quaternion Bezier (Rqbez) Interpolation

An easy shortcut to $C^2$ continuity is to ignore the mathematics of quaternions and treat the quaternion series as a 4-vector of independent variables $\left\{{\overrightarrow{q}}_i\right\}$, whose elements are then interpolated independently. Afterwards, the interpolated elements are renormalized to ensure that $\parallel q\parallel =1$. This method then is as continuous as the interpolation method implemented, most commonly cubic Bezier—thus the name, Renormalized Quaternion Bezier or RQBez [12]. Though this method does have continuous 1st and 2nd derivatives, the quaternion-as-vector assignment means that the derivatives are not physically related to the rotation. So, if used to calculate quantities such as angular moment or angular acceleration, the algorithm introduces phantom forces and torques [9].

1.5. Logarithmic Quaternion Interpolation (Lqi)

As previously discussed, we can write any quaternion as $\mathbf{q}(\theta ,\widehat{n})=exp\left(\theta \widehat{n}\right)$. In work aimed at better robotic steering, Pu et al. [13] utilized this notation to write $log\left(\mathbf{q}\right)=\left[0,\overrightarrow{r}\right]$ where $\overrightarrow{r}=\left|\theta \right|\widehat{n}\in {\mathbf{R}}^3$ and performed standard Euclidean interpolation on the vector $\overrightarrow{r}=\langle x,y,z\rangle$. This cast the problem as interpolating a 3D trajectory in Euclidean space where the components $\langle x,y,z\rangle$ are orthogonal and therefore independent. This allowed for 1D methods of interpolation of arbitrarily high continuity while avoiding the complications of spherical interpolation. Once the variables were interpolated, the resulting quaternion was calculated via the equations

$$\begin{array}{cc}\hfill q_0& =cos\left(\frac{\sqrt{x^2+y^2+z^2}}{2}\right)\hfill \\ \hfill q_1& =sin\left(\frac{\sqrt{x^2+y^2+z^2}}{2}\right)\frac{x}{\sqrt{x^2+y^2+z^2}}\hfill \\ \hfill q_2& =sin\left(\frac{\sqrt{x^2+y^2+z^2}}{2}\right)\frac{y}{\sqrt{x^2+y^2+z^2}}\hfill \\ \hfill q_3& =sin\left(\frac{\sqrt{x^2+y^2+z^2}}{2}\right)\frac{z}{\sqrt{x^2+y^2+z^2}}\hfill \end{array}$$

(16)

Using this approach, which we here refer to as Logarithmic Quaternion Interpolation method (LQI), they demonstrated their method was able to achieve the long-sought-after $C^2$ continuity for quaternions for prescribed rotational motion of a robotic arm.

1.6. The Ambiguity of the Quaternion Logarithm

Quaternions have an inherent ambiguity akin to axis-angle representations, i.e., a rotation of $\theta$ around $\widehat{n}$ is equivalent to a rotation around $-\theta$ around $-\widehat{n}$. There is also, of course, ambiguity with $\theta$, as $cos\left(\theta \right)=cos(\theta +2m\pi )$ where m is any integer ($m\in \mathit{Z}$). As Pu et al.’s application was $\mathit{prescriptive}$, they were defining a rotational path for a robotic arm to take, they had a priori knowledge about the variables $\theta$ and $\widehat{n}$ that were used to prescribe the path. Thus, the variables can be pre-prepared to avoid discontinuities around $\theta =0$. We are interested in descriptive interpolation where we are merely given the set of quaternions to calculate $(\theta ,\widehat{n})$ in a consistent way for interpolation. We achieve this by the following process Algorithm 1.   

Algorithm 1: Recovering a $C^2$ axis-angle series for logarithmic interpolation

Obviously, care must be taken for when ${\mathbf{q}}_i$ or ${\mathbf{q}}_{i-1}$ is the unit quaternion $\mathbf{1}=[1,\langle 0,0,0\rangle ]$ as the unit vector is indeterminate. As our spline choice does not require equal spacing between key frames, our process was to remove them from the interpolation process. Another solution would be to replace the ${\theta }_i$ with the nearest odd multiple of $\pi$ and assign ${\widehat{n}}_i$ as the average of the previous and next unit vector, appropriately normalized, to be utilized in the interpolation.

1.7. Modified Logarithmic Quaternion Interpolation (Mlqi)

In Pu et al.’s approach, $\mathbf{q}\left(t\right)=exp\left(\right|\theta |\widehat{n})=exp\left(\overrightarrow{r}\right)$ means that in logarithmic space, the quaternions is a trajectory on a growing and shrinking sphere. The angle $\theta$ is always positive, as it is the norm of the vector $\overrightarrow{r}$. When $\theta$ and $\widehat{n}$ are known variables and we are interested in $\mathit{prescribing}$, this does not introduce problems. However, if we are calculating $\theta$ and $\widehat{n}$ via taking the logarithm of a quaternion time series, numerical errors compound near $\theta =0$ (or even multiples of $\pi$). We explored a modified Logarithmic Quaternion Interpolation method (mLQI) of this method by writing the equations for $\widehat{n}\left(t\right)$ and $\theta \left(t\right)$ as defined in the quaternion

$$\begin{array}{c}{q}_0=cos\left(\frac{\theta }{2}\right),q_1=sin\left(\frac{\theta }{2}\right)X,q_2=sin\left(\frac{\theta }{2}\right)Y,q_3=sin\left(\frac{\theta }{2}\right)Z\end{array}$$

(17)

$$\begin{array}{c}{X}^2+Y^2+Z^2=1\end{array}$$

(18)

We then perform interpolation on $\left(\theta ,X,Y,Z\right)$, the angle and the axis components. This approach decouples the changing size of $\theta$ and the unit vector components. Obviously, this introduces an additional complexity as the variables $\langle X,Y,Z\rangle$ are elements of a unit vector and are thus coupled. We explored the performance effects of treating them as an unnormalized unit vector as well as renormalizing the results after interpolating (akin to RQBez).

2. Results and Discussion

We picked several examples of continuous quaternion trajectories to interpolate. Examples and algorithms were scripted in MATLAB to take advantage of vectorization. For all interpolations, we utilized MATLAB’s built-in “interp1” function [14] to calculate the functions and their derivatives, using the “spline” option for C-2 continuity. (For access to source code, please contact the corresponding author). We evaluated the error in the angle $\theta$, the angular momentum $\overrightarrow{\omega }$, and angular acceleration $\overrightarrow{\alpha }$ for a broad choice of key time spaces, $\Delta T$. (For the functional forms of the quaternion derivatives in each method, see Appendix A). The quaternion trajectories we used to evaluate different interpolation methods use the following generic model equation

$$\begin{array}{c}\mathbf{q}\left(t\right)=\left[sin\left(\frac{\theta }{2}\right),cos\left(\frac{\theta }{2}\right)\widehat{n}\right]\end{array}$$

(19)

$$\begin{array}{c}\widehat{n}=cos\left(\varphi \left(t\right)\right)sin\left(\psi \left(t\right)\right)\widehat{x}+sin\left(\varphi \left(t\right)\right)sin\left(\psi \left(t\right)\right)\widehat{y}+cos\left(\psi \left(t\right)\right)\widehat{z}\end{array}$$

(20)

The construction of the unit vector $\widehat{n}$ is the standard spherical coordinates, where $\varphi \in (-\infty ,\infty )$ and $\psi \in \left[0,\pi \right]$.

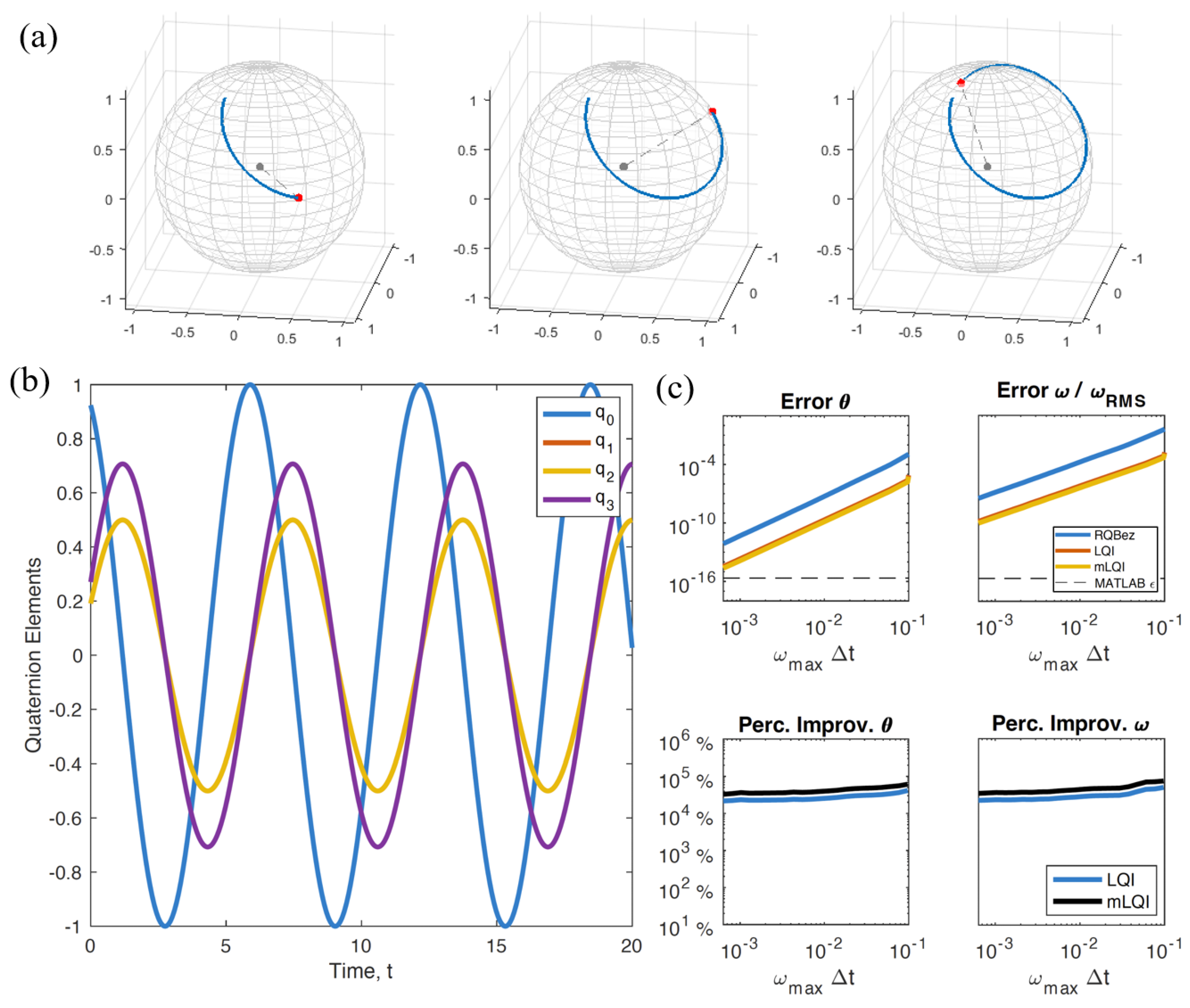
2.1. Example 1: Simple Rotation in the Angle

Our first example is the simplest rotation possible, where the unit vector is constant ($\varphi =const.$, $\psi =const.$) and the rotation angle $\theta$ linearly increases, i.e., ${\omega }_{\theta }=const.$ We applied this quaternion trajectory to the $\widehat{z}$ unit vector and plotted it in Figure 2a. As can be seen, the line sweeps out a standard circle around $\widehat{n}=\left[111\right]/\sqrt{3}$. As $\theta$ varies constantly, the components $q_i$ are sinusoidal (see Figure 2b). Looking at the error performance in Figure 2c, we can see that both LQI and mLQI outperform RQBez by a factor of 100. In the lower figures, we can see the percent improvement over RQBez is comparable between LQI and mLQI.

2.2. Example 2: Simple Mixed Rotation

We now consider a case where both the angle and unit vector are rotating. This can be thought of using the simple rotational system Example 1 as the unit vector for a quaternion, which will then rotate about at a constant rate. The trajectory is visualized in Figure 3a. This is a moderately more complex quaternion trajectory (Figure 3b), where the composited sinusoidal variations lead to constructive and destructive interference patterns in the individual components. Looking at the error performance in Figure 2c, we have separations of multiple orders of magnitude between RQBez, LQI, and mLQI, with mLQI performing a factor of 100 better than LQI.

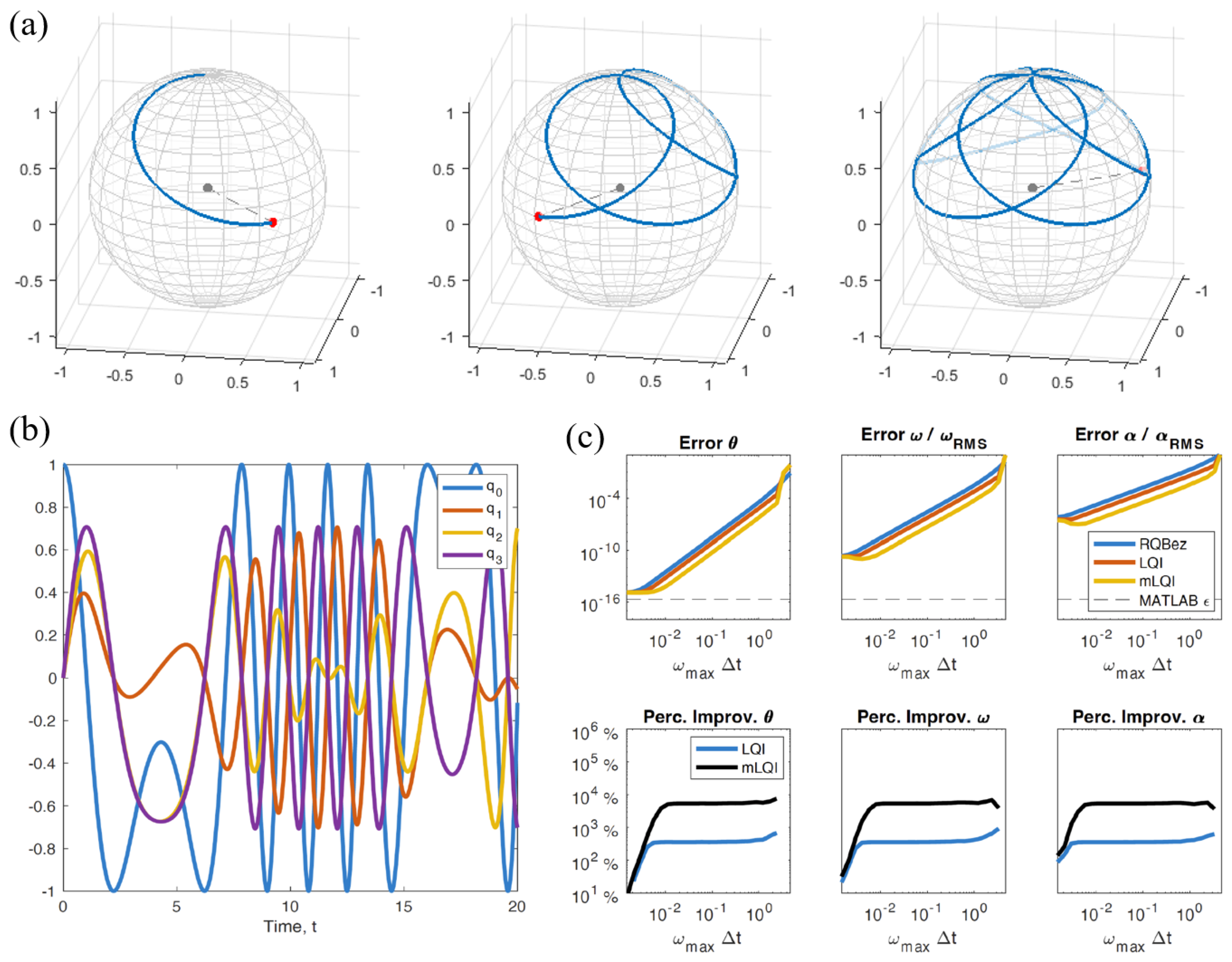
2.3. Example 3: Complex Mixed Rotation

Now we consider the system in Example 2, but where the angle has an oscillatory motion, i.e., $\theta ={\omega }_{0}sin\left({\omega }_{0}t\right)$. This is not unlike a scanning mirror system in a LIDAR, albeit somewhat exaggerated. The trajectory in Figure 2a is visibly much more complex, and the quaternion components vary wildly Figure 4. These fast fluctuations are a particular difficulty for interpolating. As can be seen in Figure 4c, similar to Example 2, we had separations of multiple orders of magnitude between RQBez, LQI, and mLQI, with our modified method performing the best overall.

2.4. Execution Time Comparison

Finally, we also investigated the execution times for all the algorithms over a broad range of key frame spacings. Using the quaternion system from Example 3, we compared time of execution for RQBez, LQI, and two version of mLQI—one where the unit vector was interpolated unnormalized and one where it was renormalized after interpolation. The results are seen in Figure 5. As can be seen, the timing performance seems to follow the same power law relationship for each method ($y\sim x^{-1}$ is shown for reference). The largest difference between methods is the function evaluation of the equations involved, particularly the derivatives. As we show in Appendix A, the equations for the quaternions and their derivatives of RQBez and LQI are complex, owing to the normalization factor. Additionally, when the interpolation in mLQI is constrained to be normalized, the method is slower than the same method unnormalized. This is reflective of the simpler equations of an unnormalized mLQI algorithm is compared to RQBez and LQI saving number-of-operation times.

3. Discussion and Conclusions

In this work, we found that interpolating quaternion time series in the logarithmic space is numerically robust across several orders of magnitude of key frame spacing. With our contribution of a time-series-aware method of taking the logarithm, we find that the original LQI method performs up to two orders of magnitude x better than the method of RQBez. Because of our concerns with errors near $\theta =0$, we also demonstrated a method mLQI for interpolating the full set of quaternion variables and found it to behave even better, outperforming RQBez by an additional two orders of magnitude. Additionally, the simpler formulation of equations of mLQI resulted in smaller execution times than either RQBez or LQI. Further refinements can be made on magnitude-preserving interpolation of the unit vector via projection methods. Additionally, we want to investigate these methods when tasked with interpolating noisy rotational time-series.