Low-Rank Matrix Completion via QR-Based Retraction on Manifolds

Abstract

Low-rank matrix completion aims to recover an unknown matrix from a subset of observed entries. In this paper, we solve the problem via optimization of the matrix manifold. Specially, we apply QR factorization to retraction during optimization. We devise two fast algorithms based on steepest gradient descent and conjugate gradient descent, and demonstrate their superiority over the promising baseline with the ratio of at least $24\%$.

1. Introduction

The problem of matrix completion (MC) has generated a great deal of interest over the last decade [1], and several variant problems have been considered, such as non-negative matrix completion (NMC) [2], structured matrix completion [3,4] (including Hankel matrices [5]), and low-rank matrix completion (LRMC) [6,7]. Because of its wide applications in sensor network localization [8], system identification [9], machine learning [10,11], computer vision [12], recommendation systems [13], etc., LRMC has drawn a great deal of attention. Let $M\in {\mathbb{R}}^{n\times n}$ be an observed matrix and $\mathrm{\Omega }\subset \left\{\right(i,j),i,j=1,\dots ,n\}$ be an index set of the observed position. Then, the desired low-rank matrix X can be recovered by solving the following rank minimization problem [14,15]:

$$\underset{X\in {\mathbb{R}}^{n\times n}}{min}\mathrm{rank}\left(X\right)\mathrm{s}.\mathrm{t}.P_{\mathrm{\Omega }}\left(X\right)=P_{\mathrm{\Omega }}\left(M\right),$$

(1)

where ${\left[P_{\mathrm{\Omega }}\left(X\right)\right]}_{ij}=X_{ij}$, $(i,j)\in \mathrm{\Omega }$ and 0, otherwise. Unfortunately, the calculation of the rank function is (non-deterministic polynomial) NP-hard, and thus all known algorithms need double exponential time on the dimension of n.

To overcome this limitation, many approaches have been proposed [13]. For instance, Candès and Recht [16] replaced the rank function with the nuclear norm, and (1) can be rewritten as

$$\underset{X}{min}{\parallel X\parallel }_{*}\mathrm{s}.\mathrm{t}.P_{\mathrm{\Omega }}\left(X\right)=P_{\mathrm{\Omega }}\left(M\right),$$

(2)

where ${\parallel X\parallel }_{*}={\sum }_i{\sigma }_i\left(X\right)$ and ${\sigma }_i\left(X\right)$ represents the i-th largest non-zero singular value. They proved that if the number of observed entries $m=\left|\mathrm{\Omega }\right|$ obeys $m\ge c{n}^{1.2}rlog\left(n\right)$ with c being some positive constant and r being the rank of X, then most matrices of rank r can be perfectly recovered with very high probability by solving a simple convex optimization program. However, when the size of the matrix is large, the computation is still burdensome. To mitigate the computational burden, Cai et al. [17] introduced the singular value thresholding algorithm. The key idea of this approach is to place the regularization term into the objective function of the nuclear norm minimization problem. On the other hand, given the rank of a matrix, Lee and Bresler [18] replaced the rank function with the Frobenius norm, and (1) can be rewritten as

$$\underset{X}{min}\frac{1}{2}{\parallel P_{\mathrm{\Omega }}\left(M\right)-P_{\mathrm{\Omega }}\left(X\right)\parallel }_F^2\mathrm{s}.\mathrm{t}.\mathrm{rank}\left(X\right)\le r.$$

(3)

According to matrix theory, the matrix $M\in {\mathbb{R}}^{n_1\times n_2}$ of rank r can be decomposed into two matrices $X\in {\mathbb{R}}^{n_1\times r}$ and $Y\in {\mathbb{R}}^{n_2\times r}$ such that $M=X{Y}^T$. A straightforward method is to determine X and Y by minimizing the residual between the original M and the recovered one (that is, $X{Y}^T$) on the sampling set [19,20]:

$$\underset{X,Y}{min}\frac{1}{2}{\parallel P_{\mathrm{\Omega }}\left(M\right)-P_{\mathrm{\Omega }}\left(X{Y}^T\right)\parallel }_F^2.$$

(4)

To solve this multiple objective optimization program, one can employ the alternating minimization technique: (i) set X first and determine Y via minimizing the residual and; (ii) fix Y and determine X in the same way.

To accelerate the completing process, a novel utilization of the rank information is definition of an inner product and a differentiable structure, which formulates a manifold-based optimization program [21,22]. Then, one can compute the Riemannian gradient and Hessian matrix to solve the following problem [14,23]:

$$\underset{X\in {\mathcal{M}}_r}{min}\parallel P_{\mathrm{\Omega }}(X-M)\parallel ,$$

(5)

where ${\mathcal{M}}_r:=\{X\in {\mathbb{R}}^{n_1\times n_2},\mathrm{rank}\left(X\right)=r\}$. Specially, Mishra et al. [24] discussed singular value decomposition, rank factorization, and QR factorization on manifolds. Following this line, Cambier and Absil [25] simultaneously considered singular value decomposition and regularization:

$$\underset{X\in {\mathcal{M}}_r}{min}\parallel P_{\mathrm{\Omega }}{(X-M)\parallel }_{l_1}+\lambda {\parallel P_{\mathrm{\Omega }}\left(X\right)\parallel }_F^2,$$

(6)

where ${\parallel X\parallel }_{l_1}={\Sigma }_{i,j}\left|X_{i,j}\right|$ and $\lambda$ is a regularization parameter. Yet, the improvement of the accuracy is not remarkable. More recently, Dong et al. [26] devised a preconditioned gradient descent algorithm for the rank factorization problem:

$$\underset{(G,H)\in {\mathbb{R}}^{m\times k}\times {\mathbb{R}}^{n\times k}}{min}\frac{1}{2}{\parallel P_{\mathrm{\Omega }}(G{H}^T-M)\parallel }_F^2,$$

(7)

which is a multiple objective problem on the product space that can be defined as a manifold. Although it shows good performance in comparison to single-objective problems, the algorithm hardly considers the structure on a per matrix basis.

In this paper, we consider QR factorization on manifolds. Different from single-objective optimization on the manifold [24,27,28], we study LRMC using multiple objective optimization in the product space ${\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}$. During iteration, we first obtain the gradient of the objective function in the tangent space and then retract it with QR factorization. Specially, we introduce a measure to characterize the degree of orthogonality of Q for retraction, based on which we design two fast algorithms and show their advantage in comparison to rank factorization [26].

The paper is organized as follows. In Section 2, we introduce some preliminaries, including basic notations, problem formulation, and the element of manifolds. In Section 3, we show algorithms based on the choice of initial point, descent direction, step size, and retraction. In Section 4, we prove convergence and analyze the reason why the proposed algorithms outperform those in [26]. In Section 5, we demonstrate the superior performance of the proposed algorithms using numerical experiments. Finally, in Section 6 we provide a conclusion.

2. Preliminary

Notation. The Euclidean inner product and norm for the product space ${\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}$, respectively, denoted with $〈·,·〉$ and $\parallel ·\parallel$, are defined by

$$〈x,y〉=Tr\left(Q_x^T{Q}_y\right)+Tr\left(R_x{R}_y^T\right)\mathrm{and}\parallel x\parallel =\sqrt{〈x,x〉},$$

(8)

for any pair of points $x=(Q_x,R_x),y=(Q_y,R_y)\in {\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}$.

Problem statement. The purpose of this paper is to solve the problem (5). With QR factorization, it becomes:

$$\underset{(Q,R)\in {\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}}{min}{f}_{\mathrm{\Omega }}(Q,R):=\frac{1}{2}{\parallel P_{\mathrm{\Omega }}(QR-M)\parallel }_F^2.$$

(9)

QR factorization. QR factorization [29] can be carried out by using Householder transformation, Givens rotations, Gram–Schmidt process, and their variants. In this paper, we choose the modified Gram–Schmidt algorithm for a more reliable procedure. (see Algorithm 7 for details.)

Geometric element on ${\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}$. The tangent space (see Figure 1) at a point $x\in {\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}$ is the finite Cartesian product of the tangent spaces of the two element matrix spaces. Then, $T_x({\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2})\simeq {\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}$ (see Section 3.5.2, [21]) where $X\simeq Y$ indicates that there is a homeomorphism between the topological space X and Y.

Comparing the performance of several metrics, we consider the following. Given two tangent vectors $\xi ,\eta \in T_x({\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2})$ (see Section 4, [26]) at point $x=(Q,R)\in {\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}$, the preconditioned metric is

$$M_x(\xi ,\eta )=Tr({\xi }_Q^T{\eta }_Q(R{R}^T+\delta I_r))+Tr\left({\xi }_R{\eta }_R^T(1+\delta )\right),$$

(10)

where $\xi =({\xi }_Q,{\xi }_R)$, $\eta =({\eta }_Q,{\eta }_R)$, $\delta >0$ is a constant, which keeps the metric well defined and positive definite if Q or R does not have full rank. Furthermore, if $\xi =\eta$, one can write ${\parallel \xi \parallel }_x^2=M_x(\xi ,\xi )$ as a kind of norm at point x.

Definition 1.

For a point $x\in {\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}$, the gradient of $f_{\mathrm{\Omega }}$ is the unique vector in $T_x({\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2})$, denoted with $\nabla f_{\mathrm{\Omega }}\left(x\right)$, such that

$$M_x(\xi ,\nabla f_{\mathrm{\Omega }}\left(x\right))=D{f}_{\mathrm{\Omega }}\left(x\right)\left[\xi \right],\forall \xi \in T_x({\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}),$$

(11)

where $D{f}_{\mathrm{\Omega }}\left(x\right)\left[\xi \right]=Tr\left({\xi }_Q^T{P}_{\mathrm{\Omega }}(QR-M)R^T\right))+Tr\left({\xi }_R{P}_{\mathrm{\Omega }}^T(QR-M)Q\right)$ is directional derivative defined [21] by

$$D{f}_{\mathrm{\Omega }}\left(x\right)\left[\xi \right]=\underset{t\to 0}{lim}\frac{f_{\mathrm{\Omega }}(x+t\xi )-f_{\mathrm{\Omega }}\left(x\right)}{t}.$$

Combing Equations (8) and (11), it follows that

$$\nabla f_{\mathrm{\Omega }}(Q,R)=({\partial }_Q{f}_{\mathrm{\Omega }}(Q,R){(R{R}^T+\delta I_r)}^{-1},{\partial }_R{f}_{\mathrm{\Omega }}(Q,R){(1+\delta )}^{-1}),$$

(12)

where ${\partial }_Q{f}_{\mathrm{\Omega }}(Q,R)=P_{\mathrm{\Omega }}(QR-M)R^T$ and ${\partial }_R{f}_{\mathrm{\Omega }}(Q,R)=Q^T{P}_{\mathrm{\Omega }}(QR-M)$.

3. Algorithms

Initial point $x^0$. Following the widely used spectral initialization [30], we apply $k-$SVD to a zero-filled matrix $M_0:=P_{\mathrm{\Omega }}\left(M\right)$ and yield three matrices $U_0,{\Sigma }_0$, and $V_0$ such that $M_0=U_0{\Sigma }_0{V}_0^T$. Then, the initial point $x^0:=(Q^0,R^0)$ is set as (see Algorithm 1 for details)

$$(Q^0,R^0)=(U_0{\Sigma }_0^{1/2},{\Sigma }_0^{1/2}{V}_0^T).$$

(13)

Algorithm 1 Initialization

Input: data M and rank r Output: initialization $x_0$       1: Use singular value decomposition (SVD) to compute $U,\Sigma ,V$ (that satisfies $M=U\Sigma V^T$).       2: Trim matrices $U_0=U(:,1:r),{\Sigma }_0=\Sigma (1:r,1:r),V_0=V(:,1:r)$.       3: Set $x_0=[U_0{\left({\Sigma }_0\right)}^{1/2};V_0{\left({\Sigma }_0^{1/2}\right)}^T]$.

Descent direction ${\eta }^t$. Here, we consider two kinds of directions, the steepest descent (SD) direction (see Algorithm 2) and the conjugate descent (CD) direction (see Algorithm 3 and Figure 1), defined, respectively, by

$$\begin{array}{cc}\hfill {\eta }^t& =-\nabla f\left(x^t\right),\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\eta }^t& =-\nabla f\left(x^t\right)+{\beta }_t{\eta }^{t-1}.\hfill \end{array}$$

(15)

Although there are several calculations of ${\beta }_t$, we adopt ${\beta }_t^{DY}={\parallel {\xi }^t\parallel }_x^2/M_x({\eta }^{t-1},\Delta {\xi }^{t-1})$ from [31] because it outperforms the others.

Algorithm 2 Steepest descent (SD) direction of the function in (9) with orthogonality of Q

Input: Data M, iterate $x_t=[Q;R^T]$, rank r, and metric constant $\delta$. Output: SD direction ${\xi }^t$       1: $S=P_{\mathrm{\Omega }}(QR-M)$.       2: $\nabla f_{\mathrm{\Omega }}\left(x^t\right)=(S{R}^T/(R{R}^T+\delta I_r),S^{T}Q/(1+\delta ))(=\nabla f,\mathrm{for}\mathrm{omitted})$.       3: ${\xi }^t=-\nabla f$

Algorithm 3 Conjugate descent (CD) direction of the function in (9)

Input: Last conjugate direction ${\eta }^{t-1}$(Set ${\eta }^0=0$), conjugate direction ${\beta }_t$. Output: Conjugate direction ${\eta }^t$.       1: Compute $\nabla f$ using Algorithm 2.       2: ${\eta }^t=-\nabla f+{\beta }_t{\eta }^{t-1}$.

Stepsize $s_t$. For the SD direction, we apply exact line search (ELS) [22] (see Algorithm 4). Let $\eta =({\eta }_Q,{\eta }_R)\in T_x({\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2})$ be a given descent direction; then,

$$\begin{array}{cc}\hfill & {argmin}_s{f}_{\mathrm{\Omega }}(Q+s{\eta }_Q,R+s{\eta }_R)\hfill \\ \hfill & ={argmin}_s\frac{1}{2}{\parallel P_{\mathrm{\Omega }}((Q+s{\eta }_Q)(R+s{\eta }_R)-M)\parallel }_F^2\hfill \\ \hfill & ={argmin}_s\frac{1}{2}{\parallel P_{\mathrm{\Omega }}\left({\eta }_Q{\eta }_R\right)s^2+P_{\mathrm{\Omega }}(Q{\eta }_R+{\eta }_{Q}R)s+P_{\mathrm{\Omega }}(QR-M)\parallel }_F^2\hfill \\ \hfill & ={argmin}_s\frac{1}{2}Tr\left[{(A{s}^2+Bs+O)}^T(A{s}^2+Bs+O)\right]\hfill \\ \hfill & ={argmin}_s\frac{1}{2}\left[Tr\left(A^{T}A\right)s^4+2Tr\left(A^{T}B\right)s^3+(2Tr\left(A^{T}O\right)+Tr\left(B^{T}B\right))s^2+2Tr\left(B^{T}O\right)s+Tr\left(O^{T}O\right)\right],\hfill \end{array}$$

where $A=P_{\mathrm{\Omega }}\left({\eta }_Q{\eta }_R\right)$, $B=P_{\mathrm{\Omega }}(Q{\eta }_R+{\eta }_{Q}R)$, and $O=P_{\mathrm{\Omega }}(QR-M)$. The differential of the formula above reads as:

$$2Tr\left(A^{T}A\right)s^3+3Tr\left(A^{T}B\right)s^2+(2Tr\left(A^{T}O\right)+Tr\left(B^{T}B\right))s+Tr\left(B^{T}O\right)=0.$$

(16)

As a cubic equation, one can obtain its roots easily. The step size $s_t$ is exactly the real positive root.

Algorithm 4 Exact line search

Input: Data M, iterate $x=[Q;R^T]$, Conjugate direction $\eta =[{\eta }_Q;{\eta }_R^T]$. Output: Step size s.       1: Set $A=P_{\mathrm{\Omega }}\left({\eta }_Q{\eta }_R\right),B=P_{\mathrm{\Omega }}(Q{\eta }_R+{\eta }_{Q}R)$ and $O=P_{\mathrm{\Omega }}(QR-M)$.       2: Furthermore, solve the cubic equation $2Tr\left(A^{T}A\right)x^3+3Tr\left(A^{T}B\right)x^2+(2Tr\left(A^{T}O\right)+Tr\left(B^{T}B\right))x+Tr\left(B^{T}O\right)=0$.       3: Let the smallest absolute value s of their solutions be the step size.

For the CD direction, we apply the inexact line search (IELS) [32] (see Algorithm 5). For this purpose, we set $s_0=-M_x({\xi }^t,{\eta }^t)/(L\parallel {\eta }^t{\parallel }_x^2)$, where $L>0$ is constant, and $\sigma \in (0,0.5]$. Then, the step size $s_t$ at the $t-$th iteration is the largest one in the set $\{s_0,0.5s_0,0.5^2{s}_0,\cdots \}$, and therefore

$$f\left(x^t\right)-f(x^t+s_t{\eta }^t)\ge -\sigma s_t{M}_x({\xi }^t,{\eta }^t).$$

(17)

Algorithm 5 Inexact line search

Input: Data M, iterate x, constant $L>0$, times limitation $im$, parameter $\sigma \in (0,0.5]$, SD direction $\xi$, and CD direction $\eta$. Output: Stepsize s.       1: Set $s_0=-M_x(\xi ,\eta )/{(L\parallel \eta \parallel }_x^2)$.       2: $k\leftarrow 0$       3: while$f_{\mathrm{\Omega }}\left(x\right)-f_{\mathrm{\Omega }}(x+s\eta )+\sigma s{M}_x(\xi ,\eta )<0\&\&k<im$do       4:    $s\leftarrow 0.5s$       5:    $k\leftarrow k+1$       6: end while

Retraction. With the descent direction $\eta =({\eta }_Q,{\eta }_R)$ and stepsize s, one can apply retraction (see Figure 1 and Algorithm 6). For this purpose, we introduce the concept of the degree of orthogonality.

Definition 2.

For a matrix $Q\in {\mathbb{R}}^{n_1\times r}$, we definite its degree of orthogonality as:

$$\mathrm{Orth}\left(Q\right)=\left|\frac{Tr\left(Q^{T}Q\right)-r}{r}\right|.$$

(18)

Algorithm 6 Retraction with QR factorization

Input: Iteration $x=[Q;R^T]$, direction $\eta =[{\eta }_Q;{\eta }_R^T]$, stepsize $s_t$ and parameter $\theta$. Output: Next iterate $x^{t+1}=(Q^{t+1},R^{t+1})$.       1: if$\mathrm{Orth}(Q^t+s_t{\eta }_Q^t)<\theta$ (see (18)) then       2:    $x^{t+1}=x^t$       3: else {obtain $\tilde{Q}$ and $\tilde{R}$ from $Q^t+s_t{\eta }_Q^t$ using Algorithm 7}       4:    $x^{t+1}=[\tilde{Q};({(R^t)}^T+s_t{({\eta }_R^t)}^T){(\tilde{R})}^T]$       5: end if

Algorithm 7 Modified Gram–Schmidt algorithm

Input: $A\in {\mathbb{R}}^{n_1\times r}$ with $\mathrm{rank}\left(A\right)=r$. Output: $Q\in {\mathbb{R}}^{n_1\times r}$ and $R\in {\mathbb{R}}^{r\times r}$.       1: for$k=1:r$do       2:    $R_{x,x}=\sqrt{{\Sigma }_{i=1}^{n_1}{A}_{i,k}^2}$       3:    for $i=1:n_1$ do       4:      $Q_{i,k}=A_{i,k}/R_{k,k}$       5:    end for       6:    for $k=k+1:r$ do       7:      $R_{k,j}={\Sigma }_{i=1}^{n_1}{Q}_{i,k}{A}_{i,j}$       8:      for $i=1:n_1$ do       9:         $A_{i,j}=A_{i,j}-Q_{i,k}{R}_{k,j}$       10:      end for       11:    end for       12: end for

Given a small parameter $\theta$, we say that the matrix $Q+s{\eta }_Q$ has good orthogonality if $\mathrm{Orth}(Q+s{\eta }_Q)<\theta$. Then, we adopt $(Q+s{\eta }_Q,R+s{\eta }_R)$ as the value for the next iterate. On the contrary, we have to decompose $Q+s{\eta }_Q$ [33] and obtain $\tilde{Q}$, $\tilde{R}$, and hence, the next iteration point $(\tilde{Q},\tilde{R}(R+s{\eta }_R))$.

In summary, we present Algorithms 8 and 9 as the whole process of solving the optimization problem (9), respectively.

Algorithm 8 QR Riemannian gradient descent (QRRGD)

Input: Function $f:{\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}\to \mathbb{R}$ (see (9)), initial point $x^0\in {\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}$ (generated by Algorithm 1), tolerance parameter $ϵ>0$ Output: $x^t$       1: $t\leftarrow 0$       2: Compute the gradient by Algorithm 2       3: while$\parallel {\xi }^t{\parallel }_x>ϵ$do       4:    Find step size $s_t$ by Algorithm 4       5:    Update via retraction (Algorithm 6): $x^{t+1}=R_{x^t}\left(s_t{\eta }^t\right)$       6:    $t\leftarrow t+1$       7:    Compute the steepest direction by Algorithm 2       8: end while

Algorithm 9 QR Riemannian conjugate gradient (QRRCG)

Input: Function $f:{\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}\to \mathbb{R}$(see (9)), initial point $x^0\in {\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}$, tolerance parameter $ϵ>0$ p Output: $x^t$       1: $t\leftarrow 0$       2: Compute the gradient using Algorithm 2       3: while$\parallel {\xi }^t{\parallel }_x>ϵ$do       4:    Find step size $s_t$ using Algorithm 4       5:    Update via retraction (Algorithm 6): $x^{t+1}=R_{x^t}\left(s_t{\eta }^t\right)$       6:    $t\leftarrow t+1$       7:    Compute the conjugate direction using Algorithm 3       8: end while

4. Analysis

4.1. Convergence

We conduct analysis of Algorithm 8 as an instance and Algorithm 9 can be proved using a similar method. First, we prove that the objective function (9) is Lipschitz continuously differentiable [34] on the product space ${\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}$ over the Euclidean geometry. Then, we demonstrate that the proposed Riemannian gradient descent direction (14) has a sufficient decrease in the function value provided that the step size is selected properly depending on the local geometry at each iteration.

The Lipschitz continuity of the gradient of f in the sublevel set [35]

$$S^0=\{x\in {\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2},f\left(x\right)\le f\left(x^0\right)\}.$$

(19)

with respect to a point $x^0\in {\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}$ is shown below.

Lemma. 1

(Lipschitz continuous). Given a point $x^0\in {\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}$, there exists a Lipschitz constant $L_0>0$ such that the gradient of f in ${\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}$ is $L_0-$Lipschitz continuous for any $x,y\in {\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}$ belonging to the sublevel set $S^0$ (19) (see [36] for details to this lemma),

$$f\left(y\right)-f\left(x\right)\le 〈\nabla f\left(x\right),y-x〉+\frac{L_0}{2}{\parallel y-x\parallel }^2.$$

(20)

Proof. 

By the definition of function (9), set $S^0$, where $S^0$ is bounded with respect to any $x<\infty$. Furthermore, let B be a closed ball that contains $S^0$. For all $x,y\in B$, according to f is $C^{\infty }$, we have

$$\begin{array}{cc}\hfill f\left(y\right)& =f\left(x\right)+{\int }_0^1〈\nabla f(x+\tau (y-x\left)\right),y-x〉d\tau \hfill \\ \hfill & =f\left(x\right)+〈f\left(x\right),y-x〉+{\int }_0^1〈\nabla f(x+\tau (y-x\left)\right)-\nabla f\left(x\right),y-x〉d\tau \hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill |f\left(y\right)-f\left(x\right)-〈\nabla f\left(x\right),y-x〉|& =|{\int }_0^1〈f(x+\tau (y-x\left)\right)-\nabla f\left(x\right),y-x〉d\tau |\hfill \\ \hfill & \le {\int }_0^1\left|〈\nabla f(x+\tau (y-x\left)\right)-\nabla f\left(x\right),y-x〉\right|d\tau \hfill \\ \hfill & \le {\int }_0^1\parallel \nabla f(x+\tau (y-x))-\nabla f\left(x\right)\parallel \parallel y-x\parallel d\tau \hfill \\ \hfill & \le \tau L_0{\parallel y-x\parallel }^{2}d\tau \hfill \\ \hfill & =\frac{L_0}{2}{\parallel y-x\parallel }^2.\hfill \end{array}$$

This means that (20) is true on B, and it functions on its subset $S^0$. □

Next, we obtain the following sufficient decrease property with Lemma 1.

Lemma 2.

At any iterate $x^t=(Q^t,R^t)$ produced by Algorithm 8 before stopping, the following sufficient decrease property holds, provided that the step size s satisfies $0<s<2H_t/L_0$ for a positive value $H_t>0$,

$$f\left(x^{t+1}\right)-f\left(x^t\right)\le -C_t\left(s\right){\parallel \nabla f\left(x^t\right)\parallel }^2,$$

(21)

where $C_t\left(s\right)=s(H_t-\frac{L_{0}s}{2})>0$ and $H_t$ is defined by

$$H_t=\delta +\min (1,{\sigma }_{\min }^2\left(R^t\right)),$$

(22)

under the gradient setting (14).

Proof. 

In Algorithm 8, at iterate $x^t\in {\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}$, the Riemannian gradient descent step is ${\eta }^t=-\nabla f\left(x^t\right)$. Let $s>0$ denote the step size for producing the next iterate: $x^{t+1}=x^t+s{\eta }^t=({\eta }_Q,{\eta }_R)$. In the gradient setting (14), the partial differentials are

$${\partial }_{Q}f\left(x\right)={\eta }_Q(R{R}^T+\delta I_r)\mathrm{and}{\partial }_{H}f\left(x\right)={\eta }_R(1+\delta ).$$

(23)

According to Lemma 1, it follows that

$$\begin{array}{cc}\hfill f\left(x^{t+1}\right)-f\left(x^t\right)& \le 〈\nabla f\left(x^t\right),x^{t+1}-x^t〉+\frac{L_0}{2}{\parallel x^{t+1}-x^t\parallel }^2\hfill \\ \hfill & =-s〈\nabla f\left(x^t\right),\nabla f\left(x^t\right)〉+\frac{L_0{s}^2}{2}{\parallel {\eta }^t\parallel }^2\hfill \\ \hfill & =-s(Tr\left({\eta }_Q^T{\eta }_Q(R{R}^T+\delta I_r)\right)+Tr\left({\eta }_R{\eta }_R^T(Q^{T}Q+\delta I_r)\right))+\frac{L_0{s}^2}{2}{\parallel {\eta }^t\parallel }^2\hfill \\ \hfill & \le -s(\delta \parallel {\eta }^t{\parallel }^2+{\sigma }_{min}^2\left(R\right)\parallel {\eta }_Q{\parallel }_F^2+{\sigma }_{min}^2\left(Q\right)\parallel {\eta }_R{\parallel }_F^2)+\frac{L_0{s}^2}{2}{\parallel {\eta }^t\parallel }^2\hfill \\ \hfill & \le -s\parallel {\eta }^t{\parallel }^2(\delta +min(1,{\sigma }_{min}^2\left(R^t\right)))+\frac{L_0{s}^2}{2}{\parallel {\eta }^t\parallel }^2\hfill \\ \hfill & =-C_t\left(s\right){\parallel \nabla f\left(x^t\right)\parallel }^2.\hfill \end{array}$$

□

Next, we prove that Algorithm 8 with the step size selected by the exact line search (16) ensures sufficient decrease at each iteration.

Lemma 3.

The iterates produced by Algorithm 8, with step size chosen by the exact line search (see Algorithm 4) satisfy the following sufficient decrease property,

$$f\left(x^{t+1}\right)-f\left(x^t\right)\le -(H_t^2/2L_0){\parallel \nabla f\left(x^t\right)\parallel }^2.$$

(24)

Proof. 

In Algorithm (8), let $\eta =-\nabla f\left(x^t\right)$ denote the Riemannian gradient descent direction at the iterate $x^t\in {\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{r\times n_2}$. From Lemmas 2 and 3, one obtains

$$f(x^t+s\eta )\le f\left(x^t\right)-C_t\left(s\right){\parallel \nabla f\left(x^t\right)\parallel }^2.$$

for $s\in [0,2H_t/L_0]$ with $H_t$ defined in (22). On the other hand, let $\widehat{s}$ be the step size computed using Algorithm 4, and the next iterate $x^{t+1}=x^t+\widehat{s}\eta$ is the minimum of f along the direction $\eta$: $f\left(x^{t+1}\right)\le f(x^t+s\eta )$ by procession, for all $s\ge 0$. Therefore,

$$\begin{array}{cc}\hfill f\left(x^{t+1}\right)& \le \underset{s\in [0,2H_t/L_0]}{min}f(x^t+s\eta )\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & \le \underset{s\in [0,2H_t/L_0]}{min}(f\left(x^t\right)-C_t\left(s\right)\parallel \nabla f\left(x^t\right){\parallel }^2)\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & =f\left(x^t\right)-(H_t^2/2L_0){\parallel \nabla f\left(x^t\right)\parallel }^2.\hfill \end{array}$$

(27)

In Equation (27), the conclusion ${max}_{s\in [0,2H_t/L_0]}{C}_t\left(s\right)={max}_{s\in [0,2H_t/L_0]}s(H_t-\frac{L_{0}s}{2})=H_t^2/2L_0$ is applied. □

In both Lemmas 2 and 3, the sufficient decrease quantity depends on the local parameter $H_t$. The quality $H_t$ is useful only when it is a strictly positive number. We address this in Proposition 1 for the gradient setting (12).

Proposition 1.

Under the same settings as in Lemmas 2 and 3, there exists a positive numerical constant $H_{*}>0$ such that the quantities (22) are lower bounded,

$$\underset{t\ge 0}{inf}{H}_t\ge H_{*}.$$

(28)

Proof. 

In the gradient setting (12),

$$\begin{array}{c}\hfill H_t=\delta +min({\sigma }_{min}^2\left(Q^t\right),{\sigma }_{min}^2\left(R^t\right))\ge \sigma >0.\end{array}$$

It is easy to find the result (28) can be ensured by $H_{*}:=\sigma$ as claimed. □

Now, we reach the main result using the following theorem.

Theorem 1.

Under the problem statement (9), given the initial point $x^0$ and the gradient setting (12), the sequence generated by Algorithm 8 with the step size (16) converges and a upper bound of the gradient norm shows as follows,

$$\parallel \nabla f\left(x^N\right)\parallel \le \sqrt{\frac{2L_0(f\left(x^0\right)-f^{*})}{H_{*}N}}$$

(29)

after N iterations, where $L_0>0$ is the Lipschitz constant in Lemma 1, the numerical constant $H_{*}>0$ is given in Proposition (28), and $f^{*}$ is a lower bound of the function value of (9).

Proof. 

The convergence of the sequence ${\left(x^t\right)}_{t\ge 0}$ is a direct result of the sufficient decrease property (21) in Lemma 2 and the boundedness of the sequence of function values $f{\left(x^t\right)}_{t\ge 0}.$

Let $N\ge 1$ denote the number of iterations needed for reaching an iterate $x^N$ such that $\parallel \nabla f\left(x^N\right)\parallel \le ϵ$, for a tolerance parameter $ϵ>0$.

Because Algorithm 8 does not terminate at $t\le N-1$, the gradient norms $\parallel \nabla f\left(x^t\right)\parallel >ϵ$ for all $t\le N-1$. Adding up the right hand sides of (24) for $t=0,\dots ,N-1$ follows

$$\begin{array}{cc}\hfill f\left(x^N\right)-f\left(x^0\right)& \le -\sum _{t=0}^{N-1}(H_t^2/2L_0){\parallel \nabla f\left(x^t\right)\parallel }^2\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill & \le -({ϵ}^2/2L_0)\sum _{t=0}^{N-1}{H}_t^2\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & =-(H_{*}/2L_0){ϵ}^{2}N.\hfill \end{array}$$

(32)

In Equation (32), Proposition 1 is applied. Therefore, the number of iterations satisfies

$$N\le \frac{2L_0(f\left(x^0\right)-f\left(x^N\right))}{H_{*}{ϵ}^2}\le \frac{2L_0(f\left(x^0\right)-f^{*})}{H_{*}{ϵ}^2}.$$

In other words, the iterate produced by the algorithm after N iteration obeys

$$\parallel \nabla f\left(x^N\right)\parallel \le \sqrt{\frac{2L_0(f\left(x^0\right)-f^{*}))}{H_{*}N}}.$$

□

4.2. Computational Cost

In this subsection, we analyze the computation cost of our QR-based method with the other. It demonstrates the reason that we can obtain better performance than the compared method. After we make a QR factorization to matrix Q, it leads to some computational cost, but what the factorization reaps, the benefits greatly exceeds what it costs using an ingenious trick.

Cost increase. In Figure 2, we mark three parts including computations in retraction as $C_1$, $C_2$, and $C_3$, respectively. For $C_1$, we compute $Tr\left(Q^{T}Q\right)$ as the leading part where $Q\in {\mathbb{R}}^{n_1\times r}$, the cost of which is $2n_1{r}^2$. For $C_2$, we compute the QR decomposition of a matrix in ${\mathbb{R}}^{n_1\times r}$ by the MGS algorithm, which costs $2n_1{r}^2$. For $C_3$, it just computes the product of matrices $\tilde{R}\in {\mathbb{R}}^{r\times r}$ and $R\in {\mathbb{R}}^{r\times n_2}$; hence, it costs $2n_2{r}^2$. Assume that the rate of the good orthogonality is $1-{\theta }_0$, and the iteration number is $k_{\mathrm{iter}}$; then, the whole increasing cost is $k_{\mathrm{iter}}(C_1+{\theta }_0(C_2+C_3))$.

Cost decrease. A simple thought is to reduce the cost in each iteration process. First, we consider the gradient of the objective function (9), and the computational costs are summarized in

Table 1. Computational costs of the gradients of the objective function.

Computation	Cost
$P_{\mathrm{\Omega }}(QR-M)R^T{(R{R}^T+\delta I_r)}^{-1}$	$(4r+1)\left|\mathrm{\Omega }\right|+2(n_1+n_2)r^2+C_{\mathrm{chol}}{r}^3$
$Q^T{P}_{\mathrm{\Omega }}(QR-M){(Q^{T}Q+\delta I_r)}^{-1}$	$(4r+1)\left|\mathrm{\Omega }\right|+2(n_1+n_2)r^2+C_{\mathrm{chol}}{r}^3$
$Q^T{P}_{\mathrm{\Omega }}(QR-M)/(1+\delta )$	$(4r+1)\left|\mathrm{\Omega }\right|$

, where $C_{\mathrm{chol}}=1/3$ is a coefficient in the Cholesky decomposition while computing the inverse. Therefore, once we compute the gradient we have $D_1=2(n_1+n_2)r^2+C_{\mathrm{chol}}{r}^3$ reductions directly with respect to algorithms without QR. Second, we consider the metric (10), and the computational costs are summarized in

Table 2. Computation costs of the metric.

Computation	Cost
$Tr\left({\xi }_Q^T{\eta }_Q(R{R}^T+\delta I_r)\right)$	$2(n_1+n_2+r)r^2$
$Tr\left({\xi }_R{\eta }_R^T(Q^{T}Q+\delta I_r)\right)$	$2(n_1+n_2+r)r^2$
$Tr\left({\xi }_R{\eta }_R^T(1+\delta )\right)$	$2n_2{r}^2$

. When we compute the metric, the reduction is $D_2=2(n_1+r)r^2$ under the QR method than those without it.

In Algorithm 8, if we find the step size $s_t$ using the exact line search (Algorithm 4), then the reduction is $k_{\mathrm{iter}}{D}_1$, because the exact line search needs not to compute the metric. Furthermore, the reduction in the computational cost at one iteration is $D_1-(C_1+{\theta }_0(C_2+C_3))=\frac{1}{3}{r}^3+2(1-{\theta }_0)n_2{r}^2-2n_1{r}^2$.

In Algorithm 9, if we find the step size $s_t$ using the inexact line search (Algorithm 5), the reduction in the worst case is $k_{\mathrm{iter}}(D_1+im{D}_2)$. Furthermore, the reduction in the computational cost at one iteration is $(D_1+im{D}_2)-(C_1+{\theta }_0(C_2+C_3))=(2im+\frac{1}{3})r^3+2(im-r)n_1{r}^2+2(1-{\theta }_0)n_2{r}^2$.

5. Numerical Experiments

This section shows a numerical comparison of our algorithms with the recent RGD/RCG algorithms [26], which outperforms existing matrix factorization models on manifolds. The experiments are divided into two parts: in the first part, we test our algorithm on synthetic data, whereas in the second part, we provide the results on an empirical dataset PeMS Traffic [37].

To assess the algorithmic performance, we use the root mean square error (RMSE). Given a matrix $M\in {\mathbb{R}}^{n_1\times n_2}$ observed on $\mathrm{\Omega }$, the RMSE of $X\in {\mathbb{R}}^{n_1\times n_2}$ with respect to M is defined by

$$\mathrm{RMSE}(X;\mathrm{\Omega })=\sqrt{{\Sigma }_{(i,j)\in \mathrm{\Omega }}{(X_{ij}-M_{ij})}^2/\left|\mathrm{\Omega }\right|}.$$

(33)

Other parameters used in experiments are as follows: (1) p is the probability of an entry being observed; (2) the stopping parameter $ϵ={10}^{-10}$ is one of the two parameters stop the iteration process when RMSE reaches it; (3) the iteration budget parameter $\lambda =250$ is another parameter that stops the iteration process when iterating a specific amount of times over it; (4) the metric parameter $\delta ={10}^{-4}$ helps the metric be well defined; (5) the orthogonality parameter $\theta =0.01$ is used to judge whether a matrix has good orthogonality; and (6) the oversampling factor $OSF\in (2.5,3)$ according to [14], defined by $OSF=\left|\mathrm{\Omega }\right|/\left(r(n_1+n_2-r)\right)$, which decides the difficulty of the problem.

In our experiment, we first fix the values of $n_1$, $n_2$, and p. Next, we determine the difficulty of recovery, which can be characterized by the over sampling factor (OSF). Following [14], we set the OSF in $(2.5,3)$. Finally, we determine the value of the rank by $r=\lfloor 11/30n_1{n}_{2}p/(n_1+n_2)\rfloor$. To ensure that the matrix M is low ranked (e.g., $r=10$), there are two methods. One is setting $n_1$ and $n_2$ as small as possible given the values of p. For example, given $p=0.2$, the values of $n_1$ and $n_2$ are about 250. Because of the small size, the problem is trivial. The other is letting p be smaller given the larger values of $n_1$ and $n_2$. This is what was performed in our experiment. For example, given $n_1=n_2=2000$ in Figure 2, we set $p=0.05$ and obtain $r=18$.

All numerical experiments were performed on a desktop with 16-core Intel i7-10700F CPUs and 32GB of memory running Windows10 and MATLAB R2022b. The source code is available at https://github.com/Cz1544252489/qrcode (accessed on 14 February 2023).

5.1. Synthetic Data

Initially, we provide some comments about the chosen rank on synthetic data. We first fix the values of $n_1$, $n_2$, and p. Next, we determine the difficulty of recovery, which can be characterized by the oversampling factor (OSF). Following [14], we set the OSF in $(2.5,3)$. Finally, we can determine the value of the rank by $r=\lfloor 11/30n_1{n}_{2}p/(n_1+n_2)\rfloor$.

We generate two observed matrices $M_1$ and $M_2$ with probability p, which is the ratio of an entry being observed defined by $M_1=FQ$ with $(F,Q^T)\in {\mathbb{R}}^{n_1\times r}\times {\mathbb{R}}^{n_2\times r}$ and $M_2=M_1/(\max \left(M_1\right)-\min \left(M_1\right))$, where $(F,Q^T)$ are composed of columns that are i.i.d. Gaussian vectors. The reason why we generate them is to test our algorithm on different scale of entries, and it will be measured by $E\left(M\right)$ that is the average of random entries.

Table 3. Computational results for Figure 3 with matrices size of $2000\times 2000$. The time is rounded to three decimal places and RMSE is rounded to five decimal places.

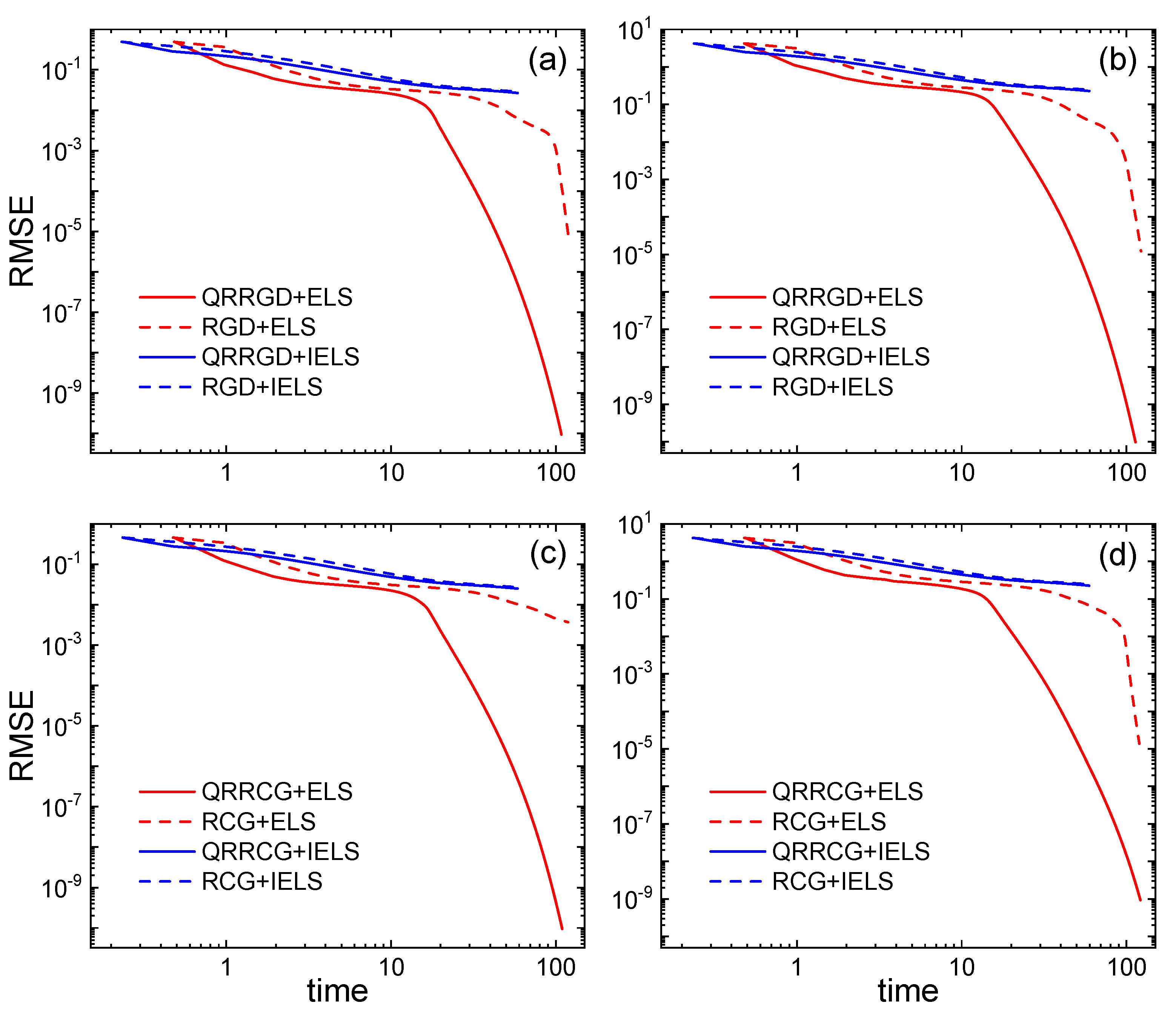
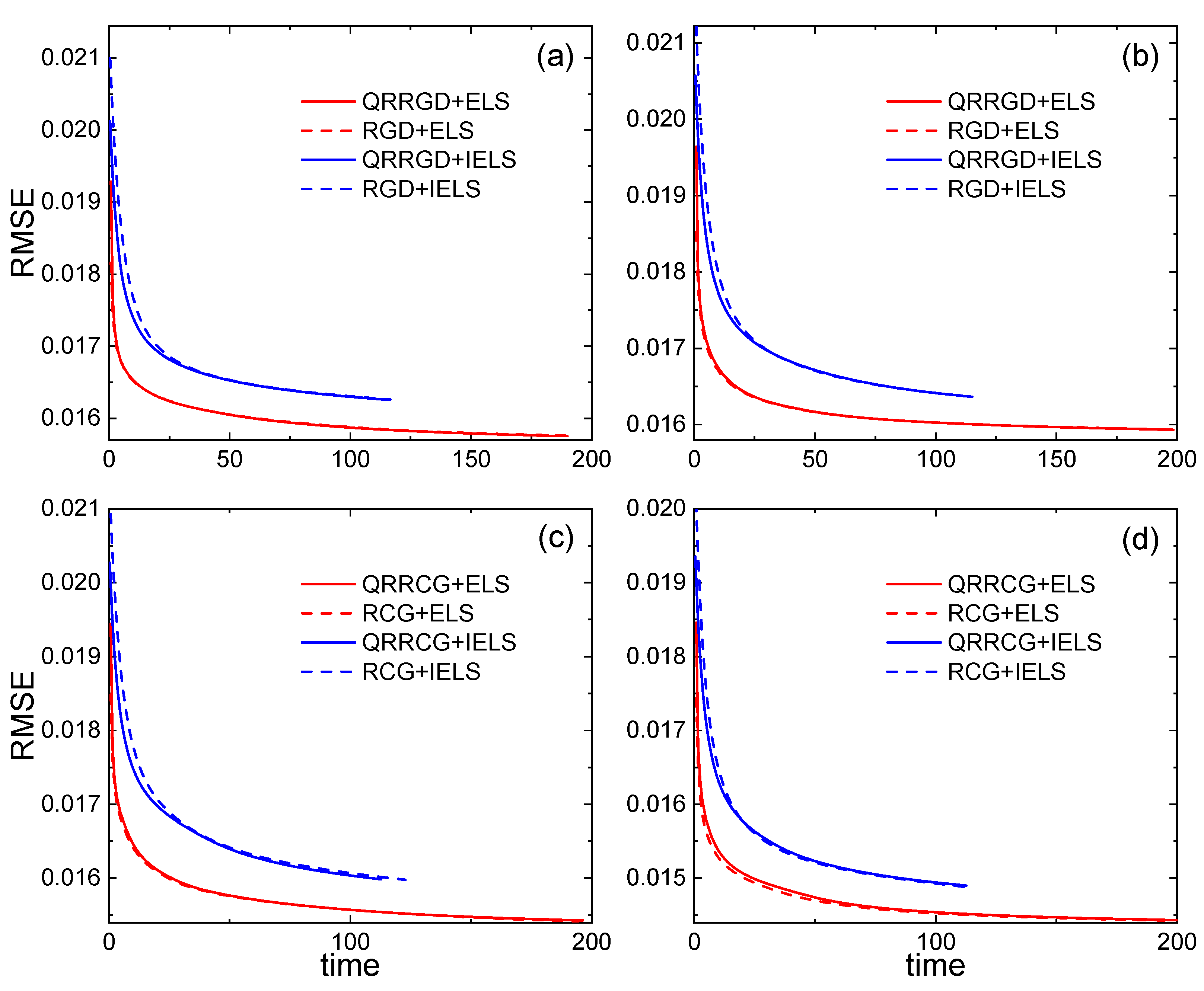
Subfigure	Method	Time	RMSE	Iteration
(a)	QRRGD+ELS	108.282	$9.42416\times {10}^{-11}$	223
	RGD+ELS	120.644	$5.65317\times {10}^{-6}$	250
	QRRGD+IELS	58.763	$2.66777\times {10}^{-2}$	250
	RGD+IELS	57.905	$2.88969\times {10}^{-2}$	250
(b)	QRRGD+ELS	113.655	$9.89826\times {10}^{-11}$	237
	RGD+ELS	122.815	$1.21759\times {10}^{-5}$	250
	QRRGD+IELS	59.640	$2.27510\times {10}^{-1}$	250
	RGD+IELS	59.400	$2.45927\times {10}^{-1}$	250
(c)	QRRCG+ELS	109.363	$9.39990\times {10}^{-11}$	227
	RCG+ELS	118.726	$3.69309\times {10}^{-3}$	250
	QRRCG+IELS	58.677	$2.50264\times {10}^{-2}$	250
	RCG+IELS	59.849	$2.68750\times {10}^{-2}$	250
(d)	QRRCG+ELS	121.740	$9.28316\times {10}^{-10}$	250
	RCG+ELS	119.905	$1.36830\times {10}^{-5}$	250
	QRRCG+IELS	59.449	$2.24703\times {10}^{-1}$	250
	RCG+IELS	58.432	$2.45275\times {10}^{-1}$	250

and

Table 4. Computational results for Figure 4 with matrices size of $4000\times 4000$. The time is rounded to three decimal places and RMSE is rounded to five decimal places.

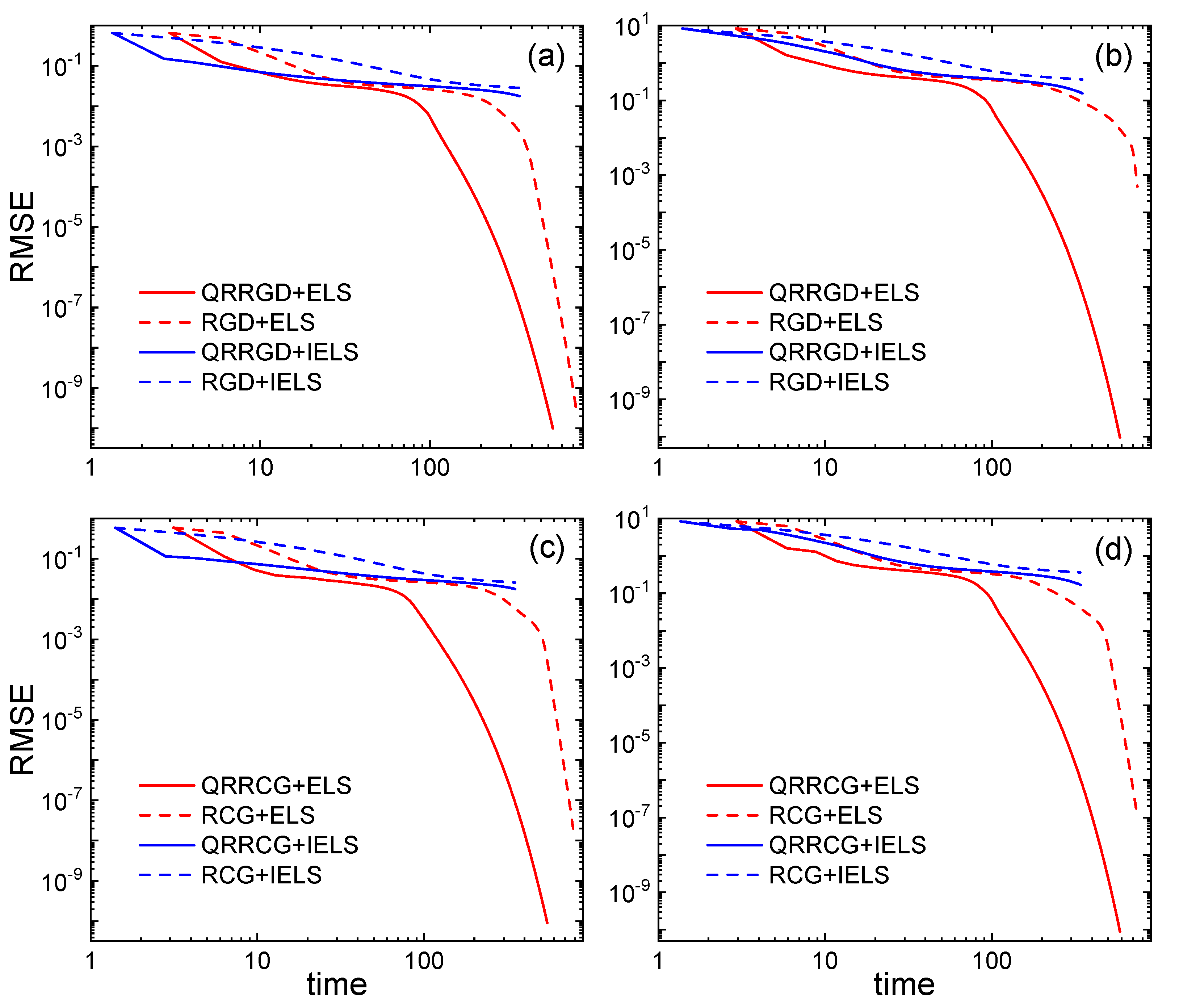
Subfigure	Method	Time	RMSE	Iteration
(a)	QRRGD+ELS	529.851	$9.89657\times {10}^{-11}$	181
	RGD+ELS	733.993	$2.40792\times {10}^{-10}$	250
	QRRGD+IELS	337.730	$1.76829\times {10}^{-2}$	250
	RGD+IELS	335.950	$2.82502\times {10}^{-2}$	250
(b)	QRRGD+ELS	586.522	$9.55942\times {10}^{-11}$	201
	RGD+ELS	745.970	$4.96694\times {10}^{-4}$	250
	QRRGD+IELS	349.708	$1.53603\times {10}^{-1}$	250
	RGD+IELS	348.213	$3.59285\times {10}^{-1}$	250
(c)	QRRCG+ELS	547.370	$9.03539\times {10}^{-11}$	173
	RCG+ELS	782.545	$1.99382\times {10}^{-8}$	250
	QRRCG+IELS	351.655	$1.77931\times {10}^{-2}$	250
	RCG+IELS	350.344	$2.56178\times {10}^{-2}$	250
(d)	QRRCG+ELS	586.297	$9.00940\times {10}^{-11}$	199
	RCG+ELS	738.357	$1.38944\times {10}^{-7}$	250
	QRRCG+IELS	341.237	$1.66425\times {10}^{-1}$	250
	RCG+IELS	338.835	$3.59287\times {10}^{-1}$	250

show the results with matrices size of $2000\times 2000$ and $4000\times 4000$. And

Table 5. Computational results for Figure 5 with matrices size ranging from $2000\times 2000$ to $8000\times 2000$. The time is rounded to three decimal places and RMSE is rounded to five decimal places.

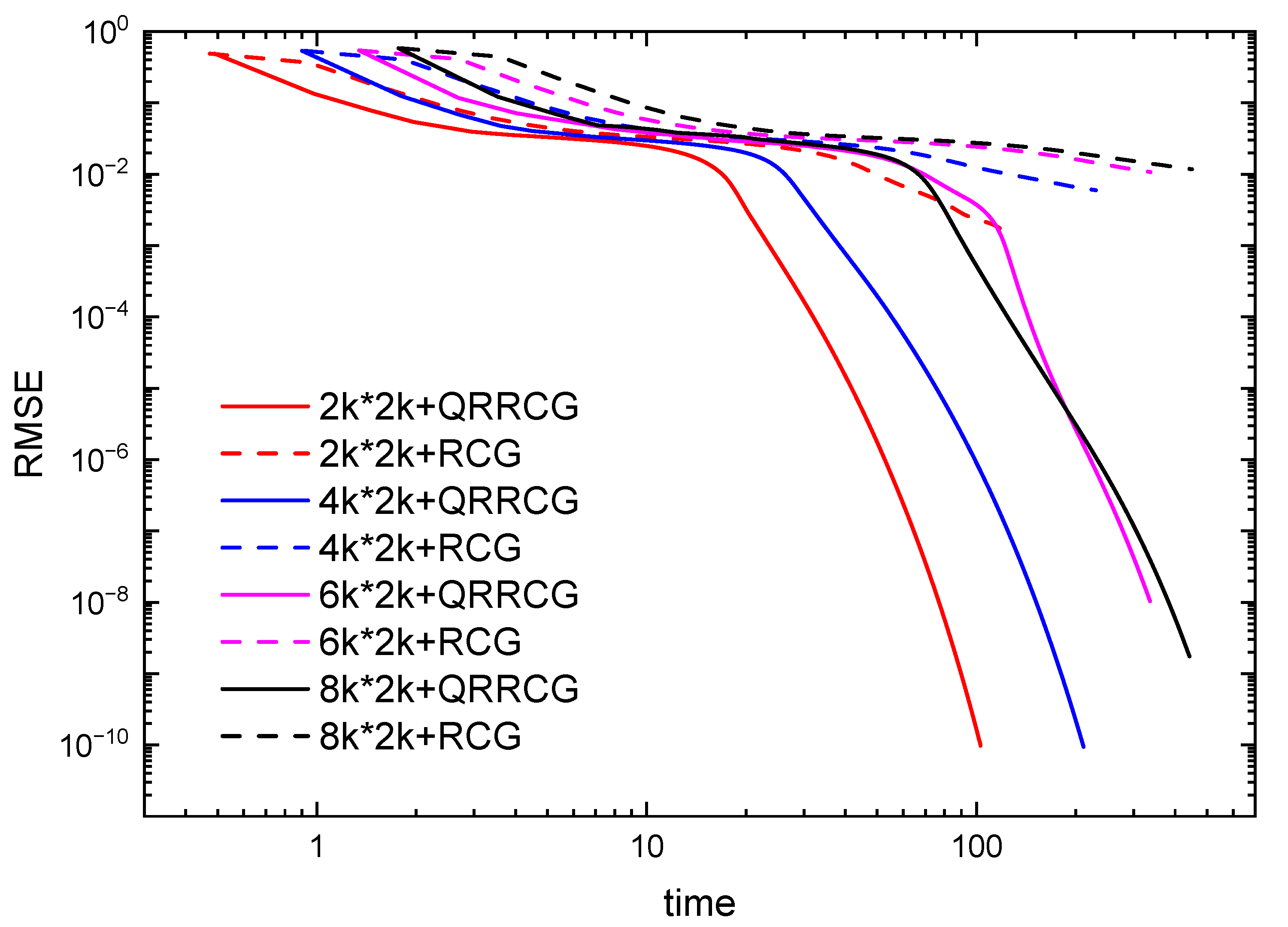
r,OSF	Size	Method	Time	RMSE	Iteration
18,2.79	$2000\times 2000$	QRRCG	102.939	$9.78333\times {10}^{-11}$	210
		RCG	118.397	$1.71532\times {10}^{-3}$	250
24,2.79	$4000\times 2000$	QRRCG	211.122	$9.43873\times {10}^{-11}$	234
		RCG	230.015	$5.98057\times {10}^{-3}$	250
27,2.79	$6000\times 2000$	QRRCG	335.745	$1.03872\times {10}^{-8}$	250
		RCG	336.917	$1.07408\times {10}^{-2}$	250
29,2.77	$8000\times 2000$	QRRCG	442.133	$1.74723\times {10}^{-9}$	250
		RCG	449.752	$1.17567\times {10}^{-1}$	250

shows the results with matrices size ranging from $2000\times 2000$ to $8000\times 2000$.

5.2. Empirical Data

In this part, we test our algorithm on the PeMS Traffic [37] dataset. It is a matrix with a size of $963\times 10560$ containing traffic occupancy rates (between 0 and 1) recorded across time by $m=963$ sensors placed along different lanes of freeways in the San Francisco Bay Area. The recordings are sampled every 10 minutes, covering a period of 15 months. The column index set corresponds to the time domain and the row index set corresponds to geographical points (sensors), which are referred to as the spatial domain. In the experiment, we use the part of test dataset; it has 173 rows and 6837 columns with $p=0.05$.

Table 6. Computational results for Figure 6 on PeMS Traffic. The time is rounded to three decimal places and RMSE is rounded to five decimal places.

Subfigure	Method	Time	RMSE	Iteration
(a)	QRG+ELS	189.945	$1.57521\times {10}^{-2}$	250
	RGD+ELS	192.104	$1.57584\times {10}^{-2}$	250
	QRRGD+IELS	116.213	$1.62539\times {10}^{-2}$	250
	RGD+IELS	116.576	$1.62615\times {10}^{-2}$	250
(b)	QRRGD+ELS	198.433	$1.59324\times {10}^{-2}$	250
	RGD+ELS	196.615	$1.59392\times {10}^{-2}$	250
	QRRGD+IELS	115.070	$1.63650\times {10}^{-2}$	250
	RGD+IELS	113.418	$1.63721\times {10}^{-2}$	250
(c)	QRRCG+ELS	196.291	$1.54291\times {10}^{-2}$	250
	RCG+ELS	194.373	$1.54170\times {10}^{-2}$	250
	QRRCG+IELS	112.798	$1.59846\times {10}^{-2}$	250
	RCG+IELS	122.820	$1.59796\times {10}^{-2}$	250
(d)	QRRCG+ELS	201.373	$1.44327\times {10}^{-2}$	250
	RCG+ELS	196.029	$1.44283\times {10}^{-2}$	250
	QRRCG+IELS	112.663	$1.48999\times {10}^{-2}$	250
	RCG+IELS	112.358	$1.48827\times {10}^{-2}$	250

shows the results on the empirical data.

As shown above, solid lines represent the results of our algorithms with QR factorization, whereas dashed lines correspond to those of the algorithms with rank factorization [26]. For synthetic data, our algorithms either yield better solutions or run with less time in comparison to [26] on most cases. Whereas for the empirical dataset, it shows a slight advantage for weak structures on earth. It has been demonstrated that the algorithms in [26] outperform the state-of-the-art methods using alternating minimization and the manifold concept.

Furthermore, we briefly measure the ratio of speedup from the compared algorithm. It can be defined by the means of speedup on all our experiment, that is, $SU={\Sigma }_{i\in E}S{U}_i/\left|E\right|$, where E is the set of experiments. Furthermore, a single speedup $S{U}_i$ defined as below:

$$S{U}_i=\left\{\begin{array}{ccc}\hfill 0& & \mathrm{if}{t}_1>t_2\mathrm{and}{ϵ}_1>{ϵ}_2\hfill \\ \hfill |\frac{t_2{ϵ}_2}{t_1{ϵ}_1}-1|& & otherwise\hfill \end{array}\right.$$

(34)

where $t_1$ and ${ϵ}_1$ are the time in seconds and theRMSE of the QR method, respectively, whereas $t_2$ and ${ϵ}_2$ are the time in seconds and the RMSE of the compared method. Finally, we obtain $SU=24.00\%$.

6. Conclusions

We have proposed two LRMC algorithms, QRRGD and QRRCG, for reconstruction of an observed matrix via QR-based retraction on manifolds. These two algorithms are computationally efficient and have higher accuracy, demonstrated by theoretical analysis of computational costs and numerical experiments with synthetic data and a real-world dataset PeMS Traffic. To improve efficacy, one could adjust the values of other parameters such as using smaller $\theta$ for orthogonality, a larger $OSF$, and a more suitable $\delta$ value for the metric. On the other hand, different conjugate methods [38], as well as the rank adaptive method [39], can be considered.