A Review of Chaotic Systems Based on Memristive Hopfield Neural Networks
Abstract
:1. Introduction
2. Introduction of Basic Knowledge
2.1. Hopfield Neural Networks
2.2. Memristor
2.3. Chaotic Dynamics
3. Memristive Hopfield Neural Networks
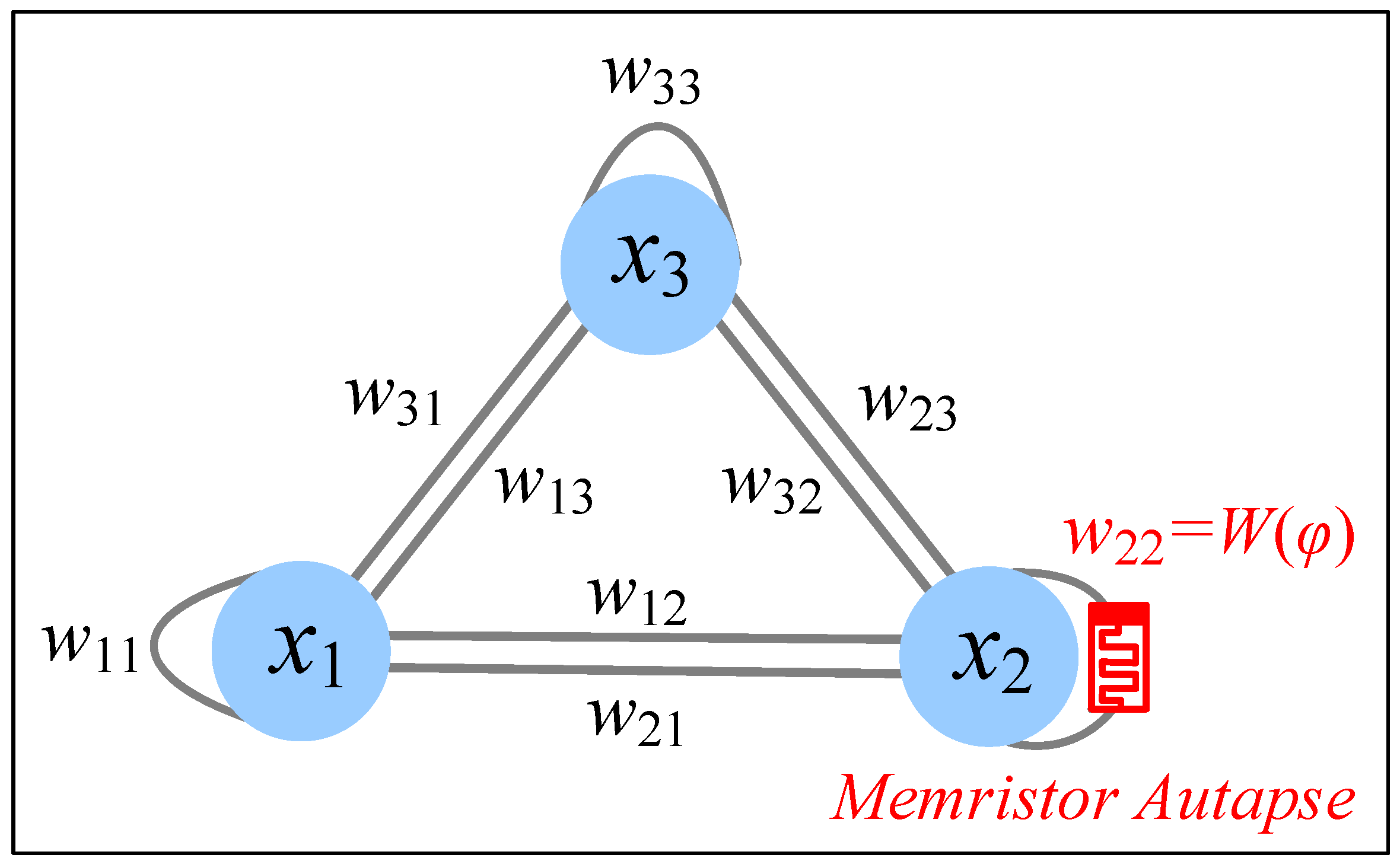
3.1. Using Memristors to Emulate Neural Synapses
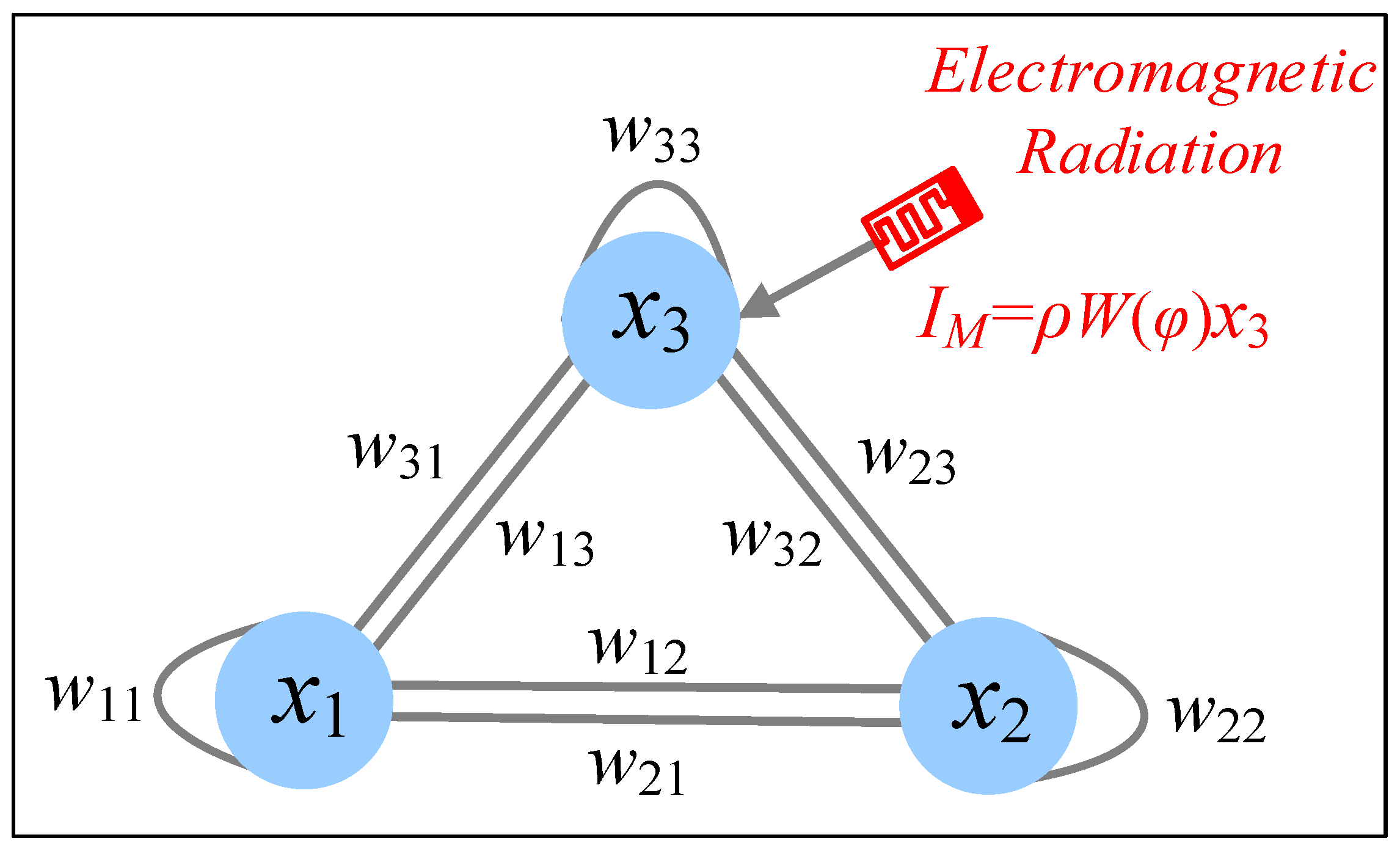
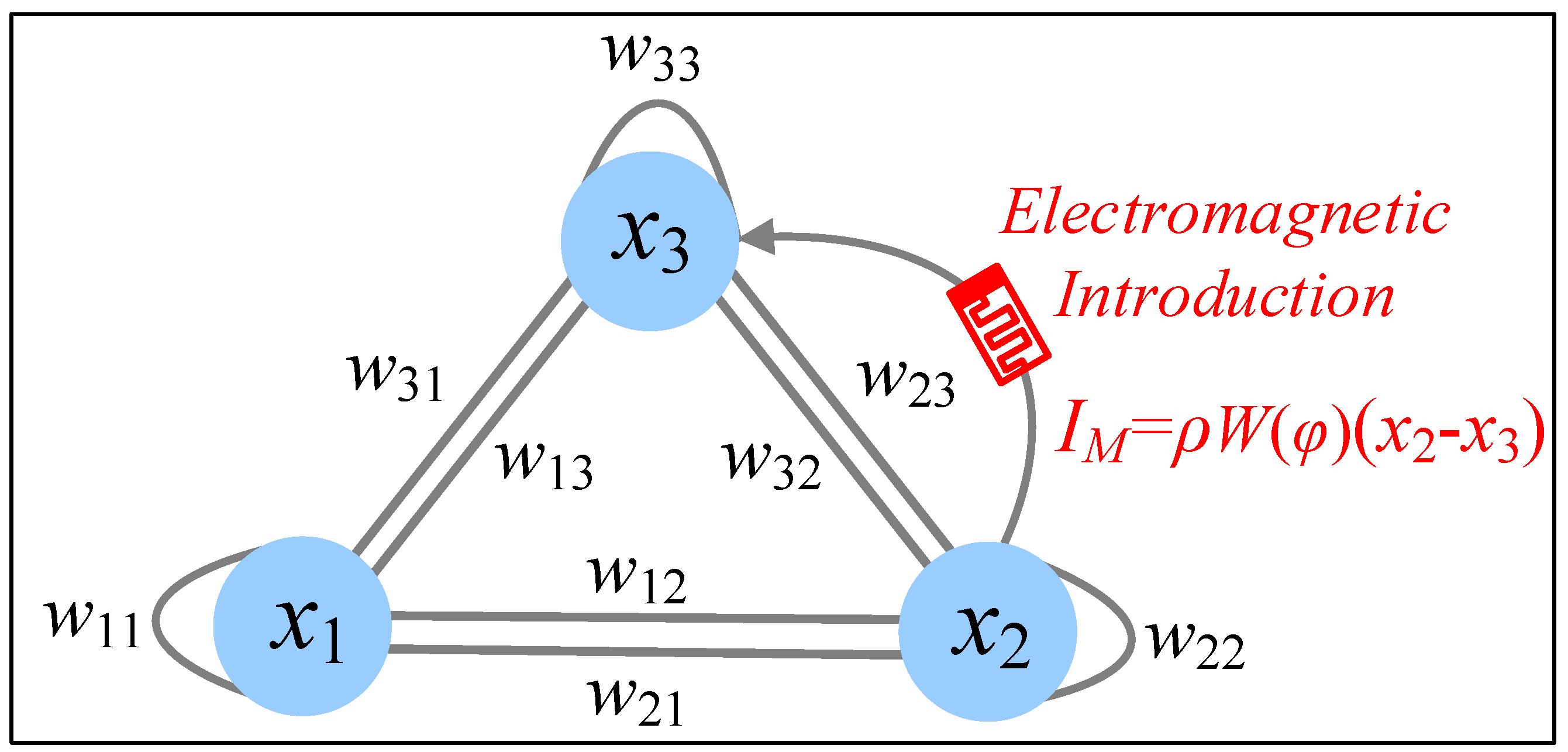
3.2. Using Memristor to Describe Electromagnetic Induction
| Dynamical Behaviors | References |
|---|---|
| Transient chaos | [114,169,173] |
| Hyperchaos | [111,118,123,169] |
| Feigenbaum tree | [147] |
| Coexisting attractors | [113,147,157,163,174,176,178,180,182] |
| Bursting firing | [148,151,166] |
| Chimera state | [156] |
| Hidden attractors | [112,152,153,170,173] |
| Synchronization | [156,158] |
| Multi-scroll attractors | [116,120,122,149,150,160,164,168,171,172,174,183] |
| Multi-structure attractors | [117,118] |
| Multistability | [124,151,155,159,166,167,173,175,177] |
| Extreme multistability | [115,116,121,152,153,154,161,162,170] |
| Hidden extreme multistability | [152,153,170] |
| Initial-offset coexisting behaviors | [116,121,154,161,162] |
4. Application and Future Works
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Huisman, J.; Weissing, F.J. Biodiversity of plankton by species oscillations and chaos. Nature 1999, 402, 407–410. [Google Scholar] [CrossRef]
- Dendrinos, D.S. Traffic-flow dynamics, a search for chaos. Chaos Solitons Fractals 1994, 4, 605–617. [Google Scholar] [CrossRef]
- Kazem, A.; Sharifi, E.; Hussain, F.K.; Saberi, M.; Hussain, O.K. Support vector regression with chaos-based firefly algorithm for stock market price forecasting. Appl. Soft. Comput. 2013, 13, 947–958. [Google Scholar] [CrossRef]
- Gu, H.; Li, C.; Li, Y.; Ge, X.; Lei, T. Various patterns of coexisting attractors in a hyperchaotic map. Nonlinear Dyn. 2023, 111, 7807–7818. [Google Scholar] [CrossRef]
- Sciamanna, M.; Shore, K.A. Physics and applications of laser diode chaos. Nat. Photonics 2015, 9, 151–162. [Google Scholar] [CrossRef] [Green Version]
- Kol’tsov, N.I.; Fedotov, V.K. Two-Dimentional Chaos in chemical reactions. Russ. J. Phys. Chem. B 2018, 12, 590–592. [Google Scholar] [CrossRef]
- Yousefpour, A.; Jahanshahi, H.; Munoz-Pacheco, J.M.; Bekiros, S.; Wei, Z. A fractional-order hyper-chaotic economic system with transient chaos. Chaos Solitons Fractals 2020, 130, 109400. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, C.; Sun, J.; Yu, F. A chaotic image encryption method based on the artificial fish swarms algorithm and the DNA coding. Mathematics 2023, 11, 767. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, W.; Xiao, X.; Yao, W.; Cai, S.; Zhang, J.; Wang, C.; Li, Y. Dynamic analysis and FPGA implementation of a new, simple 5D memristive hyperchaotic Sprott-C system. Mathematics 2023, 11, 701. [Google Scholar] [CrossRef]
- Lu, Y.M.; Wang, C.H.; Deng, Q.L.; Xu, C. The dynamics of a memristor-based Rulkov neuron with fractional-order difference. Chin. Phys. B 2022, 31, 060502. [Google Scholar] [CrossRef]
- Matsumoto, T. A chaotic attractor from Chua’s circuit. IEEE Trans. Circuits Syst. 1984, 31, 1055–1058. [Google Scholar] [CrossRef]
- Sprott, J.C. Some simple chaotic flows. Phys. Rev. E 1994, 50, R647. [Google Scholar] [CrossRef] [PubMed]
- Sprott, J.C. Some simple chaotic jerk functions. Am. J. Phys. 1997, 65, 537–543. [Google Scholar] [CrossRef]
- Chen, G.; Ueta, T. Yet another chaotic attractor. Int. J. Bifurc. Chaos 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
- Lü, J.; Chen, G. A new chaotic attractor coined. Int. J. Bifurc. Chaos 2002, 12, 659–661. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Chen, G. Chaos in the fractional order Chen system and its control. Chaos Solitons Fractals 2004, 22, 549–554. [Google Scholar] [CrossRef]
- Sun, K.; Wang, X.I.A.; Sprott, J.C. Bifurcations and chaos in fractional-order simplified Lorenz system. Int. J. Bifurc. Chaos 2010, 20, 1209–1219. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C. Simple chaotic flows with a line equilibrium. Chaos Solitons Fractals 2013, 57, 79–84. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V.; Mokaev, T.N. Homoclinic orbits, and self-excited and hidden attractors in a Lorenz-like system describing convective fluid motion, Homoclinic orbits, and self-excited and hidden attractors. Eur. Phys. J.-Spec. Top. 2015, 224, 1421–1458. [Google Scholar] [CrossRef] [Green Version]
- Bao, H.; Wang, N.; Bao, B.; Chen, M.; Jin, P.; Wang, G. Initial condition-dependent dynamics and transient period in memristor-based hypogenetic jerk system with four line equilibria. Commun. Nonlinear Sci. Numer. Simul. 2018, 57, 264–275. [Google Scholar] [CrossRef]
- Suykens, J.A.; Vandewalle, J. Generation of n-double scrolls. IEEE Trans. Circuits Syst. I 1993, 40, 861–867. [Google Scholar] [CrossRef]
- Yu, S.; Lu, J.; Leung, H.; Chen, G. Design and implementation of n-scroll chaotic attractors from a general jerk circuit. IEEE Trans. Circuits Syst. I-Regul. Pap. 2005, 52, 1459–1476. [Google Scholar]
- Yu, S.; Tang, W.K.; Lu, J.; Chen, G. Generation of nxm-wing Lorenz-like attractors from a modified Shimizu–Morioka model. IEEE Trans. Circuits Syst. II-Express Briefs 2008, 55, 1168–1172. [Google Scholar]
- Yu, S.; Jinhu, L.; Chen, G.; Yu, X. Design and implementation of grid multiwing butterfly chaotic attractors from a piecewise Lorenz system. IEEE Trans. Circuits Syst. II-Express Briefs 2010, 57, 803–807. [Google Scholar] [CrossRef]
- Yu, S.; Lu, J.; Chen, G.; Yu, X. Generating grid multiwing chaotic attractors by constructing heteroclinic loops into switching systems. IEEE Trans. Circuits Syst. II-Express Briefs 2011, 58, 314–318. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, P.; Zhao, W. Novel grid multiwing butterfly chaotic attractors and their circuit design. IEEE Trans. Circuits Syst. II-Express Briefs 2014, 62, 496–500. [Google Scholar] [CrossRef]
- Tahir, F.R.; Jafari, S.; Pham, V.T.; Volos, C.; Wang, X. A novel no-equilibrium chaotic system with multiwing butterfly attractors. Int. J. Bifurc. Chaos 2015, 25, 1550056. [Google Scholar] [CrossRef]
- Hong, Q.; Li, Y.; Wang, X.; Zeng, Z. A versatile pulse control method to generate arbitrary multidirection multibutterfly chaotic attractors. IEEE Trans. Comput-Aided Des. Integr. Circuits Syst. 2018, 38, 1480–1492. [Google Scholar] [CrossRef]
- Ye, X.; Wang, X.; Gao, S.; Mou, J.; Wang, Z. A new random diffusion algorithm based on the multi-scroll Chua’s chaotic circuit system. Opt. Lasers Eng. 2020, 127, 105905. [Google Scholar] [CrossRef]
- Rajagopal, K.; Çiçek, S.; Naseradinmousavi, P.; Khalaf, A.J.M.; Jafari, S.; Karthikeyan, A. A novel parametrically controlled multi-scroll chaotic attractor along with electronic circuit design. Eur. Phys. J. Plus 2018, 133, 354. [Google Scholar] [CrossRef]
- Wang, N.; Li, C.; Bao, H.; Chen, M.; Bao, B. Generating multi-scroll Chua’s attractors via simplified piecewise-linear Chua’s diode. IEEE Trans. Circuits Syst. I-Regul. Pap. 2019, 66, 4767–4779. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; He, P.; Li, G.; Xu, X.; Zhong, H. Multi-directional annular multi-wing chaotic system based on Julia fractals. Chaos Solitons Fractals 2022, 165, 112799. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, G.; Kuznetsov, N.V.; Li, H. Generating grid chaotic sea from system without equilibrium point. Commun. Nonlinear Sci. Numer. Simul. 2022, 107, 106194. [Google Scholar] [CrossRef]
- Wu, Q.; Hong, Q.; Liu, X.; Wang, X.; Zeng, Z. Constructing multi-butterfly attractors based on Sprott C system via non-autonomous approaches. Chaos 2019, 29, 043112. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Wu, X.; Chu, R.; Zhang, L. Selection of multi-scroll attractors in Jerk circuits and their verification using Pspice. Nonlinear Dyn. 2014, 76, 1951–1962. [Google Scholar] [CrossRef]
- Hong, Q.; Wu, Q.; Wang, X.; Zeng, Z. Novel nonlinear function shift method for generating multiscroll attractors using memristor-based control circuit. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2019, 27, 1174–1185. [Google Scholar] [CrossRef]
- Zaamoune, F.; Menacer, T.; Lozi, R.; Chen, G. Symmetries in hidden bifurcation routes to multiscroll chaotic attractors generated by saturated function series. J. Adv. Eng. Comput. 2019, 3, 511–522. [Google Scholar] [CrossRef] [Green Version]
- He, S.B.; Sun, K.H.; Zhu, C.X. Complexity analyses of multi-wing chaotic systems. Chin. Phys. B 2013, 22, 050506. [Google Scholar] [CrossRef]
- Zhang, S.; Li, C.; Zheng, J.; Wang, X.; Zeng, Z.; Chen, G. Generating any number of diversified hidden attractors via memristor coupling. IEEE Trans. Circuits Syst. I-Regul. Pap. 2021, 68, 4945–4956. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, L.; Xiang, J.; Guo, Q. Three-dimensional sine chaotic system with multistability and multi-scroll attractor. IEEE Trans. Circuits Syst. II-Express Briefs 2021, 69, 1792–1796. [Google Scholar] [CrossRef]
- Yan, D.; Ji’e, M.; Wang, L.; Duan, S.; Du, X. Generating novel multi-scroll chaotic attractors via fractal transformation. Nonlinear Dyn. 2022, 107, 3919–3944. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, C.; Yang, L. Four-wing hidden attractors with one stable equilibrium point. Int. J. Bifurc. Chaos 2020, 30, 2050086. [Google Scholar] [CrossRef]
- Sahoo, S.; Roy, B.K. Design of multi-wing chaotic systems with higher largest Lyapunov exponent. Chaos Solitons Fractals 2022, 157, 111926. [Google Scholar] [CrossRef]
- Liu, X.; Tong, X.; Wang, Z.; Zhang, M. Construction of controlled multi-scroll conservative chaotic system and its application in color image encryption. Nonlinear Dyn. 2022, 110, 1897–1934. [Google Scholar] [CrossRef]
- Yan, S.; Li, L.; Gu, B.; Cui, Y.; Wang, J.; Song, J. Design of hyperchaotic system based on multi-scroll and its encryption algorithm in color image. Integration 2023, 88, 203–221. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C. A novel multi-attractor period multi-scroll chaotic integrated circuit based on CMOS wide adjustable CCCII. IEEE Access 2019, 7, 16336–16350. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Adhikari, S.P.; Sah, M.P.; Kim, H.; Chua, L.O. Three fingerprints of memristor. IEEE Trans. Circuits Syst. I-Regul. Pap. 2013, 60, 3008–3021. [Google Scholar] [CrossRef]
- Chua, L. Everything you wish to know about memristors but are afraid to ask. Radioengineering 2015, 24, 319–368. [Google Scholar] [CrossRef]
- Muthuswamy, B.; Kokate, P.P. Memristor-based chaotic circuits. IETE Tech. Rev. 2009, 26, 417–429. [Google Scholar] [CrossRef] [Green Version]
- Cafagna, D.; Grassi, G. On the simplest fractional-order memristor-based chaotic system. Nonlinear Dyn. 2012, 70, 1185–1197. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kengne, L.K.; Kuate, P.D.K.; Chen, C. Two-memristor-based chaotic system with infinite coexisting attractors. IEEE Trans. Circuits Syst. II-Express Briefs 2020, 68, 2197–2201. [Google Scholar] [CrossRef]
- Chang, H.; Li, Y.; Chen, G.; Yuan, F. Extreme multistability and complex dynamics of a memristor-based chaotic system. Int. J. Bifurc. Chaos 2020, 30, 2030019. [Google Scholar] [CrossRef]
- Butusov, D.N.; Ostrovskii, V.Y.; Karimov, A.I.; Andreev, V.S. Semi-explicit composition methods in memcapacitor circuit simulation. Int. J. Embed. Real-Time Commun. Syst. 2019, 10, 37–52. [Google Scholar] [CrossRef]
- Ostrovskii, V.Y.; Tutueva, A.V.; Rybin, V.G.; Karimov, A.I.; Butusov, D.N. Continuation analysis of memristor-based modified Chua’s circuit. In Proceedings of the 2020 International Conference Nonlinearity, Information and Robotics (NIR), Innopolis, Russia, 3–6 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar]
- Xu, Q.; Lin, Y.; Bao, B.; Chen, M. Multiple attractors in a non-ideal active voltage-controlled memristor based Chua’s circuit. Chaos Solitons Fractals 2016, 83, 186–200. [Google Scholar] [CrossRef]
- Chen, M.; Sun, M.; Bao, H.; Hu, Y.; Bao, B. Flux–charge analysis of two-memristor-based Chua’s circuit, dimensionality decreasing model for detecting extreme multistability. IEEE Trans. Ind. Electron. 2019, 67, 2197–2206. [Google Scholar] [CrossRef]
- Kengne, J.; Negou, A.N.; Tchiotsop, D. Antimonotonicity, chaos and multiple attractors in a novel autonomous memristor-based jerk circuit. Nonlinear Dyn. 2017, 88, 2589–2608. [Google Scholar] [CrossRef]
- Hua, M.; Yang, S.; Xu, Q.; Chen, M.; Wu, H.; Bao, B. Forward and reverse asymmetric memristor-based jerk circuits. AEU-Int. J. Electron. Commun. 2020, 123, 153294. [Google Scholar] [CrossRef]
- Bao, H.; Ding, R.; Hua, M.; Wu, H.; Chen, B. Initial-condition effects on a two-memristor-based Jerk system. Mathematics 2022, 10, 411. [Google Scholar] [CrossRef]
- Xu, Q.; Cheng, S.; Ju, Z.; Chen, M.; Wu, H. Asymmetric coexisting bifurcations and multi-stability in an asymmetric memristive diode-bridge-based jerk circuit. Chin. J. Phys. 2021, 70, 69–81. [Google Scholar] [CrossRef]
- Bao, B.; Ma, Z.; Xu, J.; Liu, Z.; Xu, Q. A simple memristor chaotic circuit with complex dynamics. Int. J. Bifurc. Chaos 2011, 21, 2629–2645. [Google Scholar] [CrossRef]
- Dou, G.; Yang, H.; Gao, Z.; Li, P.; Dou, M.; Yang, W.; Guo, M.; Li, Y. Coexisting multi-dynamics of a physical SBT memristor-based chaotic circuit. Int. J. Bifurc. Chaos 2020, 30, 2030043. [Google Scholar] [CrossRef]
- Muthuswamy, B. Implementing memristor based chaotic circuits. Int. J. Bifurc. Chaos 2010, 20, 1335–1350. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, C.; Liu, Z.; Lei, T.; Chen, G. Simplified memristive Lorenz oscillator. IEEE Trans. Circuits Syst. II-Express Briefs 2022, 69, 3344–3348. [Google Scholar] [CrossRef]
- Ramamoorthy, R.; Rajagopal, K.; Leutcho, G.D.; Krejcar, O.; Namazi, H.; Hussain, I. Multistable dynamics and control of a new 4D memristive chaotic Sprott B system. Chaos Solitons Fractals 2022, 156, 111834. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C.; Joo-Chen Thio, W.; Gu, Z. A simple memristive jerk system. IET Circ. Devices Syst. 2021, 15, 388–392. [Google Scholar] [CrossRef]
- Jia, S.H.; Li, Y.X.; Shi, Q.Y.; Huang, X. Design and FPGA implementation of a memristor-based multi-scroll hyperchaotic system. Chin. Phys. B 2022, 31, 070505. [Google Scholar] [CrossRef]
- Alombah, N.H.; Fotsin, H.; Ngouonkadi, E.M.; Nguazon, T. Dynamics, analysis and implementation of a multiscroll memristor-based chaotic circuit. Int. J. Bifurc. Chaos 2016, 26, 1650128. [Google Scholar] [CrossRef]
- Yuan, F.; Wang, G.; Wang, X. Extreme multistability in a memristor-based multi-scroll hyper-chaotic system. Chaos 2016, 26, 073107. [Google Scholar] [CrossRef]
- Zhang, S.; Zheng, J.; Wang, X.; Zeng, Z.; Peng, X. A novel nonideal flux-controlled memristor model for generating arbitrary multi-double-scroll and multi-double-wing attractors. Int. J. Bifurc. Chaos 2021, 31, 2150086. [Google Scholar] [CrossRef]
- Zhang, S.; Zheng, J.; Wang, X.; Zeng, Z. Multi-scroll hidden attractor in memristive HR neuron model under electromagnetic radiation and its applications. Chaos 2021, 31, 011101. [Google Scholar] [CrossRef] [PubMed]
- Gu, S.; Peng, Q.; Leng, X.; Du, B. A novel non-equilibrium memristor-based system with multi-wing attractors and multiple transient transitions. Chaos 2021, 31, 033105. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Wen, J.; Mou, J. Dynamic analysis and DSP implementation of memristor chaotic systems with multiple forms of hidden attractors. Mathematics 2023, 11, 24. [Google Scholar] [CrossRef]
- Chang, H.; Li, Y.; Chen, G. A novel memristor-based dynamical system with multi-wing attractors and symmetric periodic bursting. Chaos 2020, 30, 043110. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Liu, C.; Liu, L.; Yao, Y.; Zheng, G. Multi-scroll hidden attractors and multi-wing hidden attractors in a 5-dimensional memristive system. Chin. Phys. B 2017, 26, 110502. [Google Scholar] [CrossRef]
- Yan, D.; Wang, L.; Duan, S.; Chen, J.; Chen, J. Chaotic attractors generated by a memristor-based chaotic system and Julia fractal. Chaos Solitons Fractals 2021, 146, 110773. [Google Scholar] [CrossRef]
- Xu, Q.; Ding, S.; Bao, H.; Chen, M.; Bao, B. Piecewise-linear simplification for adaptive synaptic neuron model. IEEE Trans. Circuits Syst. II-Express Briefs 2021, 69, 1832–1836. [Google Scholar] [CrossRef]
- Ma, M.; Lu, Y.; Li, Z.; Sun, Y.; Wang, C. Multistability and phase synchronization of Rulkov neurons coupled with a locally active discrete memristor. Fractal Fract. 2023, 7, 82. [Google Scholar] [CrossRef]
- Li, H.; Yang, Y.; Li, W.; He, S.; Li, C. Extremely rich dynamics in a memristor-based chaotic system. Eur. Phys. J. Plus 2020, 135, 579. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Z.; Wu, H.; Chen, S.; Bao, B. Two-memristor-based chaotic system and its extreme multistability reconstitution via dimensionality reduction analysis. Chaos Solitons Fractals 2019, 127, 354–363. [Google Scholar] [CrossRef]
- Li, C.; Min, F.; Li, C. Multiple coexisting attractors of the serial–parallel memristor-based chaotic system and its adaptive generalized synchronization. Nonlinear Dyn. 2018, 94, 2785–2806. [Google Scholar] [CrossRef]
- Ding, D.; Qian, X.; Hu, W.; Wang, N.; Liang, D. Chaos and Hopf bifurcation control in a fractional-order memristor-based chaotic system with time delay. Eur. Phys. J. Plus 2017, 132, 447. [Google Scholar] [CrossRef]
- Wu, J.; Wang, L.; Chen, G.; Duan, S. A memristive chaotic system with heart-shaped attractors and its implementation. Chaos Solitons Fractals 2016, 92, 20–29. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Gao, M.; Tian, Y.; Wang, C.; Iu, H.H.C. A color image encryption algorithm based on hash table, hilbert curve and hyper-chaotic synchronization. Mathematics 2023, 11, 567. [Google Scholar] [CrossRef]
- Wang, R.; Li, C.; Kong, S.; Jiang, Y.; Lei, T. A 3D memristive chaotic system with conditional symmetry. Chaos Solitons Fractals 2022, 158, 111992. [Google Scholar] [CrossRef]
- Mezatio, B.A.; Motchongom, M.T.; Tekam, B.R.W.; Kengne, R.; Tchitnga, R.; Fomethe, A. A novel memristive 6D hyperchaotic autonomous system with hidden extreme multistability. Chaos Solitons Fractals 2019, 120, 100–115. [Google Scholar] [CrossRef]
- Ma, M.; Yang, Y.; Qiu, Z.; Peng, Y.; Sun, Y.; Li, Z.; Wang, M. A locally active discrete memristor model and its application in a hyperchaotic map. Nonlinear Dyn. 2022, 107, 2935–2949. [Google Scholar] [CrossRef]
- Jin, J.; Cui, L. Fully integrated memristor and its application on the scroll-controllable hyperchaotic system. Complexity 2019, 2019, 4106398. [Google Scholar] [CrossRef] [Green Version]
- Rajagopal, K.; Vaidyanathan, S.; Karthikeyan, A.; Srinivasan, A. Complex novel 4D memristor hyperchaotic system and its synchronization using adaptive sliding mode control. Alex. Eng. J. 2018, 57, 683–694. [Google Scholar] [CrossRef]
- Wan, Q.; Zhou, Z.; Ji, W.; Wang, C.; Yu, F. Dynamic analysis and circuit realization of a novel no-equilibrium 5D memristive hyperchaotic system with hidden extreme multistability. Complexity 2020, 2020, 7106861. [Google Scholar] [CrossRef]
- Li, H.; Hua, Z.; Bao, H.; Zhu, L.; Chen, M.; Bao, B. Two-dimensional memristive hyperchaotic maps and application in secure communication. IEEE Trans. Ind. Electron. 2020, 68, 9931–9940. [Google Scholar] [CrossRef]
- Lai, Q.; Yang, L.; Liu, Y. Design and realization of discrete memristive hyperchaotic map with application in image encryption. Chaos Solitons Fractals 2022, 165, 112781. [Google Scholar] [CrossRef]
- Yu, F.; Xu, S.; Xiao, X.; Yao, W.; Huang, Y.; Cai, S.; Yin, B.; Li, Y. Dynamics analysis, FPGA realization and image encryption application of a 5D memristive exponential hyperchaotic system. Integration 2023, 90, 58–70. [Google Scholar] [CrossRef]
- Ma, M.; Xiong, K.; Li, Z.; Sun, Y. Dynamic behavior analysis and synchronization of memristor-coupled heterogeneous discrete neural Network. Mathematics 2023, 11, 375. [Google Scholar] [CrossRef]
- Li, C.; Lei, T.; Liu, Z. Offset parameter cancellation produces countless coexisting attractors. Chaos 2022, 32, 121104. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Wang, C.; Yao, W.; Lin, H. Observer-based synchronization of memristive Neural Network under DoS attacks and actuator saturation and its application to image encryption. Appl. Math. Comput. 2022, 425, 127080. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neurons with graded response have collective computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. Belarus-Agrar. Ser. 1984, 81, 3088–3092. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Das, A.; Das, P.; Roy, A.B. Chaos in a three-dimensional general model of neural network. Int. J. Bifurc. Chaos 2002, 12, 2271–2281. [Google Scholar] [CrossRef]
- Aram, Z.; Jafari, S.; Ma, J.; Sprott, J.C.; Zendehrouh, S.; Pham, V.T. Using chaotic artificial neural networks to model memory in the brain. Commun. Nonlinear Sci. Numer. Simul. 2017, 44, 449–459. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, L.; Jiang, D.; Guan, Y.; Zhang, Z. A simultaneous scrambling and diffusion color image encryption algorithm based on Hopfield chaotic neural network. IEEE Access 2019, 7, 185796–185810. [Google Scholar] [CrossRef]
- Yi, S.I.; Kumar, S.; Williams, R.S. Improved hopfield network optimization using manufacturable three-terminal electronic synapses. IEEE Trans. Circuits Syst. I-Regul. Pap. 2021, 68, 4970–4978. [Google Scholar] [CrossRef]
- Bao, B.; Chen, C.; Bao, H.; Zhang, X.; Xu, Q.; Chen, M. Dynamical effects of neuron activation gradient on Hopfield neural network, numerical analyses and hardware experiments. Int. J. Bifurc. Chaos 2019, 29, 1930010. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Chen, C.; Sun, Y.; Zhou, C.; Xu, C.; Hong, Q. Neural bursting and synchronization emulated by neural network and circuits. IEEE Trans. Circuits Syst. I-Regul. Pap. 2021, 68, 3397–3410. [Google Scholar] [CrossRef]
- Tabekoueng Njitacke, Z.; Laura Matze, C.; Fouodji Tsotsop, M.; Kengne, J. Remerging feigenbaum trees, coexisting behaviors and bursting oscillations in a novel 3D generalized Hopfield neural network. Neural Process. Lett. 2020, 52, 267–289. [Google Scholar] [CrossRef]
- Ma, J. Biophysical neurons, energy, and synapse controllability: A review. J. Zhejiang Univ.-Sci. A 2023, 24, 109–129. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Deng, Q.; Xu, C.; Deng, Z.; Zhou, C. Review on chaotic dynamics of memristive neuron and neural network. Nonlinear Dyn. 2021, 106, 959–973. [Google Scholar] [CrossRef]
- Wu, F.; Wang, C.; Jin, W.; Ma, J. Dynamical responses in a new neuron model subjected to electromagnetic induction and phase noise. Phys. A 2017, 469, 81–88. [Google Scholar] [CrossRef]
- Lv, M.; Wang, C.; Ren, G.; Ma, J.; Song, X. Model of electrical activity in a neuron under magnetic flow effect. Nonlinear Dyn. 2016, 85, 1479–1490. [Google Scholar] [CrossRef]
- Li, Q.; Tang, S.; Zeng, H.; Zhou, T. On hyperchaos in a small memristive neural network. Nonlinear Dyn. 2014, 78, 1087–1099. [Google Scholar] [CrossRef]
- Pham, V.T.; Jafari, S.; Vaidyanathan, S.; Volos, C.; Wang, X. A novel memristive neural network with hidden attractors and its circuitry implementation. China-Technol. Sci. 2016, 59, 358–363. [Google Scholar] [CrossRef]
- Bao, B.; Qian, H.; Xu, Q.; Chen, M.; Wang, J.; Yu, Y. Coexisting behaviors of asymmetric attractors in hyperbolic-type memristor based Hopfield neural network. Front. Comput. Neurosci. 2017, 11, 81. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, X.; Liu, C.; Liu, L.; Ni, J.; Yao, Y. Chaotic dynamics in a neural network under electromagnetic radiation. Nonlinear Dyn. 2018, 91, 1541–1554. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Hong, Q.; Sun, Y. A multi-stable memristor and its application in a neural network. IEEE Trans. Circuits Syst. II-Express Briefs 2020, 67, 3472–3476. [Google Scholar] [CrossRef]
- Zhang, S.; Zheng, J.; Wang, X.; Zeng, Z.; He, S. Initial offset boosting coexisting attractors in memristive multi-double-scroll Hopfield neural network. Nonlinear Dyn. 2020, 102, 2821–2841. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Xu, C.; Zhang, X.; Iu, H.H. A memristive synapse control method to generate diversified multi-structure chaotic attractors. IEEE Trans. Comput-Aided Des. Integr. Circuits Syst. 2023, 42, 942–955. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Sun, J.; Zhang, X.; Sun, Y.; Iu, H.H. Memristor-coupled asymmetric neural network, bionic modeling, chaotic dynamics analysis and encryption application. Chaos Solitons Fractals 2023, 166, 112905. [Google Scholar] [CrossRef]
- Xu, S.; Wang, X.; Ye, X. A new fractional-order chaos system of Hopfield neural network and its application in image encryption. Chaos Solitons Fractals 2022, 157, 111889. [Google Scholar] [CrossRef]
- Yu, F.; Shen, H.; Yu, Q.; Kong, X.; Sharma, P.K.; Cai, S. Privacy protection of medical data based on multi-scroll memristive Hopfield neural network. IEEE Trans. Netw. Sci. Eng. 2023, 10, 845–858. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Cui, L.; Sun, Y.; Xu, C.; Yu, F. Brain-like initial-boosted hyperchaos and application in biomedical image encryption. IEEE Trans. Ind. Inform. 2022, 18, 8839–8850. [Google Scholar] [CrossRef]
- Yu, F.; Chen, H.; Kong, X.; Yu, Q.; Cai, S.; Huang, Y.; Du, S. Dynamic analysis and application in medical digital image watermarking of a new multi-scroll neural network with quartic nonlinear memristor. Eur. Phys. J. Plus 2022, 137, 434. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Wang, C.; Cui, L.; Sun, Y.; Zhang, X.; Yao, W. Hyperchaotic memristive ring neural network and application in medical image encryption. Nonlinear Dyn. 2022, 110, 841–855. [Google Scholar] [CrossRef]
- Kandel, E.R.; Schwartz, J.H.; Jessell, T.M.; Siegelbaum, S.; Hudspeth, A.J.; Mack, S. (Eds.) Principles of Neural Science; McGraw-hill: New York, NY, USA, 2000; Volume 4, pp. 1227–1246. [Google Scholar]
- Chen, C.; Min, F.; Zhang, Y.; Bao, H. ReLU-type Hopfield neural network with analog hardware implementation. Chaos Solitons Fractals 2023, 167, 113068. [Google Scholar] [CrossRef]
- Wang, H.; Yu, Y.; Wen, G.; Zhang, S.; Yu, J. Global stability analysis of fractional-order Hopfield neural network with time delay. Neurocomputing 2015, 154, 15–23. [Google Scholar] [CrossRef]
- Debbouche, N.; Ouannas, A.; Batiha, I.M.; Grassi, G.; Kaabar, M.K.; Jahanshahi, H.; Aly, A.A.; Aljuaid, A.M. Chaotic behavior analysis of a new incommensurate fractional-order hopfield neural network system. Complexity 2021, 2021, 3394666. [Google Scholar] [CrossRef]
- Ma, C.; Mou, J.; Yang, F.; Yan, H. A fractional-order hopfield neural network chaotic system and its circuit realization. Eur. Phys. J. Plus 2020, 135, 100. [Google Scholar] [CrossRef]
- Karim, S.A.; Zamri, N.E.; Alway, A.; Kasihmuddin, M.S.M.; Ismail, A.I.M.; Mansor, M.A.; Hassan, N.F.A. Random satisfiability, A higher-order logical approach in discrete Hopfield neural network. IEEE Access 2021, 9, 50831–50845. [Google Scholar] [CrossRef]
- Rebentrost, P.; Bromley, T.R.; Weedbrook, C.; Lloyd, S. Quantum Hopfield neural network. Phys. Rev. A 2018, 98, 042308. [Google Scholar] [CrossRef] [Green Version]
- Barra, A.; Beccaria, M.; Fachechi, A. A new mechanical approach to handle generalized Hopfield neural network. Neural Netw. 2018, 106, 205–222. [Google Scholar] [CrossRef]
- Chua, L. Memristor-the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Liao, M.; Wang, C.; Sun, Y.; Lin, H.; Xu, C. Memristor-based affective associative memory neural network circuit with emotional gradual processes. Neural Comput. Appl. 2022, 34, 13667–13682. [Google Scholar] [CrossRef]
- Tan, Y.; Wang, C. A simple locally active memristor and its application in HR neurons. Chaos 2020, 30, 053118. [Google Scholar] [CrossRef] [PubMed]
- Deng, Z.; Wang, C.; Lin, H.; Sun, Y. A memristive spiking neural network circuit with selective supervised attention algorithm. In IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems; IEEE: Piscataway, NJ, USA, 2023. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.; Midya, R.; Xia, Q.; Yang, J.J. Review of memristor devices in neuromorphic computing, materials sciences and device challenges. J. Phys. D-Appl. Phys. 2018, 51, 503002. [Google Scholar] [CrossRef]
- Hong, Q.; Shi, Z.; Sun, J.; Du, S. Memristive self-learning logic circuit with application to encoder and decoder. Neural Comput. Appl. 2021, 33, 4901–4913. [Google Scholar] [CrossRef]
- Wen, Z.; Wang, C.; Deng, Q.; Lin, H. Regulating memristive neuronal dynamical properties via excitatory or inhibitory magnetic field coupling. Nonlinear Dyn. 2022, 110, 3823–3835. [Google Scholar] [CrossRef]
- Lv, M.; Ma, J. Multiple modes of electrical activities in a new neuron model under electromagnetic radiation. Neurocomputing 2016, 205, 375–381. [Google Scholar] [CrossRef]
- Xu, Q.; Ju, Z.; Ding, S.; Feng, C.; Chen, M.; Bao, B. Electromagnetic induction effects on electrical activity within a memristive Wilson neuron model. Cogn. Neurodynamics 2022, 16, 1221–1231. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, C.; Sun, Y.; Yao, W.; Lin, H. Cluster output synchronization for memristive neural network. Inf. Sci. 2022, 589, 459–477. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, C.; Deng, Q. Rulkov neural network coupled with discrete memristors. Networks 2022, 33, 214–232. [Google Scholar] [CrossRef]
- Faradja, P.; Qi, G. Analysis of multistability, hidden chaos and transient chaos in brushless DC motor. Chaos Solitons Fractals 2020, 132, 109606. [Google Scholar] [CrossRef]
- Chen, M.; Li, M.; Yu, Q.; Bao, B.; Xu, Q.; Wang, J. Dynamics of self-excited attractors and hidden attractors in generalized memristor-based Chua’s circuit. Nonlinear Dyn. 2015, 81, 215–226. [Google Scholar] [CrossRef]
- Jafari, S.; Rajagopal, K.; Hayat, T.; Alsaedi, A.; Pham, V.T. Simplest megastable chaotic oscillator. Int. J. Bifurc. Chaos 2019, 29, 1950187. [Google Scholar] [CrossRef]
- Gu, S.; He, S.; Wang, H.; Du, B. Analysis of three types of initial offset-boosting behavior for a new fractional-order dynamical system. Chaos Solitons Fractals 2021, 143, 110613. [Google Scholar] [CrossRef]
- Njitacke, Z.T.; Kengne, J.; Fotsin, H.B. A plethora of behaviors in a memristor based Hopfield neural network. Int. J. Dyn. Syst. Cont. 2019, 7, 36–52. [Google Scholar] [CrossRef]
- Xu, Q.; Song, Z.; Bao, H.; Chen, M.; Bao, B. Two-neuron-based non-autonomous memristive Hopfield neural network, numerical analyses and hardware experiments. AEU-Int. J. Electron. Commun. 2018, 96, 66–74. [Google Scholar] [CrossRef]
- Li, R.; Dong, E.; Tong, J.; Wang, Z. A novel multiscroll memristive Hopfield neural network. Int. J. Bifurc. Chaos 2022, 32, 2250130. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Zhang, H.; Chen, G. Design and analysis of multiscroll memristive hopfield neural network with adjustable memductance and application to image encryption. In IEEE Transactions on Neural Networks and Learning Systems; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Hua, M.; Bao, H.; Wu, H.; Xu, Q.; Bao, B. A single neuron model with memristive synaptic weight. Chin. J. Phys. 2022, 76, 217–227. [Google Scholar] [CrossRef]
- Doubla, I.S.; Ramakrishnan, B.; Njitacke, Z.T.; Kengne, J.; Rajagopal, K. Hidden extreme multistability and its control with selection of a desired attractor in a non-autonomous Hopfield neuron. AEU-Int. J. Electron. Commun. 2022, 144, 154059. [Google Scholar] [CrossRef]
- Doubla, I.S.; Ramakrishnan, B.; Tabekoueng, Z.N.; Kengne, J.; Rajagopal, K. Infinitely many coexisting hidden attractors in a new hyperbolic-type memristor-based HNN. Eur. Phys. J.-Spec. Top. 2022, 231, 2371–2385. [Google Scholar] [CrossRef]
- Bao, H.; Hua, M.; Ma, J.; Chen, M.; Bao, B. Offset-control plane coexisting behaviors in two-memristor-based Hopfield neural network. In IEEE Transactions on Industrial Electronics; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Shen, H.; Yu, F.; Kong, X.; Mokbel, A.A.M.; Wang, C.; Cai, S. Dynamics study on the effect of memristive autapse distribution on Hopfield neural network. Chaos 2022, 32, 083133. [Google Scholar] [CrossRef] [PubMed]
- Parastesh, F.; Jafari, S.; Azarnoush, H.; Hatef, B.; Namazi, H.; Dudkowski, D. Chimera in a network of memristor-based Hopfield neural network. Eur. Phys. J.-Spec. Top. 2019, 228, 2023–2033. [Google Scholar] [CrossRef]
- Ding, D.; Luo, J.; Shan, X.; Hu, Y.; Yang, Z.; Ding, L. Coexisting behaviors of a fraction-order novel hyperbolic-type memristor Hopfield neuron network based on three neurons. Int. J. Mod. Phys. B 2020, 34, 2050302. [Google Scholar] [CrossRef]
- Wang, Z.; Parastesh, F.; Rajagopal, K.; Hamarash, I.I.; Hussain, I. Delay-induced synchronization in two coupled chaotic memristive Hopfield neural network. Chaos Solitons Fractals 2020, 134, 109702. [Google Scholar] [CrossRef]
- Leng, Y.; Yu, D.; Hu, Y.; Yu, S.S.; Ye, Z. Dynamic behaviors of hyperbolic-type memristor-based Hopfield neural network considering synaptic crosstalk. Chaos 2020, 30, 033108. [Google Scholar] [CrossRef] [PubMed]
- Boya, B.F.B.A.; Kengne, J.; Kenmoe, G.D.; Effa, J.Y. Four-scroll attractor on the dynamics of a novel Hopfield neural network based on bi-neurons without bias current. Heliyon 2022, 8, e11046. [Google Scholar] [CrossRef] [PubMed]
- Bao, H.; Chen, Z.; Cai, J.; Xu, Q.; Bao, B. Memristive cyclic three-neuron-based neural network with chaos and global coexisting attractors. Sci. China-Technol. Sci. 2022, 65, 2582–2592. [Google Scholar] [CrossRef]
- Chen, C.; Min, F. ReLU-type memristor-based Hopfield neural network. Eur. Phys. J.-Spec. Top. 2022, 231, 2979–2992. [Google Scholar] [CrossRef]
- Ma, T.; Mou, J.; Yan, H.; Cao, Y. A new class of Hopfield neural network with double memristive synapses and its DSP implementation. Eur. Phys. J. Plus 2022, 137, 1135. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kuate, P.D.K. Generating grid multi-scroll attractors in memristive neural network. IEEE Trans. Circuits Syst. I-Regul. Pap. 2022, 70, 1324–1336. [Google Scholar] [CrossRef]
- Lai, Q.; Lai, C.; Kuate, P.D.K.; Li, C.; He, S. Chaos in a simplest cyclic memristive neural network. Int. J. Bifurc. Chaos 2022, 32, 2250042. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Yang, X.; Zi, X.; Xiao, F. A tristable locally active memristor and its application in Hopfield neural network. Nonlinear Dyn. 2022, 108, 1697–1717. [Google Scholar] [CrossRef]
- Ding, D.; Xiao, H.; Yang, Z.; Luo, H.; Hu, Y.; Zhang, X.; Liu, Y. Coexisting multi-stability of Hopfield neural network based on coupled fractional-order locally active memristor and its application in image encryption. Nonlinear Dyn. 2022, 108, 4433–4458. [Google Scholar] [CrossRef]
- Yu, F.; Kong, X.; Mokbel, A.A.M.; Yao, W.; Cai, S. Complex dynamics, hardware implementation and image encryption application of multiscroll memeristive Hopfield neural network with a novel local active memeristor. IEEE Trans. Circuits Syst. II-Express Briefs 2022, 70, 326–330. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C. Influences of electromagnetic radiation distribution on chaotic dynamics of a neural network. Appl. Math. Comput. 2020, 369, 124840. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Tan, Y. Hidden extreme multistability with hyperchaos and transient chaos in a Hopfield neural network affected by electromagnetic radiation. Nonlinear Dyn. 2020, 99, 2369–2386. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Sun, Y.; Wang, T. Generating n-scroll chaotic attractors from a memristor-based magnetized Hopfield neural network. IEEE Trans. Circuits Syst. II-Express Briefs 2022, 70, 311–315. [Google Scholar] [CrossRef]
- Wan, Q.; Li, F.; Chen, S.; Yang, Q. Symmetric multi-scroll attractors in magnetized Hopfield neural network under pulse controlled memristor and pulse current stimulation. Chaos Solitons Fractals 2023, 169, 113259. [Google Scholar] [CrossRef]
- Wan, Q.; Yan, Z.; Li, F.; Liu, J.; Chen, S. Multistable dynamics in a Hopfield neural network under electromagnetic radiation and dual bias currents. Nonlinear Dyn. 2022, 109, 2085–2101. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Yao, W.; Tan, Y. Chaotic dynamics in a neural network with different types of external stimuli. Commun. Nonlinear Sci. Numer. Simul. 2020, 90, 105390. [Google Scholar] [CrossRef]
- Chen, C.; Chen, J.; Bao, H.; Chen, M.; Bao, B. Coexisting multi-stable patterns in memristor synapse-coupled Hopfield neural network with two neurons. Nonlinear Dyn. 2019, 95, 3385–3399. [Google Scholar] [CrossRef]
- Chen, C.; Bao, H.; Chen, M.; Xu, Q.; Bao, B. Non-ideal memristor synapse-coupled bi-neuron Hopfield neural network, Numerical simulations and breadboard experiments. AEU-Int. J. Electron. Commun. 2019, 111, 152894. [Google Scholar] [CrossRef]
- Chen, C.; Min, F.; Zhang, Y.; Bao, B. Memristive electromagnetic induction effects on Hopfield neural network. Nonlinear Dyn. 2021, 106, 2559–2576. [Google Scholar] [CrossRef]
- Wan, Q.; Yan, Z.; Li, F.; Chen, S.; Liu, J. Complex dynamics in a Hopfield neural network under electromagnetic induction and electromagnetic radiation. Chaos 2022, 32, 073107. [Google Scholar] [CrossRef] [PubMed]
- Eftekhari, L.; Amirian, M.M. Stability analysis of fractional order memristor synapse-coupled hopfield neural network with ring structure. Cogn. Neurodynamics 2022. [Google Scholar] [CrossRef]
- Yu, F.; Kong, X.; Chen, H.; Yu, Q.; Cai, S.; Huang, Y.; Du, S. A 6D fractional-order memristive Hopfield neural network and its application in image encryption. Front. Phys. 2022, 10, 847385. [Google Scholar] [CrossRef]
- Dong, T.; Gong, X.; Huang, T. Zero-Hopf Bifurcation of a memristive synaptic Hopfield neural network with time delay. Neural Netw. 2022, 149, 146–156. [Google Scholar] [CrossRef]
- Ding, S.; Wang, N.; Bao, H.; Chen, B.; Wu, H.; Xu, Q. Memristor synapse-coupled piecewise-linear simplified Hopfield neural network, Dynamics analysis and circuit implementation. Chaos Solitons Fractals 2023, 166, 112899. [Google Scholar] [CrossRef]
- Yu, F.; Yu, Q.; Chen, H.; Kong, X.; Mokbel, A.A.M.; Cai, S.; Du, S. Dynamic analysis and audio encryption application in IoT of a multi-scroll fractional-order memristive Hopfield neural network. Fractal Fract. 2022, 6, 370. [Google Scholar] [CrossRef]
- Hu, S.G.; Liu, Y.; Liu, Z.; Chen, T.P.; Wang, J.J.; Yu, Q.; Deng, L.J.; Yin, Y.; Hosaka, S. Associative memory realized by a reconfigurable memristive Hopfield neural network. Nat. Commun. 2015, 6, 7522. [Google Scholar] [CrossRef] [Green Version]
- Fahimi, Z.; Mahmoodi, M.R.; Nili, H.; Polishchuk, V.; Strukov, D.B. Combinatorial optimization by weight annealing in memristive hopfield networks. Sci. Rep. 2021, 11, 16383. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Ding, R. A novel locally active time-delay memristive Hopfield neural network and its application. Eur. Phys. J.-Spec. Top. 2022, 231, 3005–3017. [Google Scholar] [CrossRef]
- Hong, Q.; Yan, R.; Wang, C.; Sun, J. Memristive circuit implementation of biological nonassociative learning mechanism and its applications. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 1036–1050. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Xu, C.; Sun, J.; Deng, Q. A memristor-based associative memory neural network circuit with emotion effect. Neural Comput. Applic. 2023. [Google Scholar] [CrossRef]
- Sun, J.; Kang, K.; Sun, Y.; Hong, Q.; Wang, C. A multi-value 3D crossbar array nonvolatile memory based on pure memristors. Eur. Phys. J.-Spec. Top. 2022, 231, 3119–3130. [Google Scholar] [CrossRef]
- Huang, L.L.; Zhang, Y.; Xiang, J.H.; Liu, J. Extreme multistability in a Hopfield neural network based on two biological neuronal systems. IEEE Trans. Circuits Syst. II-Express Briefs 2022, 69, 4568–4572. [Google Scholar] [CrossRef]
- Ostrovskii, V.; Fedoseev, P.; Bobrova, Y.; Butusov, D. Structural and parametric identification of knowm memristors. Nanomaterials 2021, 12, 63. [Google Scholar] [CrossRef]
- Yuan, F.; Li, S.; Deng, Y.; Li, Y.; Chen, G. Cu-doped TiO2− x nanoscale memristive applications in chaotic circuit and true random number generator. IEEE Trans. Ind. Electron. 2022, 70, 4120–4127. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, H.; Wang, C.; Yu, F.; Sun, J.; Du, S.; Deng, Z.; Deng, Q. A Review of Chaotic Systems Based on Memristive Hopfield Neural Networks. Mathematics 2023, 11, 1369. https://doi.org/10.3390/math11061369
Lin H, Wang C, Yu F, Sun J, Du S, Deng Z, Deng Q. A Review of Chaotic Systems Based on Memristive Hopfield Neural Networks. Mathematics. 2023; 11(6):1369. https://doi.org/10.3390/math11061369
Chicago/Turabian StyleLin, Hairong, Chunhua Wang, Fei Yu, Jingru Sun, Sichun Du, Zekun Deng, and Quanli Deng. 2023. "A Review of Chaotic Systems Based on Memristive Hopfield Neural Networks" Mathematics 11, no. 6: 1369. https://doi.org/10.3390/math11061369
APA StyleLin, H., Wang, C., Yu, F., Sun, J., Du, S., Deng, Z., & Deng, Q. (2023). A Review of Chaotic Systems Based on Memristive Hopfield Neural Networks. Mathematics, 11(6), 1369. https://doi.org/10.3390/math11061369








