Energy Flow Analysis Model of High-Frequency Vibration Response for Plates with Free Layer Damping Treatment
Abstract
:1. Introduction
2. Energy Flow Analysis Model for the Plate with FFLD Treatment
2.1. Equivalent Model of the Plate with FLD Treatment
2.2. Energy Density Equation of the FLD Plate
3. Energy Flow Analysis Model for the Plate with PFLD Treatment
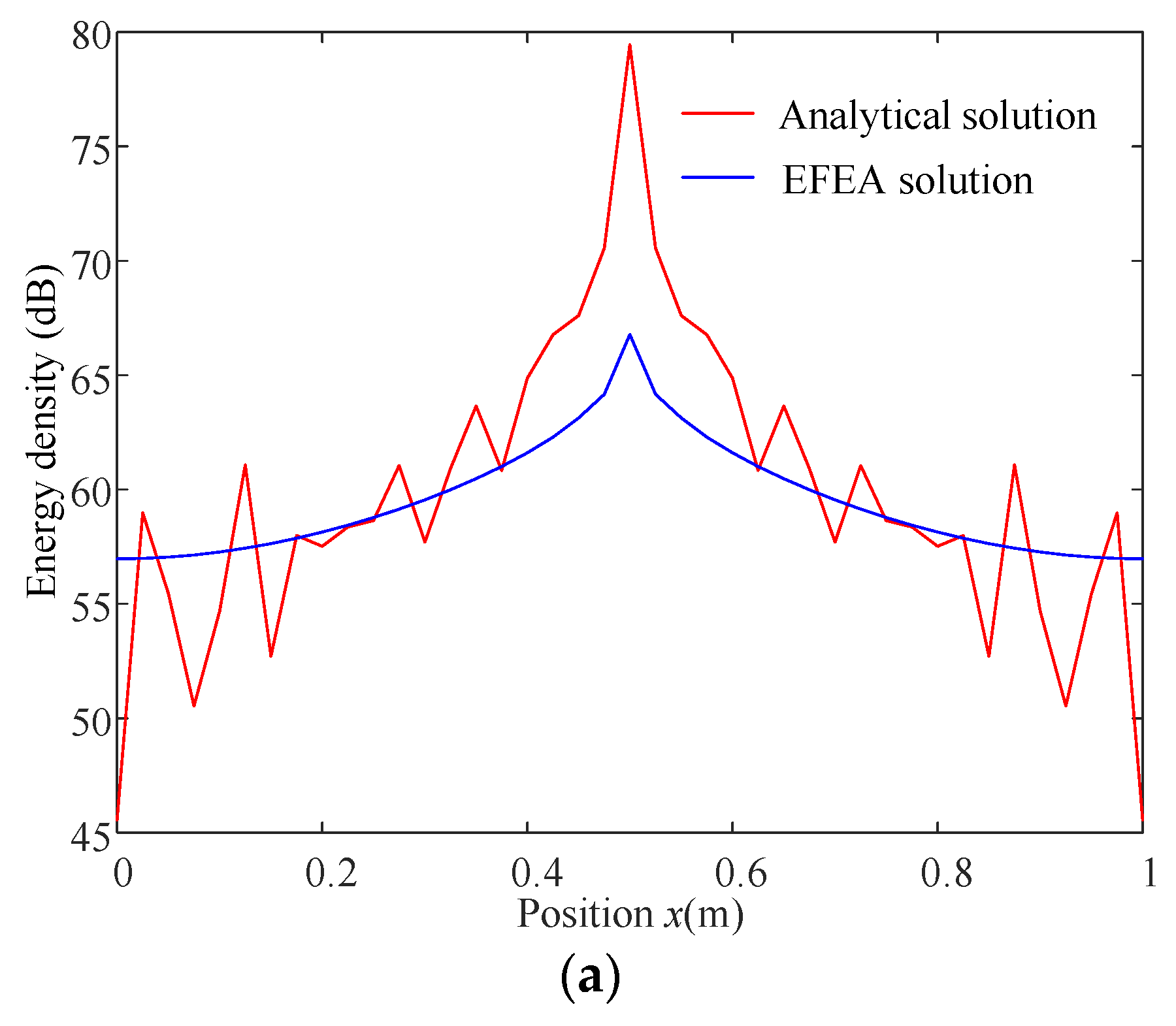
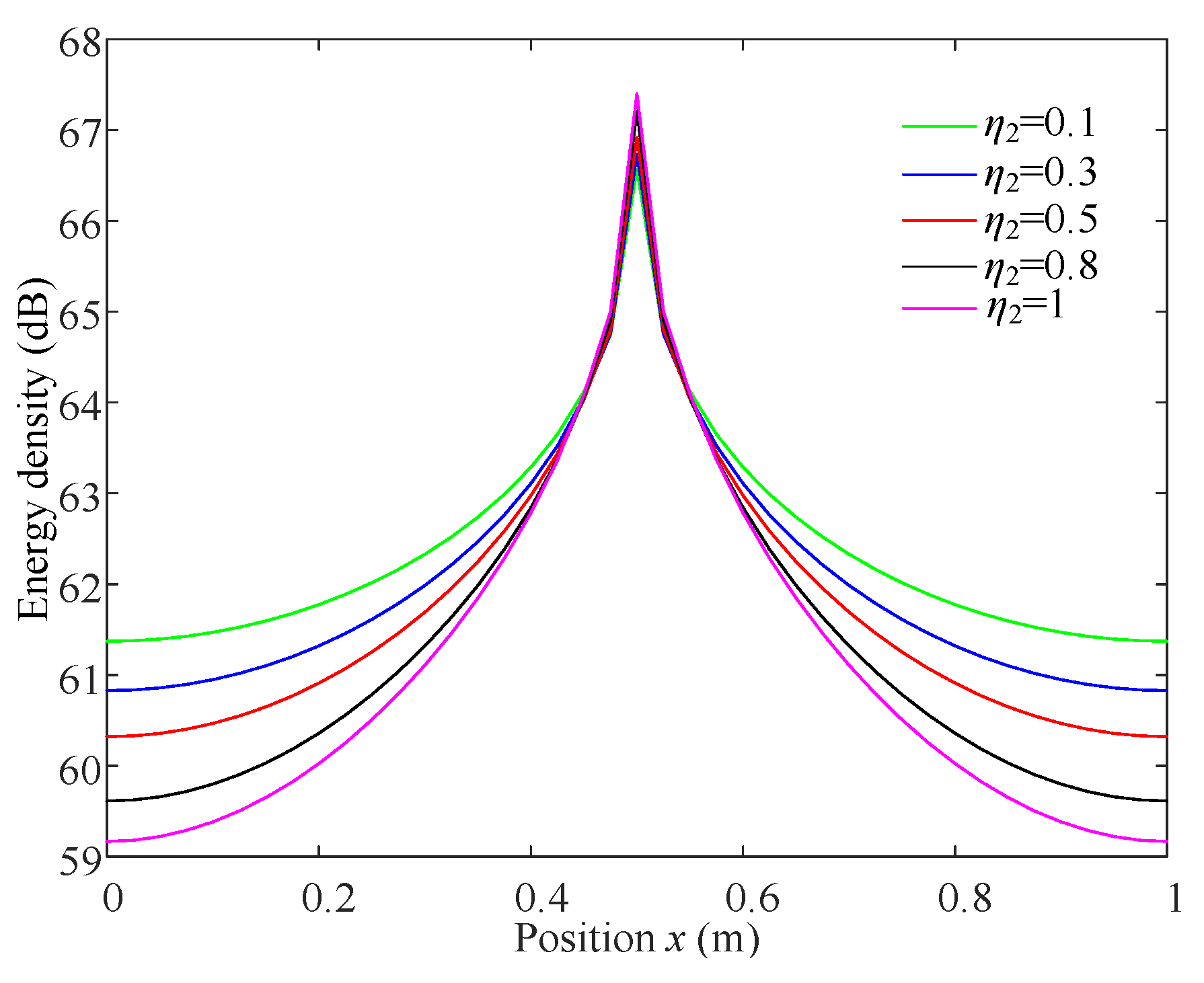
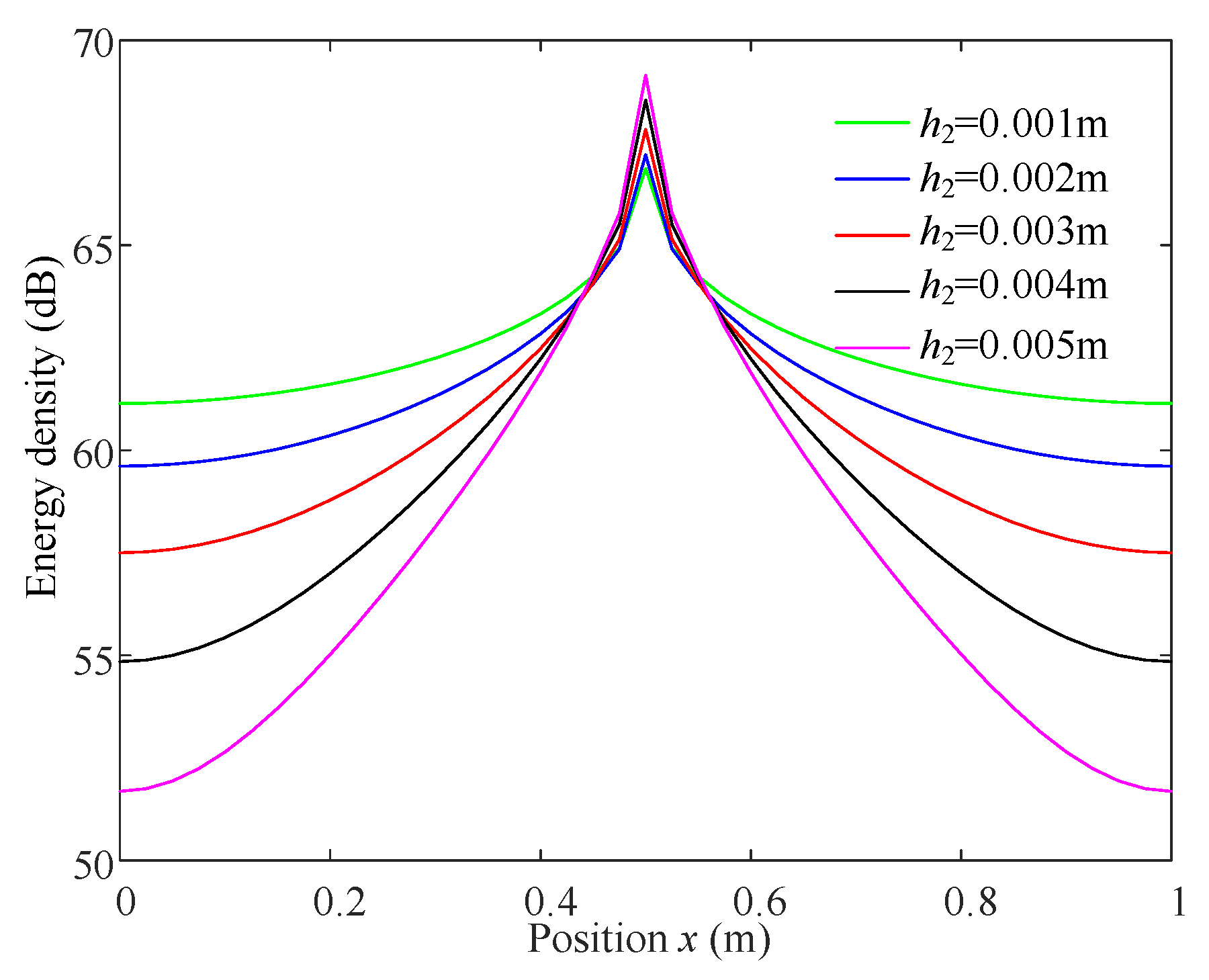
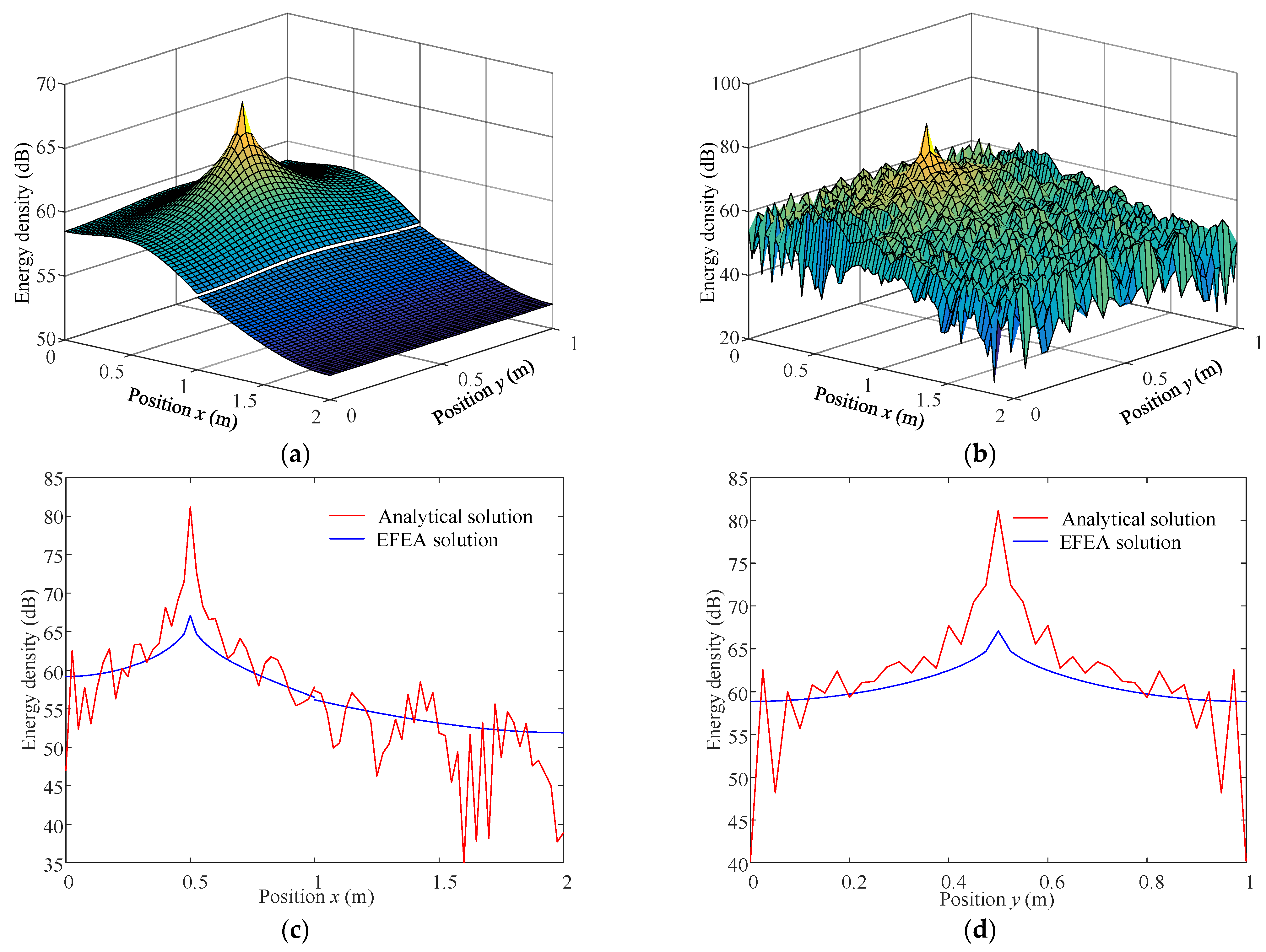
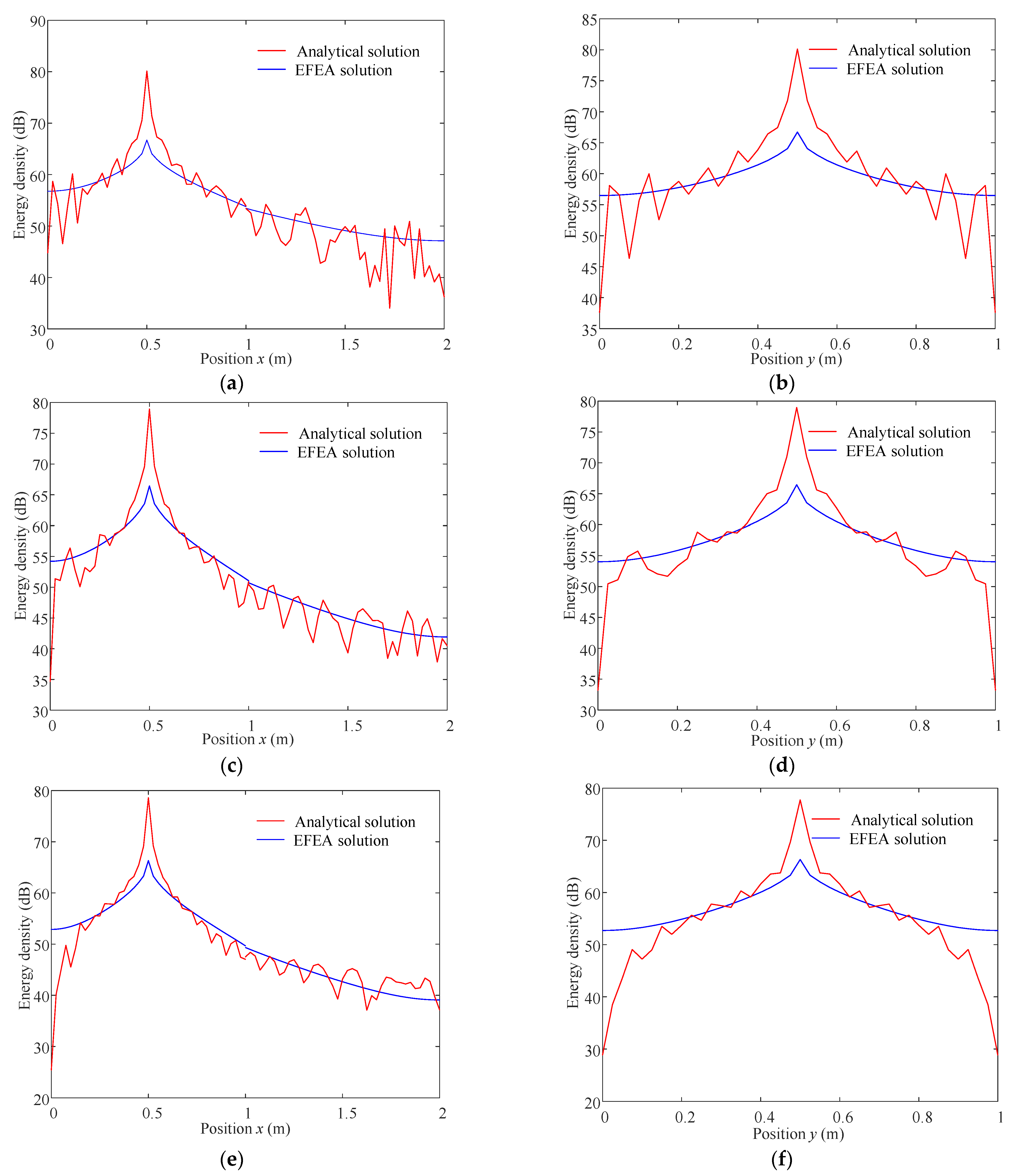
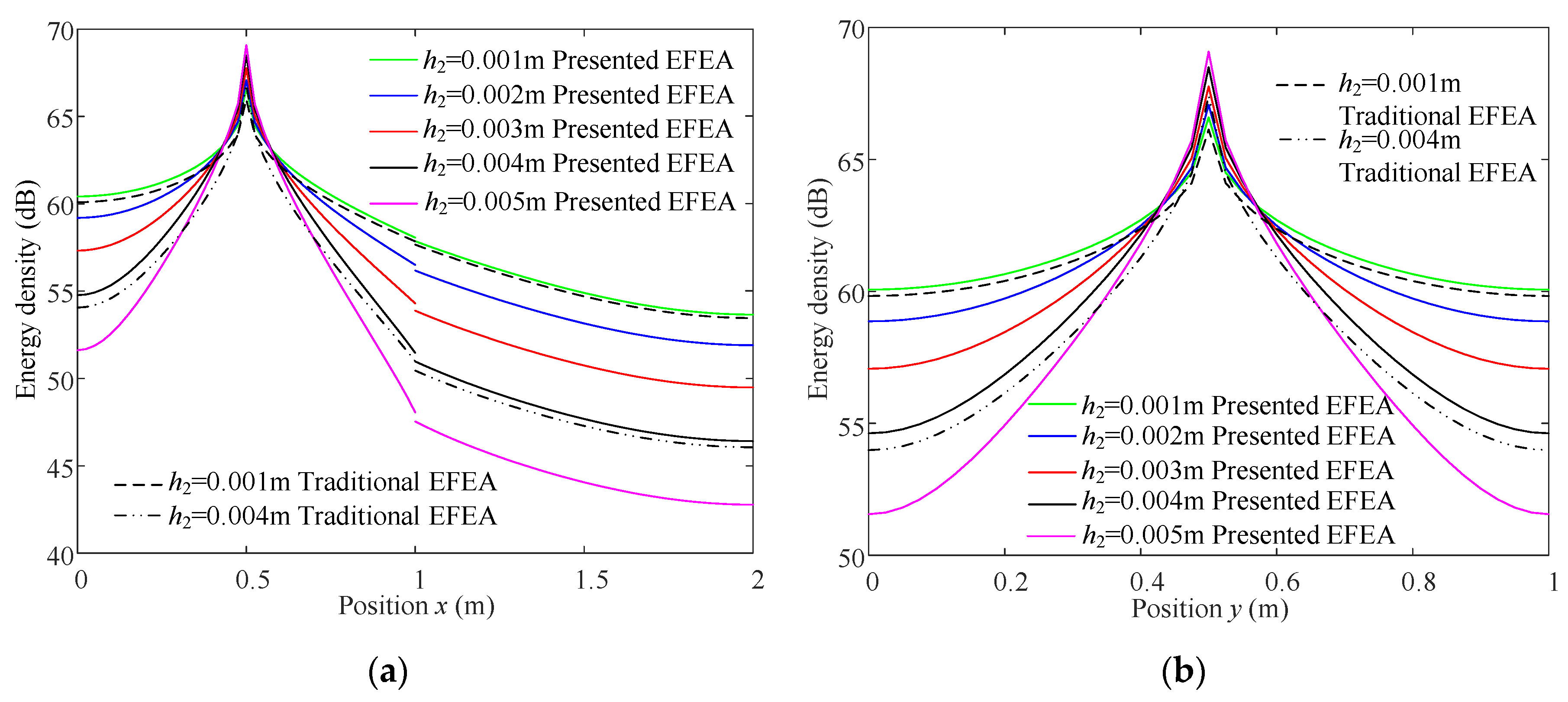
4. Verification and Discussion
4.1. Plate with FFLD Treatment
4.2. Plate with PFLD Treatment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, H.D.; Hao, Z.W.; Liu, W.; Ding, J.F.; Sun, Y.; Zhang, Q.H.; Liu, Y.Z. The shock environment prediction of satellite in the process of satellite-rocket separation. Acta Astronaut. 2019, 159, 112–122. [Google Scholar] [CrossRef]
- Wang, H.Z.; Yu, K.P.; Zhang, Z.Q.; Zeng, Y.X.; Wang, X. Prediction of the acoustic-vibration environment of an instrument cabin by using the energy finite element method. J. Vib. Shock. 2019, 38, 143–148. [Google Scholar]
- Zhao, H.D.; Ding, J.F.; Hao, Z.W.; Liu, W.; Sun, Y.; Liu, Y.Z. Study on prediction methods of pyroshock environment for complex spacecraft structures. J. Aircr. 2020, 41, 35–43. [Google Scholar]
- Yilmaz, I.; Arslan, E.; Cavdar, K. Experimental and numerical investigation of sound radiation from thin metal plates with different thickness values of free layer damping layers. Acoust. Austa. 2021, 49, 1–14. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Najafi, A. Damping characterization and viscoelastic behavior of laminated polymer matrix composites using a modified classical lamination theory. Exp. Mech. 2007, 47, 831–839. [Google Scholar] [CrossRef]
- Xia, X.J.; Xu, Z.M.; Lai, S.Y.; Zhang, Z.F.; He, Y.S. Responses of unconstrained damped vibro-acoustic systems using the wave based prediction technique. J. Vib. Shock. 2017, 36, 158–163. [Google Scholar]
- Liu, L.; Cooradi, R.; Ripamonti, F.; Rao, Z.S. Wave based method for flexural vibration of thin plate with general elastically restrained edges. J. Sound Vib. 2020, 483, 115468. [Google Scholar] [CrossRef]
- Petrone, G.; Melillo, G.; Laudiero, A.; De Rosa, S. A Statistical Energy Analysis (SEA) model of a fuselage section for the prediction of the internal Sound Pressure Level (SPL) at cruise flight conditions. Aerosp. Sci. Technol. 2019, 88, 340–349. [Google Scholar] [CrossRef]
- Gupta, P.; Parey, A. Prediction of sound transmission loss of cylindrical acoustic enclosure using statistical energy analysis and its experimental validation. J. Vib. Control 2022, 151, 544. [Google Scholar] [CrossRef] [PubMed]
- Cherif, R.; Wareing, A.; Atalla, N. Sound transmission paths through a statistical energy analysis model of mechanically linked aircraft double-walls. Noise Control Eng. J. 2020, 69, 411–421. [Google Scholar] [CrossRef]
- Poblet-Puig, J. Estimation of the coupling loss factors of structural junctions with in-plane waves by means of the inverse statistical energy analysis problem. J. Sound Vib. 2021, 493, 133–145. [Google Scholar] [CrossRef]
- Chen, Q.; Fei, Q.G.; Li, Y.B.; Wu, S.Q.; Zhang, P. Prediction of statistical energy analysis parameters in thermal environment. J. Spacecraft. Rockets 2019, 56, 687–694. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, P.; Li, Y.B.; Wu, S.Q.; Fei, Q.G. Effect of aspect ratio on statistical energy analysis parameters of L-shaped folded plate under thermal environment. J. Vib. Shock. 2018, 37, 191–196. [Google Scholar]
- Hu, W.L.; Chen, H.B.; Zhong, Q. Effects of axial force on coupling loss factor of beam structures. J. Vib. Shock. 2020, 39, 24–30. [Google Scholar]
- Gao, R.X.; Zhang, Y.H.; Kenndy, D. Optimization of mid-frequency vibration for complex built-up systems using the hybrid finite element-statistical energy analysis method. Eng. Optim. 2019, 2019, 1691546. [Google Scholar] [CrossRef]
- Zhang, L.; Li, X.H. Prediction of transient high-frequency vibration response of line-coupled plates. Acta Acust. 2018, 43, 61–68. [Google Scholar]
- Zhang, W.B.; Chen, H.L.; Zhu, D.H.; Kong, X.J. The thermal effects on high-frequency vibration of beams using energy flow analysis. J. Sound Vib. 2014, 333, 2588–2600. [Google Scholar] [CrossRef]
- Wang, D.; Xie, M.X.; Li, Y.M. High-frequency dynamic analysis of plates in thermal environments based on energy finite element method. Shock. Vib. 2015, 2015, 157208. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.L.; Yang, Z.C.; Guo, N.; Zheng, G.W. An energy finite element method for high frequency vibration analysis of beams with axial force. Appl. Math. Model. 2018, 61, 521–539. [Google Scholar] [CrossRef]
- Yan, X.Y. Energy Finite Element Analysis Developments for High Frequency Vibration Analysis of Composite Structures. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2008. [Google Scholar]
- Liu, Z.H.; Niu, J.C. Vibrational energy flow model for functionally graded beams. Compos. Struct. 2018, 186, 17–28. [Google Scholar] [CrossRef]
- Liu, Z.H.; Niu, J.C.; Jia, R.H. Vibrational energy flow model for high-frequency vibration of beams in thermal-gradient environment. CJA 2022, 43, 592–604. [Google Scholar]
- Yong, H.K.; June, Y.K. Energy flow analysis of equivalent fluid models for porous media. J. Acoust. Soc. Am. 2021, 150, 2782. [Google Scholar]
- Cho, P.E. Energy Flow Analysis of Coupled Structures. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 1993. [Google Scholar]
- Liu, Z.H.; Niu, J.C.; Gao, X. An improved approach for analysis of coupled structures in Energy Finite Element Analysis using the coupling loss factor. Comput. Struct. 2018, 210, 69–86. [Google Scholar] [CrossRef]
- Park, Y.H. Energy flow finite element analysis of general Mindlin plate structures coupled at arbitrary angles. J. Nav. Archit. Mar. Eng. 2018, 11, 435–447. [Google Scholar] [CrossRef]
- Liu, H.L.; Zhang, Z.Y.; Li, B.T.; Xie, M.; Zhen, S. Topology optimization of high frequency vibration problems using the EFEM-based approach. Thin Wall. Struct. 2021, 160, 124–136. [Google Scholar] [CrossRef]
- Yao, S.J.; Hong, S.Y.; Song, J.H.; Kwon, H.W. Vibrational energy flow models for dilatational wave in elastic solids. Adv. Mech. Eng. 2017, 9, 1–9. [Google Scholar] [CrossRef]
- Zheng, X.; Dai, W.Q.; Qiu, Y.; Hao, Z.Y. Prediction and energy contribution analysis of interior noise in a high-speed train based on modified energy finite element analysis. Mech. Syst. Signal. Process. 2019, 126, 439–457. [Google Scholar] [CrossRef]
- Chen, Z.L.; Yang, Z.C.; Wang, Y.Y.; Zhang, X. A high-frequency shock response analysis method based on energy finite element method and virtual mode synthesis and simulation. CJA 2018, 39, 182–191. [Google Scholar]
- Zhao, H.D.; Ding, J.F.; Zhu, W.H.; Sun, Y.; Liu, Y.Z. Shock response prediction of the typical structure in spacecraft based on the hybrid modeling techniques. Aerosp. Sci. Technol. 2019, 89, 460–467. [Google Scholar] [CrossRef]
- Chen, Z.L.; Yang, Z.C.; Gu, Y.S.; Guo, S.J. An energy flow model for high-frequency vibration analysis of two-dimensional panels in supersonic airflow. Math. Model. 2019, 76, 495–512. [Google Scholar] [CrossRef]
- Han, J.B.; Hong, S.Y.; Song, J.H.; Kwon, H.W. Vibrational energy flow models for the rayleigh-love and rayleigh-bishop rods. J. Sound Vib. 2014, 333, 520–540. [Google Scholar] [CrossRef]
- Han, J.B.; Hong, S.Y.; Song, J.H.; Kwon, H.W. Vibrational energy flow models for the 1-D high damping system. J. Mech. Sci. Technol. 2013, 27, 2659–2671. [Google Scholar] [CrossRef]
- Teng, X.Y.; Liu, N.; Jiang, X.D. Analytical model of high-frequency energy flow response for a beam with free layer damping. Adv. Mech. Eng. 2020, 12, 1–12. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, X.; Han, Y.; Jiang, X.; Chen, X.; Zhou, M. Energy Flow Analysis Model of High-Frequency Vibration Response for Plates with Free Layer Damping Treatment. Mathematics 2023, 11, 1379. https://doi.org/10.3390/math11061379
Teng X, Han Y, Jiang X, Chen X, Zhou M. Energy Flow Analysis Model of High-Frequency Vibration Response for Plates with Free Layer Damping Treatment. Mathematics. 2023; 11(6):1379. https://doi.org/10.3390/math11061379
Chicago/Turabian StyleTeng, Xiaoyan, Yuedong Han, Xudong Jiang, Xiangyang Chen, and Meng Zhou. 2023. "Energy Flow Analysis Model of High-Frequency Vibration Response for Plates with Free Layer Damping Treatment" Mathematics 11, no. 6: 1379. https://doi.org/10.3390/math11061379




