A Novel Multiobjective Formulation for Optimal Wind Speed Modeling via a Mixture Probability Density Function
Abstract
:1. Introduction
2. Materials and methods
2.1. Probability Density Functions
2.2. Proposed Mixture Probability Density Function
2.3. Probabilistic Indices
2.4. Problem Formulation
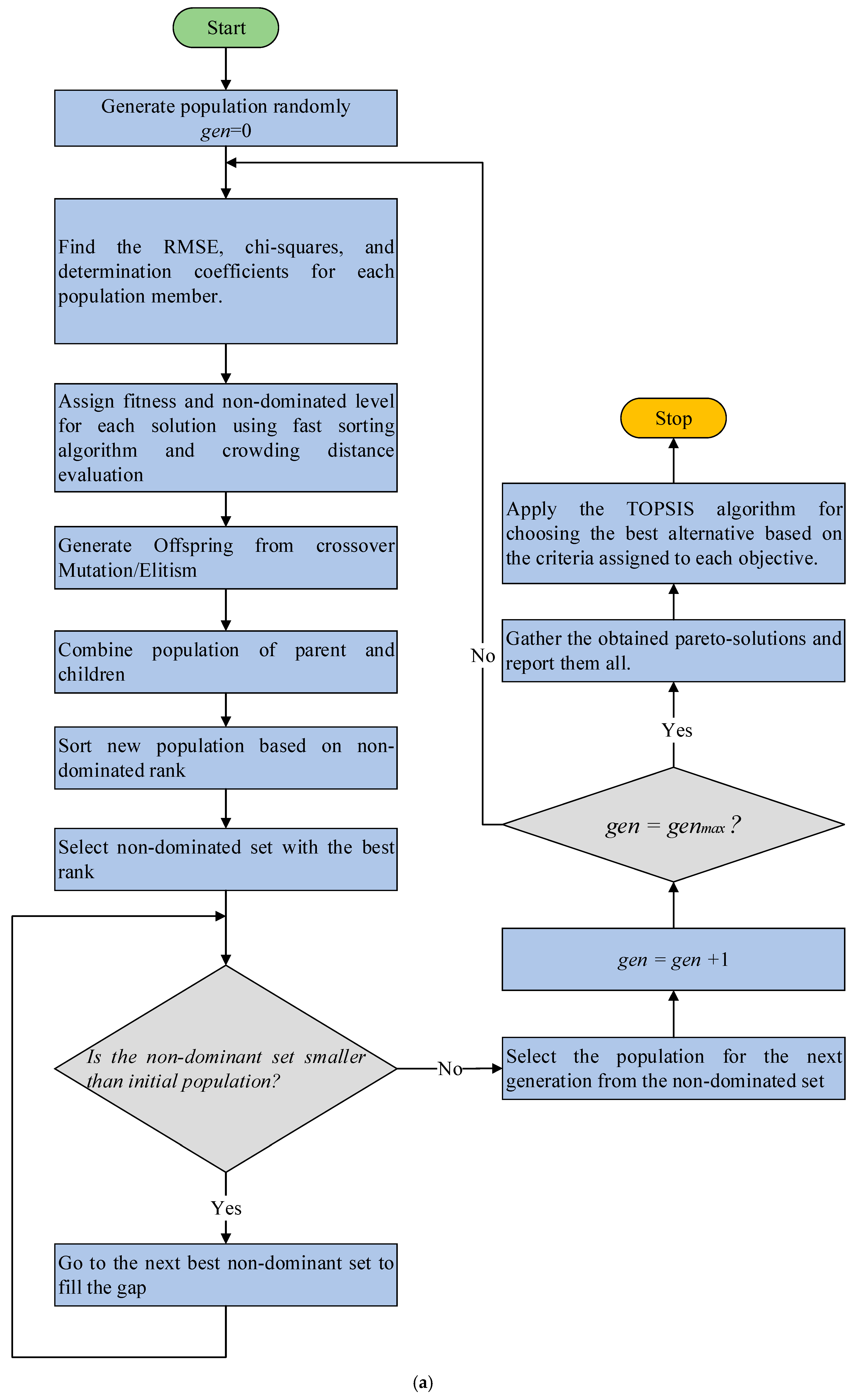
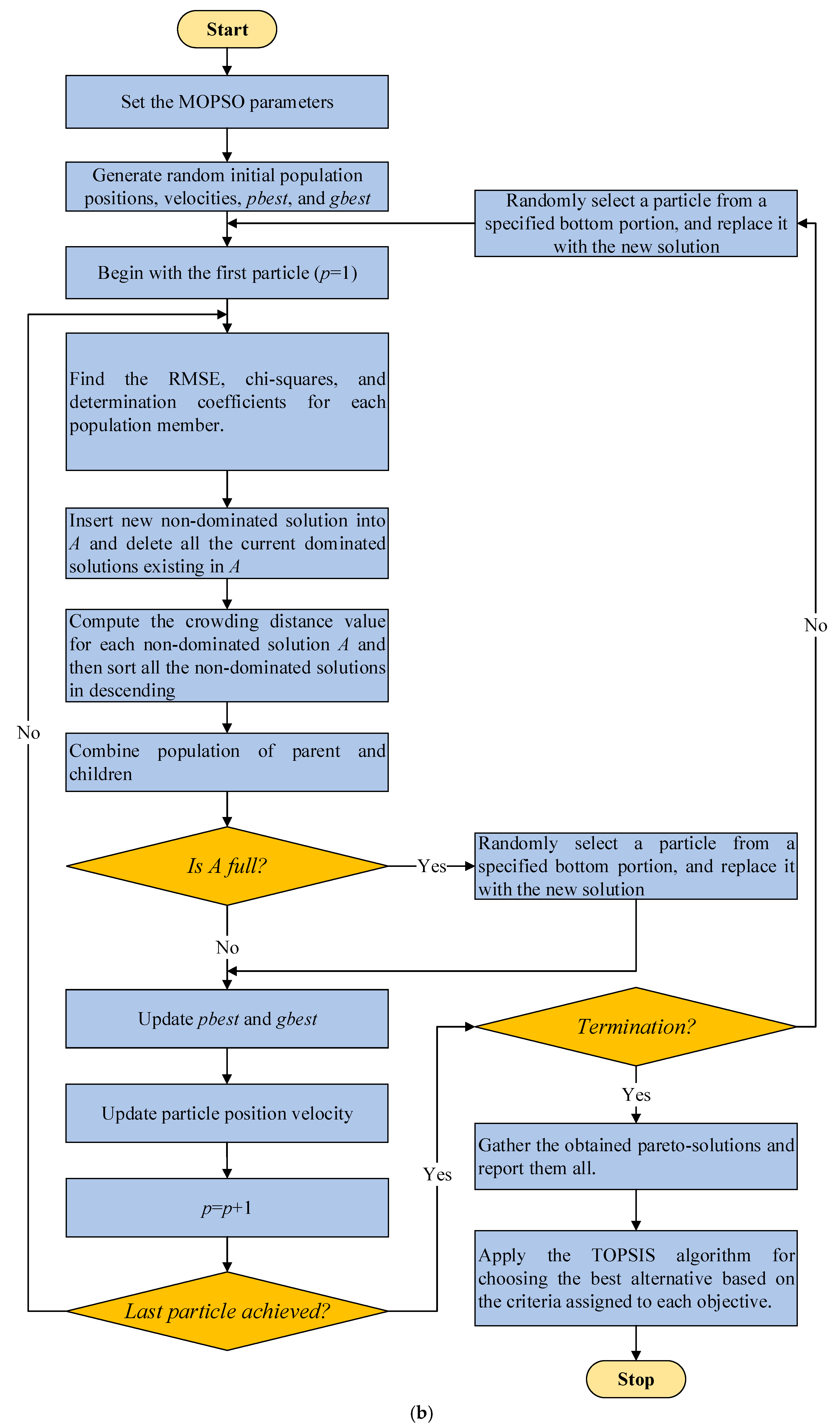
| Algorithm 1: Pseudo-code for the proposed multicriteria optimization process to optimally fit wind speed data to the proposed mixture probability density function. |
|
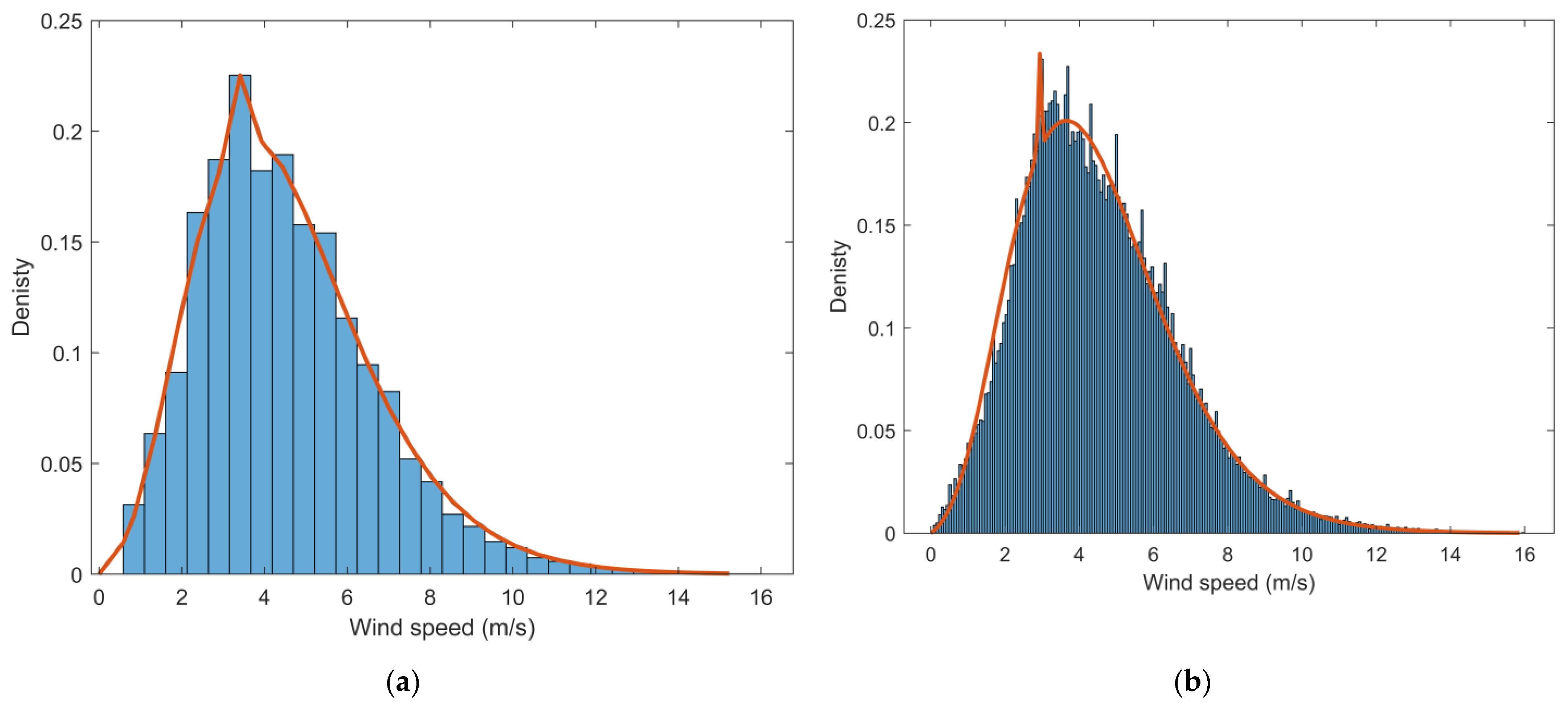
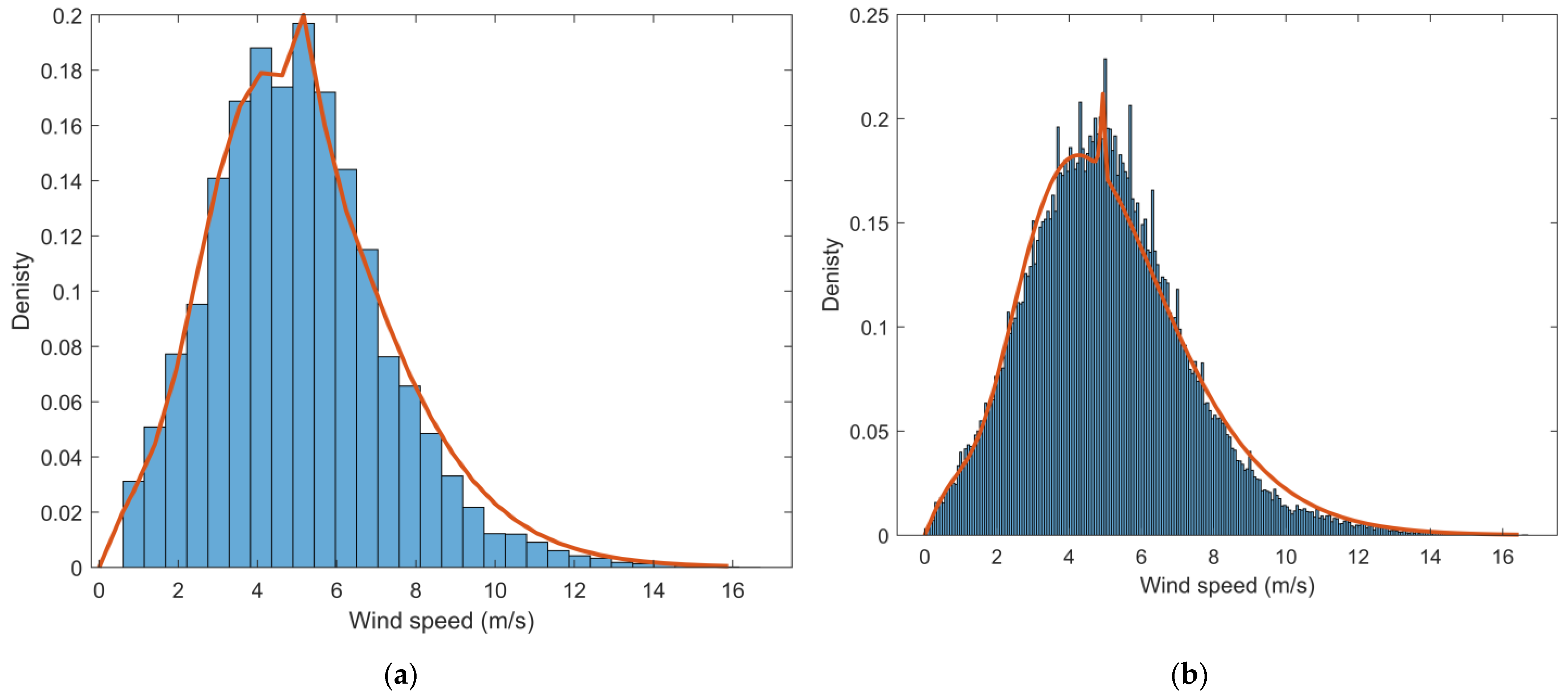
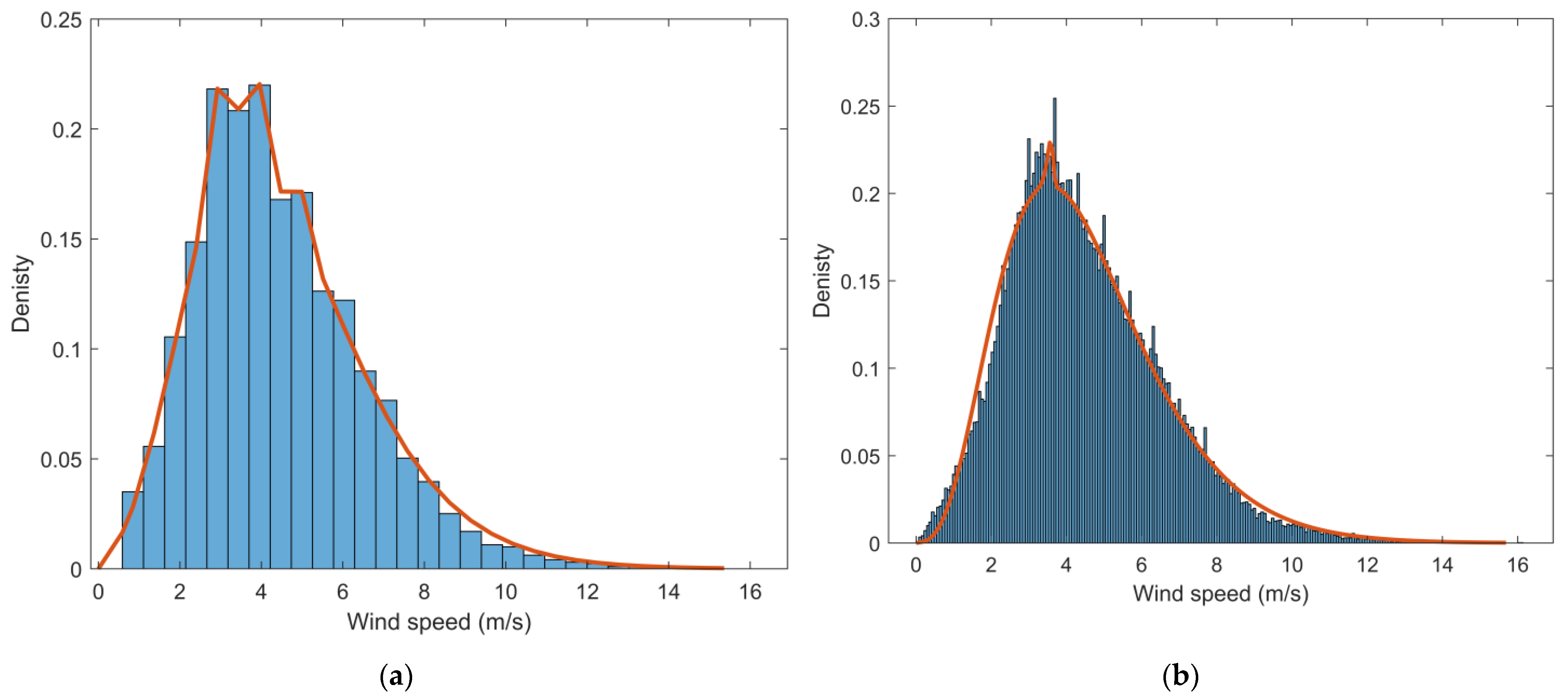
3. Results and Discussion
3.1. Equal Wind Speed Spacings
3.2. Variable Wind Speed Spacings
3.3. Comparison of NSGA-II and MOPSO
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cruz, M.R.M.; Fitiwi, D.Z.; Santos, S.F.; Catalão, J.P.S. A comprehensive survey of flexibility options for supporting the low-carbon energy future. Renew. Sustain. Energy Rev. 2018, 97, 338–353. [Google Scholar] [CrossRef]
- Muradov, N.; Veziroglu, T. “Green” path from fossil-based to hydrogen economy: An overview of carbon-neutral technologies. Int. J. Hydrogen Energy 2008, 33, 6804–6839. [Google Scholar] [CrossRef]
- Hanley, E.S.; Deane, J.; Gallachóir, B.Ó. The role of hydrogen in low carbon energy futures–A review of existing perspectives. Renew. Sustain. Energy Rev. 2018, 82, 3027–3045. [Google Scholar] [CrossRef]
- Fan, L.; Tu, Z.; Chan, S.H. Recent development of hydrogen and fuel cell technologies: A review. Energy Rep. 2021, 7, 8421–8446. [Google Scholar] [CrossRef]
- Mostafa, M.H.; Aleem, S.H.E.A.; Ali, S.G.; Abdelaziz, A.Y.; Ribeiro, P.F.; Ali, Z.M. Robust Energy Management and Economic Analysis of Microgrids Considering Different Battery Characteristics. IEEE Access 2020, 8, 54751–54775. [Google Scholar] [CrossRef]
- Mostafa, M.H.; Abdel Aleem, S.H.E.; Ali, S.G.; Ali, Z.M.; Abdelaziz, A.Y. Techno-economic assessment of energy storage systems using annualized life cycle cost of storage (LCCOS) and levelized cost of energy (LCOE) metrics. J. Energy Storage 2020, 29, 101345. [Google Scholar] [CrossRef]
- Abdel Aleem, S.H.E.; Zobaa, A.F.; Balci, M.E.; Ismael, S.M. Harmonic Overloading Minimization of Frequency-Dependent Components in Harmonics Polluted Distribution Systems Using Harris Hawks Optimization Algorithm. IEEE Access 2019, 7, 100824–100837. [Google Scholar] [CrossRef]
- Diaaeldin, I.M.; Abdel Aleem, S.H.E.; El-Rafei, A.; Abdelaziz, A.Y.; Zobaa, A.F. Hosting capacity maximization based on optimal reconfiguration of distribution networks with optimized soft open point operation. In Hosting Capacity for Smart Power Grids; Springer: Berlin/Heidelberg, Germany, 2020; ISBN 9783030400293. [Google Scholar]
- Diaaeldin, I.M.; Abdel Aleem, S.H.E.; El-Rafei, A.; Abdelaziz, A.Y.; Zobaa, A.F. Large-scale integration of distributed generation in reconfigured distribution networks considering load uncertainty. In Uncertainties in Modern Power Systems; Elsevier: Amsterdam, The Netherlands, 2021; pp. 441–484. [Google Scholar]
- Ali, Z.M.; Diaaeldin, I.M.; Abdel Aleem, S.H.E.; El-Rafei, A.; Abdelaziz, A.Y.; Jurado, F. Scenario-based network reconfiguration and renewable energy resources integration in large-scale distribution systems considering parameters uncertainty. Mathematics 2021, 9, 26. [Google Scholar] [CrossRef]
- Ismael, S.; Abdel Aleem, S.; Abdelaziz, A.; Zobaa, A. Probabilistic Hosting Capacity Enhancement in Non-Sinusoidal Power Distribution Systems Using a Hybrid PSOGSA Optimization Algorithm. Energies 2019, 12, 1018. [Google Scholar] [CrossRef] [Green Version]
- El-Fergany, A.A.; Abdelaziz, A.Y. Capacitor allocations in radial distribution networks using cuckoo search algorithm. IET Gener. Transm. Distrib. 2014, 8, 223–232. [Google Scholar] [CrossRef] [Green Version]
- Ali, Z.M.; Diaaeldin, I.M.; El-Rafei, A.; Hasanien, H.M.; Abdel Aleem, S.H.E.; Abdelaziz, A.Y. A novel distributed generation planning algorithm via graphically-based network reconfiguration and soft open points placement using Archimedes optimization algorithm. Ain Shams Eng. J. 2021, 12, 1923–1941. [Google Scholar] [CrossRef]
- Ismael, S.M.; Abdel Aleem, S.H.E.; Abdelaziz, A.Y.; Zobaa, A.F. State-of-the-art of hosting capacity in modern power systems with distributed generation. Renew. Energy 2019, 130, 1002–1020. [Google Scholar] [CrossRef]
- Khamees, A.K.; Abdelaziz, A.Y.; Eskaros, M.R.; Attia, M.A. Investigation of Different Probability Distribution Functions for Wind Speed Modelling Using Classical and Novel Metaheuristic Methods. In Proceedings of the 2021 22nd International Middle East Power Systems Conference (MEPCON), Assiut, Egypt, 14–16 December 2021; pp. 26–31. [Google Scholar]
- Akdağ, S.A.; Bagiorgas, H.S.; Mihalakakou, G. Use of two-component Weibull mixtures in the analysis of wind speed in the Eastern Mediterranean. Appl. Energy 2010, 87, 2566–2573. [Google Scholar] [CrossRef]
- Pishgar-Komleh, S.H.; Keyhani, A.; Sefeedpari, P. Wind speed and power density analysis based on Weibull and Rayleigh distributions (a case study: Firouzkooh county of Iran). Renew. Sustain. Energy Rev. 2015, 42, 313–322. [Google Scholar] [CrossRef]
- Baran, S.; Lerch, S. Log-normal distribution based Ensemble Model Output Statistics models for probabilistic wind-speed forecasting. Q. J. R. Meteorol. Soc. 2015, 141, 2289–2299. [Google Scholar] [CrossRef] [Green Version]
- Khamees, A.K.; Abdelaziz, A.Y.; Eskaros, M.R.; Attia, M.A.; Badr, A.O. The Mixture of Probability Distribution Functions for Wind and Photovoltaic Power Systems Using a Metaheuristic Method. Processes 2022, 10, 2446. [Google Scholar] [CrossRef]
- Van der Auwera, L.; de Meyer, F.; Malet, L. The use of the Weibull three-parameter model for estimating mean wind power densities. J. Appl. Meteorol. Climatol. 1980, 19, 819–825. [Google Scholar] [CrossRef]
- Carta, J.A.; Ramírez, P. Use of finite mixture distribution models in the analysis of wind energy in the Canarian Archipelago. Energy Convers. Manag. 2007, 48, 281–291. [Google Scholar] [CrossRef]
- Celik, A.N. Energy output estimation for small-scale wind power generators using Weibull-representative wind data. J. Wind. Eng. Ind. Aerodyn. 2003, 91, 693–707. [Google Scholar] [CrossRef]
- Khamees, A.K.; Abdelaziz, A.Y.; Ali, Z.M.; Alharthi, M.M.; Ghoneim, S.S.; Eskaros, M.R.; Attia, M.A. Mixture probability distribution functions using novel metaheuristic method in wind speed modeling. Ain Shams Eng. J. 2022, 13, 101613. [Google Scholar] [CrossRef]
- Brano, V.L.; Orioli, A.; Ciulla, G.; Culotta, S. Quality of wind speed fitting distributions for the urban area of Palermo, Italy. Renew. Energy 2011, 36, 1026–1039. [Google Scholar] [CrossRef]
- Labeeuw, W.; Deconinck, G. Customer sampling in a smart grid pilot. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; IEEE: Piscataway, NJ, USA, 2012. [Google Scholar]
- Salameh, Z.M.; Borowy, B.S.; Amin, A.R. Photovoltaic module-site matching based on the capacity factors. IEEE Trans. Energy Convers. 1995, 10, 326–332. [Google Scholar] [CrossRef]
- Shi, G.; Eftekharnejad, S. Impact of solar forecasting on power system planning. In Proceedings of the 2016 North American Power Symposium (NAPS), Denver, CO, USA, 18–20 September 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Tizgui, I.; El Guezar, F.; Bouzahir, H.; Benaid, B. Comparison of methods in estimating Weibull parameters for wind energy applications. Int. J. Energy Sect. Manag. 2017, 11, 650–663. [Google Scholar] [CrossRef]
- Kang, D.; Ko, K.; Huh, J. Comparative study of different methods for estimating Weibull parameters: A case study on Jeju Island, South Korea. Energies 2018, 11, 356. [Google Scholar] [CrossRef] [Green Version]
- Suwarno, I.Y.; Irwanto, M.; Hiendro, A. Analysis of wind speed characteristics using different distribution models in Medan City, Indonesia. Int. J. Power Electron. Drive Syst. 2021, 12, 1102. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, C.; Su, J.; Wang, J. Research and application based on the swarm intelligence algorithm and artificial intelligence for wind farm decision system. Renew. Energy 2019, 134, 681–697. [Google Scholar] [CrossRef]
- Saeed, M.A.; Ahmed, Z.; Yang, J.; Zhang, W. An optimal approach of wind power assessment using Chebyshev metric for determining the Weibull distribution parameters. Sustain. Energy Technol. Assess. 2020, 37, 100612. [Google Scholar] [CrossRef]
- Guedes, K.S.; de Andrade, C.F.; Rocha, P.A.; Mangueira, R.D.S.; de Moura, E.P. Performance analysis of metaheuristic optimization algorithms in estimating the parameters of several wind speed distributions. Appl. Energy 2020, 268, 114952. [Google Scholar] [CrossRef]
- Coello Coello, C.A.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation. CEC’02 (Cat. No.02TH8600), Honolulu, HI, USA, 12–17 May 2002; IEEE: New York, NY, USA, 2002; Volume 2, pp. 1051–1056. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Omar, O.A.M.; Ahmed, H.M.; Elbarkouky, R.A. Commercial wind turbines modeling using single and composite cumulative probability density functions. Int. J. Electr. Comput. Eng. (IJECE) 2021, 11, 47. [Google Scholar] [CrossRef]
- Global Wind Atlas. Available online: https://globalwindatlas.info/en (accessed on 11 February 2023).
- Hwang, C.-L.; Yoon, K. Multiple Attributes Decision Making Methods and Applications. 1981. Available online: https://www.springer.com/gp/book/9783540105589 (accessed on 11 February 2023).
- Yoon, K. A Reconciliation among Discrete Compromise Solutions. J. Oper. Res. Soc. 1987, 38, 277. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Lai, Y.-J.; Liu, T.-Y. A new approach for multiple objective decision making. Comput. Oper. Res. 1993, 20, 889–899. [Google Scholar] [CrossRef]
- Ahmadi, B.; Ceylan, O.; Ozdemir, A. Reinforcement of the distribution grids to improve the hosting capacity of distributed generation: Multi-objective framework. Electr. Power Syst. Res. 2023, 217, 109120. [Google Scholar] [CrossRef]
- Ahmadi, B.; Ceylan, O.; Ozdemir, A.; Fotuhi-Firuzabad, M. A multi-objective framework for distributed energy resources planning and storage management. Appl. Energy 2022, 314, 118887. [Google Scholar] [CrossRef]
- Fleischer, M. The measure of Pareto optima applications to multi-objective metaheuristics. Lect. Notes Comput. Sci. 2003, 2632, 519–533. [Google Scholar] [CrossRef]
- Tao, S.; Xu, Q.; Feijoo, A.; Zheng, G. Joint Optimization of Wind Turbine Micrositing and Cabling in an Offshore Wind Farm. IEEE Trans. Smart Grid 2021, 12, 834–844. [Google Scholar] [CrossRef]
- yang, J.; Zheng, S.; Song, D.; Su, M.; Yang, X.; Joo, Y.H. Comprehensive Optimization for Fatigue Loads of Wind Turbines in Complex-Terrain Wind Farms. IEEE Trans. Sustain. Energy 2021, 12, 909–919. [Google Scholar] [CrossRef]
- Zhang, N.; Sun, Q.; Yang, L.; Li, Y. Event-Triggered Distributed Hybrid Control Scheme for the Integrated Energy System. IEEE Trans. Ind. Inform. 2022, 18, 835–846. [Google Scholar] [CrossRef]
- Yang, L.; Li, X.; Sun, M.; Sun, C. Hybrid Policy-based Reinforcement Learning of Adaptive Energy Management for the Energy Transmission-constrained Island Group. IEEE Trans. Ind. Inform. 2023, 1–12. [Google Scholar] [CrossRef]
- Omar, O.A.M.; Ahmed, H.M.; Elbarkouky, R.A. Wind turbines new criteria optimal site matching under new capacity factor probabilistic approaches. Energy Syst. 2021, 2021, 1–26. [Google Scholar] [CrossRef]
- Afifi, M.A.; Marei, M.I.; Mohamad, A.M.I. Modelling, Analysis and Performance of a Low Inertia AC-DC Microgrid. Appl. Sci. 2023, 13, 3197. [Google Scholar] [CrossRef]
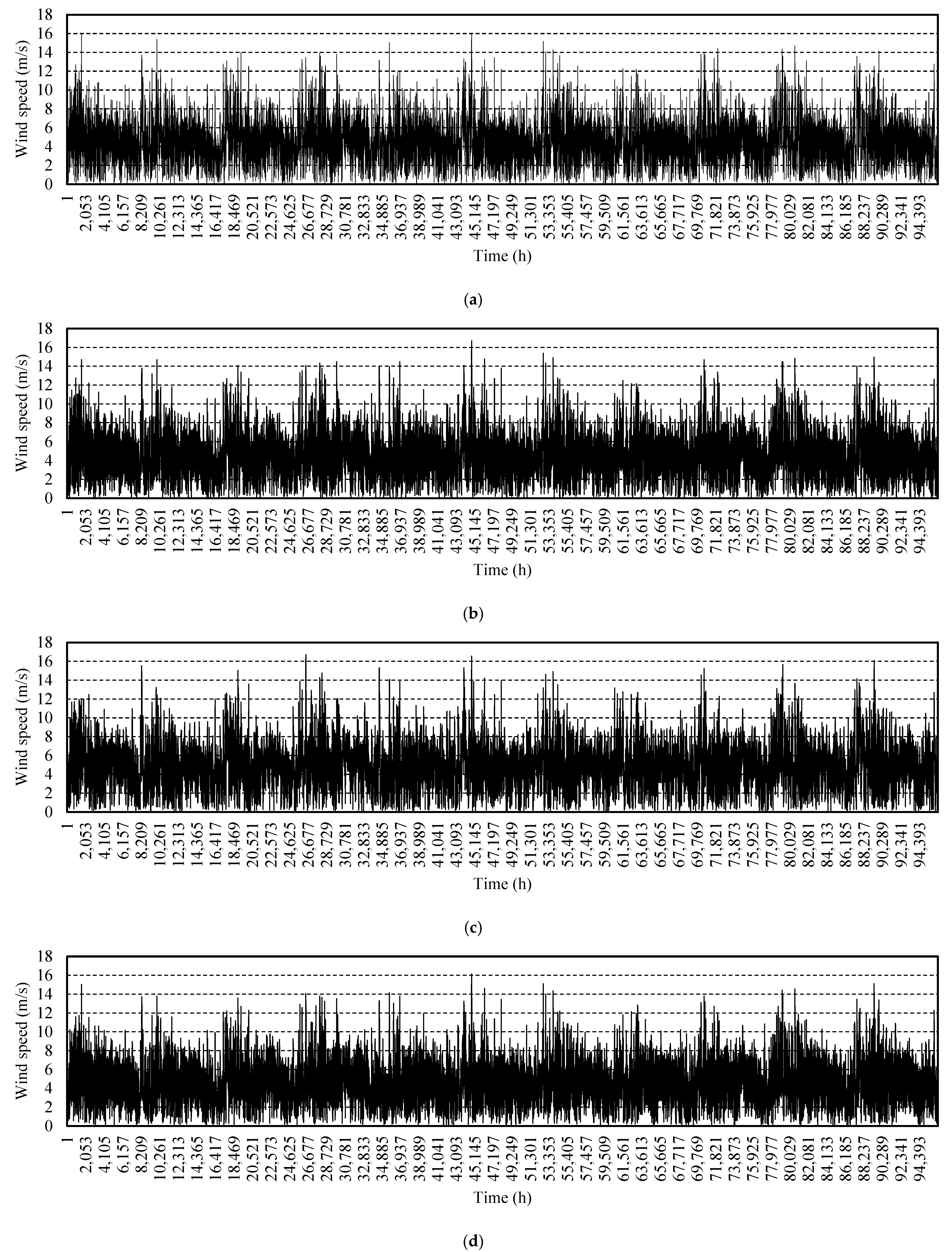
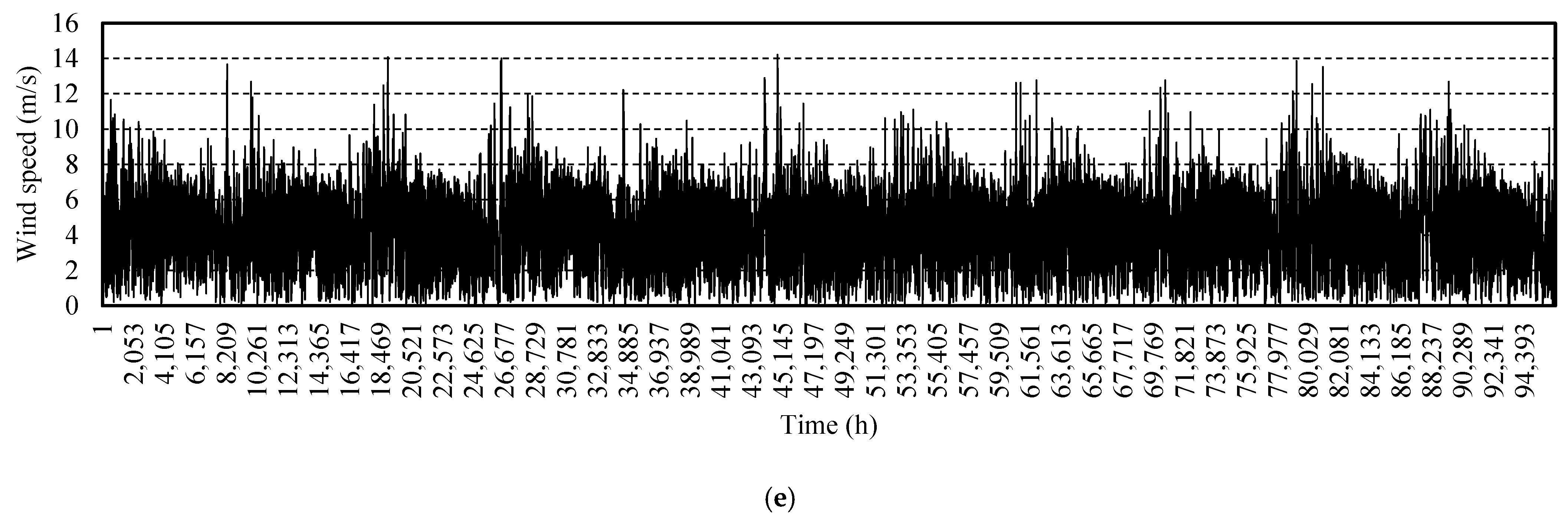



| PDF name | Equation | Parameters |
|---|---|---|
| Weibull | : shape parameter : scale parameter | |
| Gamma | : shape parameter | |
| Log-normal | : shape parameter : scale parameter | |
| Rayleigh | : scale parameter |
| Site Number | NSGA-II | MOPSO | |||||
|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.01077 | 0.97666 | 0.00012 | 0.00625 | 0.99214 | 0.00004 |
| 2 | 0.01237 | 0.96922 | 0.00015 | 0.00625 | 0.99214 | 0.00004 | |
| 3 | 0.01840 | 0.93193 | 0.00035 | 0.00540 | 0.99412 | 0.00003 | |
| 2 | 1 | 0.01097 | 0.97548 | 0.00012 | 0.00783 | 0.98750 | 0.00006 |
| 2 | 0.01182 | 0.97154 | 0.00014 | 0.00723 | 0.98933 | 0.00005 | |
| 3 | 0.02853 | 0.83421 | 0.00084 | 0.00113 | 0.99973 | 0.000001 | |
| 3 | 1 | 0.00367 | 0.99687 | 0.000014 | 0.00338 | 0.99735 | 0.00001 |
| 2 | 0.00703 | 0.98852 | 0.000051 | 0.00283 | 0.99815 | 0.00001 | |
| 3 | 0.01208 | 0.96616 | 0.000151 | 0.00192 | 0.99915 | 0.00000 | |
| 4 | 1 | 0.01005 | 0.97987 | 0.000104 | 0.00579 | 0.99333 | 0.00003 |
| 2 | 0.01552 | 0.95201 | 0.000249 | 0.00579 | 0.99332 | 0.00003 | |
| 3 | 0.01629 | 0.94714 | 0.000275 | 0.00579 | 0.99333 | 0.00003 | |
| 5 | 1 | 0.01127 | 0.97703 | 0.000131 | 0.00774 | 0.98919 | 0.00006 |
| 2 | 0.00850 | 0.98695 | 0.000074 | 0.00474 | 0.99594 | 0.00002 | |
| 3 | 0.01600 | 0.95374 | 0.000265 | 0.00777 | 0.98909 | 0.00006 | |
| Site Number | NSGA-II | MOPSO | |||||
|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.00378 | 0.99713 | 0.00003 | 0.00269 | 0.99855 | 0.00001 |
| 2 | 0.00386 | 0.99700 | 0.00003 | 0.00269 | 0.99855 | 0.00001 | |
| 3 | 0.00910 | 0.98335 | 0.00017 | 0.00302 | 0.99816 | 0.00002 | |
| 2 | 1 | 0.00553 | 0.99401 | 0.00006 | 0.00392 | 0.99699 | 0.00003 |
| 2 | 0.00764 | 0.98860 | 0.00012 | 0.00388 | 0.99705 | 0.00003 | |
| 3 | 0.02006 | 0.92126 | 0.00084 | 0.00221 | 0.99904 | 0.00001 | |
| 3 | 1 | 0.00901 | 0.98174 | 0.00017 | 0.00877 | 0.98273 | 0.00016 |
| 2 | 0.00941 | 0.98012 | 0.00018 | 0.00418 | 0.99608 | 0.00004 | |
| 3 | 0.03002 | 0.79738 | 0.00187 | 0.00531 | 0.99366 | 0.00006 | |
| 4 | 1 | 0.00551 | 0.99421 | 0.00006 | 0.00437 | 0.99637 | 0.00004 |
| 2 | 0.00791 | 0.98810 | 0.00013 | 0.00303 | 0.99826 | 0.00002 | |
| 3 | 0.01302 | 0.96771 | 0.00035 | 0.00418 | 0.99668 | 0.00004 | |
| 5 | 1 | 0.01279 | 0.97174 | 0.00051 | 0.00547 | 0.99477 | 0.00006 |
| 2 | 0.01335 | 0.96923 | 0.00055 | 0.00930 | 0.98486 | 0.00018 | |
| 3 | 0.02308 | 0.90804 | 0.00166 | 0.00930 | 0.98486 | 0.00018 | |
| Site Number | NSGA-II | MOPSO | |||||
|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.00757 | 0.98874 | 0.00018 | 0.00583 | 0.99331 | 0.00011 |
| 2 | 0.00781 | 0.98802 | 0.00019 | 0.00600 | 0.99292 | 0.00011 | |
| 3 | 0.00781 | 0.98802 | 0.00019 | 0.00601 | 0.99291 | 0.00011 | |
| 2 | 1 | 0.00728 | 0.98963 | 0.00017 | 0.00693 | 0.99062 | 0.00015 |
| 2 | 0.01531 | 0.95420 | 0.00073 | 0.00646 | 0.99185 | 0.00013 | |
| 3 | 0.01501 | 0.95599 | 0.00070 | 0.00378 | 0.99720 | 0.00004 | |
| 3 | 1 | 0.00940 | 0.98015 | 0.00028 | 0.00888 | 0.98231 | 0.00025 |
| 2 | 0.00947 | 0.97987 | 0.00028 | 0.00503 | 0.99431 | 0.00008 | |
| 3 | 0.00947 | 0.97987 | 0.00028 | 0.00664 | 0.99012 | 0.00014 | |
| 4 | 1 | 0.00850 | 0.98652 | 0.00022 | 0.00705 | 0.99072 | 0.00015 |
| 2 | 0.00875 | 0.98570 | 0.00024 | 0.00683 | 0.99128 | 0.00015 | |
| 3 | 0.01455 | 0.96047 | 0.00066 | 0.00393 | 0.99712 | 0.00005 | |
| 5 | 1 | 0.01279 | 0.97174 | 0.00051 | 0.01085 | 0.97966 | 0.00037 |
| 2 | 0.01335 | 0.96923 | 0.00055 | 0.01100 | 0.97909 | 0.00038 | |
| 3 | 0.02308 | 0.90804 | 0.00166 | 0.00795 | 0.98907 | 0.00020 | |
| Site Number | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0.00034 | 0.99454 | 0.00476 | 0.00036 | 73.79385 | 31.70703 | 4.58715 | 0.00000 | 0.14127 | 68.98417 |
| 2 | 1 | 0.00000 | 0.46317 | 0.00000 | 0.15381 | 40.35879 | 52.73686 | 4.55628 | 32.28912 | 53.80212 | 3.08534 | |
| 2 | 0.00000 | 0.38181 | 0.00120 | 0.00000 | 27.25824 | 68.94476 | 4.87313 | 10.49539 | 29.27796 | 37.76996 | ||
| 3 | 1 | 0.00363 | 0.00000 | 0.01140 | 0.00000 | 53.24860 | 17.27855 | 53.58056 | 29.09172 | 82.68204 | 79.97628 | |
| 2 | 0.01046 | 0.59690 | 0.00000 | 0.30576 | 85.03399 | 18.89028 | 4.55835 | 57.89836 | 95.61217 | 3.18172 | ||
| 3 | 0.00339 | 0.00000 | 0.00305 | 0.06542 | 74.13813 | 80.12175 | 67.48028 | 59.15287 | 77.12520 | 4.14649 | ||
| 2 | 1 | 1 | 0.00000 | 0.93619 | 0.00001 | 0.06380 | 42.29673 | 40.00127 | 4.67366 | 47.89578 | 63.84122 | 2.93954 |
| 2 | 1 | 0.00312 | 0.29239 | 0.00312 | 0.27655 | 59.85635 | 67.81208 | 5.08736 | 90.33011 | 31.44685 | 3.85625 | |
| 2 | 0.00074 | 0.00439 | 0.00122 | 0.41848 | 14.39543 | 87.70615 | 29.67952 | 51.12360 | 31.67918 | 3.09742 | ||
| 3 | 1 | 0.00000 | 0.06065 | 0.00000 | 0.23550 | 58.39489 | 80.55814 | 5.86088 | 27.32205 | 23.62730 | 3.25214 | |
| 2 | 0.04392 | 0.22702 | 0.00204 | 0.20465 | 70.97043 | 50.58780 | 4.83515 | 44.31630 | 13.10943 | 2.78105 | ||
| 3 | 0.00036 | 0.20202 | 0.01206 | 0.01180 | 42.98833 | 97.77294 | 4.77987 | 48.23871 | 10.40638 | 73.34310 | ||
| 3 | 1 | 1 | 0.00008 | 0.79294 | 0.00006 | 0.20692 | 62.46275 | 47.86930 | 5.45810 | 42.67871 | 72.18348 | 3.29967 |
| 2 | 1 | 0.00059 | 0.37752 | 0.00000 | 0.00029 | 48.52595 | 33.06928 | 5.26438 | 48.55042 | 27.14744 | 64.93494 | |
| 2 | 0.03049 | 0.34396 | 0.00079 | 0.24636 | 6.37485 | 18.59843 | 5.40582 | 57.45784 | 32.64139 | 3.75803 | ||
| 3 | 1 | 0.03058 | 0.31613 | 0.00000 | 0.01436 | 86.74505 | 16.95936 | 5.30614 | 110.02295 | 109.94055 | 53.50350 | |
| 2 | 0.00438 | 0.00784 | 0.02601 | 0.02267 | 40.87161 | 25.94324 | 59.53822 | 55.79216 | 74.74296 | 66.49486 | ||
| 3 | 0.00000 | 0.34241 | 0.00589 | 0.22974 | 48.01248 | 70.81428 | 5.09028 | 42.42671 | 37.93132 | 3.33625 | ||
| 4 | 1 | 1 | 0.00000 | 0.99196 | 0.00000 | 0.00804 | 50.39877 | 38.65348 | 4.54251 | 57.70120 | 64.43584 | 0.51050 |
| 2 | 1 | 0.00082 | 0.55058 | 0.00111 | 0.00002 | 58.22308 | 54.34909 | 4.52033 | 68.20038 | 42.90745 | 44.47037 | |
| 2 | 0.00001 | 0.44574 | 0.00098 | 0.00074 | 65.74181 | 42.79643 | 4.57082 | 39.46333 | 49.92005 | 41.76769 | ||
| 3 | 1 | 0.01843 | 0.37132 | 0.00711 | 0.00711 | 100.80900 | 23.27993 | 4.68969 | 5.21841 | 24.45806 | 63.15324 | |
| 2 | 0.00000 | 0.00897 | 0.00000 | 0.25849 | 93.43002 | 55.97088 | 38.23371 | 80.30763 | 16.09118 | 2.91898 | ||
| 3 | 0.00109 | 0.27949 | 0.03128 | 0.01670 | 85.56484 | 69.20576 | 4.62985 | 26.15153 | 20.36618 | 73.51160 | ||
| 5 | 1 | 1 | 0.00000 | 1.00000 | 0.00000 | 0.00000 | 93.58844 | 62.72201 | 4.52723 | 91.81758 | 31.06219 | 55.05638 |
| 2 | 1 | 0.00220 | 0.00000 | 0.00000 | 0.23560 | 38.40924 | 80.26567 | 63.15395 | 41.28379 | 91.10511 | 3.17433 | |
| 2 | 0.00085 | 0.56303 | 0.00278 | 0.19554 | 54.54940 | 90.12121 | 4.68333 | 92.85935 | 94.94080 | 3.44225 | ||
| 3 | 1 | 0.03576 | 0.14250 | 0.00158 | 0.14397 | 4.44326 | 20.08993 | 4.87683 | 62.12001 | 78.51489 | 3.38791 | |
| 2 | 0.01290 | 0.01042 | 0.02693 | 0.13176 | 42.83066 | 20.97307 | 55.61803 | 12.77200 | 105.65023 | 3.62303 | ||
| 3 | 0.02093 | 0.19415 | 0.06682 | 0.21228 | 92.34193 | 76.29295 | 4.27876 | 61.69388 | 71.89037 | 2.84531 |
| Site Number | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0.01821 | 0.96666 | 0.00000 | 0.01513 | 3.37535 | 15.02806 | 4.65127 | 86.33833 | 89.92111 | 0.73477 |
| 2 | 1 | 0.00120 | 0.91121 | 0.00366 | 0.06386 | 94.49952 | 34.89852 | 4.67373 | 39.70831 | 5.23394 | 3.13871 | |
| 2 | 0.00364 | 0.01498 | 0.00022 | 0.00122 | 3.44163 | 98.89050 | 1.35853 | 98.27957 | 92.78617 | 95.40006 | ||
| 3 | 1 | 0.00454 | 0.39526 | 0.00035 | 0.17120 | 57.49185 | 29.55937 | 4.70232 | 53.42064 | 28.91840 | 3.07179 | |
| 2 | 0.00267 | 0.00007 | 0.00014 | 0.00000 | 98.60259 | 0.05260 | 87.46580 | 7.99455 | 47.69958 | 3.84613 | ||
| 3 | 0.00364 | 0.42077 | 0.00069 | 0.00069 | 3.39093 | 86.53919 | 4.76569 | 92.12256 | 18.34722 | 76.94156 | ||
| 2 | 1 | 1 | 0.00022 | 0.99152 | 0.00000 | 0.00827 | 3.56125 | 90.62619 | 4.63615 | 32.34890 | 100.00000 | 0.60339 |
| 2 | 1 | 0.00004 | 0.44466 | 0.00001 | 0.00059 | 61.93793 | 11.45986 | 4.75095 | 93.26458 | 35.38043 | 0.68524 | |
| 2 | 0.00433 | 0.44259 | 0.00001 | 0.10778 | 3.61378 | 93.54713 | 4.75204 | 56.47268 | 10.98078 | 2.89341 | ||
| 3 | 1 | 0.00276 | 0.67577 | 0.00033 | 0.00016 | 5.73793 | 100.00000 | 4.91475 | 77.00172 | 95.07571 | 98.29700 | |
| 2 | 0.00303 | 0.00139 | 0.00004 | 0.18126 | 5.15555 | 85.17888 | 48.63691 | 6.94460 | 25.38179 | 3.17867 | ||
| 3 | 0.06753 | 0.00618 | 0.00024 | 0.06130 | 3.54492 | 6.70900 | 70.40451 | 9.44477 | 92.23108 | 3.18446 | ||
| 3 | 1 | 1 | 0.00000 | 0.96999 | 0.00000 | 0.03001 | 85.84468 | 73.37492 | 5.31757 | 94.37597 | 24.62790 | 0.93811 |
| 2 | 1 | 0.00021 | 0.37095 | 0.00000 | 0.00051 | 93.96757 | 91.55658 | 5.68172 | 53.04907 | 89.84384 | 95.68243 | |
| 2 | 0.26747 | 0.00016 | 0.00287 | 0.35783 | 5.47647 | 3.80692 | 85.08386 | 0.06256 | 0.18635 | 3.55755 | ||
| 3 | 1 | 0.00348 | 0.00044 | 0.00044 | 0.00000 | 5.63902 | 98.36905 | 5.10485 | 97.94978 | 99.77773 | 1.49898 | |
| 2 | 0.00469 | 0.95568 | 0.00012 | 0.00000 | 5.16733 | 97.94739 | 5.31828 | 54.66384 | 33.97096 | 1.67987 | ||
| 3 | 0.00000 | 0.00008 | 0.00004 | 0.03502 | 88.65839 | 99.35837 | 61.42782 | 70.84273 | 19.28514 | 0.96339 | ||
| 4 | 1 | 1 | 0.05474 | 0.93121 | 0.00000 | 0.01405 | 3.44476 | 5.69593 | 4.67193 | 13.14709 | 74.36018 | 0.69841 |
| 2 | 1 | 0.00259 | 0.00000 | 0.00001 | 0.00001 | 2.91999 | 93.67475 | 85.95537 | 67.18377 | 90.97950 | 3.07029 | |
| 2 | 0.00000 | 0.98644 | 0.00000 | 0.01096 | 28.21660 | 1.16557 | 4.60459 | 72.68700 | 99.30794 | 0.59264 | ||
| 3 | 1 | 0.03486 | 0.25170 | 0.00027 | 0.22097 | 3.81408 | 13.67664 | 4.77332 | 96.86787 | 98.86956 | 3.06168 | |
| 2 | 0.00526 | 0.23869 | 0.00000 | 0.00019 | 4.94044 | 85.60790 | 4.91013 | 1.59959 | 98.42046 | 81.38206 | ||
| 3 | 0.01927 | 0.22188 | 0.00676 | 0.00014 | 2.87242 | 19.75791 | 4.77571 | 40.28597 | 48.74096 | 99.75578 | ||
| 5 | 1 | 1 | 0.00398 | 0.86969 | 0.00968 | 0.11665 | 5.31591 | 100.00000 | 4.60534 | 0.00000 | 0.33532 | 2.90385 |
| 2 | 1 | 0.00407 | 0.97775 | 0.00000 | 0.01818 | 5.31612 | 100.00000 | 4.52537 | 8.12529 | 77.09078 | 0.70752 | |
| 2 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 84.42821 | 75.58742 | 48.06149 | 88.04431 | 12.17536 | 75.14713 | ||
| 3 | 1 | 0.39641 | 0.39505 | 0.00024 | 0.00030 | 5.19388 | 3.23347 | 4.37112 | 40.45326 | 36.80202 | 60.87665 | |
| 2 | 0.00001 | 0.00038 | 0.00019 | 0.18097 | 52.34119 | 45.15843 | 78.13708 | 5.86943 | 3.34522 | 2.65902 | ||
| 3 | 0.00045 | 0.00001 | 0.00016 | 0.02584 | 96.82498 | 2.58698 | 94.49701 | 70.61560 | 91.64219 | 2.78155 |
| Site Number | NSGA-II | MOPSO | |||||
|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.00788 | 0.98786 | 0.00141 | 0.00951 | 0.98232 | 0.00205 |
| 2 | 0.00819 | 0.98690 | 0.00152 | 0.00682 | 0.99090 | 0.00106 | |
| 3 | 0.01706 | 0.94310 | 0.00660 | 0.00718 | 0.98994 | 0.00117 | |
| 2 | 1 | 0.00777 | 0.98847 | 0.00139 | 0.00722 | 0.99006 | 0.00120 |
| 2 | 0.00769 | 0.98871 | 0.00137 | 0.00639 | 0.99221 | 0.00094 | |
| 3 | 0.00717 | 0.99018 | 0.00119 | 0.00722 | 0.99006 | 0.00120 | |
| 3 | 1 | 0.00996 | 0.97804 | 0.00239 | 0.00605 | 0.99191 | 0.00088 |
| 2 | 0.01115 | 0.97246 | 0.00300 | 0.00612 | 0.99171 | 0.00090 | |
| 3 | 0.01496 | 0.95046 | 0.00539 | 0.00864 | 0.98347 | 0.00180 | |
| 4 | 1 | 0.00803 | 0.98821 | 0.00145 | 0.00604 | 0.99332 | 0.00082 |
| 2 | 0.00733 | 0.99017 | 0.00121 | 0.01978 | 0.92842 | 0.00879 | |
| 3 | 0.00722 | 0.99047 | 0.00117 | 0.00804 | 0.98818 | 0.00145 | |
| 5 | 1 | 0.01137 | 0.97784 | 0.00273 | 0.00686 | 0.99193 | 0.00099 |
| 2 | 0.01137 | 0.97783 | 0.00273 | 0.01168 | 0.97661 | 0.00288 | |
| 3 | 0.01140 | 0.97771 | 0.00274 | 0.00704 | 0.99151 | 0.00105 | |
| Site Number | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0.0002 | 0.8444 | 0.0000 | 0.1554 | 48.425 | 44.339 | 4.669 | 41.365 | 56.543 | 3.020 |
| 2 | 1 | 0.0017 | 0.6721 | 0.0025 | 0.0021 | 6.149 | 63.774 | 4.726 | 33.273 | 45.119 | 71.640 | |
| 2 | 0.0003 | 0.3188 | 0.0020 | 0.0005 | 43.398 | 49.205 | 4.234 | 18.297 | 46.592 | 39.919 | ||
| 3 | 1 | 0.00000 | 0.14944 | 0.06649 | 0.20311 | 55.683 | 30.748 | 4.510 | 63.154 | 97.451 | 3.653 | |
| 2 | 0.01027 | 0.00187 | 0.01447 | 0.22116 | 60.377 | 35.709 | 78.467 | 57.418 | 53.484 | 3.377 | ||
| 3 | 0.00495 | 0.20368 | 0.00000 | 0.12456 | 42.480 | 68.215 | 4.903 | 73.196 | 22.711 | 3.414 | ||
| 2 | 1 | 1 | 0.00000 | 1.00000 | 0.00000 | 0.00000 | 54.213 | 48.625 | 4.582 | 27.172 | 44.266 | 41.026 |
| 2 | 1 | 0.00002 | 0.91132 | 0.00003 | 0.08856 | 49.728 | 44.948 | 4.678 | 35.551 | 49.427 | 2.750 | |
| 2 | 0.00000 | 0.00003 | 0.00003 | 0.00001 | 75.194 | 48.409 | 14.680 | 4.062 | 40.727 | 10.036 | ||
| 3 | 1 | 0.07615 | 0.37523 | 0.00010 | 0.00024 | 4.363 | 3.110 | 4.616 | 10.767 | 64.974 | 25.395 | |
| 2 | 0.00024 | 0.48102 | 0.00036 | 0.05832 | 98.824 | 22.681 | 4.705 | 19.240 | 78.937 | 2.999 | ||
| 3 | 0.00006 | 0.00026 | 0.00026 | 0.00778 | 23.999 | 33.205 | 25.256 | 18.865 | 68.288 | 0.444 | ||
| 3 | 1 | 1 | 0.00000 | 0.95662 | 0.04337 | 0.00000 | 69.044 | 63.562 | 5.233 | 0.000 | 0.825 | 46.606 |
| 2 | 1 | 0.00000 | 0.99528 | 0.00000 | 0.00000 | 50.286 | 5.686 | 5.222 | 67.739 | 26.628 | 50.970 | |
| 2 | 0.00022 | 0.00101 | 0.00155 | 0.00194 | 37.671 | 38.236 | 48.929 | 65.213 | 33.951 | 35.914 | ||
| 3 | 1 | 0.01790 | 0.10200 | 0.01711 | 0.16985 | 84.899 | 62.419 | 5.231 | 30.359 | 81.995 | 3.771 | |
| 2 | 0.00509 | 0.24629 | 0.00000 | 0.19175 | 60.529 | 64.694 | 5.039 | 46.647 | 65.495 | 3.643 | ||
| 3 | 0.00835 | 0.21782 | 0.00653 | 0.01731 | 83.843 | 36.780 | 5.329 | 24.729 | 45.280 | 59.468 | ||
| 4 | 1 | 1 | 0.00000 | 0.98961 | 0.00000 | 0.01039 | 55.636 | 53.742 | 4.524 | 85.219 | 42.310 | 0.481 |
| 2 | 1 | 0.00002 | 0.98496 | 0.00003 | 0.00980 | 48.350 | 39.747 | 4.514 | 14.155 | 26.492 | 0.487 | |
| 2 | 0.00516 | 0.00001 | 0.00001 | 0.00003 | 3.634 | 87.108 | 57.749 | 63.339 | 16.895 | 37.124 | ||
| 3 | 1 | 0.02622 | 0.11545 | 0.00000 | 0.08101 | 6.792 | 13.172 | 5.370 | 98.985 | 73.486 | 4.193 | |
| 2 | 0.20249 | 0.23195 | 0.00144 | 0.11972 | 3.780 | 4.559 | 4.324 | 91.330 | 0.110 | 4.321 | ||
| 3 | 0.05869 | 0.00130 | 0.00027 | 0.16147 | 5.664 | 9.177 | 81.345 | 8.644 | 80.996 | 2.809 | ||
| 5 | 1 | 1 | 0.00000 | 0.76647 | 0.00000 | 0.23353 | 53.558 | 75.748 | 4.661 | 39.797 | 37.620 | 2.931 |
| 2 | 1 | 0.00000 | 0.41577 | 0.00000 | 0.23707 | 40.008 | 60.686 | 4.690 | 59.175 | 91.911 | 2.936 | |
| 2 | 0.00000 | 0.34716 | 0.00000 | 0.00000 | 50.291 | 53.204 | 4.634 | 43.035 | 42.309 | 30.106 | ||
| 3 | 1 | 0.00001 | 0.18816 | 0.00000 | 0.00002 | 55.752 | 58.751 | 4.618 | 58.510 | 58.645 | 72.007 | |
| 2 | 0.00002 | 0.26503 | 0.00001 | 0.24116 | 56.536 | 64.118 | 4.581 | 31.815 | 46.300 | 2.964 | ||
| 3 | 0.00000 | 0.30557 | 0.00000 | 0.00002 | 49.509 | 39.171 | 4.760 | 37.036 | 15.008 | 48.917 |
| Site Number | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0.71401 | 0.00000 | 0.00000 | 0.28599 | 4.55643 | 2.57959 | 97.38555 | 87.80310 | 26.76532 | 4.45092 |
| 2 | 1 | 0.00051 | 0.75905 | 0.00480 | 0.21317 | 100.00000 | 78.93519 | 4.79506 | 93.09646 | 37.09961 | 3.01302 | |
| 2 | 0.02103 | 0.00107 | 0.00023 | 0.00014 | 3.145 | 9.304 | 96.366 | 0.429 | 39.610 | 98.845 | ||
| 3 | 1 | 0.31049 | 0.00003 | 0.00030 | 0.00059 | 4.56479 | 2.22783 | 95.71619 | 95.62623 | 0.82070 | 100.00000 | |
| 2 | 0.00003 | 0.33572 | 0.00001 | 0.00018 | 72.563 | 81.813 | 4.641 | 70.750 | 39.824 | 49.771 | ||
| 3 | 0.00515 | 0.34737 | 0.00013 | 0.00000 | 2.955 | 83.338 | 4.782 | 99.382 | 78.309 | 62.951 | ||
| 2 | 1 | 1 | 0.00000 | 0.98877 | 0.00000 | 0.01123 | 42.49486 | 99.11726 | 4.58684 | 40.24957 | 98.33208 | 0.49573 |
| 2 | 1 | 0.00005 | 0.95083 | 0.01507 | 0.00379 | 93.86458 | 67.05292 | 4.67894 | 0.01003 | 0.73239 | 0.53725 | |
| 2 | 0.02964 | 0.00058 | 0.00001 | 0.00004 | 3.317 | 7.608 | 1.157 | 0.000 | 96.174 | 78.740 | ||
| 3 | 1 | 0.00000 | 0.33870 | 0.00000 | 0.00000 | 95.85218 | 88.92973 | 4.59392 | 84.23408 | 90.74424 | 97.69710 | |
| 2 | 0.00000 | 0.33216 | 0.00000 | 0.00000 | 95.340 | 30.944 | 4.587 | 0.657 | 86.978 | 96.636 | ||
| 3 | 0.00000 | 0.31786 | 0.00000 | 0.01127 | 57.419 | 93.756 | 4.580 | 66.668 | 45.022 | 0.497 | ||
| 3 | 1 | 1 | 0.28131 | 0.66437 | 0.00000 | 0.05432 | 5.44750 | 3.55836 | 5.30209 | 81.05400 | 58.40800 | 1.18226 |
| 2 | 1 | 0.00004 | 0.00017 | 0.00006 | 0.01955 | 94.82906 | 5.07351 | 7.34059 | 26.43792 | 29.42188 | 3.67992 | |
| 2 | 0.18047 | 0.75892 | 0.00004 | 0.04074 | 5.648 | 4.297 | 5.163 | 86.680 | 69.339 | 0.982 | ||
| 3 | 1 | 0.00001 | 0.35346 | 0.00000 | 0.00000 | 95.82083 | 94.46366 | 5.24176 | 34.60687 | 71.87913 | 7.45724 | |
| 2 | 0.00536 | 0.24103 | 0.00002 | 0.03192 | 4.944 | 96.758 | 5.263 | 47.223 | 1.018 | 0.865 | ||
| 3 | 0.00000 | 0.36815 | 0.00001 | 0.00002 | 45.800 | 34.308 | 5.274 | 9.265 | 93.706 | 76.604 | ||
| 4 | 1 | 1 | 0.04979 | 0.93428 | 0.00000 | 0.01593 | 3.38081 | 6.42380 | 4.62992 | 16.16983 | 42.17319 | 0.60484 |
| 2 | 1 | 0.00000 | 0.00000 | 0.00000 | 1.00000 | 81.75708 | 39.00862 | 100.00000 | 99.99985 | 23.80490 | 3.43200 | |
| 2 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 97.990 | 58.772 | 99.779 | 99.828 | 81.813 | 53.125 | ||
| 3 | 1 | 0.00039 | 0.00000 | 0.00050 | 0.00065 | 47.15409 | 0.52431 | 97.70312 | 99.66505 | 3.66957 | 99.97253 | |
| 2 | 0.00532 | 0.00000 | 0.00066 | 0.00142 | 3.583 | 47.404 | 99.897 | 98.599 | 4.632 | 99.815 | ||
| 3 | 0.00100 | 0.96516 | 0.00023 | 0.02466 | 70.379 | 16.386 | 4.553 | 4.757 | 87.988 | 2.746 | ||
| 5 | 1 | 1 | 0.38471 | 0.59667 | 0.00000 | 0.01863 | 5.15268 | 3.30579 | 4.07631 | 24.63107 | 7.26524 | 0.56759 |
| 2 | 1 | 0.00000 | 0.97334 | 0.00000 | 0.00000 | 96.03999 | 18.92268 | 4.53098 | 3.58419 | 36.69862 | 36.10664 | |
| 2 | 0.00000 | 0.02666 | 0.00000 | 0.00000 | 98.882 | 76.903 | 1.421 | 91.753 | 98.591 | 0.561 | ||
| 3 | 1 | 0.32427 | 0.00021 | 0.00015 | 0.00000 | 5.18747 | 3.43628 | 97.42475 | 18.64058 | 9.66750 | 10.81575 | |
| 2 | 0.00012 | 0.23193 | 0.00017 | 0.00550 | 48.676 | 60.676 | 4.321 | 29.575 | 54.779 | 0.416 | ||
| 3 | 0.00000 | 0.22487 | 0.00000 | 0.21279 | 93.373 | 99.473 | 4.342 | 99.654 | 90.231 | 2.804 |
| Case Study | Variable Wind Speed Spacings | Thirty Equal Wind Speed Spacings | ||
|---|---|---|---|---|
| Site | NSGA-II | MOPSO | NSGA-II | MOPSO |
| 1 | 0.3014 | 0.2949 | 0.2900 | 0.2870 |
| 2 | 0.2484 | 0.2553 | 0.2886 | 0.3000 |
| 3 | 0.2920 | 0.2972 | 0.2713 | 0.2834 |
| 4 | 0.3060 | 0.2973 | 0.3050 | 0.3127 |
| 5 | 0.3019 | 0.2786 | 0.2657 | 0.2837 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diaaeldin, I.M.; Attia, M.A.; Khamees, A.K.; Omar, O.A.M.; Badr, A.O. A Novel Multiobjective Formulation for Optimal Wind Speed Modeling via a Mixture Probability Density Function. Mathematics 2023, 11, 1463. https://doi.org/10.3390/math11061463
Diaaeldin IM, Attia MA, Khamees AK, Omar OAM, Badr AO. A Novel Multiobjective Formulation for Optimal Wind Speed Modeling via a Mixture Probability Density Function. Mathematics. 2023; 11(6):1463. https://doi.org/10.3390/math11061463
Chicago/Turabian StyleDiaaeldin, Ibrahim Mohamed, Mahmoud A. Attia, Amr K. Khamees, Othman A. M. Omar, and Ahmed O. Badr. 2023. "A Novel Multiobjective Formulation for Optimal Wind Speed Modeling via a Mixture Probability Density Function" Mathematics 11, no. 6: 1463. https://doi.org/10.3390/math11061463
APA StyleDiaaeldin, I. M., Attia, M. A., Khamees, A. K., Omar, O. A. M., & Badr, A. O. (2023). A Novel Multiobjective Formulation for Optimal Wind Speed Modeling via a Mixture Probability Density Function. Mathematics, 11(6), 1463. https://doi.org/10.3390/math11061463









