Distributed Optimization Control for Heterogeneous Multiagent Systems under Directed Topologies
Abstract
1. Introduction
2. Preliminaries
2.1. Notations
2.2. Graph Theory
3. Problem Description
4. Main Results
4.1. DOCP for MASs with Continuous Communications
4.2. DOCP for MASs with ETC
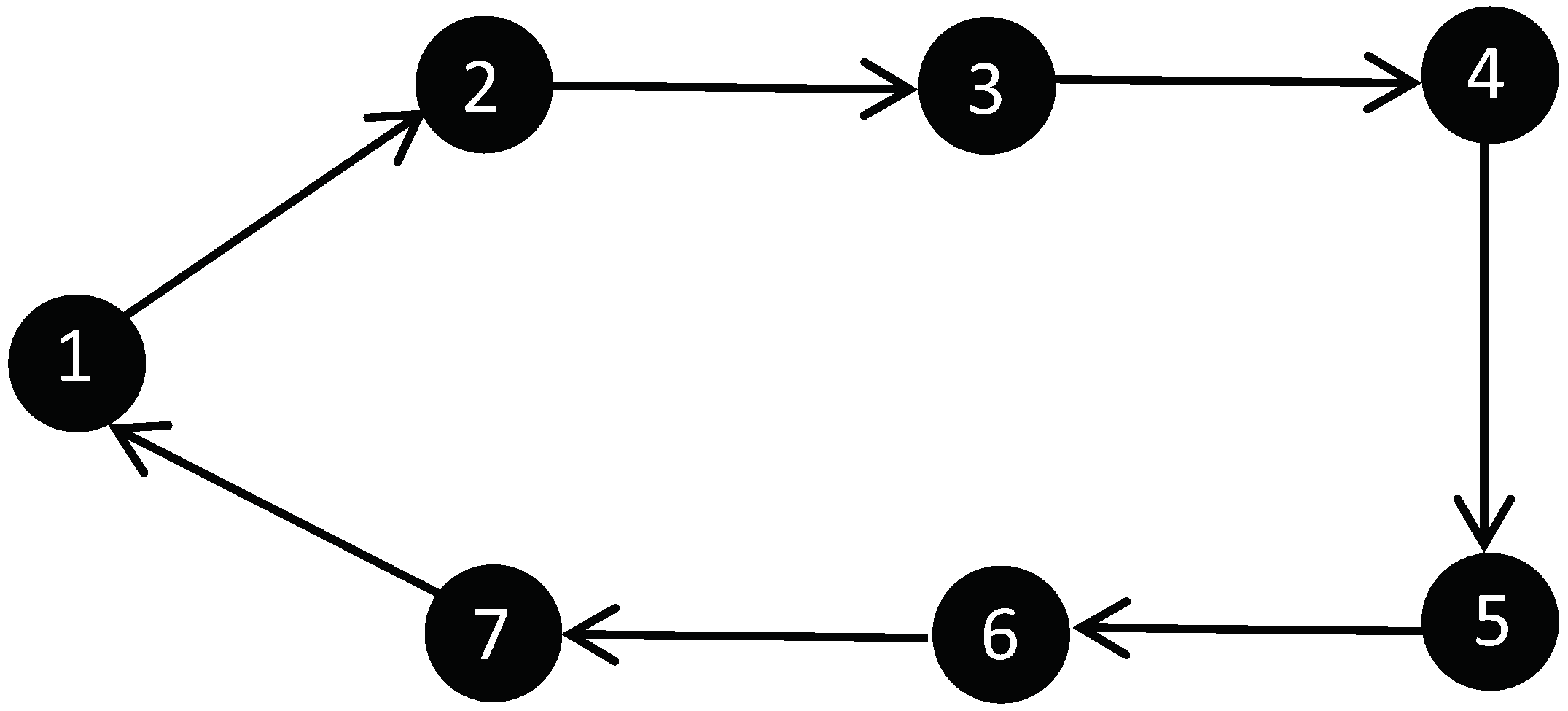
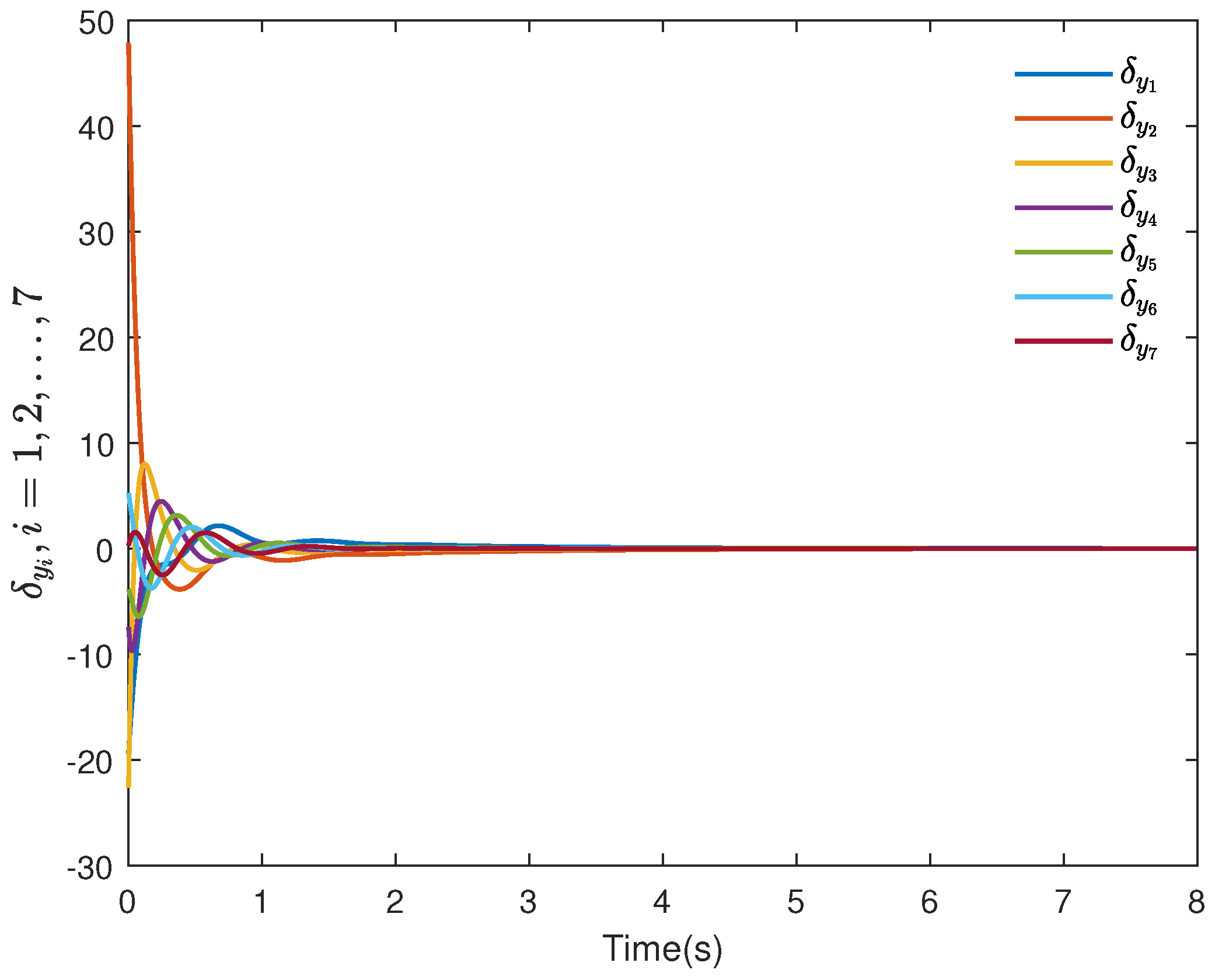
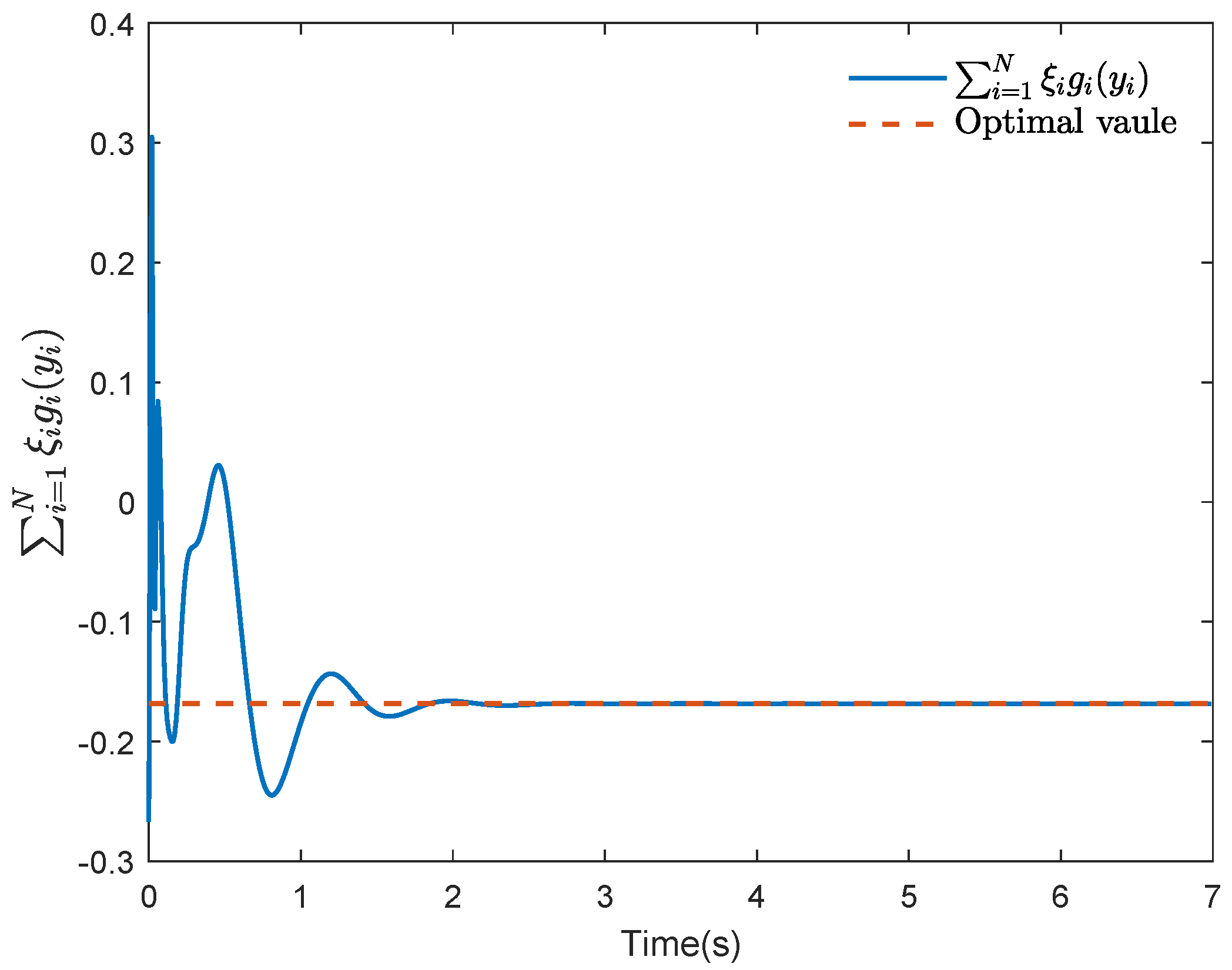
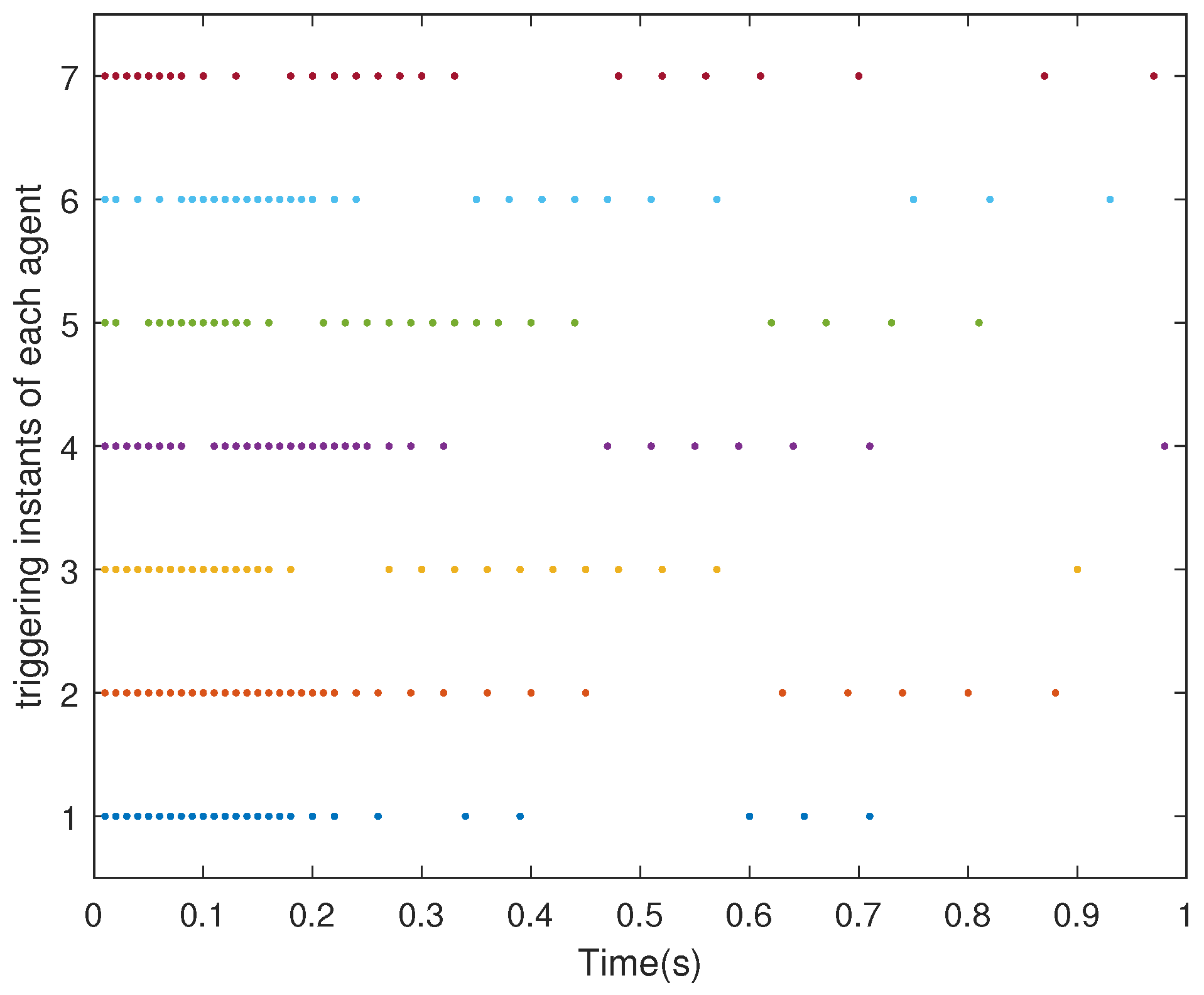
5. Illustrative Examples
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, F.; Chen, J. Minimum-energy distributed consensus control of multiagent systems: A network approximation approach. IEEE Trans. Autom. Control 2019, 65, 1144–1159. [Google Scholar] [CrossRef]
- Meng, M.; Xiao, G.; Zhai, C.; Li, G.; Wang, Z. Distributed consensus of heterogeneous multi-agent systems subject to switching topologies and delays. J. Frankl. Inst. 2020, 357, 6899–6917. [Google Scholar] [CrossRef]
- Yan, M.; Ma, W.; Zuo, L.; Yang, P. Dual-mode distributed model predictive control for platooning of connected vehicles with nonlinear dynamics. Int. J. Control Autom. Syst. 2019, 17, 3091–3101. [Google Scholar] [CrossRef]
- Li, Z.; Gao, L.; Chen, W.; Xu, Y. Distributed adaptive cooperative tracking of uncertain nonlinear fractional-order multi-agent systems. IEEE CAA J. Autom. Sin. 2020, 7, 292–300. [Google Scholar] [CrossRef]
- Fu, Q.; Shen, Q.; Jia, Z. Cooperative adaptive tracking control for unknown nonlinear multi-agent systems with signal transmission faults. Circuits Syst. Signal Process. 2020, 39, 1335–1352. [Google Scholar] [CrossRef]
- Chen, C.; Zhou, X.; Li, Z.; He, Z.; Li, Z.; Lin, X. Novel complex network model and its application in identifying critical components of power grid. Phys. A Stat. Mech. Its Appl. 2018, 512, 316–329. [Google Scholar] [CrossRef]
- Chen, F.; Chen, Z.; Xiang, L.; Liu, Z.; Yuan, Z. Reaching a consensus via pinning control. Automatica 2009, 45, 1215–1220. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, G.P.; Su, H.; Wang, X. Robust global coordination of networked systems with input saturation and external disturbances. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 7788–7800. [Google Scholar] [CrossRef]
- Liu, C.; Li, R.; Liu, B. Group-bipartite consensus of heterogeneous multi-agent systems over signed networks. Phys. A Stat. Mech. Its Appl. 2022, 592, 126712. [Google Scholar] [CrossRef]
- Cai, J.; Feng, J.; Wang, J.; Zhao, Y. Event-Based Leader-Following Synchronization of Coupled Harmonic Oscillators Under Jointly Connected Switching Topologies. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 958–962. [Google Scholar] [CrossRef]
- Zhang, Q.; Gong, Z.; Yang, Z.; Chen, Z. Distributed convex optimization for flocking of nonlinear multi-agent systems. Int. J. Control Autom. Syst. 2019, 17, 1177–1183. [Google Scholar] [CrossRef]
- Yi, P.; Li, L. Distributed Nonsmooth Convex Optimization over Markovian Switching Random Networks with Two Step-Sizes. J. Syst. Sci. Complex. 2021, 34, 1–21. [Google Scholar] [CrossRef]
- Chen, J.; Kai, S. Cooperative transportation control of multiple mobile manipulators through distributed optimization. Sci. China Inf. Sci. 2018, 61, 1–17. [Google Scholar] [CrossRef]
- Wu, Z.; Li, Z.; Yu, J. Designing Zero-Gradient-Sum Protocols for Finite-Time Distributed Optimization Problem. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 1–9. [Google Scholar] [CrossRef]
- Chen, W.; Ren, W. Event-triggered zero-gradient-sum distributed consensus optimization over directed networks. Automatica 2016, 65, 90–97. [Google Scholar] [CrossRef]
- Gharesifard, B.; Cortés, J. Distributed Continuous-Time Convex Optimization on Weight-Balanced Digraphs. IEEE Trans. Autom. Control 2014, 59, 781–786. [Google Scholar] [CrossRef]
- Yang, S.; Liu, Q.; Wang, J. Distributed Optimization Based on a Multiagent System in the Presence of Communication Delays. IEEE Trans. Syst. Man Cybern. Syst 2017, 47, 717–728. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Su, H.; Lam, J. Reduced-order interval observer based consensus for MASs with time-varying interval uncertainties. Automatica 2022, 135, 109989. [Google Scholar] [CrossRef]
- Chen, S.; Garcia, A.; Shahrampour, S. On Distributed Non-convex Optimization: Projected Subgradient Method For Weakly Convex Problems in Networks. IEEE Trans. Autom. Control 2021, 67, 1. [Google Scholar]
- Mo, L.; Liu, X.; Cao, X.; Yu, Y. Distributed second-order continuous-time optimization via adaptive algorithm with nonuniform gradient gains. J. Syst. Sci. Complex. 2020, 33, 1914–1932. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Y.; Wen, G.; Chen, G. Distributed Optimization for Linear Multiagent Systems: Edge- and Node-Based Adaptive Designs. IEEE Trans. Autom. Control 2017, 62, 3602–3609. [Google Scholar] [CrossRef]
- Huang, B.; Zou, Y.; Meng, Z.; Ren, W. Distributed Time-Varying Convex Optimization for a Class of Nonlinear Multiagent Systems. IEEE Trans. Autom. Control 2020, 65, 801–808. [Google Scholar] [CrossRef]
- Zhang, Y.; Deng, Z.; Hong, Y. Distributed optimal coordination for multiple heterogeneous Euler–Lagrangian systems. Automatica 2017, 79, 207–213. [Google Scholar] [CrossRef]
- Li, Z.; Wu, Z.; Li, Z.; Ding, Z. Distributed Optimal Coordination for Heterogeneous Linear Multiagent Systems With Event-Triggered Mechanisms. IEEE Trans. Autom. Control 2020, 65, 1763–1770. [Google Scholar] [CrossRef]
- Mao, S.; Dong, Z.w.; Du, W.; Tian, Y.C.; Liang, C.; Tang, Y. Distributed Non-Convex Event-Triggered Optimization over Time-varying Directed Networks. IEEE Trans. Ind. Inform. 2021, 18, 4737–4748. [Google Scholar] [CrossRef]
- Wang, X.; Hong, Y.; Ji, H. Distributed Optimization for a Class of Nonlinear Multiagent Systems With Disturbance Rejection. IEEE Trans. Cybern. 2016, 46, 1655–1666. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Yu, Y.; Li, X.; Xie, L. Exponential convergence of distributed optimization for heterogeneous linear multi-agent systems over unbalanced digraphs. Automatica 2022, 141, 110259. [Google Scholar] [CrossRef]
- Yan, J.; Yu, H. Distributed optimization of multiagent systems in directed networks with time-varying delay. J. Control. Sci. Eng. 2017, 2017, 7937916. [Google Scholar] [CrossRef]
- Yang, F.; Yu, Z.; Huang, D.; Jiang, H. Distributed optimization for second-order multi-agent systems over directed networks. Mathematics 2022, 10, 3803. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Cai, S.; Zhou, F.; He, Q. Fixed-time cluster lag synchronization in directed heterogeneous community networks. Phys. A Stat. Mech. Its Appl. 2019, 525, 128–142. [Google Scholar] [CrossRef]
- Ruan, X.; Xu, C.; Feng, J.; Wang, J.; Zhao, Y. Adaptive dynamic event-triggered control for multi-agent systems with matched uncertainties under directed topologies. Phys. A Stat. Mech. Its Appl. 2022, 586, 126450. [Google Scholar] [CrossRef]
- Kia, S.S.; Cortés, J.; Martínez, S. Distributed convex optimization via continuous-time coordination algorithms with discrete-time communication. Automatica 2015, 55, 254–264. [Google Scholar] [CrossRef]
- Wu, Z.; Li, Z.; Ding, Z.; Li, Z. Distributed Continuous-Time Optimization With Scalable Adaptive Event-Based Mechanisms. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 3252–3257. [Google Scholar] [CrossRef]
- Mazo, M.; Tabuada, P. Decentralized Event-Triggered Control Over Wireless Sensor/Actuator Networks. IEEE Trans. Autom. Control 2011, 56, 2456–2461. [Google Scholar] [CrossRef]
- Cai, J.; Feng, J.; Wang, J.; Zhao, Y. Tracking Consensus of Multi-agent Systems Under Switching Topologies via Novel SMC: An Event-Triggered Approach. IEEE Trans. Netw. Sci. Eng. 2022, 9, 2150–2163. [Google Scholar] [CrossRef]
- Deng, Z.; Wang, X.; Hong, Y. Distributed optimisation design with triggers for disturbed continuous-time multi-agent systems. IET Contr. Theory Appl. 2017, 11, 282–290. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Huang, B.; Han, J. A distributed Newton–Raphson-based coordination algorithm for multi-agent optimization with discrete-time communication. Neural Comput. Appl. 2020, 32, 4649–4663. [Google Scholar] [CrossRef]
- Wan, P.; Lemmon, M.D. Event-triggered distributed optimization in sensor networks. In Proceedings of the 2009 International Conference on Information Processing in Sensor Networks, San Francisco, CA, USA, 13–16 April 2009; pp. 49–60. [Google Scholar]
- Li, R.; Yang, G.H. Consensus Control of a Class of Uncertain Nonlinear Multiagent Systems via Gradient-Based Algorithms. IEEE Trans. Cybern. 2019, 49, 2085–2094. [Google Scholar] [CrossRef]
- Lin, P.; Ren, W.; Yang, C.; Gui, W. Distributed Continuous-Time and Discrete-Time Optimization With Nonuniform Unbounded Convex Constraint Sets and Nonuniform Stepsizes. IEEE Trans. Autom. Control 2019, 64, 5148–5155. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Wu, C.W.; Chua, L. Synchronization in an array of linearly coupled dynamical systems. IEEE Trans. Circuits Syst. I-Fundam. Theor. Appl. 1995, 42, 430–447. [Google Scholar]
- Godsil, C.; Royle, G.F. Algebraic Graph Theory; Springer: Berlin/Heidelberg, Germany, 2001; Volume 207. [Google Scholar]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Bhat, S.P.; Bernstein, D.S. Geometric homogeneity with applications to finite-time stability. Math. Control Signal Syst. 2005, 17, 101–127. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Liu, D.; Feng, J.; Zhao, Y. Distributed Optimization Control for Heterogeneous Multiagent Systems under Directed Topologies. Mathematics 2023, 11, 1479. https://doi.org/10.3390/math11061479
Wang J, Liu D, Feng J, Zhao Y. Distributed Optimization Control for Heterogeneous Multiagent Systems under Directed Topologies. Mathematics. 2023; 11(6):1479. https://doi.org/10.3390/math11061479
Chicago/Turabian StyleWang, Jingyi, Danqi Liu, Jianwen Feng, and Yi Zhao. 2023. "Distributed Optimization Control for Heterogeneous Multiagent Systems under Directed Topologies" Mathematics 11, no. 6: 1479. https://doi.org/10.3390/math11061479
APA StyleWang, J., Liu, D., Feng, J., & Zhao, Y. (2023). Distributed Optimization Control for Heterogeneous Multiagent Systems under Directed Topologies. Mathematics, 11(6), 1479. https://doi.org/10.3390/math11061479






