Analysis and Forecasting of International Airport Traffic Volume

Abstract

Globalization has resulted in increases in air transportation demand and air passenger traffic. With the increases in air traffic, airports face challenges related to infrastructure, air services, and future development. Air traffic forecasting is essential to ensuring appropriate investment in airports. In this study, we combined fuzzy theory with support vector regression (SVR) to develop a fuzzy SVR (FSVR) model for forecasting international airport traffic. This model was used to predict the air traffic volumes at the world’s 10 busiest airports in terms of air traffic in 2018. The predictions were made for the period from August 2014 to December 2019. For fuzzy time series, the developed FSVR model can consider historical air traffic changes. The FSVR model can suitably divide air traffic changes into appropriate fuzzy sets, generate membership function values, and establish fuzzy relations to produce fuzzy interpolated values with minimal errors. Thus, in the prediction of continuous data, the fuzzy data with the smallest errors can be subjected to SVR to find the optimal hyperplane model with the minimum distance to the appropriate support vector sample points. The performance of the proposed model was compared with those of five other models. Of the compared models, the FSVR model exhibited the lowest mean absolute percentage error (MAPE), mean absolute error, and root mean square error for all types of traffic at all of the airports analyzed; all of the MAPE values were below 2.5. The FSVR model can predict future growth trends in air traffic, air passenger flows, aircraft flows, and logistics. An airport authority can use this model to analyze the existing operational facilities and service capacity, find bottlenecks in airport operations, and create a blueprint for future development. The findings revealed that implementing a hybrid modeling approach, specifically the FSVR model, can significantly enhance the performance of the SVR model. The FSVR model allows airlines to predict traffic growth patterns, identify viable new destinations, optimize their schedules or fleet, make accurate marketing decisions, and plan traffic effectively. The FSVR model can guide the timely construction of appropriate airport facilities with accurate predictions. Rapid, cost-effective, efficient, and balanced transportation planning enables the provision of fast, cost-effective, comfortable, safe, and convenient passenger and cargo services while ensuring the proper planning of the airport’s capacity for land-side transportation connections.

1. Introduction

Globalization has brought about numerous changes in people’s lives [1]. The International Fund has identified four fundamental aspects of globalization: trade and international exchange, capital and investment, population flow, and the diffusion of knowledge. The world market has become integrated into a global village through international trade and investment growth [2]. Air transport is a global industry that is a catalyst for interconnectedness and globalization [3]. Air travel can be undertaken for purposes such as sightseeing and entertainment, attending business meetings, and delivering commercial goods to international destinations worldwide. Air traffic has increased considerably over the past years. The Air Passenger Traffic Forecast Report noted that the demand for air passenger traffic has grown strongly and that the aviation industry’s center of gravity has shifted eastward over time [4]. By 2022, the volume of air passenger traffic was expected to be double the level of 2021, and the average annual growth rate of air passenger traffic was expected to reach 3.5%. By 2037, the number of air passengers is expected to be 8.2 billion [5]. Air transportation in various countries is gaining momentum. The development prospects for the aviation industry are bright, and this industry will flourish and lead the development of the world economy in the future. The aviation industry can benefit from better interconnection. However, the International Air Transport Association indicated that airports and air traffic control may be unable to cope with the increasing passenger demand. Governments and infrastructure operators should plan strategically for future development [6], and their decisions have a strong influence on the value created in their region [7].

The era of low-cost carriers (LCCs) began with the founding of Southwest Airlines in 1971 as the world’s first LCC [8]. LCCs have created transportation demand and have become a source of economic growth over the past decade. In 2008, LCCs provided approximately 3.6 billion seats in the air transport industry, which increased to approximately 5.3 billion seats by the end of 2017. The market share of LCCs increased from 21% in 2007 to 29% in 2017. The market share of LCCs on intercontinental routes increased from 4.4% in 2008 to 11.4% in 2017. Moreover, the market share of LCCs on regional routes increased from 23.6% to 31.4% during the aforementioned period. LCCs have thus experienced considerable growth over the past 15 years.

The aviation industry continues to develop as air traffic continues to grow. The governments of various countries should solve infrastructure bottlenecks when developing their domestic aviation markets [3]. With the emergence of new infrastructure and aviation services, the demand for air transportation has increased over time. However, forecasting airport traffic accurately is essential for determining precise returns on investment and avoiding investment wastage. Therefore, governments must conduct suitable traffic forecasting and planning for the aviation industry [6] and develop efficient air infrastructure and air services if their countries are to meet national economic development goals [7].

Models used for aviation management forecasting range from simple techniques to more complex approaches. Wang et al. conducted a study on forecasting the tourism demand in Hong Kong, comparing the effectiveness of three forecasting techniques. These techniques involved the use of a combination of models such as the autoregressive integrated moving average (ARIMA) model, the autoregressive distributed lag model, the error correction model, and the vector autoregressive model. Their results indicated that superior forecasting results were obtained when using combinations of the aforementioned models, rather than when using any model alone [9]. Therefore, when it is unknown which model in a set of models produces the best predictions, the predictions of the several models can be combined to obtain suitable results. Saayman modeled and predicted tourism in South Africa from its major intercontinental tourism markets [10] by using a naive forecasting model, the Holt–Winters exponential smoothing (ETS) model [11], the ARIMA model [12], and the seasonal ARIMA (SARIMA) model [13]. Their results indicated that, of the aforementioned models, the SARIMA model was the most accurate in forecasting the tourist arrivals in three time intervals: 3, 6, and 12 months. Saayman concluded that univariate forecasting methods are relatively accurate in predicting the number of tourists that will visit South Africa, especially in the short run. However, the SARIMA model has limitations in its policy applications due to its inability to assess the impact of external events on tourist arrivals [10]. Hassani compared the performance of different models in forecasting the number of tourists arriving in Europe in terms of their root mean square error (RMSE) and direction of change [14]. They found that the singular spectrum analysis R model, the singular spectrum analysis V model, and the ARIMA model, as well as the Box-Cox transformation, the autoregressive moving average error, the trend, and the seasonal component model [15], were superior to other models. To determine the terminal capacity required to support the long-term growth of Taoyuan International Airport in Taiwan, Suryani developed a system dynamics model for predicting the future air cargo demand [16]. Alexander and Merkert developed a gravity-based model for predicting airfreight demand. They evaluated gravity models to predict and provide accurate explanations for the effects of major economic events, such as a global financial crisis, on airfreight demand [17]. The least accurate models have been found to be the ETS [11], AR fractionally integrated MA, AR, and weighted AR [18] models. The computational modeling is mainly based on artificial neural networks [19,20,21] and the support vector machine (SVM) model [22,23,24], and complex numerical models work together with physical descriptions of the processes without empirical analysis [25]. Cao et al. explored and analyzed subway passenger traffic diversion laws during holidays by using the predictions of an ARIMA model and a SVM model [26]. However, in terms of prediction accuracy, no single model is superior to the alternative models under all conditions. Traditional time series analysis models are not superior to machine learning prediction models. Although traditional time series analysis and predictive models may be among the best models for predicting a given time series, they still have many limitations when applied in practice. The problem of predicting values that approximate historical data cannot be solved by traditional methods [27]. The forecasting performances of the support vector regression (SVR) and ARIMA models, which have unique advantages and disadvantages, has not been compared.

The advantages of using the SVR model to produce accurate predictions become less apparent as the length of the time series forecast increases. Further improvements can be made to the original ML in various ways, given that hybrid models can produce effective predictions. One solution for improvement is to use a fuzzy system with the SVR to allow different input points to contribute in different ways to the learning of the decision surface. The advantages of these models can be combined using a fuzzy time series (FTS) [28]. Tai proposed an improved FTS (IFTS) model that uses historical data to make predictions about the penetration of salt and the total population, and their model had a higher prediction accuracy than did other fuzzy SVR models [29]. The results show that the hybrid model can be more accurate in time series predictions because it reduces the influence of outliers. In summary, hybrid models can achieve better prediction results than can single models.

In the present study, a self-developed fuzzy SVR (FSVR) model based on an IFTS was used to accurately predict international airport traffic. The FSVR model was developed using an improved fuzzy set to perform SVR, which approximates the fuzzy upper and lower bounds to generate numerical predictions. The model parameters have been studied to determine the optimal values for each data set in use. The results of testing the proposed model on a large number of data sets with different characteristics showed that the proposed model outperforms the existing models such as Holt–Winters’ (ADD), ETS, ARIMA, SARIMA, and SVR. Airport traffic data are represented as fuzzy values and can be used for membership functions to simulate economic expertise and knowledge. Seasonal time series are suitable for interpolating historical data and predicting future data. The proposed FSVR model can efficiently and accurately solve time series and nonlinear problems. The contributions of this study are as follows. First, we developed and optimized an FSVR model for forecasting international airport traffic volumes. Second, we validated the ability of the developed FSVR model to perform well under multiple parameters. Third, robust statistical indicators were calculated to determine the accuracy of the proposed model. These indicators were obtained by comparing the model forecasts with observation data published on the websites of various airports. However, the airport traffic volume can be violently affected by the negative phenomena such as a worldwide infectious disease [30,31]. Our proposed method can only be applied to a continuous periodic sequence, and negative phenomena can affect the accuracy of the forecast obtained using the proposed method [32].

2. Methods

2.1. Support Vector Regression

SVR is a supervised learning model that extends the traditional SVM algorithm [33]. This model uses the ε-insensitive loss function of the training data for regression analysis, which allows the prediction of continuous data [34]. The SVR algorithm constructs a hyperplane to minimize the distance from the farthest sample point to the hyperplane. To transform nonlinear problems into linear problems, the SVR algorithm maps the training data into a high-dimensional feature space. The training data are represented by {(x_i, y_i); i = 1, 2, …, N; x_i ∈ Rⁿ; y_i ∈ R}, where x_i is an n-dimensional input value, y_i is the actual output value, and N is the size of the data set. The SVR function is defined as

$$y=f\left(x_i\right)={\omega }^T\phi \left(x_i\right)+b$$

(1)

The predicted value f(x_i) is represented by a linear combination of the feature functions of the input φ(x_i). Moreover, the adjustment factors ω and b are estimated using a penalty function as follows:

$$R\left(C\right)=\frac{1}{2}{\parallel \omega \parallel }^2+C·\frac{1}{n}{\displaystyle \sum }_{i=1}^n\parallel y_i-f{\left(x\right)\parallel }_{\epsilon }$$

(2)

$${\left|y-f\left(x\right)\right|}_{\epsilon }=\{\begin{array}{c}0, \left|y-f\left(x\right)\right|\le \epsilon \\ \left|y-f\left(x\right)\right|-\epsilon , otherwise\end{array}$$

(3)

The balance between model complexity and training error rate is controlled by the penalty coefficient C and the maximum tolerable error ε. To handle the infeasible constraints of the optimization problem, the slack variables ${\xi }_i$ and ${\xi }_i^{*}$ are introduced as follows:

$$\begin{gathered} \underset{\omega b{\xi }^{(*)}}{\min }\frac{1}{2}{\parallel \omega \parallel }^2+C{\displaystyle \sum }_{i=1}^n\left({\xi }_i+{\xi }_i^{*}\right), \\ \mathrm{subject} \mathrm{to} \{\begin{array}{c}-y_i+{\omega }^T\phi \left(x_i\right)+b\le \epsilon +{\xi }_i^{},\left(i=1,\dots , m\right), \\ y_i-{\omega }^T\phi \left(x_i\right)-b\le \epsilon +{\xi }_i^{*},\left(i=1,\dots , m\right), \\ {\xi }_i^{*}\ge 0, \left(i=1,\dots , m\right),\end{array} \end{gathered}$$

(4)

A small ε value can lead to overfitting, whereas a large ε value can lead to underfitting. The Lagrangian equations for a dual optimization problem are expressed as follows:

$$\begin{gathered} \underset{{\alpha }_{i,}{\alpha }_i^{*}}{\min }\frac{1}{2}{\displaystyle \sum }_{i,j=1}^n{y}_i\left({\alpha }_i-{\alpha }_i^{*}\right)\left({\alpha }_j-{\alpha }_j^{*}\right)k\left(x_i,x_j\right)+{\displaystyle \sum }_{i=1}^n\left(\left(\epsilon -y_i\right){\alpha }_i+\left(\epsilon +y_i\right){\alpha }_i^{*}\right), \\ \mathrm{Subject} \mathrm{to}\{\begin{array}{c}{\displaystyle {\displaystyle \sum }_{i=1}^n}\left({\alpha }_i-{\alpha }_i^{*}\right)=0, \\ 0\le {\alpha }_i^{*}\le C, \left(i=1,\dots ,m\right)\end{array} \end{gathered}$$

(5)

An SVR function is expressed as follows:

$$f\left(x\right)={\displaystyle \sum }_{i=1}^n\left({\alpha }_i-{\alpha }_i^{*}\right)k\left(x_i , x\right)+b$$

(6)

where ${\alpha }_i$ and ${\alpha }_i^{*}$ represent Lagrange multipliers and k(x_i, x) represent the kernel function. By performing additive decomposition on univariate time series models, the SVR model can be constructed so that the kernel function class is closed under additive decomposition. Commonly used kernel functions for the SVR model include spline, Gaussian radial basis function (RBF), linear, polynomial, and matching hidden Markov model (MHMM) kernels [35]. The Gaussian RBF kernel is widely used for nonlinear mapping, especially when considering the interactions between two time series, and performs well under the additive decomposition of these kernel functions [36]. The Gaussian RBF kernel constructs a nonlinear decision hyperplane in the input space using the following formula:

$$k\left(x_i, x\right)=exp\left(-\sigma \parallel x-x_i\parallel {}^2\right)$$

(7)

where σ represents the kernel width, and x and x_i are input vectors. In SVR, there are three main parameters that strongly affect performance, and they are the penalty coefficient C, the kernel parameter, and the width ε of the insensitive loss function. C is used to balance the relationship between model complexity and training error, while ε is used to control the width of the SVR sensitive region and the number of support vectors. For the Gaussian RBF kernel, the kernel parameter affects the distribution and range characteristics of the training sample data, thus affecting the width of the local neighborhood.

2.2. Fuzzy Set Design

Let U = {u₁, u₂, ..., u_m} denote the complete set of objects under discussion, which is called the universe. Each element in the universe is represented by u. The fuzzy set of U is defined as follows:

A = {μ_A(u₁)/u₁, μ_A(u₂)/u₂, ..., μ_A(u_m)/u_m}

(8)

where μ_A(u_i) is the membership function that maps the elements of universe U to the range [0,1]. The membership function μ_A(u_i): U → [0, 1] indicates the degree of membership of element u_i in set A, where i is an integer from 1 to m. The membership degree ranges from 0 to 1.

Let X(t) be a sequence of values with t = 1, 2, ..., and let X be an element in universe U. If a real number f_i(t) is given such that f_i(t) is in the range [0, 1], then f_i(t) is defined as a fuzzy subset. The collection of f₁(t), f₂(t), ..., f_i(t) is called the fuzzy time series of X(t), which is denoted F(t). The deviation between the original prediction and the estimated data—which is represented as {${\widehat{X}}_i$}, i = 1, 2, ..., n—is evaluated using metrics such as the mean square error, mean absolute error (MAE), mean absolute percentage error (MAPE), symmetric MAPE, mean absolute scaled error, and RMSE. A smaller variance indicates a more accurate model prediction. Suppose that the data set X_i corresponds to the time t_i, where i = 1, 2, ..., n.

2.3. Fuzzy SVR

The FSVR model developed in this study is based on the IFTS model [29], which uses dynamic, probabilistic, and comprehensive rules for the handling of uncertainties in raw data [37,38]. The IFTS model is based on the concept of variation between two consecutive periods and the fuzzy relationship between the elements in a series. For seasonal and nonseasonal time series, this model can perform fuzzy historical interpolation and make predictions about the future. All of the parameters of the proposed IFTS model are calculated using the appropriate methods to accommodate data sets with different characteristics. The IFTS model is more effective in prediction and forecasting than are alternative models and is included in the R program as a function and thus is convenient to implement. The steps of the IFTS model are outlined in Algorithm 1, and additional information is provided in the subsequent text [29].

Algorithm 1: Fuzzy time series using IFTS model

Definition:   The interval between the smallest and largest variations in the data set is contained in the universal set U.   Ui = Xi+1 − Xi, i = 1, 2, ..., n − 1   U = [Min, Max]

Input:   Air traffic: The data set Xi of passengers, aircraft movements, and freight corresponds to the time ti, i=1, 2, …, n.

Output:   Fuzzy model of the time series of the air traffic volume with the lowest RMSE value.

1 $$\begin{gathered} \mathrm{Divide} U \mathrm{into} m \mathrm{equal} \mathrm{intervals} \mathrm{of} \mathrm{fuzzy} \mathrm{sets} u_i, i=1, 2, \dots , m. \mathrm{Find} \mathrm{the} \mathrm{midpoints} \\ \mathrm{of} \mathrm{the} \mathrm{intervals} \left(u_i^0, i=1,\dots , m\right) \end{gathered}$$ with initial values m = 5, 6, 7, …, 11.

2 Calculation of the C-value of each interval $t=0, \mathrm{initial} \mathrm{values} k=500, \epsilon =1\mathrm{e}-06, a^{\left(0\right)}=0, b^{\left(0\right)}=1, \mathsf{\Delta }{C}^{\left(0\right)}=0.5, n^{\left(0\right)}=1$

3 If t = i and i ≥ 1

4  $\mathrm{Compute} \mathsf{\Delta }{C}^{\left(t\right)}=\frac{b^{\left(t\right)}-a^{\left(t\right)}}{k}, and C_i^{\left(t\right)}$

5   $\mathrm{If} a=0 \mathrm{and} b=1, C_i^{\left(t\right)}=a^{\left(t\right)}+i△C^{\left(t\right)}, i=1, 2, \dots , k-1$

6  If a = 0 and b ≠$1, C_i^{\left(t\right)}=a^{\left(t\right)}+i△C^{\left(t\right)}, i=1, 2, \dots , k$

7  If a ≠$0 \mathrm{and} b=1, C_i^{\left(t\right)}=a^{\left(t\right)}+i△C^{\left(t\right)}, i=0, 1, 2, \dots , k-1$

8  If a ≠ 0 and b ≠$1, C_i^{\left(t\right)}=a^{\left(t\right)}+i△C^{\left(t\right)}, i=0, 1, 2, \dots , k$

9  IFTS to find $C_l^{\left(t\right)}$$, 0\le l\le k$

10  Find $C=C_l^{\left(m\right)}$$\mathrm{until} b^{\left(m\right)}-a^{\left(m\right)}<\epsilon$

11 Determination of the respective values of the set of the fuzzy set with C, $\mu {\mathsf{A}}_i\left(u_i\right)=\frac{1}{1+{\left[C\times \left(U_i-u_i^0\right)\right]}^2}, i=1, 2, \dots , m$

12 Choose a base corresponding to the previous time intervals, w = 12 (1 < w < n).

13 Calculation of the fuzzy relationship matrix $R^w\left(t\right)=O^w\left(t\right){{\displaystyle \cap }}^{}K\left(t\right)=\left[\begin{array}{c}\begin{array}{c}{R}_{11}\\ R_{21}\end{array} \begin{array}{c}{R}_{12}\\ R_{22}\end{array} \begin{array}{c}\dots \\ \dots \end{array} \begin{array}{c}{R}_{1j}\\ R_{2j}\end{array}\\ \begin{array}{c}\dots \\ R_{i1}\end{array} \begin{array}{c}\dots \\ R_{i2}\end{array} \begin{array}{c}\dots \\ \dots \end{array} \begin{array}{c}\dots \\ R_{ij}\end{array}\end{array}\right]$.

14 Define F$$\begin{gathered} \left(t\right) \mathrm{as} \mathrm{the} \mathrm{fuzzy} \mathrm{forecast} \mathrm{of} \mathrm{the} \mathrm{variations} \mathrm{at} \mathrm{the} \mathrm{moment} t. \\ Ft=\left[E\left(R_{11}, R_{21},\dots , R_{i1}\right) E\left(R_{12}, R_{22},\dots , R_{i2}\right)\dots E\left(R_{1j}, R_{2j},\dots , R_{ij}\right)\right] \end{gathered}$$ where $E\left(R_{1k}, R_{2k},\dots , R_{ik}\right)=\frac{R_{1k}+R_{2k}+\dots +R_{ik}}{w-2},k=1, 2,\dots , j$

15 Forecast 7(m(7)×w(1)) fuzzy model data for the time series, forecast value, and the   result is calculated for the value t = w based on the variations in the result of the   previous values (t − 1, ..., t − w).

16  $\widehat{X}\left(t\right)=X\left(t-1\right)+V\left(t\right)$ $\mathrm{where} V\left(t\right)=\frac{{{\displaystyle \sum }}_{i=1}^w{\mu }_t\left(u_i\right)\times u_m^i}{{{\displaystyle \sum }}_{i=1}^w{\mu }_t\left(u_i\right)}$

17 The data from each fuzzy model are compared with the real data. The RMSE is   calculated for all of the fuzzy model data. We use the RMSE as the evaluation   criterion to compare with the listed models.

The five steps used to construct an IFTS model [29] for the fuzzy set between X_i+1 and X_i are as follows:

Step 1: Calculate the change between successive time periods in the data set X_i, and determine the minimum (Min) and maximum (Max) values of universe U [39].

U_i = X_i+1 − X_i, i = 1, 2, ..., n − 1

(9)

Step 2: Divide the universe U into m equal-length intervals, each denoted by u_i (i = 1, 2, ..., m), where the growth rate of each interval can vary at different times. Next, compute the midpoint of each interval, denoted by $u_i^0$ (i = 1, 2, ..., m).

Step 3: On the basis of the fuzzy set between X_i+1 and X_i, determine the corresponding value of the fuzzy set A_i of F(t). The fuzzy sets A₁, A₂, ..., A_m are defined as follows:

A_i = {μA_i(u_i)/u_i}, u_i∈U, μA_i∈[0, 1]

(10)

$$\mu {\mathsf{A}}_i\left(u_i\right)=\frac{1}{1+{\left[C\times \left(U_i-u_i^0\right)\right]}^2}, i=1, 2, \dots , m$$

(11)

where C is a constant, with C ∈ (0, 1); U_i is the change between successive time periods, calculated in step 1; and $u_i^0$ is the midpoint of each time period, calculated in step 2.

Step 4: Select an interval cardinality w (1 < w < n). Based on the chosen value of w, compute the fuzzy relation matrix R^w(t). This step generates a computation matrix O^w(t) of size i × j, where i is the number of rows and j is the number of columns. Depending on the number of interval changes, the computation matrix is aligned with the data at times t − 2, t − 3, ..., t − w. Additionally, a 1 × j matrix K(t) is obtained to represent the fuzzy change row matrix at time t − 1. Finally, the obtained fuzzy relation matrix R(t) is combined with the fuzzy relation matrices from other time instants to form the relation matrix R(t), as Equation (12).

$$R\left(t\right)=O^w\left(t\right){{\displaystyle \cap }}^{}K\left(t\right)=\left[\begin{array}{c}\begin{array}{c}{R}_{11}\\ R_{21}\end{array} \begin{array}{c}{R}_{12}\\ R_{22}\end{array} \begin{array}{c}\dots \\ \dots \end{array} \begin{array}{c}{R}_{1j}\\ R_{2j}\end{array}\\ \begin{array}{c}\dots \\ R_{i1}\end{array} \begin{array}{c}\dots \\ R_{i2}\end{array} \begin{array}{c}\dots \\ \dots \end{array} \begin{array}{c}\dots \\ R_{ij}\end{array}\end{array}\right]$$

(12)

The fuzzy time series F(t) is expressed as follows:

$$Ft=\left[E\left(R_{11}, R_{21},\dots , R_{i1}\right) E\left(R_{12}, R_{22},\dots , R_{i2}\right)\dots E\left(R_{1j}, R_{2j},\dots , R_{ij}\right)\right]$$

(13)

where

$$E\left(R_{1k}, R_{2k},\dots , R_{ik}\right)=\frac{R_{1k}+R_{2k}+\dots +R_{ik}}{w-2},k=1, 2,\dots , j$$

(14)

Step 5: Forecast the data for time t by using the following equation:

$$\widehat{X}\left(t\right)=X\left(t-1\right)+V\left(t\right)$$

(15)

$$V\left(t\right)=\frac{{{\displaystyle \sum }}_{i=1}^w{\mu }_t\left(u_i\right)\times u_m^i}{{{\displaystyle \sum }}_{i=1}^w{\mu }_t\left(u_i\right)}$$

(16)

where μ_t(u_i) is a component of F(t). The term V(t) is calculated on the basis of the variation in the data throughout the time series and the previous V(t) values. X(t − 1) is the actual value at time t − 1, and $\widehat{X}\left(t\right)$ is the forecasted value at time t. The value of $\widehat{X}\left(t\right)$ is influenced by X(t − 1) and V(t). The calculation method is described in the following text.

Group data changes between consecutive time periods and assign those with larger changes to more clusters. Equation (12) shows the fuzzy relationship between the universe and the fuzzy sets. The time t is predicted in accordance with the result of t = w, which is derived from the change values of t − 1, t − 2, …, t − w. The obtained results are compared with the actual values to evaluate the model’s accuracy, and the error is estimated. The constant C influences the value of μA_i(u_i), and the criterion for the evaluation of the prediction model is used to determine the optimal value of C. The model evaluation process involves the following steps:

Step 1: Define the values of k and ε, where k represents the number of divisions in each iteration and ε represents the error in C. A smaller value of ε results in a longer computation time.

Step 2: For t = 0, allocate the initial values as follows: a⁽⁰⁾ = 0 and b⁽⁰⁾ = 1.

Step 3: For t = i, i ≥ 1, calculate the terms $a^{\left(t\right)}$, $b^{\left(t\right)}$, and $△C^{\left(t\right)}$ as follows:

$$a^{\left(t\right)}=a^{\left(t-1\right)}+\left[n^{\left(t-1\right)}-1\right]△C^{\left(t-1\right)},$$

(17)

$$b^{\left(t\right)}=a^{\left(t-1\right)}+\left[n^{\left(t-1\right)}+1\right]△C^{\left(t-1\right)},$$

(18)

$$△C^{\left(t\right)}=\frac{b^{\left(t\right)}-a^{\left(t\right)}}{k}, \mathrm{and} C_i^{\left(t\right)},$$

(19)

Depending on the values of a and b, calculate the values of $C_i^{\left(t\right)}$ as follows:

• if a = 0 and b = 1, then $C_i^{\left(t\right)}=a^{\left(t\right)}+i△C^{\left(t\right)}, i=1, 2, \dots , k-1,$
• if a = 0 and b $\ne$ 1, then $C_i^{\left(t\right)}=a^{\left(t\right)}+i△C^{\left(t\right)}, i=1, 2, \dots , k,$
• if a $\ne$ 0 and b $=$ 1, then $C_i^{\left(t\right)}=a^{\left(t\right)}+i△C^{\left(t\right)}, i=0, 1, \dots , k-1,$
• if a $\ne$ 0 and b $\ne$ 1, then $C_i^{\left(t\right)}=a^{\left(t\right)}+i△C^{\left(t\right)}, i=0, 1, \dots , k.$

Step 4: Calculate the IFTS by using $C_i^{\left(t\right)}$, and find $C_l^{\left(t\right)}$ to optimize the CEF model.

Step 5: Repeat Steps 3 and 4 to find C = $C_l^{\left(m\right)}$ until b^(m) − a^(m) < ε.

The “division of intervals for the universal set” algorithm in the IFTS model consists of the following steps:

Step 1: If t = 0, ε > 0 is a small positive number. In this case, the initializing sequence’s cluster elements are defined as $Z^{\left(0\right)}=\left(z_1^{\left(0\right)}, z_2^{\left(0\right)}, \dots , z_n^{\left(0\right)}\right)=\left(x_1, x_2, \dots , x_n\right)$.

Step 2: Update each fuzzy data point by using the following formula:

$$z_i^{\left(t+1\right)}=\frac{{{\displaystyle \sum }}_{i^{\prime }=1}^{n}f\left(z_i^{\left(t\right)}, z_{i^{\prime }}^{\left(t\right)} \right)· z_{i^{\prime }}^{\left(t\right)}}{{{\displaystyle \sum }}_{i^{\prime }=1}^{n}f\left(z_i^{\left(t\right)}, z_{i^{\prime }}^{\left(t\right)} \right)}$$

(20)

where f($z_i^{\left(t\right)}, z_{i^{\prime }}^{\left(t\right)}$) is a truncated Gaussian kernel. This kernel is defined as follows:

$$f\left(z_i^{\left(t\right)}, z_{i^{\prime }}^{\left(t\right)}\right)=\{\begin{array}{c}\exp \left(-\frac{d}{\lambda }\right) if d=d\left(z_i^{\left(t\right)},z_i^{\prime \left(t\right)}\right)\le d_s,\\ 0 if d>d_s,\end{array}$$

(21)

where $d\left(z_i^{\left(t\right)},z_i^{\prime \left(t\right)}\right)$ is the Euclidean distance between $z_i^{\left(t\right)}$ and $z_i^{\prime \left(t\right)}$. Moreover, d_s is the average value of all pairs of data element distances. Calculate the parameter d_s as follows:

$$d_s=\frac{2}{n\left(n-1\right)}{\displaystyle \sum }_{i<i^{\prime }}d\left(x_i, x_i^{\prime }\right)$$

(22)

where n is the number of data points and λ depends on d_s. If λ approaches 0, the data have n intervals, and if λ approaches infinity, the data have one interval.

Step 3: Step 2 is repeated until the condition $ma{x}_i\left\{d\left(z_i^{\left(t\right)},z_i^{\left(t+1\right)}\right)\right\}<\epsilon$ i is satisfied. When the elements of the data set converge to the representative element $z_i^{\left(t\right)}$, i ranges from 1 to m. After the computation is complete, a sequence containing m representative elements is obtained, where m represents the interval value for partitioning the entire set.

The IFTS model described in the aforementioned text was used to fuzzify an original air traffic time series. The fuzzy time series data were used as independent regression variables for an SVR model, and fuzzy reasoning was implemented to generate corresponding fuzzy data. The SVR model was trained for air traffic volume prediction by using independent regression variables. Various factors affecting the partition of the fuzzy set were considered in the fuzzification process. These factors are as follows:

• Flight schedules in winter and summer based on each airport’s time zone.
• The role of each airport in the global air transportation network and the unique functions it performs based on its geographic location.
• Consecutive public holidays in each region.
• Off-peak and peak tourism needs or the effects of major events, such as the Olympics or a world’s fair, on air traffic.

Flight seasons are divided into winter and summer, covering flights from November 1 to March 31 of the following year, and from April 1 to October 31, respectively. The main fuzzy set is constructed based on flight schedules and flight frequency tables and includes five fuzzy sets: summer peak, winter peak, intermediate transition, summer off-peak, and winter off-peak. In addition, other factors affecting air traffic, such as light peaks, local tourist demand, and national holidays, are also considered. The number of fuzzy sets is between 5 and 10, and the seasonal factors and time intervals are set to 12 months. Using the IFTS model, a fuzzy data model with seven fuzzy sets (m = 7) and a time interval of 12 months is generated. The RMSE of each fuzzy set is calculated, and the group with the smallest RMSE is selected as the input data for the AR independent variable. The interval cardinality is used as the fuzzy extraction parameter for 12 periods, and the fuzzy relationship matrix is calculated within these 12 periods, dividing the fuzzy sets into 12 groups. The original data are used as the dependent variable for SVR, while the independent variable is fuzzy. The data are divided into training and test sets to determine the optimal SVR parameters and construct the proposed SVR prediction model.

2.4. Evaluation Criteria

The MAPE, MAE, and RMSE were used to evaluate indicators to determine the optimal prediction model. These indicators are expressed as follows:

$$MAPE=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left|\frac{Y_i-{\widehat{Y}}_i}{Y_i}\right|\times 100$$

(23)

$$RMSE=\sqrt{\frac{1}{n}\times {\displaystyle \sum }_{i=1}^n{\left({\widehat{Y}}_i-Y_i\right)}^2}$$

(24)

$$MAE=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left|Y_i-{\widehat{Y}}_i\right|$$

(25)

where $Y_i$ is the actual value, ${\widehat{Y}}_i$ is the forecasted value, and n is the number of forecast periods. The MAPE is a relative indicator that is independent of the unit and magnitude of the actual and forecasted values. The difference between the predicted and actual values can be determined objectively by using the MAPE. The MAPE is used to compare the overall prediction accuracy of the models in an easy and quick manner. A lower MAPE indicates a higher prediction accuracy. According to Lewis, four categories of the MAPE exist: very accurate, solid, adequate, and imprecise.

RMSE is a statistical measure used to quantify the deviation between predicted and actual values. It is calculated as the square root of the ratio of the average deviation between the actual and predicted data to the number of observations. The RMSE is sensitive to small errors in a set of measurements and thus can suitably reflect the measurement precision. Consequently, it is used as a standard for evaluating the accuracy of a measurement process.

The MAE is the average of the absolute residuals between each predicted value and the actual value. This parameter is a convenient tool for measuring errors and ranges from 0 to infinity. When the predicted and actual values are in perfect agreement, the MAE is 0, and the prediction model is perfect.

3. Results and Discussion

This study focused on the International Airport Association’s time series of the air traffic at the 10 airports with the most passenger traffic globally in 2018, namely the Hartsfield–Jackson Atlanta International Airport (ATL) in the United States, Beijing Capital International Airport (PEK) in China, Dubai International Airport (DXB) in the United Arab Emirates, Los Angeles International Airport (LAX) in the United States, Tokyo International (Haneda) Airport (HND) in Japan, Chicago O’Hare International Airport (ORD) in the United States, London Heathrow Airport (LHR) in the United Kingdom, Hong Kong International Airport (HKG) in China, Shanghai Pudong International Airport (PVG) in China, and Paris Charles de Gaulle International Airport (CDG) in France [40].

Airports Council International defines air passenger traffic as the total number of passengers carried by departing and arriving aircraft when counting transit passengers only once. In this study, monthly passenger traffic data were collected for the aforementioned airports for the period between August 2014 and December 2019. These data were obtained from Airports Council International’s statistical report or from the official websites of the relevant airports. The time series interval was 1 month, and 1950 data records were collected for air passenger traffic at each airport. Among these records, 1590 data records from August 2014 to December 2018 were used as the training set data; the remaining 360 records from January to December 2019 were used as the testing set data. The training set was used to train various prediction models (i.e., the Holt–Winters, ETS, ARIMA, SARIMA, SVR, and FSVR models), which were then used to make predictions for the data from January to December 2019. The predicted values were compared with the test set to determine the models’ accuracy.

Table 1. Statistics on passenger traffic data of top ten airports.

Airport	Min.	Max.	Mean	Med.	Q1	Q3	IQR	SD	CV
Atlanta	683.399	1021.628	873.448	873.326	832.123	930.807	98.684	76.045	8.706
Beijing	697.669	904.566	796.969	809.755	761.501	825.617	64.116	51.011	6.401
Dubai	519.871	837.648	701.710	697.906	658.181	761.679	103.499	71.989	10.259
Los Angeles	495.060	846.982	684.953	686.525	635.694	727.552	91.858	80.092	11.693
Haneda, Tokyo	549.112	864.140	682.344	675.672	647.462	720.944	73.482	60.881	8.922
O’Hare	477.124	815.502	665.597	674.528	624.477	724.487	100.010	82.183	12.347
Heathrow, London	495.388	781.485	647.829	652.789	595.435	693.046	97.612	68.516	10.576
Hong Kong	484.500	682.600	591.153	590.200	563.019	622.100	59.081	43.636	7.382
Pudong, Shanghai	427.736	682.594	567.193	578.441	521.474	621.585	100.111	64.557	11.382
Charles de Gaulle, Paris	434.976	747.421	578.939	575.432	515.323	649.627	134.305	78.270	13.520
Total	5264.834	8184.566	6790.132	6814.575	6354.687	7277.444	922.757	677.180	101.188

Unit: 10,000 tons; Min.: minimum value; Max.: maximum value; Mean: average value; Med.: median; Q1: first quartile; Q3: third quartile; IQR: interquartile range; SD: standard deviation; CV: coefficient of variation.

indicates the number of passengers handled at each of the airports considered.

In the collected time series data, T_t is the trend term, S_t is the seasonal term, and R_t is the residual term. The formula for additive decomposition used to decompose the trend and seasonality of the air traffic volume is as follows:

$$y_t=T_t+S_t+R_t$$

(26)

The trend strength is defined by Equation (27) and is between 0 and 1. Moreover, Equation (28) defines the seasonality strength. A time series has no seasonality if the seasonality strength is close to 0 [11].

$$F_T=\underset{}{max}\left(0, 1-\frac{Var(R_t)}{Var(T_t+R_t)}\right)$$

(27)

$$F_s=\underset{}{max}\left(0, 1-\frac{Var(R_t)}{Var(S_t+R_t)}\right)$$

(28)

Table 2. Seasonality and trend strength of the major air traffic volume at top ten airports.

Airport	Freight Volume
	Seasonal	Trend
Atlanta (ATL)	0.95	0.83
Beijing (PEK)	0.74	0.84
Dubai (DXB)	0.82	0.74
Los Angeles LAX	0.99	0.98
Haneda (HND)	0.93	0.91
O’Hare (ORD)	0.98	0.90
Heathrow, London (LHR)	0.98	0.87
Hong Kong (HKG)	0.82	0.79
Pudong (PVG)	0.86	0.97
Charles de Gaulle (CDG)	0.97	0.90

shows the strength of the seasonal and trend components of the air traffic volume. For passenger traffic, PEK had the lowest seasonal strength, at 0.74, whereas DXB, HKG, and PVG had seasonal strengths higher than 0.8. The remaining six airports had seasonal strengths of above 0.9 (0.94–0.97). Thus, the results indicated that the 10 airports considered exhibited seasonal traffic patterns and that most of them exhibited strong seasonal patterns. Regarding flight operations, PEK and DXB had low seasonal strengths of 0.69 and 0.53, respectively; HKG and PVG exhibited moderate seasonal strengths of 0.88 and 0.81, respectively; and the other six airports exhibited moderate to high seasonal strengths.

Regarding passenger volume, LAX, HND, ORD, PVG, and CDG exhibited high trend strengths of between 0.90 and 0.98; ATL, PEK, and LHR exhibited moderate trend strengths of 0.83–0.87; and DXB and HKG exhibited relatively low trend strengths of 0.74 and 0.79, respectively. The passenger volume trends were moderately to highly strong at all airports.

In the FSVR model developed here, historical air traffic data were used as the input, and the functional correlation between the dependent and independent variables was used to obtain predictions. Airlines estimate their passenger traffic demand for each quarter and apply for a fixed schedule, which is allocated by the international conference each year. The annual flight schedule is divided into winter and summer seasons, and each airport exhibits strong seasonal trends in its passenger traffic (Table 2).

Therefore, the changes in the current air traffic were hypothesized to exhibit 1- or 12-period lags with respect to the changes in the historical air traffic data. The functional relationship of the data was calculated through SVR to fit the data that lag by 1 period or 12 periods. The optimal number of lags for the dependent variable y in the self-regression was determined by calculating the RMSE and MAPE values. The calculation of the traffic volume for ATL using the SVM function in R software is described as an example. In this example, the three most important SVM parameters were set to default values as follows: the penalty coefficient C was set as 1, the kernel parameter of the Gaussian kernel function (RBF) σ was set as 1, and the width of the insensitive loss function ε was set as 0.1. The results of the SVR self-regression lag analysis for the air traffic of ATL are presented in

Table 3. Analysis table of the number of post-regression periods of SVR auto-regression for air traffic volume at Atlanta International Airport.

	Category	Passenger Traffic Volume
Data		RMSE	MAPE	No. of Support Vectors
lagged 12-period traffic data		40.133	3.127	41
lagged one period of traffic data		78.358	7.165	46

. Regarding passenger traffic volume and aircraft take-off and landing frequency, the 12-period-lagged data were better than the 1-period-lagged data for use as independent-variable data in the SVR model. In contrast, for freight volume, the 1-period-lagged data were better than the 12-period-lagged data for use as independent-variable data in the SVR model. Therefore, in the SVR model in this study, 12-period-lagged data were used as the independent-variable data for the passenger traffic volume and aircraft take-off and landing frequency, while 1-period-lagged data were used as the independent-variable data for the freight volume.

The grid search method in R can be used to select C, σ, and ε. This method trains the model for each set of parameter combinations, checks its performance, and selects the best performing model. To ensure the reliability of the model and the adaptability of the above parameters during the training process, the optimization function built into the e1071 application package in R is used to adjust the parameters and perform cross-validation automatically. Therefore, the parameters are set as C = [2⁰, 2^0.1, 2^0.1, …, 2¹⁴], σ = [2⁻¹⁰, 2^−9.9, 2^−9.8, …, 2⁰], and ε = [2⁻¹⁰, 2^−9.9, 2^−9.8, …, 2⁰].

Peaks and seasonal patterns are characteristics of air passenger and flight traffic. In addition, other parameters can affect traffic volume time series, such as the aviation policy of the relevant government and the airport’s geography. Therefore, the data for different airports are divided into different fuzzy sets for the calculation of the membership function through fuzzy theory. Tai’s IFT model and SVR model were used to fuzzify the air traffic volume data in the development of the FSVR model. The fuzzified traffic volume was then used as the independent variable for the SVR self-regression model. During the fuzzification process, the domain of the traffic volume time series data was defined by partitioning it into fuzzy sets with different increments, resulting in low root mean square error fuzzy data. The factors affecting air traffic—such as national and regional holidays, travel seasons, winter and summer flight schedules, and passenger demand—were considered when defining the fuzzy sets for air traffic volume. The number of fuzzy sets (m) was set between 5 and 10. In addition, the cardinality w for the previous time interval was set to 12 in accordance with the characteristics of the 12-month flight cycle; thus, 7 fuzzy data sets were obtained for 12 periods. From these data sets, the fuzzy data with the minimum RMSE were selected as the optimal input for FSVR self-regression.

The 10 airports considered in this study were divided into 3 regions: North America, Middle East and Europe, and Asia. The experimental results indicated that the best number of fuzzy sets for each airport’s fuzzy air traffic time series could be obtained from the minimum RMSE of the fuzzy data by using the IFTS model. The best number of fuzzy sets of passenger traffic for each North American airport, each Middle Eastern and European airport, PVG, and HKG was between five and seven. The best number of fuzzy sets of passenger traffic for PEK was 9 or 10, and the corresponding number for HND was 8 or 9.

The IFTS model uses historical changes in data to establish the domains and the fuzzy relationship. Similar elements in a time series are grouped into appropriate fuzzy sets by using fuzzy classification algorithms, which help produce fuzzy interpolated time series with low error. In this study, the fuzzy relationship matrix was calculated using the data for the previous 12 periods. As presented in

Table 4. The RMSE of fuzzy time series.

Passenger Traffic Volume	lag12-RMSE	Fuzzy-RMSE
Atlanta	35.716	22.249
Los Angeles	37.987	3.395
O’Hare	35.375	20.546
Heathrow, London	20.545	6.294
Charles de Gaulle, Paris	29.313	21.063
Dubai	42.874	19.204
Beijing	44.234	6.520
Pudong, Shanghai	46.301	6.448
Hong Kong	28.882	16.088
Haneda, Tokyo	35.335	1.268

, lower RMSE values were obtained with the fuzzy time series produced by the IFTS model than with the 12-period-lagged data.

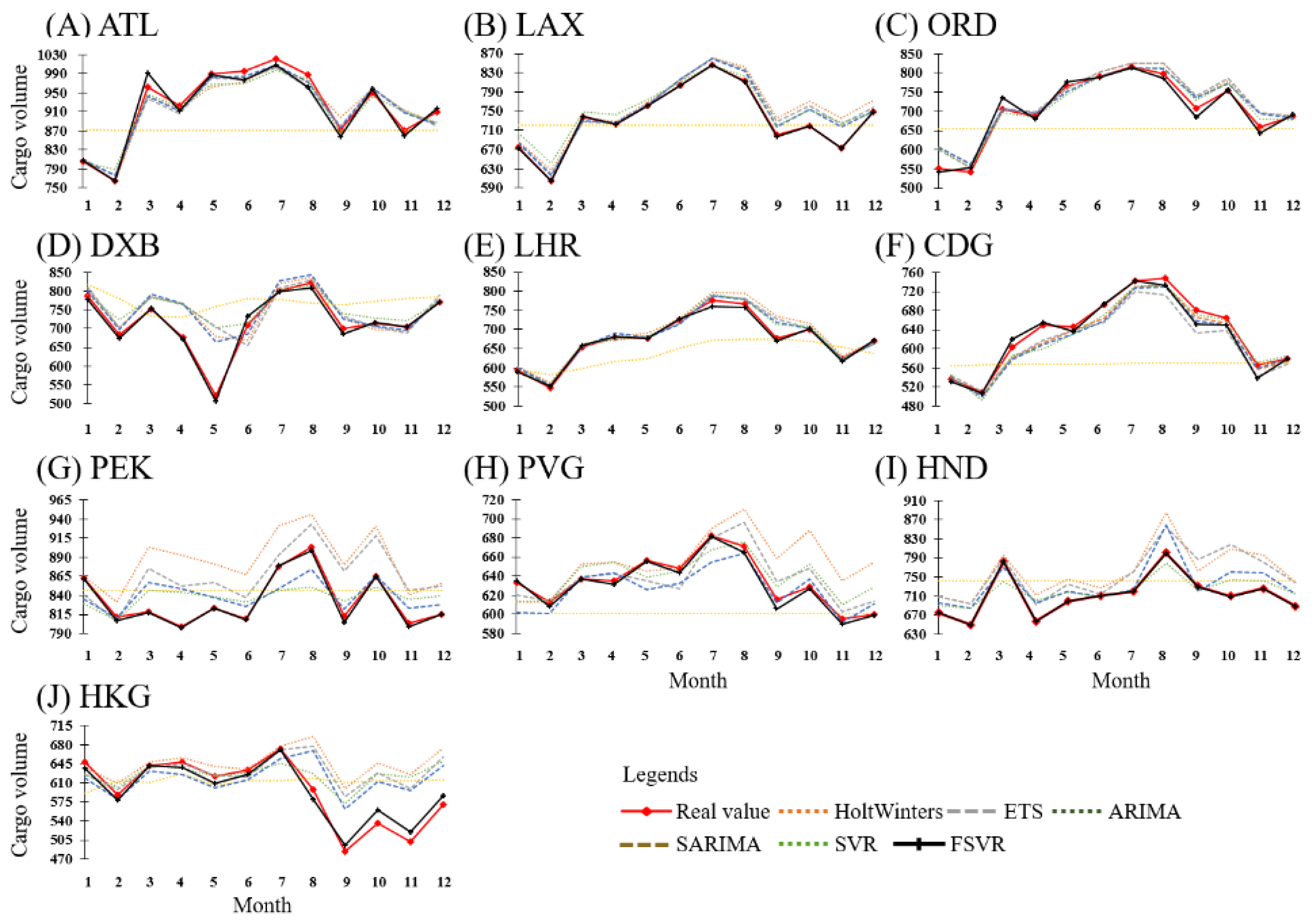
As shown in

Table 5. The experimental results of the traffic volume forecast model MAPE, MAE, and MAPE values.

Airport	Criteria	Holt–Winters’(ADD)	ETS	ARIMA	SARIMA	SVR	FSVR
ATL	MAPE(%)	1.909	1.937	8.453	1.535	1.884	1.253
	MAE	17.735	17.881	79.074	14.076	17.258	11.883
	RMSE	21.142	20.724	91.516	17.022	20.289	14.902
LAX	MAPE(%)	3.215	2.525	7.018	2.005	2.803	0.159
	MAE	22.910	18.110	51.619	14.404	19.347	1.141
	RMSE	29.386	23.160	66.035	19.008	24.440	1.536
ORD	MAPE(%)	2.797	2.800	12.196	2.552	2.361	1.633
	MAE	18.425	18.798	86.249	16.341	15.445	11.132
	RMSE	23.847	24.055	98.817	22.518	20.433	14.195
DXB	MAPE(%)	5.977	6.583	10.346	5.533	5.875	1.462
	MAE	37.844	41.236	66.789	35.242	35.922	9.399
	RMSE	56.545	63.778	88.062	52.941	61.619	14.215
LHR	MAPE(%)	2.209	1.579	6.842	1.371	1.297	0.742
	MAE	15.034	10.712	47.682	9.363	8.954	5.146
	RMSE	21.129	16.437	56.534	14.031	12.541	6.464
CDG	MAPE(%)	2.197	3.480	12.079	2.597	2.306	1.710
	MAE	14.284	22.949	81.276	16.947	14.674	10.824
	RMSE	17.266	26.569	98.765	20.448	18.977	14.642
PEK	MAPE(%)	6.282	4.387	3.980	2.454	3.149	0.320
	MAE	52.029	36.329	33.107	20.441	26.378	2.643
	RMSE	57.558	39.975	34.907	24.637	29.246	3.655
PVG	MAPE(%)	4.149	2.022	5.331	2.111	2.316	0.542
	MAE	25.945	12.894	34.741	13.573	14.591	3.401
	RMSE	32.565	15.317	42.404	17.056	16.664	4.408
HND	MAPE(%)	6.875	6.112	6.573	3.658	3.112	0.048
	MAE	48.921	43.354	45.884	26.005	21.975	0.343
	RMSE	54.773	50.451	52.102	30.997	25.721	0.447
HKG	MAPE(%)	9.508	7.868	9.124	7.746	7.500	2.021
	MAE	51.452	42.581	50.676	43.002	40.529	11.512
	RMSE	71.429	59.519	62.067	52.722	56.814	13.262
Ave. of MAPE(%)		4.512	3.929	8.194	3.156	3.260	0.989
Ave. of MAE		30.458	26.484	57.710	20.939	21.507	6.742
Ave. of RMSE		38.564	33.999	69.121	27.138	28.674	8.773

Bold means the lowest value. Underline means the value > 10.

, the SARIMA model exhibited lower MAEs than did the Holt–Winters, ETS, ARIMA, and SVR models in forecasting the passenger traffic for ATL, LAX, DXB, and PEK. The SVR model exhibited lower MAEs than did the other aforementioned models in forecasting the passenger traffic for ORD, LHR, HND, and HKG. Among the aforementioned five models, the Holt–Winters additive model and ETS model exhibited the lowest MAEs in forecasting the passenger traffic for CDG and PVG, respectively. The proposed FSVR model exhibited lower MAEs than did the aforementioned five models in forecasting passenger traffic for all of the considered airports. The lowest average MAE among those of the six models was exhibited by the FSVR model (6.742), followed by the SARIMA and SVR models (20.939 and 21.507, respectively). The average MAE of the FSVR model was 67%–68% lower than those of the SARIMA and SVR models.

The MAPE values for the predicted passenger traffic were below 10% for all airports except ORD, DXB, and CDG. Thus, the models achieved high prediction accuracy. The FSVR model had lower MAPE values than those of the other five models. The average MAPE of the FSVR model was 0.989, which was approximately 68% lower than that of the SARIMA model (3.156), which had the second-lowest average MAPE. According to the RMSE values presented in Table 5, the ARIMA model was the least accurate in predicting the passenger traffic at all airports. The Holt–Winters model performed well for CDG, and the ETS model performed well for PVG. The SARIMA model exhibited the second-lowest RMSE values in its predictions for ATL, LAX, DXB, PEK, and HKG. The SVR model exhibited the second-lowest RMSE values for ORD, LHR, and HND. Among the six models, the FSVR model exhibited the lowest RMSE values in predicting the passenger traffic for all airports. The average RMSE value of the FSVR model was 8.773, which was 67% lower than that of the SARIMA model (27.138), which had the second-lowest average RMSE. Among the compared models, the FSVR model provided the best results in terms of MAE, MAPE, and RMSE for forecasting international airport passenger traffic. The relevant parameters of each forecasting model are listed in

Table 6. Parameters related to each forecasting model of traffic volume.

Airport	Holt–Winters’ (ADD)(α, β, γ)	ETS (α, β, γ)	ARIMA (p, d, q)	SARIMA (p, d, q)(P, D, Q)S	SVR (ε, C, σ)	FSVR (ε, C, σ)
ATL	(0.3242271, 0.03419252, 0)	(0.2486, 0.0001, 0.0009)	(1,1,0)	(0,1,1)(0,1,1)	(0.07943282, 1448.155, 0.0002511886)	(0.0001, 8192, 0.026125)
LAX	(0.9180541, 0, 0.2935654)	(0.6199, 0.0001, 0.0001)	(0,1,0)	(0,1,1)(0,1,1)	(0.225, 1024, 0.05)	(0.0001, 1024, 0.0002)
ORD	(0.3964889, 0, 0.8077017)	(0.6426, 0.0001, 0.0001)	(0,1,0)	(1,0,0)(0,1,1) with drift	(0.1584893, 4, 0.1995262)	(0.02209709, 22.62742, 0.125)
DXB	(0.01336716, 1, 0.2483901)	(0.0491, 0.0491, 0.0001)	(5,0,0) with non-zero mean	(0,0,0)(1,1,0) with drift	(0.2, 32, 0.0006)	(0.16, 1024, 0.04)
LHR	(0.4530443, 0.009712022, 0.6942027)	(0.1388, 0.0001, 0.0001)	(1,0,0) with non-zero mean	(1,0,0)(0,1,1) with drift	(0.1, 128, 0.009)	(0.0125, 1.24, 0.3125)
CDG	(0.06164469, 0.6310111, 0.6988015)	(0.3959, N, 0.0001)	(2,1,2) with drift	(0,1,1)(0,1,0)	(0.153, 1024, 1.022)	(0.151, 30, 0.01)
PEK	(0.07326602, 0.0240825, 0.7191751)	(0.0083, 0.0001, 0.0209)	(0,1,1)	(0,0,3)(1,0,1) with non-zero mean	(0.001, 0.757, 0.51)	(0.015625, 64, 0.00390625)
PVG	(0.5797924, 0, 0)	(0.0363, 0.0001, 0.0009)	(0,1,1)	(1,0,1)(1,0,0) with non-zero mean	(0.329877, 63.09573, 0.00390625)	(0.03125, 90.50967, 0.001953125)
HND	(0.4796565, 0, 0.9722993)	(0.0898, 0.0001, 0.0001)	(0,1,1)	(1,0,1)(1,0,0) with non-zero mean	(0.0001, 0.630957, 0.01625)	(0.001953125, 14.92853, 0.001953125)
HKG	(0.2538931, 0.02770604, 0.2855045)	(0.0001, 0.0001, 0.0001)	(3,1,0)	(1,0,3)(1,0,0) with non-zero mean	(0.556, 2.098, 0.971)	(0.01, 512, 0.0315)

, and the comparison of the actual and forecasted values for 2019 is displayed in Figure 1.

The passenger traffic at DXB decreased by 3.2 million people in 2019 because of temporary runway closures, the bankruptcy of Jet Airways, which is a popular airline flying to and from DXB, and the disruptions caused by the inability of Flydubai, which is Dubai’s second-largest airline carrier after Emirates, to acquire Boeing 737 MAX aircraft. In 2019, PEK faced several challenges, such as the escalation of trade tensions between the US and China, geopolitical conflicts, and financial market volatility. In addition, the opening of Daxing Airport in September 2019 resulted in the relocation of some flights from PEK, further reducing its transportation capacity. PEK recorded 594,329 take-offs and landings in 2019, and this number represented a decrease of 3.2% compared with the numbers for 2018. Moreover, the passenger throughput at PEK in 2019 was 100,011,438, which was 1% lower than that in 2018. Airline operations at HKG were considerably affected by the prolonged political turmoil and complex geopolitical environment in Hong Kong from the second half of 2019, which resulted in the passenger traffic in 2019 (71.5 million passengers) being 4.2% lower than that in 2018. HKG was closed several times because of protests and violence, which resulted in travel warnings from approximately 40 countries and led to a decline in the overall business volume, with flight movements 1.9% lower and a total cargo volume 6.1% lower (at 4.8 million tons) in 2019 compared with the corresponding values in 2018. The decline in passenger traffic was particularly pronounced on routes to and from mainland China and Southeast Asia.

The FSVR model produces accurate fuzzy historical interpolations because it uses Tai’s IFTS model, which is suitable for nonseasonal time series, and because it considers historical changes in traffic volume. The combination of an SVR model, which maps data to high-dimensional feature spaces, with fuzzy theory, which is used to transform nonlinear problems into linear or nearly linear problems, enables the accurate prediction of an airport’s air traffic volume. The predictions obtained using the proposed FSVR model for the air traffic volumes at DXB, PEK, and HKG in 2019 and the corresponding actual air traffic volumes are displayed in Figure 2.

Accurate forecasting of the air traffic demand is of paramount importance not only to private airports, airlines, and related industries, but also to governments and international aviation organizations [41]. In this study, we have tested the performance of the proposed model using data from the national level, which can be applied at the corporate level. The results demonstrate FSVR’s high accuracy and show that it outperforms SVR and performs well across all airport types. Forecasting the air traffic demand can help private airports plan staffing, queuing, and equipment to reduce wait times and improve service levels [42]. For airlines, accurate forecasts can be instrumental in the determination of route availability, frequency, and capacity. In addition, the results of the forecasting can assist policy makers and organizations in determining the capacity and scope of the aviation industry, allowing them to reach appropriate agreements with other countries and companies to achieve maximum efficiency and profit. Notably, air demand forecasting can also help the aviation industry anticipate market demands, adapt to market changes, and manage resources and finances more effectively [43].

4. Conclusions

In this study, the proposed FSVR model uses the IFTS model proposed by Tai to fuzzify time series data on air traffic volume. Because the IFTS model can be applied to nonseasonal time series, the FSVR model can consider historical changes in a fuzzy time series. Fuzzy classification algorithms appropriately divide similar elements in a time series into appropriate fuzzy sets, generate membership functions, and establish fuzzy relationships. The fuzzy data with the smallest error are then subjected to SVR to predicting continuous data and find the best hyperplane model with the minimum distance to the appropriate support vector sample points. The passenger volumes of the world’s 10 busiest international airports in terms of passenger traffic in 2018 (ATL, PEK, DXB, LAX, HND, ORD, LHR, HKG, PVG, and CDG) were predicted using the proposed FSVR model and five other models. The predictions were made based on data from August 2014 to December 2019. The developed FSVR model provided accurate prediction results for the air passenger volume at each of the airports considered. Of the compared models, the proposed FSVR model exhibited the lowest MAPE, MAE, and RMSE values for its air traffic predictions for all of the airports considered. The average MAPE, MAE, and RMSE values obtained with the proposed model were 0.989, 6.742, and 8.773, respectively, and all of the MAPE values were below 2.5. This study represents the first application of FSVR to the prediction of airport traffic. The results demonstrate the high accuracy of FSVR, which outperforms the SVR model and performs well across different airport types. In future airport traffic forecasting research, multivariate techniques can be used to account for the interdependence of variables.