A Novel Adaptive Finite-Time Position Tracking Control Strategy for Teleoperation System with Varying Communication Delays

Abstract

Based on the traditional control approach, the position-tracking performance of the teleoperation system with communication delay is generally asymptotically stable. In practical applications, the closed-loop system is expected to achieve stable and finite-time convergence performance. A novel finite-time bilateral control scheme for a telerobotics system with communication delay is presented in this paper. On the basis of the traditional proportional damping injection control, this paper proposes and designs a new finite-time control method by introducing the non-integer power to the position error, velocity, and the combined error with position error and velocity. In comparison to existing proportional damping injection and finite-time control structures, the proposed method not only achieves the finite-time convergence performance of position tracking, but it also has the advantages of a simple structure and fewer gain coefficients. The controller also incorporates the radial basis function (RBF) neural network and adaptive approach to compensate unknown dynamics and external forces, thus also avoiding the measurement of force signals. The Lyapunov–Krasovskii function is then defined, and it is demonstrated that the position tracking of closed-loop teleoperation system has bounded stability and finite-time control performance. The simulation experiment is also performed, and the results further illustrated the bounded stability of the system. Moreover, compared to the position tracking errors of other non-finite-time control methods, it is demonstrated that the proposed finite-time control scheme has a faster convergence rate and higher convergence precision.

1. Introduction

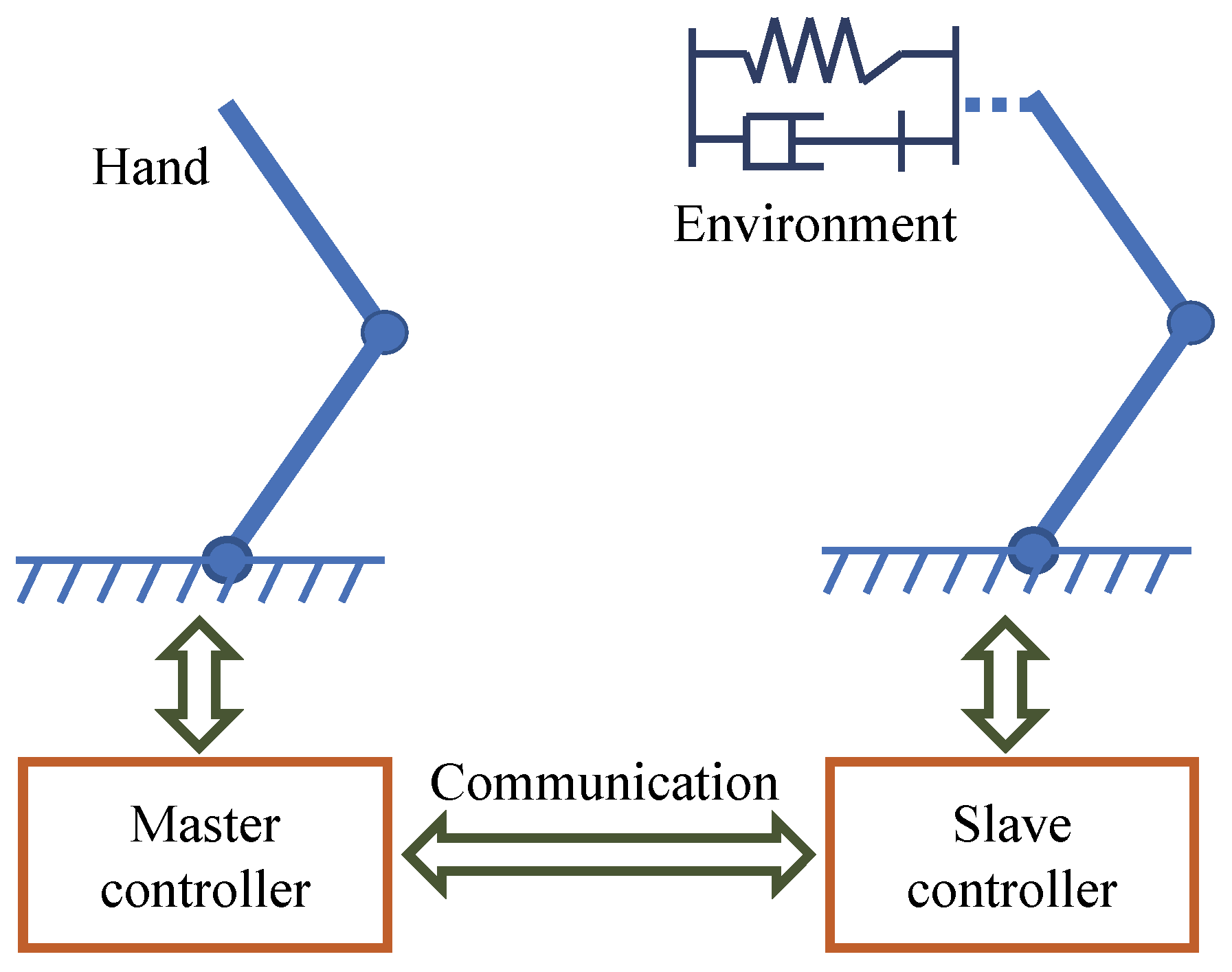
The telerobotics system combines the intelligence of the operator and the operation ability of the robot, it can achieve a variety of operational tasks in a hazardous and dangerous environment. Based on these excellent characteristics, teleoperation systems have been widely used in nuclear radiation, space, deep sea, and complex industrial environments, and play an important role in these engineering applications [1,2]. In a typical teleoperation system, the operator controls the movement of the master robot, while the slave robot is regulated to achieve the position-tracking movement of the master robot [3]. Generally, two controllers are introduced at the master end and the slave end, respectively, to realize position-tracking control. This control structure is also defined as the bilateral control. The operator can sense the interaction condition between the robot and task environment based on bilateral control. The position/force signals of the master robot and the slave robot need to be transmitted to each other’s controller through the communication channel to achieve position tracking and force feedback. Compared with the unilateral control mode, the bilateral control mode provides the operator with better telepresence feedback of the operation force, which improves the operation’s precision and efficiency.

In bilateral control of teleoperation systems, the position/force signals of the master robot and the slave robot are always transmitted through the communication channel to each other’s controller to achieve position tracking and force feedback. Nevertheless, the communication delay cannot be inevitable. This fact creates an inconsistent factor, i.e., the position signals with time delay will reduce the tracking performance and stability of the teleoperation system, and may even cause system instability [3]. In general, stability is regarded as the most fundamental performance for the communication delay teleoperation system [4]. Currently, passive theory and the Lyapunov method are commonly used to analyze the stability of a teleoperation system and design an appropriate structure for position control. For a teleoperation system, communication delay factor can be equivalent to injecting additional energy. Therefore, the passivity theory is to reduce the energy of the communication process by designing an effective controller, which can ensure the passivity of the closed-loop system and maintain the stability of system. The passive theory-based control methods of the telerobotics system have the scattering method [5,6], the traditional wave method, and improved wave variable method [7,8]. However, the passivity assumptions of the master and slave sides are insufficient for engineering practice conditions. Then, numerous scholars have employed the Lyapunov theory to analyze the stability of the time-delay teleoperation system and to develop the control strategy. Some typical control strategies based on the Lyapunov method include $H_{\infty }$ control [9], adaptive control [10,11,12], sliding mode control [13], output feedback control [14], feedforward-feedback position control [15], and so on. These methods have produced effective position tracking controllers for teleoperation systems with fixed or time-varying communication delays.

Comparative to other control methods, the proportional damping injection (P+d) is a control strategy for time-delayed telerobotics with a simple structure and good control performance. The main component of damping injection control is to utilize damping terms to eliminate superfluous energy and maintain the stability of the time-delay system. Proportional plus damping and proportional differential plus damping (PD+d) are often part of the damping injection controller’s fundamental construction [16]. The Lyapunov—Krasovskii method is usually employed for the design of damping injection controllers and the analysis of closed-loop system stability. Some improved damping injection controllers have been proposed and designed. In [17], a PD controller without speed measurement is proposed for the teleoperation system, and a first-order filter is designed for speed estimation. For a teleoperation system with passive and nonpassive injected force, Islam [18] developed a novel PD+d control approach, and symmetric and asymmetric communication delays were also taken into consideration. In [19,20,21], three novel P+d-like controllers are presented to guarantee the position/force-tracking performances for the network telerobitics system. In [22], the authors present three strategies that adjust the damping and stiffness of the bilateral teleoperation system to maintain the stable teleoperation. In [23], a simplified P+d control with gravity compensation is presented, and the effectiveness of the controller is also verified by experiments. The gravity torque of the robot is commonly defined as the known information to construct the controller in the above damping injection control approach. For practical systems, gravity torque may be difficult to obtain accurately, and the effect of friction torque and other additional injection forces could weaken the control performance of the teleoperation system. Adaptive control is a very effective way to solve the problem of model uncertainty and has been successfully applied in teleoperation systems. In addition, adaptive control can contribute to ensure the passivity and stability of the delay teleoperation system. Scholars have proposed some new damping injection control methods combining adaptive strategy. In [24], a nonlinear proportional plus nonlinear damping (nP+nD) controller based on adaptive environmental force term is presented. In [25], an adaptive fuzzy logic system is utilized to estimate uncertain torques, and an improved PD+d controller is proposed. In our previous work [26], the adaptive method combined with RBF neural network was used to build an improved damping injection controller. However, the control scheme designed based on the above work only achieves asymptotic stability of the closed-loop system. It implies that the synchronization error between the master and slave robots can converge to zero when the time becomes infinite. The stability performance of finite time can ensure the system converges to a small neighborhood in a finite time, which has faster convergence speed, higher convergence accuracy, and better anti-interference ability. It can be seen that finite-time stability has more engineering application value than asymptotic stability.

The finite-time control method has also been researched and developed by some scholars for the time-delay teleoperation system. Yang [27] presented an adaptive fuzzy finite-time control strategy to address the control issue of a teleoperation system with uncertain dynamics. In [28], an adaptive finite-time control method is proposed to address the actuator saturation problem. In some work [29,30,31,32,33], several finite-time control structures are proposed to realize the position tracking control of telerobotics system with the factors of model parameter uncertainty, varying communication delay, actuator saturation, output constraints, etc. These finite-time controllers are basically based on the nonsingular terminal sliding mode (NTSM) and auxiliary variables combined with speed and position errors. The research work is still relatively insufficient in spite of the development of finite-time control methods for teleoperation systems. There are still some challenges and problems that need to be solved.

The first issue is how to simplify the finite-time control scheme to reduce the complexity of controller design. The existing finite-time controller has some disadvantages, such as the complex design process and many controller gain parameters. What is far more important is that the impact of communication delay on stability cannot be obtained in the above finite time approaches. Yang [34] proposed a new continuous nonsmooth proportional damping injection finite-time control method, which successfully simplified the finite-time controller for the teleoperation system. However, the author did not consider the unknown gravity torque, friction torque, and non-zero external force. In our paper, we expect to reduce the amount of fractional power to simplify the selection constraints of controller parameters. The second one is how to establish the relationship between communication delay, controller gain, and fractional power parameters. In this paper, we expect to use Lyapunov–Krasovskii functional for stability analysis and further establish this relationship. The last problem is how to deal with the unknown gravity, friction, and external torques, and the radial basis function (RBF) neural network and adaptive method are utilized to implement the compensation of unknown dynamics and external forces.

Based on the line of analyzing the existing work and comparing it with our previous work, the fundamental contributions of this paper are summarized as follows:

• In this paper, a novel simplified finite-time adaptive proportional damping injection control strategy is proposed for the teleoperation system with asymmetric varying communication delay. Compared with most of the existing proportional damping injection control methods (such as [19,20,21,22,23,24,25,35] and our previous work in [26]), the proposed control structure achieves the finite-time tracking performance of the master–slave robot position, and the method presented above only achieves the asymptotically stability performance. Compared with the only existing finite-time proportional damping injection control strategy in [34], the proposed controller is more concise and has fewer controller gain parameters, which is more convenient to use in the actual teleoperation system.
• The RBF neural network and the adaptive control method are presented to realize the estimation and compensation of external forces. Compared with some existing control methods, such as [18,19,20,21,24,25,26], the proposed method does not require us to measure and estimate the external forces. In addition, the unknown dynamics can also be compensated.

The remainder of this paper is organized as follows. In Section 2, we describe the dynamic models and properties of the teleoperation system, the definition of the RBF neural network, and some related mathematical definitions and lemmas. In Section 3, the proposed adaptive finite-time control method based on the P+d control scheme is proposed and the stability of the closed-loop system is also discussed. In Section 4, simulation experiments are implemented to verify the stability and good position-tracking performance of the system. Finally, this work is concluded in Section 5.

2. Problem Statement

In this section, the dynamic model and some important properties of the teleoperation system are described first, and then the objectives of the system control, the concepts and properties of the RBF neural network, and some concepts and lemmas of mathematics and control theory are also stated later.

2.1. Teleoperation System Dynamics

A typical dynamic model of the telerobotics system is composed of the master robot dynamic, slave robot dynamic, and a communication model. For the master and slave robots, if they are assumed to be the manipulators with n rotational degree of freedom (dof), the dynamic models in joint space can be defined as

$$\begin{array}{cc}\hfill & {\mathit{M}}_m\left({\mathit{q}}_m\right){\ddot{\mathit{q}}}_m+{\mathit{C}}_m\left({\dot{\mathit{q}}}_m,{\mathit{q}}_m\right){\dot{\mathit{q}}}_m+{\mathit{G}}_m\left({\mathit{q}}_m\right)+{\mathit{F}}_m={\mathit{\tau }}_m-{\mathit{\tau }}_h,\hfill \\ \hfill & {\mathit{M}}_s\left({\mathit{q}}_s\right){\ddot{\mathit{q}}}_s+{\mathit{C}}_s\left({\dot{\mathit{q}}}_s,{\mathit{q}}_s\right){\dot{\mathit{q}}}_s+{\mathit{G}}_s\left({\mathit{q}}_s\right)+{\mathit{F}}_s={\mathit{\tau }}_s-{\mathit{\tau }}_e,\hfill \end{array}$$

(1)

where for $j=m,s$, ${\mathit{q}}_j\in {\mathcal{R}}^n$, ${\dot{\mathit{q}}}_j\in {\mathcal{R}}^n$, and ${\ddot{\mathit{q}}}_j\in {\mathcal{R}}^n$ are, respectively, defined as the position, velocity and acceleration vectors of the master/slave robot at time $t\in {\mathcal{R}}^{+}$. ${\mathit{M}}_j\left({\mathit{q}}_j\right)\in {\mathcal{R}}^{n\times n}$ is the inertia matrix of the robot, ${\mathit{C}}_j\left({\dot{\mathit{q}}}_j,{\mathit{q}}_j\right)\in {\mathcal{R}}^{n\times n}$ is the coriolis and centrifugal matrix, ${\mathit{G}}_j\left({\mathit{q}}_j\right)\in {\mathcal{R}}^n$ is the gravitational torque. ${\mathit{F}}_j\in {\mathcal{R}}^n$ is friction and external interference torques. The torques exerted by the operator and the environmental is ${\mathit{\tau }}_h,{\mathit{\tau }}_e\in {\mathcal{R}}^n$. The values of ${\mathit{\tau }}_h$ and ${\mathit{\tau }}_e$ are related to the force ${\mathit{F}}_h$ applied by the operator to the master robot, and the force ${\mathit{F}}_e$ applied by the environment to the slave robot, which can be further described as ${\mathit{\tau }}_h={\mathit{J}}_m^T{\mathit{F}}_h$ and ${\mathit{\tau }}_e={\mathit{J}}_s^T{\mathit{F}}_e$. The Jacobian matrices of the master and slave robots are defined as ${\mathit{J}}_m$ and ${\mathit{J}}_s$, respectively. The control torques of the master and slave robots are defined as ${\mathit{\tau }}_m$ and ${\mathit{\tau }}_s$.

The robot dynamics in Equation (1) are nonlinear and have time-varying parameters. For $j=m,s$ are defined as the master and slave robots, respectively, and there are some important properties as follows [36,37]

Property 1.

The inertia matrix ${\mathit{M}}_j\left({\mathit{q}}_j\right)$ is positively symmetrical. Moreover, the following inequalities are held if the maximum eigenvalue $M_{j,max}$ and minimum eigenvalue $M_{j,min}$ are satisfied with

$$\begin{array}{c}\hfill 0<M_{j,min}\mathit{I}\le {\mathit{M}}_j\left({\mathit{q}}_j\right)\le M_{j,max}\mathit{I}<\infty \end{array}$$

Property 2.

For any nonzero vector $\mathit{x}\in {\mathcal{R}}^n$, the following equation always holds

$$\begin{array}{c}\hfill {\mathit{x}}^T({\dot{\mathit{M}}}_j-2{\mathit{C}}_j)\mathit{x}=0.\end{array}$$

Property 3.

For all position and velocity vectors ${\mathit{q}}_j,{\dot{\mathit{q}}}_j\in {\mathcal{R}}^n$, there exists a positive positive scalar $c_j$ and the following inequality is always satisfied

$$\begin{array}{c}\hfill \parallel {\mathit{C}}_j({\mathit{q}}_j,{\dot{\mathit{q}}}_j){\dot{\mathit{q}}}_j\parallel \le c_j\parallel {\mathit{q}}_j\parallel \parallel {\dot{\mathit{q}}}_j\parallel .\end{array}$$

Property 4.

The time derivative of ${\mathit{C}}_j({\mathit{q}}_j,{\dot{\mathit{q}}}_j)$ is bounded if the velocity and acceleration ${\dot{\mathit{q}}}_j,{\ddot{\mathit{q}}}_j$ are all bounded.

Property 5.

The gravitational torque ${\mathit{G}}_j$ and friction torque ${\mathit{F}}_j$ are all bounded.

The variable delay signals of the forward and backward communication channels are defined as $d_m\left(t\right)$ and $d_s\left(t\right)$. In the control structure of the bilateral teleoperation system, the position information of the master and the slave side ${\mathit{q}}_m$ and ${\mathit{q}}_s$ are transmitted to the other side through the communication channel, which will cause the transmission delay and can be described as ${\mathit{q}}_m(t-d_m\left(t\right))$ and ${\mathit{q}}_s(t-d_s\left(t\right))$. In order to simplify the expression in the controller and stability derivation process, ${\mathit{q}}_{md}$ and ${\mathit{q}}_{sd}$ are introduced here to replace the expression ${\mathit{q}}_m(t-d_m\left(t\right))$ and ${\mathit{q}}_s(t-d_s\left(t\right))$, respectively.

In the design of a bilateral control scheme, it is necessary to make some assumptions about communication delay, operator force, and external force signals:

Assumption 1.

The asymmetric time-varying communication delays $d_m\left(t\right)$ and $d_s\left(t\right)$ are bounded. There are two positive constants ${\overline{d}}_m,{\overline{d}}_s\in {\mathcal{R}}^{+}$ to satisfy the boundedness of communication delays as

$$\begin{array}{cc}\hfill & 0\le d_m\left(t\right)\le {\overline{d}}_m,\hfill \\ \hfill & 0\le d_s\left(t\right)\le {\overline{d}}_s.\hfill \end{array}$$

Assumption 2.

The operator force ${\mathit{F}}_h$ and environment force ${\mathit{F}}_e$ are also bounded, and they have $\parallel {\mathit{F}}_h\parallel \le {\overline{F}}_h,{\overline{F}}_h\ge 0$ and $\parallel {\mathit{F}}_e\parallel \le {\overline{F}}_e,{\overline{F}}_e\ge 0$.

Control Objectives The control objective of this study is to develop a finite-time controller to guarantee the finite-time position-tracking control performance of the time-delay teleoperation system. This means the tracking errors $\parallel \mathit{q}\left(t\right)-{\mathit{q}}_s\left(t\right)\parallel$ should converge to a very small domain of 0 within the fixed time.

2.2. RBF Neural Network

The radial basis function (RBF) neural network is a commonly used three-layer feedforward neural network. One of its most important properties is that it can approximate any nonlinear function [38]. Therefore, it is used to deal with laws that are difficult to analyze in the system. In addition, it also has a good generalization ability and fast learning speed. In nonlinear function approximation, data classification, system modeling, and control system design, RBF neural networks are frequently utilized because of the aforementioned characteristics. In the adaptive control method, RBF neural network is employed to estimate the unknown dynamics of the system. The radial basis function is the key part of the RBF neural network, and the Gaussian function is usually selected as the radial basis kernel function. The concept of RBF neural network can be stated as follows [39].

For a continuous function $G\left(x\right):{\mathcal{R}}^l\to {\mathcal{R}}^b$, $\mathit{x}\in {\mathcal{R}}^a$ is the input vector, then the function $F\left(x\right)$ can be redefined by RBF neural network as

$$\begin{array}{c}\hfill G\left(x\right)={\mathit{W}}^T\mathit{\phi }\left(\mathit{x}\right)+w.\end{array}$$

(2)

where $\mathit{W}\in {\mathcal{R}}^{k\times l}$ is the weight matrix, k is the number of network nodes. $\mathit{\phi }={\left[{\phi }_1,{\phi }_2,\dots ,{\phi }_k\right]}^T$ can also be calculated based on the Gaussian basis function as

$$\begin{array}{c}\hfill {\phi }_i=e^{-\frac{{\left(\mathit{x}-{\mathit{b}}_i\right)}^T\left(\mathit{x}-{\mathit{b}}_i\right)}{2c^2}},i=1,2,\dots ,d.\end{array}$$

${\mathit{b}}_i\in {\mathcal{R}}^a$ is the the Gaussian center vector of the i-th node. c is the width of Gaussian function. w is the bounded approximate error.

Remark 1.

It should be mentioned that the weight matrix of the network is formed and obtained by the Lyapunov stability criterion in the adaptive control approach with RBF neural network. The developed adaptive learning laws can guarantee the convergence and stability of the closed-loop system. A variety of neural network input values should be considered in determining the Gauss-centered vector of i-the node ${\mathit{b}}_i$. With specifying an appropriate width of c, the input data values of the neural network should fall inside the domain of Gaussian functions.

Remark 2.

With the definition of the Gaussian basis function, it can be seen that for all input vectors $\mathit{x}$, the Gauss function ${\phi }_i$ is always bounded. This property will be used in the system stability analysis.

It is a different procedure for the RBF neural network to build the adaptive control structure and directly estimate the unknown function. In general, the RBF neural network is employed in adaptive control design to replace the uncertain element of the model and normalize the input data using the radial basis function. Based on the defined weight error vector, a Lyapunov function can be developed, and the learning rate of the neural network’s weight coefficient can also be solved while guaranteeing the closed-loop system’s stability. Therefore, the learning rate (also defined as the adaptive law) should be calculated during the stability analysis of the closed-loop system. From a certain point of view, the Lyapunov function constructed by a weight error can be regarded as its cost function.

2.3. Fundamentals of Mathematics and Lemma

The $L_2$ norm of a time function $f:\mathcal{R}\to {\mathcal{R}}^n$ is shown as ${\parallel f\parallel }_{L_2}=({\int }_0^{\infty }{\parallel f\left(t\right)\parallel }^{2}dt{)}^{1/2}$. The $L_{\infty }$ norm of a time function $f:\mathcal{R}\to {\mathcal{R}}^n$ is defined as ${\parallel f\parallel }_{L_{\infty }}={sup}_{t\in [0,\infty )}{\parallel f\left(t\right)\parallel }_{\infty }$. The definition of $L_2$ and $L_{\infty }$ spaces can be given based on the definition of $L_2$ and $L_{\infty }$ norms. The $L_2$ and $L_{\infty }$ spaces are defined as the sets $f:\mathcal{R}\to {\mathcal{R}}^n,{\parallel f\left(t\right)\parallel }_{L_2}<+\infty$ and $f:\mathcal{R}\to {\mathcal{R}}^n,{\parallel f\left(t\right)\parallel }_{L_{\infty }}<+\infty$. For any time vector $\mathit{x}={[x_1,x_2,\dots ,x_n]}^T\in {\mathcal{R}}^n$, the function $\mathrm{sig}{\left(\mathit{x}\right)}^p$ is defined as $\mathrm{sig}\left(\mathit{x}\right)=\left[\right|x_1{|}^p\mathrm{sign}\left(x_1\right),|x_2{|}^p\mathrm{sign}\left(x_2\right),\dots ,|x_n{|}^p\mathrm{sign}\left(x_n\right)]$, where p is a positive constant. The derivative of $\mathrm{sig}{\left(\mathit{x}\right)}^p$ can be calculated as $d\mathrm{sig}{\left(\mathit{x}\right)}^p/dt=p\dot{\mathit{x}}\mathrm{diag}{(x_1,x_2,\dots ,x_n)}^{p-1}$.

Before designing the finite-time control structure, the definition of finite-time control for nonlinear systems is given here [40]. Consider the nonlinear system $\dot{\mathit{x}}=f(\mathit{x},t),$$\mathit{x}\left(0\right)={\mathit{x}}_0,\mathit{x}\in {\mathcal{R}}^n$, f characterizes a continuous mapping $f:U_0\to {\mathcal{R}}^n$ on an open neighborhood $U_0$ of the origin. The zero solution ${\mathit{x}}_t(0,{\mathit{x}}_0)$ of the system is finite-time stable if it is Lyapunov stable and finite-time convergent in a neighborhood $U\subset U_0$. The finite time convergence means that there exists a function $T_x:U\backslash 0\to (0,\infty )$, $U\subseteq W$ is an open neighborhood of the origin, such that $\forall {\mathit{x}}_0\in W$ and for $t\in [0,T_x\left({\mathit{x}}_0\right)]$, ${lim}_{t\to T_x\left({\mathit{x}}_0\right)}{\mathit{x}}_t(0,{\mathit{x}}_0)=0$. The zero solution is globally finite-time stable when $W=\mathcal{R}$.

Lemma 1

([41]). Considering a system as $\dot{\mathit{x}}$, $\mathit{x}\left(0\right)={\mathit{x}}_0$, the system is finite-time stable if there exists a continuous positive differentiable function $V:U\backslash 0\to {\mathcal{R}}^{+}$ and the following inequality can be always established

$$\begin{array}{c}\hfill \dot{V}\left(\mathit{x}\right)\le -{\rm Y}{V}^{\sigma }\left(\mathit{x}\right)+\Psi ,\mathit{x}\in U_0\backslash 0\end{array}$$

where $0<\sigma <1$, ${\rm Y}>0$ and $\Psi >0$, $U_0\subset U\backslash 0$ is an open neighborhood of origin. If $U_0=U$ the system is globally finite-time stable, and there exists a positive scalar v satisfying $0<v<1$, which can make the system converge to a neighborhood $\Pi$ in finite-time T as

$$\begin{array}{cc}\hfill T\le & \frac{V^{1-\sigma }\left(0\right)}{{\rm Y}v(1-\sigma )}\hfill \\ \hfill \Pi =& max\left\{\mathit{x}\left|V\le {\left[\frac{\Psi }{{\rm Y}(1-v)}\right]}^{1/\Psi }\right.\right\}\hfill \end{array}$$

Several mathematical lemmas are also given below for the analysis of system stability.

Lemma 2

([34]). For any real numbers A, B, and $0<b\le 1$, the following two inequalities hold

$$\begin{array}{cc}\hfill & {|\mathrm{sig}\left(A\right)}^b-\mathrm{sig}{\left(B\right)}^b|\le 2^{1-b}{|A-B|}^{\sigma }\hfill \\ \hfill & {\left(\left|A\right|+\left|B\right|\right)}^b\le {\left|A\right|}^b+{\left|B\right|}^b\hfill \end{array}$$

Lemma 3

([34]). For any time vectors $\mathit{A}\left(t\right),\mathit{B}\left(t\right)\in {\mathcal{R}}^n$, $p>0$, and a real value function $r\left(\mathit{A}\right(t),\mathit{B}(t\left)\right)>0$, the following inequality holds

$$\begin{array}{cc}\hfill & {\mathit{A}}^T\left(t\right){\int }_{t-T\left(t\right)}^t\mathrm{sig}{\left(\mathit{B}\left(\xi \right)\right)}^{p}d\xi -{\int }_{t-T\left(t\right)}^t\frac{pr{(\mathit{A}\left(t\right),\mathit{B}\left(t\right))}^{-\frac{1}{p}}}{1+p}{\mathit{B}}^T\left(\xi \right)\mathrm{sig}{\left(\mathit{B}\left(\xi \right)\right)}^{p}d\xi \hfill \\ \hfill \le & \overline{T}\frac{r\left(\mathit{A}\right(t),\mathit{B}(t\left)\right)}{1+p}{\mathit{A}}^T\left(t\right)\mathrm{sig}{\left(\mathit{A}\left(\xi \right)\right)}^p\hfill \end{array}$$

where $0<T\left(t\right)\le \overline{T}$.

3. Adaptive Finite Time Proportional Plus Damping Control Design

3.1. Controller Design

In this subsection, a novel finite-time adaptive position tracking control method is proposed. As stated in the introduction chapter, on the one hand, the gravitational torque and friction torque are difficult to obtain accurately in the actual robot system. On the other hand, the operator’s torque and the environmental torque need to be measured by the multi-dimensional force sensors. According to the relevant properties of the system dynamic models, the gravity, friction, operator, and environment torques are all bounded. Therefore, the RBF neural network is employed to estimate the gravity, friction, and operator/environment torques in the finite time control scheme design in our work.

Firstly, the unknown dynamics of the gravitational torques ${\mathit{G}}_m,{\mathit{G}}_s$, friction torques ${\mathit{F}}_m,{\mathit{F}}_s$, and and operator and environment torques ${\mathit{\tau }}_h$ and ${\mathit{\tau }}_e$ are approximated and compensated using the RBF neural network. These unknown dynamics can be defined by neural networks as follows

$$\begin{array}{cc}\hfill & {\mathit{G}}_m\left({\mathit{q}}_m\right)+{\mathit{F}}_m+{\mathit{\tau }}_h={\mathit{W}}_m^T{\mathit{\phi }}_m\left({\mathit{x}}_m\right)+{\mathit{w}}_m,\hfill \\ \hfill & {\mathit{G}}_s\left({\mathit{q}}_s\right)+{\mathit{F}}_s+{\mathit{\tau }}_e={\mathit{W}}_s^T{\mathit{\phi }}_s\left({\mathit{x}}_s\right)+{\mathit{w}}_s.\hfill \end{array}$$

(3)

where for $j=m,s$, ${\mathit{W}}_j\in {\mathcal{R}}^{l\times n}$ is the ideal RBF neural network weight matrix with l nodes, ${\mathit{\omega }}_j$ is the bounded estimation error, ${\mathit{x}}_j={\left[{\mathit{q}}_j^T,{\dot{\mathit{q}}}_j^T\right]}^T$ is the input vector. ${\mathit{\phi }}_j\left({\mathit{x}}_j\right)\in {\mathcal{R}}^{l\times 1}$ is the Gaussian basis function vector which can be calculated by

$$\begin{array}{c}\hfill {\phi }_{j,i}=e^{-\frac{{\left({\mathit{x}}_j-{\mathit{b}}_{j,i}\right)}^T\left({\mathit{x}}_j-{\mathit{b}}_{j,i}\right)}{2c_j^2}},i=1,2,\dots ,l.\end{array}$$

(4)

${\mathit{b}}_{j,i}\in {\mathcal{R}}^{1\times ln}$ is the Gaussian center function vector of i-th hidden layer node. $c_j$ is the width of Gaussian function.

The telerobotics system description can then be represented as

$$\begin{array}{cc}\hfill & {\mathit{M}}_m\left({\mathit{q}}_m\right){\ddot{\mathit{q}}}_m+{\mathit{C}}_m\left({\dot{\mathit{q}}}_m,{\mathit{q}}_m\right){\dot{\mathit{q}}}_m+{\mathit{W}}_m^T{\mathit{\phi }}_m\left({\mathit{x}}_m\right)+{\mathit{w}}_m={\mathit{\tau }}_m,\hfill \\ \hfill & {\mathit{M}}_s\left({\mathit{q}}_s\right){\ddot{\mathit{q}}}_s+{\mathit{C}}_s\left({\dot{\mathit{q}}}_s,{\mathit{q}}_s\right){\dot{\mathit{q}}}_s+{\mathit{W}}_s^T{\mathit{\phi }}_s\left({\mathit{x}}_s\right)+{\mathit{w}}_s={\mathit{\tau }}_s.\hfill \end{array}$$

(5)

In order to better design and construct the finite-time control structure, the following auxiliary variables ${\mathit{s}}_m$ and ${\mathit{s}}_s$ are introduced in the master–slave robot side.

$$\begin{array}{c}\hfill {\mathit{s}}_m={\mathit{q}}_m\left(t\right)-{\mathit{q}}_{sd}+{\dot{\mathit{q}}}_m\left(t\right),\\ \hfill {\mathit{s}}_s={\mathit{q}}_s\left(t\right)-{\mathit{q}}_{md}+{\dot{\mathit{q}}}_s\left(t\right).\end{array}$$

(6)

The following control laws of master and slave robots are designed as

$$\begin{array}{cc}\hfill {\mathit{\tau }}_m=& K_m\mathrm{sig}{\left({\mathit{s}}_m\right)}^{\sigma }-2K_m\mathrm{sig}{\left({\mathit{q}}_m-{\mathit{q}}_{sd}\right)}^{\sigma }-{\mathit{\alpha }}_m\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }+{\widehat{\mathit{W}}}_m{\mathit{\phi }}_m\left({\mathit{x}}_m\right)+{\widehat{\mathit{w}}}_m,\hfill \\ \hfill {\mathit{\tau }}_s=& K_s\mathrm{sig}{\left({\mathit{s}}_s\right)}^{\sigma }-2K_s\mathrm{sig}{\left({\mathit{q}}_s-{\mathit{q}}_{md}\right)}^{\sigma }-{\mathit{\alpha }}_s\mathrm{sig}{\left({\dot{\mathit{q}}}_s\right)}^{\sigma }+{\widehat{\mathit{W}}}_s{\mathit{\phi }}_s\left({\mathit{x}}_s\right)+{\widehat{\mathit{w}}}_s.\hfill \end{array}$$

(7)

where for $j=m,s$, $K_j$ and ${\alpha }_j$ are the gain coefficients of controllers, $o<\sigma <1$ presents the power coefficient, ${\widehat{\mathit{W}}}_j$ and ${\widehat{\mathit{\omega }}}_j$ are defined as the adaptive estimate terms of the ideal approximate weight matrix ${\mathit{W}}_j$ and estimation error ${\mathit{\omega }}_j$.

Remark 3.

The finite-time control laws designed in this paper are based on the traditional proportional-damping injection control and are improved by combining it with the finite-time control method. In the teleoperation system, the time-varying communication delays will disturb the position error of the master and the slave side, which will further cause oscillation and even instability of the system. To maintain the stability of the closed-loop system, the damping term is used to weaken and disperse the detrimental energy of the system. The finite-time control structure is constructed by introducing power $0<\sigma <1$ on the proportional error term and damping term as $sig{\left({\mathit{q}}_j-{\mathit{q}}_{j^{\prime }d}\right)}^{\sigma }$ and $sig{\left({\dot{\mathit{q}}}_j\right)}^{\sigma }$, when $j=m,s$, there has $j^{\prime }=s,m$. If the power is small, the tracking error can have a fast convergence speed, but the control values would have oscillations. When the power is closer to 1, the control performance is more similar to the traditional proportional damping injection control method. The specific analysis will be described in the simulation part later.

Remark 4.

For one thing, the crucial improvements of this paper over our previous work in [26] are to realize the finite-time control efficiency of the closed-loop system and develop a simpler finite-time controller. In [26] only the asymptotically stability of the position tracking control is achieved. The non-singular terminal sliding mode or auxiliary variable must be developed first for the typical finite-time controller of the teleoperation system, and finite-time control laws can be designed based on their non-integer power terms. The calculation of the control law will be accompanied by a large number of mathematical operations, which is inconvenient for engineering implementation and application. For another, compared with the work in [34], the proposed finite-time controller has few weight coefficients which can avoid the constraints on the controller implementation caused by more controller gain selections. This study also presents a novel finite-time stability analysis approach, which differs from [34].

Remark 5.

In the proposed control scheme, the adaptive method is not only utilized to compensate the uncertain dynamics, but also used to estimate the external torques of the operator and the environment. In [26], the operator and environmental force information need to be measured and transmitted back to the controller for compensation to achieve better position-tracking control performance. In [34], the gravity torque in the controller is believed to be accurate, and the influences of friction moment, operator, and environment are ignored. The control approach stated in this paper addresses the major challenges well. The adaptive rates can be developed based on Lyapunov theory and assure the passivity of the parameter estimation. For a teleoperation system, the introduction of an adaptive method can further improve the passivity and stability of a closed-loop system. In our work, the forms of adaptive learning rates are designed as

$$\begin{array}{cc}\hfill & {\dot{\widehat{\mathit{W}}}}_m=-{\Lambda }_{m1}{\mathit{\phi }}_m\left({\mathit{x}}_m\right){\dot{\mathit{q}}}_m,\hfill \\ \hfill & {\dot{\widehat{\mathit{w}}}}_m=-{\Lambda }_{m2}{\dot{\mathit{q}}}_m,\hfill \\ \hfill & {\dot{\widehat{\mathit{W}}}}_s=-{\Lambda }_{s1}{\mathit{\phi }}_s\left({\mathit{x}}_s\right){\dot{\mathit{q}}}_s,\hfill \\ \hfill & {\dot{\widehat{\mathit{w}}}}_s=-{\Lambda }_{s2}{\dot{\mathit{q}}}_s.\hfill \end{array}$$

(8)

3.2. System Stability Analysis

To ensure the finite-time control performance of the closed-loop teleoperation system, the following two theorems are proposed to show the main results of this paper. Firstly, global asymptotic stability and the boundedness of state signals will be proved based on the Lyapunov method in Theorem 1. Secondly, the finite time control of closed-loop teleoperation will be proved based on Lemma 1 in Theorem 2.

Theorem 1.

In the network telerobotics system in (1), with the presented control laws in (7), adaptive laws in (8), the bounded asymmetric time-varying communication delays, bounded human and environmental forces, and unknown gravity and friction torques, the closed-loop system is stable, and the signals of the system ${\dot{\mathit{q}}}_m$, ${\dot{\mathit{q}}}_s$, ${\mathit{q}}_m-{\mathit{q}}_s$, ${\tilde{\mathit{W}}}_m$, ${\tilde{\mathit{W}}}_s$, ${\tilde{\mathit{\omega }}}_m$, ${\tilde{\mathit{\omega }}}_s$ are all bounded if there exist appropriate positive controller gain coefficients ${\alpha }_m,{\alpha }_s,K_m,K_s$ and a positive real constant K which can meet the following relationships with the upper bound ${\overline{d}}_m$ and ${\overline{d}}_s$ of master–slave communication delays as

$$\begin{array}{cc}\hfill & {\alpha }_m\ge 2^{1-\sigma }{K}_m+{\overline{d}}_{m}K+2{\overline{d}}_s{\left(\frac{K_m}{1+\sigma }\right)}^{1+\sigma }\left(\frac{\sigma }{K}\right)\hfill \\ \hfill & {\alpha }_s\ge 2^{1-\sigma }{K}_m+{\overline{d}}_{s}K+2{\overline{d}}_m{\left(\frac{K_m}{1+\sigma }\right)}^{1+\sigma }\left(\frac{\sigma }{K}\right)\hfill \end{array}$$

(9)

Theorem 2.

For the bilateral teleoperation system in (1), if Theorem 1 is established and the positive controller gain coefficients satisfy ${\alpha }_m\ge 2K_m$ and $\frac{{\alpha }_s{K}_m}{K_s}\ge 2K_m$, then the finite time control performance of closed-loop teleoperation system can be guaranteed.

First, the proof of Theorem 1 is given as follows

Proof. 

Consider the teleoperation system (1), define the state of the system where ${\mathit{x}}_t={[{\mathit{q}}_m,{\mathit{q}}_s,{\dot{\mathit{q}}}_m,{\dot{\mathit{q}}}_s,{\tilde{\mathit{W}}}_m,{\tilde{\mathit{\omega }}}_m,{\tilde{\mathit{W}}}_s,{\tilde{\mathit{\omega }}}_s]}^T$, choose the following Lyapunov–Krasovskii function $V\left({\mathit{x}}_t\right)=V_1\left({\mathit{x}}_t\right)+V_2\left({\mathit{x}}_t\right)+V_3\left({\mathit{x}}_t\right)+V_4\left({\mathit{x}}_t\right)$, where

$$\begin{array}{cc}\hfill V_1& =\frac{1}{2}{\dot{\mathit{q}}}_m^T{\mathit{M}}_m{\dot{\mathit{q}}}_m+\frac{K_m}{2K_s}{\dot{\mathit{q}}}_s^T{\mathit{M}}_s{\dot{\mathit{q}}}_s,\hfill \\ \hfill V_2& =\frac{K_m}{\sigma +1}\sum _{i=1}^n{\left|q_{mi}-q_{si}\right|}^{\sigma +1},\hfill \\ \hfill V_3& ={\int }_{-{\overline{d}}_m}^0{\int }_{t+\delta }^{t}K{\dot{\mathit{q}}}_m^T\left(\xi \right){\dot{\mathit{q}}}_m\left(\xi \right)d\xi d\delta +{\int }_{-{\overline{d}}_s}^0{\int }_{t+\delta }^{t}K{\dot{\mathit{q}}}_s^T\left(\xi \right){\dot{\mathit{q}}}_s\left(\xi \right)d\xi d\delta ,\hfill \\ \hfill V_4& =\frac{{\Lambda }_{m1}^{-1}}{2}\mathrm{tr}\left({\tilde{\mathit{W}}}_m^T{\tilde{\mathit{W}}}_m\right)+\frac{{\Lambda }_{m2}^{-1}}{2}{\tilde{\mathit{w}}}_m^T{\tilde{\mathit{w}}}_m+\frac{{\Lambda }_{s1}^{-1}{K}_m}{2K_s}\mathrm{tr}\left({\tilde{\mathit{W}}}_s^T{\tilde{\mathit{W}}}_s\right)+\frac{{\Lambda }_{s2}^{-1}{K}_m}{2K_s}{\tilde{\mathit{w}}}_s^T{\tilde{\mathit{w}}}_s.\hfill \end{array}$$

(10)

It is obvious that $V_1$, $V_2$, $V_3$, and $V_4$ are all positive.

With the property of the robotic system, control laws in (7), the time derivative of $V_1$ can be computed as

$$\begin{array}{cc}\hfill {\dot{V}}_1=& {\dot{\mathit{q}}}_m^T\left[K_m\mathrm{sig}{\left({\mathit{s}}_m\right)}^{\sigma }-K_m\mathrm{sig}{\left({\mathit{q}}_m-{\mathit{q}}_{sd}\right)}^{\sigma }-K_m\mathrm{sig}{\left({\mathit{q}}_m-{\mathit{q}}_{sd}\right)}^{\sigma }-{\alpha }_m\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }\right.\hfill \\ \hfill & +{\widehat{\mathit{W}}}_m{\mathit{\phi }}_m\left({\mathit{x}}_m\right)+{\widehat{\mathit{w}}}_m-{\mathit{W}}_m{\mathit{\phi }}_m\left({\mathit{x}}_m\right)-{\mathit{w}}_m]\hfill \\ \hfill & +\frac{K_m}{K_s}{\dot{\mathit{q}}}_s^T\left[K_s\mathrm{sig}{\left({\mathit{s}}_s\right)}^{\sigma }-K_s\mathrm{sig}{\left({\mathit{q}}_s-{\mathit{q}}_{md}\right)}^{\sigma }-K_s\mathrm{sig}{\left({\mathit{q}}_s-{\mathit{q}}_{md}\right)}^{\sigma }-{\alpha }_s\mathrm{sig}{\left({\dot{\mathit{q}}}_s\right)}^{\sigma }\right.\hfill \\ \hfill & +{\widehat{\mathit{W}}}_s{\mathit{\phi }}_s\left({\mathit{x}}_s\right)+{\widehat{\mathit{w}}}_s-{\mathit{W}}_s{\mathit{\phi }}_s\left({\mathit{x}}_s\right)-{\mathit{w}}_s]\hfill \end{array}$$

(11)

Considering Lemma 2, we can obtain the following formula

$$\begin{array}{cc}\hfill {\dot{V}}_1\le & K_m\left|{\dot{\mathit{q}}}_m^T\right|\left|\mathrm{sig}{\left({\mathit{s}}_m\right)}^{\sigma }-\mathrm{sig}{\left({\mathit{q}}_m-{\mathit{q}}_{sd}\right)}^{\sigma }\right|\hfill \\ \hfill & +{\dot{\mathit{q}}}_m^T\left[-K_m\mathrm{sig}{\left({\mathit{q}}_m-{\mathit{q}}_{sd}\right)}^{\sigma }-{\alpha }_m\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }+{\tilde{\mathit{W}}}_m{\mathit{\phi }}_m\left({\mathit{x}}_m\right)+{\tilde{\mathit{w}}}_m\right]\hfill \\ \hfill & +K_m\left|{\dot{\mathit{q}}}_s^T\right|\left|\mathrm{sig}{\left({\mathit{s}}_s\right)}^{\sigma }-\mathrm{sig}{\left({\mathit{q}}_s-{\mathit{q}}_{md}\right)}^{\sigma }\right|\hfill \\ \hfill & +\frac{K_m}{K_s}{\dot{\mathit{q}}}_s^T\left[-K_s\mathrm{sig}{\left({\mathit{q}}_s-{\mathit{q}}_{md}\right)}^{\sigma }-{\alpha }_s\mathrm{sig}{\left({\dot{\mathit{q}}}_s\right)}^{\sigma }+{\tilde{\mathit{W}}}_s{\mathit{\phi }}_s\left({\mathit{x}}_s\right)+{\tilde{\mathit{w}}}_s\right]\hfill \\ \hfill \le & 2^{1-\sigma }{K}_m\left|{\dot{\mathit{q}}}_m^T\right|{\left|{\mathit{s}}_m-{\mathit{q}}_m+{\mathit{q}}_{sd}\right|}^{\sigma }+2^{1-\sigma }{K}_m\left|{\dot{\mathit{q}}}_s^T\right|{\left|{\mathit{s}}_s-{\mathit{q}}_s+{\mathit{q}}_{md}\right|}^{\sigma }\hfill \\ \hfill & +{\dot{\mathit{q}}}_m^T\left[-K_m\mathrm{sig}{\left({\mathit{q}}_m-{\mathit{q}}_{sd}\right)}^{\sigma }-{\alpha }_m\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }+{\tilde{\mathit{W}}}_m{\mathit{\phi }}_m\left({\mathit{x}}_m\right)+{\tilde{\mathit{w}}}_m\right]\hfill \\ \hfill & +\frac{K_m}{K_s}{\dot{\mathit{q}}}_s^T\left[-K_s\mathrm{sig}{\left({\mathit{q}}_s-{\mathit{q}}_{md}\right)}^{\sigma }-{\alpha }_s\mathrm{sig}{\left({\dot{\mathit{q}}}_s\right)}^{\sigma }+{\tilde{\mathit{W}}}_s{\mathit{\phi }}_s\left({\mathit{x}}_s\right)+{\tilde{\mathit{w}}}_s\right]\hfill \\ \hfill =& 2^{1-\sigma }{K}_m{\dot{\mathit{q}}}_m^T\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }+2^{1-\sigma }{K}_m{\dot{\mathit{q}}}_s^T\mathrm{sig}{\left({\dot{\mathit{q}}}_s\right)}^{\sigma }\hfill \\ \hfill & +{\dot{\mathit{q}}}_m^T\left[-K_m\mathrm{sig}{\left({\mathit{q}}_m-{\mathit{q}}_{sd}\right)}^{\sigma }-{\alpha }_m\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }+{\tilde{\mathit{W}}}_m{\mathit{\phi }}_m\left({\mathit{x}}_m\right)+{\tilde{\mathit{w}}}_m\right]\hfill \\ \hfill & +\frac{K_m}{K_s}{\dot{\mathit{q}}}_s^T\left[-K_s\mathrm{sig}{\left({\mathit{q}}_s-{\mathit{q}}_{md}\right)}^{\sigma }-{\alpha }_s\mathrm{sig}{\left({\dot{\mathit{q}}}_s\right)}^{\sigma }+{\tilde{\mathit{W}}}_s{\mathit{\phi }}_s\left({\mathit{x}}_s\right)+{\tilde{\mathit{w}}}_s\right].\hfill \end{array}$$

(12)

The derivative of $V_2$ is

$$\begin{array}{c}\hfill {\dot{V}}_2=K_m{\left({\dot{\mathit{q}}}_m-{\dot{\mathit{q}}}_s\right)}^T\mathrm{sig}\left({\mathit{q}}_m-{\mathit{q}}_s\right).\end{array}$$

(13)

Combining Equations (12) and (13), it can be obtained as

$$\begin{array}{cc}\hfill {\dot{V}}_1+{\dot{V}}_2\le & 2^{1-\sigma }{K}_m{\dot{\mathit{q}}}_m^T\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }+2^{1-\sigma }{K}_m{\dot{\mathit{q}}}_s^T\mathrm{sig}{\left({\dot{\mathit{q}}}_s\right)}^{\sigma }\hfill \\ \hfill & +K_m{\dot{\mathit{q}}}_m\mathrm{sig}{\left({\mathit{q}}_m-{\mathit{q}}_s\right)}^{\sigma }-K_m{\dot{\mathit{q}}}_m\mathrm{sig}{\left({\mathit{q}}_m-{\mathit{q}}_{sd}\right)}^{\sigma }\hfill \\ \hfill & +K_m{\dot{\mathit{q}}}_s\mathrm{sig}{\left({\mathit{q}}_m-{\mathit{q}}_s\right)}^{\sigma }-K_m{\dot{\mathit{q}}}_s\mathrm{sig}{\left({\mathit{q}}_s-{\mathit{q}}_{md}\right)}^{\sigma }\hfill \\ \hfill & -{\alpha }_m{\dot{\mathit{q}}}_m^T\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }+{\dot{\mathit{q}}}_m^T\left[{\tilde{\mathit{W}}}_m{\mathit{\phi }}_m\left({\mathit{x}}_m\right)+{\tilde{\mathit{w}}}_m\right]\hfill \\ \hfill & -\frac{{\alpha }_s{K}_m}{K_s}{\dot{\mathit{q}}}_s^T\mathrm{sig}{\left({\dot{\mathit{q}}}_s\right)}^{\sigma }+\frac{K_m}{K_s}{\dot{\mathit{q}}}_s^T\left[{\tilde{\mathit{W}}}_s{\mathit{\phi }}_s\left({\mathit{x}}_s\right)+{\tilde{\mathit{w}}}_s\right]\hfill \end{array}$$

(14)

For $K_m{\dot{\mathit{q}}}_m^T\mathrm{sig}{\left({\mathit{q}}_m-{\mathit{q}}_s\right)}^{\sigma }-K_m{\dot{\mathit{q}}}_m^T\mathrm{sig}{\left({\mathit{q}}_m-{\mathit{q}}_{sd}\right)}^{\sigma }$, the following inequality can be obtained

$$\begin{array}{cc}\hfill & K_m{\dot{\mathit{q}}}_m^T\mathrm{sig}{\left({\mathit{q}}_m-{\mathit{q}}_s\right)}^{\sigma }-K_m{\dot{\mathit{q}}}_m^T\mathrm{sig}{\left({\mathit{q}}_m-{\mathit{q}}_{sd}\right)}^{\sigma }\hfill \\ \hfill \le & K_m\left|{\dot{\mathit{q}}}_m^T\right|\left|\mathrm{sig}{\left({\mathit{q}}_m-{\mathit{q}}_s\right)}^{\sigma }-\mathrm{sig}{\left({\mathit{q}}_m-{\mathit{q}}_{sd}\right)}^{\sigma }\right|\hfill \\ \hfill \le & 2^{1-\sigma }{K}_m\left|{\dot{\mathit{q}}}_m^T\right|\left|{\mathit{q}}_s-{\mathit{q}}_{sd}\right|\hfill \\ \hfill =& 2^{1-\sigma }{K}_m\left|{\dot{\mathit{q}}}_m^T\right|{\left|{\int }_{t-d_s}^t{\dot{\mathit{q}}}_s\left(\xi \right)d\xi \right|}^{\sigma }\hfill \end{array}$$

(15)

Then, based on ${\dot{V}}_1$ and ${\dot{V}}_2$, we have

$$\begin{array}{cc}\hfill {\dot{V}}_1+{\dot{V}}_2\le & -\left({\alpha }_m-2^{1-\sigma }{K}_m\right){\dot{\mathit{q}}}_m^T\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }+2^{1-\sigma }{K}_m\left|{\dot{\mathit{q}}}_m^T\right|{\left|{\int }_{t-d_s}^t{\dot{\mathit{q}}}_s\left(\xi \right)d\xi \right|}^{\sigma }\hfill \\ \hfill & +{\dot{\mathit{q}}}_m^T\left[{\tilde{\mathit{W}}}_m{\mathit{\phi }}_m\left({\mathit{x}}_m\right)+{\tilde{\mathit{w}}}_m\right]\hfill \\ \hfill & -\left(\frac{{\alpha }_s{K}_m}{K_s}-2^{1-\sigma }{K}_m\right){\dot{\mathit{q}}}_s^T\mathrm{sig}{\left({\dot{\mathit{q}}}_s\right)}^{\sigma }+2^{1-\sigma }{K}_m\left|{\dot{\mathit{q}}}_m^T\right|{\left|{\int }_{t-d_s}^t{\dot{\mathit{q}}}_s\left(\xi \right)d\xi \right|}^{\sigma }\hfill \\ \hfill & +\frac{K_m}{K_s}{\dot{\mathit{q}}}_s^T\left[{\tilde{\mathit{W}}}_s{\mathit{\phi }}_s\left({\mathit{x}}_s\right)+{\tilde{\mathit{w}}}_s\right]\hfill \end{array}$$

(16)

For each element ${\left|{\int }_{t-d_s}^t{\dot{q}}_{si}\left(\xi \right)d\xi \right|}^{\sigma },i=1,2,\dots ,n$ in the integral vector ${\left|{\int }_{t-d_s}^t{\dot{\mathit{q}}}_s\left(\xi \right)d\xi \right|}^{\sigma }$, along with the definition of integral and Lemma 2, we can further obtain

$$\begin{array}{cc}\hfill {\left|{\int }_{t-d_s}^t{\dot{q}}_{si}\left(\xi \right)d\xi \right|}^{\sigma }=& {\left|\underset{n\to \infty }{lim}\sum _{ik=0}^{n-1}\frac{d_s}{n}{\dot{q}}_{si}\left(t-d_s+\frac{k{d}_s}{n}\right)\right|}^{\sigma }\hfill \\ \hfill \le & \underset{n\to \infty }{lim}\sum _{ik=0}^{n-1}{\left|\frac{d_s}{n}{\dot{q}}_{si}\left(t-d_s+\frac{k{d}_s}{n}\right)\right|}^{\sigma }\hfill \\ \hfill =& {\int }_{t-d_s}^t{\left|{\dot{q}}_{si}\left(\xi \right)d\xi \right|}^{\sigma }d\xi \hfill \end{array}$$

(17)

Then there are the following vector inequalities

$$\begin{array}{cc}\hfill & {\left|{\int }_{t-d_s}^t{\dot{\mathit{q}}}_s\left(\xi \right)d\xi \right|}^{\sigma }\le {\int }_{t-d_s}^t{\left|{\dot{\mathit{q}}}_s\left(\xi \right)d\xi \right|}^{\sigma }d\xi \hfill \\ \hfill & {\left|{\int }_{t-d_m}^t{\dot{\mathit{q}}}_m\left(\xi \right)d\xi \right|}^{\sigma }\le {\int }_{t-d_m}^t{\left|{\dot{\mathit{q}}}_m\left(\xi \right)d\xi \right|}^{\sigma }d\xi \hfill \end{array}$$

(18)

Therefore, we can further express (16) as

$$\begin{array}{cc}\hfill {\dot{V}}_1+{\dot{V}}_2\le & -\left({\alpha }_m-2^{1-\sigma }{K}_m\right){\dot{\mathit{q}}}_m^T\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }+2^{1-\sigma }{K}_m\left|{\dot{\mathit{q}}}_m^T\right|{\int }_{t-d_s}^t{\left|{\dot{\mathit{q}}}_s\left(\xi \right)\right|}^{\sigma }d\xi \hfill \\ \hfill & +{\dot{\mathit{q}}}_m^T\left[{\tilde{\mathit{W}}}_m{\mathit{\phi }}_m\left({\mathit{x}}_m\right)+{\tilde{\mathit{w}}}_m\right]\hfill \\ \hfill & -\left(\frac{{\alpha }_s{K}_m}{K_s}-2^{1-\sigma }{K}_m\right){\dot{\mathit{q}}}_s^T\mathrm{sig}{\left({\dot{\mathit{q}}}_s\right)}^{\sigma }+2^{1-\sigma }{K}_m\left|{\dot{\mathit{q}}}_m^T\right|{\int }_{t-d_s}^t{\left|{\dot{\mathit{q}}}_s\left(\xi \right)\right|}^{\sigma }d\xi \hfill \\ \hfill & +\frac{K_m}{K_s}{\dot{\mathit{q}}}_s^T\left[{\tilde{\mathit{W}}}_s{\mathit{\phi }}_s\left({\mathit{x}}_s\right)+{\tilde{\mathit{w}}}_s\right]\hfill \end{array}$$

(19)

The derivative of $V_3$ can be expressed as

$$\begin{array}{cc}\hfill {\dot{V}}_3=& {\overline{d}}_{m}K{\dot{\mathit{q}}}_m\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }-K{\int }_{t-{\overline{d}}_m}^t{\dot{\mathit{q}}}_m\left(\xi \right)\mathrm{sig}{\left({\dot{\mathit{q}}}_m\left(\xi \right)\right)}^{\sigma }d\xi \hfill \\ \hfill & +{\overline{d}}_{s}K{\dot{\mathit{q}}}_s\mathrm{sig}{\left({\dot{\mathit{q}}}_s\right)}^{\sigma }-K{\int }_{t-{\overline{d}}_s}^t{\dot{\mathit{q}}}_s\left(\xi \right)\mathrm{sig}{\left({\dot{\mathit{q}}}_s\left(\xi \right)\right)}^{\sigma }d\xi \hfill \\ \hfill \le & {\overline{d}}_{m}K{\dot{\mathit{q}}}_m\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }-K{\int }_{t-d_m}^t{\dot{\mathit{q}}}_m\left(\xi \right)\mathrm{sig}{\left({\dot{\mathit{q}}}_m\left(\xi \right)\right)}^{\sigma }d\xi \hfill \\ \hfill & +{\overline{d}}_{s}K{\dot{\mathit{q}}}_s\mathrm{sig}{\left({\dot{\mathit{q}}}_s\right)}^{\sigma }-K{\int }_{t-d_s}^t{\dot{\mathit{q}}}_s\left(\xi \right)\mathrm{sig}{\left({\dot{\mathit{q}}}_s\left(\xi \right)\right)}^{\sigma }d\xi \hfill \end{array}$$

(20)

Combining Equations (19) and (20), we have

$$\begin{array}{cc}\hfill {\dot{V}}_1+{\dot{V}}_2+{\dot{V}}_3\le & -\left({\alpha }_m-2^{1-\sigma }{K}_m\right){\dot{\mathit{q}}}_m^T\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }+2^{1-\sigma }{K}_m\left|{\dot{\mathit{q}}}_m^T\right|{\int }_{t-d_s}^t{\left|{\dot{\mathit{q}}}_s\left(\xi \right)\right|}^{\sigma }d\xi \hfill \\ \hfill & +{\dot{\mathit{q}}}_m^T\left[{\tilde{\mathit{W}}}_m{\mathit{\phi }}_m\left({\mathit{x}}_m\right)+{\tilde{\mathit{w}}}_m\right]\hfill \\ \hfill & -\left(\frac{{\alpha }_s{K}_m}{K_s}-2^{1-\sigma }{K}_m\right){\dot{\mathit{q}}}_s^T\mathrm{sig}{\left({\dot{\mathit{q}}}_s\right)}^{\sigma }+2^{1-\sigma }{K}_m\left|{\dot{\mathit{q}}}_m^T\right|{\int }_{t-d_s}^t{\left|{\dot{\mathit{q}}}_s\left(\xi \right)\right|}^{\sigma }d\xi \hfill \\ \hfill & +\frac{K_m}{K_s}{\dot{\mathit{q}}}_s^T\left[{\tilde{\mathit{W}}}_s{\mathit{\phi }}_s\left({\mathit{x}}_s\right)+{\tilde{\mathit{w}}}_s\right]\hfill \\ \hfill & +{\overline{d}}_{m}K{\dot{\mathit{q}}}_m\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }-K{\int }_{t-d_m}^t{\dot{\mathit{q}}}_m\left(\xi \right)\mathrm{sig}{\left({\dot{\mathit{q}}}_m\left(\xi \right)\right)}^{\sigma }d\xi \hfill \\ \hfill & +{\overline{d}}_{s}K{\dot{\mathit{q}}}_s\mathrm{sig}{\left({\dot{\mathit{q}}}_s\right)}^{\sigma }-K{\int }_{t-d_s}^t{\dot{\mathit{q}}}_s\left(\xi \right)\mathrm{sig}{\left({\dot{\mathit{q}}}_s\left(\xi \right)\right)}^{\sigma }d\xi \hfill \end{array}$$

(21)

Let $\left|{\dot{\mathit{q}}}_m^T\right|={\mathit{A}}^T$, $\sigma =p$, $r\left(t\right)={\left(\frac{2^{1-\sigma }{K}_m\sigma }{K\left(1+\sigma \right)}\right)}^{\sigma }$, with Lemma 3, we can obtain

$$\begin{array}{cc}\hfill & 2^{1-\sigma }{K}_m\left|{\dot{\mathit{q}}}_m^T\right|{\int }_{t-d_s}^t{\left|{\dot{\mathit{q}}}_s\left(\xi \right)\right|}^{\sigma }d\xi -K{\int }_{t-d_s}^t{\dot{\mathit{q}}}_s\left(\xi \right)\mathrm{sig}{\left({\dot{\mathit{q}}}_s\left(\xi \right)\right)}^{\sigma }d\xi \hfill \\ \hfill \le & {\overline{d}}_s{\left(\frac{K_m{2}^{1-\sigma }}{1+\sigma }\right)}^{1+\sigma }{\left(\frac{\sigma }{K}\right)}^{\sigma }{\dot{\mathit{q}}}_m^T\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }\hfill \\ \hfill \le & 2{\overline{d}}_s{\left(\frac{K_m}{1+\sigma }\right)}^{1+\sigma }{\left(\frac{\sigma }{K}\right)}^{\sigma }{\dot{\mathit{q}}}_m^T\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }\hfill \end{array}$$

(22)

According to the same method and derivation process, the following inequality can also be further obtained

$$\begin{array}{cc}\hfill & 2^{1-\sigma }{K}_m\left|{\dot{\mathit{q}}}_s^T\right|{\int }_{t-d_m}^t{\left|{\dot{\mathit{q}}}_m\left(\xi \right)\right|}^{\sigma }d\xi -K{\int }_{t-d_m}^t{\dot{\mathit{q}}}_m\left(\xi \right)\mathrm{sig}{\left({\dot{\mathit{q}}}_m\left(\xi \right)\right)}^{\sigma }d\xi \hfill \\ \hfill \le & 2{\overline{d}}_m{\left(\frac{K_m}{1+\sigma }\right)}^{1+\sigma }{\left(\frac{\sigma }{K}\right)}^{\sigma }{\dot{\mathit{q}}}_2^T\mathrm{sig}{\left({\dot{\mathit{q}}}_2\right)}^{\sigma }\hfill \end{array}$$

(23)

Then

$$\begin{array}{cc}\hfill & {\dot{V}}_1+{\dot{V}}_2+{\dot{V}}_3\hfill \\ \hfill \le & -\left[{\alpha }_m-2^{1-\sigma }{K}_m-{\overline{d}}_{m}K-2{\overline{d}}_s{\left(\frac{K_m}{1+\sigma }\right)}^{1+\sigma }{\left(\frac{\sigma }{K}\right)}^{\sigma }\right]{\dot{\mathit{q}}}_m^T\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }\hfill \\ \hfill & -\left[\frac{{\alpha }_s{K}_m}{K_s}-2^{1-\sigma }{K}_m-{\overline{d}}_{s}K-{\overline{d}}_m{\left(\frac{K_m}{1+\sigma }\right)}^{1+\sigma }{\left(\frac{\sigma }{K}\right)}^{\sigma }\right]{\dot{\mathit{q}}}_s^T\mathrm{sig}{\left({\dot{\mathit{q}}}_s\right)}^{\sigma }\hfill \\ \hfill & +{\dot{\mathit{q}}}_m^T\left[{\tilde{\mathit{W}}}_m{\mathit{\phi }}_m\left({\mathit{x}}_m\right)+{\tilde{\mathit{w}}}_m\right]+\frac{K_m}{K_s}{\dot{\mathit{q}}}_s^T\left[{\tilde{\mathit{W}}}_s{\mathit{\phi }}_s\left({\mathit{x}}_s\right)+{\tilde{\mathit{w}}}_s\right]\hfill \end{array}$$

(24)

Finally, the derivative of $V_4$ can be computed as

$$\begin{array}{cc}\hfill & {\dot{V}}_4={\Lambda }_{m1}^{-1}\mathrm{tr}\left({\tilde{\mathit{W}}}_m^T{\dot{\tilde{\mathit{W}}}}_m\right)+{\Lambda }_{m2}^{-1}{\tilde{\mathit{\omega }}}_m^T{\dot{\tilde{\mathit{\omega }}}}_m+\frac{K_m}{K_s{\Lambda }_{s1}}\mathrm{tr}\left({\tilde{\mathit{W}}}_s^T{\dot{\tilde{\mathit{W}}}}_s\right)+\frac{K_m}{K_s{\Lambda }_{s2}}{\tilde{\mathit{\omega }}}_s^T{\dot{\tilde{\mathit{\omega }}}}_s\hfill \end{array}$$

(25)

where ${\tilde{\mathit{W}}}_m={\widehat{\mathit{W}}}_m-{\mathit{W}}_m$, ${\tilde{\mathit{\omega }}}_m={\widehat{\mathit{\omega }}}_m-{\mathit{\omega }}_m$, ${\tilde{\mathit{W}}}_s={\widehat{\mathit{W}}}_s-{\mathit{W}}_s$, ${\tilde{\mathit{\omega }}}_s={\widehat{\mathit{\omega }}}_s-{\mathit{\omega }}_s$

$$\begin{array}{cc}\hfill & {\dot{V}}_4={\Lambda }_{m1}^{-1}\mathrm{tr}\left({\tilde{\mathit{W}}}_m^T{\dot{\widehat{\mathit{W}}}}_m\right)+{\Lambda }_{m2}^{-1}{\tilde{\mathit{\omega }}}_m^T{\dot{\widehat{\mathit{\omega }}}}_m+\frac{K_m}{K_s{\Lambda }_{s1}}\mathrm{tr}\left({\tilde{\mathit{W}}}_s^T{\dot{\widehat{\mathit{W}}}}_s\right)+\frac{K_m}{K_s{\Lambda }_{s2}}{\tilde{\mathit{\omega }}}_s^T{\dot{\widehat{\mathit{\omega }}}}_s\hfill \end{array}$$

(26)

Based on the adaptive rate, we can further obtain

$$\begin{array}{cc}\hfill & {\dot{V}}_4=-{\dot{\mathit{q}}}_m\left[{\tilde{\mathit{W}}}_m^T{\mathit{\phi }}_m\left({\mathit{x}}_m\right)+{\mathit{\omega }}_m^T\right]-\frac{K_m}{K_s}{\dot{\mathit{q}}}_s\left[{\tilde{\mathit{W}}}_s^T{\mathit{\phi }}_s\left({\mathit{x}}_s\right)+{\mathit{\omega }}_s^T\right]\hfill \end{array}$$

(27)

Finally, we can obtain that

$$\begin{array}{cc}\hfill & {\dot{V}}_1+{\dot{V}}_2+{\dot{V}}_3+{\dot{V}}_4\hfill \\ \hfill \le & -\left({\alpha }_m-{\psi }_m\right){\dot{\mathit{q}}}_m^T\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }-\left({\alpha }_s-{\psi }_s\right){\dot{\mathit{q}}}_s^T\mathrm{sig}{\left({\dot{\mathit{q}}}_s\right)}^{\sigma }\hfill \end{array}$$

(28)

where ${\psi }_m=2^{1-\sigma }{K}_m+{\overline{d}}_{m}K+2{\overline{d}}_s{\left(\frac{K_m}{1+\sigma }\right)}^{1+\sigma }\left(\frac{\sigma }{K}\right)$, ${\psi }_s=2^{1-\sigma }{K}_m+{\overline{d}}_{s}K+2{\overline{d}}_m{\left(\frac{K_m}{1+\sigma }\right)}^{1+\sigma }\left(\frac{\sigma }{K}\right)$

Based on the controller gain coefficient condition set in Theorem 1, we have ${\alpha }_m\ge {\psi }_m$ and ${\alpha }_s\ge {\psi }_s$, and an important conclusion can be obtained as

$$\begin{array}{cc}\hfill & \dot{V}={\dot{V}}_1+{\dot{V}}_2+{\dot{V}}_3+{\dot{V}}_4\le 0\hfill \end{array}$$

(29)

Obviously, the closed-loop teleoperation system is stable. In addition, the following conclusions can be obtained that the velocities ${\dot{\mathit{q}}}_m,{\dot{\mathit{q}}}_s\in {\mathcal{L}}_{\infty }$, the position-tracking error ${\mathit{q}}_m-{\mathit{q}}_s\in {\mathcal{L}}_{\infty }$, the adaptive parameter errors ${\tilde{\mathit{W}}}_m,{\tilde{\mathit{W}}}_s,{\tilde{\mathit{\omega }}}_m,{\tilde{\mathit{\omega }}}_s\in {\mathcal{L}}_{\infty }$. As ${\mathit{q}}_m-{\mathit{q}}_{sd}={\mathit{q}}_m-{\mathit{q}}_s+{\int }_{t-d_s}^t{\dot{\mathit{q}}}_{s}d\xi$, then ${\mathit{q}}_m-{\mathit{q}}_{sd}\in {\mathcal{L}}_{\infty }$. Similarly, ${\mathit{q}}_s-{\mathit{q}}_{md},{\mathit{s}}_m,{\mathit{s}}_s\in {\mathcal{L}}_{\infty }$ can be further obtained. In order to prove the global asymptotic stability of the system, it is also necessary to prove the boundedness of the acceleration signals ${\ddot{\mathit{q}}}_m$ and ${\ddot{\mathit{q}}}_s$.

Firstly, taking the analysis of the master robot as an example, based on the dynamics model and control law of the master robot, the following expression of acceleration can be obtained as

$$\begin{array}{c}\hfill {\ddot{\mathit{q}}}_m={\mathit{M}}_m^{-1}\left[-{\mathit{C}}_m{\dot{\mathit{q}}}_m+K_m\mathrm{sig}{\left({\mathit{s}}_m\right)}^{\sigma }-2K_m\mathrm{sig}{\left({\mathit{q}}_m-{\mathit{q}}_{sd}\right)}^{\sigma }-{\alpha }_m\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }+{\tilde{\mathit{W}}}_m^T{\mathit{\phi }}_m+{\tilde{\mathit{\omega }}}_m\right]\end{array}$$

(30)

With the ${\mathit{q}}_m,{\mathit{q}}_m-{\mathit{q}}_{sd}\in {\mathcal{L}}_{\infty }$, and Property 1, 3, and 4, it can be deduced that ${\ddot{\mathit{q}}}_m\in {\mathcal{L}}_{\infty }$. Considering the slave robot, we can get a similar conclusion as ${\ddot{\mathit{q}}}_s\in {\mathcal{L}}_{\infty }$. With Barbalt’s Lemma, it is obvious that there has ${\dot{\mathit{q}}}_m,{\dot{\mathit{q}}}_s\to 0$, when $t\to \infty$.

Based on the above formula, it can be found that if ${\mathit{q}}_m-{\mathit{q}}_s$ is held, we must prove ${\ddot{\mathit{q}}}_m\to 0$ and bounded ${\stackrel{⃛}{\mathit{q}}}_m$. By differentiation of the above equation on both sides, there is

$$\begin{array}{cc}\hfill {\stackrel{⃛}{\mathit{q}}}_m=& \frac{d{\mathit{M}}_m^{-1}}{dt}\left[-{\mathit{C}}_m{\dot{\mathit{q}}}_m+K_m\mathrm{sig}{\left({\mathit{s}}_m\right)}^{\sigma }-2K_m\mathrm{sig}{\left({\mathit{q}}_m-{\mathit{q}}_{sd}\right)}^{\sigma }-{\alpha }_m\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }+{\tilde{\mathit{W}}}_m^T{\mathit{\phi }}_m+{\tilde{\mathit{\omega }}}_m\right]\hfill \\ \hfill & +{\mathit{M}}_m^{-1}\left[-{\mathit{C}}_m{\ddot{\mathit{q}}}_m-{\dot{\mathit{C}}}_m{\dot{\mathit{q}}}_m+K_m\sigma \mathrm{diag}{\left|{\mathit{s}}_m\right|}^{\sigma -1}\dot{{\mathit{s}}_m}+{\tilde{\mathit{W}}}_m^T{\dot{\mathit{\phi }}}_m+{\dot{\widehat{\mathit{W}}}}_m^T{\mathit{\phi }}_m+{\dot{\mathit{\omega }}}_m\right.\hfill \\ \hfill & \left.-2K_m\sigma \mathrm{diag}{\left|{\mathit{q}}_m-{\mathit{q}}_{sd}\right|}^{\sigma -1}({\dot{\mathit{q}}}_m-(1-{\dot{d}}_s){\dot{\mathit{q}}}_s)-{\alpha }_m\sigma \mathrm{diag}{\left|{\dot{\mathit{q}}}_m\right|}^{\sigma -1}\ddot{{\mathit{q}}_m}\right]\hfill \end{array}$$

(31)

Based on the above properties and conclusions, it is obvious that ${\stackrel{⃛}{\mathit{q}}}_m,{\stackrel{⃛}{\mathit{q}}}_s\in {\mathcal{L}}_{\infty }$. Therefore, with Barbalt’s Lemma, ${\ddot{\mathit{q}}}_m,{\ddot{\mathit{q}}}_s\to 0$ when $t\to \infty$. Finally, based on the definition of the RBF neural network, we know that ${\mathit{q}}_m-{\mathit{q}}_s\to 0$ when $t\to \infty$ can be ensured.

This completes the proof. □

Next, based on the conclusion of Theorem 1, the proof of the finite-time control performance of Theorem 2 is given here.

Proof. 

The proof of this theorem is investigated using the following Lyapunov function $\overline{V}$ as

$$\begin{array}{c}\hfill \overline{V}=\frac{1}{2}{\dot{\mathit{q}}}_m^T{\mathit{M}}_m{\dot{\mathit{q}}}_m+\frac{1}{2}{\dot{\mathit{q}}}_s^T{\mathit{M}}_s{\dot{\mathit{q}}}_s\end{array}$$

(32)

Based on the previous proof process, the derivative of $\overline{V}$ can be expressed as

$$\begin{array}{cc}\hfill \dot{\overline{V}}=& {\dot{\mathit{q}}}_m^T\left[2K_m\mathrm{sig}{\left({\mathit{s}}_m\right)}^{\sigma }-2K_m\mathrm{sig}{\left({\mathit{q}}_m-{\mathit{q}}_{sd}\right)}^{\sigma }-{\alpha }_m\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }\right.\hfill \\ \hfill & +{\tilde{\mathit{W}}}_m{\mathit{\phi }}_m\left({\mathit{x}}_m\right)+{\tilde{\mathit{\omega }}}_m-K_m\mathrm{sig}{\left({\mathit{s}}_m\right)}^{\sigma }]\hfill \\ \hfill & +\frac{K_m}{K_s}{\dot{\mathit{q}}}_s^T\left[2K_s\mathrm{sig}{\left({\mathit{s}}_s\right)}^{\sigma }-2K_s\mathrm{sig}{\left({\mathit{q}}_s-{\mathit{q}}_{md}\right)}^{\sigma }-{\alpha }_s\mathrm{sig}{\left({\dot{\mathit{q}}}_s\right)}^{\sigma }\right.\hfill \\ \hfill & +{\tilde{\mathit{W}}}_s{\mathit{\phi }}_s\left({\mathit{x}}_s\right)+{\tilde{\mathit{\omega }}}_s-K_s\mathrm{sig}{\left({\mathit{s}}_s\right)}^{\sigma }]\hfill \end{array}$$

(33)

With Lemma 2, we can obtain

$$\begin{array}{cc}\hfill \dot{\overline{V}}\le & -\left({\alpha }_m-2K_m\right){\dot{\mathit{q}}}_m^T\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }+{\dot{\mathit{q}}}_m^T\left[{\tilde{\mathit{W}}}_m{\mathit{\phi }}_m\left({\mathit{x}}_m\right)+{\tilde{\mathit{\omega }}}_m-K_m\mathrm{sig}{\left({\mathit{s}}_m\right)}^{\sigma }\right]\hfill \\ \hfill & -\left(\frac{{\alpha }_s{K}_m}{K_s}-2K_m\right){\dot{\mathit{q}}}_s^T\mathrm{sig}{\left({\dot{\mathit{q}}}_s\right)}^{\sigma }+{\dot{\mathit{q}}}_s^T\left[{\tilde{\mathit{W}}}_s{\mathit{\phi }}_s\left({\mathit{x}}_s\right)+{\tilde{\mathit{\omega }}}_s-K_s\mathrm{sig}{\left({\mathit{s}}_s\right)}^{\sigma }\right]\hfill \end{array}$$

(34)

Based on boundedness in Theorem 1 of ${\tilde{\mathit{W}}}_m,{\tilde{\mathit{W}}}_s,{\tilde{\mathit{\omega }}}_m,{\tilde{\mathit{\omega }}}_s,{\mathit{s}}_m,{\mathit{s}}_s,{\mathit{\phi }}_m,{\mathit{\phi }}_s,{\dot{\mathit{q}}}_m,{\dot{\mathit{q}}}_s$, there is

$$\begin{array}{cc}\hfill \dot{\overline{V}}\le & -{\kappa }_m{\dot{\mathit{q}}}_m^T\mathrm{sig}{\left({\dot{\mathit{q}}}_m\right)}^{\sigma }-{\kappa }_s{\dot{\mathit{q}}}_s^T\mathrm{sig}{\left({\dot{\mathit{q}}}_s\right)}^{\sigma }+{\Phi }_m+{\Phi }_s\hfill \end{array}$$

(35)

where ${\kappa }_m={\alpha }_m-2K_m$, ${\kappa }_s=\frac{{\alpha }_s{K}_m}{K_s}-2K_m$, $\left|{\dot{\mathit{q}}}_m^T\right|\left|{\tilde{\mathit{W}}}_m{\mathit{\phi }}_m\left({\mathit{x}}_m\right)+{\tilde{\mathit{\omega }}}_m-K_m\mathrm{sig}{\left({\mathit{s}}_m\right)}^{\sigma }\right|\le {\Phi }_m$, $\left|{\dot{\mathit{q}}}_s^T\right|\left|{\tilde{\mathit{W}}}_s{\mathit{\phi }}_s\left({\mathit{x}}_s\right)+{\tilde{\mathit{\omega }}}_s-K_s\mathrm{sig}{\left({\mathit{s}}_s\right)}^{\sigma }\right|\le {\Phi }_s$. if $\Phi ={\Phi }_m+{\Phi }_s$, we can get

$$\begin{array}{cc}\hfill \dot{\overline{V}}\le & -\frac{2^{\frac{\sigma +1}{2}}{\kappa }_m}{{\left[{\lambda }_{max}\left({\mathit{M}}_m\right)\right]}^{\frac{\sigma +1}{2}}}{\left(\frac{1}{2}{\dot{\mathit{q}}}_m^T{\mathit{M}}_m{\dot{\mathit{q}}}_m\right)}^{\frac{\sigma +1}{2}}-\frac{2^{\frac{\sigma +1}{2}}{\kappa }_s}{{\left[{\lambda }_{max}\left({\mathit{M}}_s\right)\right]}^{\frac{\sigma +1}{2}}}{\left(\frac{1}{2}{\dot{\mathit{q}}}_s^T{\mathit{M}}_s{\dot{\mathit{q}}}_m\right)}^{\frac{\sigma +1}{2}}+\Phi \hfill \end{array}$$

(36)

If ${\rm Y}$ is defined as

$$\begin{array}{c}\hfill {\rm Y}=min\left\{\frac{2^{\frac{\sigma +1}{2}}{\kappa }_m}{{\left[{\lambda }_{max}\left({\mathit{M}}_m\right)\right]}^{\frac{\sigma +1}{2}}},\frac{2^{\frac{\sigma +1}{2}}{\kappa }_s}{{\left[{\lambda }_{max}\left({\mathit{M}}_s\right)\right]}^{\frac{\sigma +1}{2}}}\right\}\end{array}$$

(37)

Then with the Lemma 2

$$\begin{array}{cc}\hfill \dot{\overline{V}}\le & -{\rm Y}\left[{\left(\frac{1}{2}{\dot{\mathit{q}}}_m^T{\mathit{M}}_m{\dot{\mathit{q}}}_m\right)}^{\frac{\sigma +1}{2}}+{\left(\frac{1}{2}{\dot{\mathit{q}}}_s^T{\mathit{M}}_s{\dot{\mathit{q}}}_m\right)}^{\frac{\sigma +1}{2}}\right]+\Phi \hfill \\ \hfill \le & -{\rm Y}{\left[\left(\frac{1}{2}{\dot{\mathit{q}}}_m^T{\mathit{M}}_m{\dot{\mathit{q}}}_m\right)+\left(\frac{1}{2}{\dot{\mathit{q}}}_s^T{\mathit{M}}_s{\dot{\mathit{q}}}_m\right)\right]}^{\frac{\sigma +1}{2}}+\Phi \hfill \\ \hfill \le & -{\rm Y}{\overline{V}}^{\frac{\sigma +1}{2}}+\Phi \hfill \end{array}$$

(38)

Finally, invoking Lemma 1 and according to Theorem 1, the finite-time control performance of the closed-loop teleoperation system is obtained. This completes the proof. □

4. Simulation Results and Analysis

In this section, simulation experiments are designed and implemented to analyze and verify the effectiveness of the proposed control structure. The simulation is implemented in the Simulink environment of MATLAB 2021b. In the simulation, a pair of two manipulators with 2-dof revolute joints is employed. In addition, in order to better simulate the interaction process between the operator, teleoperation system, and environment, the operator dynamic is introduced at the master robot side and the environment contact model is also employed at the slave robot side. These models are assumed to be stiffness-damping models. The detailed mathematical descriptions of operator force ${\mathit{F}}_h$ and environmental force ${\mathit{F}}_e$ are shown as

$$\begin{array}{cc}\hfill {\mathit{F}}_h& =b_h{\dot{\mathit{X}}}_m+k_h\left({\mathit{X}}_m-{\mathit{X}}_{m0}\right)+{\mathit{f}}_h\hfill \\ \hfill {\mathit{F}}_e& =b_e{\dot{\mathit{X}}}_s+k_e\left({\mathit{X}}_s-{\mathit{X}}_{s0}\right)\hfill \end{array}$$

(39)

where for $j=m,s$, ${\mathit{X}}_j$ and ${\dot{\mathit{X}}}_j$ are the end position and velocity vectors of the master/slave robots in the Cartesian coordinate system. ${\mathit{X}}_j$ can be obtained through the forward kinematic of the robot, and ${\dot{\mathit{X}}}_j$ can be calculated through Jacobian matrices with the joint velocities. $b_h$ and $k_h$ are the damping and stiffness coefficients of the operator force dynamic. $b_e$ and $k_e$ are the damping and stiffness coefficients of the environment force model, respectively. ${\mathit{f}}_h$ is the external operator force vector. In this simulation, the values of $k_h$ and $k_e$ are set as 10 N/(m/s), $b_n$ is 5 N/(m/s), and $b_e$ is 2 N/(m/s). ${\mathit{X}}_{m0}$ and ${\mathit{X}}_{s0}$ are set as ${[1.366,1]}^{T}m$. The principle diagram of the simulation is shown in Figure 1.

The dynamic matrices and vectors ${\mathit{M}}_j$, ${\mathit{C}}_j$, ${\mathit{G}}_j$, and ${\mathit{F}}_j$ are defined as follows [37]

$$\begin{array}{c}\hfill {\mathit{M}}_j=\left[\begin{array}{cc}{m}_{j11}& m_{j12}\\ m_{j21}& m_{j22}\end{array}\right],{\mathit{C}}_j=\left[\begin{array}{cc}{c}_{j11}& c_{j12}\\ c_{j21}& c_{j22}\end{array}\right],{\mathit{G}}_j=\left[\begin{array}{c}{g}_{j1}\\ g_{j2}\end{array}\right],{\mathit{F}}_j=\left[\begin{array}{c}{f}_{j1}\\ f_{j2}\end{array}\right].\end{array}$$

where $m_{j11}=l_{j1}^2(m_{j1}+m_{j2})+l_{j2}{m}_{j2}(2l_{j1}cos{q}_{j2}+l_{j2})$, $m_{j12}=m_{j21}=l_{j2}^2{m}_{j2}+l_{j1}{l}_{j2}{m}_{j2}$$cos{q}_{j2}$, $m_{22}=l_{j2}^2{m}_{j2}$, $c_{11}=-l_{j1}{l}_{j2}{m}_{j2}sin{q}_{j2}{\dot{\dot{q}}}_{j2}$, $c_{12}=-l_{j1}{l}_{j2}{m}_{j2}sin{q}_{j2}({\dot{q}}_{j1}+{\dot{q}}_{j2})$, $c_{21}=l_{j1}{l}_{j2}{m}_{j2}$$sin{q}_{j2}$, $c_{22}=0$, $g_{j1}=(m_{j1}+m_{j2})l_{j1}gcos\left(q_{j1}\right)+m_{j2}{l}_{j2}gcos(q_{j1}+q_{j2})$, $g_{j2}=m_{j2}{l}_{j2}gcos(q_{j1}+q_{j2})$, $f_{j1}=0.5{\dot{q}}_{j1}+0.2\mathrm{sign}\left({\dot{q}}_{j1}\right)$, and $f_{j2}=0.5{\dot{q}}_{j2}+0.2\mathrm{sign}\left({\dot{q}}_{j2}\right)$. For simplicity, the parameters of the master robot are defined as [24 $m_{m1}=4.0$ kg, $m_{m2}=0.5$ kg, $l_{m1}=l_{m2}=1.0$ m. The parameters of the slave robot are set as $m_{s1}=3.4$ kg, $m_{s2}=0.25$ kg, $l_{s1}=l_{s2}=1.0$ m.

The time-varying communication delays are considered in the simulation experiments, which are shown in Figure 2. The curves of the external force ${\mathit{f}}_h$ applied by the operator in the x-direction and y-direction are shown in Figure 3. It can be seen that from 2 to 7 s, the operator applied an external force in the negative x-direction and positive y-direction to change the end position of the master robot. Then, the external force injected by the operator disappears to zero. However, it should be noted that at this time, the operator and environment still have forces acting on the master and slave robots. This simulation factor is not available in some related work.

Theorems 1 and 2 are used to set controller gains in the simulation to guarantee the stability and finite-time control performance of closed-loop teleoperation systems. In the master and slave controllers, the controller gain parameters are selected as $K_m=K_s=0.8$, ${\alpha }_m={\alpha }_s=5$, $\sigma =8/11$. The gains of adaptive learning rate are selected as ${\Lambda }_{m1}={\Lambda }_{s1}=0.9$, ${\Lambda }_{m2}={\Lambda }_{s2}=0.9$. The initial joint position of the master and slave robots are ${\mathit{q}}_{m0}={[pi/4,pi/6]}^T$ and ${\mathit{q}}_{s0}={[pi/6,pi/8]}^T$, respectively. The initial joint velocities ${\dot{\mathit{q}}}_{m0}$ and ${\dot{\mathit{q}}}_{s0}$ are zeros.

We carried out three parts of simulation experiments to verify the stability of the closed-loop system, the influence of power on the control performance, and the advantages of finite-time control performance. The results of these simulations are shown in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17, respectively.

4.1. Verification of System Stability

Figure 4 and Figure 5 show the position-tracking performances of the closed-loop system. Figure 4 represents that the joints of master and slave robots have position deviation with the action of the extra force of the operator. When the extra injection forces of the operator are removed, the joint positions of the master and the slave robots quickly realize mutual tracking. Figure 5 gives the results of the joint position difference between the master robot and the slave robot at the same time. These results vividly present the position tracking effect of the master and slave robots. Seven to eight seconds after the injection forces are removed, the master robot and slave robot quickly realize the position-tracking performance without static error. These results demonstrate that stable and efficient position-tracking control performance can be achieved with the proposed control method. In addition, the results also verify some important conclusions obtained from the above theorem proving.

Figure 6 shows the curves of operator force and environmental force. The upper subfigure is the operator force, and the lower one is the environmental force. It can be seen that in the teleoperation system, the operator exerts a non-zero force on the master robot, and the environment also exerts a force on the slave robot. In addition, the stability of the operator and environmental force results further shows that the closed-loop system is stable. Figure 7 shows the control values of the master and slave controllers.

In order to verify the boundedness of adaptive learning parameters, the curves of adaptive learning parameters ${\widehat{\mathit{W}}}_m$, ${\widehat{\mathit{W}}}_s$, ${\widehat{\mathit{\omega }}}_m$, and ${\widehat{\mathit{\omega }}}_s$ are also shown in Figure 8 and Figure 9 below.

The above simulation results verify the statement of Theorem 1 and the conclusions obtained from its proof expression. The whole closed-loop teleoperation system is stable, and the state variables for constructing the Lyapunov function are also bounded.

4.2. Effect of the Power Coefficient

In the second part of the simulation, the influences of the power parameter $\sigma$ of the master and slave controllers are shown and analyzed. We choose the different power values of $\sigma$ as $\sigma =1,8/11,5/11,2/11$. In this simulation, the initial position status of the master and slave robots are all set to 0. Figure 10 and Figure 11 show the control results based on these power parameters.

From Figure 10 and Figure 11, it can be seen that the larger the power is, the slower the convergence rate has. When $\sigma =1$, the control scheme is degraded to the traditional proportional damping injection controller. However, the faster convergence speed will cause the oscillation of the control torque, which further limits its application in the actual robot system. It also further shows that the finite-time control structure proposed in this paper has a faster convergence rate than the traditional proportional damping injection control structure.

4.3. Comparison of Control Performance

For this subsection, we chose three representative P+d control methods, applied them in the simulation, and compared the results of these methods with the proposed control scheme to confirm the effectiveness. There are three instances created based on these P+d control strategies. Case 1: in [23], De Lima proposed a simplified P+d control method, and gravity compensation is also considered in the controller. In the simulation experiment, the gravity torque vector of the control law in case 1 is inaccurate, and we intend to demonstrate the benefits of the adaptive method in our method by evaluating the position-tracking performance with Case 1. Case 2: in [12], Yang introduced the adaptive term to compensate for the gravity torque and proposed an adaptive P+d control strategy. Case 3: in [22], this control strategy employs hybrid control terms, and a new control scheme is designed based on the P+d control approach. In Case 3, the operator and environment torques need to be measured and sent into the controllers. In the proposed approach, the RBF neural network is introduced to estimate the external force, and we expect to evaluate the performance of external force estimation by analyzing and contrasting the method of Case 3. Additionally, as these three comparison approaches are non-finite-time performance control structures, we expect to validate the efficacy of the proposed control method by contrasting the simulation results of these non-finite-time methods. Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17 show the detailed simulation results and comparisons.

The joint position-tracking performances based on the Case 1 method are given in Figure 12 and Figure 13. These results show that the position-tracking performances of the master and slave robots can reach stability after the additional injection forces are removed. The time when the final tracking error converges into the stable region is around 10.5 s. From the curve of position-tracking errors in Figure 13, it can be seen that the proposed control approach has a higher convergence accuracy and speed than the Case 1 method.

Figure 14 and Figure 15 show the joint position tracking of the master and slave robots with the method in Case 2. It can be seen that the position-tracking performance in the method of Case 2 has steady-state errors in the first joint. In the control structure of Case 2, the authors only introduce the adaptive control method in the slave controller. However, the proposed finite-time control scheme still has advantages in the convergence speed and accuracy of position tracking.

Figure 16 and Figure 17 show the joint position tracking of the master/slave robots with the method in Case 3. In Case 3, the author has proved that with the action of operator force and environmental force, when $t\to \infty$, ${\mathit{q}}_m-{\mathit{q}}_s\to 0$ is held. Therefore, theoretically, if the time is long enough, the convergence precision of Case 3 is similar to the finite-time control method we proposed. The simulation results illustrate this point. However, it is clear that the convergence speed of the finite-time control performance is faster, demonstrating the efficacy of the suggested control method.

The comparisons of these three P+d control methods show that the proposed finite-time control scheme has higher convergence speed and accuracy in position tracking error performances. From Figure 15, Figure 16 and Figure 17, it can be seen that based on the proposed method, the position errors of the master–slave robot have converged to a small neighborhood of 0 in about 8 s, while the performances with Case 1 and Case 2 have converged to a relatively stable state in about 11 s and 9.5 s, respectively, and neither of them can converge to the small neighborhood of 0, which means that there are steady-state errors. The root mean square error (RMSE) index is introduced here to quantify the speed and accuracy of position-tracking performances of the proposed approach and these three methods. The RMSE is defined as follows:

$$\begin{array}{c}\hfill RMSE=\sqrt{\frac{1}{n}\sum _{i=1}^n{\left(e_i\right)}^2}\end{array}$$

(40)

where $e_i$ represents the position tracking error of each joint of the robot, n denotes the length of the error sequence. The smaller the RMSE, the faster the tracking and the higher the accuracy of the position performance. In order to avoid the impact of the extra force, only the RMSE values of the system after 8 seconds are analyzed and calculated. The RMSEs of the position tracking errors with these three control schemes are shown in

Table 1. RMSE of position-tracking errors with different control methods.

Index	Proposed	Case1	Case2	Case3
RMSE of joint 1	0.0036	0.1573	0.3371	0.0127
RMSE of joint 2	0.0092	0.2126	0.0132	0.0099

. It can be seen that the tracking errors with the proposed control method have smaller RMSE values, which means that the master and slave robots have better position-tracking performance.

5. Conclusions

This paper presents a new finite-time controller for the time-delay teleoperation system, whereas the majority of existing proportional damping injection controllers only achieve asymptotic position-tracking stability. Based on the conventional structure of proportional damping injection control, a finite-time control structure is designed by introducing non-integer power terms, and position tracking finite-time control performance is achieved. Compared with other finite-time control strategies, the proposed control strategy has a simple structure and fewer gain parameters. In addition, the RBF neural network and adaptive method are employed to estimate the uncertain dynamics and external injection forces. In the proof of stability, the stability and boundedness of the system and state are demonstrated, followed by the finite-time convergence performance, which offers a novel approach to the finite-time performance analysis of damping injection control. Simulation results prove the bounded stability of the closed-loop system and present that the proposed method has a faster convergence speed and higher convergence precision than other methods. However, some considerable works still need to take place. First, experiments should be performed to validate the proposed control strategy. Second, the study of the communication environment is mostly predicated on the ideal condition, and the analysis of packet loss and other issues are needed. Finally, further improvement of this finite-time control structure should be considered.