Significance of Weissenberg Number, Soret Effect and Multiple Slips on the Dynamic of Biconvective Magnetohydrodynamic Carreau Nanofuid Flow
Abstract
:1. Introduction
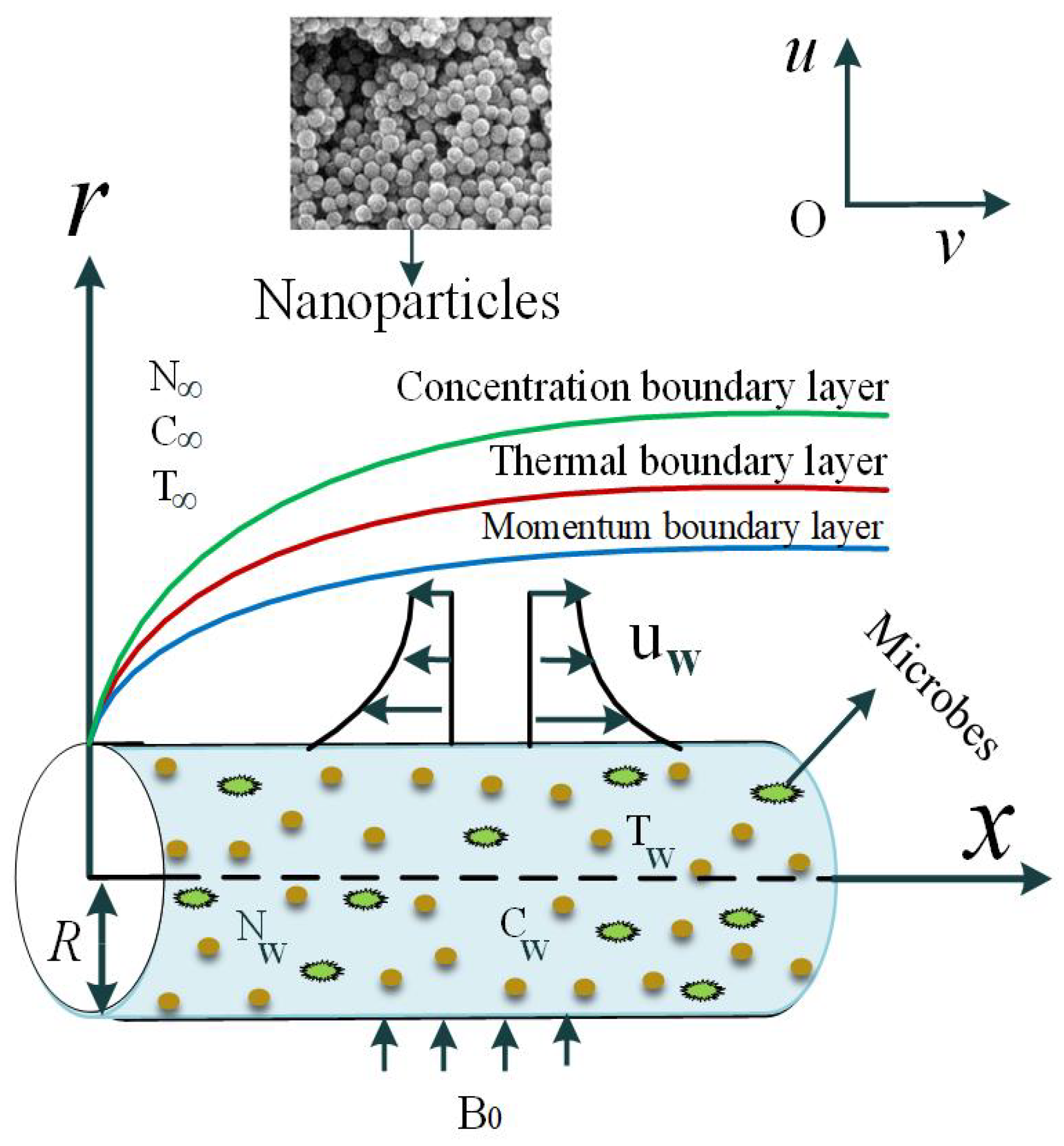
2. Problem Description
3. Physical Quantities
4. Engineering Quantities
5. Implementation of Method
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
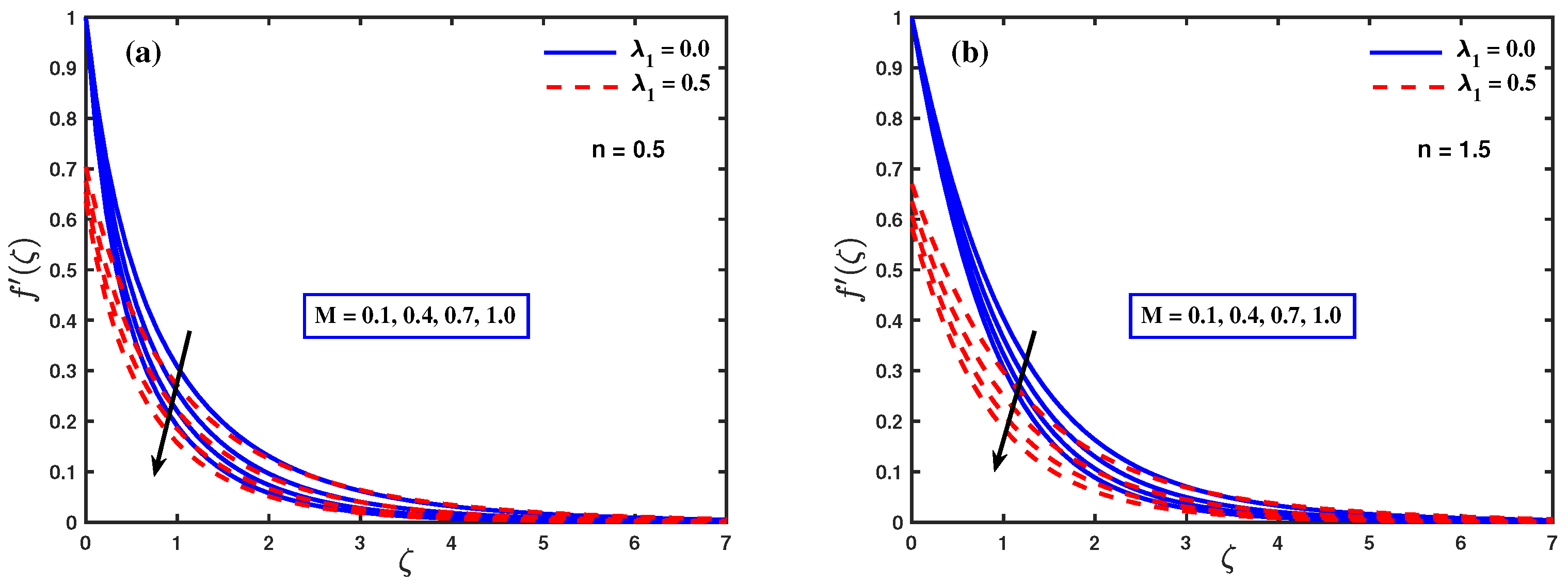
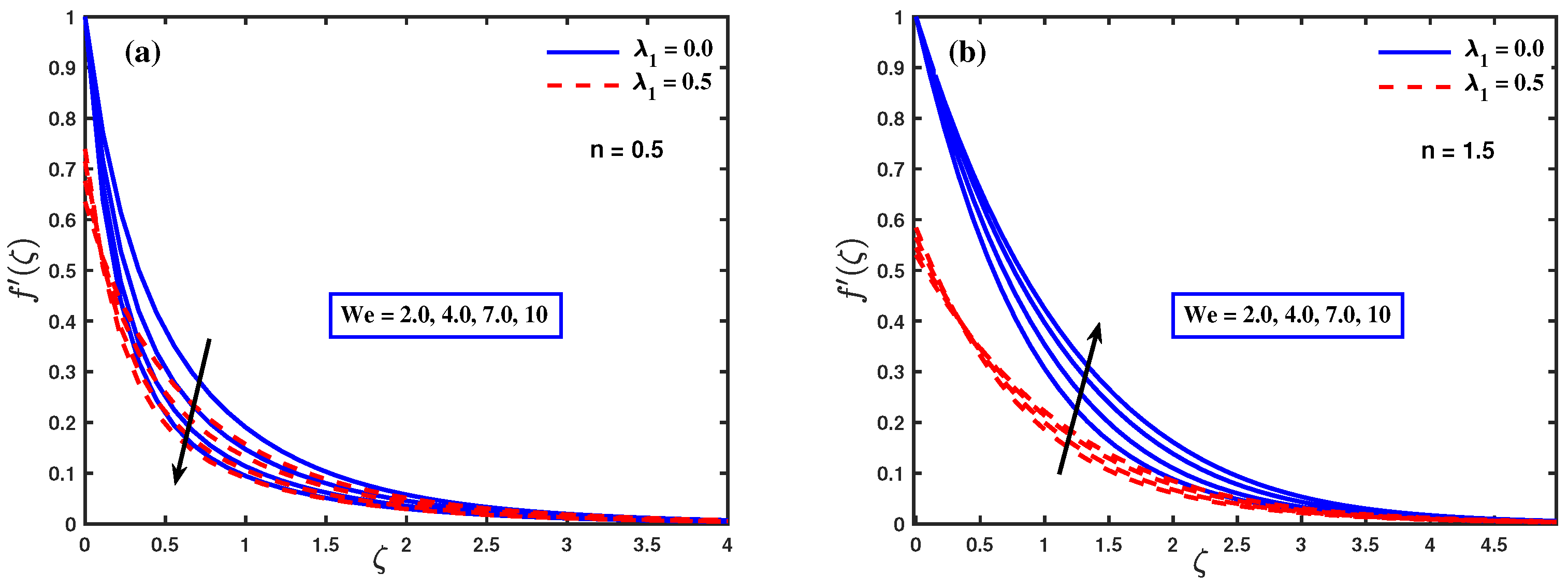
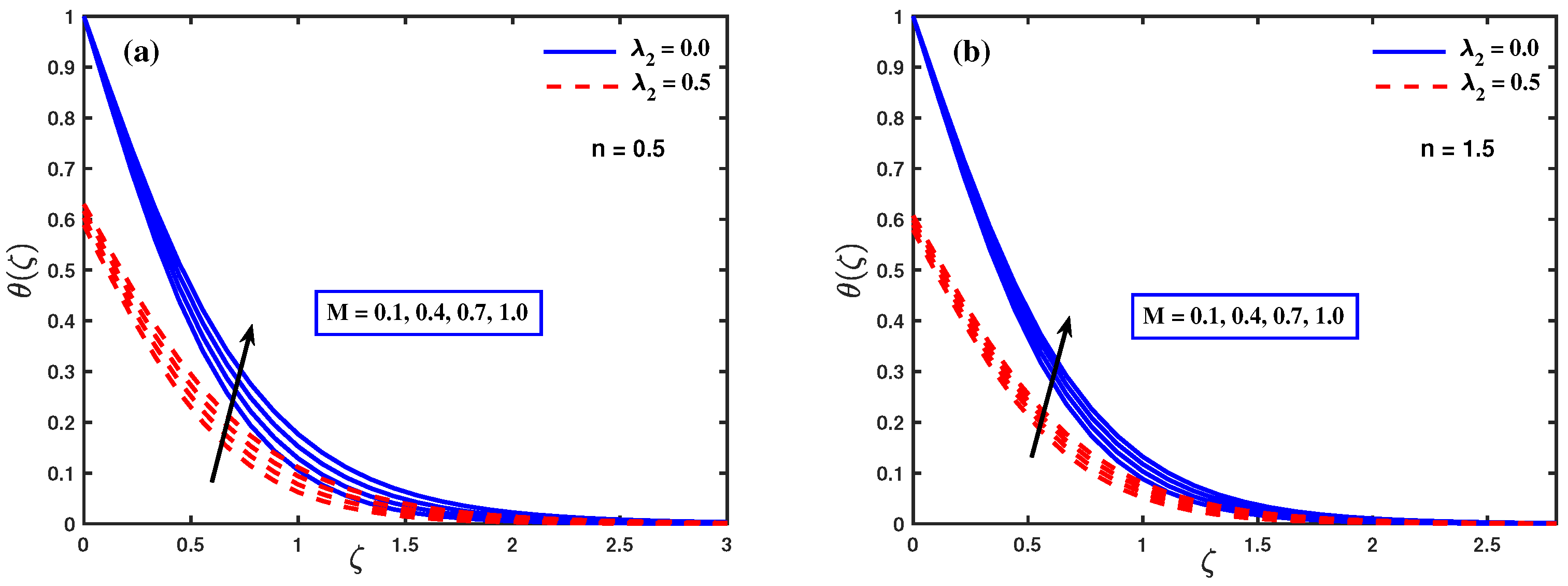
6. Results and Discussion
7. Concluding Remarks
- The temperature distribution is declining with Prandtl number and thermal slip parameter.
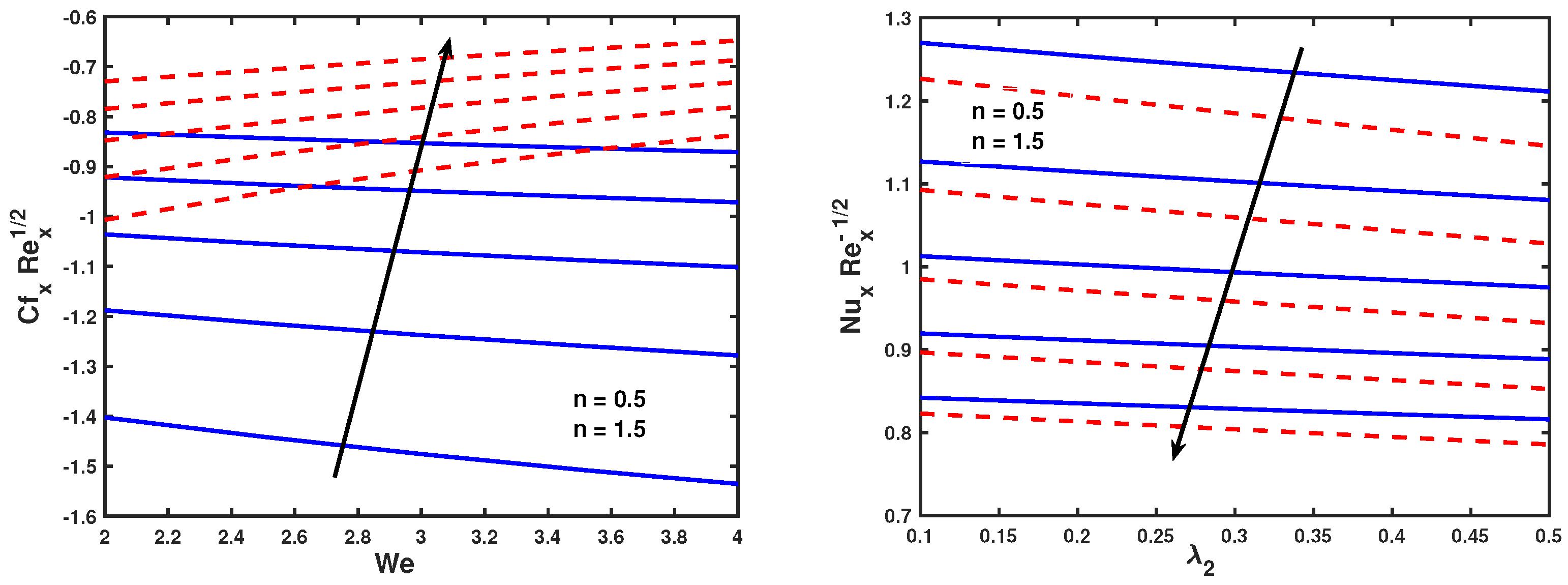
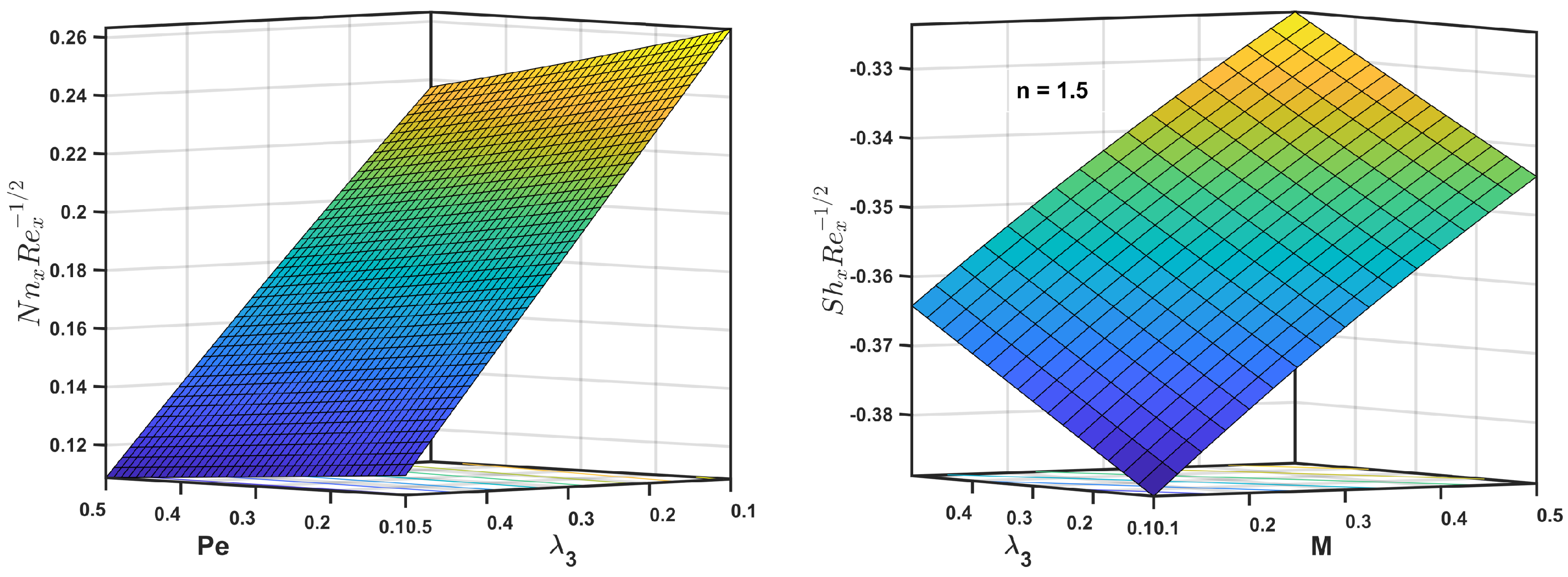
- Nusselt number and local skin friction are intensified with the curvature parameter and diminished with the velocity slip parameter for both and .
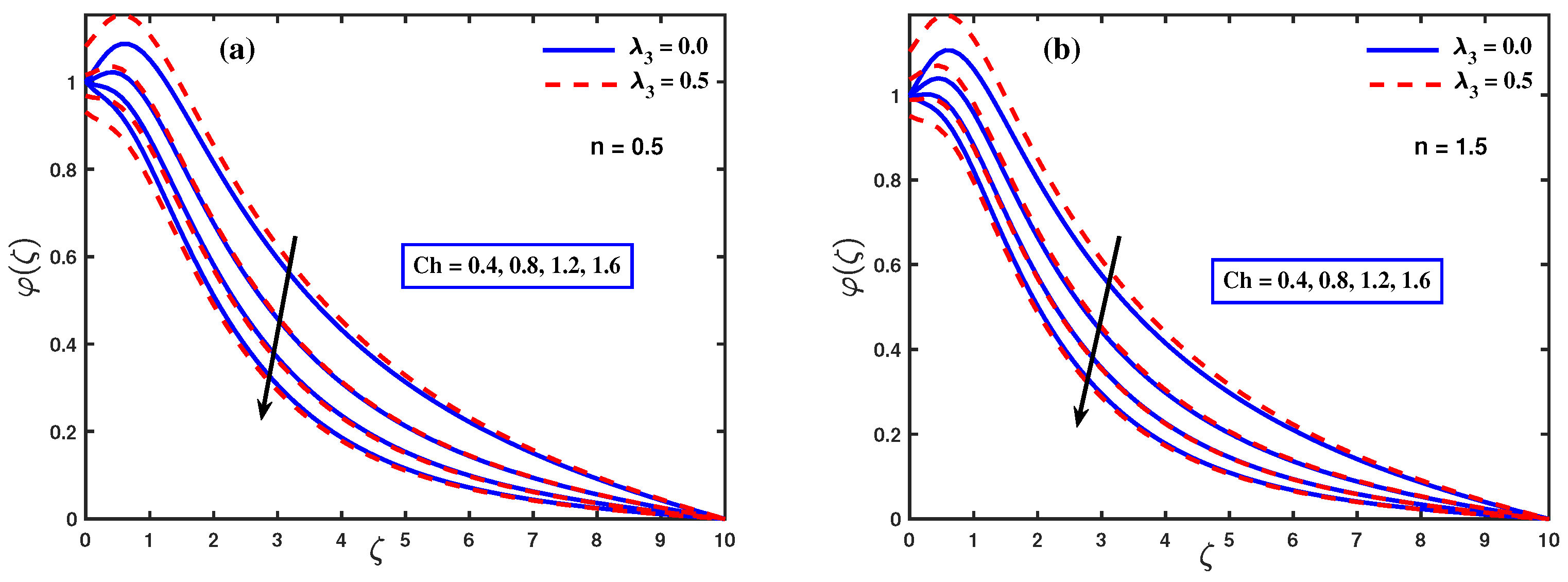
- The concentration profile and motile concentration profile diminish with the chemical reaction factor and , respectively.
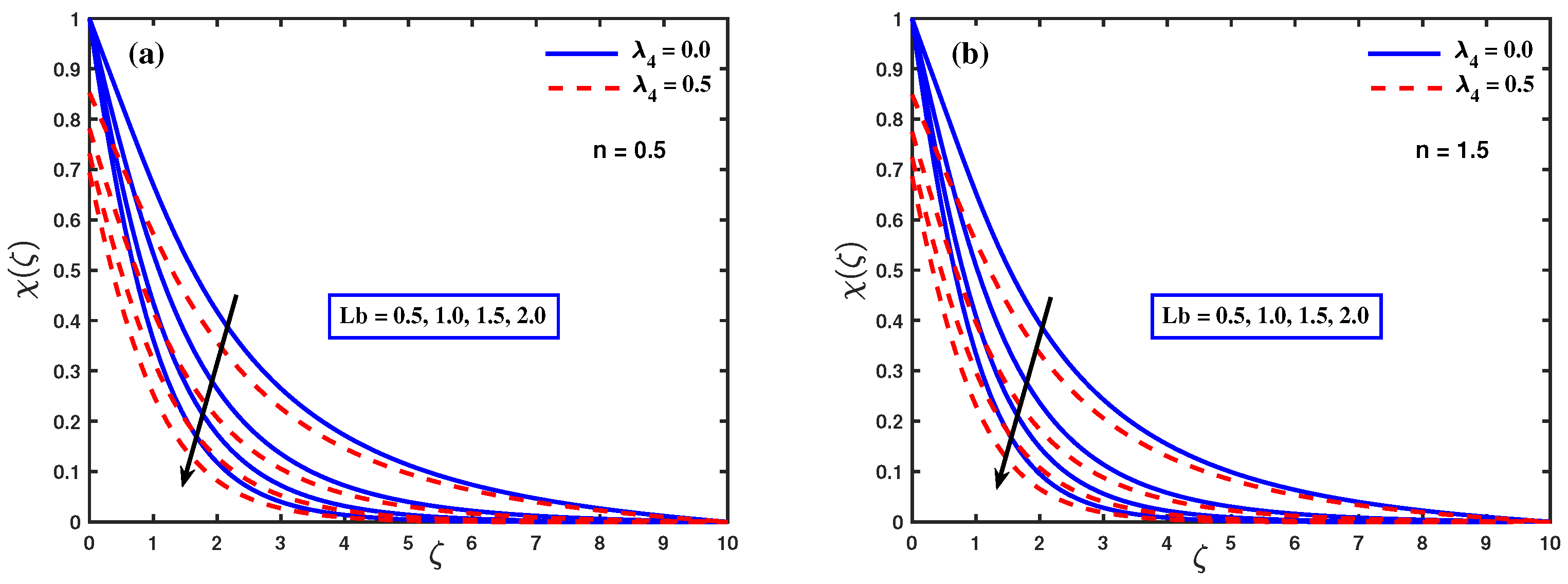
- Thermal diffusivity declines as the values of increase, creating a drop in boundary layer thickness and temperature in both cases.
- Weissenberg number demonstrates a different nature on the velocity profile, skin friction, and heat transfer; these are reduced for shear diminishing and increased when shear condensing .
- The magnetic parameter M with the simultaneous effect of velocity slip creates a decreasing impact on the velocity field for shear thinning and shear thickening.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| fluid velocity components (m s−1) | uniform magnetic field (Am−1) | ||
| f | non-dimensional radial velocity component (m s−1) | a | reference velocity, m/s |
| l | characteristic length m | R | radius of the cylinder, m |
| cylindrical coordinates | Reynolds number | ||
| ambient temperature (K (Kelvin)) | T | fluid temperature (K (Kelvin)) | |
| fluid temperature at the cylinder (K (Kelvin)) | C | fluid concentration | |
| ambient nanoparticle concentration | n | power-law index | |
| nanoparticle concentration at the disc | Brownian diffusivity | ||
| thermophoretic diffusion | Prandtl number | ||
| b | chemotaxis constant | microorganisms diffusion coefficient | |
| maximum cell swimming speed | ambient concentration of microorganisms | ||
| N | concentration of microorganisms | surface concentration of microorganisms | |
| reference concentration of microorganisms | M | magnetic field parameter | |
| local drag coefficient | local Nusselt number | ||
| local motile microorganism number | local Sherwood number | ||
| curvature parameter | heat source | ||
| Peclet number | chemical reaction parameter | ||
| Lewis number | w | micro-organism difference parameter | |
| traditional Lewis number | Soret number | ||
| Weissenberg number | velocity slip parameter | ||
| thermal slip parameter | concentration slip parameter | ||
| motile microbes slip parameter | non-dimensional temperature | ||
| density () | dimensionless variable | ||
| k | thermal conductivity () | specific heat capacity () | |
| viscosity () | Boltzmann’s constant ( | ||
| kinematic viscosity () | electrical conductivity () |
References
- Basir, M.; Faisal, M.; Kumar, R.; Sarojamma, G.; Narayana, P.; Raza, J.; Mahmood, A. Exploration of thermal-diffusion and diffusion-thermal effects on the motion of temperature-dependent viscous fluid conveying microorganism. Arab. J. Sci. Eng. 2019, 44, 8023–8033. [Google Scholar] [CrossRef]
- Areekara, S.; Sabu, A.S.; Mathew, A.; Saravanan, B. Statistical analysis on the stratification effects of bioconvective EMHD nanofluid flow past a stretching sheet: Application in theranostics. Heat Transf. 2021, 50, 6680–6702. [Google Scholar] [CrossRef]
- Saranya, S.; Radha, K. Review of nanobiopolymers for controlled drug delivery. Polym.-Plast. Technol. Eng. 2014, 53, 1636–1646. [Google Scholar] [CrossRef]
- Liu, X.; Ali, B.; Mujeed, S.; Abdal, S. Finite element simulation of multi-slip effects on unsteady MHD bioconvective micropolar nanofluid flow over a sheet with solutal and thermal convective boundary conditions. Coatings 2019, 9, 842. [Google Scholar]
- Sk, M.T.; Das, K.; Kundu, P.K. Multiple slip effects on bioconvection of nanofluid flow containing gyrotactic microorganisms and nanoparticles. J. Mol. Liq. 2016, 220, 518–526. [Google Scholar] [CrossRef]
- Habibishandiz, M.; Saghir, M. A critical review of heat transfer enhancement methods in the presence of porous media, nanofluids, and microorganisms. Therm. Sci. Eng. Prog. 2022, 30, 101267. [Google Scholar] [CrossRef]
- Ali, B.; Habib, D.; Al Mdallal, Q. Finite element analysis on the thermo-convective non-isothermal nanofluid flow in MHD Hall generator system with Soret and Dufour effects. Case Stud. Therm. Eng. 2022, 39, 102389. [Google Scholar] [CrossRef]
- Khan, M.; Azam, M.; Alshomrani, A. Effects of melting and heat generation/absorption on unsteady Falkner-Skan flow of Carreau nanofluid over a wedge. Int. J. Heat Mass Transf. 2017, 110, 437–446. [Google Scholar] [CrossRef]
- Azam, M.; Khan, M.; Alshomrani, A. Unsteady radiative stagnation point flow of MHD Carreau nanofluid over expanding/contracting cylinder. Int. J. Mech. Sci. 2017, 130, 64–73. [Google Scholar] [CrossRef]
- Hsiao, K.L. To promote radiation electrical MHD activation energy thermal extrusion manufacturing system efficiency by using Carreau-Nanofluid with parameters control method. Energy 2017, 130, 486–499. [Google Scholar] [CrossRef]
- Salahuddin, T.; Hussain, A.; Malik, M.; Awais, M.; Khan, M. Carreau nanofluid impinging over a stretching cylinder with generalized slip effects: Using finite difference scheme. Results Phys. 2017, 7, 3090–3099. [Google Scholar] [CrossRef]
- Jagadha, S.; Hari Shing Naik, S.; Durgaprasad, P.; Naresh Kumar, A.; Naikoti, K. Radiative Newtonian Carreau nanofluid through stretching cylinder considering the first-order chemical reaction. Int. J. Ambient. Energy 2021, 43, 4959–4967. [Google Scholar] [CrossRef]
- Mallawi, F.; Ullah, M.Z. Conductivity and energy change in Carreau nanofluid flow along with magnetic dipole and Darcy-Forchheimer relation. Alex. Eng. J. 2021, 60, 3565–3575. [Google Scholar] [CrossRef]
- Ahmad, B.; Ahmad, M.O.; Ali, L.; Ali, B.; Hussein, A.K.; Shah, N.A.; Chung, J.D. Significance of the Coriolis force on the dynamics of Carreau–Yasuda rotating nanofluid subject to Darcy–forchheimer and gyrotactic microorganisms. Mathematics 2022, 10, 2855. [Google Scholar] [CrossRef]
- Kumar, P.; Poonia, H.; Ali, L.; Areekara, S. The numerical simulation of nanoparticle size and thermal radiation with the magnetic field effect based on tangent hyperbolic nanofluid flow. Case Stud. Therm. Eng. 2022, 37, 102247. [Google Scholar] [CrossRef]
- Ali, L.; Ali, B.; Ghori, M.B. Melting effect on Cattaneo–Christov and thermal radiation features for aligned MHD nanofluid flow comprising microorganisms to leading edge: FEM approach. Comput. Math. Appl. 2022, 109, 260–269. [Google Scholar] [CrossRef]
- Ramzan, M.; Farooq, M.; Hayat, T.; Alsaedi, A.; Cao, J. MHD stagnation point flow by a permeable stretching cylinder with Soret-Dufour effects. J. Cent. South Univ. 2015, 22, 707–716. [Google Scholar] [CrossRef]
- Akbari, S.; Faghiri, S.; Poureslami, P.; Hosseinzadeh, K.; Shafii, M.B. Analytical solution of non-Fourier heat conduction in a 3-D hollow sphere under time-space varying boundary conditions. Heliyon 2022, 8, e12496. [Google Scholar] [CrossRef]
- Faghiri, S.; Akbari, S.; Shafii, M.B.; Hosseinzadeh, K. Hydrothermal analysis of non-Newtonian fluid flow (blood) through the circular tube under prescribed non-uniform wall heat flux. Theor. Appl. Mech. Lett. 2022, 12, 100360. [Google Scholar] [CrossRef]
- Gulzar, M.M.; Aslam, A.; Waqas, M.; Javed, M.A.; Hosseinzadeh, K. A nonlinear mathematical analysis for magneto-hyperbolic-tangent liquid featuring simultaneous aspects of magnetic field, heat source and thermal stratification. Appl. Nanosci. 2020, 10, 4513–4518. [Google Scholar] [CrossRef]
- Rehman, S.U.; Fatima, N.; Ali, B.; Imran, M.; Ali, L.; Shah, N.A.; Chung, J.D. The Casson dusty nanofluid: Significance of Darcy–forchheimer law, magnetic field, and non-Fourier heat flux model subject to stretch surface. Mathematics 2022, 10, 2877. [Google Scholar] [CrossRef]
- Ali, L.; Manan, A.; Ali, B. Maxwell Nanofluids: FEM Simulation of the Effects of Suction/Injection on the Dynamics of Rotatory Fluid Subjected to Bioconvection, Lorentz, and Coriolis Forces. Nanomaterials 2022, 12, 3453. [Google Scholar] [CrossRef]
- Pandey, A.K.; Kumar, M. Boundary layer flow and heat transfer analysis on Cu-water nanofluid flow over a stretching cylinder with slip. Alex. Eng. J. 2017, 56, 671–677. [Google Scholar] [CrossRef]
- Siddique, I.; Salamat, N.; Hussain, S.; Abdal, S. The significance of magnetohydrodynamics Sutterby nanofluid flow with concentration depending properties across stretching/shrinking sheet and porosity. Int. J. Mod. Phys. B 2022, 36, 2250223. [Google Scholar]
- Islam, S.; Khan, A.; Kumam, P.; Alrabaiah, H.; Shah, Z.; Khan, W.; Zubair, M.; Jawad, M. Radiative mixed convection flow of maxwell nanofluid over a stretching cylinder with joule heating and heat source/sink effects. Sci. Rep. 2020, 10, 17823. [Google Scholar] [CrossRef]
- Pandey, A.K.; Kumar, M. Natural convection and thermal radiation influence on nanofluid flow over a stretching cylinder in a porous medium with viscous dissipation. Alex. Eng. J. 2017, 56, 55–62. [Google Scholar] [CrossRef] [Green Version]
- Sulochana, C.; Sandeep, N. Stagnation point flow and heat transfer behavior of Cu–water nanofluid towards horizontal and exponentially stretching/shrinking cylinders. Appl. Nanosci. 2016, 6, 451–459. [Google Scholar] [CrossRef] [Green Version]
- Ali, L.; Ali, B.; Liu, X.; Ahmed, S.; Shah, M.A. Analysis of bio-convective MHD Blasius and Sakiadis flow with Cattaneo-Christov heat flux model and chemical reaction. Chin. J. Phys. 2022, 77, 1963–1975. [Google Scholar] [CrossRef]
- Shah, J.; Ali, F.; Khan, N.; Ahmad, Z.; Murtaza, S.; Khan, I.; Mahmoud, O. MHD flow of time-fractional Casson nanofluid using generalized Fourier and Fick’s laws over an inclined channel with applications of gold nanoparticles. Sci. Rep. 2022, 12, 17364. [Google Scholar] [CrossRef] [PubMed]
- Khan, N.; Ali, F.; Arif, M.; Ahmad, Z.; Aamina, A.; Khan, I. Maxwell nanofluid flow over an infinite vertical plate with ramped and isothermal wall temperature and concentration. Math. Probl. Eng. 2021, 2021, 3536773. [Google Scholar] [CrossRef]
- Murtaza, S.; Ahmad, Z.; Ali, I.E.; Akhtar, Z.; Tchier, F.; Ahmad, H.; Yao, S.W. Analysis and Numerical Simulation of Fractal-Fractional Order Non-Linear Couple Stress Nanofluid with Cadmium Telluride Nanoparticles. J. King Saud-Univ.-Sci. 2023, 35, 102618. [Google Scholar] [CrossRef]
- Iqbal, T.; Ali, B. Finite element analysis of the impact of particles aggregation on the thermal conductivity of nanofluid under chemical reaction. Waves Random Complex Media 2023, 9, 1–21. [Google Scholar]
- Shah, N.A.; Mahsud, Y.; Aziz, M.; Tlili, I. Analytical solutions for unsteady electrohydrodynamics flows of Maxwell fluids in microchannels with circular cross section. Phys. Fluids 2020, 32, 013107. [Google Scholar] [CrossRef]
- Naz, R.; Noor, M.; Shah, Z.; Sohail, M.; Kumam, P.; Thounthong, P. Entropy generation optimization in MHD pseudoplastic fluid comprising motile microorganisms with stratification effect. Alex. Eng. J. 2020, 59, 485–496. [Google Scholar] [CrossRef]
- Mousa, H.; Ali, B.; Abd Allah, Z.; Hussain, S.; Siddique, I.; Huang, Y. Insight into significance of thermal stratification and radiation on dynamics of micropolar water based TiO2 nanoparticle via finite element simulation. J. Mater. Res. Technol. 2022, 19, 4209–4219. [Google Scholar]
- Chen, S.B.; Shahmir, N.; Ramzan, M.; Sun, Y.L.; Aly, A.A.; Malik, M. Thermophoretic particle deposition in the flow of dual stratified Casson fluid with magnetic dipole and generalized Fourier’s and Fick’s laws. Case Stud. Therm. Eng. 2021, 26, 101186. [Google Scholar] [CrossRef]
- Prasannakumara, B. Numerical simulation of heat transport in Maxwell nanofluid flow over a stretching sheet considering magnetic dipole effect. Partial Differ. Equ. Appl. Math. 2021, 4, 100064. [Google Scholar] [CrossRef]
- Shampine, L.F.; Shampine, L.F.; Gladwell, I.; Thompson, S. Solving ODEs with Matlab; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Sabu, A.S.; Areekara, S.; Mathew, A. Effects of multislip and distinct heat source on MHD Carreau nanofluid flow past an elongating cylinder using the statistical method. Heat Transf. 2021, 50, 5652–5673. [Google Scholar] [CrossRef]
- Khan, W.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Khan, I.; Ullah, S.; Malik, M.; Hussain, A. Numerical analysis of MHD Carreau fluid flow over a stretching cylinder with homogenous-heterogeneous reactions. Results Phys. 2018, 9, 1141–1147. [Google Scholar] [CrossRef]

| n | BVP5C [39] | RKF45 [39] | RK4 [39] | Current Result | ||
|---|---|---|---|---|---|---|
| 0.5 | 1 | 0.2 | 0.989702 | 0.989709 | 0.989709 | 0.989701 |
| 2 | 0.4 | 0.901331 | 0.901343 | 0.901343 | 0.901342 | |
| 3 | 0.6 | 0.830948 | 0.830972 | 0.830972 | 0.830949 | |
| 1.5 | 1 | 0.2 | 1.145708 | 1.145708 | 1.145708 | 1.145704 |
| 2 | 0.4 | 1.367059 | 1.367061 | 1.367061 | 1.367058 | |
| 3 | 0.6 | 1.611580 | 1.611585 | 1.611585 | 1.611580 |
| Pop [40] | Sabu [39] | Current Results | |
|---|---|---|---|
| 0.7 | 0.4539 | 0.453932 | 0.453933 |
| 2.0 | 0.9113 | 0.911359 | 0.911359 |
| 7.0 | 1.8954 | 1.895428 | 1.895422 |
| 20 | 3.3539 | 3.354174 | 3.354172 |
| n | M | ||||||
|---|---|---|---|---|---|---|---|
| 0.5 | 0.5 | - | - | - | 1.038195 | 0.845774 | −0.244909 |
| - | 1.5 | - | - | - | 0.875339 | 1.006156 | −0.135125 |
| - | 2.5 | - | - | - | 0.619765 | 1.119215 | 0.051506 |
| - | - | 0.1 | - | - | 0.952643 | 0.921192 | −0.275204 |
| - | - | 0.4 | - | - | 0.964925 | 0.960081 | −0.040858 |
| - | - | 0.7 | - | - | 0.977579 | 0.996118 | 0.157372 |
| - | - | - | 2 | - | 0.964925 | 0.960081 | −0.040858 |
| - | - | - | 3 | - | 0.917302 | 0.872254 | −0.006914 |
| - | - | - | 4 | - | 0.870742 | 0.808093 | 0.026700 |
| - | - | - | - | 0.2 | 0.964925 | 0.960081 | −0.040858 |
| - | - | - | - | 0.4 | 0.845168 | 0.816136 | 0.047052 |
| - | - | - | - | 0.6 | 0.718793 | 0.707215 | 0.140396 |
| 1.5 | 0.5 | - | - | - | 1.088769 | 1.082961 | −0.275481 |
| - | 1.5 | - | - | - | 0.982632 | 1.342749 | −0.208953 |
| - | 2.5 | - | - | - | 0.879563 | 1.531233 | −0.138016 |
| - | - | 0.1 | - | - | 1.028744 | 1.187827 | −0.323431 |
| - | - | 0.4 | - | - | 1.042463 | 1.295725 | −0.093998 |
| - | - | 0.7 | - | - | 1.052298 | 1.392372 | 0.104310 |
| - | - | - | 2 | - | 1.042463 | 1.295725 | −0.093998 |
| - | - | - | 3 | - | 1.047745 | 1.357226 | −0.096997 |
| - | - | - | 4 | - | 1.050866 | 1.406824 | −0.098531 |
| - | - | - | - | 0.2 | 1.042463 | 1.295725 | −0.093998 |
| - | - | - | - | 0.4 | 0.888681 | 0.987318 | 0.016635 |
| - | - | - | - | 0.6 | 0.745529 | 0.804817 | 0.121383 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, P.; Poonia, H.; Ali, L.; Shah, N.A.; Chung, J.D. Significance of Weissenberg Number, Soret Effect and Multiple Slips on the Dynamic of Biconvective Magnetohydrodynamic Carreau Nanofuid Flow. Mathematics 2023, 11, 1685. https://doi.org/10.3390/math11071685
Kumar P, Poonia H, Ali L, Shah NA, Chung JD. Significance of Weissenberg Number, Soret Effect and Multiple Slips on the Dynamic of Biconvective Magnetohydrodynamic Carreau Nanofuid Flow. Mathematics. 2023; 11(7):1685. https://doi.org/10.3390/math11071685
Chicago/Turabian StyleKumar, Pardeep, Hemant Poonia, Liaqat Ali, Nehad Ali Shah, and Jae Dong Chung. 2023. "Significance of Weissenberg Number, Soret Effect and Multiple Slips on the Dynamic of Biconvective Magnetohydrodynamic Carreau Nanofuid Flow" Mathematics 11, no. 7: 1685. https://doi.org/10.3390/math11071685
APA StyleKumar, P., Poonia, H., Ali, L., Shah, N. A., & Chung, J. D. (2023). Significance of Weissenberg Number, Soret Effect and Multiple Slips on the Dynamic of Biconvective Magnetohydrodynamic Carreau Nanofuid Flow. Mathematics, 11(7), 1685. https://doi.org/10.3390/math11071685







