Fuzzy Discretization on the Multinomial Naïve Bayes Method for Modeling Multiclass Classification of Corn Plant Diseases and Pests
Abstract
:1. Introduction
2. Related Work
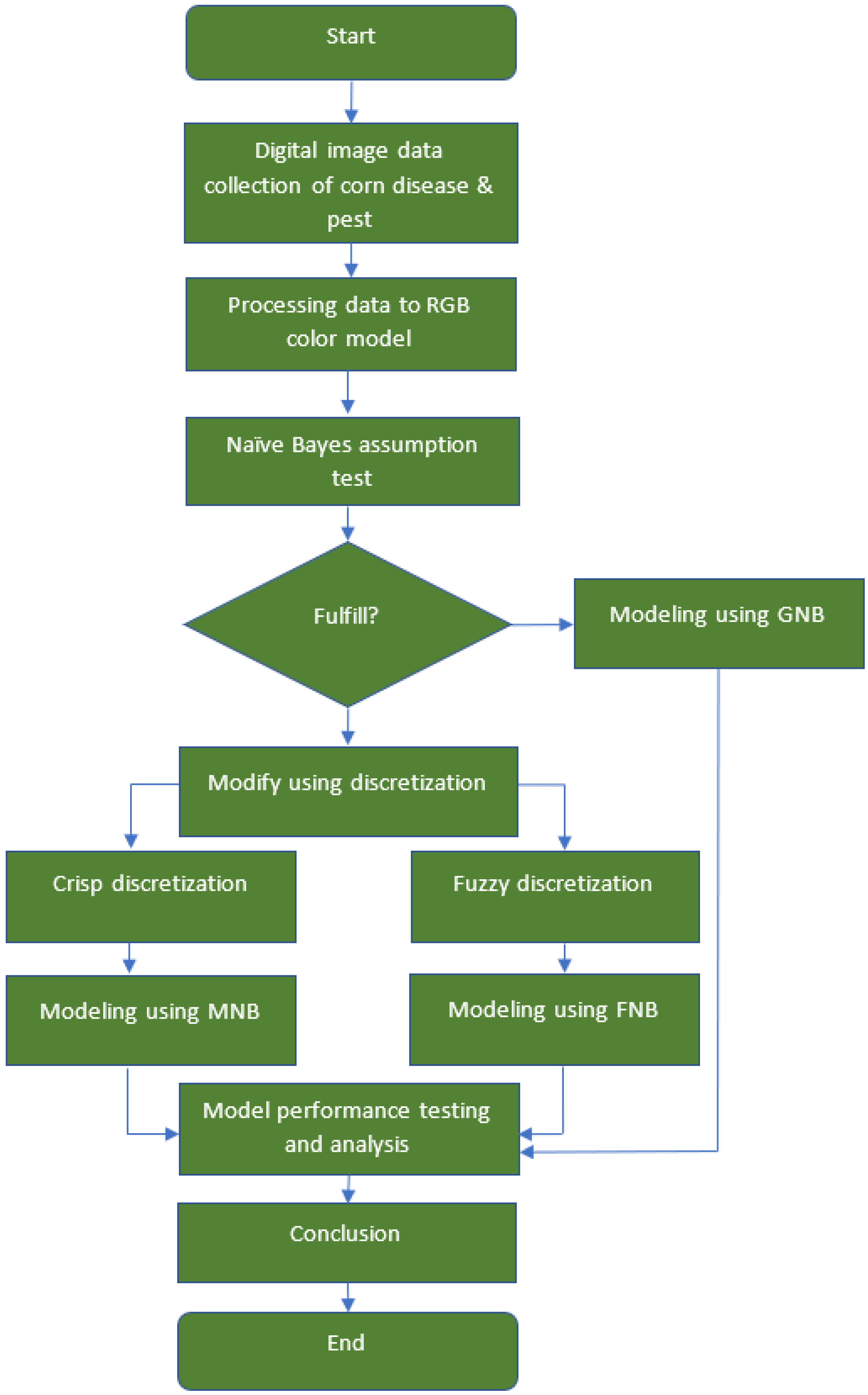
3. Materials and Methods
3.1. Crisp and Fuzzy Discretization
3.2. Type of Fuzzy Membership Function
3.3. Multinomial Naïve Bayes
4. Empirical Application
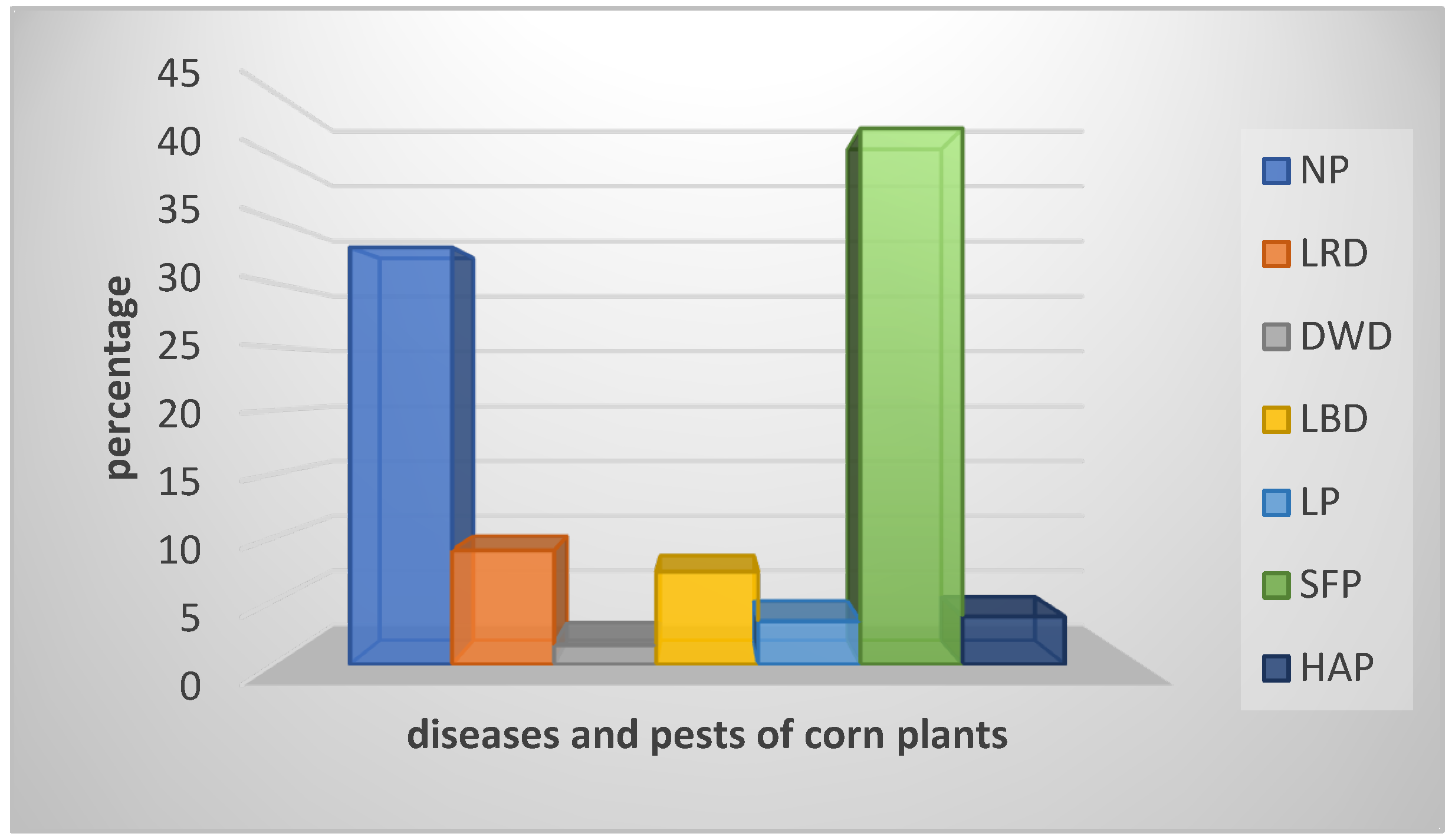
4.1. Description and Exploration of Dataset
4.2. Modelings
4.3. Result and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Q.; Huang, M. Rough fuzzy model based feature discretization in intelligent data preprocess. J. Cloud Comput. 2021, 10, 5. [Google Scholar] [CrossRef]
- Roy, A.; Pal, S.K. Fuzzy discretization of feature space for a rough set classifier. Pattern Recognit. Lett. 2003, 24, 895–902. [Google Scholar] [CrossRef]
- Shanmugapriya, M.; Nehemiah, H.K.; Bhuvaneswaran, R.S.; Arputharaj, K.; Sweetlin, J.D. Fuzzy Discretization based Classification of Medical Data. Res. J. Appl. Sci. Eng. Technol. 2017, 14, 291–298. [Google Scholar] [CrossRef]
- Algehyne, E.A.; Jibril, M.L.; Algehainy, N.A.; Alamri, O.A.; Alzahrani, A.K. Fuzzy Neural Network Expert System with an Improved Gini Index Random Forest-Based Feature Importance Measure Algorithm for Early Diagnosis of Breast Cancer in Saudi Arabia. Big Data Cogn. Comput. 2022, 6, 13. [Google Scholar] [CrossRef]
- Fernandez, S.; Ito, T.; Cruz-Piris, L.; Marsa-Maestre, I. Fuzzy Ontology-Based System for Driver Behavior Classification. Sensors 2022, 22, 7954. [Google Scholar] [CrossRef]
- Eftekhari, M.; Mehrpooya, A.; Farid, S.-M.; Vicenc, T. How Fuzzy Concepts Contribute to Machine Learning; Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Chen, H.L.; Hu, Y.C.; Lee, M.Y. Evaluating appointment of division managers using fuzzy multiple attribute decision making. Mathematics 2021, 9, 2417. [Google Scholar] [CrossRef]
- Altay, A.; Cinar, D. Fuzzy decision trees. In Studies in Fuzziness and Soft Computing, 1st ed.; Springer: Cham, Switzerland, 2016; pp. 221–261. [Google Scholar] [CrossRef]
- Resti, Y.; Irsan, C.; Amini, M.; Yani, I.; Passarella, R.; Zayanti, D.A. Performance Improvement of Decision Tree Model using Fuzzy Membership Function for Classification of Corn Plant Diseases and Pests. Sci. Technol. Indones. 2022, 7, 284–290. [Google Scholar] [CrossRef]
- Femina, B.T.; Sudheep, E.M. A Novel Fuzzy Linguistic Fusion Approach to Naive Bayes Classifier for Decision Making Applications. Int. J. Adv. Sci. Eng. Inf. Technol. 2020, 10, 1889–1897. [Google Scholar] [CrossRef]
- Resti, Y.; Burlian, F.; Yani, I.; Zayanti, D.A.; Sari, I.M. Improved the Cans Waste Classification Rate of Naive Bayes using Fuzzy Approach. Sci. Technol. Indones. 2020, 5, 75–78. [Google Scholar] [CrossRef]
- Yazgi, T.G.; Necla, K. An Aggregated Fuzzy Naive bayes Data Classifier. J. Comput. Appl. Math. 2015, 286, 17–27. Available online: https://www.ptonline.com/articles/how-to-get-better-mfi-results (accessed on 12 December 2022).
- Sadollah, A. Introductory Chapter: Which Membership Function is Appropriate in Fuzzy System? In Fuzzy Logic Based in Optimization Methods and Control Systems and Its Applications; InTechOpen: London, UK, 2018; pp. 3–6. [Google Scholar] [CrossRef] [Green Version]
- Resti, Y.; Irsan, C.; Putri, M.T.; Yani, I.; Anshori; Suprihatin, B. Identification of Corn Plant Diseases and Pests Based on Digital Images using Multinomial Naïve Bayes and K-Nearest Neighbor. Sci. Technol. Indones. 2022, 7, 29–35. [Google Scholar] [CrossRef]
- Panigrahi, K.P.; Das, H.; Sahoo, A.K.; Moharana, C.S. Maize Leaf Disease Detection and Classification Using Machine Learning Algorithms; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Kusumo, B.S.; Heryana, A.; Mahendra, O.; Pardede, H.F. Machine Learning-based for Automatic Detection of Corn-Plant Diseases Using Image Processing. In Proceedings of the 2018 International Conference on Computer, Control, Informatics and its Applications (IC3INA), Tangerang, Indonesia, 1–2 November 2018; pp. 93–97. [Google Scholar] [CrossRef]
- Syarief, M.; Setiawan, W. Convolutional neural network for maize leaf disease image classification. Telkomnika Telecommun. Comput. Electron. Control. 2020, 18, 1376–1381. [Google Scholar] [CrossRef]
- Sibiya, M.; Sumbwanyambe, M. A Computational Procedure for the Recognition and Classification of Maize Leaf Diseases Out of Healthy Leaves Using Convolutional Neural Networks. AgriEngineering 2019, 1, 119–131. [Google Scholar] [CrossRef] [Green Version]
- Haque, M.A.; Marwaha, S.; Deb, C.K.; Nigam, S.; Arora, A.; Hooda, K.S.; Soujanya, P.L.; Aggarwal, S.K.; Lall, B.; Kumar, M.; et al. Deep learning-based approach for identification of diseases of maize crop. Sci. Rep. 2022, 12, 1–14. [Google Scholar] [CrossRef]
- Xian, T.S.; Ngadiran, R. Plant Diseases Classification using Machine Learning. J. Phys. Conf. Ser. 2021, 1962, 1–12. [Google Scholar] [CrossRef]
- Ngugi, L.C.; Abelwahab, M.; Abo-Zahhad, M. Recent Advances in Image Processing Techniques for Automated Leaf Pest an Diseas Recognition—A Review. Inf. Process. Agric. 2021, 8, 27–51. [Google Scholar] [CrossRef]
- Domingues, T.; Brandão, T.; Ferreira, J.C. Machine Learning for Detection and Prediction of Crop Diseases and Pests: A Comprehensive Survey. Agriculture 2022, 12, 1350. [Google Scholar] [CrossRef]
- Kasinathan, T.; Singaraju, D.; Sriniuasulu, R.U. Insect classification and detection in field crops using modern machine learning techniques. Inf. Process. Agric. 2021, 8, 446–457. [Google Scholar] [CrossRef]
- Almadhor, A.; Rauf, H.T.; Lali, M.I.U.; Damaševičius, R.; Alouffi, B.; Alharbi, A. Ai-driven framework for recognition of guava plant diseases through machine learning from dslr camera sensor based high resolution imagery. Sensors 2021, 21, 3830. [Google Scholar] [CrossRef]
- Hossain, E.; Hossain, M.F.; Rahaman, M.A. A Color and Texture Based Approach for the Detection and Classification of Plant Leaf Disease Using KNN Classifier. In Proceedings of the 2019 International Conference on Electrical, Computer and Communication Engineering (ECCE), Cox’sBazar, Bangladesh, 7–9 February 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Rajesh, B.; Vardhan, M.V.S.; Sujihelen, L. Leaf Disease Detection and Classification by Decision Tree. In Machine Learning Foundations; Springer: Cham, Switzerland, 2020; pp. 141–165. [Google Scholar] [CrossRef]
- AAgghey, Z.; Mwinuka, L.J.; Pandhare, S.M.; Dida, M.A.; Ndibwile, J.D. Detection of username enumeration attack on ssh protocol: Machine learning approach. Symmetry 2021, 13, 2192. [Google Scholar] [CrossRef]
- Akbar, F.; Hussain, M.; Mumtaz, R.; Riaz, Q.; Wahab, A.W.A.; Jung, K.H. Permissions-Based Detection of Android Malware Using Machine Learning. Symmetry 2022, 14, 718. [Google Scholar] [CrossRef]
- Hsu, S.C.; Chen, I.C.; Huang, C.L. Image classification using naive bayes classifier with pairwise local observations. J. Inf. Sci. Eng. 2017, 33, 1177–1193. [Google Scholar] [CrossRef]
- Pan, Y.; Gao, H.; Lin, H.; Liu, Z.; Tang, L.; Li, S. Identification of bacteriophage virion proteins using multinomial Naïve bayes with g-gap feature tree. Int. J. Mol. Sci. 2018, 19, 1779. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Daniele, S.; Jonathan, M.G.; Federico, A.; Biganzoli, E.M.; Ian, O.E. A Non-parametric Version of the Naive Bayes Classifier. Knowl. Based Syst. 2011, 24, 775–784. [Google Scholar] [CrossRef] [Green Version]
- Mazhar, T.; Malik, M.A.; Nadeem, M.A.; Mohsan, S.A.H.; Haq, I.; Karim, F.K.K.; Mostafa, S.M.M. Movie Reviews Classification through Facial Image Recognition and Emotion Detection Using Machine Learning Methods. Symmetry 2022, 14, 2607. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Cham, Switzerland, 2013. [Google Scholar] [CrossRef]
- Bae, J.-H.; Yu, G.-H.; Lee, J.-H.; Vu, D.T.; Anh, L.H.; Kim, H.-G.; Kim, J.-Y. Superpixel Image Classification with Graph Convolutional Neural Networks Based on Learnable Positional Embedding. Appl. Sci. 2022, 12, 9176. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, J.J.; Li, R. Enhanced Unsupervised Graph Embedding via Hierarchical Graph Convolution Network. Math. Probl. Eng. 2020, 2020, 5702519. [Google Scholar] [CrossRef]
- Yu, D.; Yang, Y.; Zhang, R.; Wu, Y. Knowledge embedding based graph convolutional network. In Proceedings of the WWW’21: The Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 1619–1628. [Google Scholar] [CrossRef]
- Giordano, M.; Maddalena, L.; Manzo, M.; Guarracino, M.R. Adversarial attacks on graph-level embedding methods: A case study. Ann. Math. Artif. Intell. 2022. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, J.; Zhang, Y.; Wu, H.; Zhao, C.; Teng, G.; Li, J. A Plant Disease Recognition Method Based on Fusion of Images and Graph Structure Text. Front. Plant Sci. 2022, 12, 1–12. [Google Scholar] [CrossRef]
- Hudec, M. Fuzziness in Information Systems: How to Deal with Crisp and Fuzzy Data in Selection, Classification, and Summarization, 1st ed.; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef] [Green Version]
- Yunus, M. Optimasi Penentuan Nilai Parameter Himpunan Fuzzy dengan Teknik Tuning System. MATRIK J. Manajemen Tek. Inform. dan Rekayasa Komput. 2018, 18, 21–28. [Google Scholar] [CrossRef]
- Resti, Y.; Kresnawati, E.S.; Dewi, N.R.; Zayanti, D.A.; Eliyati, N. Diagnosis of diabetes mellitus in women of reproductive age using the prediction methods of naive bayes, discriminant analysis, and logistic regression. Sci. Technol. Indones. 2021, 6, 96–104. [Google Scholar] [CrossRef]
- Lee, C.F.; Tzeng, G.H.; Wang, S.Y. A new application of fuzzy set theory to the Black-Scholes option pricing model. Expert Syst. Appl. 2005, 29, 330–342. [Google Scholar] [CrossRef]
- Dinesh, S.; Dash, T. Reliable Evaluation of Neural Network for Multiclass Classification of Real-world Data. arXiv 2016, arXiv:1612.00671. [Google Scholar]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Ramasubramanian, K.; Singh, A. Machine Learning Using R With Time Series and Industry-Based Use Cases in R, 2nd ed.; Apress: New Delhi, India, 2019. [Google Scholar] [CrossRef]
- De Diego, I.M.; Redondo, A.R.; Fernández, R.R.; Navarro, J.; Moguerza, J.M. General Performance Score for classification problems. Appl. Intell. 2022, 52, 12049–12063. [Google Scholar] [CrossRef]
- Lubis, A.A.N.; Anwar, R.; Soekarno, B.P.; Istiaji, B.; Dewi, S.; Herawati, D. Serangan Ulat Grayak Jagung (Spodoptera frugiperda) pada Tanaman Jagung di Desa Petir, Kecamatan Daramaga, Kabupatem Bogor dan Potensi Pengendaliannya Menggunakan Metarizhium Rileyi. J. Pus. Inov. Masyarkat 2020, 2, 931–939. [Google Scholar]
- Firmansyah, E.; Ramadhan, R.A.M. Tingkat serangan Spodoptera frugiperda J.E. Smith pada pertanaman jagung di Kota Tasikmalaya dan perkembangannya di laboratorium. Agrovigor J. Agroekoteknologi 2021, 14, 87–90. [Google Scholar] [CrossRef]
- Székely, G.J.; Rizzo, M.L. A new test for multivariate normality. J. Multivar. Anal. 2005, 93, 58–80. [Google Scholar] [CrossRef] [Green Version]
- Resti, Y.; Desi, H.S.; Zayanti, D.A.; Eliyati, N. Classification of Diseases Aand Pests Of Maize using Multinomial Logistic Regression Based on Resampling Technique of K-Fold Cross-Validation. Indones. J. Eng. Sci. 2022, 3, 69–76. [Google Scholar] [CrossRef]

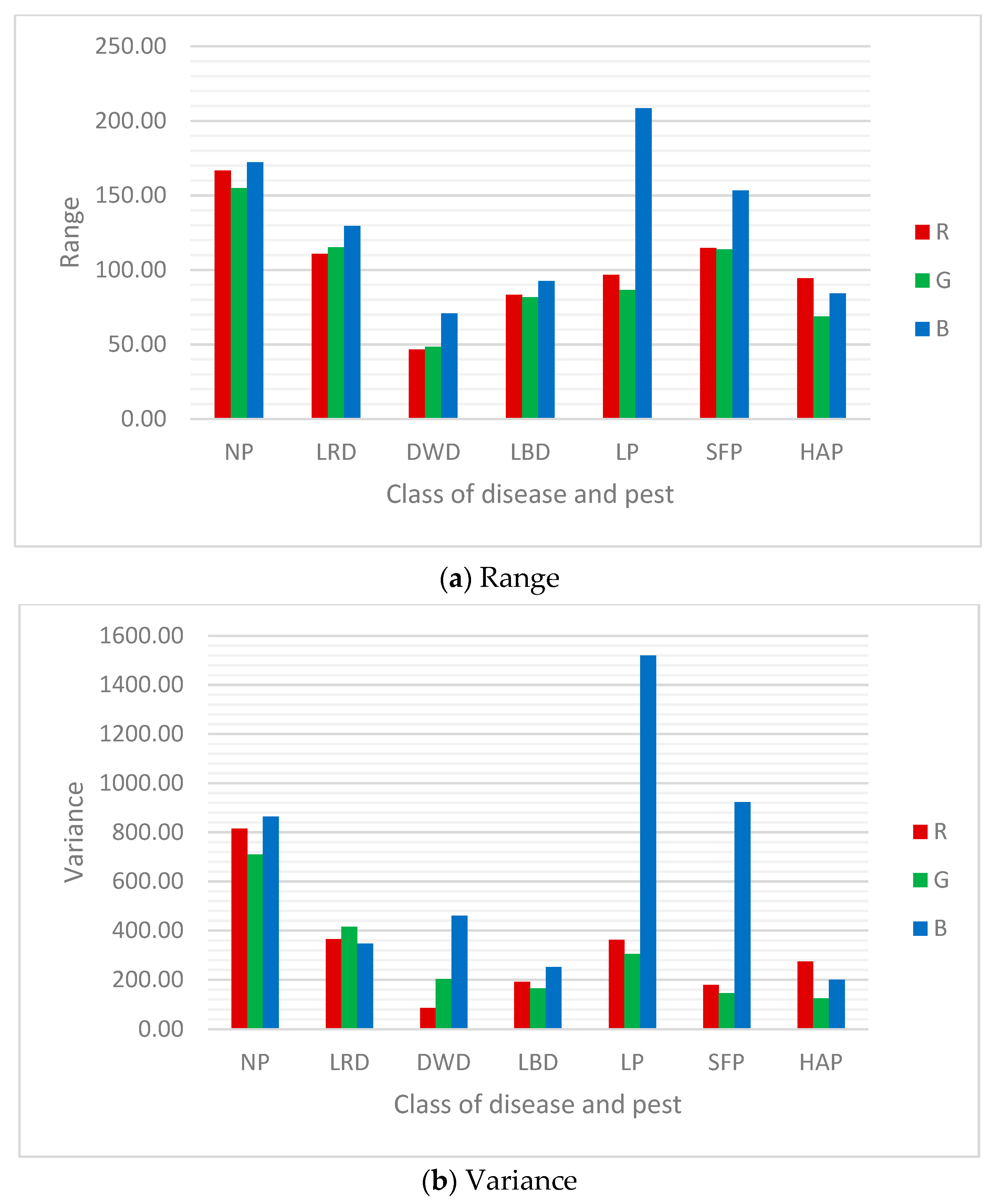
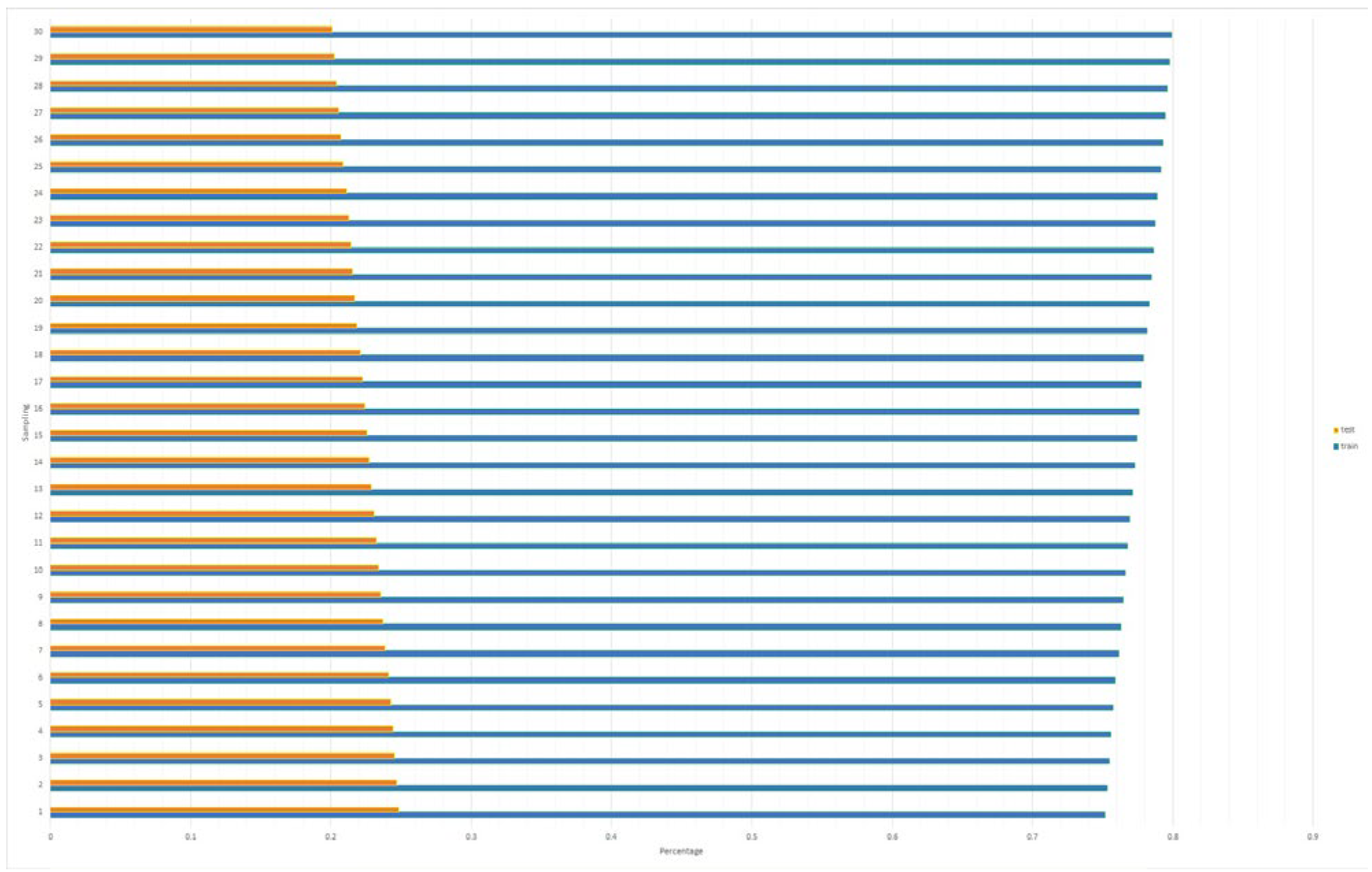
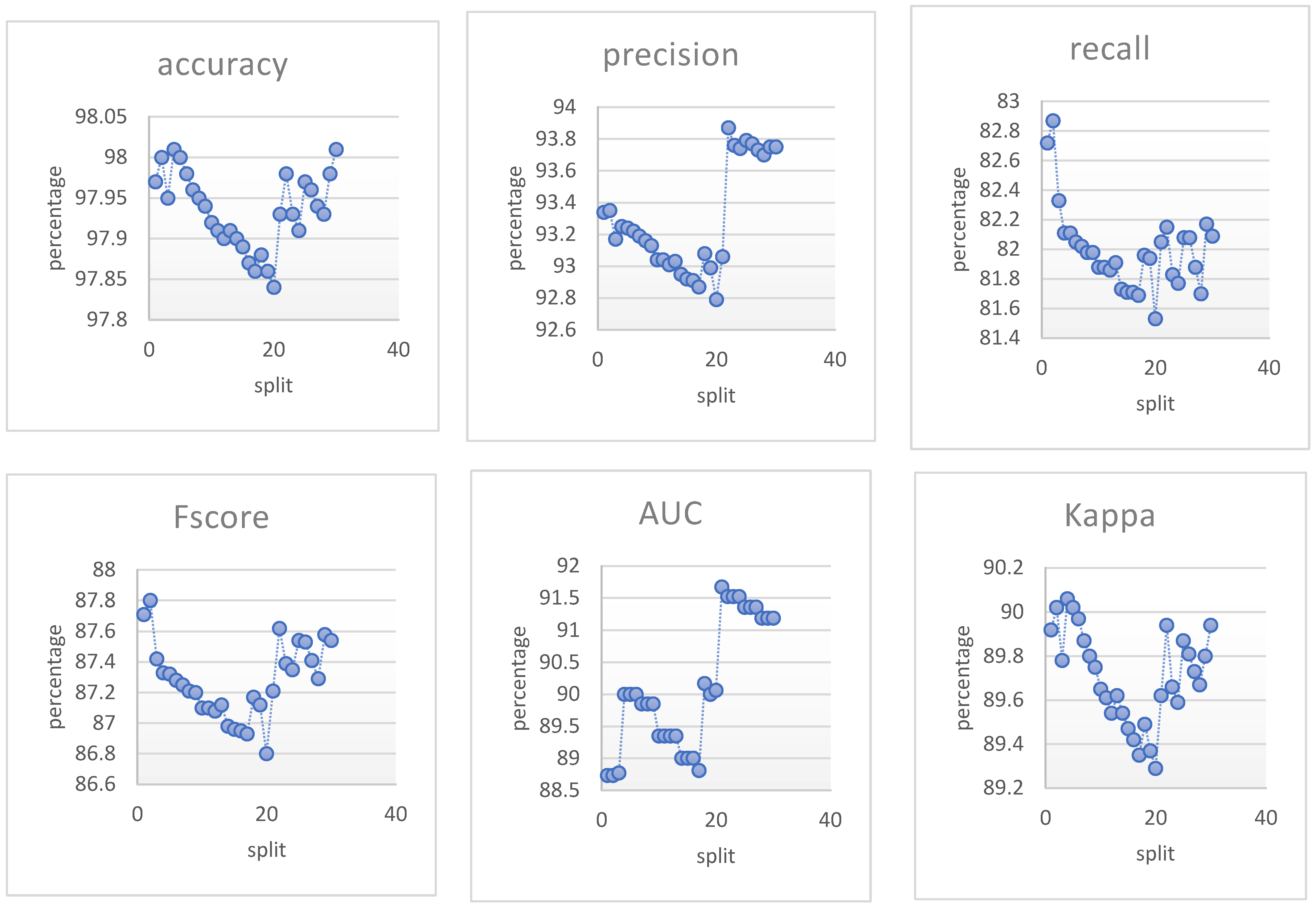
| Class | Mean of Pixel Value in Channel | Std. Dev. of Pixel Value in Channel | ||||
|---|---|---|---|---|---|---|
| Red | Green | Blue | Red | Green | Blue | |
| NP | 129.13 | 157.58 | 118.20 | 28.55 | 26.63 | 29.39 |
| LRD | 125.19 | 134.25 | 102.63 | 19.10 | 20.38 | 18.61 |
| DWD | 152.88 | 146.40 | 51.40 | 9.26 | 14.24 | 21.46 |
| LBD | 117.03 | 122.94 | 101.62 | 13.81 | 12.83 | 15.87 |
| LP | 195.71 | 199.24 | 134.67 | 19.01 | 17.46 | 38.97 |
| SFP | 120.58 | 150.04 | 64.54 | 13.36 | 12.04 | 30.37 |
| HAP | 163.26 | 149.15 | 89.35 | 16.53 | 11.16 | 14.12 |
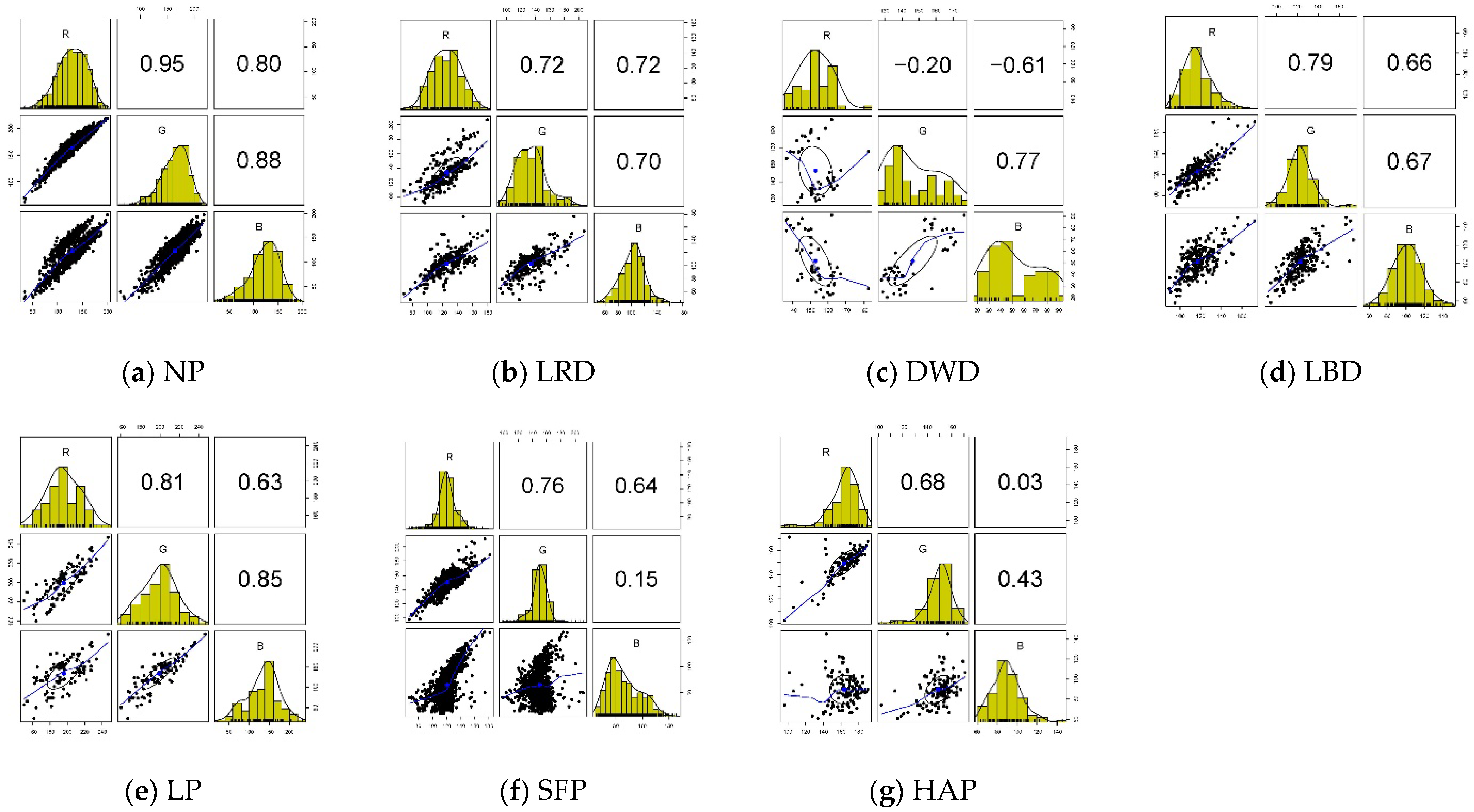
| Henze-Zirkler Test | Class of Corn Diseases and Pests | ||||||
|---|---|---|---|---|---|---|---|
| LRD | DWD | LBD | LP | SFP | HAP | NP | |
| Statistic | 5.55 | 1.67 | 1.89 | 2.31 | 11.68 | 4.49 | 18.89 |
| p-value | 0.00 | 7.2 × 10−6 | 2.56 × 10−7 | 1.64 × 10−9 | 0.00 | 0.00 | 0.00 |
| 1 | [32.77, 75.55] | [63.00, 99.70] | [12.18, 56.11] |
| 2 | [75.56, 118.34] | [99.71, 136.40] | [56.12, 100.03] |
| 3 | [118.35, 161.12] | [136.41, 173.10] | [100.04, 143.95] |
| 4 | [161.13, 203.90] | [173.11, 209.80] | [143.96, 187.87] |
| 5 | [203.91, 246.68] | [209.81, 246.50] | [187.88, 231.80] |
| Model | ||||
|---|---|---|---|---|
| FMNB1 | 1 | [32.77, 57.64, 85.55] | [63.00, 83.41, 109.70] | [12.18, 34.74, 66.11] |
| 2 | [72.64, 66.54, 128.34] | [93.41, 118.42, 146.40] | [49.74, 74.79, 110.03] | |
| 3 | [102.64, 137.62, 171.12] | [131.45, 156.43, 183.10] | [89.79, 119.80, 153,95] | |
| 4 | [152.64,181.60, 213.90] | [168.47, 188.46,, 219.80] | [134.81, 167,81, 197.87] | |
| 5 | [206.02, 220.04, 246.68] | [175.20, 189.23, 246.50] | [192.29, 206.33,231.80] | |
| FMNB2 | 1 | [32.77,44.77, 62.77, 90.55] | [63.00, 78.00, 93.00, 114.70] | [12.18, 27.17, 42.18, 71.11] |
| 2 | [55.77, 75.76, 97.77, 133.34] | [86.00, 106.00, 128.00, 151.40] | [35.18,55.16, 77.18, 115.03] | |
| 3 | [83.77, 103.76, 125.77, 176.12] | [114.00, 106.00, 128.00, 188.10] | [63.18, 83.17, 105.17, 158.95] | |
| 4 | [111.76, 131.77, 153.76, 218.90] | [142.00, 162.00, 184.01, 224.80] | [91.18, 111.17, 133.18, 202.87] | |
| 5 | [139.77, 159.76, 181.76, 246.68] | [170.00, 190.02, 212.01, 246.50] | [119.18, 139.17, 161.16, 231.80] | |
| FMNB3 | 1 | [32.77, 88.64] | [63.00, 113.41] | [12.18, 66.74] |
| 2 | [51.54, 93.06, 135.57] | [65.10,92.09, 155.08] | [30.03, 78.91, 120.79] | |
| 3 | [114.00, 127.85, 174.68] | [105.37, 153.79, 195.21] | [80.10, 125.17, 160.24] | |
| 4 | [143.11,150.44, 225.77] | [164.28, 179.19, 200.09] | [145.19, 182.06, 198.93] | |
| 5 | [206.02, 220.04, 246.68] | [175.20, 246.50] | [192.29, 231.80] | |
| FMNB4 | 1 | [32.77, 88.64] | [63.00, 113.41] | [12.18, 66.74] |
| 2 | [96.64, 116.64, 138.63, 133.34] | [121.41, 141.42, 163.44, 151.40] | [74.74, 94.70, 116.73, 115.03] | |
| 3 | [124.64, 144.63, 166.62, 176.12] | [149.41, 169.44, 169.42, 188.10] | [102.74, 122.72, 144.70, 158.95] | |
| 4 | [152.64, 172.62, 194.64, 218.90] | [177.41, 197.42, 219.40, 224.80] | [130.74, 150.72, 172.71, 202.87] | |
| 5 | [206.02, 246.68] | [175.20, 246.50] | [192.29, 231.80] | |
| FMNB5 | 1 | [32.77, 60.64, 88.50] | [63.00, 82.41, 101.81] | [12.18, 43.74, 75.30] |
| 2 | [71.54, 96.06, 120.57] | [85.10, 115.09, 145.08] | [56.03, 87.91, 119.79] | |
| 3 | [109.00, 127.85, 146.68] | [109.37, 137.79, 166.21] | [99.10, 128.17, 157.24] | |
| 4 | [131.11, 166.44, 201.77] | [135.28, 171.19, 207.09] | [143.19, 171.06, 198.93] | |
| 5 | [170.02, 208.35, 246.68] | [169.20, 207.85, 246.50] | [187.29, 209.55, 231.80] | |
| FMNB6 | 1 | [32.77, 60.64, 88.50] | [63.00, 82.41, 101.81] | [12.18, 43.74, 75.30] |
| 2 | [71.54, 87.50, 106.15, 120.57] | [85.10, 109.55, 126.18, 145.08] | [56.03, 68.62, 87.58, 119.79] | |
| 3 | [109.00, 126.41, 139.04, 146.68] | [109.37, 146.44, 163.07, 166.21] | [99.10, 112.51, 131.47, 157.24] | |
| 4 | [131.11, 150.30, 181.93, 201.77] | [135.28, 183.33, 199.96, 207.09] | [137.44, 156.40, 175.36, 194.33] | |
| 5 | [170.02, 208.35, 246.68] | [169.20, 207.85, 246.50] | [187.29, 209.55, 231.80] | |
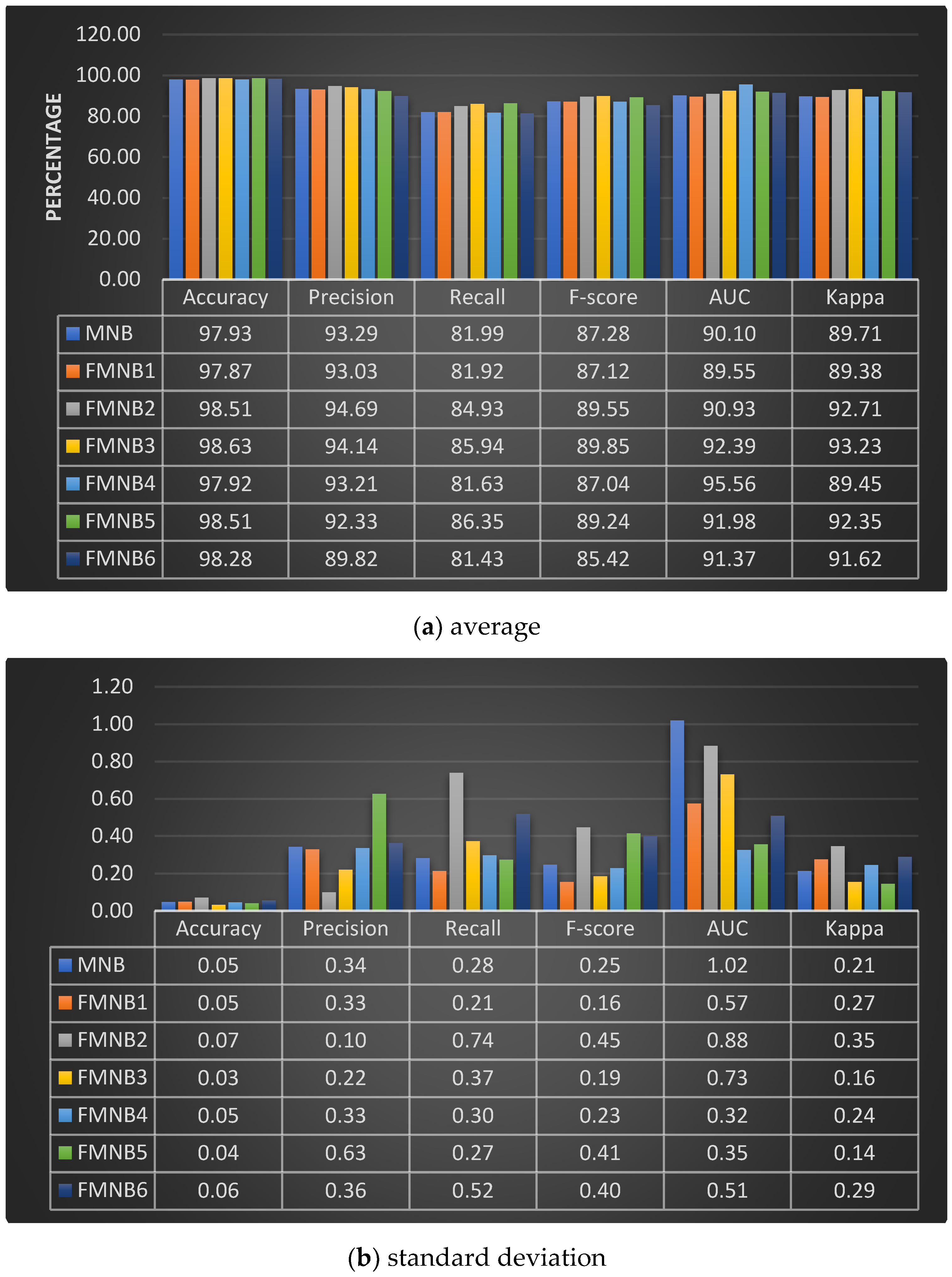
| Metrics | Source of Var. | Sum of Squares | Mean Squares | F | p-Value | F-Criteria |
|---|---|---|---|---|---|---|
| Accuracy | between | 9.14 | 2.29 | 876.63 | 2 × 10−100 | 2.43 |
| within | 0.38 | 0.00 | ||||
| Precision | between | 441.47 | 110.37 | 790.85 | 2.37 × 10−97 | |
| within | 20.24 | 0.14 | ||||
| Recall | between | 621.85 | 155.46 | 703.45 | 7.73 × 10−94 | |
| within | 32.05 | 0.22 | ||||
| Fscore | between | 425.96 | 106.49 | 853.80 | 1.2 × 10−99 | |
| within | 18.08 | 0.12 | ||||
| AUC | between | 96.41 | 24.10 | 44.09 | 3.57 × 10−24 | |
| within | 79.27 | 0.55 | ||||
| Kappa | between | 225.68 | 56.42 | 962.04 | 3 × 10−103 | |
| within | 8.50 | 0.06 |
| Comparison Model | Absolute Mean Difference | |||||
|---|---|---|---|---|---|---|
| Accuracy | Precision | Recall | Fscore | AUC | Kappa | |
| MNB vs. FMNB2 | 0.57 | 1.41 | 2.94 | 2.27 | 0.83 | 3.01 |
| MNB vs. FMNB3 | 0.70 | 0.85 | 3.95 | 2.57 | 2.29 | 3.52 |
| MNB vs. FMNB5 | 0.57 | 0.96 | 4.36 | 1.96 | 1.88 | 2.65 |
| MNB vs. FMNB6 | 0.35 | 3.47 | 0.57 | 1.86 | 1.27 | 1.91 |
| FMNB2 vs. FMNB3 | 0.12 | 0.56 | 1.01 | 0.31 | 1.46 | 0.52 |
| FMNB2 vs. FMNB3 | 0.00 | 2.36 | 1.42 | 0.31 | 1.05 | 0.36 |
| FMNB2 vs. FMNB3 | 0.23 | 4.88 | 3.50 | 4.13 | 0.44 | 1.09 |
| FMNB3 vs. FMNB5 | 0.12 | 1.81 | 0.41 | 0.61 | 0.41 | 0.88 |
| FMNB3 vs. FMNB6 | 0.35 | 4.32 | 4.51 | 4.43 | 1.02 | 1.61 |
| FMNB5 vs. FMNB6 | 0.23 | 2.51 | 4.92 | 3.82 | 0.61 | 0.73 |
| Prediction Method/ Dataset/Number of Class | Combination of Fuzzy Membership Functions | Performance of Original Model (%) | Performance of Fuzzy Approach Model (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Accu | Prec | Rec | Spec | Accu | Prec | Rec | Spec | ||
| NN-RF/breast cancer SA/two (Algehyne et al. [4]) | all trapezoidal | 95.61 | - | 88.45 | 93.56 | 99.33 | - | 99.41 | 99.24 |
| GA/driver behavior (Fernandez et al. [5]) | linear and triangular trapezoidal (only for age) | - | - | - | - | - | 82.00 | 87.00 | - |
| DTID3/Corn Diseases and Pests (Resti et al. [9]) | S and triangular | 94.53 | 84.31 | 83.07 | 96.72 | 97.76 | 89.83 | 94.87 | 98.66 |
| NB/ Heart Disease Status (Femina and Sudheep [10]) | all triangular | 87.60 | - | 88.63 | 79.10 | 91.63 | - | 92.68 | 90.19 |
| NB/ Types of Cans Waste (Resti et al. [11]) | linear and triangular | 50.26 | - | - | - | 85.19 | - | - | - |
| NB/heart disease (Yazgi and Necla [12]) | all trapezoidal | 74.00 | - | - | - | 81.50 | - | - | - |
| Proposed method | linear and triangular | 97.93 | 93.29 | 81.99 | 98.79 | 98.63 | 94.14 | 85.94 | 99.21 |
| Paper | No of Class | No of Obs. | Evaluation Method | Classification Method | Performance Metric (%) | |||
|---|---|---|---|---|---|---|---|---|
| Accu | Prec | Rec | Fscore | |||||
| Panigrahi et al. [15] | 2 | 3823 | Hold out with a ratio of 90:10 | DT | 74.35 | - | 75.00 | 75.00 |
| KNN | 76.16 | - | 75.00 | 76.00 | ||||
| NB | 77.46 | - | 78.00 | 75.50 | ||||
| SVM | 77.56 | - | 78.50 | 78.50 | ||||
| RF | 79.23 | - | 79.00 | 81.50 | ||||
| Kusumo et al. [16] | 4 | 3852 | 10-CV | DT | 77.00 | - | - | - |
| NB | 78.00 | - | - | - | ||||
| RF | 88.00 | - | - | - | ||||
| SVML | 89.00 | - | - | - | ||||
| SVMR | 87.00 | - | - | - | ||||
| Sibiya and Sumbwanyambe [18] | 4 | 100 | Hold out with a ratio of 70:30 | CNN | 92.85 | - | - | - |
| Haque [19] | 4 | 5939 | Hold out with a ratio of 70:30 | CNN | 95.71 | - | - | - |
| Syarief and Setiawan [17] | 4 | 200 | 10-CV | DT | 83.30 | - | 83.58 | - |
| KNN | 93.30 | - | 94.72 | - | ||||
| SVM | 93.50 | - | 95.08 | - | ||||
| Resti et al. [14] | 6 | 761 | Hold out with a ratio of 80:20 | MNB | 92.72 | 79.88 | 79.24 | 78.17 |
| KNN | 98.54 | 88.57 | 94.38 | 93.59 | ||||
| Resti et al. [9] | 6 | 761 | 10-CV | DT | 94.53 | 84.31 | 83.07 | 83.58 |
| FDT | 97.76 | 89.39 | 94.87 | 93.29 | ||||
| Resti et al. [50] | 7 | 4616 | 5-CV | LR | 99.85 | 98.59 | 98.15 | 98.37 |
| Proposed Method | 7 | 3172 | Monte Carlo | MNB | 97.93 | 93.29 | 81.99 | 87.28 |
| FNB3 | 98.63 | 94.14 | 85.94 | 89.95 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Resti, Y.; Irsan, C.; Neardiaty, A.; Annabila, C.; Yani, I. Fuzzy Discretization on the Multinomial Naïve Bayes Method for Modeling Multiclass Classification of Corn Plant Diseases and Pests. Mathematics 2023, 11, 1761. https://doi.org/10.3390/math11081761
Resti Y, Irsan C, Neardiaty A, Annabila C, Yani I. Fuzzy Discretization on the Multinomial Naïve Bayes Method for Modeling Multiclass Classification of Corn Plant Diseases and Pests. Mathematics. 2023; 11(8):1761. https://doi.org/10.3390/math11081761
Chicago/Turabian StyleResti, Yulia, Chandra Irsan, Adinda Neardiaty, Choirunnisa Annabila, and Irsyadi Yani. 2023. "Fuzzy Discretization on the Multinomial Naïve Bayes Method for Modeling Multiclass Classification of Corn Plant Diseases and Pests" Mathematics 11, no. 8: 1761. https://doi.org/10.3390/math11081761
APA StyleResti, Y., Irsan, C., Neardiaty, A., Annabila, C., & Yani, I. (2023). Fuzzy Discretization on the Multinomial Naïve Bayes Method for Modeling Multiclass Classification of Corn Plant Diseases and Pests. Mathematics, 11(8), 1761. https://doi.org/10.3390/math11081761








