Efficient Solution of Burgers’, Modified Burgers’ and KdV–Burgers’ Equations Using B-Spline Approximation Functions
Abstract
:1. Introduction
2. B-Spline Basis
- is a polynomial of degree on .
- .
- The sum of the basis functions are identical unity or .
- Each on .
- Each basis function has one maximum value, except in the case of .
3. Quadratic Basis and Orthogonal Collocation on Finite Elements
Numerical Example
4. Application to Burgers’ Equation
5. Application of Quazilinearization to Burgers’ Equation
6. Stability of the Quadratic B-Spline Collocation Method
7. Convergence of the Method
8. Numerical Examples and Simulations for Burgers’ Equation
- 1.
- 2.
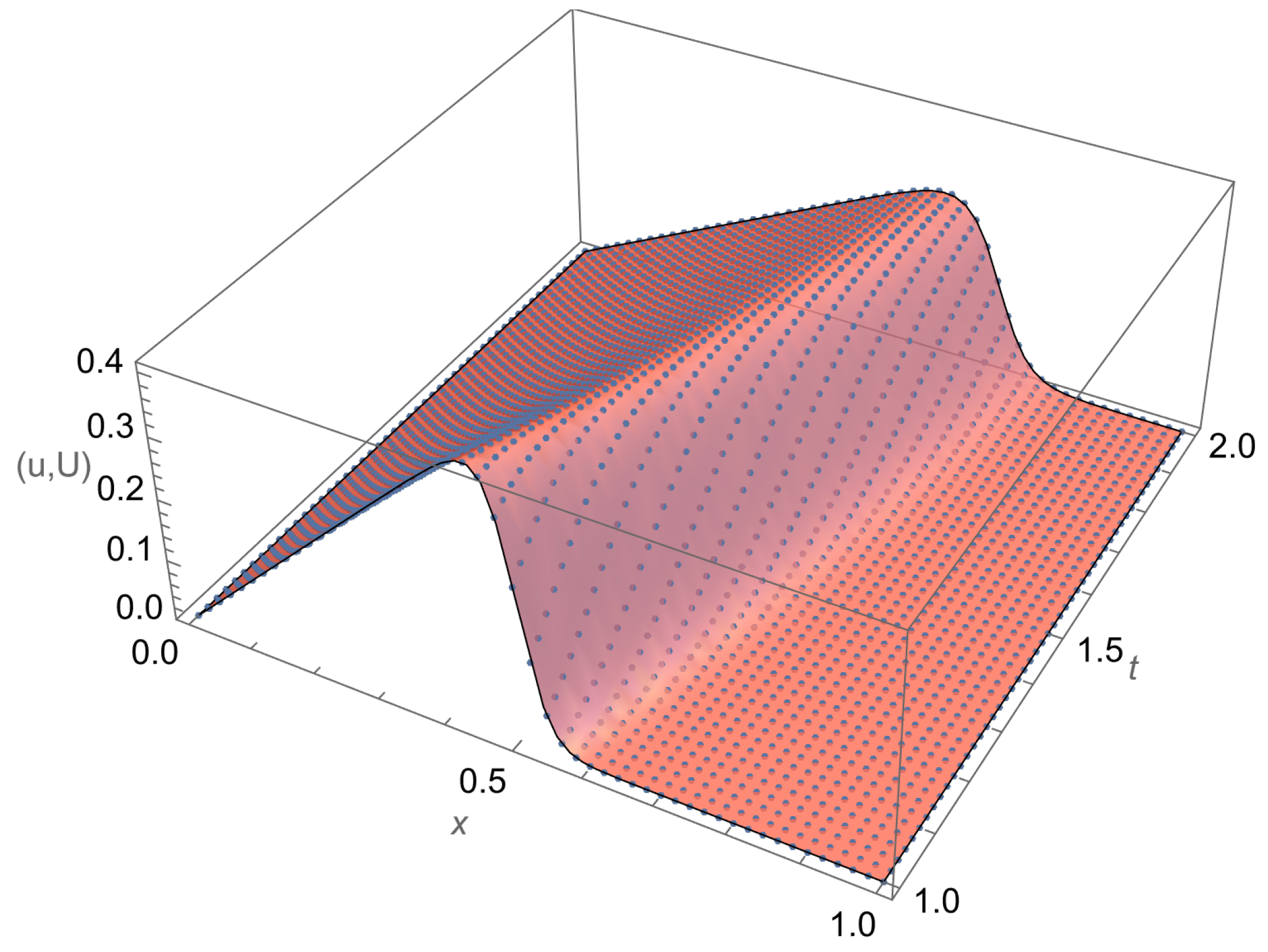
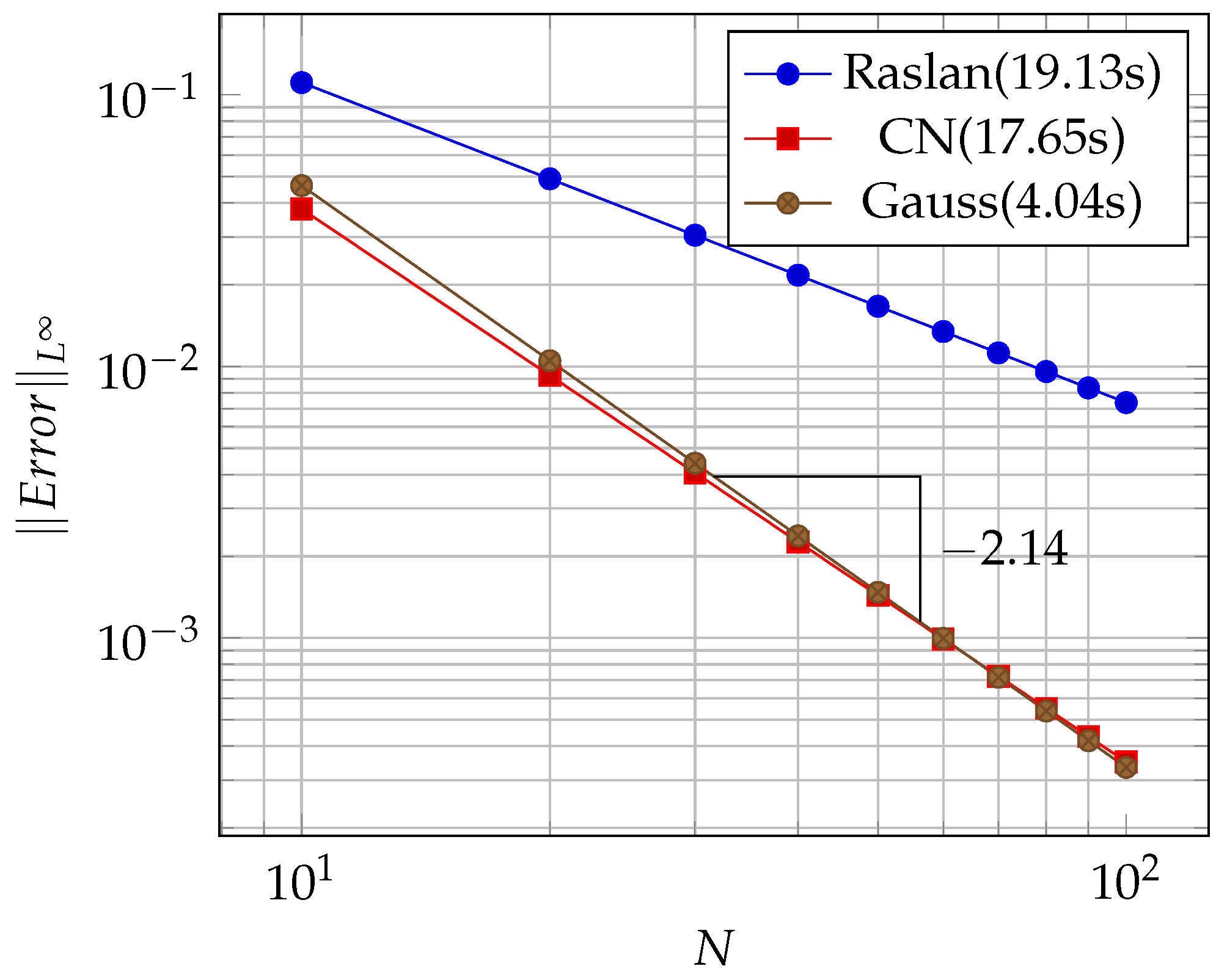
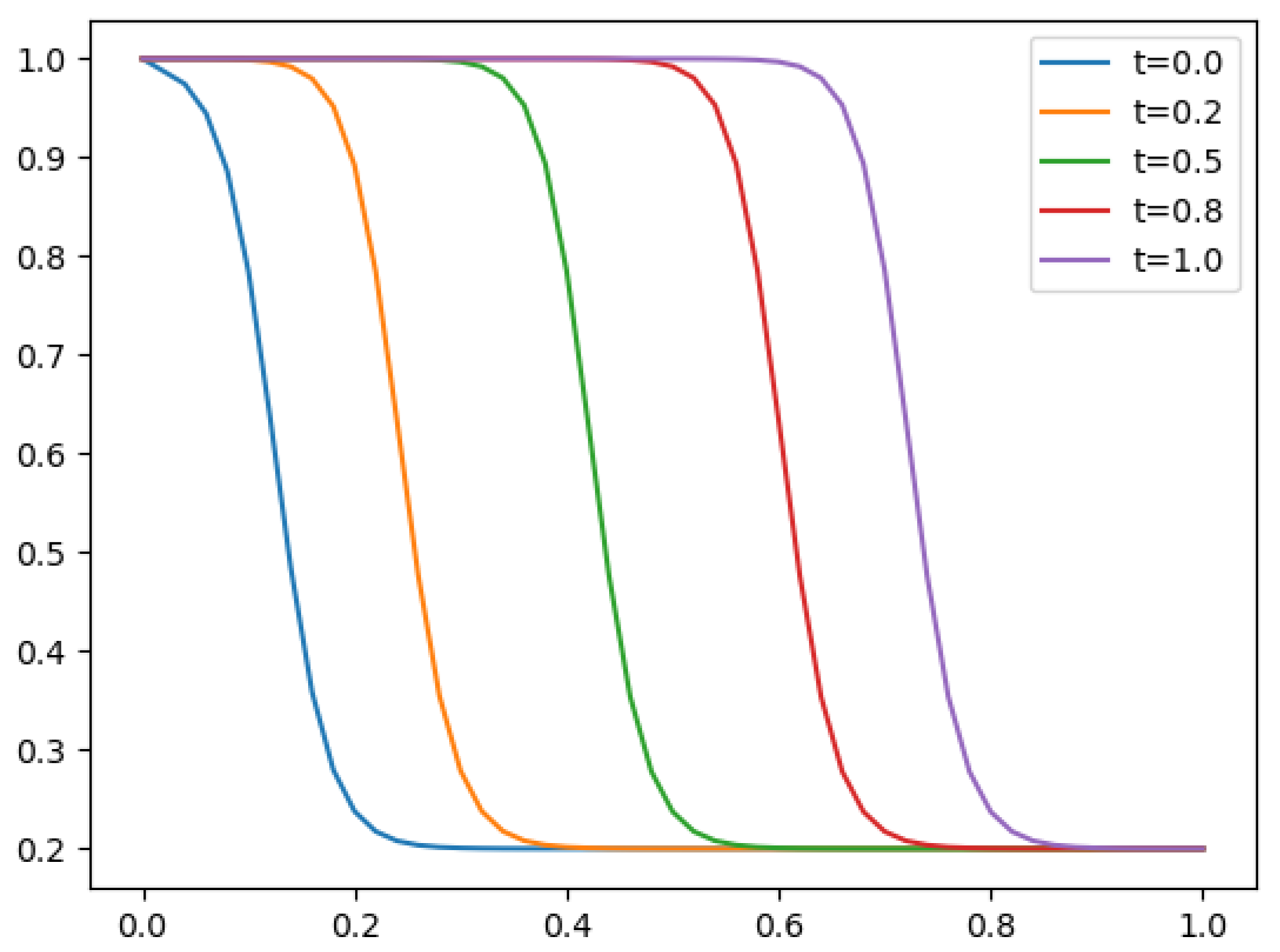
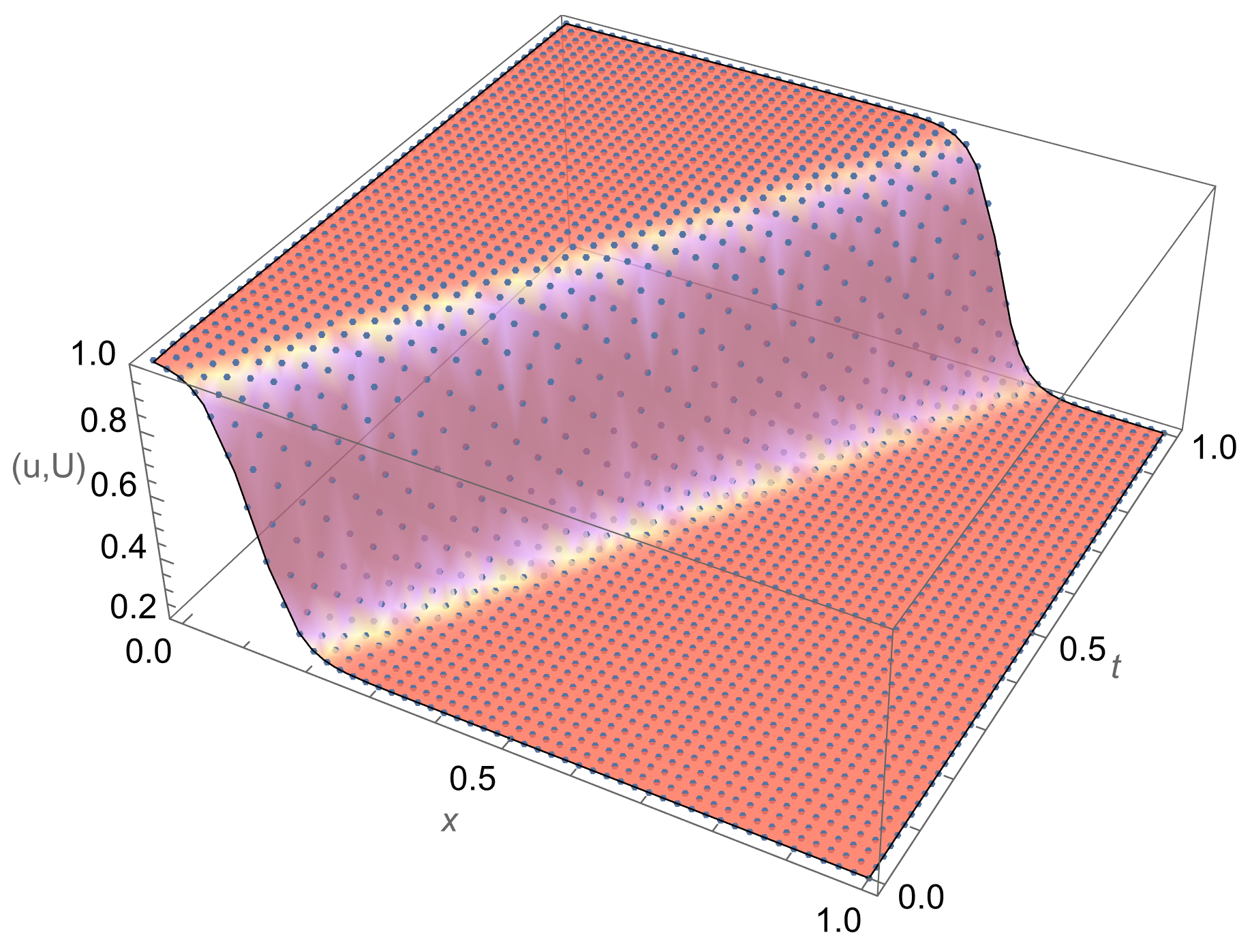
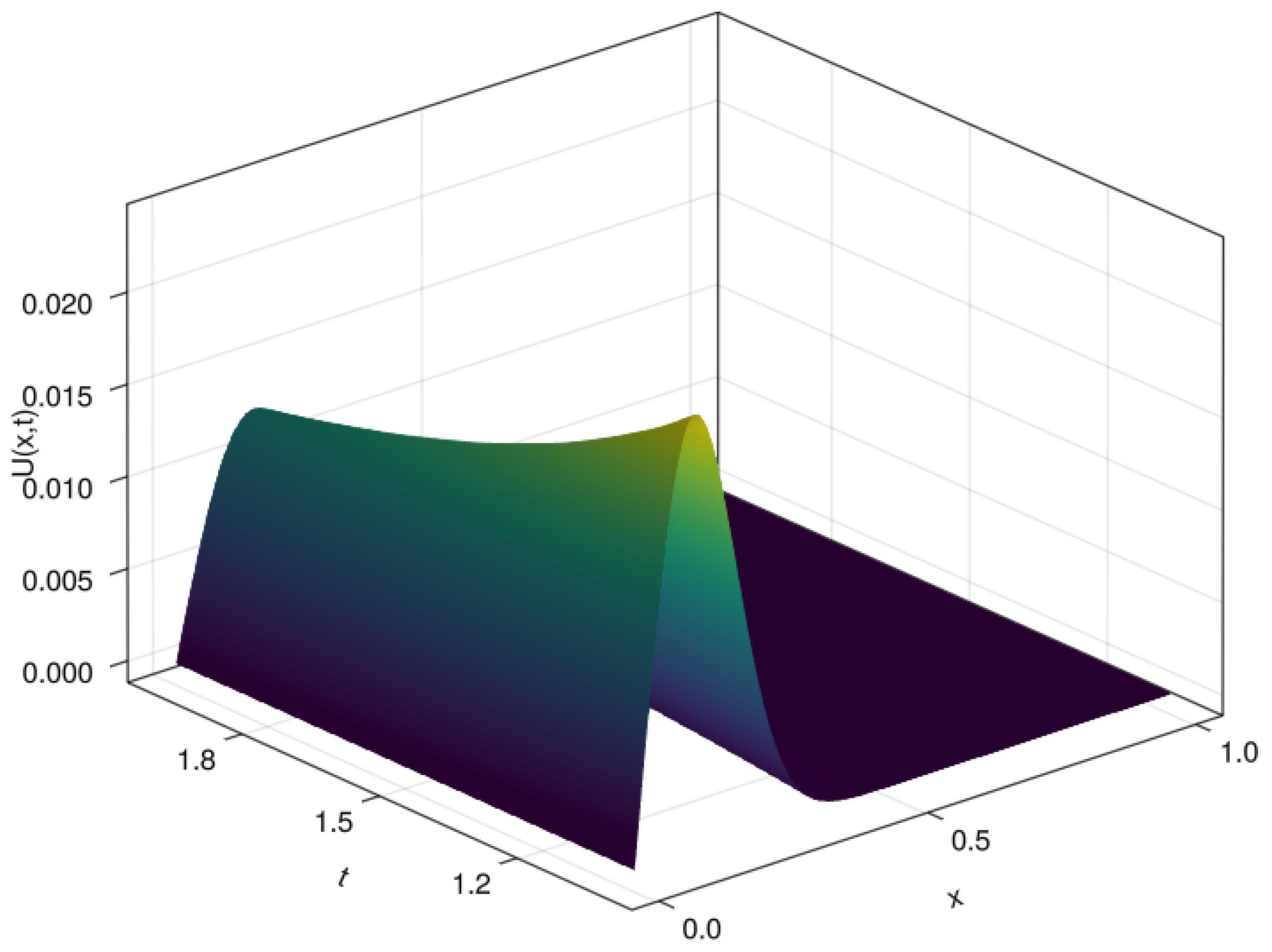
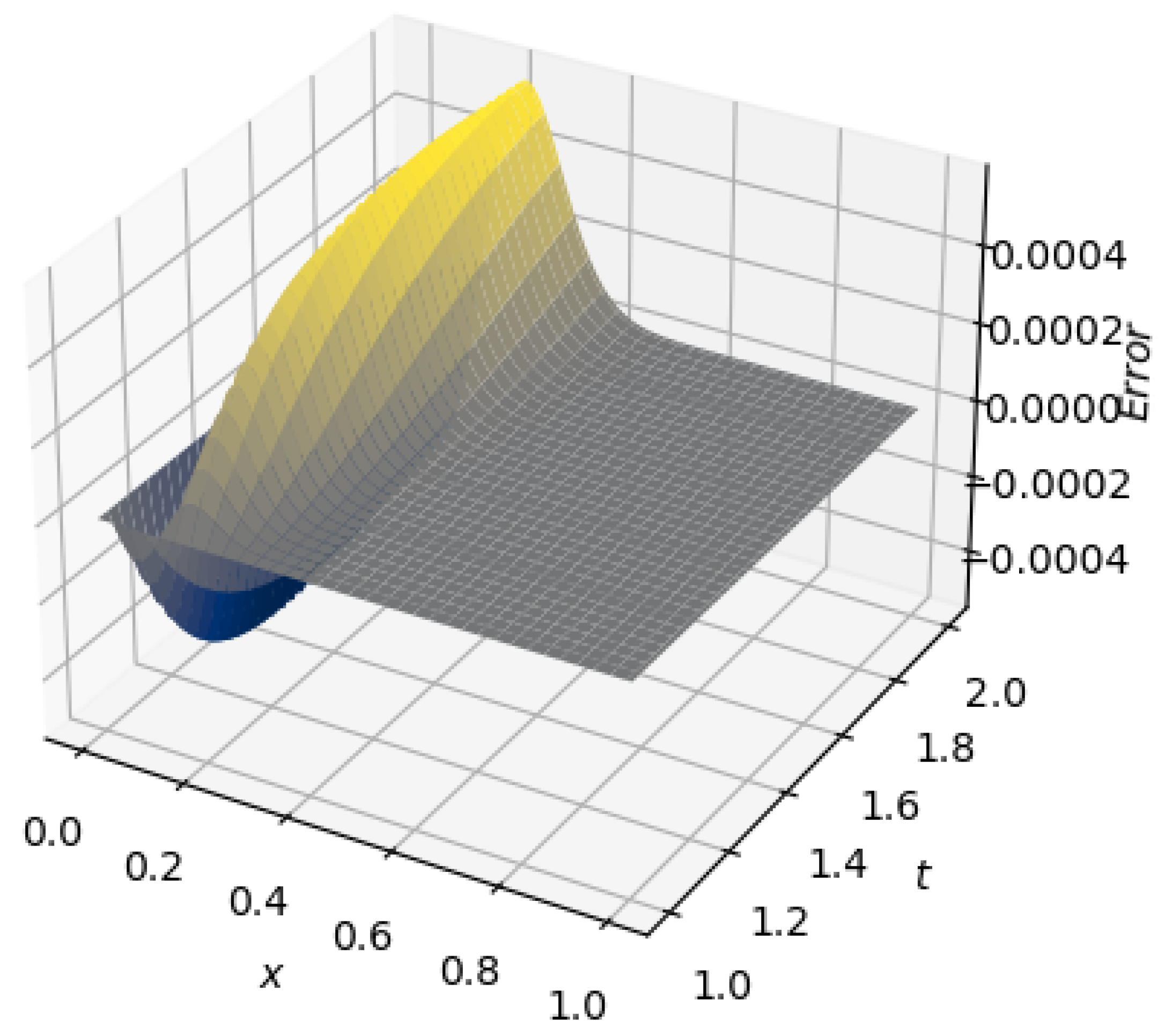
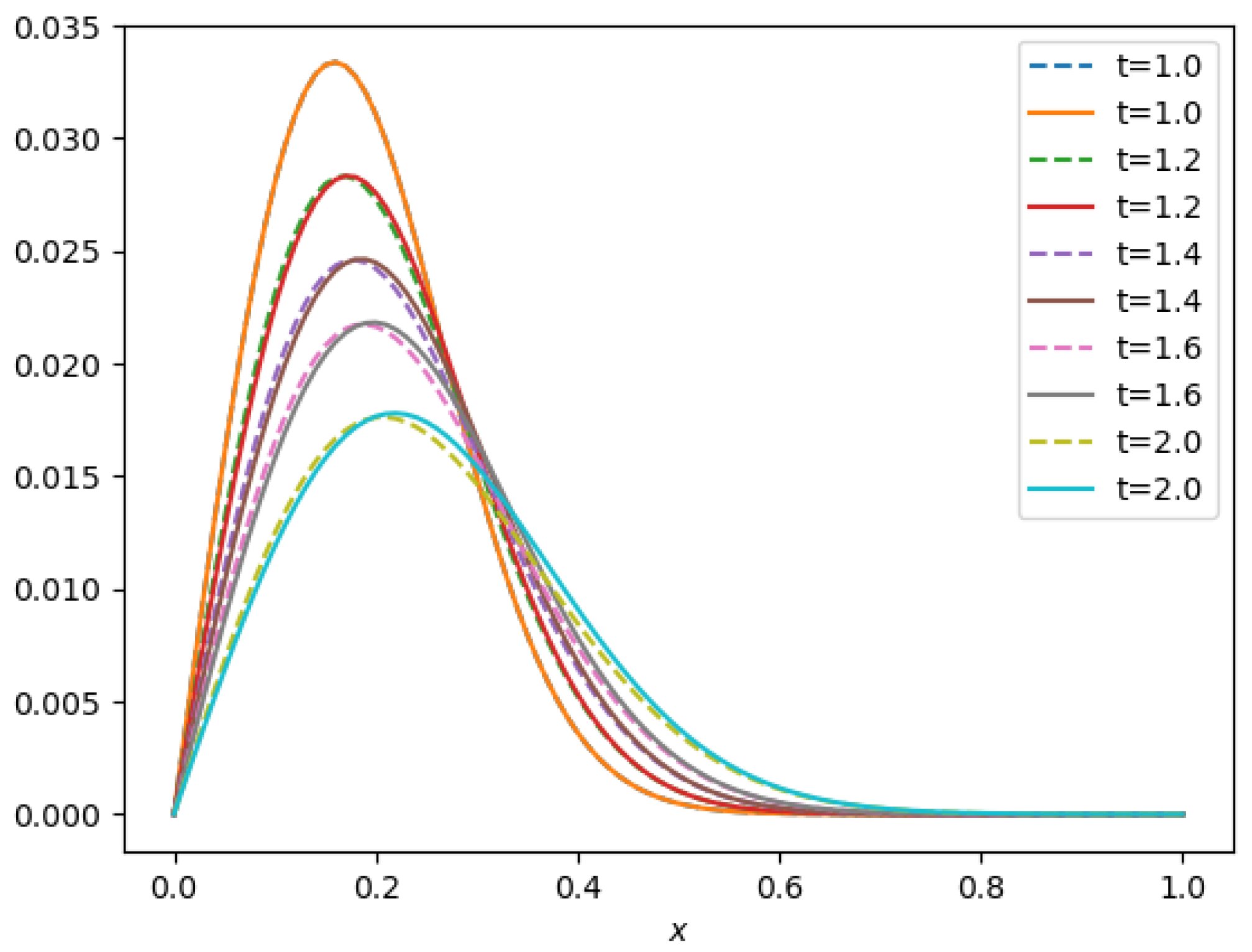
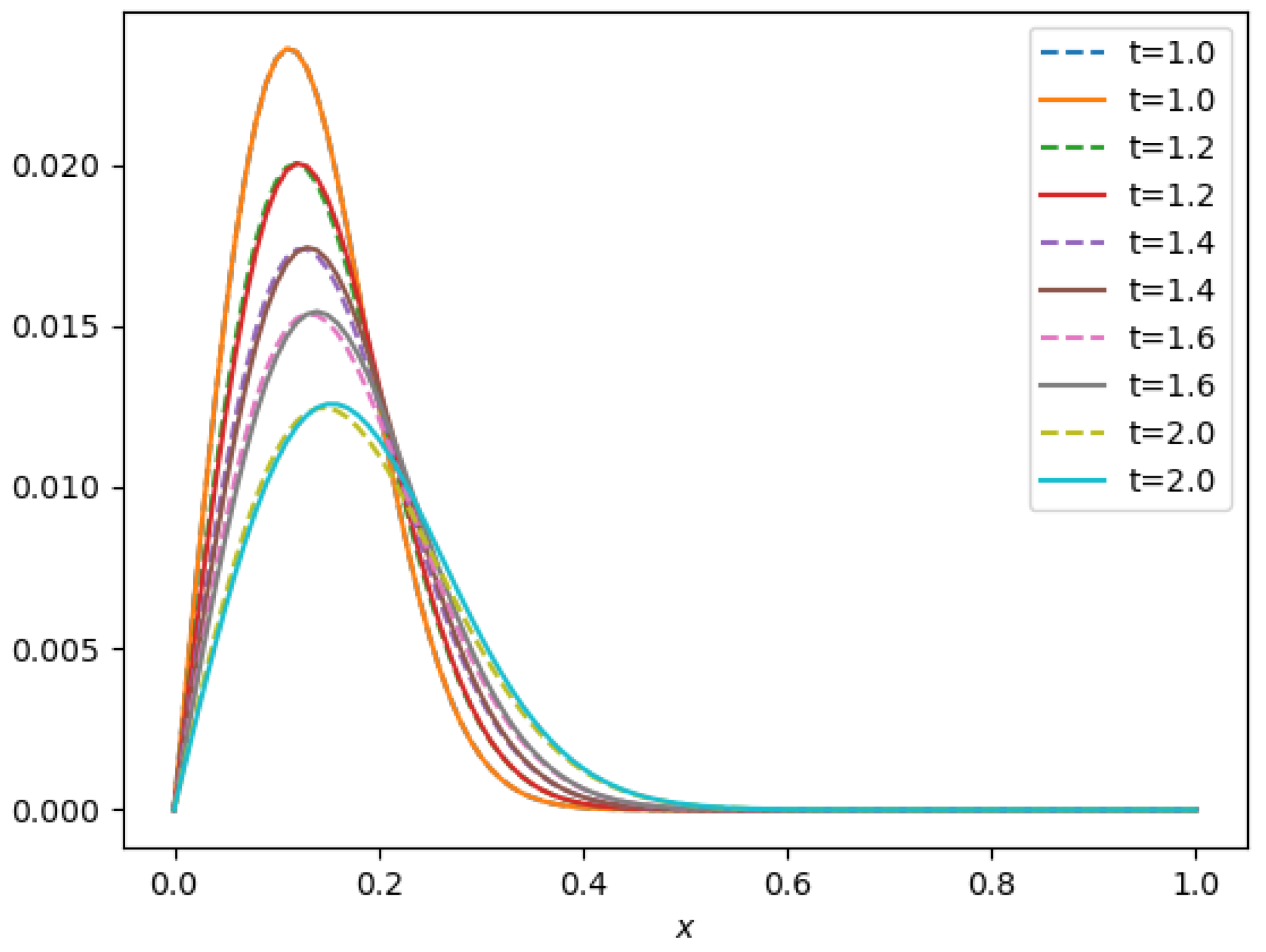
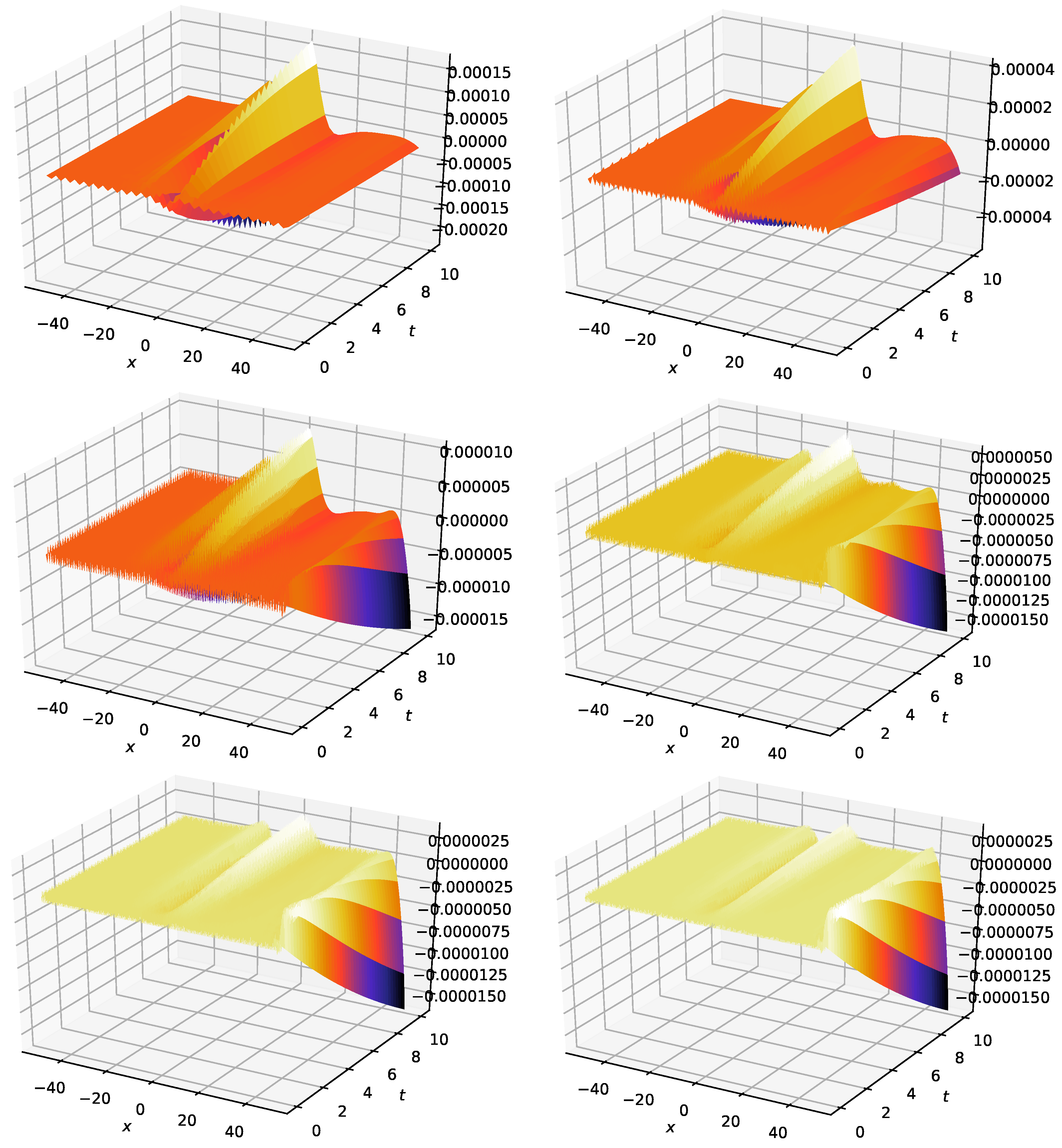
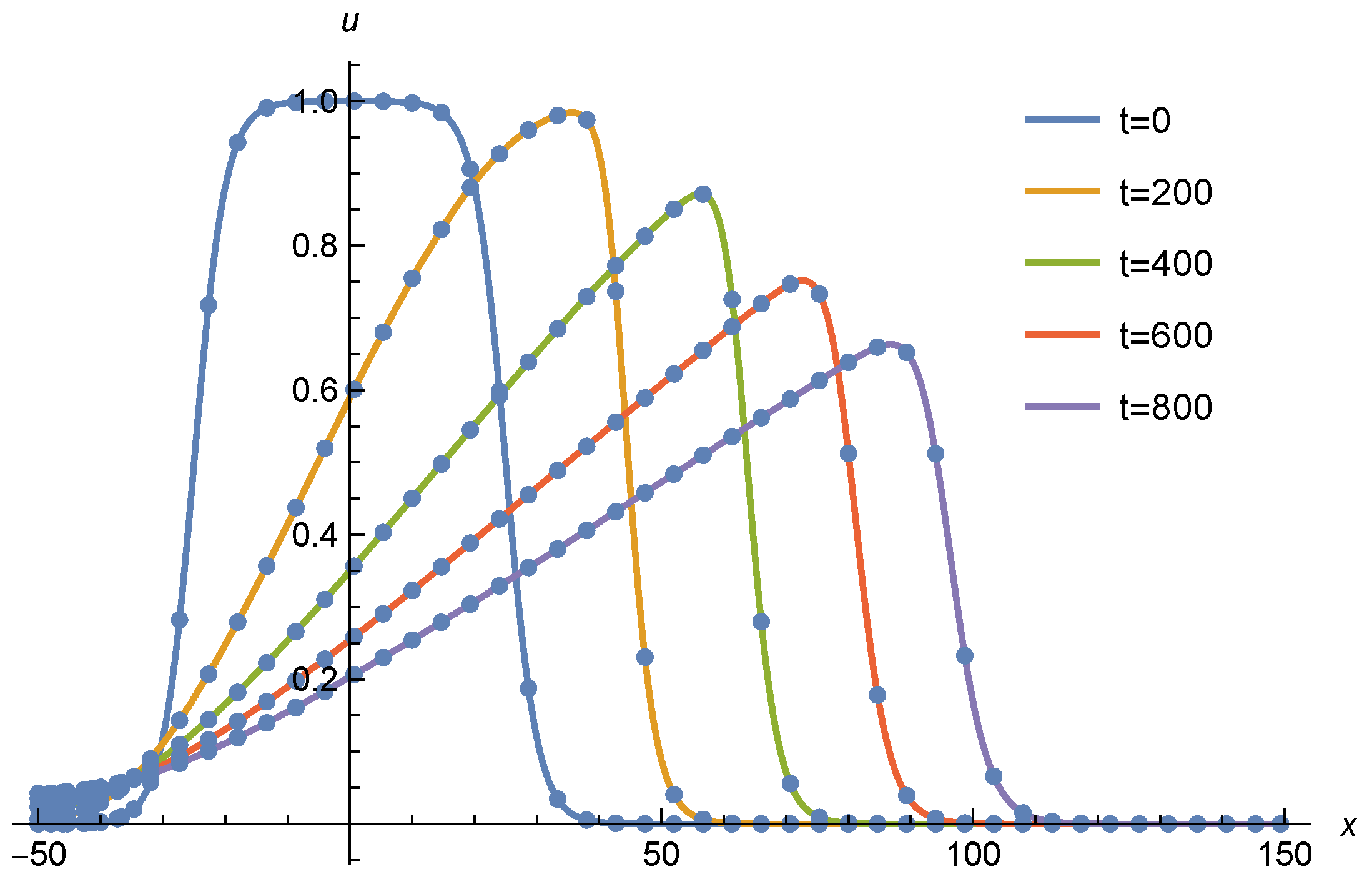
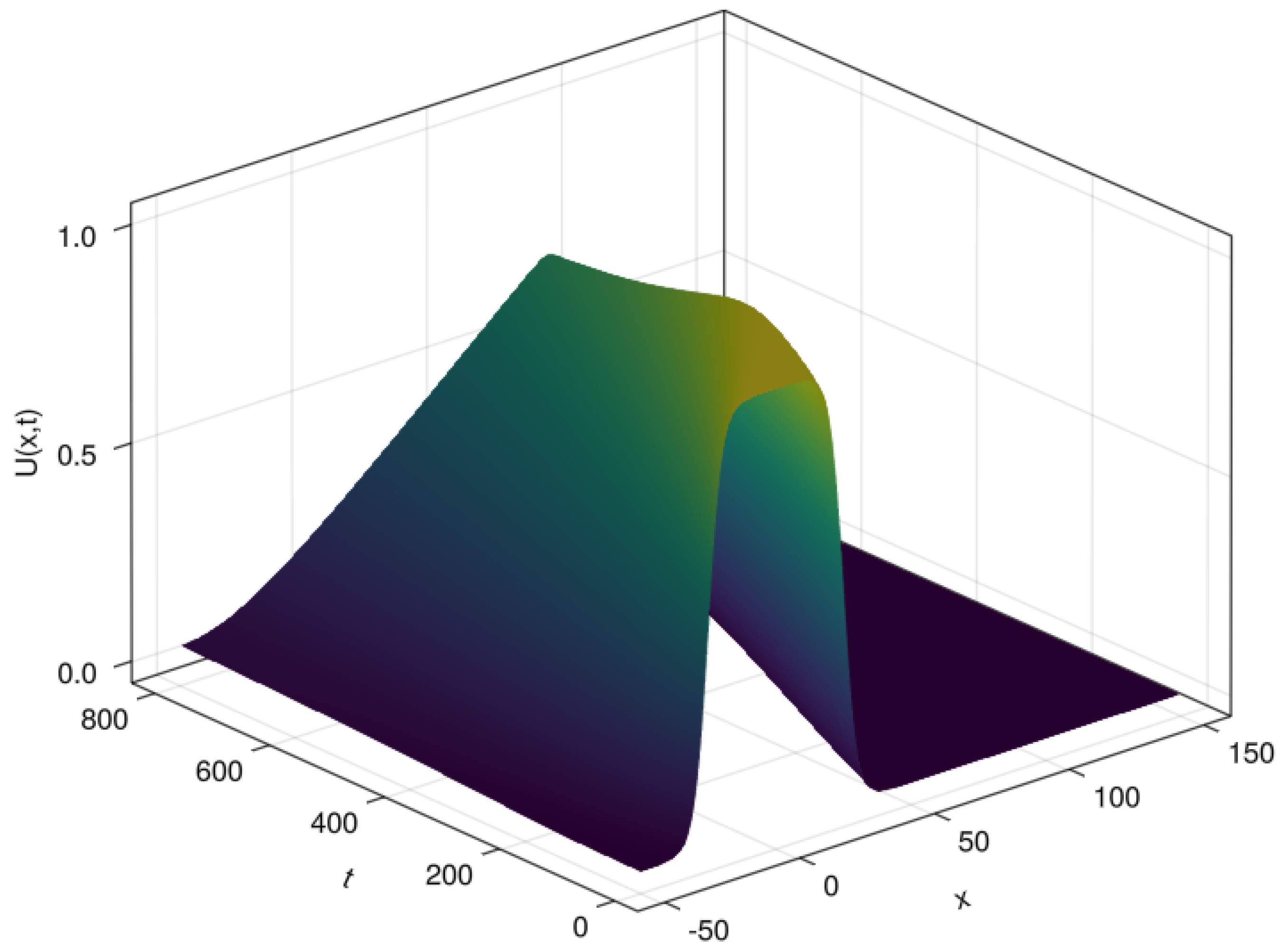
- A travelling wave solution of Burgers’ Equation (14), which is of the formwith the initial conditionand the boundary conditions , where , and are constants, is considered. We compare the norms of the errors at various times when the number of partitions of the space interval [0, 1] is , the number of time steps is and the final time is . Figure 3 shows the profiles at some values of t for all x. The graph of the exact solution is overlaid onto that of the approximate solution in Figure 4. The exact and approximate solutions match perfectly on the computational domain. It is clearly shown in Figure 5 that our method has convergence order two and is three times faster than CN.
9. Modified Burgers’ Equation
10. Numerical Simulations for the Modified Burgers’ Equation
11. Cubic B-Splines
12. Application of the Cubic B-Spline OCFE Method to KdV–Burgers’ Equation
13. Numerical Simulations for KdV–Burgers’ Equation
14. A Case of KdV–Burgers’ Equation That Does Not Have an Exact Solution
15. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Arora, S.; Kaur, I.; Tilahun, W. An exploration of quintic Hermite splines to solve Burgers’ equation. Arab. J. Math. 2020, 9, 19–36. [Google Scholar] [CrossRef] [Green Version]
- Botella, O.; Shariff, K. B-spline methods in fluid dynamics. Int. J. Comput. Fluid Dyn. 2003, 17, 133–149. [Google Scholar] [CrossRef]
- Singh, P.; Parumasur, N.; Bansilal, C. Orthogonal collocation on finite elements Using quintic Hermite basis. Aust. J. Math. Anal. Appl. 2021, 18, 1–12. [Google Scholar]
- Young, L.C. Orthogonal collocation revisited. Comput. Methods Appl. Mech. Engrg. 2019, 345, 1033–1076. [Google Scholar] [CrossRef]
- Biazar, J.; Ghazvini, H. Exact solutions for nonlinear Burgers’ equation by homotopy perturbation method. Numer. Methods Partial Differ. Equ. 2009, 25, 833–842. [Google Scholar] [CrossRef]
- Inc, M. On numerical solution of Burgers’ equation by homotopy analysis method. Phys. Lett. A 2008, 372, 356–360. [Google Scholar] [CrossRef]
- Hassanien, I.A.; Salama, A.A.; Hosham, H.A. Fourth-order finite difference method for solving Burgers’ equation. Appl. Math. Comput. 2005, 170, 781–800. [Google Scholar] [CrossRef]
- Zeidan, D.; Chau, C.K.; Lu, T.T.; Zheng, W.Q. Mathematical studies of the solution of Burgers’ equations by Adomian decomposition method. Math. Methods Appl. Sci. 2020, 43, 2171–2188. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Darvishi, M.T. A numerical solution of Burgers’ equation by modified Adomian method. Appl. Math. Comput. 2005, 163, 1265–1272. [Google Scholar] [CrossRef]
- Moghimi, M.; Hejazi, F.S. Variational iteration method for solving generalized Burgers’–Fisher and Burgers’ Equations. Chaos Solit. Fractals 2007, 33, 1756–1761. [Google Scholar] [CrossRef]
- Hall, C.A.; Meyer, W.W. Optimal error bounds for cubic spline interpolation. J. Approx. Theory 1976, 16, 105–122. [Google Scholar] [CrossRef] [Green Version]
- Mittal, R.C.; Jain, R.K. Redefined cubic B-splines collocation method for solving convection–diffusion equations. Appl. Math. Model. 2012, 36, 5555–5573. [Google Scholar] [CrossRef]
- Bialecki, B.; Fairweather, G. Orthogonal spline collocation method for partial differential equations. J. Comput. Appl. Math. 2001, 128, 55–82. [Google Scholar] [CrossRef] [Green Version]
- Ali, A.H.A.; Gardner, G.A.; Gardner, L.R.T.A. Collocation Solution for Burgers’ Equation Using Cubic B-Spline Finite Elements. Comput. Methods Appl. Mech. Eng. 1992, 100, 325–337. [Google Scholar] [CrossRef]
- Arora, G.; Singh, B.K. Numerical solution of Burgers’ equation with modified cubic B-spline differential quadrature method. Appl. Math. Comput. 2013, 22, 166–177. [Google Scholar] [CrossRef]
- Bialecki, B.; Fisher, N. Maximum norm convergence analysis of extrapolated Crank-Nicolson orthogonal spline collocation for Burgers’ equation in one space variable. J. Differ. Equ. Appl. 2018, 24, 1621–1642. [Google Scholar] [CrossRef]
- Bialecki, B.; Fairweather, G.; Karageorghis, A.; Maack, J. A quadratic spline collocation method for the Dirichlet biharmonic problem. Numer. Algorithms 2020, 83, 165–199. [Google Scholar] [CrossRef]
- De Boor, C.; Swartz, B. Collocation at Gaussian points. SIAM J. Numer. Anal. 1973, 10, 582–606. [Google Scholar] [CrossRef]
- Khalifa, A.K.A.; Eilbeck, J.C. Collocation with quadratic and cubic splines. IMA J. Numer. Anal. 1982, 2, 111–121. [Google Scholar] [CrossRef]
- Soliman, A.A.; Raslan, K.R. Collocation Method Using Quadratic B-Spline for the Rlw Equation. Int. J. Comput. Math. 2001, 78, 399–412. [Google Scholar] [CrossRef]
- Kumari, A.; Kukreja, V. Error bounds for septic Hermite interpolation and its implementation to study modified Burgers’ equation. Numer. Algorithms 2022, 89, 1799–1821. [Google Scholar] [CrossRef]
- Irk, D. Sextic b-spline collocation method for the modified Burgers’ equation. Kybernetes 2009, 38, 1599–1620. [Google Scholar] [CrossRef]
- Bratsos, A.G.; Khaliq, A.Q. An exponential time differencing method of lines for the Burgers’ and the modified Burgers’ equations. Numer. Methods Partial Differ. Equ. 2018, 34, 2024–2039. [Google Scholar] [CrossRef]
- Ramadan, M.A.; El-Danaf, T.S. Numerical treatment for the modified Burgers’ equation. Math. Comput. Simul. 2005, 70, 90–98. [Google Scholar] [CrossRef]
- Lakshmi, C.; Awasthi, A. Robust numerical scheme for nonlinear modified Burgers’ equation. Int. J. Comput. Math. 2018, 95, 1910–1926. [Google Scholar] [CrossRef]
- Kaya, D. An application of the decomposition method for the KdVb equation. Appl. Math. Comput. 2004, 152, 279–288. [Google Scholar] [CrossRef]
- Soliman, A.A. A numerical simulation and explicit solutions of KdV- Burgers’ and Lax’s seventh-order KdV equations. Chaos Solit. Fractals 2006, 29, 294–302. [Google Scholar] [CrossRef]
- Zaki, S.I. A quintic B-spline finite elements scheme for the KdVB equation. Comput. Methods Appl. Mech. Engrg. 2000, 188, 121–134. [Google Scholar] [CrossRef]
- Helal, M.; Mehanna, M.S.A. Comparison between two different methods for solving KdV–Burgers’ equation. Chaos Solit. Fractals 2006, 28, 320–326. [Google Scholar] [CrossRef]
- Demiray, H. A note on the exact travelling wave solution to the KdV–Burgers’ equation. Wave Motion 2003, 38, 367–369. [Google Scholar] [CrossRef]
- Wang, M. Exact solutions for a compound KdV-Burgers’ equation. Phys. Lett. A 1996, 213, 279–287. [Google Scholar] [CrossRef]
- Jeffrey, A.; Mohamad, M.N. Exact solutions to the KdV-Burgers’ equation. Wave Motion 1991, 14, 369–375. [Google Scholar] [CrossRef]
- Wazzan, L.A. Modified Tanh–Coth method for solving the KdV and the KdV–Burgers’ equations. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 443–450. [Google Scholar] [CrossRef]
- Kudryashov, N.A. On new travelling wave solutions of the KdV and the KdV–Burgers’ equations. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1891–1900. [Google Scholar] [CrossRef]
- Ramadan, M.A.; Aly, H.S. New approach for solving of extended KdV Equation. AJBAS 2023, 4, 96–109. [Google Scholar] [CrossRef]
- Raslan, K.R.A. Collocation solution for Burgers’ equation using quadratic B-spline finite elements. Int. J. Comput. Math. 2003, 80, 931–938. [Google Scholar] [CrossRef]


| h | Khalifa [19] | OCFE |
|---|---|---|
| 1.76 | 2.12 | |
| 1.93 | 2.03 | |
| 1.96 | 2.00 |
| t | Present | Raslan [36] | CN | Present | Raslan [36] | CN |
|---|---|---|---|---|---|---|
| 1.2 | 0.002389 | 0.009445 | 0.002455 | 0.003594 | 0.014613 | 0.003630 |
| 1.4 | 0.002140 | 0.009192 | 0.002201 | 0.003779 | 0.019857 | 0.003762 |
| 1.6 | 0.001868 | 0.008531 | 0.001905 | 0.003589 | 0.024209 | 0.003546 |
| 1.8 | 0.001653 | 0.010477 | 0.001667 | 0.003310 | 0.027808 | 0.003258 |
| 2 | 0.001431 | 0.012058 | 0.001426 | 0.003025 | 0.030687 | 0.002972 |
| t | Present | Raslan [36] | CN |
|---|---|---|---|
| 1 | 0.124967 | 0.124817 | 0.124967 |
| 1.2 | 0.124059 | 0.124317 | 0.124059 |
| 1.4 | 0.123291 | 0.123954 | 0.123291 |
| 1.6 | 0.122626 | 0.123602 | 0.122626 |
| 1.8 | 0.122039 | 0.123264 | 0.122039 |
| 2 | 0.121513 | 0.122940 | 0.000000 |
| x | Present | Exact | Raslan [36] |
|---|---|---|---|
| 0.365 | 0.182978 | 0.182473 | 0.185924 |
| 0.415 | 0.206938 | 0.207419 | 0.215954 |
| 0.465 | 0.232783 | 0.232227 | 0.235308 |
| 0.605 | 0.289358 | 0.288192 | 0.293358 |
| 0.645 | 0.274683 | 0.274869 | 0.279174 |
| 0.695 | 0.181949 | 0.180506 | 0.150321 |
| 0.725 | 0.095053 | 0.098406 | 0.096996 |
| 0.765 | 0.028298 | 0.029633 | 0.030028 |
| 0.805 | 0.006413 | 0.006911 | 0.007348 |
| 0.845 | 0.001254 | 0.001413 | 0.001598 |
| 0.915 | 6.11 × 10 | 7.05 × 10 | 0.000140 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parumasur, N.; Adetona, R.A.; Singh, P. Efficient Solution of Burgers’, Modified Burgers’ and KdV–Burgers’ Equations Using B-Spline Approximation Functions. Mathematics 2023, 11, 1847. https://doi.org/10.3390/math11081847
Parumasur N, Adetona RA, Singh P. Efficient Solution of Burgers’, Modified Burgers’ and KdV–Burgers’ Equations Using B-Spline Approximation Functions. Mathematics. 2023; 11(8):1847. https://doi.org/10.3390/math11081847
Chicago/Turabian StyleParumasur, Nabendra, Rasheed A. Adetona, and Pravin Singh. 2023. "Efficient Solution of Burgers’, Modified Burgers’ and KdV–Burgers’ Equations Using B-Spline Approximation Functions" Mathematics 11, no. 8: 1847. https://doi.org/10.3390/math11081847
APA StyleParumasur, N., Adetona, R. A., & Singh, P. (2023). Efficient Solution of Burgers’, Modified Burgers’ and KdV–Burgers’ Equations Using B-Spline Approximation Functions. Mathematics, 11(8), 1847. https://doi.org/10.3390/math11081847






