A Novel Integrated Heuristic Optimizer Using a Water Cycle Algorithm and Gravitational Search Algorithm for Optimization Problems
Abstract
:1. Introduction
- (1)
- A crude niching technique was designed and adopted to define the sea, rivers and their corresponding streams in the WCA, and a non-linear setting was introduced to adjust the total number of rivers and the sea during the search process. Thereby, a modified WCA is presented, which could possess a better balance between exploration and exploitation.
- (2)
- To further strengthen the adaptivity and robustness of the algorithm for various search stages and problems, the resulting water cycle search and gravitational search were further integrated according to their history performance within certain iterations.
- (3)
- The binomial crossover operation was additionally introduced in the proposed algorithm when the gravitational search or modified water cycle search were executed. This might further promote control over the transmission of the search information.
2. The Classical GSA and WCA
2.1. Gravitational Search Algorithm
2.2. Water Cycle Algorithm
3. Proposed Algorithm
3.1. Modified WCA
| Algorithm 1 Modified niching approach. |
|
| Algorithm 2 The framework of the MWCA. |
|
3.2. The Hybridization of MWCA and GSA
3.3. The Crossover Operation
| Algorithm 3 The framework of the HMWCA. |
|
3.4. Complexity Analysis
4. Numerical Experiments
4.1. The Sensitivities of Parameters and
4.2. The Effectiveness of the Proposed Components in the HMWCA
- (1)
- HMWCA1: the method in the original WCA [38] was used to form the sea, rivers and streams instead of the modified niching method in the HMWCA.
- (2)
- HMWCA2: the population was only updated by the water cycle search in the HMWCA during the whole search process.
- (3)
- HMWCA3: after the water cycle search or gravitational search at each generation, the binomial crossover operation is not further used in the HMWCA.
- (4)
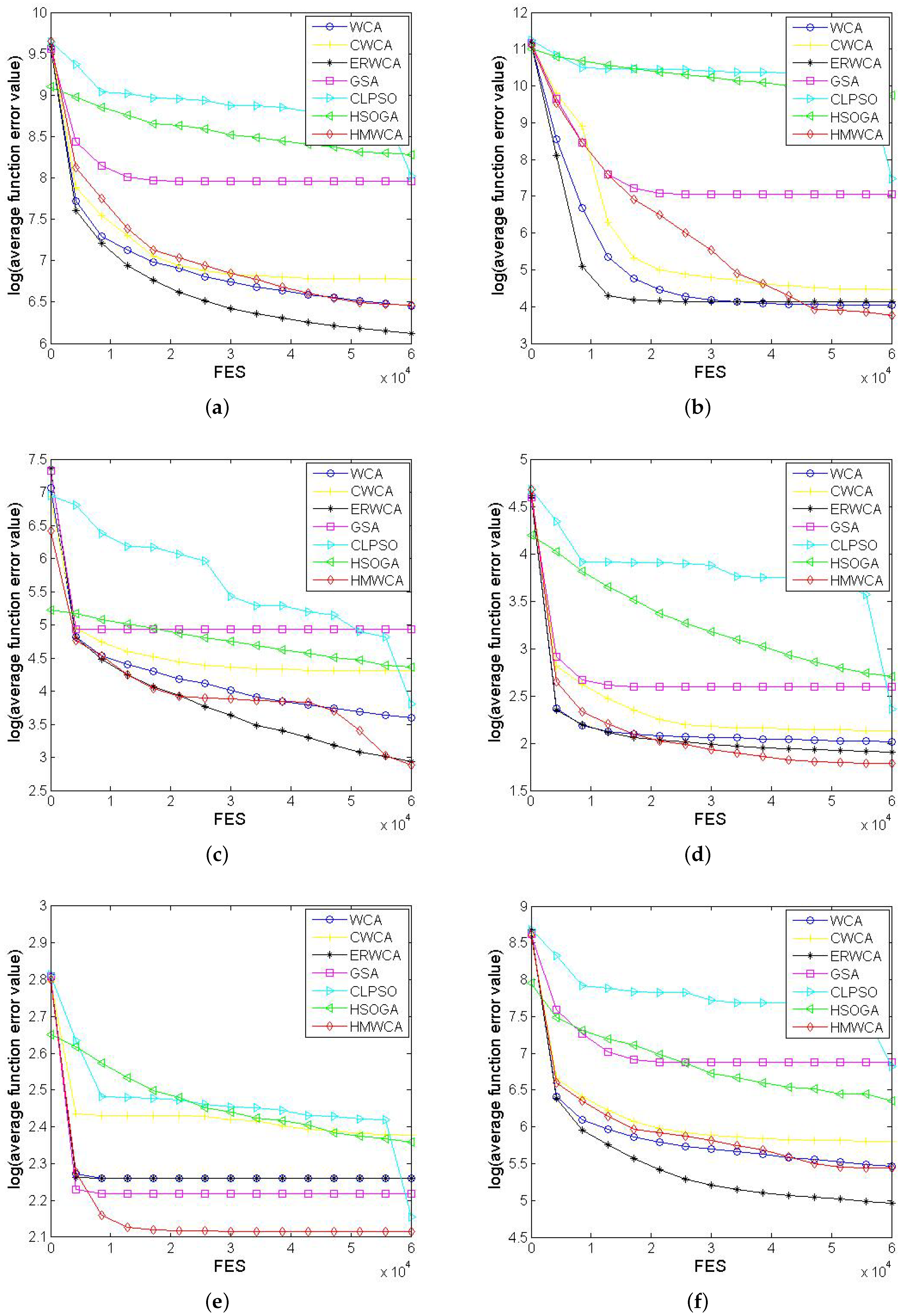
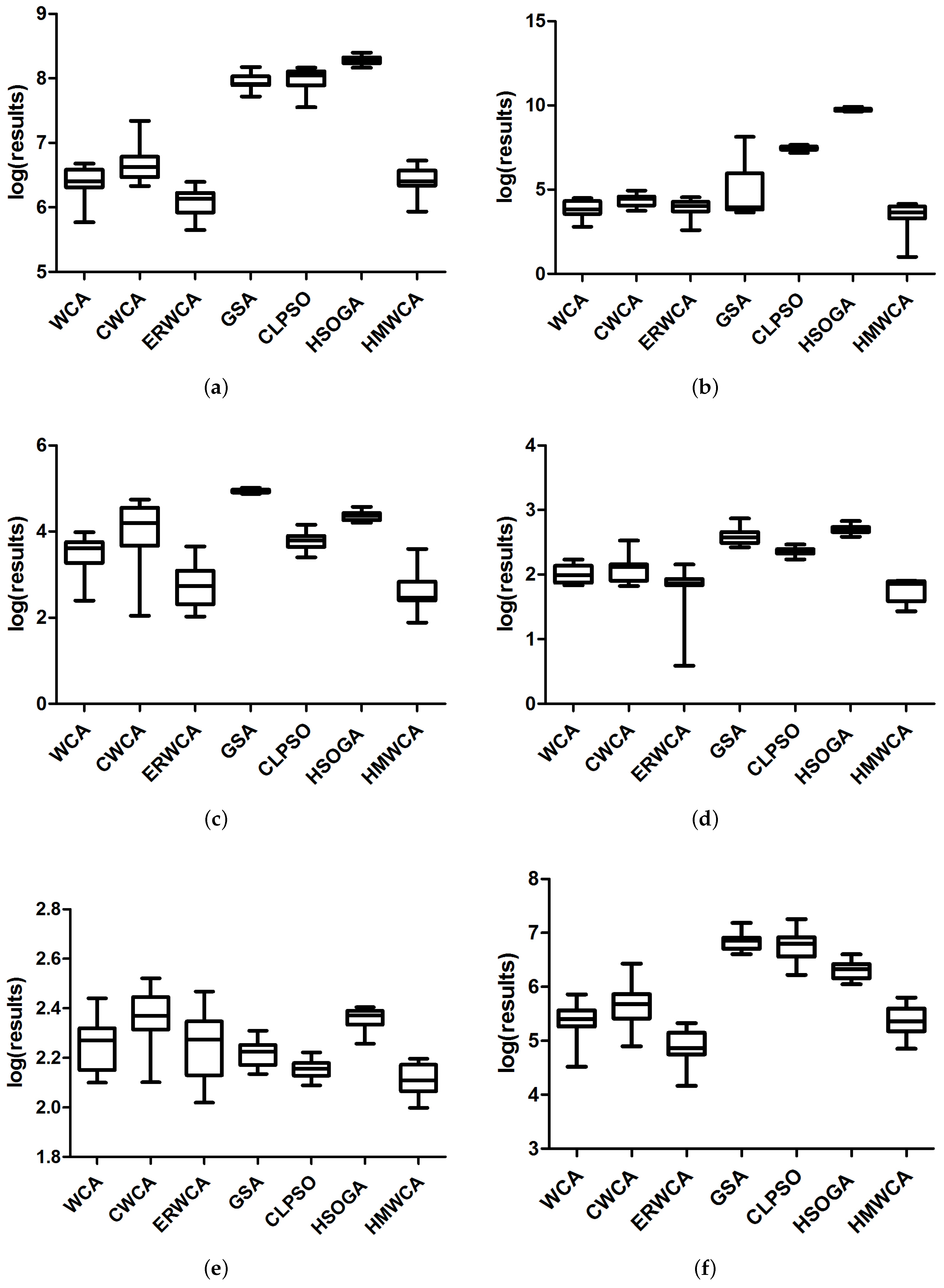
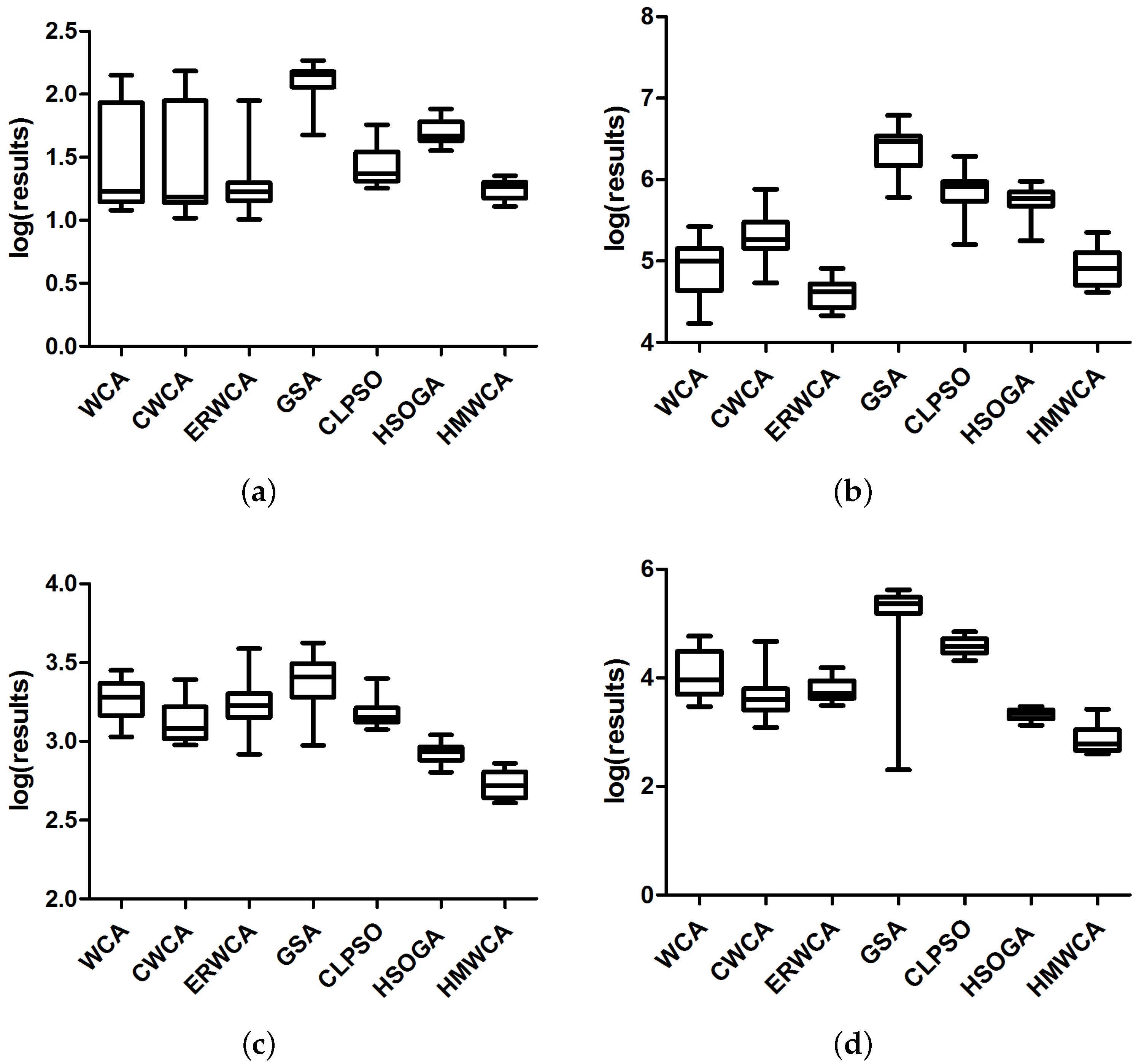
4.3. Comparisons and Discussion
4.4. Algorithm Efficiency
4.5. Application
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sha, D.Y.; Hsu, C.Y. A new particle swarm optimization for the open shop scheduling problem. Comput. Oper. Res. 2008, 35, 3243–3261. [Google Scholar] [CrossRef]
- Zhang, B.; Pan, Q.K.; Meng, L.L.; Lu, C.; Mou, J.H.; Li, J.Q. An automatic multi-objective evolutionary algorithm for the hybrid flowshop scheduling problem with consistent sublots. Knowl.-Based Syst. 2022, 238, 107819. [Google Scholar] [CrossRef]
- Das, R.; Akay, B.; Singla, R.K.; Singh, K. Application of artificial bee colony algorithm for inverse modelling of a solar collector. Inverse Probl. Sci. Eng. 2017, 25, 887–908. [Google Scholar] [CrossRef]
- Omran, M.G.; Engelbrecht, A.P.; Salman, A.A. Differential evolution methods for unsupervised image classification, 2008. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC 2005), Edinburgh, UK, 2–4 September 2005. [Google Scholar]
- Zhang, Z.; Han, Y. Discrete sparrow search algorithm for symmetric traveling salesman problem. Appl. Soft Comput. 2022, 118, 108469. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization, 1995. In Proceedings of the Icnn95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology. In Control and Artificial Intelligence; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Storn, R. Differential evolution-a simple and efficient heuristic for global optimization over continuous space. J. Glob. Optim. 1997, 11, 341. [Google Scholar] [CrossRef]
- Colorni, A. Distributed optimization by ant colonies. In Proceedings of the First European Conference on Artificial Life, Paris, France, 11–13 December 1991. [Google Scholar]
- Ying, T.; Zhu, Y. Fireworks Algorithm for Optimization, 2010. In Proceedings of the First International Conference, ICSI 2010, Beijing, China, 12–15 June 2010. [Google Scholar]
- Sun, G.; Zhao, R.; Lan, Y. Joint operations algorithm for large-scale global optimization. Appl. Soft Comput. 2016, 38, 1025–1039. [Google Scholar] [CrossRef]
- Jain, M.; Singh, V.; Rani, A. A novel nature-inspired algorithm for optimization: Squirrel search algorithm. Swarm Evol. Comput. 2018, 44, 148–175. [Google Scholar] [CrossRef]
- Wagdy, A.; Khater, A.; Hadi, A.A. Gaining-sharing knowledge based algorithm for solving optimization problems Algorithm. Int. J. Mach. Learn. Cybern. 2020, 11, 1501–1529. [Google Scholar]
- Ma, Z.Q.; Wu, G.H.; Suganthan, P.N.; Song, A.J.; Luo, Q.Z. Performance assessment and exhaustive listing of 500+ nature-inspired metaheuristic algorithms. Swarm Evol. Comput. 2023, 77, 101248. [Google Scholar] [CrossRef]
- Ilonen, J.; Kamarainen, J.K.; Lampinen, J. Differential Evolution Training Algorithm for Feed-Forward Neural Networks. Neural Process. Lett. 2003, 17, 93–105. [Google Scholar] [CrossRef]
- Bello, R.; Gomez, Y.; Nowe, A.; Garcia, M.M. Two-Step Particle Swarm Optimization to Solve the Feature Selection Problem, 2007. In Proceedings of the International Conference on Intelligent Systems Design & Applications, Rio de Janeiro, Brazil, 20–24 October 2007. [Google Scholar]
- Cuevas, E.; Zaldivar, D.; Perez-Cisneros, M. A novel multi-threshold segmentation approach based on differential evolution optimization. Expert Syst. Appl. 2010, 37, 5265–5271. [Google Scholar] [CrossRef]
- Li, J.Y.; Zhan, Z.H.; Tan, K.C.; Zhang, J. A Meta-knowledge transfer-based differential evolution for multitask optimization. IEEE Trans. Evol. Comput. 2022, 26, 719–734. [Google Scholar] [CrossRef]
- Liao, Z.W.; Mi, X.Y.; Pang, Q.S.; Sun, Y. History archive assisted niching differential evolution with variable neighborhood for multimodal optimization. Swarm Evol. Comput. 2023, 76, 101206. [Google Scholar] [CrossRef]
- Chen, J.X.; Gong, Y.J.; Chen, W.N.; Li, M.T.; Zhang, J. Elastic differential evolution for automatic data clustering. IEEE Trans. Cybern. 2021, 51, 4134–4147. [Google Scholar] [CrossRef]
- Hrstka, O.; Kuerová, A. Improvement of real coded genetic algorithm based on differential operators preventing premature convergence. Adv. Eng. Softw. 2004, 35, 237–246. [Google Scholar] [CrossRef] [Green Version]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Sun, G.; Zhang, A.; Wang, Z.; Yao, Y.; Ma, J.; Couples, G.D. Locally informed Gravitational Search Algorithm. Knowl.-Based Syst. 2016, 104, 134–144. [Google Scholar] [CrossRef]
- Yu, M.; Zhang, Y.; Chen, K.; Zhang, D. Integration of process planning and scheduling using a hybrid GA/PSO algorithm. Int. J. Adv. Manuf. Technol. 2015, 78, 583–592. [Google Scholar] [CrossRef]
- Yan, X.Q.; Tian, M.N. Differential evolution with two-level adaptive mechanism for numerical optimization. Knowl.-Based Syst. 2022, 241, 108209. [Google Scholar] [CrossRef]
- Li, Y.Z.; Wang, S.H.; Yang, H.Y.; Chen, H.; Yang, B. Enhancing differential evolution algorithm using leader-adjoint populations. Inf. Sci. 2023, 622, 235–268. [Google Scholar] [CrossRef]
- Xu, H.Q.; Gu, S.; Fan, Y.C.; Li, X.S.; Zhao, Y.F.; Zhao, J.; Wang, J.J. A strategy learning framework for particle swarm optimization algorithm. Inf. Sci. 2023, 619, 126–152. [Google Scholar] [CrossRef]
- Zuo, X.; Li, X. A DE and PSO based hybrid algorithm for dynamic optimization problems. Soft Comput. 2014, 18, 1405–1424. [Google Scholar] [CrossRef]
- Zheng, Y.J.; Xu, X.L.; Ling, H.F.; Chen, S.Y. A hybrid fireworks optimization method with differential evolution operators. Neurocomputing 2015, 148, 75–82. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Suganthan, P.N.; Reynolds, R.G. CADE: A hybridization of Cultural Algorithm and Differential Evolution for numerical optimization. Inf. Sci. 2017, 378, 215–241. [Google Scholar] [CrossRef]
- Lynn, N.; Suganthan, P.N. Ensemble particle swarm optimizer. Appl. Soft Comput. 2017, 55, 533–548. [Google Scholar] [CrossRef]
- Shehadeh, H.A. A hybrid sperm swarm optimization and gravitational search algorithm (HSSOGSA) for global optimization. Neural Comput. Appl. 2021, 33, 11739–11752. [Google Scholar] [CrossRef]
- Chen, H. Hierarchical Learning Water Cycle Algorithm. Appl. Soft Comput. 2020, 86, 105935. [Google Scholar] [CrossRef]
- Taib, H.; Bahreininejad, A. Data clustering using hybrid water cycle algorithm and a local pattern search method. Adv. Eng. Softw. 2021, 153, 102961. [Google Scholar] [CrossRef]
- Veeramani, C.; Senthil, S. An improved Evaporation Rate-Water Cycle Algorithm based Genetic Algorithm for solving generalized ratio problems. RAIRO-Oper. Res. 2020, 55, S461–S480. [Google Scholar] [CrossRef]
- Li, W.; Liang, P.; Sun, B.; Sun, Y.; Huang, Y. Reinforcement learning-based particle swarm optimization with neighborhood differential mutation strategy. Swarm Evol. Comput. 2023, 78, 101274. [Google Scholar] [CrossRef]
- Saryazdi, N.P. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M. Water cycle algorithm—A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110, 151–166. [Google Scholar] [CrossRef]
- Sadollah, A.; Eskandar, H.; Bahreininejad, A.; Kim, J.H. Water cycle algorithm with evaporation rate for solving constrained and unconstrained optimization problems. Appl. Soft Comput. 2015, 30, 58–71. [Google Scholar] [CrossRef]
- Heidari, A.A.; Abbaspour, R.A.; Jordehi, A.R. An efficient chaotic water cycle algorithm for optimization tasks. Neural Comput. Appl. 2017, 28, 57–85. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H. Chaotic gravitational constants for the gravitational search algorithm. Appl. Soft Comput. 2017, 53, 407–419. [Google Scholar] [CrossRef]
- Wang, H. A hierarchical gravitational search algorithm with an effective gravitational constant. Swarm Evol. Comput. 2019, 46, 118–139. [Google Scholar] [CrossRef]
- Lei, Z.; Gao, S.; Gupta, S.; Cheng, J.; Yang, G. An aggregative learning gravitational search algorithm with self-adaptive gravitational constants. Expert Syst. Appl. 2020, 152, 113396. [Google Scholar] [CrossRef]
- Qiao, Y. A simple water cycle algorithm with percolation operator for clustering analysis. Soft Comput. 2019, 23, 4081–4095. [Google Scholar] [CrossRef]
- Osaba, E.; Del, J.; Sadollah, A.; Nekane, B.M. A discrete water cycle algorithm for solving the symmetric and asymmetric traveling salesman problem. Appl. Soft Comput. 2018, 71, 277–290. [Google Scholar] [CrossRef]
- Kudkelwar, S. An application of evaporation-rate-based water cycle algorithm for coordination of over-current relays in microgrid. Sadhana Acad. Proc. Eng. Sci. 2020, 45, 237. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, H.; Luo, H. Research on the construction of stock portfolios based on multiobjective water cycle algorithm and KMV algorithm. Appl. Soft Comput. 2022, 115, 108186. [Google Scholar] [CrossRef]
- Nasir, M.; Sadollah, A.; Choi, Y.H.; Kim, J.H. A comprehensive review on water cycle algorithm and its applications. Neural Comput. Appl. 2020, 32, 17433–17488. [Google Scholar] [CrossRef]
- Mittal, H.; Tripathi, A.; Pandey, A.C.; Pal, R. Gravitational search algorithm: A comprehensive analysis of recent variants. Multimed. Tools Appl. 2021, 80, 7581–7608. [Google Scholar] [CrossRef]
- Oshi, S.K. Chaos embedded opposition based learning for gravitational search algorithm. Appl. Intell. 2023, 53, 5567–5586. [Google Scholar]
- Wang, Y.R.; Gao, S.C.; Yu, Y.; Cai, Z.H.; Wang, Z.Q. A gravitational search algorithm with hierarchy and distributed framework. Knowl.-Based Syst. 2021, 218, 106877. [Google Scholar] [CrossRef]
- Chen, C.H.; Wang, X.J.; Dong, H.C.; Wang, P. Surrogate-assisted hierarchical learning water cycle algorithm for high-dimensional expensive optimization. Swarm Evol. Comput. 2022, 75, 101169. [Google Scholar] [CrossRef]
- Ye, J.; Xie, L.; Wang, H. A water cycle algorithm based on quadratic interpolation for high-dimensional global optimization problems. Appl. Intell. 2023, 53, 2825–2849. [Google Scholar] [CrossRef]
- Price, K.V.; Storn, R.M.; Lampinen, J.A. Differential Evolution—A Practical Approach to Global Optimization. Nat. Comput. 2005, 141, 2. [Google Scholar]
- Liang, J.J.; Qu, B.Y.; Suganthan, P.N. Problem definitions and evaluation criteria for the CEC 2014 special session and competition on single objective real-parameter numerical optimization. In Computational Intelligence Laboratory, Zhengzhou University, Zhengzhou China and Technical Report; Nanyang Technological University: Singapore, 2013. [Google Scholar]
- Das, S.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for CEC 2011 Competition on Testing Evolutionary Algorithms on Real World Optimization Problems; Jadavpur University: Kolkata, India; Nanyang Technological University: Singapore, 2011. [Google Scholar]
- Sheng, W.; Swift, S.; Zhang, L.; Liu, X. A weighted sum validity function for clustering with a hybrid niching genetic algorithm. IEEE Trans. Syst. Man, Cybern. Part (Cybern.) 2005, 35, 1156–1167. [Google Scholar] [CrossRef] [Green Version]
- Udit, H.; Swagatam, D.; Dipankar, M. A cluster-based differential evolution algorithm with external archive for optimization in dynamic environments. IEEE Trans. Cybern. 2013, 43, 881–897. [Google Scholar]
- Zhang, J.Q.; Sanderson, A.C. JADE: Adaptive Differential Evolution With Optional External Archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Epitropakis, M.G.; Plagianakos, V.P.; Vrahatis, M.N. Balancing the exploration and exploitation capabilities of the differential evolution algorithm. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008. [Google Scholar]
- Jiang, Z.Y.; Cai, Z.X.; Wang, Y. Hybrid Self-Adaptive Orthogonal Genetic Algorithm for Solving Global Optimization Problems. J. Softw. 2010, 21, 1296–1307. [Google Scholar] [CrossRef]

| Functions | Statistical | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Item | ||||||||||
| 5 | 5 | Mean Error | 4.97 × 10 | 4.04 × 10 | 1.01 × 10 | 1.39 × 10 | 4.91 × 10 | 2.71 × 10 | 7.06 × 10 | 2.17 × 10 |
| Std Dev | 3.31 × 10 | 7.79 × 10 | 4.80 × 10 | 3.28 × 10 | 3.19 × 10 | 3.31 × 10 | 3.25 × 10 | 2.84 × 10 | ||
| 8 | Mean Error | 4.78 × 10 | 2.89 × 10 | 7.59 × 10 | 1.22 × 10 | 4.73 × 10 | 2.07 × 10 | 7.54 × 10 | 2.22 × 10 | |
| Std Dev | 2.78 × 10 | 3.24 × 10 | 3.23 × 10 | 2.74 × 10 | 4.15 × 10 | 1.35 × 10 | 3.09 × 10 | 2.09 × 10 | ||
| 10 | Mean Error | 7.97 × 10 | 2.00 × 10 | 6.49 × 10 | 1.33 × 10 | 8.00 × 10 | 2.92 × 10 | 8.78 × 10 | 2.44 × 10 | |
| Std Dev | 7.17 × 10 | 2.34 × 10 | 3.75 × 10 | 4.48 × 10 | 3.46 × 10 | 1.87 × 10 | 1.76 × 10 | 5.89 × 10 | ||
| 10 | 5 | Mean Error | 6.45 × 10 | 1.05 × 10 | 6.25 × 10 | 1.35 × 10 | 4.72 × 10 | 2.27 × 10 | 8.21 × 10 | 2.34 × 10 |
| Std Dev | 3.67 × 10 | 2.52 × 10 | 2.48 × 10 | 1.99 × 10 | 3.34 × 10 | 2.16 × 10 | 2.27 × 10 | 3.80 × 10 | ||
| 8 | Mean Error | 5.01 × 10 | 1.27 × 10 | 6.95 × 10 | 1.36 × 10 | 4.01 × 10 | 1.53 × 10 | 6.21 × 10 | 2.16 × 10 | |
| Std Dev | 2.85 × 10 | 2.85 × 10 | 3.37 × 10 | 3.03 × 10 | 2.84 × 10 | 1.01 × 10 | 2.83 × 10 | 4.54 × 10 | ||
| 10 | Mean Error | 4.46 × 10 | 2.39 × 10 | 7.63 × 10 | 1.20 × 10 | 4.54 × 10 | 1.06 × 10 | 8.03 × 10 | 2.29 × 10 | |
| Std Dev | 2.59 × 10 | 1.84 × 10 | 5.03 × 10 | 1.62 × 10 | 3.30 × 10 | 4.84 × 10 | 2.76 × 10 | 2.93 × 10 | ||
| 15 | 5 | Mean Error | 2.90 × 10 | 7.61 × 10 | 6.11 × 10 | 1.31 × 10 | 2.75 × 10 | 1.00 × 10 | 7.58 × 10 | 2.29 × 10 |
| Std Dev | 1.26 × 10 | 1.17 × 10 | 2.12 × 10 | 1.79 × 10 | 1.75 × 10 | 6.50 × 10 | 3.14 × 10 | 2.90 × 10 | ||
| 8 | Mean Error | 4.31 × 10 | 1.29 × 10 | 7.65 × 10 | 1.37 × 10 | 5.74 × 10 | 1.38 × 10 | 7.97 × 10 | 2.15 × 10 | |
| Std Dev | 1.79 × 10 | 1.34 × 10 | 3.07 × 10 | 3.05 × 10 | 5.52 × 10 | 7.06 × 10 | 2.82 × 10 | 4.34 × 10 | ||
| 10 | Mean Error | 4.63 × 10 | 2.18 × 10 | 7.55 × 10 | 1.20 × 10 | 4.33 × 10 | 2.03 × 10 | 7.65 × 10 | 2.20 × 10 | |
| Std Dev | 2.59 × 10 | 2.00 × 10 | 3.97 × 10 | 2.72 × 10 | 2.48 × 10 | 9.98 × 10 | 3.14 × 10 | 1.62 × 10 | ||
| 20 | 5 | Mean Error | 3.72 × 10 | 1.13 × 10 | 8.22 × 10 | 1.41 × 10 | 4.80 × 10 | 1.89 × 10 | 6.77 × 10 | 2.21 × 10 |
| Std Dev | 2.60 × 10 | 1.75 × 10 | 3.07 × 10 | 2.31 × 10 | 3.53 × 10 | 1.10 × 10 | 2.89 × 10 | 2.04 × 10 | ||
| 8 | Mean Error | 6.91 × 10 | 2.25 × 10 | 8.13 × 10 | 1.41 × 10 | 2.87 × 10 | 2.91 × 10 | 8.21 × 10 | 2.24 × 10 | |
| Std Dev | 3.05 × 10 | 3.72 × 10 | 3.63 × 10 | 2.46 × 10 | 1.34 × 10 | 2.62 × 10 | 3.00 × 10 | 2.92 × 10 | ||
| 10 | Mean Error | 4.29 × 10 | 1.36 × 10 | 7.70 × 10 | 1.27 × 10 | 4.46 × 10 | 1.25 × 10 | 7.47 × 10 | 2.16 × 10 | |
| Std Dev | 2.52 × 10 | 1.17 × 10 | 3.43 × 10 | 1.93 × 10 | 3.96 × 10 | 7.27 × 10 | 3.00 × 10 | 2.97 × 10 | ||
| Functions | HMWCA1 | HMWCA2 | HMWCA3 | HMWCA4 | HMWCA |
|---|---|---|---|---|---|
| Mean Error ± Std Dev /Rank | Mean Error ± Std Dev /Rank | Mean Error ± Std Dev /Rank | Mean Error ± Std Dev /Rank | Mean Error ± Std Dev /Rank | |
| 6.34 × 106 ± 3.14 × 106 /2 | 7.37 × 106 ± 5.28 × 106 /3 | 3.04 × 107 ± 1.07 × 107 /5 | 1.03 × 107 ± 2.53 × 106 /4 | 2.90 × 106 ± 1.26 × 106 /1 | |
| 1.47 × 10 ± 1.52 × 10 /3 | 1.54 × 10 ± 4.94 × 10 /1 | 2.36 × 10 ± 2.68 × 10 /5 | 8.03 × 10 ± 8.77 × 10 /4 | 5.80 × 10 ± 4.72 × 10 /2 | |
| 2.71 × 10 ± 3.26 × 10 /3 | 5.08 × 10 ± 8.21 × 10 /1 | 2.89 × 10 ± 7.60 × 10 /5 | 1.86 × 10 ± 8.72 × 10 /4 | 7.61 × 10 ± 1.17 × 10 /2 | |
| 1.20 × 10 ± 4.56 × 10 /3 | 8.12 × 10 ± 4.56 × 10 /2 | 1.91 × 10 ± 4.55 × 10 /4 | 2.14 × 10 ± 3.35 × 10 /5 | 6.11 × 10 ± 2.12 × 10 /1 | |
| 2.00 × 10 ± 4.48 × 10 /1 | 2.00 × 10 ± 1.86 × 10 /1 | 2.00 × 10 ± 3.35 × 10 /1 | 2.01 × 10 ± 6.87 × 10 /5 | 2.00 × 10 ± 2.12 × 10 /1 | |
| 2.64 × 10 ± 3.60 × 10 /3 | 2.61 × 10 ± 4.05 × 10 /2 | 3.04 × 10 ± 3.32 × 10 /4 | 5.27 × 10 ± 5.90 × 10 /5 | 2.42 × 10 ± 2.93 × 10 /1 | |
| 8.62 × 10 ± 1.05 × 10 /3 | 3.52 × 10 ± 3.86 × 10 /2 | 1.29 × 10 ± 3.79 × 10 /5 | 6.43 × 10 ± 2.87 × 10 /4 | 1.10 × 10 ± 1.18 × 10 /1 | |
| 1.10 × 10 ± 1.48 × 10 /2 | 8.26 × 10 ± 1.88 × 10 /1 | 1.33 × 10 ± 2.95 × 10 /4 | 2.30 × 10 ± 2.23 × 10 /5 | 1.10 × 10 ± 2.94 × 10 /2 | |
| 1.41 × 10 ± 3.01 × 10 /2 | 1.46 × 10 ± 4.55 × 10 /3 | 1.47 × 10 ± 2.66 × 10 /4 | 2.77 × 10 ± 4.49 × 10 /5 | 1.31 × 10 ± 1.79 × 10 /1 | |
| 2.64 × 10 ± 4.46 × 10 /3 | 2.12 × 10 ± 4.83 × 10 /2 | 3.39 × 10 ± 6.39 × 10 /4 | 4.67 × 10 ± 1.05 × 10 /5 | 1.82 × 10 ± 4.59 × 10 /1 | |
| 3.70 × 10 ± 6.28 × 10 /2 | 3.95 × 10 ± 7.07 × 10 /3 | 3.95 × 10 ± 6.05 × 10 /3 | 6.77 × 10 ± 1.14 × 10 /5 | 3.56 × 10 ± 5.39 × 10 /1 | |
| 6.24 × 10 ± 2.83 × 10 /2 | 1.03 × 10 ± 4.80 × 10 /3 | 1.32 × 10 ± 6.11 × 10 /4 | 1.65 × 10 ± 6.49 × 10 /5 | 6.21 × 10 ± 2.09 × 10 /1 | |
| 4.99 × 10 ± 1.40 × 10 /3 | 4.80 × 10 ± 1.13 × 10 /2 | 5.39 × 10 ± 1.26 × 10 /4 | 5.77 × 10 ± 1.04 × 10 /5 | 4.20 × 10 ± 6.11 × 10 /1 | |
| 2.85 × 10 ± 5.61 × 10 /1 | 3.33 × 10 ± 1.07 × 10 /5 | 3.04 × 10 ± 4.05 × 10 /2 | 3.17 × 10 ± 4.21 × 10 /4 | 3.05 × 10 ± 5.20 × 10 /3 | |
| 5.12 × 10 ± 2.21 × 10 /3 | 3.44 × 10 ± 1.13 × 10 /2 | 5.15 × 10 ± 1.73 × 10 /4 | 1.36 × 10 ± 2.19 × 10 /5 | 3.11 × 10 ± 9.66 × 10 /1 | |
| 1.24 × 10 ± 6.40 × 10 /2 | 1.28 × 10 ± 5.10 × 10 /4 | 1.27 × 10 ± 4.50 × 10 /3 | 2.21 × 10 ± 2.92 × 10 /5 | 1.21 × 10 ± 5.98 × 10 /1 | |
| 5.13 × 10 ± 3.13 × 10 /2 | 7.28 × 10 ± 6.17 × 10 /3 | 1.14 × 10 ± 9.40 × 10 /4 | 1.99 × 10 ± 1.23 × 10 /5 | 2.75 × 10 ± 1.75 × 10 /1 | |
| 1.08 × 10 ± 1.33 × 10 /2 | 4.32 × 10 ± 7.55 × 10 /4 | 1.70 × 10 ± 2.14 × 10 /3 | 4.75 × 10 ± 4.96 × 10 /5 | 5.19 × 10 ± 3.36 × 10 /1 | |
| 1.71 × 10 ± 3.84 × 10 /2 | 1.56 × 10 ± 3.27 × 10 /1 | 2.51 × 10 ± 3.54 × 10 /4 | 5.86 × 10 ± 3.28 × 10 /5 | 1.79 × 10 ± 3.05 × 10 /3 | |
| 5.51 × 10 ± 3.94 × 10 /3 | 5.37 × 10 ± 6.11 × 10 /2 | 6.59 × 10 ± 5.28 × 10 /4 | 2.72 × 10 ± 1.09 × 10 /5 | 3.80 × 10 ± 2.14 × 10 /1 | |
| 1.90 × 10 ± 2.03 × 10 /2 | 2.48 × 10 ± 1.69 × 10 /3 | 3.45 × 10 ± 2.61 × 10 /4 | 1.31 × 10 ± 7.29 × 10 /5 | 1.00 × 10 ± 6.50 × 10 /1 | |
| 7.39 × 10 ± 1.76 × 10 /3 | 6.36 × 10 ± 1.84 × 10 /1 | 8.24 × 10 ± 2.30 × 10 /4 | 1.44 × 10 ± 3.84 × 10 /5 | 6.37 × 10 ± 1.27 × 10 /2 | |
| 3.14 × 10 ± 4.68 × 10 /1 | 3.14 × 10 ± 2.00 × 10 /1 | 3.26 × 10 ± 8.14 × 10 /4 | 3.37 × 10 ± 2.96 × 10 /5 | 3.14 × 10 ± 5.50 × 10 /1 | |
| 2.31 × 10 ± 3.31 × 10 /2 | 2.44 × 10 ± 6.21 × 10 /4 | 2.29 × 10 ± 2.83 × 10 /1 | 2.80 × 10 ± 1.14 × 10 /5 | 2.31 × 10 ± 6.54 × 10 /2 | |
| 2.12 × 10 ± 2.75 × 10 /3 | 2.06 × 10 ± 8.45 × 10 /1 | 2.11 × 10 ± 3.58 × 10 /2 | 2.30 × 10 ± 7.12 × 10 /5 | 2.12 × 10 ± 1.61 × 10 /3 | |
| 1.01 × 10 ± 1.15 × 10 /2 | 1.01 × 10 ± 1.62 × 10 /2 | 1.01 × 10 ± 7.34 × 10 /2 | 1.60 × 10 ± 5.15 × 10 /5 | 1.00 × 10 ± 1.18 × 10 /1 | |
| 8.07 × 10 ± 3.40 × 10 /3 | 8.33 × 10 ± 3.08 × 10 /4 | 6.44 × 10 ± 3.39 × 10 /1 | 1.68 × 10 ± 1.11 × 10 /5 | 7.58 × 10 ± 3.14 × 10 /2 | |
| 5.80 × 10 ± 1.83 × 10 /4 | 4.87 × 10 ± 9.00 × 10 /1 | 1.52 × 10 ± 7.50 × 10 /5 | 5.44 × 10 ± 1.14 × 10 /3 | 5.43 × 10 ± 1.18 × 10 /2 | |
| 3.02 × 10 ± 2.74 × 10 /5 | 2.19 × 10 ± 2.01 × 10 /1 | 2.51 × 10 ± 3.53 × 10 /3 | 2.63 × 10 ± 4.03 × 10 /4 | 2.29 × 10 ± 2.90 × 10 /2 | |
| 1.04 × 10 ± 5.44 × 10 /3 | 9.79 × 10 ± 3.11 × 10 /2 | 1.55 × 10 ± 2.83 × 10 /5 | 1.63 × 10 ± 6.12 × 10 /4 | 9.38 × 10 ± 7.82 × 10 /1 | |
| Sum Rank | 75 | 67 | 107 | 141 | 44 |
| Average Rank | 2.5 | 2.23 | 3.57 | 4.7 | 1.47 |
| Algorithms | Parameter Setting |
|---|---|
| GSA | , , |
| HSOGA | , , , , , , |
| CLPSO | , , , , m = 5 |
| WCA | , , |
| CWCA | , , , , , , |
| ER_WCA | , , |
| HMWCA | , , , , , |
| Function | Algorithm | WCA | CWCA | ER_WCA | GSA | CLPSO | HSOGA | HMWCA |
|---|---|---|---|---|---|---|---|---|
| Mean Error | 2.82 × 10 − | 6.00 × 10 + | 1.32 × 10 − | 9.10 × 10 + | 1.04 × 10 + | 1.91 × 10 + | 2.90 × 10 | |
| Std Dev /Rank | 1.05 × 10 /2 | 4.88 × 10 /4 | 6.07 × 10 /1 | 2.37 × 10 /5 | 3.12 × 10 /6 | 2.49 × 10 /7 | 1.26 × 10 /3 | |
| Mean Error | 1.07 × 10 + | 2.93 × 10 + | 1.36 × 10 + | 1.12 × 10 + | 2.93 × 10 + | 5.68 × 10 + | 5.80 × 10 | |
| Std Dev /Rank | 1.01 × 10 /2 | 2.12 × 10 /4 | 1.04 × 10 /3 | 3.17 × 10 /5 | 7.69 × 10 /6 | 1.00 × 10 /7 | 4.72 × 10 /1 | |
| Mean Error | 3.99 × 10 + | 2.02 × 10 + | 8.53 × 10 + | 8.71 × 10 + | 6.46 × 10 + | 2.30 × 10+ | 7.61 × 10 | |
| Std Dev /Rank | 2.56 × 10 /3 | 1.85 × 10 /4 | 9.62 × 10 /2 | 7.63 × 10 /7 | 2.94 × 10 /5 | 5.09 × 10 /6 | 1.17 × 10 /1 | |
| Mean Error | 1.03 × 10 + | 1.36 × 10 + | 7.99 × 10 + | 3.92 × 10 + | 2.30 × 10 + | 5.02 × 10 + | 6.11 × 10 | |
| Std Dev /Rank | 3.22 × 10 /3 | 6.46 × 10 /4 | 2.71 × 10 /2 | 1.07 × 10 /6 | 2.80 × 10 /5 | 6.48 × 10 /7 | 2.12 × 10 /1 | |
| Mean Error | 2.01 × 10 + | 2.01 × 10 + | 2.01 × 10 + | 2.00 × 10 ≈ | 2.07 × 10 + | 2.10 × 10 + | 2.00 × 10 | |
| Std Dev /Rank | 8.27 × 10 /3 | 6.84 × 10 /3 | 9.23 × 10 /3 | 5.71 × 10 /1 | 5.05 × 10 /6 | 5.92 × 10 /7 | 2.73 × 10 /1 | |
| Mean Error | 3.10 × 10 + | 2.52 × 10 + | 3.03 × 10 + | 2.47 × 10 + | 2.30 × 10 − | 3.17 × 10 + | 2.42 × 10 | |
| Std Dev /Rank | 3.45 × 10 /6 | 3.28 × 10 /4 | 3.55 × 10 /5 | 2.11 × 10 /3 | 1.61 × 10 /1 | 1.86 × 10 /7 | 2.93 × 10 /2 | |
| Mean Error | 2.19 × 10 + | 9.12 × 10 + | 1.13 × 10 + | 1.33 × 10 + | 1.19 × 10 + | 4.27 × 10 + | 1.10 × 10 | |
| Std Dev /Rank | 1.90 × 10 /3 | 4.97 × 10 /4 | 1.30 × 10 /2 | 1.69 × 10 /6 | 6.56 × 10 /5 | 6.12 × 10 /7 | 1.18 × 10 /1 | |
| Mean Error | 1.51 × 10 + | 7.45 × 10 − | 1.73 × 10 + | 1.41 × 10 + | 1.80 × 10 − | 1.36 × 10 + | 1.10 × 10 | |
| Std Dev /Rank | 2.99 × 10 /6 | 2.68 × 10 /2 | 4.28 × 10 /7 | 1.22 × 10 /5 | 3.23 × 10 /1 | 1.04 × 10 /4 | 2.94 × 10 /3 | |
| Mean Error | 1.82 × 10 + | 2.39 × 10 + | 1.82 × 10 + | 1.65 × 10 + | 1.43 × 10 + | 2.28 × 10 + | 1.31 × 10 | |
| Std Dev /Rank | 4.10 × 10 /4 | 5.35 × 10 /7 | 4.93 × 10 /4 | 2.11 × 10 /3 | 1.22 × 10 /2 | 1.88 × 10 /6 | 1.79 × 10 /1 | |
| Mean Error | 4.00 × 10 + | 1.84 × 10 + | 3.64 × 10 + | 3.85 × 10 + | 3.71 × 10 + | 1.89 × 10 + | 1.82 × 10 | |
| Std Dev /Rank | 8.84 × 10 /7 | 6.25 × 10 /2 | 6.58 × 10 /4 | 4.76 × 10 /6 | 1.02 × 10 /5 | 1.85 × 10 /3 | 4.59 × 10 /1 | |
| Mean Error | 4.23 × 10 + | 3.72 × 10 + | 4.55 × 10 + | 4.48 × 10 + | 4.44 × 10 + | 7.22 × 10 + | 3.56 × 10 | |
| Std Dev /Rank | 1.02 × 10 /3 | 6.81 × 10 /2 | 7.33 × 10 /6 | 6.12 × 10 /5 | 2.79 × 10 /4 | 3.29 × 10 /7 | 5.39 × 10 /1 | |
| Mean Error | 1.40 × 10 + | 3.60 × 10 − | 1.51 × 10 + | 5.59 × 10 − | 9.08 × 10 + | 2.61 × 10 + | 6.21 × 10 | |
| Std Dev /Rank | 5.34 × 10 /5 | 1.08 × 10 /2 | 5.67 × 10 /6 | 4.62 × 10 /1 | 1.52 × 10 /4 | 4.56 × 10 /7 | 2.09 × 10 /3 | |
| Mean Error | 5.41 × 10 + | 7.67 × 10 + | 5.62 × 10 + | 3.66 × 10 − | 3.89 × 10 − | 9.30 × 10 + | 4.20 × 10 | |
| Std Dev /Rank | 1.19 × 10 /4 | 1.31 × 10 /6 | 1.56 × 10 /5 | 6.61 × 10 /1 | 4.75 × 10 /2 | 1.77 × 10 /7 | 6.11 × 10 /3 | |
| Mean Error | 3.46 × 10 + | 9.83 × 10 + | 4.69 × 10 + | 5.43 × 10 + | 3.43 × 10 + | 1.43 × 10 + | 3.05 × 10 | |
| Std Dev /Rank | 1.32 × 10 /3 | 3.64 × 10 /6 | 2.33 × 10 /4 | 1.50 × 10 /5 | 3.30 × 10 /2 | 3.63 × 10 /7 | 5.20 × 10 /1 | |
| Mean Error | 3.24 × 10 + | 2.65 × 10 − | 4.88 × 10 + | 3.28 × 10 + | 2.65 × 10 − | 7.75 × 10 + | 3.11 × 10 | |
| Std Dev /Rank | 1.19 × 10 /4 | 1.41 × 10 /1 | 3.34 × 10 /6 | 1.37 × 10 /5 | 2.92 × 10 /1 | 4.76 × 10 /7 | 9.66 × 10 /3 | |
| Mean Error | 1.27 × 10 + | 1.21 × 10 ≈ | 1.29 × 10 + | 1.37 × 10 + | 1.19 × 10 − | 1.31 × 10 + | 1.21 × 10 | |
| Std Dev /Rank | 4.62 × 10 /4 | 5.50 × 10 /2 | 4.58 × 10 /5 | 2.02 × 10 /7 | 3.18 × 10 /1 | 2.63 × 10 /6 | 5.98 × 10 /2 | |
| Mean Error | 2.91 × 10 + | 6.40 × 10 + | 9.12 × 10 − | 7.50 × 10 + | 6.60 × 10 + | 2.24 × 10 + | 2.75 × 10 | |
| Std Dev /Rank | 1.75 × 10 /3 | 5.92 × 10 /4 | 5.37 × 10 /1 | 2.83 × 10 /7 | 3.85 × 10 /6 | 8.12 × 10 /5 | 1.75 × 10 /2 | |
| Mean Error | 5.26 × 10 + | 1.33 × 10 + | 5.01 × 10 + | 5.24 × 10 + | 5.31 × 10 + | 2.04 × 10 + | 5.19 × 10 | |
| Std Dev /Rank | 6.44 × 10 /4 | 1.04 × 10 /5 | 6.27 × 10 /3 | 4.55 × 10 /2 | 4.55 × 10 /6 | 7.96 × 10 /7 | 3.36 × 10 /1 | |
| Mean Error | 3.99 × 10 + | 4.75 × 10 + | 2.38 × 10 + | 1.32 × 10 + | 2.78 × 10 + | 5.15 × 10 + | 1.79 × 10 | |
| Std Dev /Rank | 4.12 × 10 /4 | 4.52 × 10 /5 | 2.31 × 10 /2 | 3.63 × 10 /7 | 1.04 × 10 /3 | 1.17 × 10 /6 | 3.05 × 10 /1 | |
| Mean Error | 4.46 × 10 + | 2.57 × 10 + | 1.04 × 10 − | 2.48 × 10 + | 1.11 × 10 + | 1.64 × 10 + | 3.80 × 10 | |
| Std Dev /Rank | 3.42 × 10 /3 | 1.66 × 10 /6 | 7.08 × 10 /1 | 1.21 × 10 /7 | 4.72 × 10 /4 | 5.58 × 10 /5 | 2.14 × 10 /2 | |
| Mean Error | 1.03 × 10 + | 2.34 × 10 + | 4.19 × 10 + | 2.74 × 10 + | 8.31 × 10 + | 5.99 × 10 + | 1.00 × 10 | |
| Std Dev /Rank | 6.59 × 10 /2 | 1.62 × 10 /3 | 1.66 × 10 /4 | 1.35 × 10 /7 | 4.29 × 10 /6 | 1.89 × 10 /5 | 6.50 × 10 /1 | |
| Mean Error | 6.43 × 10 + | 6.81 × 10 + | 6.66 × 10 + | 1.17 × 10 + | 4.01 × 10 − | 6.38 × 10 + | 6.37 × 10 | |
| Std Dev /Rank | 2.50 × 10 /4 | 2.46 × 10 /6 | 1.98 × 10 /5 | 3.02 × 10 /7 | 1.07 × 10 /1 | 1.32 × 10 /3 | 1.27 × 10 /2 | |
| Mean Error | 3.15 × 10 + | 3.16 × 10 + | 3.15 × 10 + | 2.69 × 10 − | 3.20 × 10 + | 3.45 × 10 + | 3.14 × 10 | |
| Std Dev /Rank | 1.70 × 10 /3 | 1.67 × 10 /5 | 9.38 × 10 /3 | 7.39 × 10 /1 | 1.59 × 10 /6 | 2.54 × 10 /7 | 5.50 × 10 /2 | |
| Mean Error | 2.43 × 10 + | 2.45 × 10 + | 2.43 × 10 + | 2.03 × 10 − | 2.35 × 10 + | 2.09 × 10 − | 2.31 × 10 | |
| Std Dev /Rank | 1.02 × 10 /5 | 6.35 × 10 /7 | 1.07 × 10 /5 | 6.21 × 10 /1 | 3.03 × 10 /4 | 3.45 × 10 /2 | 6.54 × 10 /3 | |
| Mean Error | 2.21 × 10 + | 2.12 × 10 ≈ | 2.24 × 10 + | 2.02 × 10 − | 2.17 × 10 + | 2.04 × 10 − | 2.12 × 10 | |
| Std Dev /Rank | 1.02 × 10 /6 | 7.77 × 10 /3 | 9.17 × 10 /7 | 3.38 × 10 /1 | 2.58 × 10 /5 | 2.09 × 10 /2 | 1.61 × 10 /3 | |
| Mean Error | 1.13 × 10 + | 1.01 × 10 + | 1.09 × 10 + | 1.98 × 10 + | 1.01 × 10 + | 1.01 × 10 + | 1.00 × 10 | |
| Std Dev /Rank | 3.30 × 10 /6 | 2.15 × 10 /2 | 2.75 × 10 /5 | 1.19 × 10 /7 | 7.98 × 10 /2 | 3.53 × 10 /2 | 1.18 × 10 /1 | |
| Mean Error | 9.20 × 10 + | 9.36 × 10 + | 1.04 × 10 + | 1.81 × 10 + | 4.94 × 10 − | 1.07 × 10 + | 7.58 × 10 | |
| Std Dev /Rank | 3.69 × 10 /3 | 2.75 × 10 /4 | 3.34 × 10 /5 | 4.19 × 10 /7 | 4.79 × 10 /1 | 3.53 × 10 /6 | 3.14 × 10 /2 | |
| Mean Error | 1.89 × 10 + | 1.39 × 10 + | 1.82 × 10 + | 2.52 × 10 + | 1.51 × 10 + | 8.46 × 10 + | 5.43 × 10 | |
| Std Dev /Rank | 5.19 × 10 /6 | 4.32 × 10 /3 | 6.15 × 10 /5 | 8.18 × 10 /7 | 2.96 × 10 /4 | 1.14 × 10 /2 | 1.18 × 10 /1 | |
| Mean Error | 5.44 × 10 + | 7.23 × 10 + | 8.48 × 10 + | 1.44 × 10 + | 9.69 × 10 + | 8.30 × 10 + | 2.29 × 10 | |
| Std Dev /Rank | 9.48 × 10 /6 | 2.49 × 10 /5 | 8.97 × 10 /7 | 7.19 × 10 /4 | 5.71 × 10 /3 | 2.40 × 10 /2 | 2.90 × 10 /1 | |
| Mean Error | 1.82 × 10 + | 6.71 × 10 + | 6.51 × 10 + | 2.28 × 10 + | 4.04 × 10 + | 2.19 × 10 + | 9.38 × 10 | |
| Std Dev /Rank | 1.75 × 10 /5 | 9.54 × 10 /4 | 3.24 × 10 /3 | 1.09 × 10 /7 | 1.46 × 10 /6 | 4.75 × 10 /2 | 7.82 × 10 /1 | |
| Average Rank | 4.07 | 3.97 | 4.37 | 4.77 | 3.77 | 5.27 | 1.7 | |
| + | 29 | 25 | 27 | 24 | 23 | 29 | ||
| - | 1 | 3 | 3 | 5 | 7 | 1 | ||
| ≈ | 0 | 2 | 0 | 1 | 0 | 0 | ||
| Function | Algorithm | WCA | CWCA | ER_WCA | GSA | CLPSO | HSOGA | HMWCA |
|---|---|---|---|---|---|---|---|---|
| Mean Error | 7.78 × 10 + | 2.38 × 10 + | 5.50 × 10 − | 3.93 × 10 + | 2.37 × 10 + | 7.62 × 10 + | 6.76 × 10 | |
| Std Dev /Rank | 1.84 × 10 /3 | 1.18 × 10 /4 | 1.41 × 10 /1 | 3.05 × 10 /6 | 6.61 × 10 /5 | 1.24 × 10 /7 | 2.17 × 10 /2 | |
| Mean Error | 1.31 × 10 − | 1.16 × 10 + | 8.17 × 10 − | 2.04 × 10 + | 1.25 × 10 + | 5.15 × 10 + | 3.93 × 10 | |
| Std Dev /Rank | 8.55 × 10 /2 | 2.61 × 10 /4 | 9.44 × 10 /1 | 3.40 × 10 /6 | 2.83 × 10 /4 | 5.66 × 10 /7 | 2.58 × 10 /3 | |
| Mean Error | 1.07 × 10 − | 1.05 × 10 + | 5.07 × 10 − | 1.56 × 10 + | 6.01 × 10 + | 1.67 × 10 + | 1.50 × 10 | |
| Std Dev /Rank | 4.72 × 10 /2 | 3.77 × 10 /4 | 3.33 × 10 /1 | 9.58 × 10 /6 | 1.15 × 10 /4 | 1.73 × 10 /7 | 6.75 × 10 /3 | |
| Mean Error | 1.40 × 10 − | 4.81 × 10 + | 1.04 × 10 − | 2.91 × 10 + | 7.83 × 10 + | 7.37 × 10 + | 2.03 × 10 | |
| Std Dev /Rank | 5.19 × 10 /2 | 2.94 × 10 /4 | 4.73 × 10 /1 | 6.40 × 10 /6 | 8.79 × 10 /5 | 1.28 × 10 /7 | 3.04 × 10 /3 | |
| Mean Error | 2.01 × 10 + | 2.03 × 10 + | 2.01 × 10 + | 2.00 × 10 ≈ | 2.08 × 10 + | 2.12 × 10 + | 2.00 × 10 | |
| Std Dev /Rank | 1.35 × 10 /3 | 9.38 × 10 /5 | 9.13 × 10 /3 | 1.06 × 10 /1 | 3.21 × 10 /6 | 5.27 × 10 /7 | 3.58 × 10 /1 | |
| Mean Error | 5.91 × 10 + | 4.91 × 10 − | 5.84 × 10 + | 5.30 × 10 + | 5.14 × 10 − | 6.71 × 10 + | 5.16 × 10 | |
| Std Dev /Rank | 4.80 × 10 /6 | 4.63 × 10 /1 | 7.92 × 10 /5 | 2.74 × 10 /4 | 2.27 × 10 /2 | 1.86 × 10 /7 | 3.18 × 10 /3 | |
| Mean Error | 4.30 × 10 − | 1.01 × 10 + | 8.53 × 10 − | 2.02 × 10 + | 1.09 × 10 + | 5.09 × 10 + | 4.64 × 10 | |
| Std Dev /Rank | 2.06 × 10 /2 | 2.74 × 10 /4 | 7.12 × 10 /1 | 3.14 × 10 /6 | 2.70 × 10 /5 | 6.57 × 10 /7 | 1.93 × 10 /3 | |
| Mean Error | 3.00 × 10 + | 2.21 × 10 + | 3.03 × 10 + | 2.77 × 10 + | 9.14 × 10 − | 3.97 × 10 + | 1.93 × 10 | |
| Std Dev /Rank | 3.96 × 10 /5 | 4.77 × 10 /3 | 6.53 × 10 /6 | 1.80 × 10 /4 | 8.54 × 10 /1 | 2.59 × 10 /7 | 2.86 × 10 /2 | |
| Mean Error | 4.01 × 10 + | 5.14 × 10 + | 3.94 × 10 + | 3.55 × 10 + | 3.76 × 10 + | 5.54 × 10 + | 2.58 × 10 | |
| Std Dev /Rank | 7.32 × 10 /5 | 7.88 × 10 /6 | 5.73 × 10 /4 | 2.82 × 10 /2 | 2.54 × 10 /3 | 3.21 × 10 /7 | 6.46 × 10 /1 | |
| Mean Error | 7.29 × 10 + | 4.26 × 10 − | 6.93 × 10 + | 7.52 × 10 + | 2.49 × 10 − | 7.41 × 10 + | 4.72 × 10 | |
| Std Dev /Rank | 8.50 × 10 /5 | 1.10 × 10 /2 | 8.71 × 10 /4 | 7.19 × 10 /7 | 2.68 × 10 /1 | 5.42 × 10 /6 | 8.04 × 10 /3 | |
| Mean Error | 8.08 × 10 + | 7.19 × 10 + | 7.80 × 10 + | 8.17 × 10 + | 9.29 × 10 + | 1.39 × 10 + | 6.88 × 10 | |
| Std Dev /Rank | 1.40 × 10 /4 | 6.86 × 10 /2 | 1.03 × 10 /3 | 8.54 × 10 /5 | 4.63 × 10 /6 | 4.12 × 10 /7 | 5.96 × 10 /1 | |
| Mean Error | 2.16 × 10 + | 6.29 × 10 − | 2.13 × 10 + | 1.28 × 10 − | 1.18 × 10 − | 4.07 × 10 + | 1.24 × 10 | |
| Std Dev /Rank | 6.70 × 10 /6 | 1.85 × 10 /2 | 8.20 × 10 /5 | 6.79 × 10 /1 | 1.34 × 10 /3 | 3.90 × 10 /7 | 2.90 × 10 /4 | |
| Mean Error | 6.25 × 10 + | 8.01 × 10 + | 6.31 × 10 + | 2.87 × 10 + | 5.36 × 10 − | 4.98 × 10 + | 5.81 × 10 | |
| Std Dev /Rank | 8.50 × 10 /3 | 1.40 × 10 /5 | 1.50 × 10 /4 | 5.98 × 10 /6 | 7.86 × 10 /1 | 3.24 × 10 /7 | 5.33 × 10 /2 | |
| Mean Error | 4.15 × 10 + | 2.62 × 10 + | 3.84 × 10 + | 4.33 × 10 + | 4.88 × 10 + | 1.18 × 10 + | 3.30 × 10 | |
| Std Dev /Rank | 1.92 × 10 /3 | 5.25 × 10 /5 | 1.32 × 10 /2 | 7.20 × 10 /6 | 8.13 × 10 /4 | 1.33 × 10 /7 | 3.79 × 10 /1 | |
| Mean Error | 8.77 × 10 − | 1.05 × 10 + | 1.26 × 10 + | 9.76 × 10 + | 7.27 × 10 + | 2.16 × 10 + | 1.07 × 10 | |
| Std Dev /Rank | 2.33 × 10 /1 | 3.36 × 10 /6 | 4.38 × 10 /3 | 6.07 × 10 /5 | 3.30 × 10 /4 | 7.80 × 10 /7 | 1.84 × 10 /2 | |
| Mean Error | 2.24 × 10 + | 2.14 × 10 − | 2.24 × 10 + | 2.26 × 10 + | 2.14 × 10 − | 2.30 × 10 + | 2.16 × 10 | |
| Std Dev /Rank | 6.51 × 10 /4 | 5.88 × 10 /1 | 5.65 × 10 /4 | 3.45 × 10 /6 | 3.12 × 10 /1 | 1.55 × 10 /7 | 9.07 × 10 /3 | |
| Mean Error | 7.90 × 10 − | 4.06 × 10 + | 3.34 × 10 − | 2.69 × 10 + | 4.03 × 10 + | 7.84 × 10 + | 1.73 × 10 | |
| Std Dev /Rank | 2.82 × 10 /2 | 2.50 × 10 /4 | 1.55 × 10 /1 | 1.07 × 10 /5 | 1.36 × 10 /6 | 1.69 × 10 /7 | 5.87 × 10 /3 | |
| Mean Error | 2.77 × 10 + | 5.49 × 10 + | 2.92 × 10 + | 3.16 × 10 + | 9.25 × 10 + | 8.58 × 10 + | 2.13 × 10 | |
| Std Dev /Rank | 1.92 × 10 /2 | 2.22 × 10 /4 | 2.07 × 10 /3 | 6.70 × 10 /6 | 4.50 × 10 /5 | 1.70 × 10 /7 | 1.15 × 10 /1 | |
| Mean Error | 6.39 × 10 + | 6.91 × 10 + | 7.20 × 10 + | 1.72 × 10 + | 9.43 × 10 + | 3.85 × 10 + | 5.22 × 10 | |
| Std Dev /Rank | 3.00 × 10 /2 | 3.31 × 10 /3 | 2.59 × 10 /4 | 3.22 × 10 /6 | 1.20 × 10 /5 | 5.60 × 10 /7 | 3.23 × 10 /1 | |
| Mean Error | 6.07 × 10 − | 7.20 × 10 + | 2.53 × 10 − | 1.99 × 10 + | 4.90 × 10 + | 7.17 × 10 + | 1.81 × 10 | |
| Std Dev /Rank | 3.89 × 10 /2 | 3.24 × 10 /6 | 1.67 × 10 /1 | 8.45 × 10 /7 | 1.00 × 10 /4 | 2.48 × 10 /5 | 1.34 × 10 /3 | |
| Mean Error | 4.71 × 10 − | 1.83 × 10 + | 2.03 × 10 − | 4.58 × 10 + | 1.21 × 10 + | 1.65 × 10 + | 9.98 × 10 | |
| Std Dev /Rank | 2.64 × 10 /2 | 1.16 × 10 /4 | 1.16 × 10 /1 | 1.08 × 10 /5 | 4.48 × 10 /6 | 6.04 × 10 /7 | 5.53 × 10 /3 | |
| Mean Error | 1.50 × 10 + | 1.51 × 10 + | 1.55 × 10 + | 2.15 × 10 + | 1.48 × 10 + | 2.25 × 10 + | 1.13 × 10 | |
| Std Dev /Rank | 3.82 × 10 /3 | 3.31 × 10 /4 | 3.86 × 10 /5 | 3.95 × 10 /6 | 2.17 × 10 /2 | 1.88 × 10 /7 | 2.89 × 10 /1 | |
| Mean Error | 3.45 × 10 + | 3.59 × 10 + | 3.44 × 10 + | 2.55 × 10 − | 3.92 × 10 + | 3.31 × 10 − | 3.37 × 10 | |
| Std Dev /Rank | 1.28 × 10 /5 | 1.39 × 10 /6 | 2.69 × 10 /4 | 1.52 × 10 /1 | 1.08 × 10 /7 | 7.84 × 10 /2 | 1.70 × 10 /3 | |
| Mean Error | 3.00 × 10 + | 2.97 × 10 + | 3.08 × 10 + | 2.40 × 10 − | 2.93 × 10 + | 2.17 × 10 − | 2.84 × 10 | |
| Std Dev /Rank | 9.52 × 10 /6 | 1.63 × 10 /5 | 1.16 × 10 /7 | 1.66 × 10 /2 | 1.91 × 10 /4 | 6.62 × 10 /1 | 1.13 × 10 /3 | |
| Mean Error | 2.45 × 10 + | 2.24 × 10 − | 2.44 × 10 + | 2.04 × 10 − | 2.54 × 10 + | 2.03 × 10 − | 2.27 × 10 | |
| Std Dev /Rank | 1.03 × 10 /6 | 9.48 × 10 /3 | 1.11 × 10 /5 | 5.55 × 10 /2 | 7.41 × 10 /7 | 1.69 × 10 /1 | 1.25 × 10 /4 | |
| Mean Error | 1.75 × 10 + | 1.25 × 10 + | 2.32 × 10 − | 2.00 × 10 + | 1.24 × 10 − | 1.07 × 10 − | 1.50 × 10 | |
| Std Dev /Rank | 7.59 × 10 /5 | 6.78 × 10 /7 | 1.01 × 10 /3 | 1.00 × 10 /6 | 3.78 × 10 /2 | 5.61 × 10 /1 | 5.27 × 10 /4 | |
| Mean Error | 1.87 × 10 + | 1.62 × 10 − | 1.85 × 10 + | 3.25 × 10 + | 1.63 × 10 − | 2.00 × 10 + | 1.67 × 10 | |
| Std Dev /Rank | 1.26 × 10 /5 | 1.07 × 10 /1 | 1.28 × 10 /4 | 4.99 × 10 /7 | 1.80 × 10 /2 | 4.42 × 10 /6 | 1.62 × 10 /3 | |
| Mean Error | 3.64 × 10 + | 2.81 × 10 + | 3.65 × 10 + | 5.93 × 10 + | 4.24 × 10 + | 8.26 × 10 + | 4.74 × 10 | |
| Std Dev /Rank | 1.03 × 10 /4 | 6.16 × 10 /3 | 9.26 × 10 /5 | 1.41 × 10 /7 | 8.98 × 10 /6 | 1.17 × 10 /2 | 4.71 × 10 /1 | |
| Mean Error | 1.23 × 10+ | 9.22 × 10 + | 1.08 × 10 + | 2.02 × 10 − | 5.93 × 10 + | 5.19 × 10 + | 2.37 × 10 | |
| Std Dev /Rank | 1.06 × 10 /7 | 1.88 × 10 /5 | 7.85 × 10 /6 | 3.72 × 10 /1 | 2.02 × 10 /4 | 2.06 × 10 /3 | 1.73 × 10 /2 | |
| Mean Error | 4.31 × 10 + | 1.65 × 10 + | 1.88 × 10 + | 3.17 × 10 + | 2.41 × 10 + | 7.38 × 10 + | 1.91 × 10 | |
| Std Dev /Rank | 5.51 × 10 /4 | 3.71 × 10 /2 | 4.31 × 10 /3 | 3.72 × 10 /7 | 8.66 × 10 /6 | 7.47 × 10 /5 | 4.21 × 10 /1 | |
| Average Rank | 3.7 | 3.83 | 3.33 | 4.77 | 4.03 | 5.73 | 2.33 | |
| + | 22 | 24 | 21 | 24 | 22 | 26 | ||
| - | 8 | 6 | 9 | 5 | 8 | 4 | ||
| ≈ | 0 | 0 | 0 | 1 | 0 | 0 | ||
| Function | ||||||
|---|---|---|---|---|---|---|
| HMWCA | 54.22 s | 55.87 s | 53.23 s | 54.98 s | 59.72 s | 56.70 s |
| WCA | 30.70 s | 24.16 s | 31.03 s | 25.37 s | 29.44 s | 28.16 s |
| GSA | 116.60 s | 115.87 s | 115.40 s | 116.58 s | 115.99 s | 116.55 s |
| Algorithm | Best (Result) | Worse (Result) | Average Value | Standard Deviation |
|---|---|---|---|---|
| WCA | 3.62 × 10 | 2.57 × 10 | 3.09 × 10 | 4.00 × 10 |
| CWCA | 3.35 × 10 | 2.46 × 10 | 3.02 × 10 | 3.14 × 10 |
| ER_WCA | 3.44 × 10 | 2.68 × 10 | 2.93 × 10 | 2.34 × 10 |
| HMWCA | 3.27 10 is versio | 2.29 × 10 | 2.77 × 10 | 3.16 × 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, M.; Liu, J.; Yue, W.; Zhou, J. A Novel Integrated Heuristic Optimizer Using a Water Cycle Algorithm and Gravitational Search Algorithm for Optimization Problems. Mathematics 2023, 11, 1880. https://doi.org/10.3390/math11081880
Tian M, Liu J, Yue W, Zhou J. A Novel Integrated Heuristic Optimizer Using a Water Cycle Algorithm and Gravitational Search Algorithm for Optimization Problems. Mathematics. 2023; 11(8):1880. https://doi.org/10.3390/math11081880
Chicago/Turabian StyleTian, Mengnan, Junhua Liu, Wei Yue, and Jie Zhou. 2023. "A Novel Integrated Heuristic Optimizer Using a Water Cycle Algorithm and Gravitational Search Algorithm for Optimization Problems" Mathematics 11, no. 8: 1880. https://doi.org/10.3390/math11081880
APA StyleTian, M., Liu, J., Yue, W., & Zhou, J. (2023). A Novel Integrated Heuristic Optimizer Using a Water Cycle Algorithm and Gravitational Search Algorithm for Optimization Problems. Mathematics, 11(8), 1880. https://doi.org/10.3390/math11081880





