Blockchain-Assisted Hybrid Harris Hawks Optimization Based Deep DDoS Attack Detection in the IoT Environment

Abstract

The Internet of Things (IoT) is developing as a novel phenomenon that is applied in the growth of several crucial applications. However, these applications continue to function on a centralized storage structure, which leads to several major problems, such as security, privacy, and a single point of failure. In recent years, blockchain (BC) technology has become a pillar for the progression of IoT-based applications. The BC technique is utilized to resolve the security, privacy, and single point of failure (third-part dependency) issues encountered in IoT applications. Conversely, the distributed denial of service (DDoS) attacks on mining pools revealed the existence of vital fault lines amongst the BC-assisted IoT networks. Therefore, the current study designs a hybrid Harris Hawks with sine cosine and a deep learning-based intrusion detection system (H3SC-DLIDS) for a BC-supported IoT environment. The aim of the presented H3SC-DLIDS approach is to recognize the presence of DDoS attacks in the BC-assisted IoT environment. To enable secure communication in the IoT networks, BC technology is used. The proposed H3SC-DLIDS technique designs a H3SC technique by integrating the concepts of Harris Hawks optimization (HHO) and sine cosine algorithm (SCA) for feature selection. For the intrusion detection process, a long short-term memory auto-encoder (LSTM-AE) model is utilized in this study. Finally, the arithmetic optimization algorithm (AOA) is implemented for hyperparameter tuning of the LSTM-AE technique. The proposed H3SC-DLIDS method was experimentally validated using the BoT-IoT database, and the results indicate the superior performance of the proposed H3SC-DLIDS technique over other existing methods, with a maximum accuracy of 99.05%.

1. Introduction

With the evolution of the internet, the Internet of Things (IoT) has developed as an innovative technology and has penetrated the day-to-day life activities of human beings [1]. The IoT-based applications, namely RFID-based identity management systems, supply chain management and healthcare, empowering society and individuals directly. This technology has become auspicious for modeling, as well as data analysis, through a combination of machine learning (ML) and cloud computing (CC) [2] techniques. IoT-based development brings about tremendous growth in several domains. An application is typically built and run in an IoT environment based on computing architecture and centralized storage [3]. The centralized storage methods are prone to several privacy and security breaches. The basic working model will have some limitations in assisting the growth of IoT-assisted systems in the near future. Therefore, there is a need to develop a distributed storage or decentralized model to overcome such issues [4]. Blockchain (BC) technology is one of the emerging decentralization-related architectures. To deal with billions of transactions generated by IoT systems, the distributed computing process uses a point-to-point computing mechanism. This reduces the cost of storage and computing with the help of storage and computing abilities of numerous idle devices that are installed in unused places [5].

Additional protection systems should be applied to increase security to achieve safe storage and secure transmission and ensure the privacy of several individuals [6]. The BC technique is a suitable, secure, and dependable technique that can be leveraged for this purpose. Since the cost of constructing data storage and data center is high, it is not feasible to improve the existing disaster recovery system [7]. Thus, when it comes to enhancing disaster recovery capabilities, the main issue to be addressed is to reduce storage costs. BC, which links centralized and distributed services, can halt an attack successfully on vital network structures [8]. Intrusion detection systems (IDSs) have a primary task to perform, i.e., to observe the anomalous performance in a network or a host. Today, the current IDSs are not very effective in identifying the extensive range of threats. Collaborative IDs have certain abilities to at least identify a few threats and transfer it for further processing. IDSs can be categorized into two types based on where the IDSs are deployed, i.e., network-based ID systems (NIDSs) and host-based ID systems (HIDSs) [9]. By placing packet sniffers in the network, the NIDS monitors the network at different points. Such packet sniffers choose the data and transfer it to the analysis units, where a comparison is conducted between the current system and the anomaly [10]. The application of various DL methods to identify the attacks with binary classification and classify different kinds of attacks with multi-class classification, has become an active research domain.

The current study designs a hybrid Harris Hawks with sine cosine and a deep-learning-based intrusion detection system (H3SC-DLIDS) for a BC-supported IoT environment. The proposed model allows the BC technology to communicate in the IoT environment securely. In addition, the H3SC-DLIDS technique designs a H3SC technique for feature selection with the LSTM_AE model for classification. Moreover, the arithmetic optimization algorithm (AOA) is applied as a hyperparameter optimizer of the LSTM-AE method. The performance of the proposed H3SC-DLIDS technique was validated in the study using the BoT-IoT dataset. In short, some of the key contributions of the study are listed herewith.

• A novel H3SC-DLIDS technique comprising H3SC-based feature selection, LSTM-AE-based classification and AOA-based hyperparameter tuning is presented in this study for DDoS attack detection in the IoT network. To the best of the researcher’s knowledge, no authors proposed this H3SC-DLIDS technique so far in the literature.
• A new H3SC technique has been developed by integrating the characteristics of the HHO algorithm and SCA for an optimal selection of the features.
• An AOA has been presented in this study with an LSTM-AE model for attack detection.
• Hyperparameter optimization of the LSTM-AE model using the AOA algorithm and cross-validation, helps in boosting the predictive outcome of the proposed model for unseen data.

The rest of the paper is organized as follows: Section 2 provides the related works, and Section 3 offers the proposed model. Then, Section 4 details the analytical results and Section 5 concludes the paper.

2. Related Works

Heidari et al. [11] suggested a BC-based radial basis function neural networks (RBFNNs) prototype. The suggested technique can enhance the veracity of the information, as well as its repository for smart policy-making across the diverse IoDs. In this study, the authors further deliberated the enforcement of BC to generate the distributed forecasting analysis and a prototype for efficient practice and distribution of the DL techniques in a distributed manner. In the literature [12], a new peculiar IDS structure was proposed for IoT networks by employing the DL method. In particular, a screening-based aspect selection, deep neural network (DNN), prototype was the introduction, in which the tremendously associated factors were dropped. Additionally, the prototype was adjusted with several constraints and hyper-constraints.

Mansour [13] established a new poor and rich optimizing with a DL prototype for BC-enabled intrusion detection in the CPS atmosphere, abbreviated as the PRO-DLBIDCPS method. The suggested PRO-DLBIDCPS method primarily presented the Adaptive Harmony Search Algorithm (AHSA) method for the selection of the factor subsets appropriately. For invasion identification and categorization, an attention-founded bi-directional gated recurrent neural network (Bi-GRNN) prototype was enforced. In the study conducted earlier [14], the FIDChain IDS was suggested by employing the weightless ANN in a federated learning (FL) manner. This was done so to confirm the confidentiality of information in the healthcare industry and to parallelly improve the BC technology. Such a model gives a dispersed register for combining the local weights, and later distributing the enhanced worldwide weights after standardizing and averting the lethal outbreaks. This process provided complete clarity and stability over the dispersed structure, with insignificant overhead. When the recognition prototype is enforced at the edge, it safeguards the cloud in case of any outbreaks. This occurs because it stops the information from its gateway at a minimal recognition period and low processing by calculating the volume as FL pacts with lesser sets of information.

Sarhan et al. [15] suggested an ordered BC-based FL outline to develop a safe and confidentiality-conserved co-operative IoT invasion identification method. The authors also accentuated and exhibited the significance of distributing the cyber hazard intelligence amongst inter-organizational IoT networks to enhance the recognition competency of the prototype. The suggested ML-based invasion identification outline follows an ordered FL construction method to confirm the confidentiality of the education process, as well as the organizational info. The authors [16] suggested a deep blockchain framework (DBF) to accomplish security-oriented dispersed invasion identification and confidentiality-based BC with clever contracts in IoT networks. The invasion identification technique was also implemented by the BiLSTM DL protocol to pact with the chronological network info, and was evaluated by employing the info sets of BoT-IoT, as well as UNSW-NB15. In the study conducted earlier [17], an empirical intelligent agent (EIA) was developed with an exclusive Swarm-NN technique to identify the invaders in an edge-centric IoMT outline. The most significant result of the suggested policy was the identification of the outbreaks when data transfer occurred over a network and an effective analysis of the health info at the network edge with great precision.

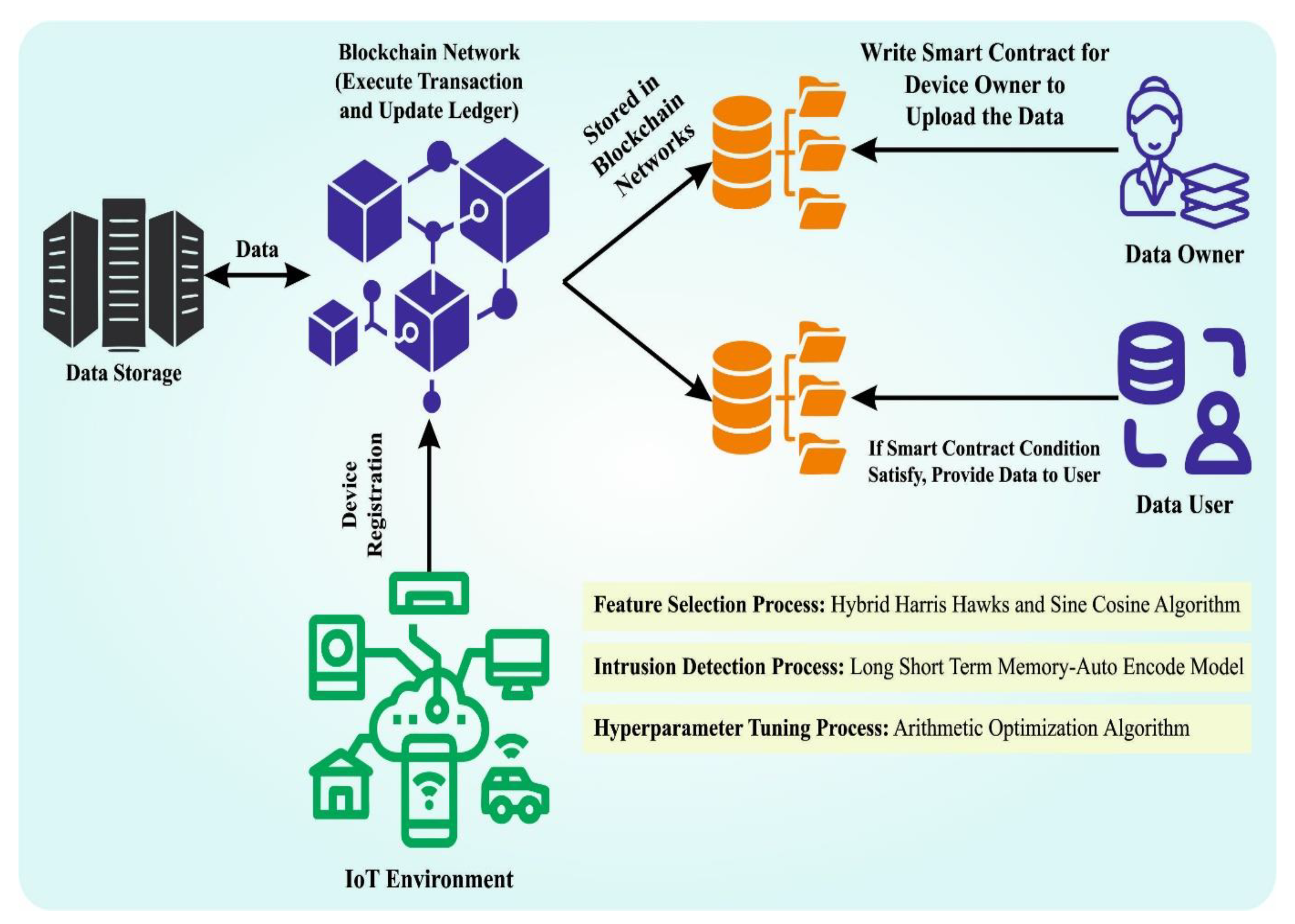
3. The Proposed Model

In the current study, the authors have developed a new H3SC-DLIDS algorithm for the identification of DDoS attacks in the BC-assisted IoT environment. To enable secure communication in the IoT networks, BC technology is used. It comprises three stages, such as feature subset selection using the H3SC approach, LSTM-AE-based DDoS attack detection, and AOA-based parameter tuning. Figure 1 illustrates the overall procedure of the proposed H3SC-DLIDS approach.

3.1. BC Technology

To enable secure communication in the IoT networks, BC technology is used. BC technology is a decentralized P2P network, in which a registered node validates every transaction and records it in a dispersed and immutable ledger [18]. The consensus method assures the integrity of the network. Particularly, no centralized authority exists in this mechanism to validate the produced event: every single transaction must be authenticated by the BC node with the help of a mutual agreement (consensus). Some conventional types of consensuses are briefed herewith.

• Proof-of-importance (PoI): the node that can construct a block has the maximal amount of transactions.
• Proof-of-stake (PoS): the node with high wealth has a higher opportunity to contribute from the consensus, and constructs the block.
• Proof-of-work (PoW): a transaction can be approved once the node accepts its P2P network.
• Proof-of-authority (PoA): certain nodes are allowed to produce novel blocks and protect the BC. It is to be noted that the aforementioned process features potential benefits and probable disadvantages, too, primarily based on the basic $\mathrm{P}2\mathrm{P}$ network architecture.

$\mathrm{PoS}$ and $\mathrm{PoW}$ refer to the conventional methods that are used to accomplish the consensus among the $\mathrm{P}2\mathrm{P}$ nodes. Nevertheless, it becomes apparent that the PoS method is demonstrated for attacking, since the mining cost is approximately zero. On the other hand, the PoW method requires higher computational resources. Both PoI and PoA are effective alternatives, since both are energy-friendly and achieved improved performance. Furthermore, the BC technique presents two methods to create a network of permissioned and permission-less BCs. Particularly, the permissioned BC (private BC) limits the implementation of the tasks and access to the nodes that belong to the network. Successively, permission-less BC (public BC) enables a possible candidate to be a node and belongs to the network. The node on this BC might implement the rest of the errands, once it provides the physical capability (for instance, mine blocks, authenticate transactions, etc.). The BC technique has a proper characteristic, i.e., it is capable of selecting the levels of decentralization in a network, partially decentralized or else the completely centralized ones. To be specific, the closed permissioned BC gets completely centralized. Finally, the data stored is noticeable to the participant node, whereas the open permissioned BC is partially decentralized, since every entity can read the stored data.

3.2. Design of H3SC-Based Feature Selection

At the initial stage, the H3SC-DLIDS technique designs a new H3SC technique for feature subset selection [19]. Likewise, it is predicted to improve the solution’s quality, as well as the convergence behavior. Furthermore, the performance of a hybrid mechanism might result in generating a highly efficient search, because it greatly jumps at regular intervals in the searching area to escape from the local optimum issues. Hence, it produces several diverse solutions. In the hierarchical form of the presented H3SC technique, the bottommost layer of the SCA upgrades an individual that is generated by the HHO at the topmost layer. There exists an $M$ HHO search agent at the topmost layer that corresponds to the bottommost layer’s $M$ group count. All the groups in the bottommost layer comprise the $N$ population. The implementation of the SCA, at the bottommost layer, is the early stage during the updating procedure of the novel location. Then, based on the attained optimum solution, the position of the individual is upgraded in the topmost layer. Consequently, novel equations that represent the exploitation, as well as exploration phases, are generated. The exploration stage of the H3SC technique is implemented using the mathematical expression given below.

$$\begin{gathered} Y_{t+1}^i \\ =\left\{\begin{array}{c}{y}_{\mathrm{rand}}-{\mathrm{r}}_{2 }|y_{\mathrm{rand}}-2{\mathrm{r}}_2\left[{\mathrm{y}}_{\mathrm{t}}+{\mathrm{r}}_8 sin \left(r_9\right)\times \left|r_{10}{\mathrm{p}}_t^{\mathrm{i}}-{\mathrm{y}}_{\mathrm{t}}\right|\right]|, c\ge 0.5\&r_{11}<0.5\\ y_{rand}-r_2\left|y_{rand}-2r_2\left[y_t+r_8 cos\left(r_9\right)\times \left|r_{10}{\mathrm{p}}_t^{\mathrm{i}}-y_t\right|\right]\right|, c\ge 0.5\&r_{11}\ge 0.5\\ y_{prey}-y_m-r_3\left[l{b}_t+r_4\left[u{b}_t-l{b}_t\right]\right], c<0.5\end{array}\right. \end{gathered}$$

(1)

In Equation (1), $Y_{t+1}^i$ represents the position of the $t^{th}$ individual from the topmost layer that is equivalent to the $i^{th}$searching component in the bottommost layer. $y_t$ defines the position of the $t$^th topmost layer searching agent. $t$ denotes the existing number of iterations$.$ $y_{prey}=p_i^t$ characterizes the better location attained up to the existing iteration.$c$ and $r_2,$ $r_3,$ $r_4,$ $r_{11}$ indicate the random parameters. $y_m,$ $lb$, and $ub$ denote the average mean, upper, and lower boundaries correspondingly.

$$\begin{gathered} r_8=2-t\left(\frac{2}{T}\right) \\ {r}_9=2\pi \cdot rand() \\ {r}_{10}=2\cdot rand() \end{gathered}$$

(2)

The exploitation stage is implemented by the abovementioned besieging strategy.

Tough besiege: hawks follow this strategy to capture the prey with the lowest energy when escaping the hunt. This is represented as $r\ge 0.5$ and $E<0.5$. The presented hybrid technique implements these strategies as given below.

$$Y_{t+1}^i=\left\{\begin{array}{l}{\mathrm{y}}_{prey}-E\left|y_{prey}-2r_2\left[{\mathrm{y}}_{\mathrm{t}}+r_8\sin \left(r_9\right)\times \left|r_{10}{p}_i^t-y_t\right|\right]\right|,{ \mathrm{r}}_{11}<0.5\hfill \\ y_{prey}-E\left|y_{prey}-2r_2\left[y_t+r_8\cos \left(r_9\right)\times \left|r_{10}{p}_i^t-y_t\right|\right]\right|, r_{11}\ge 0.5\hfill \end{array}\right.$$

(3)

$$E=2E_0\left(1-\frac{t}{T}\right), t=\left\{1,2,3, \dots , T\right\}$$

(4)

Tough besiege with progressive quick dives: if the prey’s energy gets depleted, this besiege is determined viz., $r<0.5$ and $E<0.5$

$$Y_{t+1}^i=\left\{\begin{array}{l}ZifF\left(Z\right)<F\left(y_t\right)\&\hfill \\ y_t=\left\{\begin{array}{c}{y}_t+{\mathrm{r}}_8\sin \left(r_9\right)\times \left|r_{10}{p}_i^t-y_t\right|,r_{11}<0.5\\ y_t+{\mathrm{r}}_8\cos \left(r_9\right)\times \left|r_{10}{p}_i^t-y_t\right|,r_{11}\ge 0.5\end{array}\right.\hfill \\ X if F\left(X\right)<F\left(y_t\right)\&\hfill \\ y_t=\left\{\begin{array}{c}{y}_t+{\mathrm{r}}_8\sin \left(r_9\right)\times \left|r_{10}{p}_i^t-y_t\right|,r_{11}<0.5\\ y_t+{\mathrm{r}}_8\cos \left(r_9\right)\times \left|r_{10}{p}_i^t-y_t\right|,r_{11}\ge 0.5\end{array}\right.\hfill \end{array}\right.$$

(5)

where $Z=X+S\times LF\left(D\right)$, $X=y_{prey}-E\left|J{y}_{prey}-y_m\right|$,

$S=Random vector of 1\times D$, $r_7=Random parameter, and D=Dimension.$

$$J=2\left(1-r_7\right)$$

(6)

$$LF\left(D\right)=\frac{\beta \times u}{|v{|}^{\frac{1}{\sigma }}}\times 0.01$$

(7)

$$\beta =\left(\frac{\sin \left(\frac{\pi \sigma }{2}\right)\times \mathsf{\Gamma }\left(1+\sigma \right)}{\mathsf{\Gamma }\left(\frac{1+\sigma }{2}\right)\times \sigma \times 2^{\left(\frac{\sigma -1}{2}\right)}}\right)$$

(8)

Mild besiege: this is implemented by the hawks if $r\ge 0.5$ and $E\ge 0.5$

$$Y_{t+1}^i=\left\{\begin{array}{l}{y}_{prey}-\left[{\mathrm{y}}_t+r_8\sin \left(r_9\right)\times \left|r_{10}{p}_i^t-y_t\right|\right]-E|y_{prey}-\hfill \\ 2r_2\left[y_t+r_8\sin \left(r_9\right)\times \left|r_{10}{p}_i^t-y_t\right|\right]|,r_{11}<0.5\hfill \\ y_{prey}-\left[y_t+r_8\cos \left(r_9\right)\times \left|r_{10}{p}_i^t-y_t\right|\right]-E|y_{prey}-\hfill \\ 2r2\left[y_t+r_8\cos \left(r_9\right)\times \left|r_{10}{p}_i^t-y_t\right|\right]|,r_{11}\ge 0.5\hfill \end{array}\right.$$

(9)

Mild besiege with progressive quick dives: here, the prey has sufficient energy $E\ge 0.5$ to flee the hunt. However, the hawk generates a mild besiege $r<0.5$.

$$Y_{t+1}^i=\left\{\begin{array}{c}Z\mathrm{if}F\left(Z\right)<F\left(y_t\right)\&y_t=\\ \left\{\begin{array}{c}{y}_t+r_8\sin \left(r_9\right)\times \left|r_{10}{p}_i^t-y_t\right|,r_{11}<0.5\\ y_t+r_8\cos \left(r_9\right)\times \left|r_{10}{p}_i^t-y_t\right|,r_{11}\ge 0.5\end{array}\right.\\ XifF\left(X\right)<F\left(y_t\right)\&y_t=\\ \left\{\begin{array}{c}{y}_t+r_8\sin {(r_9)}^{}\times \left|r_{10}{p}_i^t-y_t\right|,r_{11}<0.5\\ y_t+r_8\cos \left(r_9\right)\times \left|r_{10}{p}_i^t-y_t\right|,r_{11}\ge 0.5\end{array}\right.\end{array}\right.,$$

(10)

where

$$Z=X+S\times LF\left(D\right)$$

$$X=y_{prey}-E\left|J{y}_{prey}-y_t\right|$$

In the presented method, the objective is incorporated into a single-objective equation so that the present weight recognizes every important objective [20]. A fitness function is adopted here that integrates both the objectives of FS as follows.

$$Fitness\left(X\right)=\alpha \cdot E\left(X\right)+\beta \times \left(1-\frac{\left|R\right|}{\left|N\right|}\right)$$

(11)

In Equation (11), $Fitness$($X$) characterizes the fitness value of the subset $X,$ $E\left(X\right)$ symbolizes the classifier rate of the errors based on the features chosen in X subset, $\left|R\right|$ and $\left|N\right|$ represents the number of the selected and original features correspondingly,$\alpha \in \left[0,1\right]$ and $\beta =\left(1-\alpha \right)$, where $\alpha$ and $\beta$ indicate the weight of the classifier error and reduction ratio correspondingly.

3.3. Optimal LSTM-AE-Based DDoS Attack Detection

The LSTM-AE model is used for an accurate identification of DDoS attacks. AE is a class of NNs that is utilized for a competent reconstruction of unlabeled datasets [21]. The AE learns a representation of the presented data by training the network to disregard the irrelevant parts of data, for instance noise. It learns the design of the standard procedure when detecting anomalies. All other items that do not follow these patterns are categorized as anomalies. Initially, the encoder maps the input as $h,$ i.e., hidden representation after which the decoder maps the data of the hidden space to the reconstruction of the input value. In a simple case provided with a single hidden state, the encoded step of AE, i.e., $x\in {ℝ}^d$ is mapped to $h\in {ℝ}^p$. Employing this data is defined as latent space $h$, as given below.

$$h=\sigma \left(Wx+b\right)$$

(12)

Here, $h$ refers to the frequently suggested hidden space or representation. $\sigma$ implies the activation function such as the ReLU activation function or sigmoid. $W$ signifies the weighted matrix and $b$ denotes the bias vector that is commonly initialized arbitrarily than the training progress; it can be upgraded gradually with BP. Afterwards, the decoding process obtains the hidden depiction $h,$ which ultimately attempts to recreate the encoded input. Specifically, the decoder put efforts for mapping the hidden illustration $h$ to recreate$x^{\prime }$. In the preceding notation, this function is expressed.

$$x^{\prime }={\sigma }^{\prime }\left(W^{\prime }h+b^{\prime }\right)$$

(13)

Here, $\sigma$ denotes an activation function while $b$ and $W$ refer to the bias vector and weight matrix correspondingly. It is noted that $x^{\prime },$ ${\sigma }^{\prime },$ and $b^{\prime }$ are different in their encoded counterparts. Finally, the AEs are trained to minimize the loss function and also deal with reconstruction errors. For instance, a case of reconstructing the loss can be the MSE.

$$L\left(x, x^{\prime }\right)=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{(x-x^{\prime })}^2=\frac{1}{n}{\displaystyle \sum }_{i=1}^n(x-{\sigma }^{\prime }(W^{\prime }(\sigma {(Wx+b))+b^{\prime }))}^2$$

(14)

LSTM-AE has been established on this univariate time series data to perform the classification. Figure 2 represents the structure of LSTM-AE model. This model is used to provide a lookback window that dictates the time series patch obtained by the network. Based on the experience, the LSTM network obtains a 2D array, with a size of $n\mathrm{x}f$ as input at every timestep. The dimensions of this array are related to $n$ previous timestep, whereas the network assumes that at every input, the $f$ feature contains the database. The LSTM layer contains several cells, as the count of time points whenever the network views back at every time $t$. During the order of the LSTM layer, every cell of the previous layer creates a resultant for constructing the 2D array and the subsequent layer needs.

To generate the reconstructed input, the resultant of the final LSTM layer is multiplied by the$2D$ array. In effect, this array is a vector of lengths that are equivalent to the unit count from every cell of the final LSTM layer. This repeats for $f$ times used several times as a feature count from the input. Finally, the study aims at mitigating the divergence between the input and reconstructed models, thus producing a minimum reconstruction error as determined in (3). This stipulation makes sure the reliability of the reconstructs to ground true data.

Finally, the AOA-based hyperparameter tuning process is executed to modify the hyperparameter values of the LSTM-AE model. The AOA technique exploits the distribution behaviors of the arithmetical operator at the time of calculation, namely, division (D), multiplication (M), subtraction (S), and addition (A) [22]. The presented method exploits the math-optimizer-accelerated $\left(MOA\right)$ function to choose from the exploration and exploitation search stages, as expressed by Equation (15):

$$MOA\left(iter\right)= \mathrm{Min}+iter\times \left(\frac{ \mathrm{Max} - \mathrm{Min} }{{\mathrm{Max}}_{-}iter}\right)$$

(15)

Here, $iter$ denotes the current iteration, ${\mathrm{Max}}_{-}iter$ indicates the maximal amount of iterations, $\mathrm{and} \mathrm{Max}$ and$\mathrm{Min}$indicate the maximal and minimal values of the accelerated function, correspondingly. During the exploration stage, the AOA model exploits two major approaches, such as the division (D) and multiplication (M) search processes, to search for the best solution. The novel location updating the formula for the exploration stage is presented below.

$$x_{i,j}\left(iter+1\right)=\left\{\begin{array}{l}best\left(xj\right)÷\left(MOP+\in \right)\times \left(\left(u{b}_j-l{b}_j\right)\times \mu +l{b}_j\right), r2<0.5\hfill \\ best\left(xj\right)\times MOP\times \left(\left(u{b}_j-l{b}_j\right)\times \mu +l{b}_j\right), otherwise\hfill \end{array}\right.$$

(16)

In Equation (9), $x_{i,j}\left(iter+1\right)$ indicates the $j$-$th$ location of the $i$-$th$ solution during the existing iteration, and $best({\chi }_j)$ represents the $j$-$th$ location in the optimum solution, and $\mu$ represents the control parameter. Here, MOP represents the math optimizer probability that is evaluated as follows:

$$MOP\left(iter\right)=1-\frac{ite{r}^{\frac{1}{\alpha }}}{{\mathrm{Max}}_{-}ite{r}^{\frac{1}{\alpha }}}.$$

(17)

In Equation (10), $\alpha$ indicates a sensitive parameter. During the exploration stage, the AOA method exploits two major approaches, such as the addition (D) and the subtraction (S) search strategies, to achieve a high-dense solution.

$$x_{i,j}\left(iter+1\right)=\left\{\begin{array}{l}best\left(xj\right)-MOP\times \left(\left(u{b}_j-l{b}_j\right)\times \mu +l{b}_j\right), r2<0.5\hfill \\ best\left(xj\right)+MOP\times \left(\left(u{b}_j-l{b}_j\right)\times \mu +l{b}_j\right), otherwise\hfill \end{array}\right.$$

(18)

Fitness choice is an essential aspect of the AOA manner. The encoder solution was employed in this study to determine the aptitude (goodness) of the candidate results. A positive integer is used to represent the better performance of the candidate solutions. In this study, the minimum classification error rate is considered to be the fitness function, as given in Equation (19).

$$fitness\left(x_i\right)=\frac{number of misclassified samples}{Total number of samples}\ast 100$$

(19)

4. Results and Discussion

The proposed model was simulated using the Python 3.6.5 tool (Netherlands) on a PC configured with i5-8600k, GeForce 1050Ti 4GB, 16GB RAM, 250GB SSD, and 1TB HDD. The parameter settings are given herewith: learning rate: 0.01, dropout: 0.5, batch size: 5, epoch count: 50, and activation: ReLU.

In this section, the experimental outcomes achieved by the proposed H3SC-DLIDS approach on the BoT-IoT dataset is discussed [23]. The results were examined under two aspects, such as the binary dataset and the multiclass dataset. The binary dataset includes a total of 2056 samples under two classes, as briefed in

Table 1. Details of the binary dataset.

BoT-IoT Binary Dataset
Class	No. of Instances
Attack	1579
Normal	477
Total Number of Samples	2056

. Next, the multiclass dataset has a total of 2056 samples under five classes, as shown in

Table 2. Details of the multiclass dataset.

BoT-IoT Multiclass Dataset
Class	No. of Instances
DDoS	500
DoS	500
Recon	500
Theft	79
Normal	477
Total Number of Instances	2056

. The BoT-IoT dataset consists of network traffic data, captured using a real-time IoT network infrastructure and a variety of devices such as cameras, smart home devices, and wearable fitness trackers. The dataset includes various attack scenarios, such as DDoS attacks, port scans, and malware infections. The attacks were generated by simulating different botnet behaviors, such as Mirai, Bashlite, and IoT Reaper. The dataset contains 10 features and the presented H3SC technique selected six features.

The confusion matrix generated by the proposed H3SC-DLIDS technique under binary class is demonstrated in Figure 3. The figure highlights the efficiency of the proposed H3SC-DLIDS technique in terms of identifying 1555 attack samples and 457 normal samples.

In

Table 3. Classification results of the H3SC-DLIDS approach on a binary dataset.

Class	$\mathit{A}\mathit{c}\mathit{c}{\mathit{u}}_{\mathit{b}\mathit{a}\mathit{l}}$	$\mathit{P}\mathit{r}\mathit{e}{\mathit{c}}_{\mathit{n}}$	$\mathit{R}\mathit{e}\mathit{c}{\mathit{a}}_{\mathit{l}}$	${\mathit{F}}_{\mathit{s}\mathit{c}\mathit{o}\mathit{r}\mathit{e}}$	$\mathit{A}\mathit{U}{\mathit{C}}_{\mathit{s}\mathit{c}\mathit{o}\mathit{r}\mathit{e}}$
Attack	98.48%	98.73%	98.48%	98.60%	97.14%
Normal	95.81%	95.01%	95.81%	95.41%	97.14%
Average	97.14%	96.87%	97.14%	97.01%	97.14%

and Figure 4, the overall classification results of the H3SC-DLIDS technique on the binary dataset are portrayed. The experimental values infer the productive results attained by the proposed H3SC-DLIDS technique amongboth classes. In addition, it should be noted that the H3SC-DLIDS technique reached an average $acc{u}_{bal}$ of 97.14%, $pre{c}_n$ of 96.87%, $rec{a}_l$ of 97.14%, $F_{score}$ of 97.01%, and an $AU{C}_{score}$ of 97.14%.

Figure 5 portrays the accuracy outcomes achieved by the proposed H3SC-DLIDS method during the training and validation processes upon the binary dataset. The figure infers that the proposed H3SC-DLIDS method accomplished high accuracy values with an increase in the number of epochs. Further, the increase in the validation accuracy values over training accuracy values reveals that the proposed H3SC-DLIDS approach learns the binary dataset efficiently.

The loss analysis was conducted upon the proposed H3SC-DLIDS method at the time of training and validation using the binary dataset and the results are shown in Figure 6. The results infer that the H3SC-DLIDS approach reached closer values of training and validation losses. The H3SC-DLIDS method can be inferred to learn the binary dataset efficiently.

The confusion matrix generated by the proposed H3SC-DLIDS method under the multiclass dataset is shown in Figure 7. The figure illustrates the efficiency of the proposed H3SC-DLIDS method in terms of the identification of 490 DDoS samples, 493 DoS samples, 490 Recon samples, 68 Theft samples, and 466 normal samples.

In

Table 4. Classification results of the proposed H3SC-DLIDS approach on the multiclass dataset.

Class	$\mathit{A}\mathit{c}\mathit{c}{\mathit{u}}_{\mathit{b}\mathit{a}\mathit{l}}$	$\mathit{P}\mathit{r}\mathit{e}{\mathit{c}}_{\mathit{n}}$	$\mathit{R}\mathit{e}\mathit{c}{\mathit{a}}_{\mathit{l}}$	${\mathit{F}}_{\mathit{s}\mathit{c}\mathit{o}\mathit{r}\mathit{e}}$	$\mathit{A}\mathit{U}{\mathit{C}}_{\mathit{s}\mathit{c}\mathit{o}\mathit{r}\mathit{e}}$
DDoS	98.98%	97.80%	98.00%	97.90%	98.65%
DoS	99.12%	97.82%	98.60%	98.21%	98.95%
Recon	98.88%	97.42%	98.00%	97.71%	98.58%
Theft	99.17%	91.89%	86.08%	88.89%	92.89%
Normal	99.08%	98.31%	97.69%	98.00%	98.59%
Average	99.05%	96.65%	95.67%	96.14%	97.53%

and Figure 8, the overall classification outcomes of the proposed H3SC-DLIDS algorithm on the multiclass dataset are displayed. The experimental values infer the effectual outcomes of the presented H3SC-DLIDS approach among both classes. Further, the H3SC-DLIDS technique yielded an average $acc{u}_{bal}$ of 99.05%, $pre{c}_n$ of 96.65%, $rec{a}_l$ of 95.67%, $F_{score}$ of 96.14%, and an $AU{C}_{score}$ of 97.53%.

Figure 9 exhibits the accuracy outcomes of the H3SC-DLIDS method during the training and validation processes using the multiclass dataset. The results represent the H3SC-DLIDS approach reaching high accuracy values with an increase in the number of epochs. Further, the increase in the validation accuracy values over training accuracy values demonstrates that the H3SC-DLIDS methodology learns the multiclass dataset effectively.

The loss analysis was conducted for the H3SC-DLIDS approach during the training and validation phases using the multiclass dataset and the results are shown in Figure 10. The figure emphasizes that the H3SC-DLIDS algorithm reaches closer values of training and validation losses. The H3SC-DLIDS method was proven to learn the multiclass dataset efficiently.

Figure 11 reveals the classification results of the H3SC-DLIDS method under binary and multiclass datasets. Figure 11a–c shows the PR analysis outcomes of the H3SC-DLIDS method under binary and multiclass datasets. The figures infer that the proposed H3SC-DLIDS approach gained a maximum PR performance under all the classes. Eventually, Figure 11b–d exemplifies the ROC examination results achieved by the proposed H3SC-DLIDS method under binary and multiclass datasets. The figure depicts that the H3SC-DLIDS methodology has potential outcomes with higher ROC values under distinct class labels.

A comparative analysis was conducted between the proposed H3SC-DLIDS method and other methods, and the results are shown in

Table 5. Comparative analysis results of the proposed H3SC-DLIDS technique and other systems.

Methods	$\mathit{A}\mathit{c}\mathit{c}{\mathit{u}}_{\mathit{b}\mathit{a}\mathit{l}}$	$\mathit{P}\mathit{r}\mathit{e}{\mathit{c}}_{\mathit{n}}$	$\mathit{R}\mathit{e}\mathit{c}{\mathit{a}}_{\mathit{l}}$	${\mathit{F}}_{\mathit{s}\mathit{c}\mathit{o}\mathit{r}\mathit{e}}$
H3SC-DLIDS	99.05%	96.65%	95.67%	96.14%
AE-MLP Model	98.19%	95.91%	93.31%	95.13%
IDS-IoT Model	97.40%	95.80%	94.90%	95.53%
XGBoost Model	97.09%	94.28%	92.13%	95.05%
RF Model	97.00%	94.98%	93.69%	94.57%
DT Model	95.21%	92.43%	92.51%	93.26%

and Figure 12 [24,25]. The experimental values infer that the DT model accomplished a poor performance over other approaches. Next, the IDS-IoT, XGBoost and RF methods reached closer classification results.

Contrastingly, the AE-MLP model produced a reasonable outcome. Nevertheless, the H3SC-DLIDS technique outperformed all other models with a maximum $acc{u}_y$ of 99.05%, $pre{c}_n$ of 96.65%, $rec{a}_l$ of 95.67%, and a $F_{score}$ of 96.14%. The results infer that the H3SC-DLIDS technique can achieve effectual results compared to other techniques.

5. Conclusions

In this study, the authors have established a novel H3SC-DLIDS methodology for the identification of DDoS attacks in the BC-assisted IoT environment. To enable secure communication within IoT networks, BC technology is used. In this study, the H3SC-DLIDS technique designs a new H3SC technique for the feature selection process, by combining the concepts of HHO and SCA techniques. For the intrusion detection process, the LSTM-AE model is used. At the final stage, the AOA is used for the hyperparameter tuning of the LSTM-AE system. The experimental performance of the H3SC-DLIDS system was validated using two datasets, such as the BoT-IoT dataset and the multiclass dataset. The outcomes indicate the superior performance of the proposed H3SC-DLIDS algorithm over other existing algorithms. In the future, the performance of the H3SC-DLIDS method can be improved by implementing ensemble fusion-based DL methods.