Three-Dimensional Unsteady Mixed Convection Flow of Non-Newtonian Nanofluid with Consideration of Retardation Time Effects
Abstract
:1. Introduction
2. Problem Formulation
3. Homotopy Analytical Method
4. Convergence of HAM
5. Conclusions
- ❖
- A reduction in the flow intensity due to the increase in the porosity parameter is noticed.
- ❖
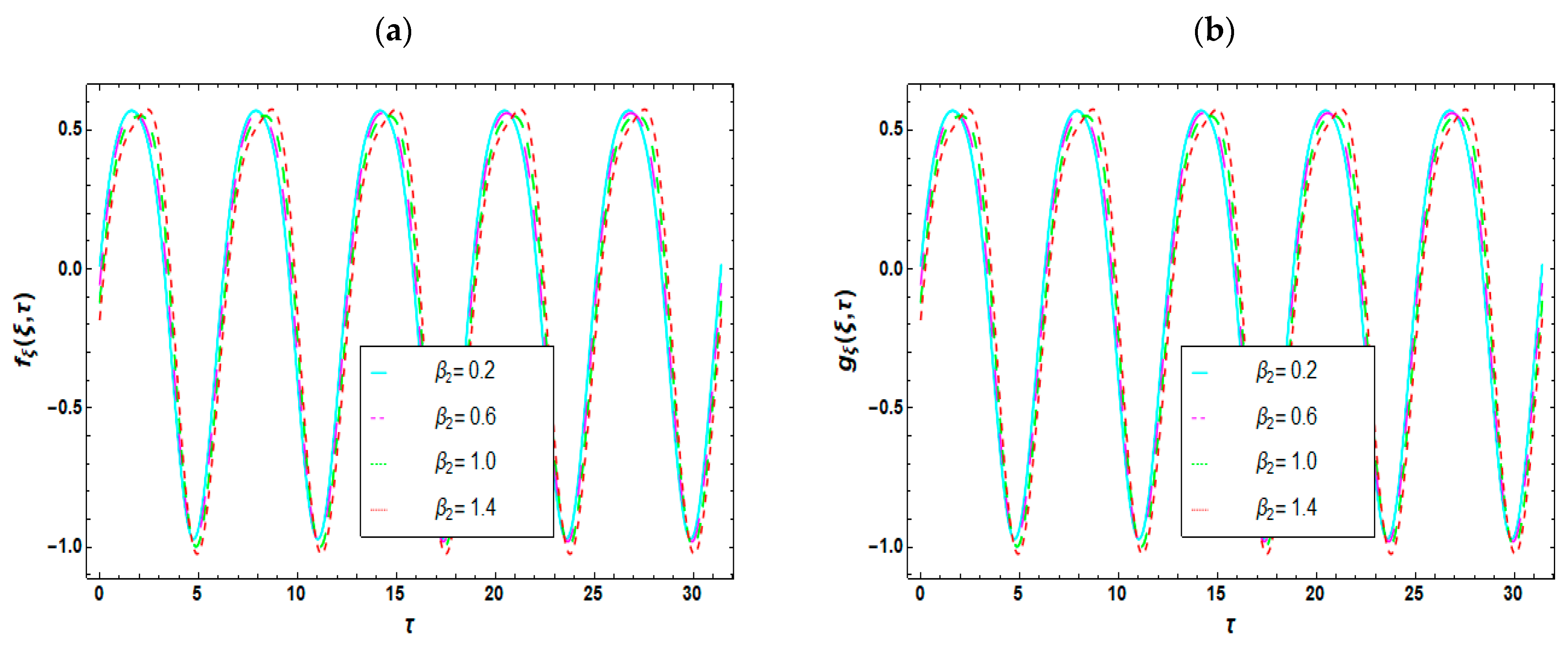
- No phase shift of the oscillating velocity is encountered for all the considered parameters.
- ❖
- An augmentation of the velocity magnitude occurs when the oscillation frequency ratio is increased.
- ❖
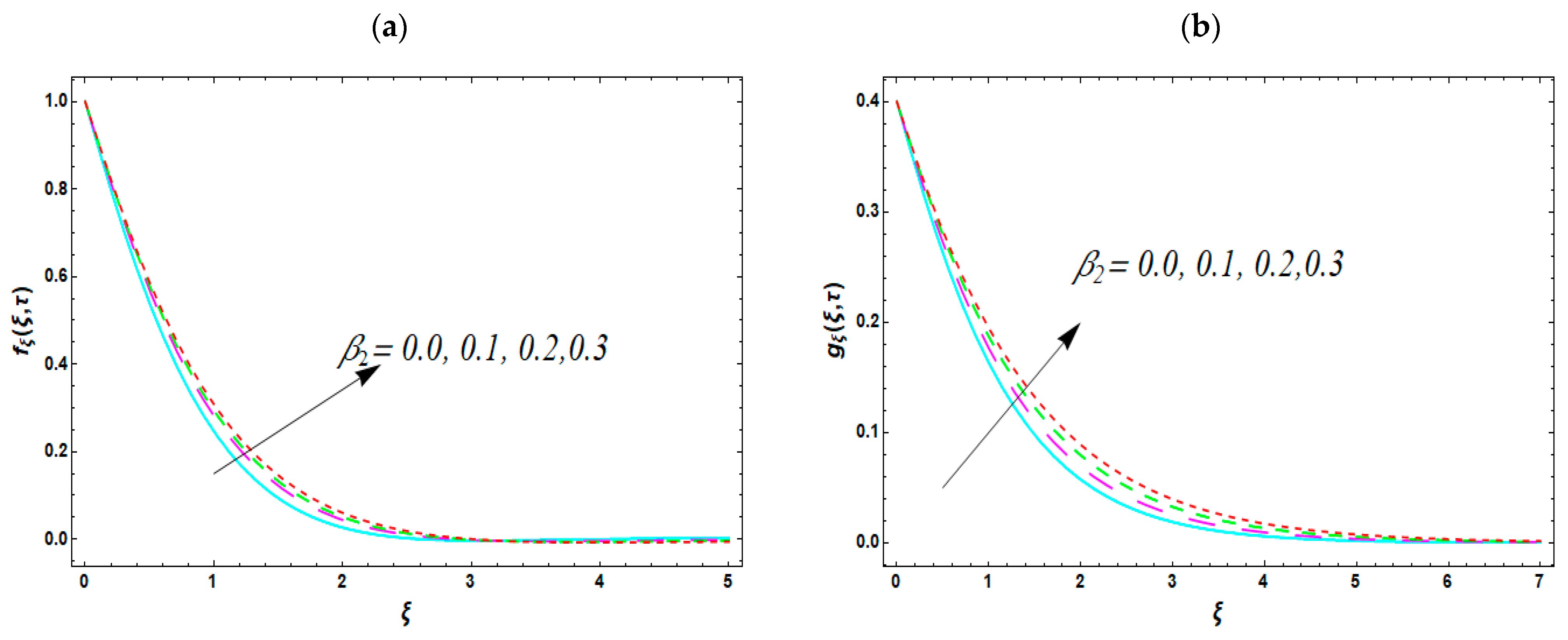
- The retardation parameter causes an increase in velocity.
- ❖
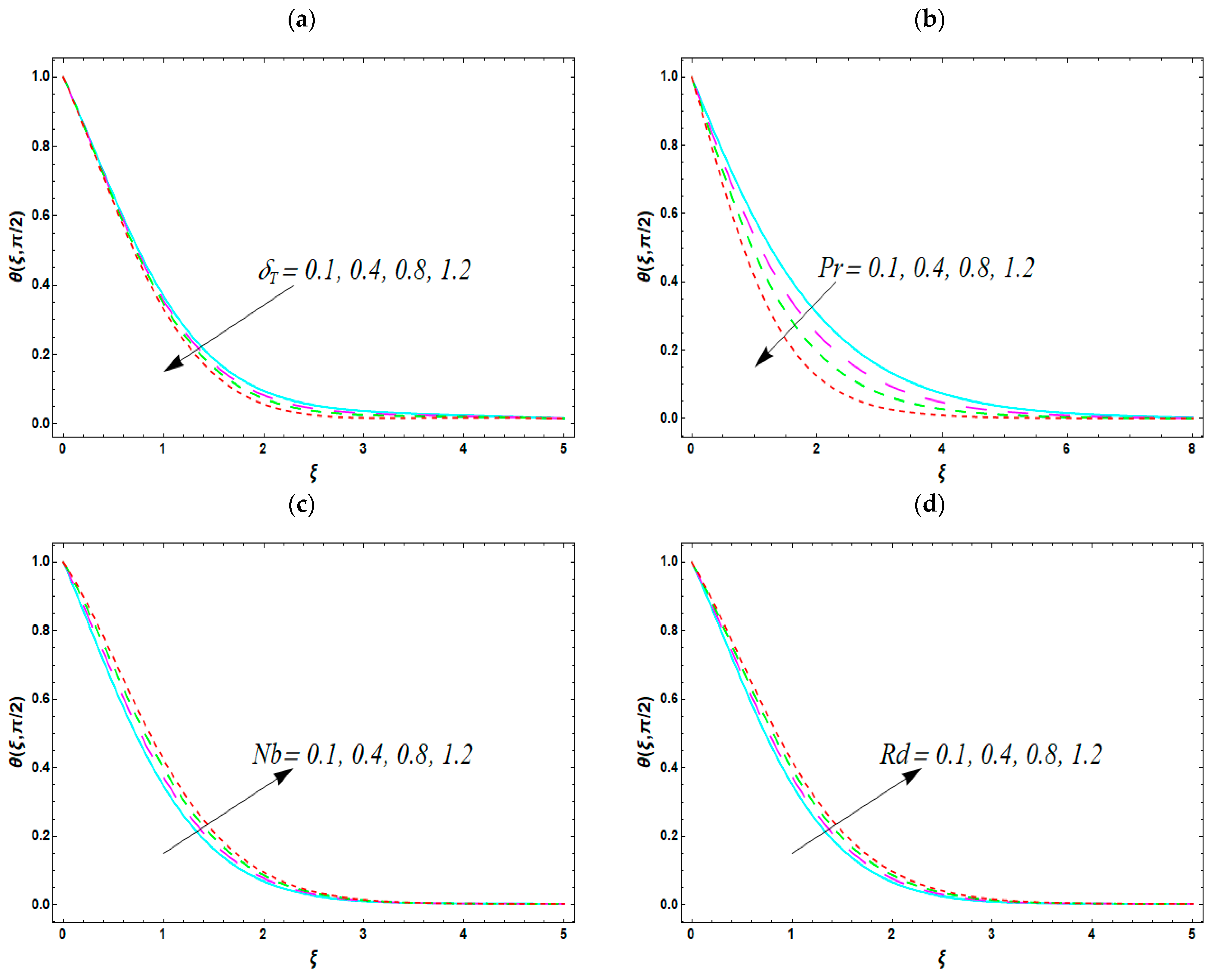
- The increase in the thermal relaxation factor causes a reduction in temperature.
- ❖
- The porosity parameters enhance the thermal and concentration profiles.
- ❖
- An augmentation of the heat transfer occurs when the radiative parameter is increasing.
- ❖
- Lower concentrations are encountered for higher values of the Prandtl and Lewis numbers.
- ❖
- The local Nusselt number increases with the Lewis and Prandtl numbers.
- ❖
- The current analysis can be extended by modifying the model, evaluating the entropy generation, performing a sensitivity analysis, considering hybrid nanofluids, using an artificial neural network, etc.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| velocity components | |
| frequency | |
| time | |
| relaxation time | |
| retardation time | |
| Brownian diffusion | |
| kinematic viscosity | |
| chemical reaction rate | |
| thermal expression coefficient | |
| thermal diffusivity | |
| thermal relaxation coefficient | |
| concentration relaxation coefficient | |
| Stefan–Boltzmann constant | |
| mean absorption coefficient | |
| retardation time | |
| Brownian motion | |
| Lewis number | |
| chemical reaction | |
| stretching ratio constant | |
| reaction constant | |
| thermal relaxation constant | |
| concentration relaxation constant | |
| S | ratio of frequency to stretching rate |
| Pr | Prandtl number |
| thermophoresis |
References
- Choi, S.U.S. Enhancing Thermal Conductivity of Fluids with Nanoparticles. 231; American Society of Mechanical Engineers: New York, NY, USA, 1995; pp. 99–106. [Google Scholar]
- Buongiorno, J. Convective Transport in Nanofluids. J. Heat Transfer. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Hayat, T.; Kiyani, M.; Ahmad, I.; Ahmad, B. On analysis of magneto Maxwell nano-material by surface with variable thickness. Int. J. Mech. Sci. 2017, 131–132, 1016–1025. [Google Scholar] [CrossRef]
- Sui, J.; Zheng, L.; Zhang, X. Boundary layer heat and mass transfer with Cattaneo–Christov double-diffusion in upper-convected Maxwell nanofluid past a stretching sheet with slip velocity. Int. J. Therm. Sci. 2016, 104, 461–468. [Google Scholar] [CrossRef]
- Hsiao, K.-L. Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int. J. Heat Mass Transf. 2017, 112, 983–990. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Free and circular jets cooled by single phase nanofluids. Eur. J. Mech.—B/Fluids 2019, 76, 1–6. [Google Scholar] [CrossRef]
- Ahmed, J.; Khan, M.; Ahmad, L. Stagnation point flow of Maxwell nanofluid over a permeable rotating disk with heat source/sink. J. Mol. Liq. 2019, 287, 110853. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Buongiorno model in a nanofluid filled asymmetric channel fulfilling zero net particle flux at the walls. Int. J. Heat Mass Transf. 2018, 126, 974–979. [Google Scholar] [CrossRef]
- Tlili, I.; Waqas, H.; Almaneea, A.; Khan, S.U.; Imran, M. Activation Energy and Second Order Slip in Bioconvection of Oldroyd-B Nanofluid over a Stretching Cylinder: A Proposed Mathematical Model. Processes 2019, 7, 914. [Google Scholar] [CrossRef]
- Abbasi, A.; Farooq, W.; Tag-ElDin, E.S.M.; Khan, S.U.; Khan, M.I.; Guedri, K.; Elattar, S.; Waqas, M.; Galal, A.M. Heat Transport Exploration for Hybrid Nanoparticle (Cu, Fe3O4)—Based Blood Flow via Tapered Complex Wavy Curved Channel with Slip Features. Micromachines 2022, 13, 1415. [Google Scholar] [CrossRef]
- Kiranakumar, H.V.; Thejas, R.; Naveen, C.S.; MIjaz Khan Prasanna, G.D.; Reddy, S.; Oreijah, M.; Guedri, K.; Bafakeeh, O.T.; Jameel, M. A review on electrical and gas-sensing properties of reduced graphene oxide-metal oxide nanocomposites. Biomass Convers. Biorefin. 2022, 1–11. [Google Scholar] [CrossRef]
- Waqas, H.; Oreijah, M.; Guedri, K.; Khan, S.U.; Yang, S.; Yasmin, S.; Khan, M.I.; Bafakeeh, O.T.; Tag-ElDin, E.S.M.; Galal, A.M. Gyrotactic Motile Microorganisms Impact on Pseudoplastic Nanofluid Flow over a Moving Riga Surface with Exponential Heat Flux. Crystals 2022, 12, 1308. [Google Scholar] [CrossRef]
- Chu, Y.-M.; Khan, M.I.; Abbas, T.; Sidi, M.O.; Alharbi, K.A.M.; Alqsair, U.F.; Khan, S.U.; Malik, M. Radiative thermal analysis for four types of hybrid nanoparticles subject to non-uniform heat source: Keller box numerical approach. Case Stud. Therm. Eng. 2022, 40, 102474. [Google Scholar] [CrossRef]
- Habib, D.; Salamat, N.; Abdal, S.; Siddique, I.; Ang, M.C.; Ahmadian, A. On the role of bioconvection and activation energy for time dependent nanofluid slip transpiration due to extending domain in the presence of electric and magnetic fields. Ain Shams Eng. J. 2021, 13, 101519. [Google Scholar] [CrossRef]
- Xia, W.-F.; Haq, F.; Saleem, M.; Khan, M.I.; Khan, S.U.; Chu, Y.-M. Irreversibility analysis in natural bio-convective flow of Eyring-Powell nanofluid subject to activation energy and gyrotactic microorganisms. Ain Shams Eng. J. 2021, 12, 4063–4074. [Google Scholar] [CrossRef]
- Waqas, M.; Sadiq, M.A.; Bahaidarah, H.M. Gyrotactic bioconvection stratified flow of magnetized micropolar nanoliquid configured by stretchable radiating surface with Joule heating and viscous dissipation. Int. Commun. Heat Mass Transf. 2022, 138, 106229. [Google Scholar] [CrossRef]
- Liu, X.; Adibi, M.; Shahgholi, M.; Tlili, I.; Sajadi, S.M.; Abdollahi, A.; Li, Z.; Karimipour, A. Phase change process in a porous Carbon-Paraffin matrix with different volume fractions of copper oxide Nanoparticles: A molecular dynamics study. J. Mol. Liq. 2022, 366, 120296. [Google Scholar] [CrossRef]
- Mekheimer, K.S.; Abo-Elkhair, R.E.; Abdelsalam, S.I.; Ali, K.K.; Moawad, A.M.A. Biomedical simulations of nanoparticles drug delivery to blood hemodynamics in diseased organs: Synovitis problem. Int. Commun. Heat Mass Transfer 2022, 130, 105756. [Google Scholar] [CrossRef]
- Kumar, K.G.; Ramesh, G.; Gireesha, B.; Gorla, R. Characteristics of Joule heating and viscous dissipation on three-dimensional flow of Oldroyd B nanofluid with thermal radiation. Alex. Eng. J. 2018, 57, 2139–2149. [Google Scholar] [CrossRef]
- Sajid, M.; Ahmed, B.; Abbas, Z. Steady mixed convection stagnation point flow of MHD Oldroyd-B fluid over a stretching sheet. J. Egypt. Math. Soc. 2015, 23, 440–444. [Google Scholar] [CrossRef]
- Irfan, M.; Khan, M.; Khan, W.A.; Sajid, M. Thermal and solutal stratifications in flow of Oldroyd-B nanofluid with variable conductivity. Appl. Phys. A 2018, 124, 674. [Google Scholar] [CrossRef]
- Bai, Y.; Tang, Q.; Zhang, Y. Unsteady MHD oblique stagnation slip flow of Oldroyd-B nanofluids by coupling Cattaneo-Christov double diffusion and Buongiorno model. Chin. J. Phys. 2022, 79, 451–470. [Google Scholar] [CrossRef]
- Roy, N.C.; Pop, I. Dual solutions of magnetohydrodynamic mixed convection flow of an Oldroyd-B nanofluid over a shrinking sheet with heat source/sink. Alex. Eng. J. 2021, 61, 5939–5948. [Google Scholar] [CrossRef]
- Mabood, F.; Abbasi, A.; Farooq, W.; Hussain, Z.; Badruddin, I. Effects of non-linear radiation and chemical reaction on Oldroyd-B nanofluid near oblique stagnation point flow. Chin. J. Phys. 2022, 77, 1197–1208. [Google Scholar] [CrossRef]
- Aziz, S.; Ahmad, I.; Ali, N.; Khan, S.U. Magnetohydrodynamic mixed convection 3-D simulations for chemically reactive couple stress nanofluid over periodically moving surface with thermal radiation. J. Therm. Anal. Calorim. 2020, 146, 435–448. [Google Scholar] [CrossRef]
- Ahmad, I.; Aziz, S.; Khan, S.U.; Ali, N. Periodically moving surface in an Oldroyd-B fluid with variable thermal conductivity and Cattaneo-Christov heat flux features. Heat Transf. 2020, 49, 3246–3266. [Google Scholar] [CrossRef]
- Ahmad, I.; Aziz, S.; Ali, N.; Khan, S.U. Radiative unsteady hydromagnetic 3D flow model for Jeffrey nanofluid configured by an accelerated surface with chemical reaction. Heat Transf. 2020, 50, 942–966. [Google Scholar] [CrossRef]
- Liao, S.J. Homotopy Analysis Method in Nonlinear Differential Equations; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Al-Qudah, A.; Odibat, Z.; Shawagfeh, N. A linearization-based computational algorithm of homotopy analysis method for nonlinear reaction–diffusion systems. Math. Comput. Simul. 2021, 194, 505–522. [Google Scholar] [CrossRef]
- Yang, Y.; Liao, S. Comparison between homotopy analysis method and homotopy renormalization method in fluid mechanics. Eur. J. Mech.—B/Fluids 2023, 97, 187–198. [Google Scholar] [CrossRef]


| 0.2 | 0.1 | 0.3 | 0.3 | 0.51425 |
| 0.4 | 0.56789 | |||
| 0.8 | 0.60670 | |||
| 0.3 | 0.4 | 0.62317 | ||
| 0.6 | 0.64209 | |||
| 0.8 | 0.66324 | |||
| 0.2 | 0.48359 | |||
| 0.4 | 0.4556 | |||
| 0.6 | 0.427857 | |||
| 0.2 | 0.48053 | |||
| 0.6 | 0.46475 | |||
| 0.8 | 0.428857 |
| 0.2 | 0.3 | 0.754231 | |
| 0.6 | 0.83544 | ||
| 0.8 | 0.93567 | ||
| 0.3 | 0.2 | 0.64567 | |
| 0.6 | 0.72675 | ||
| 0.8 | 0.74534 | ||
| 0.2 | 0.63556 | ||
| 0.4 | 0.58324 | ||
| 0.6 | 0.53677 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayadi, B.; Ghachem, K.; Al-Khaled, K.; Khan, S.U.; Kriaa, K.; Maatki, C.; Zahi, N.; Kolsi, L. Three-Dimensional Unsteady Mixed Convection Flow of Non-Newtonian Nanofluid with Consideration of Retardation Time Effects. Mathematics 2023, 11, 1892. https://doi.org/10.3390/math11081892
Ayadi B, Ghachem K, Al-Khaled K, Khan SU, Kriaa K, Maatki C, Zahi N, Kolsi L. Three-Dimensional Unsteady Mixed Convection Flow of Non-Newtonian Nanofluid with Consideration of Retardation Time Effects. Mathematics. 2023; 11(8):1892. https://doi.org/10.3390/math11081892
Chicago/Turabian StyleAyadi, Badreddine, Kaouther Ghachem, Kamel Al-Khaled, Sami Ullah Khan, Karim Kriaa, Chemseddine Maatki, Nesrine Zahi, and Lioua Kolsi. 2023. "Three-Dimensional Unsteady Mixed Convection Flow of Non-Newtonian Nanofluid with Consideration of Retardation Time Effects" Mathematics 11, no. 8: 1892. https://doi.org/10.3390/math11081892
APA StyleAyadi, B., Ghachem, K., Al-Khaled, K., Khan, S. U., Kriaa, K., Maatki, C., Zahi, N., & Kolsi, L. (2023). Three-Dimensional Unsteady Mixed Convection Flow of Non-Newtonian Nanofluid with Consideration of Retardation Time Effects. Mathematics, 11(8), 1892. https://doi.org/10.3390/math11081892







