Unsteady Hydromagnetic Flow over an Inclined Rotating Disk through Neural Networking Approach

Abstract

The goal of this research is to examine how a magnetic field affects the unsteady flow of a hybrid nanofluid over a spinning disk that is inclined and stretched while the flow is surrounded by a non-Darcy porous medium. Furthermore, for heat transmission mechanisms, Joule heating and viscous dissipation are considered. The current article is made more realistic by imposing thermal radiation to enhance the heat transmission system under the effects of convection. Moreover, thermal and velocity slip conditions have also been incorporated into the current study. The equations that administer the flow problem along with constraints at the boundaries are converted to dimension-free form by employing a set of appropriate similarity transformations, which are then solved by the numerical technique Runge-Kutta method of order four (RK-4). The new and advanced trend for the convergence of the obtained results is validated through a neural networking approach. The temperature of hybrid nanofluid is augmented by an increase in the porosity parameter, the unsteadiness factor, the Eckert number, the magnetic field, and the Forchheimmer number, while for the values of the radiation factor, the thermal heat is decreasing near the disk and increasing away from the disk. The precision of the obtained results has been ensured by comparing them with established results, with good agreement among these results.

1. Introduction

The era of nanofluid and the concept of thermal cooling became prominent when Choi [1] developed nanofluid at Argemon National Laboratory, which has proved to be a better coolant than conventional liquids such as kerosene oil, water, etc. Nanofluids are colloidal suspensions of nanoparticles such as Al₂O₃, CuO, TiO_2, etc. in base fluids such as water, oil, and engine oil. Due to their three important properties, namely, enlarged thermal conductivity, high heat transfer capability, and increased critical heat flux, the nanofluids are used in power generation tools, transport machinery, the treatment of cancer-infected tissues, electronic gadgets, and space cooling instruments, etc. Seth et al. [2] studied the consequences of thermal radiation and mixed convection on MHD nanofluid flow and discovered that for ramping thermal and isothermal plates, the thermal diffusion and radiation have decreased the Nusselt number at the plate surface. While a base fluid’s thermal conductivity is amplified with the growth of nanoparticles due to their remarkable thermophysical properties, in some situations it causes the nanofluids’ heat capacity to diminish, according to Higano et al. [3]. Keeping in view these issues, Turcu et al. [4] prepared the hybrid nanofluid with two different particles by suspending them in pure fluid. A novel nanotechnology fluid is identified as a hybrid nanofluid that is fabricated by distributing two distinct nanoparticles into a pure fluid. Recent studies suggest that hybrid nanofluids, particularly those operating at very high temperatures, can successfully replace convectional cooling. A hybrid nanofluid is made up of the composition of two or more nanoparticles suspended in the base fluid created by Muneeshwaran et al. [5]. When compared to nanofluid containing just one kind of nanoparticle, the coordinated impact of hybrid nanofluid resulted in an enhancement in heat transfer, as observed by Sajid and Ali [6]. The hybrid nanofluid has better thermal flow properties in comparison to a simple pure fluid or nanofluid comprising one type of nanoparticle.

Nowadays, the investigator’s attention is attracted by hybrid nanofluid flow over rotary geometries, which is used in numerous applications in biomedical sciences, engineering fields, and computer technology, including expensive medical equipment for most of the dangerous disease treatments, transport, and electronic robots [7,8,9]. Karman [10] was the first to use a rotating plane to study fluid flow and to analyze the problem using the momentum-integral approach. Von Karman’s problem was then extended by Milavcic and Wang [11] by introducing the slip effect at the disk’s surface. In this regard, using a viscous liquid flow due to a rotating geometry, Turkyilmazoglu and Senel [12] numerically investigated the fluid flow with a porous effect to analyze the heat and mass transfer phenomena. Devi and Devi [13] investigated the combined effects of Newtonian heating and suction/injection on a hydromagnetic hybrid nanofluid flow past a rotating plate. Later, these authors [14] expanded their research by running the same hybrid nanofluid flow past a stretchable rotating sheet. Many researchers, such as [15,16], have a keen interest due to the important applications of heat transfer analysis over a rotating plane such as gas turbines, aeronautical technology, etc.

There are various examples of fluid dynamics systems with microscale dimensions where flow regions satisfy no-slip conditions at the boundary of the problem and cannot be used. The reason behind this is that the fluid behavior is associated with the flow, which is often responsible for a slip flow regime that differs from essentially conventional flow. The no-slip boundary is also insufficient for different situations in fluid dynamics, especially in many suspensions, polymer solutions, mixed emulsions, and foams, where it can be found that partial slip is quite suitable and an appropriate constraint at the boundary to derive the best results. Due to their valuable role in the polymer, thin film, cosmetics, and electrochemical industries, several scientists have been motivated to investigate multiple flows with suitable partial slip conditions. The cumulative influence of slip and convective constraint at the boundary of the flow of suspended CNT (carbon nanotube) nanofluids has been investigated by Akbar et al. [17]. They have deduced that the growing values of the non-dimensional slip factor have reduced the fluid regime and increased the fluid temperature in the thermal boundary layer. For stable non-zero slip conditions, the rate of thermal flow is reduced with the impact of the magnetic field, as discussed by Turkyilmazoglu [18]. The impact of the thermally radiative and naturally convective flow of fluid over a cylindrical surface is investigated by Pandey and Kumar [19]. The effect of nonlinear thermal radiation on nanofluid flow and thermal diffusion has been explored by Nayak et al. [20].

It has been discussed recently by Zhang et al. [21] that heat transfer and fluid flow are promoted by thermal radiation in a confined cavity. Thermal radiation is essential in the manufacturing of machines for applications in space technology, where they transmit high thermal conductivity at extremely high temperatures. These radiations must be kept low to achieve a significant heat transfer rate, as discussed by Nayak [22]. The generation of heat creates thermal energy in the boundary layer and augments the temperature of the fluid. Therefore, heat generation is intended as a source of thermal transportation rate in the thermal layer at the boundary. Gang et al. [23] investigated the MHD flow of nanofluid with internal heat absorption/generation using the Bongiorno model. Thermal flow over a disk surface is more suitable for increasing the thermal conductivity of nanofluids using convection boundary conditions. Guedri et al. [24] examined the effects of thermal radiation on ternary hybrid nanofluid flow past a nonlinearly stretched surface. Khan et al. [25] used gold nanoparticles in blood to discuss the flow between two surfaces subject to the impact of microorganisms. Ibrahim et al. [26] discussed chemically reactive effects on mixed convective MHD flow past a nonlinearly stretched porous sheet. Thumma et al. [27] examined in their study that multiple heat sources are the reason for raising the thermal profiles.

2. Novelty/Originality

The goal of this research is to look at the problem of unsteady three-dimensional hybrid nanofluid flow across the inclined rotating and stretching disk, which is new work and has not been discussed before. The below-mentioned points further emphasized the novelty of the current work:

• A time-dependent magnetic field embedded in a non-Darcy porous medium has been considered.
• At the same time, the condition of the convective boundary is taken into account.
• Thermal radiation is considered the more realistic physical problem.
• Joule heating and viscous dissipation are employed in the energy equation.
• Velocity slip and thermal slip conditions have been used along the inclined disk.
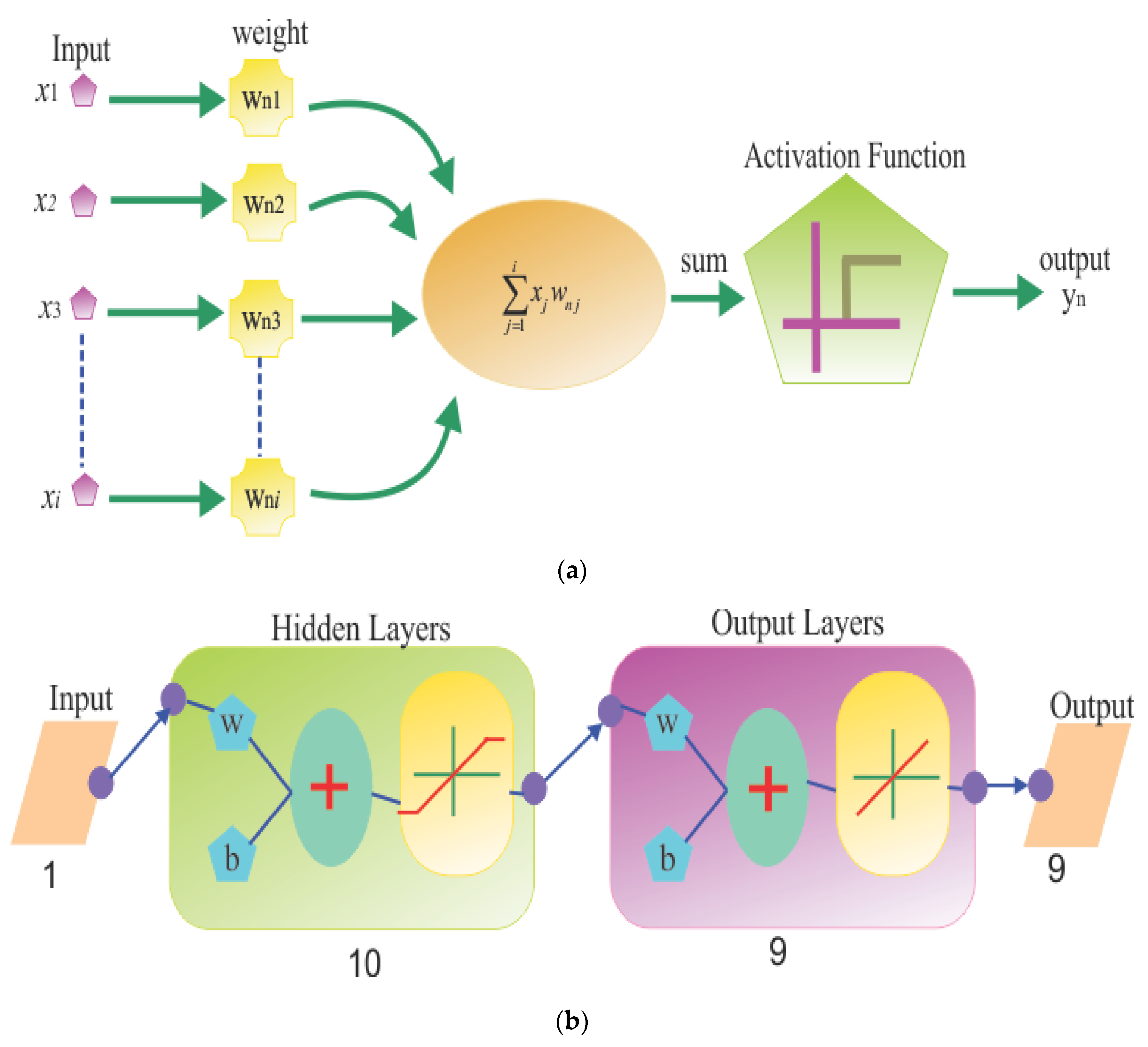
• The RK-4 method is used to get solutions from the dimensionless form of modeled equations. Neural networking is used to validate the convergence of obtained results and make the model more precise and meaningful.

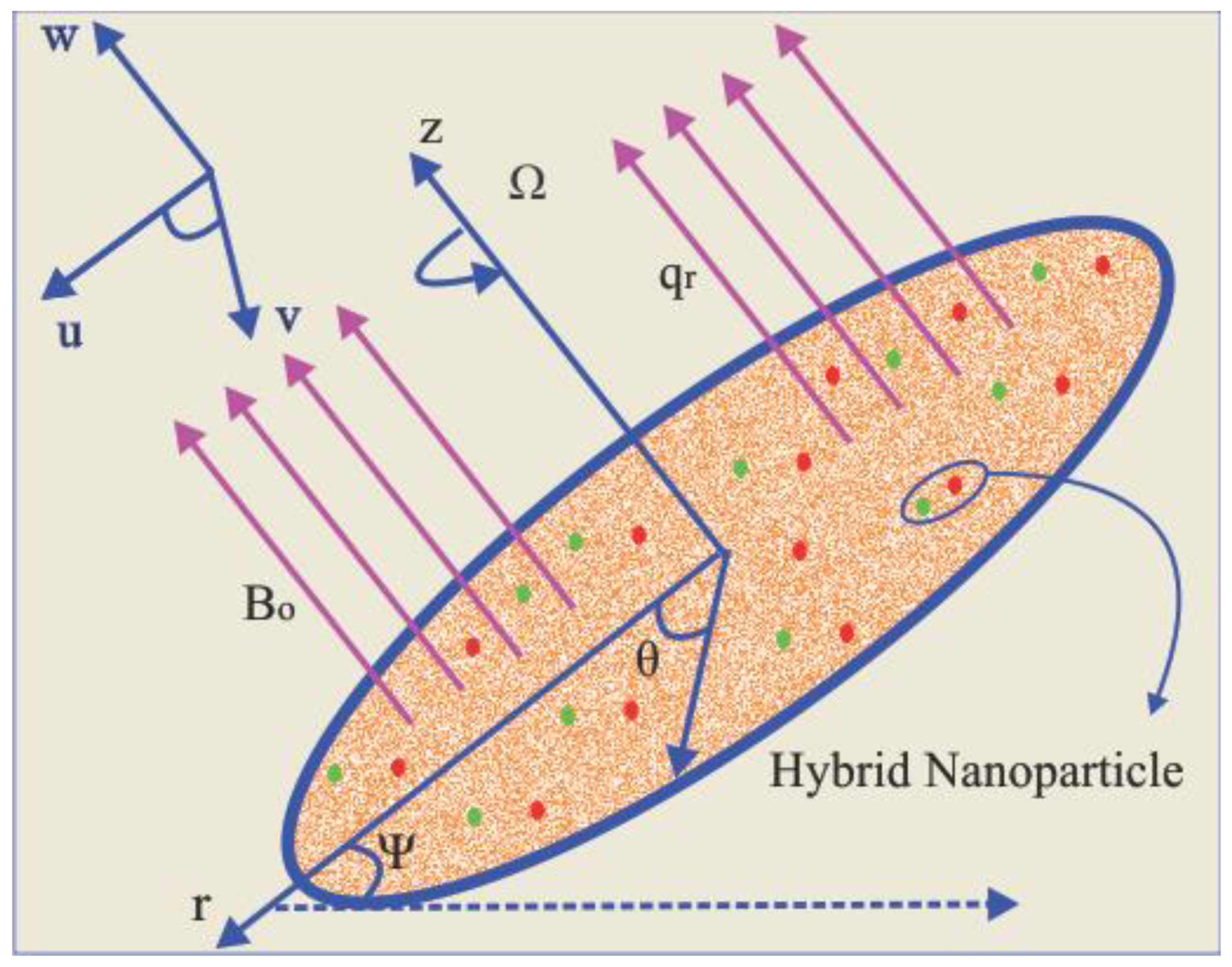
3. Materials and Methods

We consider an unsteady MHD flow of incompressible nanofluid over an inclined, rotating, and stretching disk subject to heat radiation and Joule heating. The disk is surrounded by a non-Darcy porous medium and is placed at $xy$-plane i.e., at $z=0$ and rotates with a uniform angular velocity $\mathsf{\Omega }$. The components of velocity $u,v$ and $w$ are considered along $r,\theta$ and $z$ directions. $B_0$ is the strength of the magnetic field along the z-axis. The relations of slip conditions are suggested to evaluate profiles of velocity and temperature. The flow is taken along $r$ direction due to the disk’s motion (see Figure 1) and also, nanoparticles are kept under control over $z\ge 0$. In the present work, the magnetic Reynolds number is assumed to be so small, i.e., ${\mathrm{Re}}_m<<1$ in the flow region, that the induced magnetic field is ignored. For an unsteady porous medium, we have a variable kinematic viscosity as $\upsilon \left(t\right)=\upsilon /1-\alpha t$, while the effect of the magnetic field has been observed mathematically as $B_0\left(t\right)=B_0/\left(1-\alpha t\right)$ [28] and the thermal expansion term is defined as $\beta \left(t\right)=\beta /(1-\alpha t)$.

Keeping in view all the above-stated suppositions, the leading equations are exhibited as [29,30,31,32,33]:

$$\frac{\partial u}{\partial r}+\frac{u}{r}+\frac{\partial w}{\partial z}=0,$$

(1)

$$\begin{array}{c}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial r}+w\frac{\partial u}{\partial z}-\frac{v^2}{r}={\upsilon }_{hnf}\left(\frac{{\partial }^{2}u}{\partial r^2}+\frac{1}{r}\frac{\partial u}{\partial r}-\frac{u}{r^2}+\frac{{\partial }^{2}u}{\partial z^2}\right)-\frac{{\sigma }_{hnf}{B}_0{}^2\left(t\right)}{{\rho }_{hnf}}u\\ -\frac{F_0}{{\rho }_{hnf}}{u}^2-\frac{{\upsilon }_{hnf}}{k_0}u+\frac{{\left(\rho {\beta }_T\right)}_{hnf}}{{\rho }_{hnf}}\left(T-T_{\infty }\right)g\mathrm{Sin}\left(\psi \right),\end{array}$$

(2)

$$\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial r}+w\frac{\partial v}{\partial z}+\frac{uv}{r}={\upsilon }_{hnf}\left(\frac{{\partial }^{2}v}{\partial r^2}+\frac{1}{r}\frac{\partial v}{\partial r}-\frac{v}{r^2}+\frac{{\partial }^{2}v}{\partial z^2}\right)-\frac{{\sigma }_{hnf}{B}_0{}^2\left(t\right)}{{\rho }_{hnf}}v-\frac{F_0}{{\rho }_{hnf}}{v}^2-\frac{{\upsilon }_{hnf}}{k_0}v,$$

(3)

$$\frac{\partial w}{\partial t}+u\frac{\partial w}{\partial r}+w\frac{\partial w}{\partial z}={\upsilon }_{hnf}\left(\frac{{\partial }^{2}w}{\partial r^2}+\frac{1}{r}\frac{\partial w}{\partial r}-\frac{w}{r^2}+\frac{{\partial }^{2}w}{\partial z^2}\right)-\frac{F_0}{{\rho }_{hnf}}{w}^2-\frac{{\upsilon }_{hnf}}{k_0}w+\frac{{\left(\rho {\beta }_T\right)}_{hnf}}{{\rho }_{hnf}}\left(T-T_{\infty }\right)g\mathrm{Cos}\left(\psi \right),$$

(4)

$$\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z}={\alpha }_{hnf}\left(\frac{{\partial }^{2}T}{\partial r^2}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{{\partial }^{2}T}{\partial z^2}\right)+\frac{{\sigma }_{hnf}{B}_0{}^2\left(t\right)}{{\left(\rho c_p\right)}_{hnf}}\left(u^2+v^2\right)-\frac{1}{{(\rho c_p)}_{hnf}}\frac{\partial q_r}{\partial z}+\frac{{\mu }_{hnf}}{{(\rho c_p)}_{hnf}}\left({\left(\frac{\partial u}{\partial z}\right)}^2+{\left(\frac{\partial v}{\partial z}\right)}^2\right).$$

(5)

Constraints at boundaries are described as:

$$\begin{array}{c}u=L_1\frac{\partial u}{\partial z}, v=\frac{\mathsf{\Omega }r}{\left(1-at\right)}+L_1\frac{\partial v}{\partial z}, w=0, T=T_w+L_2\frac{\partial T}{\partial z} \mathrm{at} \eta =0,\\ u\to 0, v\to 0, w\to 0, T\to T_{\infty }\} \mathrm{at} \eta \to \infty .\end{array}\}$$

(6)

Thermal radiation flux $q_r$ (comes from the Rosseland approximation) is written as:

$$q_r=-\frac{4{\sigma }^{*}}{3k^{*}}\frac{{\partial }^{4}T}{\partial z^4},$$

(7)

where ${\sigma }^{*}$ and $k^{*}$ are the Stefan-Boltzmann constant and the mean absorption coefficient, respectively. Using Taylor’s expansion of $T^4$ and deleting of the higher order terms, we then have $T^4\approx 4T_{\infty }^3-3T_{\infty }^4$ so that Equation (5) reduced to

$$\begin{array}{c}\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z}={\alpha }_{hnf}\left(\frac{{\partial }^{2}T}{\partial r^2}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{{\partial }^{2}T}{\partial z^2}\right)+\frac{{\sigma }_{hnf}B{\left(t\right)}^2}{{\left(\rho c_p\right)}_{hnf}}\left(u^2+v^2\right)\\ -\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k^{*}{(\rho c_p)}_{hnf}}\frac{{\partial }^{2}T}{\partial z^2}+\frac{{\mu }_{hnf}}{{(\rho c_p)}_{hnf}}\left({\left(\frac{\partial u}{\partial z}\right)}^2+{\left(\frac{\partial v}{\partial z}\right)}^2\right).\end{array}$$

(8)

The experimental values of water, copper, and alumina are presented in

Table 1. The Experimental values of Copper, Aluminium Oxide, and Water [34].

Material	$\mathbf{\rho } (\mathbf{k}\mathbf{g}/{\mathbf{m}}^3)$	${\mathit{C}}_{\mathit{p}} (\mathbf{j}/\mathbf{k}\mathbf{g}\mathbf{K})$	$\mathit{k} (\mathbf{W}/\mathbf{m}\mathbf{K})$	${\mathit{\beta }}_{\mathit{T}} \left({\mathit{k}}^{-1}\right)$	$\mathit{\sigma } \left(\mathit{S}/\mathit{m}\right)$
Water $\left(H_{2}O\right)$	3594	4179	0.492	$21\times {10}^{-5}$	$5.5\times {10}^{-6}$
Copper $\left(Cu\right)$	8933	385	401	$16.7\times {10}^{-5}$	$59.6\times {10}^6$
Alumina $\left(A{l}_2{O}_3\right)$	4907	700	3.7	$12.7\times {10}^{-6}$	$1.1\times {10}^7$

, and the thermophysical characteristics of the hybrid nanofluid are presented in

Table 2. The thermophysical properties of Hybrid Nanofluid [35].

Properties	Mathematical Models
Viscosity	$\frac{{\mu }_{hnf}}{{\mu }_f}=\frac{1}{{\left(1-{\varphi }_1\right)}^{2.5}{\left(1-{\varphi }_2\right)}^{2.5}}$
Density	$\frac{{\rho }_{hnf}}{{\rho }_f}=\left(1-{\varphi }_2\right)\left[\left(1-{\varphi }_1\right)+{\varphi }_1\left(\frac{{\rho }_1}{{\rho }_f}\right)\right]+{\varphi }_2\left(\frac{{\rho }_2}{{\rho }_f}\right)$
Thermal Capacity	$\frac{{\left(\rho c_p\right)}_{hnf}}{{\left(\rho c_p\right)}_f}=\left(1-{\varphi }_2\right)\left[\left(1-{\varphi }_1\right)+{\varphi }_1\left(\frac{{\left(\rho c_p\right)}_1}{{\left(\rho c_p\right)}_f}\right)\right]+{\varphi }_2\left(\frac{{\left(\rho c_p\right)}_2}{{\left(\rho c_p\right)}_f}\right)$
Thermal Expansion	$\frac{{\left({\beta }_T\right)}_{hnf}}{{\left({\beta }_T\right)}_f}=\left(1-{\varphi }_2\right)\left[\left(1-{\varphi }_1\right)+{\varphi }_1\left(\frac{{\left({\beta }_T\right)}_1}{{\left({\beta }_T\right)}_f}\right)\right]+{\varphi }_2\left(\frac{{\left({\beta }_T\right)}_2}{{\left({\beta }_T\right)}_f}\right)$
Thermal Conductivity	$\frac{k_{hnf}}{k_{nf}}=\frac{k_2+2k_{nf}-2{\varphi }_2\left(k_{nf}-k_2\right)}{k_2+2k_{nf}+{\varphi }_2\left(k_{nf}-k_2\right)}, \frac{k_{nf}}{k_f}=\frac{k_1+2k_f-2{\varphi }_1\left(k_f-k_1\right)}{k_1+2k_f+{\varphi }_1\left(k_f-k_1\right)},$
Electrical Conductivity	$\frac{{\sigma }_{hnf}}{{\sigma }_f}=\left[1+\frac{3\left(\frac{{\sigma }_2}{{\sigma }_{nf}}-1\right){\varphi }_2}{\left(\frac{{\sigma }_2}{{\sigma }_{nf}}+2\right)-\left(\frac{{\sigma }_2}{{\sigma }_{nf}}-1\right){\varphi }_2}\right], \frac{{\sigma }_{nf}}{{\sigma }_f}=\left[1+\frac{3\left(\frac{{\sigma }_1}{{\sigma }_f}-1\right){\varphi }_1}{\left(\frac{{\sigma }_1}{{\sigma }_f}+2\right)-\left(\frac{{\sigma }_1}{{\sigma }_f}-1\right){\varphi }_1}\right]$

.

The similarity transformations are given below [36].

$$\begin{array}{c}u=\frac{r\mathsf{\Omega }}{\left(1-at\right)}{f}^{\prime }\left(\eta \right), v=\frac{r\mathsf{\Omega }}{\left(1-at\right)}g\left(\eta \right), w=-\sqrt{\frac{2\mathsf{\Omega }{\upsilon }_f}{\left(1-at\right)}}f\left(\eta \right), \\ T=T_{\infty }+\left(T_w-T_{\infty }\right)\mathsf{\Theta }\left(\eta \right), \eta =z\sqrt{\frac{2\mathsf{\Omega }}{\left(1-at\right){\upsilon }_f}}\end{array}\}$$

(9)

Substituting Equation (9), in Equations (1)–(4), (6), and (8), we then get the following equations:

$$\begin{array}{c}\left(2f^{‴}\left(\eta \right)-\lambda f^{\prime }\left(\eta \right)\right)+2f\left(\eta \right)f^{″}\left(\eta \right)-\frac{{\upsilon }_f}{{\upsilon }_{hnf}}\left\{S\left(\eta f^{″}\left(\eta \right)+f^{\prime }\left(\eta \right)\right)+f^{\prime }{\left(\eta \right)}^2-g{\left(\eta \right)}^2\right\}\\ -\frac{{\mu }_f}{{\mu }_{hnf}}\left\{Fr{f}^{\prime }{\left(\eta \right)}^2+\frac{{\sigma }_{hnf}}{{\sigma }_f}M{f}^{\prime }\left(\eta \right)-\frac{Gr}{\mathrm{Re}}\frac{{\left(\rho \beta \right)}_{hnf}}{{\left(\rho \beta \right)}_f}\mathrm{Sin}\left(\psi \right)\mathsf{\Theta }\left(\eta \right)\right\}=0,\end{array}$$

(10)

$$\begin{array}{c}\left(2g^{″}\left(\eta \right)-\lambda g\left(\eta \right)\right)+\frac{{\upsilon }_f}{{\upsilon }_{hnf}}\left\{2f\left(\eta \right)g^{\prime }\left(\eta \right)-2g\left(\eta \right)f^{\prime }\left(\eta \right)-S\left(g\left(\eta \right)+\frac{\eta }{2}{g}^{\prime }\left(\eta \right)\right)\right\}\\ +2\mathrm{Re}\left(g\left(\eta \right)-f^{\prime }\left(\eta \right)\right)-\frac{{\mu }_f}{{\mu }_{hnf}}\left\{Frg{\left(\eta \right)}^2+\frac{{\sigma }_{hnf}}{{\sigma }_f}Mg\left(\eta \right)\right\}=0,\end{array}$$

(11)

$$\begin{array}{c}\frac{1}{\mathrm{Pr}}\left(\frac{k_{hnf}}{k_f}+\frac{4}{3}Rd\right){\mathsf{\Theta }}^{″}\left(\eta \right)+\frac{{\left(\rho c_p\right)}_{hnf}}{{\left(\rho c_p\right)}_f}\left(f\left(\eta \right)-\frac{S\eta }{4}\right){\mathsf{\Theta }}^{\prime }\left(\eta \right)+\frac{{\sigma }_{hnf}}{{\sigma }_f}\frac{EcM}{2}\left(g{\left(\eta \right)}^2+f^{\prime }{\left(\eta \right)}^2\right)\\ +\frac{{\mu }_{hnf}}{{\mu }_f}Ec\left(g^{\prime }{\left(\eta \right)}^2+f^{″}{\left(\eta \right)}^2\right)=0\end{array}$$

(12)

Related constraints at boundaries include

$$\begin{array}{c}f\left(0\right)=0, f^{\prime }\left(0\right)=\epsilon f^{″}\left(0\right), g\left(0\right)=1+\epsilon g^{\prime }\left(0\right), \mathsf{\Theta }\left(0\right)=1+\gamma {\mathsf{\Theta }}^{\prime }\left(0\right)\\ f^{\prime }(\infty )\to 0,g(\infty )\to 0,\mathsf{\Theta }(\infty )\to 0.\end{array}\}$$

(13)

During non-dimensionalization, the following parameters are obtained:

$$\begin{array}{l}\lambda =\frac{{\upsilon }_f}{\mathsf{\Omega }{k}_0},S=\frac{a}{\mathsf{\Omega }},Fr=\frac{r{F}_0}{{\rho }_f},M=\frac{B_0^2{\sigma }_f}{\mathsf{\Omega }{\rho }_f},\tau =\frac{Gr}{R_e^2}=\frac{g\left(T_w-T_{\infty }\right){\left(\rho \beta \right)}_f}{r{\mathsf{\Omega }}^2{\rho }_f},Rd=\frac{4T_{\infty }^3{\sigma }^{*}}{k^{*}{k}_f},\\ \mathrm{Pr}=\frac{{\upsilon }_f}{{\alpha }_f},Ec=\frac{r^2{\mathsf{\Omega }}^2}{\left(T_w-T_{\infty }\right){\left(c_p\right)}_f},\epsilon =L_1\sqrt{\frac{2\mathsf{\Omega }}{{\upsilon }_f}},\gamma =L_2\sqrt{\frac{2\mathsf{\Omega }}{{\upsilon }_f}},\end{array}$$

(14)

Dimension-free forms of skin friction and an effective local Nusselt number are described as

$$\sqrt{{\mathrm{Re}}_r}{C}_f=\frac{{\mu }_{hnf}}{{\mu }_f}{f}^{″}\left(0\right),$$

(15)

$$\sqrt{{\mathrm{Re}}_r}{C}_g=\frac{{\mu }_{hnf}}{{\mu }_f}{g}^{\prime }\left(0\right),$$

(16)

$$\frac{Nu}{\sqrt{{\mathrm{Re}}_r}}=-\left(\frac{k_{hnf}}{k_f}+\frac{4}{3}Rd\right){\mathsf{\Theta }}^{\prime }\left(0\right).$$

(17)

4. Solution Methodology

The RK-4 method is generally used to get solutions for first-order ordinary differential equations (ODEs). As a consequence, the higher-order system is reduced to the first-order system. The series solutions for Equations (10)–(12) subject to Equation (13) have been established by taking the RK-4 method [37]. The first-order system is then resolved by the RK-4 method to get the function solution (y) in terms of (x).

The transformed equations are altered into first-order differential equations by selecting the variables as:

$$x_1=\eta ,x_2=f,x_3=f^{\prime },x_4=f^{″},x_5=g,x_6=g^{\prime },x_7=\mathsf{\Theta },x_8={\mathsf{\Theta }}^{\prime }.$$

(18)

The transformed model in the first-order system is written as:

$$\begin{array}{l}{D}_{\eta }{x}_4=\frac{1}{2}\left[\lambda x_3-2x_2{x}_4+\frac{{\upsilon }_f}{{\upsilon }_{hnf}}\left[S\left(x_1{x}_4+x_3\right)+x_3{}^2-x_5{}^2\right]-\frac{{\mu }_f}{{\mu }_{hnf}}\left[Fr{x}_3{}^2+\frac{{\sigma }_{hnf}}{{\sigma }_f}M{x}_3\right]-x_7\frac{Gr}{\mathrm{Re}}\frac{{\left(\rho \beta \right)}_{hnf}}{{\left(\rho \beta \right)}_f}Sin\psi ,\right]\\ D_{\eta }{x}_6=\frac{1}{2}\left[\lambda x_5-\frac{{\upsilon }_f}{{\upsilon }_{hnf}}\left[2x_2{x}_6-2x_5{x}_3-S\left(x_5+\frac{1}{2}{x}_2{x}_6\right)+2\mathrm{Re}\left(x_5-x_3\right)\right]-\frac{{\mu }_f}{{\mu }_{hnf}}\left[Fr{x}_5{}^2+\frac{{\sigma }_{hnf}}{{\sigma }_f}M{x}_5\right],\right] \\ D_{\eta }{x}_8=\mathrm{Pr}{\left(\frac{4}{3}Rd+\frac{k_{hnf}}{k_f}\right)}^{-1}\left[-\frac{{\left(\rho \beta \right)}_{hnf}}{{\left(\rho \beta \right)}_f}\left[\left(x_2+\frac{1}{4}{x}_{1}S\right)+x_8\right]-\frac{{\sigma }_{hnf}EcM}{2{\sigma }_f}\left[x_5{}^2+x_4{}^2\right]\right] . \end{array}$$

(19)

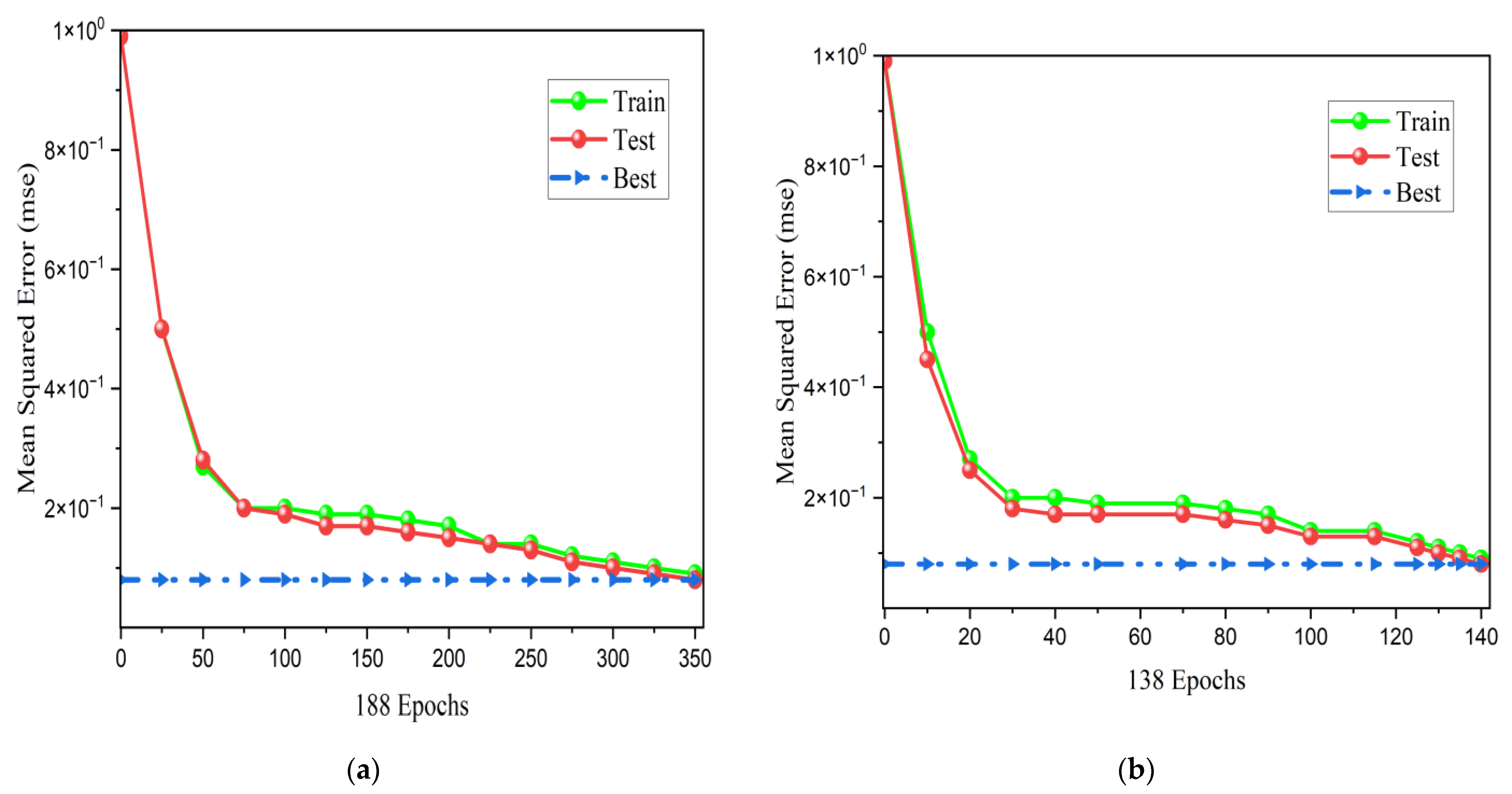
Validation of Results

The results obtained from nonlinear Equations (10)–(12) with Equation (13) are numerically validated using the neural networking approach, and a strong convergence is obtained.

5. Results and Discussion

This work examines how a magnetic field affects the unsteady flow of a hybrid nanofluid past a spinning disk that is inclined and stretched. Furthermore, the heat transmission mechanism takes Joule heating effects into account. Using an appropriate similarity transformation, the mathematical model is converted into a set of non-linear equations with boundary conditions, which are then solved by the RK-4 method. The effects of various factors on different flow profiles have been discussed in the following paragraphs.

The experimental values for the solid nanoparticles and base liquids are displayed in Table 1. The thermophysical properties of the solid nanoparticles are shown in Table 2.

Table 3. Numerical values of skin frictions for values of an inertial factor $\lambda$ with $\epsilon =2.25$.

Parameter	[38]		[39]		Present Data
$\lambda$	$f^{″}\left(0\right)$	$g^{\prime }\left(0\right)$	$f^{″}\left(0\right)$	$g^{\prime }\left(0\right)$	$f^{″}\left(0\right)$	$g^{\prime }\left(0\right)$
0.0	0.259534	−0.416784	0.25953	−0.416780	0.259420	−0.416750
0.2	0.191176	−0.509536	0.19118	−0.509540	0.191170	−0.509480
0.4	0.146057	−0.599523	0.14606	−0.599520	0.146015	−0.599530
0.6	0.116699	−0.680355	0.11670	−0.680360	0.116620	−0.680280
0.8	0.096762	−0.751543	0.099676	−0.751540	0.096764	−0.750430

is used to authenticate the obtained results with the existing literature.

Table 4. The statistical outcomes for Nusselt number and skin friction.

Parameters					$\frac{{\mathit{\mu }}_{\mathit{h}\mathit{n}\mathit{f}}}{{\mathit{\mu }}_{\mathit{f}}}{\mathit{f}}^{″}\left(0\right)$	$\frac{{\mathit{\mu }}_{\mathit{h}\mathit{n}\mathit{f}}}{{\mathit{\mu }}_{\mathit{f}}}{\mathit{g}}^{\prime }\left(0\right)$	$-\left(\frac{{\mathit{k}}_{\mathit{h}\mathit{n}\mathit{f}}}{{\mathit{k}}_{\mathit{f}}}+\frac{4}{3}\mathit{R}\mathit{d}\right){\mathsf{\Theta }}^{\prime }\left(0\right)$
$S$	Ec	$\varphi ={\varphi }_1+{\varphi }_2$	Rd	M
2.0	2.0	0.01	0.1	0.1	0.373177	0.3837321	0.37176219
3.0					0.412823	0.4835287	0.1818329
4.0					0.448879	0.541342	0.0617321
	3.0				0.44323	0.431423	0.3834210
	4.0				0.44312	0.43111	0.399643
		0.02			0.378378	0.384281	0.3932165
		0.03			0.361757	0.385210	0.42107
			0.2		0.3722328	0.382187	0.4032654
			0.3		0.3721557	0.383210	0.41873214
				0.2	0.4231013	0.3864328	0.3972135
				0.3	0.4322872	0.3878421	0.4012313

demonstrates the numerical outputs for skin friction and the Nusselt number by varying different physical flow factors. The unsteadiness factor reduces the heat transfer rate while improving skin friction because of its larger values. The Eckert number decreases the drag force for its higher values while increasing the thermal field for the same augmented values of the Eckert number. The nanoparticle volume fraction increases the heat transfer rate for its higher values, and the same effect is observed for skin friction and growth in the magnetic field parameter. The radiation parameter reduces skin friction while increasing the heat transfer rate for larger values of Rd.

The influence of the velocity slip factor upon radial velocity $g\left(\eta \right)$ and azimuthal velocity $f^{\prime }\left(\eta \right)$ is depicted in Figure 2a,b. It has been perceived that azimuthal velocity characteristics $f^{\prime }\left(\eta \right)$ are augmenting with growth in $\epsilon$ on the interval, $0\le \eta \le 3$ whereas on the interval $3<\eta \le 10$ the behavior of $f^{\prime }\left(\eta \right)$ is compact. When slip occurs in the case of azimuthal velocity, such slip flow increases, and consequently nanofluid velocity $f^{\prime }\left(\eta \right)$ upsurges, as portrayed in Figure 2a. In contrast, the radial velocity $g\left(\eta \right)$ is opposed by the slip factor, as depicted in Figure 2b, because with higher values of $\epsilon$ there is a reduction in the values of $g\left(\eta \right)$. In Figure 2c the effects of thermal slip condition $\gamma$ upon temperature profiles have been depicted, with a declining manner in the behavior of $\mathsf{\Theta }\left(\eta \right)$ due to the decay in temperature at the wall of the inclined disk. Actually, with a growth in the values, of γ there is a decay in the rate of thermal transportation from the hotter zone of the inclined disk, due to which the liquid particles become slower, which causes a depreciation in the temperature of nanoparticles.

The influence of the Forchheimer number $Fr$ is elaborated in Figure 3a,b, against the radial and azimuthal velocity profiles denoted by $f^{\prime }\left(\eta \right)$ and $g\left(\eta \right)$, respectively. Since the Forchheimer number is directly related to the porosity of the medium and the drag coefficient, the velocity profile decreases as the inertia coefficient increases. Consequently, the convective constraints progress, causing a reduction in velocity that resembles a greater Forchheimer number, as depicted in Figure 3a,b. From Figure 3c, it is observed that the temperature $\mathsf{\Theta }\left(\eta \right)$ of fluid increases with an increase in the Forchheimer number when all other parameters are kept as $\gamma =0$, $Ec=0.3$, $\mathrm{Pr}=0.3$&$Rd=0.3$. Physically, energy is transformed into heat as the fluid flow reduces, which helps to raise the temperature in the flow separation. The intensity of the flow is reduced as the non-Darcy parameter is increased, but the thermal boundary layer thickness is improved.

The variation of the porosity parameter $\lambda$ is elaborated in Figure 4a,b against radial and azimuthal velocity profiles when all the other parameters are kept as ${\varphi }_1,{\varphi }_2=0.02,$ $Fr=0.3,$ $M=1,$ $S=1,$ $Gr=0.5,$ & $\epsilon =0$. It is perceived that the porosity parameter decreases in both directions for the velocity components. Since the porosity parameter restricts the flow of the fluid on the surface of the disk, raising the value of the porosity parameter causes the width of the boundary layer to rise, which results in the velocity falling. This is because the growth in the porous medium resists the flow of fluid, resulting in flow retardation as depicted in Figure 4a,b. Figure 4c displays the effect of the porosity factor on temperature distribution for $\gamma =0,$ $Ec=0.3,$ $\mathrm{Pr}=0.3,$ & $Rd=0.3$. When the permeability of the porosity parameter is increased, then the temperature of the fluid rises, as portrayed in Figure 4c.

In Figure 5a,b, variations of the magnetic parameter $M$ are demonstrated against radial and azimuthal velocity profiles when all the other parameters are kept as ${\varphi }_1,{\varphi }_2=0.02,$ $Fr=0.3,$ $\lambda =0.3,$ $S=1,$ $Gr=0.5,$ & $\epsilon =0$. As stated in the Lorentz force, a slower body force is exerted by a magnetic field that opposes the direction of the applied magnetic field. With an increase in the values of the non-dimensional magnetic factor, the slower body motion increases and, hence, the velocity decreases, in both directions, as shown in Figure 5a,b. In Figure 5c, the effects of the magnetic parameter are elaborated against the temperature field when all other parameters are kept as $\gamma =0,$ $Ec=0.3,$ $\mathrm{Pr}=0.3,$ & $Rd=0.3$. As discussed above, the magnetic parameter depends on Lorentz force, which generates flow resistance; due to this, a small increment in temperature is observed by increasing the magnetic field. The transverse magnetic field is opposed to the transportation process. It is worth mentioning that high resistance on the fluid particles produces heat in the flow region, which intensifies the magnetic parameter as portrayed in Figure 5c.

In Figure 6a,b, the influence of the unsteadiness parameter $S$ is displayed against radial and azimuthal velocity profiles, when all the other parameters are tuned as ${\varphi }_1,{\varphi }_2=0.02,$ $Fr=0.3,$ $\lambda =0.3,$ $M=1,$ $Gr=0.5,$ & $\epsilon =0$. Here, the velocity in both $r$ and $\theta$ directions declines with the increase in the unsteadiness factor. The velocity along the disk drops as the unsteadiness parameter increases, which implies a decrease in the width of the momentum layer at the boundary close to the wall, as portrayed in Figure 6a,b. Figure 6c illustrates the impact of the unsteadiness parameter on temperature distribution when all other parameters are kept as $\gamma =0,$ $Ec=0.3,$ $\mathrm{Pr}=0.3,$ & $Rd=0.3$. When the value of the unsteadiness parameter increases, then a rise in temperature distribution occurs.

For numerous values of the thermal Grashof number $Gr$, the flow characteristics are sketched in Figure 7a,b against radial and azimuthal velocity profiles when all the other parameters are tuned as ${\varphi }_1,{\varphi }_2=0.02,$ $Fr=0.3,$ $\lambda =0.3,$ $M=1,$ $\epsilon =0$ & $S=0.5$. The growth in $Gr$ signifies the impact of thermal buoyancy force on hydrodynamic vicious force. It is noticed that there is a growth in velocity characteristics due to an upsurge in buoyancy thermal force. Actually, with growth in $Gr$ the upper values of velocity characteristics, they grow up sharply near the permeable disk and then decline gradually to free stream flow as depicted in Figure 7a,b. Figure 7c illustrates the of the Grashof number impact on temperature distribution when all other parameters are kept as $\gamma =0,$ $Ec=0.3,$ $\mathrm{Pr}=0.3,$ & $Rd=0.3$. When the value of the Grashof number increases, then a decline in temperature distribution occurs. The decreasing behavior of temperature vanishes the thickness of the thermal boundary layer.

In Figure 8a, it is observed that when the Eckert number $Ec$ increases, the temperature rises when all other parameters are kept as $\gamma =0,$ $\mathrm{Pr}=0.3,$ & $Rd=0.3$. In physical terms, the Eckert number is a ratio of frictional heat in a system. As a result, the thermal phase with a higher Eckert number is subjected to more frictional heating, increasing the temperature. The impact of $\mathrm{Pr}$ (Prandtl number) on thermal flow is labeled in Figure 8b when all other parameters are kept as $\gamma =0,$ $Ec=0.3,$ & $Rd=0.3$. A visible reduction in thermal characteristics is noticed with the increase in $\mathrm{Pr}$. Actually, $\mathrm{Pr}$ is in inverse relation to thermal diffusions; therefore, higher values of $\mathrm{Pr}$ low thermal diffusion occur due to which thermal characteristics decline. Figure 8c elaborates on the effect on temperature distribution of the radiation parameter $Rd$ when all other parameters are kept as $\gamma =0,$ $Ec=0.3,$ & $\mathrm{Pr}=0.3$. For growth in $Rd$, the thermal distribution near the laminar disk reduces and improves away from the disk, resulting in less heat transfer to the nanofluid in the boundary layer area. This is due to the fact that the radiation parameter tends to oppose the flow as the parameter values increase.

The neuronal network as mentioned in [40,41] is developed using a data source that considers variants related to the nanofluid motion mechanism proposed in regions 0 and 4. The RK-4 strategy, which uses configuration parameters for the first-order solution, coherence goal, and acceptance rate to solve prevalent mathematical equations, is adapted to support the proposed neural network approach. The Neural Network Fitting Tool (NF) is then used in a similar sequence. Figure 9a illustrates a unique neural network model. The suggested network’s structure is presented in Figure 9b, and the BRT-ANN is constructed employing the NF tool with the appropriate settings for unseen neurons, testing datasets, training datasets, and validation datasets. The software is used to form the weight function of a neural network through Bayesian regulation feedback. To achieve optimization, the suggested BRT-ANN incorporates a multilayer neuronal network structure with Bayesian regulation and retroactive propagation. Figure 10a,b show the convergence of the proposed model at the various interval as per the neural networking strategy.

6. Conclusions

In this work, the unsteady flow of the hybrid nanofluid over an inclined rotating stretching disk is scrutinized by using slip conditions and magnetic effects. The impact of conventional flow is examined with thermal radiation and Joule heating. The RK-4 method is implemented to obtain results for the proposed modeled equations. The main observations of the present investigation are summarized below.

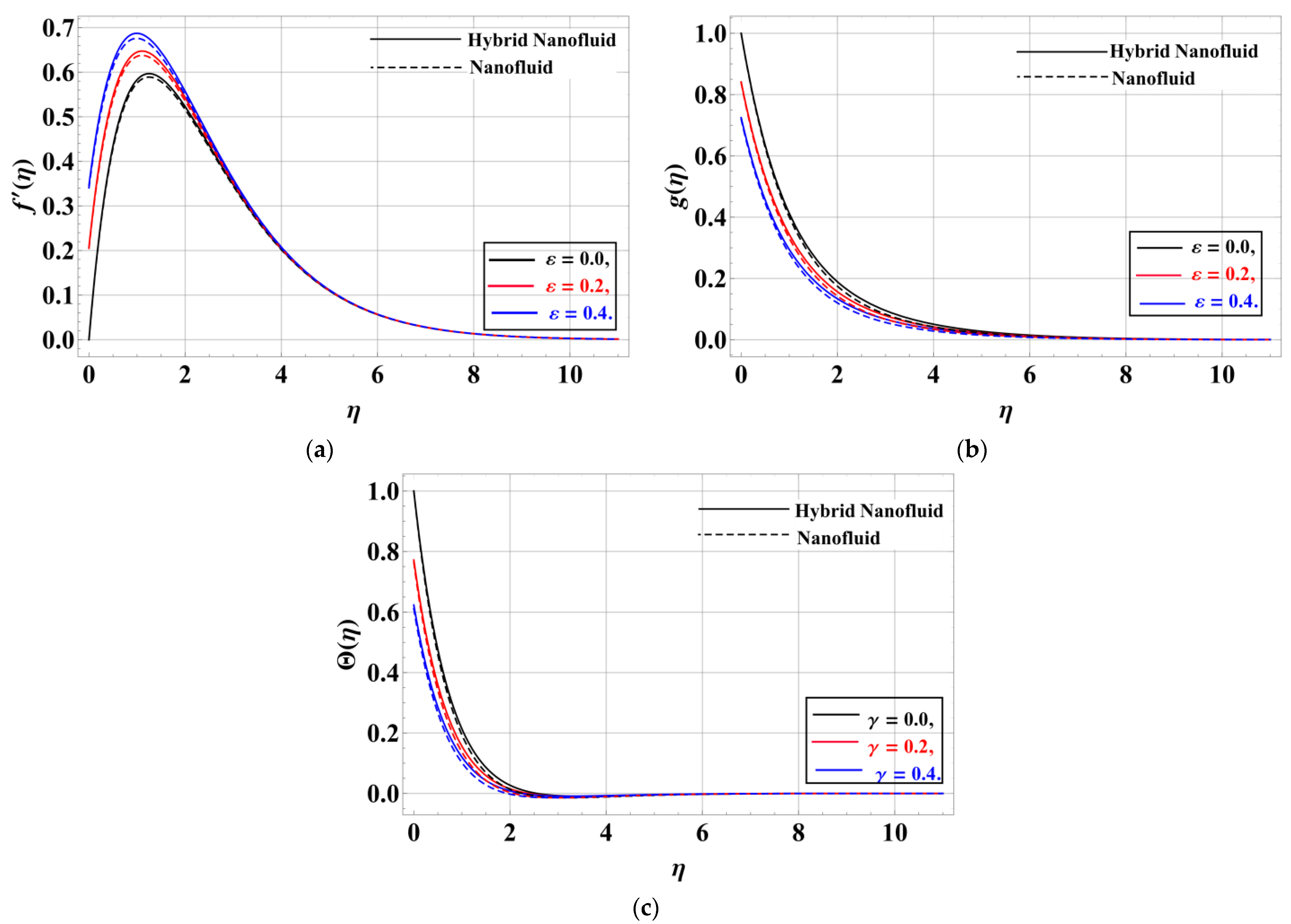
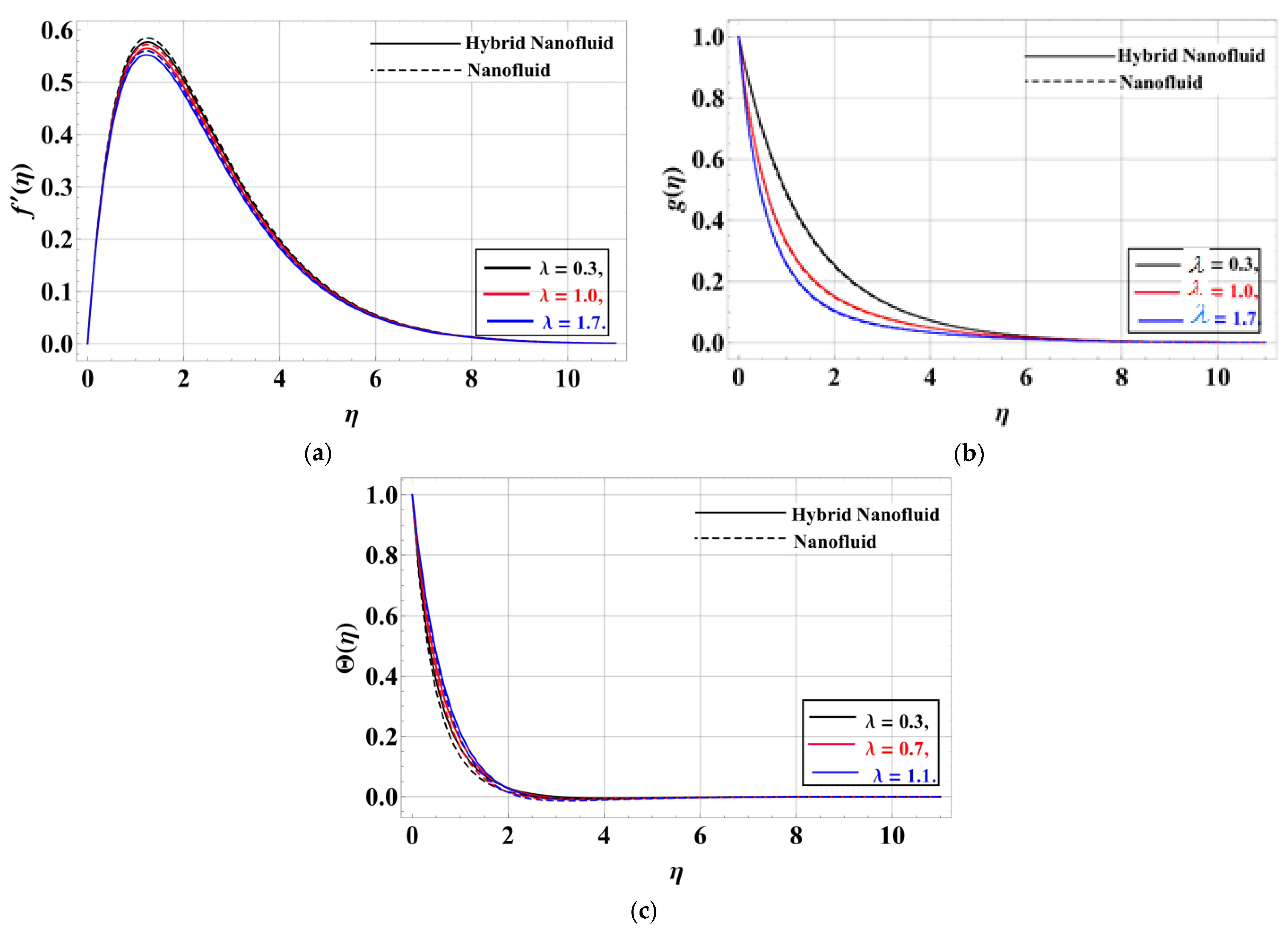
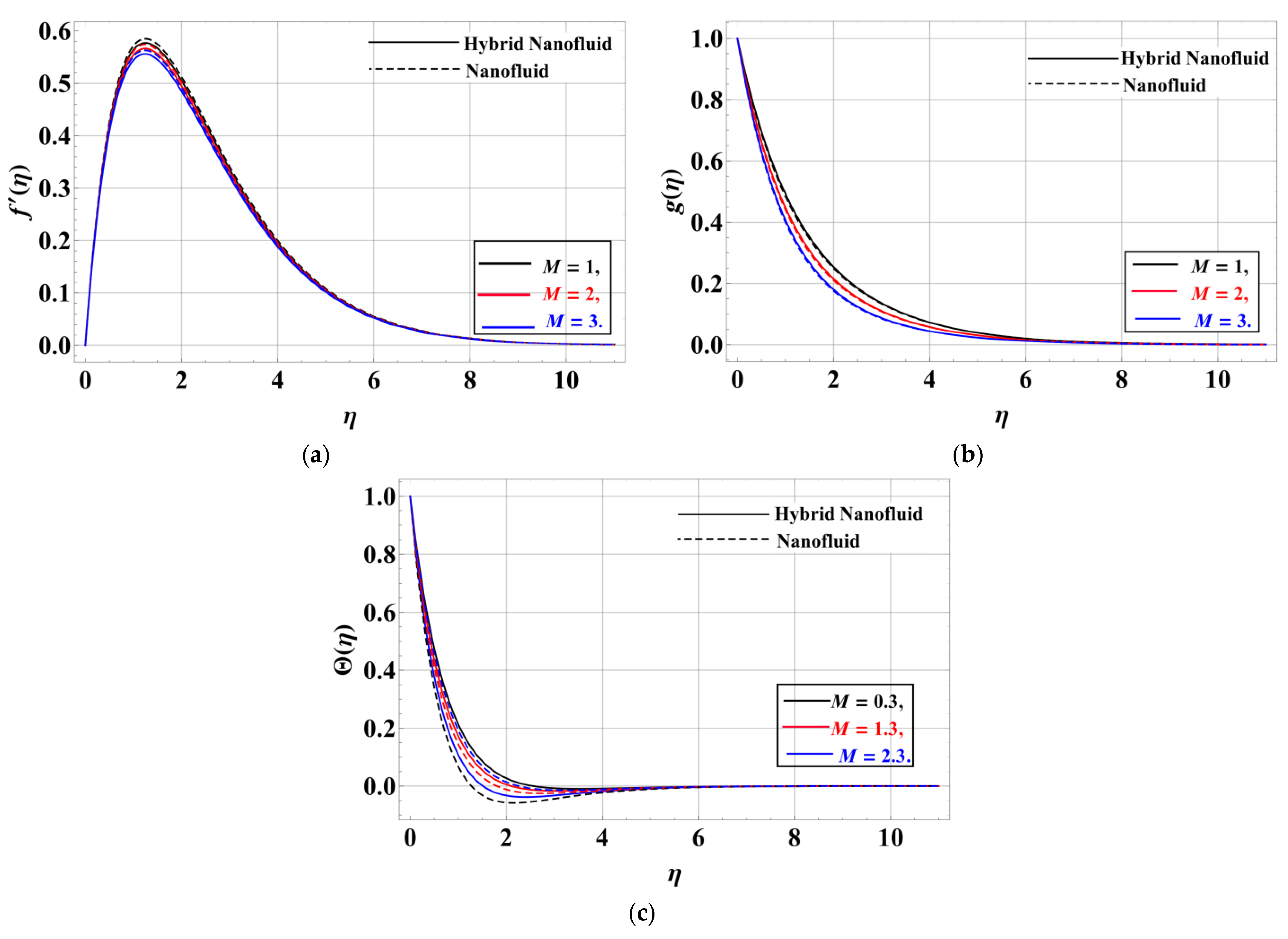
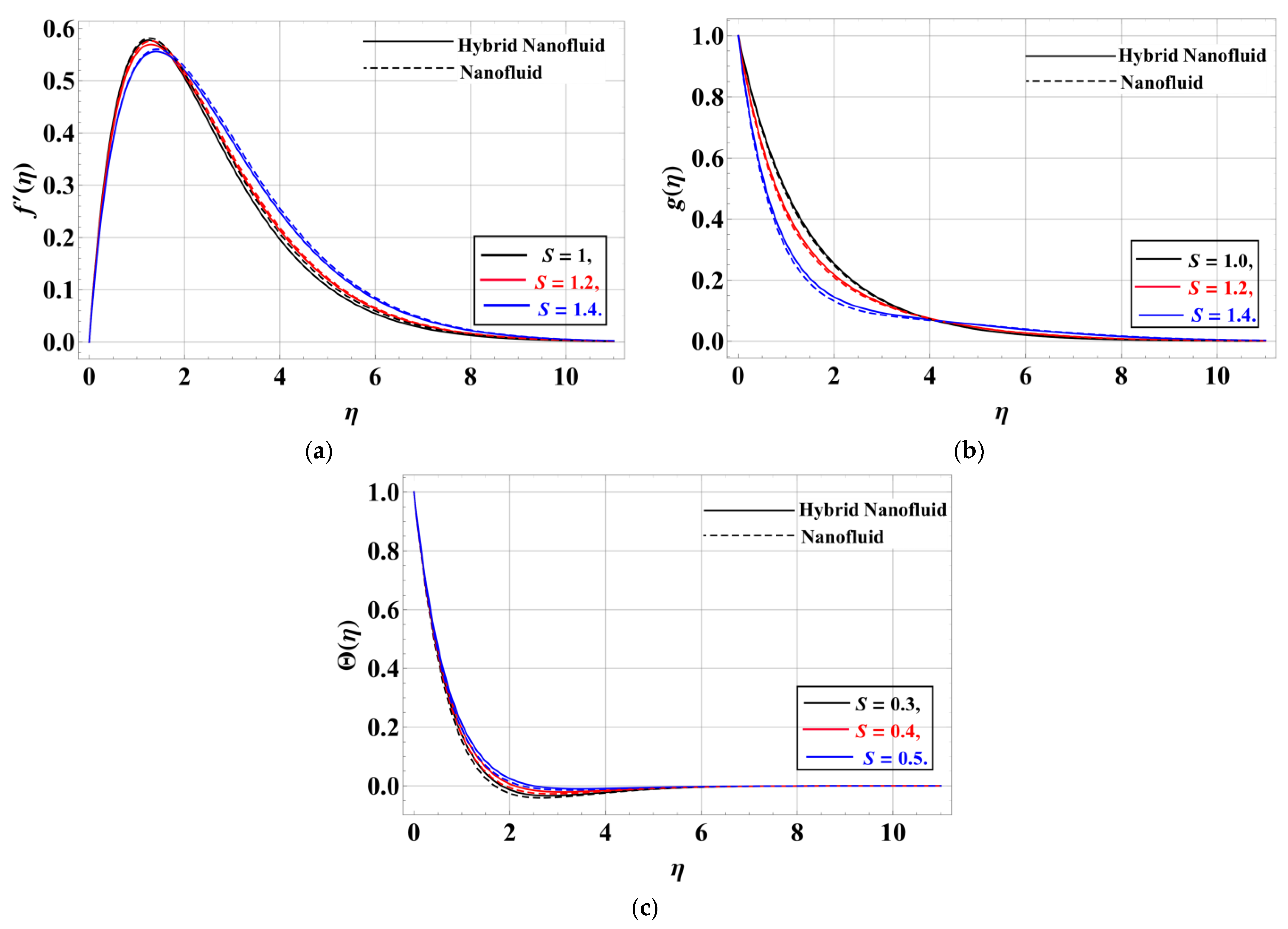
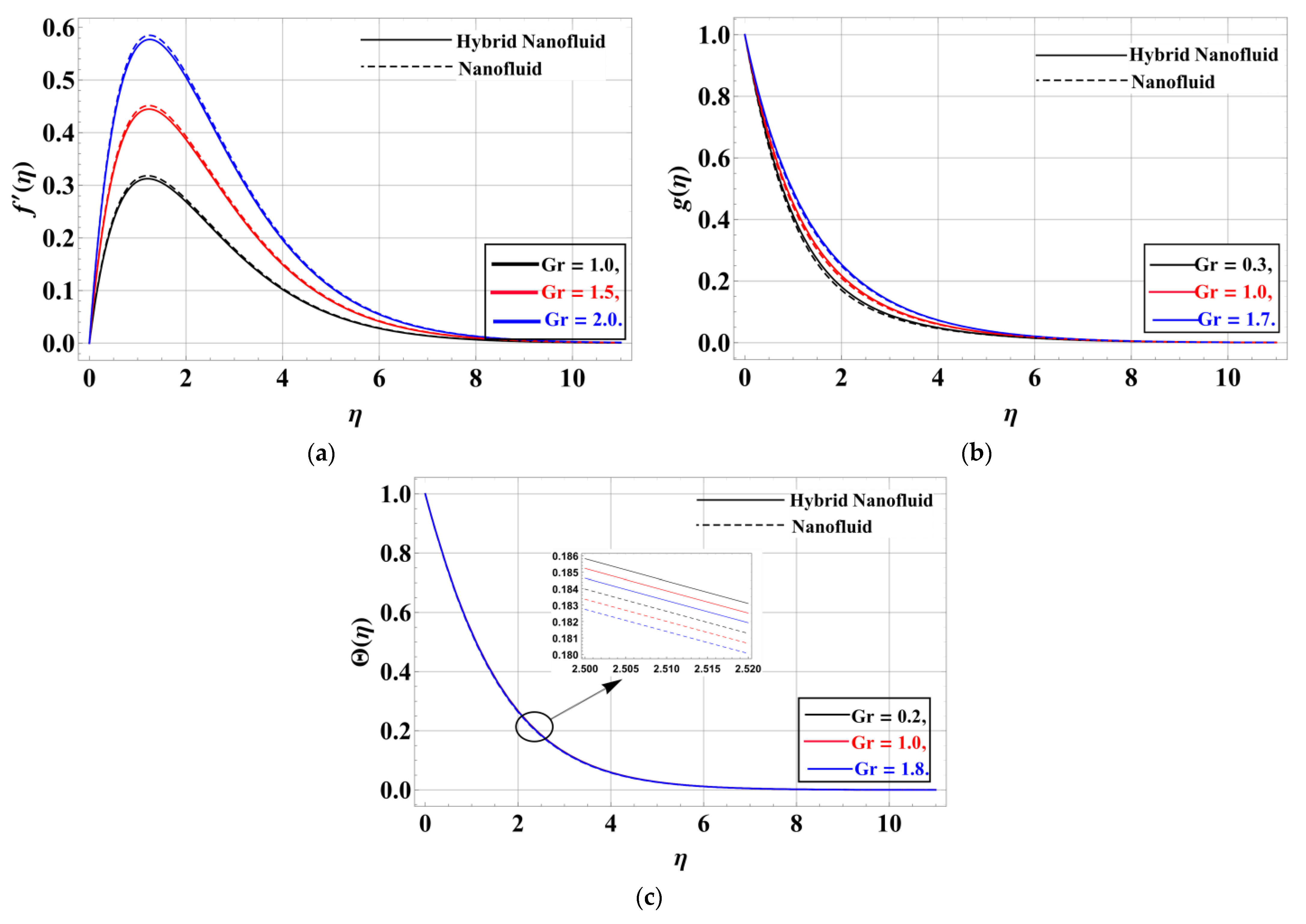
• The velocity profile along $r,$ and $\theta$ directions of the hybrid nanofluid is retarded by increasing the values of the porosity factor, unsteadiness parameter, Forchheimmer number, and magnetic field.
• The slip factor efficiently controls the growth in velocity variations.
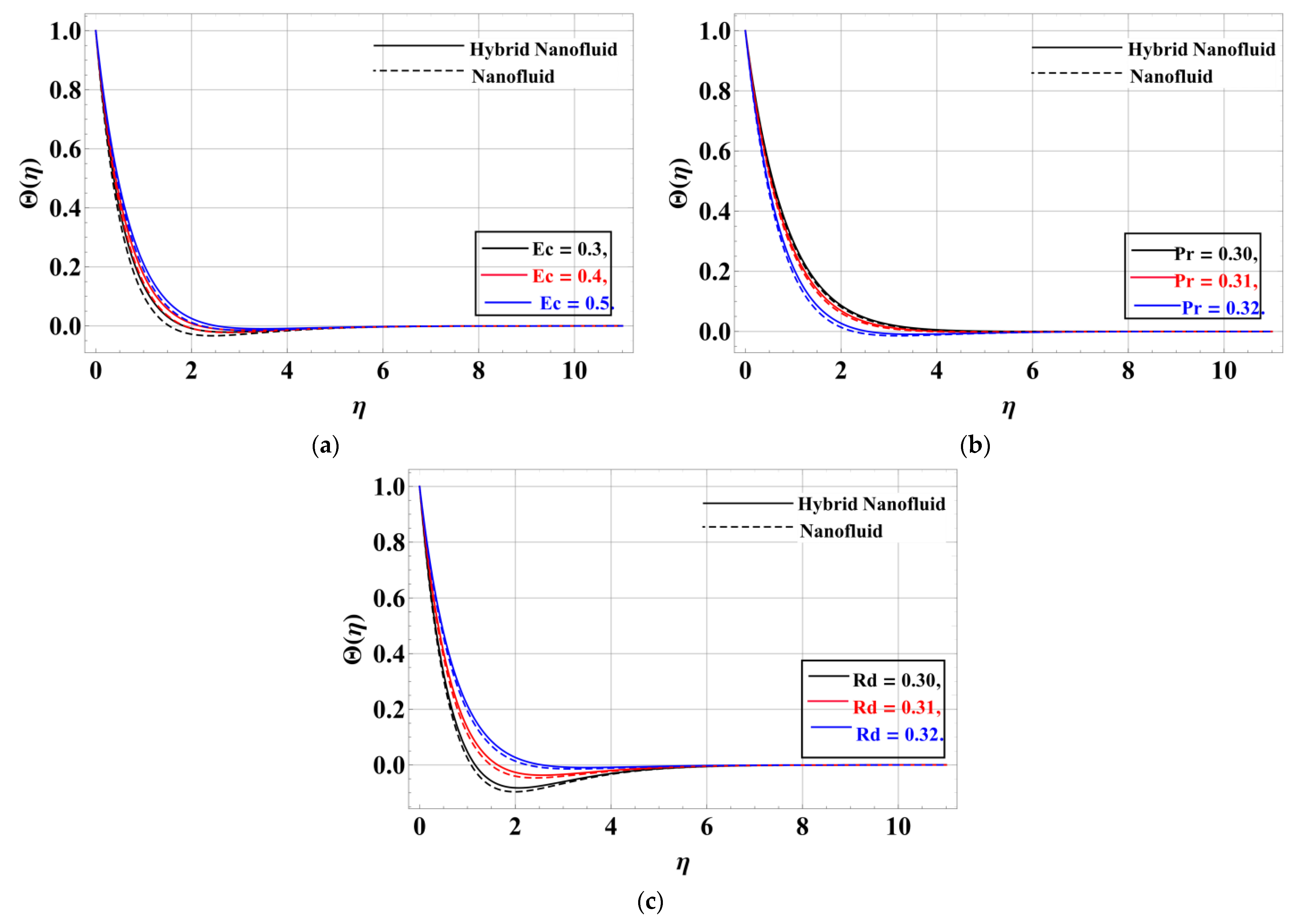
• The fluid heat gets lower with the increase in the thermal slip factor.
• The temperature of the hybrid nanofluid is increased by increasing the values of the porosity parameter, the unsteadiness factor, the Eckert number, the magnetic field, and the Forchheimmer number, while for the values of the radiation factor, the thermal heat is retarded near the disk and increases away from the disk.
• The porosity of the medium and the magnetic field are significant for the skin friction coefficient along the $r$ direction when the values of other parameters are fixed. While in $\theta$-direction the skin friction and Forchheimmer number are significant, other parameters are to be fixed.
• The magnetic and radiation factors are significant for the Nusselt number when the other parameters are fixed.
• The physical quantity, i.e., the local Nusselt number, increases to meet the increasing values of the Prandtl number.
• The convergence of the results is verified through the neural network and machine-learning approach.