Event-Triggered Extended Dissipativity Fuzzy Filter Design for Nonlinear Markovian Switching Systems against Deception Attacks
Abstract
1. Introduction, Notations, and Outline
1.1. Bibliographic Review
1.2. Objective and Outline
- (i)
- (ii)
- This work introduces a novel adaptive-event-triggered communication scheme that improves the use of network resources as opposed to [50,51,52], which assumed the triggering parameters are constant. This mechanism was shown to alleviate network bandwidth and reduce system conservatism effectively by comparing it with other strategies [35,48,53,54].
- (iii)
- As described in [30,55], an improved matrix decoupling approach, which can be implemented by selecting some constants, provides greater flexibility when designing filters. This study, in contrast to previous studies, used a meta-heuristic technique based on PSO to identify the parameters accurately.
1.3. Notations
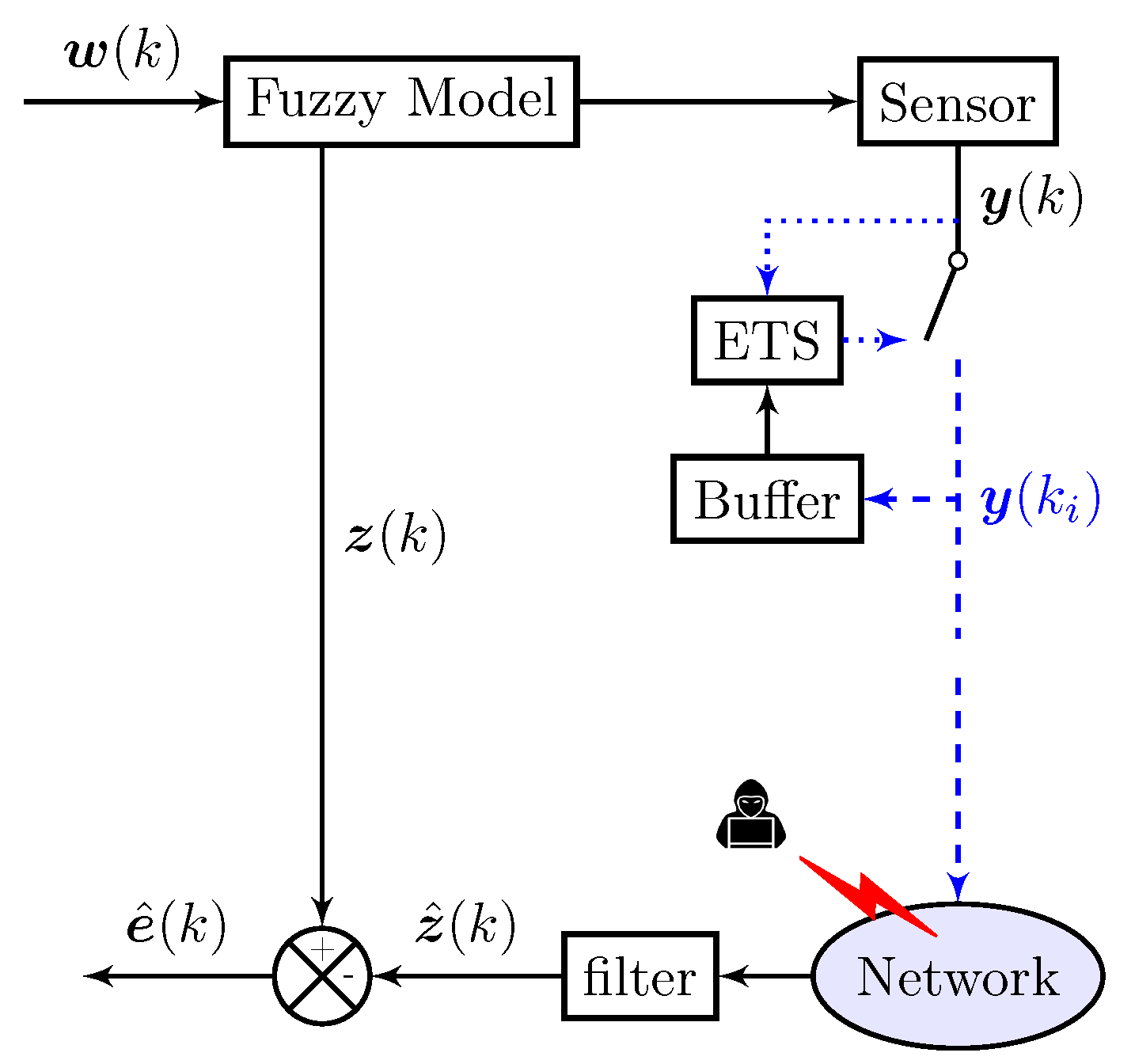
2. System Description and Problem Formulation
2.1. Markovian Jump T-S-Fuzzy-Model-Based NCS
2.2. Event-Triggered Schemes
- Case 1
- If , we define . It is obvious that .
- Case 2
- If , we define the intervals . Due to , there exists a positive integer such thatObviously, we obtainTherefore, we have , . In the first case, we define ; in the second case, is defined asFollowing the above discussion, the following relationship holds using (9):
2.3. Deception Attacks
2.4. Fuzzy Filter
2.5. Problem Formulation
- 1.
- System (19) is mean-squared stable;
- 2.
- Under zero initial conditions, the following criterion holds for :where , and matrices , , and satisfy the following assumption:
- (i)
- ;
- (ii)
- .
3. Main Results
3.1. Extended Dissipative Analysis
3.2. Filter Design
4. Optimization-Based Filter Design Algorithm
- (i)
- Dissipative/ passivity performances:
- (ii)
- / performances:
| Algorithm 1 Determining the minimum performances and filter gains |
|
5. Numerical Applications
5.1. Computational Framework and Algorithm
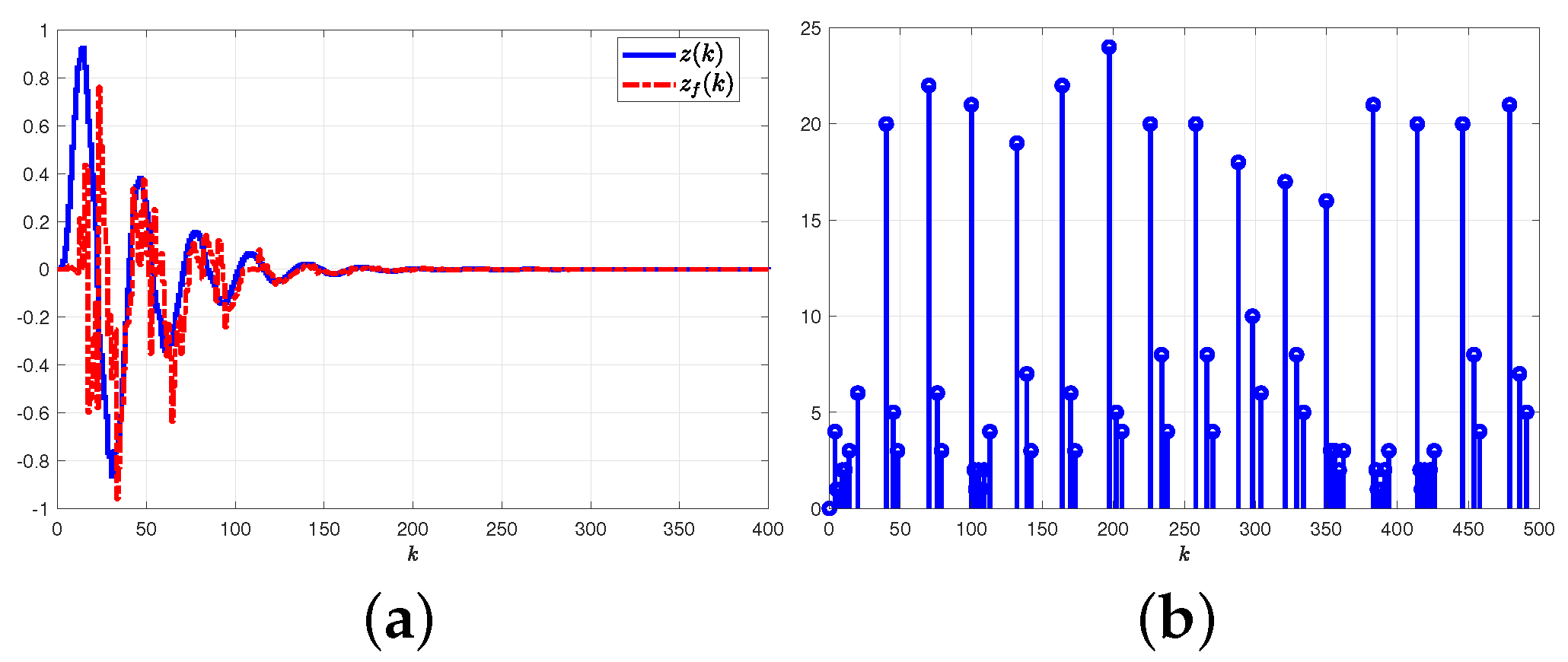
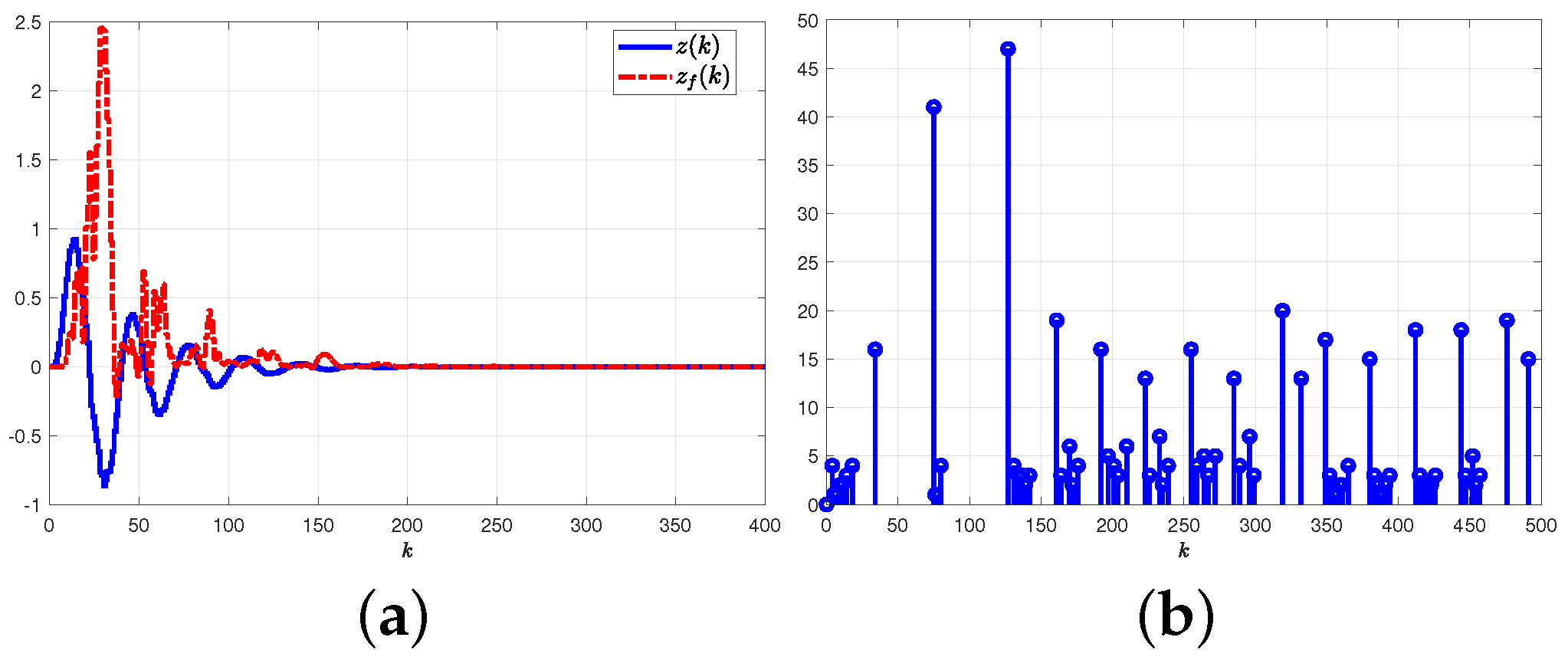
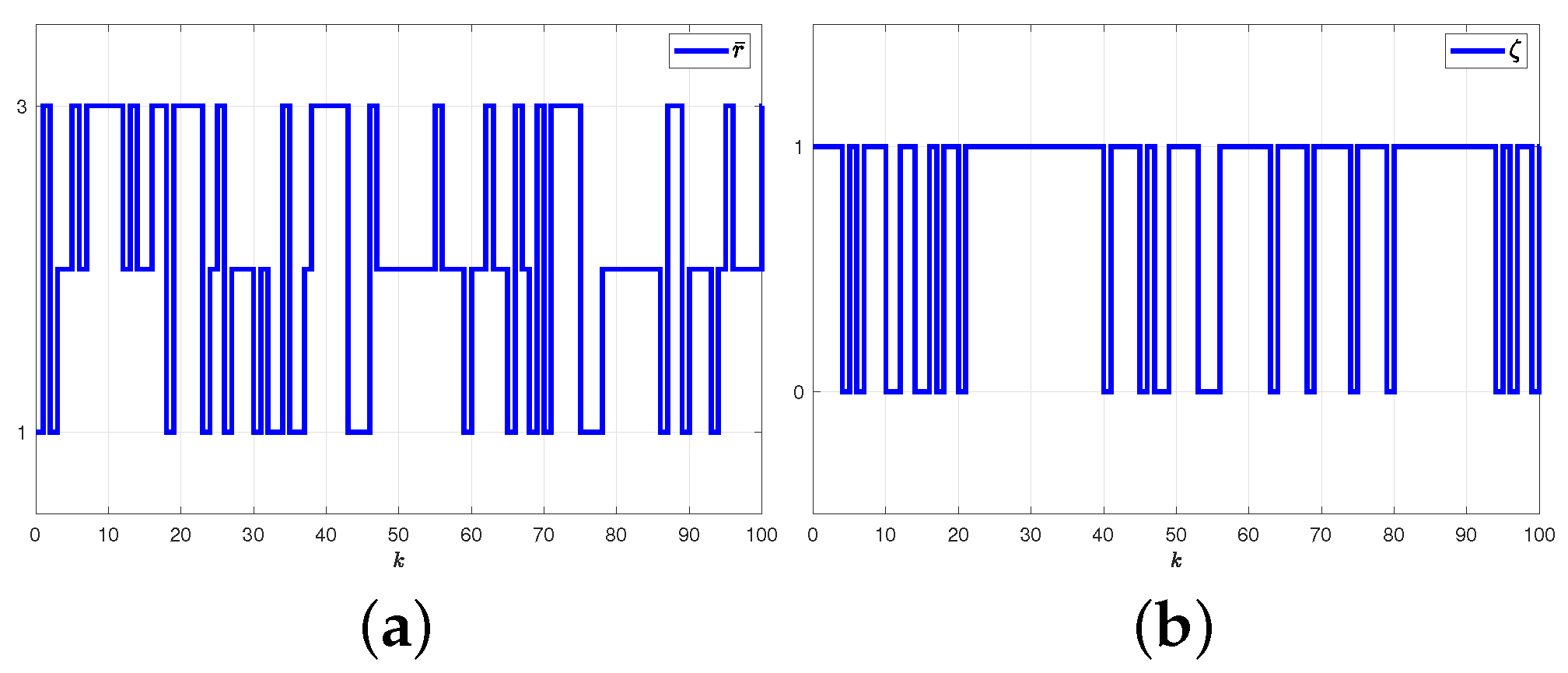
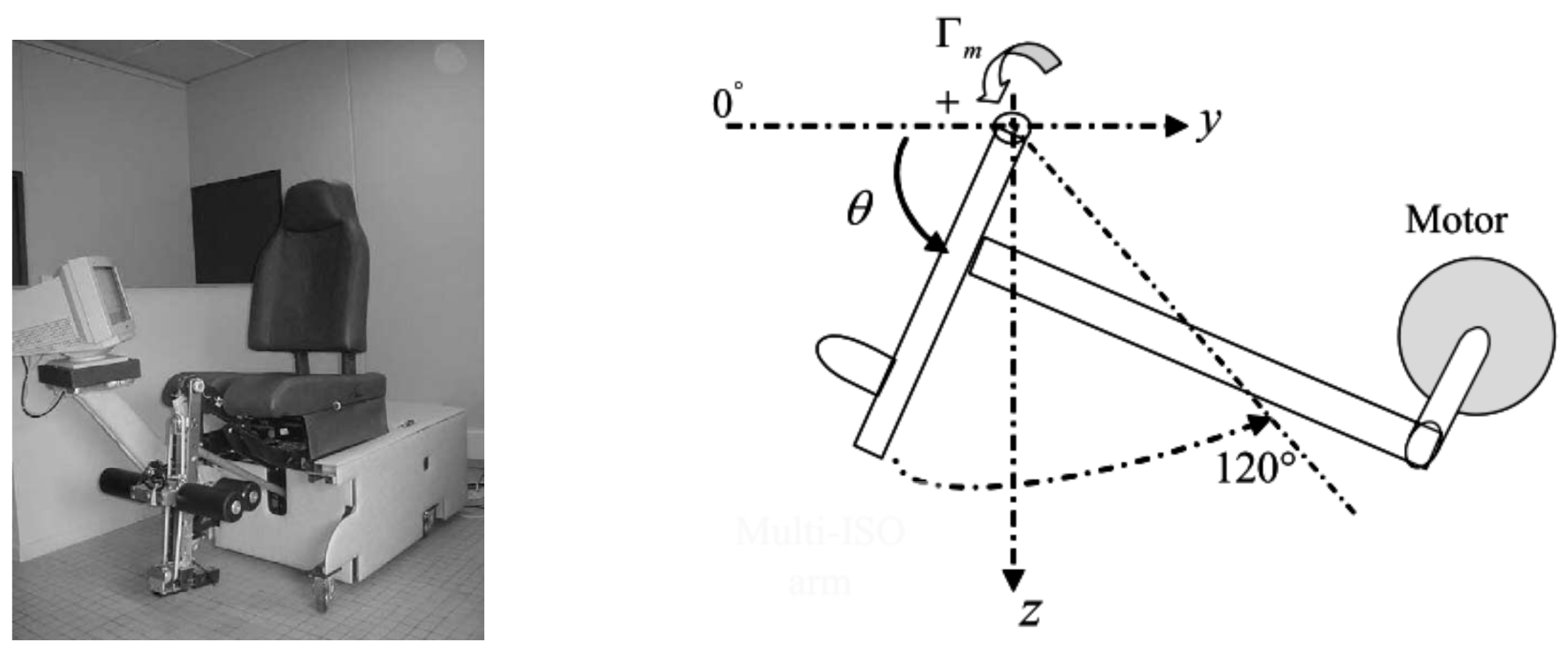
5.2. Single-Link Robot Arm System
- Case I: passivity filtering:
- Case II: dissipativity filtering:
- Case III: filtering:
- Case IV:
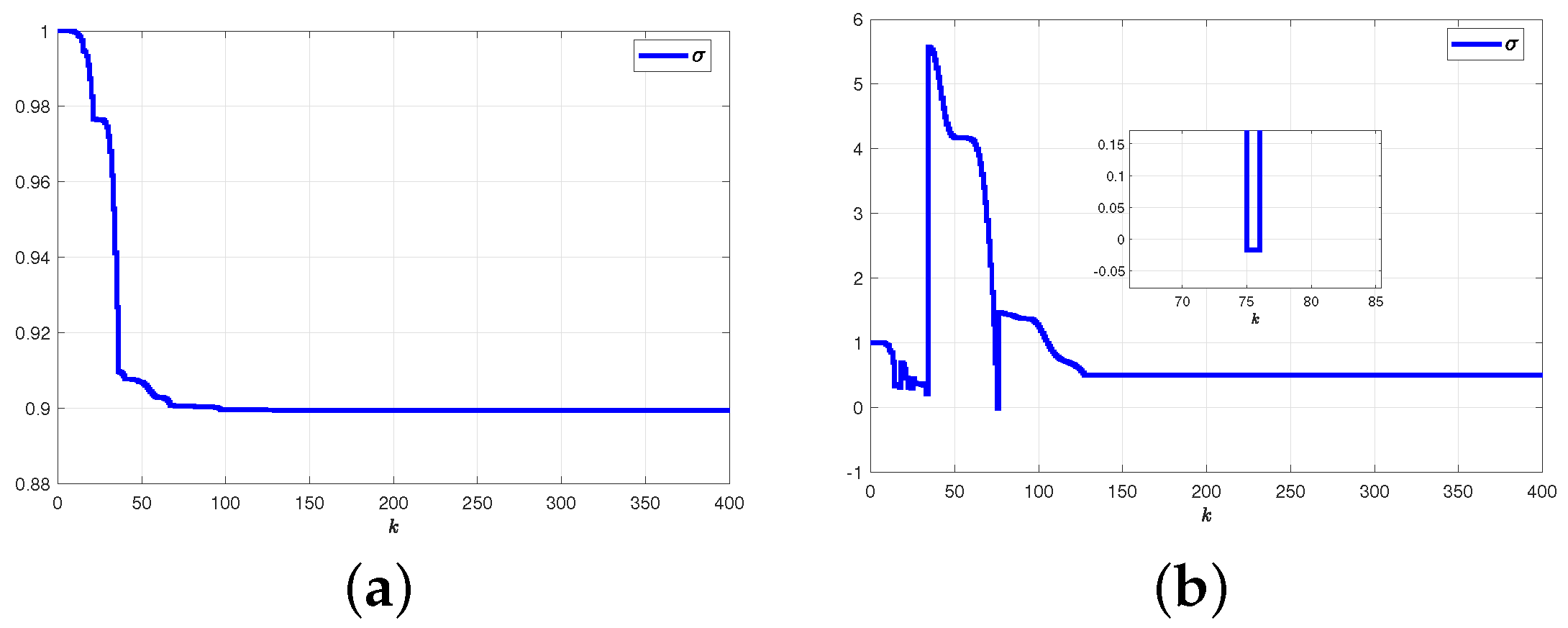
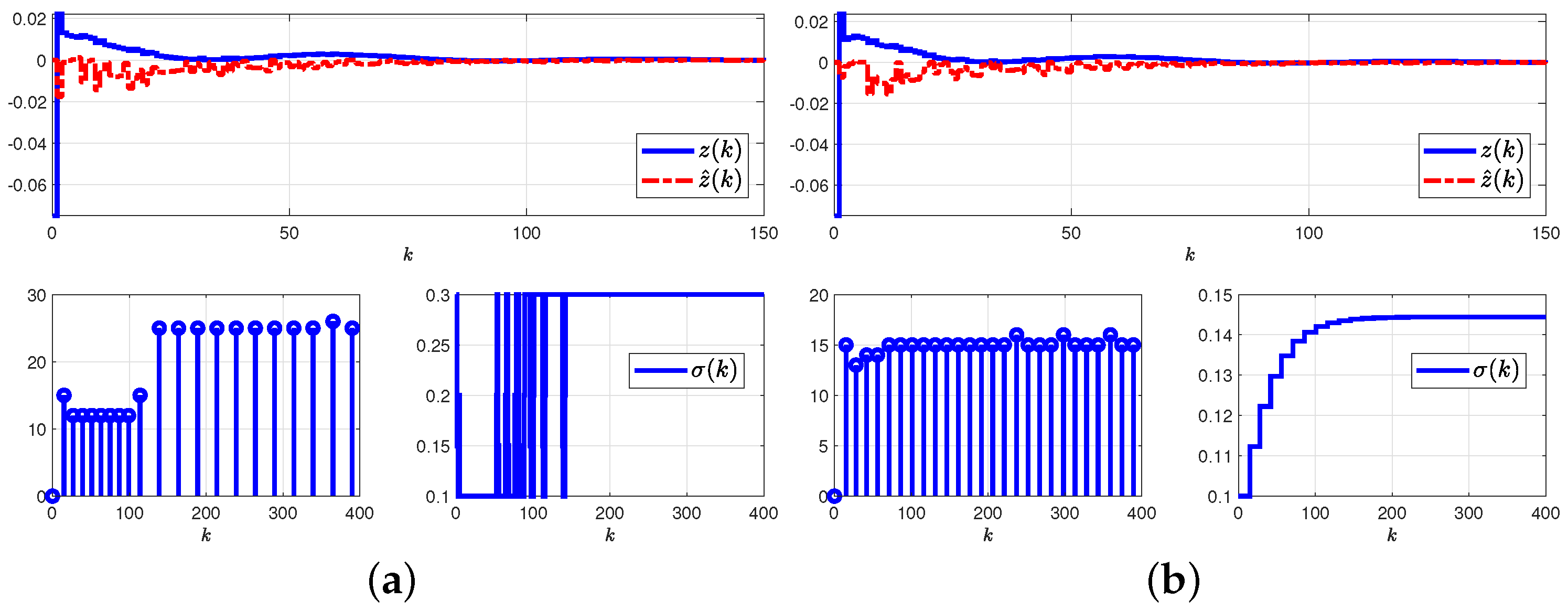
5.2.1. Results and Graphical Plots
5.2.2. Comparative Explanations
5.3. A Lower Limbs Rehabilitation System
5.4. Comparative Explanations
- To handle nonlinear network systems, a linear filter was designed in [26] using Type-1 fuzzy models, which may lead to conservative results. As an alternative, we took a more general approach based on a Markovian jump Type-2 fuzzy model to design an IT2 fuzzy filter with extended dissipativity performance.
- Different from [49,62], the filter design method described in [26] was based on an improved matrix decoupling approach that uses appropriate selected scalars. The selection of these parameters can be achieved either by a numerical analysis or by using meta-heuristic techniques, such as the PSO method addressed in this study.
6. Conclusions, Limitations, and Future Work
6.1. Concluding Remarks
6.2. Limitations
6.3. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hou, L.; Chen, D.; He, C. Finite-time nonfragile dissipative control for discrete-time neural networks with Markovian jumps and mixed time-delays. Complexity 2019, 2019, 5748923. [Google Scholar] [CrossRef]
- Sathishkumar, M.; Sakthivel, R.; Alzahrani, F.; Kaviarasan, B.; Ren, Y. Mixed H∞ and passivity-based resilient controller for nonhomogeneous Markovian jump systems. Nonlinear Anal. Hybrid Syst. 2019, 31, 86–99. [Google Scholar] [CrossRef]
- Cheng, J.; Park, J.H.; Cao, J.; Qi, W. A hidden mode observation approach to finite-time SOFC of Markovian switching systems with quantization. Nonlinear Dyn. 2020, 100, 509–521. [Google Scholar] [CrossRef]
- Cheng, J.; Park, J.H.; Zhao, X.; Karimi, H.R.; Cao, J. Quantized Nonstationary Filtering of Networked Markov Switching RSNSs: A Multiple Hierarchical Structure Strategy. IEEE Trans. Autom. Control. 2020, 65, 4816–4823. [Google Scholar] [CrossRef]
- Li, H.; Shi, P.; Yao, D.; Wu, L. Observer-based adaptive sliding mode control for nonlinear Markovian jump systems. Automatica 2016, 64, 133–142. [Google Scholar] [CrossRef]
- Ma, Y.; Jia, X.; Zhang, Q. Robust finite-time non-fragile memory H∞ control for discrete-time singular Markovian jumping systems subject to actuator saturation. J. Frankl. Inst. 2017, 354, 8256–8282. [Google Scholar] [CrossRef]
- Wu, B.; Zhao, Y. Dissipative Control for Fuzzy Singular Markov Jump Systems With State-Dependent Noise and Asynchronous Modes. IEEE Access 2021, 9, 25691–25702. [Google Scholar] [CrossRef]
- Qi, W.; Park, J.; Cheng, J.; Chen, X. Stochastic stability and L1-gain analysis for positive nonlinear semi-Markovian jump systems with time-varying delay via TS fuzzy model approach. Fuzzy Sets Syst. 2019, 371, 110–122. [Google Scholar] [CrossRef]
- Kavikumar, R.; Sakthivel, R.; Kwon, O.; Kaviarasan, B. Reliable non-fragile memory state feedback controller design for fuzzy Markovian jump systems. Nonlinear Anal. Hybrid Syst. 2020, 35, 100828. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, Z. Asynchronous Extended Dissipative Filtering for T-S Fuzzy Markov Jump Systems. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 3915–3925. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Q.; Yan, X.G.; Spurgeon, S.K. Integral sliding mode control for Markovian jump T-S fuzzy descriptor systems based on the super-twisting algorithm. Iet Control. Theory Appl. 2017, 11, 1134–1143. [Google Scholar] [CrossRef]
- Lv, C.; Chen, J.; Lv, X.; Zhang, Z. Finite-time H∞ control for interval Type-2 fuzzy singular systems via switched fuzzy models and static output feedback. Nonlinear Anal. Hybrid Syst. 2022, 45, 101206. [Google Scholar] [CrossRef]
- Zhao, T.; Wei, Z.; Dian, S.; Xiao, J. Observer-based H∞ controller design for interval Type-2 T-S fuzzy systems. Neurocomputing 2016, 177, 9–25. [Google Scholar] [CrossRef]
- Song, W.; Tong, S. Fuzzy decentralized output feedback event-triggered control for interval Type-2 fuzzy systems with saturated inputs. Inf. Sci. 2021, 575, 639–653. [Google Scholar] [CrossRef]
- Alshammari, O.; Kchaou, M.; Jerbi, H.; Ben Aoun, S.; Leiva, V. A Fuzzy Design for a Sliding Mode Observer-Based Control Scheme of Takagi–Sugeno Markov Jump Systems under Imperfect Premise Matching with Bio-Economic and Industrial Applications. Mathematics 2022, 10, 3309. [Google Scholar] [CrossRef]
- Wang, S.; Feng, J.; Zhang, H. Robust fault tolerant control for a class of networked control systems with state delay and stochastic actuator failures. Int. J. Adapt. Control. Signal Process. 2014, 28, 798–811. [Google Scholar] [CrossRef]
- Latrech, C.; Kchaou, M.; Guéguen, H. Networked non-fragile H∞ static output feedback control design for vehicle dynamics stability: A descriptor approach. Eur. J. Control. 2018, 40, 13–26. [Google Scholar] [CrossRef]
- Wang, B.; Chen, W.; Wang, J.; Zhang, B.; Zhang, Z.; Qiu, X. Cooperative Tracking Control of Multiagent Systems: A Heterogeneous Coupling Network and Intermittent Communication Framework. IEEE Trans. Cybern. 2019, 49, 4308–4320. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Z.; Sheng, W.; Alsaadi, F.E.; Alsaadi, F.E. Dynamic event-triggered mechanism for H∞ non-fragile state estimation of complex networks under randomly occurring sensor saturations. Inf. Sci. 2020, 509, 304–316. [Google Scholar] [CrossRef]
- Chen, M.; Karimi, H.R.; Sun, J. Observer-based finite time H∞ control of nonlinear discrete time-varying systems with an adaptive-event-triggered Mechanism. J. Frankl. Inst. 2020, 357, 11668–11689. [Google Scholar] [CrossRef]
- Chu, X.; Li, M. H∞ non-fragile observer-based dynamic-event-triggered sliding mode control for nonlinear networked systems with sensor saturation and dead-zone input. ISA Trans. 2019, 94, 93–107. [Google Scholar] [CrossRef] [PubMed]
- Qi, W.; Zong, G.; Zheng, W.X. Adaptive Event-Triggered SMC for Stochastic Switching Systems With Semi-Markov Process and Application to Boost Converter Circuit Model. IEEE Trans. Circuits Syst. I: Regul. Pap. 2021, 68, 786–796. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, P.; Agarwal, R.K.; Shi, Y. Event-Based Dissipative Analysis for Discrete Time-Delay Singular Jump Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1232–1241. [Google Scholar] [CrossRef]
- Wang, X.L.; Yang, G.H. Event-triggered fault detection for discrete-time T-S fuzzy systems. ISA Trans. 2018, 76, 18–30. [Google Scholar] [CrossRef] [PubMed]
- Song, X.; Men, Y.; Zhou, J.; Zhao, J.; Shen, H. Event-triggered H∞ control for networked discrete-time Markov jump systems with repeated scalar nonlinearities. Appl. Math. Comput. 2017, 298, 123–132. [Google Scholar] [CrossRef]
- Chen, Q.X.; Chang, X.H. Resilient filter of nonlinear network systems with dynamic event-triggered mechanism and hybrid cyber-attack. Appl. Math. Comput. 2022, 434, 127419. [Google Scholar] [CrossRef]
- Tian, E.; Wang, Z.; Zou, L.; Yue, D. Probabilistic-constrained filtering for a class of nonlinear systems with improved static event-triggered communication. Int. J. Robust Nonlinear Control. 2019, 29, 1484–1498. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, N.; Li, Y.; Xie, X. H∞ filter design for discrete-time networked systems with adaptive-event-triggered mechanism and hybrid cyber-attacks. J. Frankl. Inst. 2021, 358, 9325–9345. [Google Scholar] [CrossRef]
- Dong, S.; Fang, M.; Shi, P.; Wu, Z.G.; Zhang, D. Dissipativity-Based Control for Fuzzy Systems With Asynchronous Modes and Intermittent Measurements. IEEE Trans. Cybern. 2020, 50, 2389–2399. [Google Scholar] [CrossRef]
- Liu, J.; Yin, T.; Cao, J.; Yue, D.; Karimi, H.R. Security Control for T-S Fuzzy Systems With Adaptive Event-Triggered Mechanism and Multiple Cyber-Attacks. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 6544–6554. [Google Scholar] [CrossRef]
- Hsieh, C.S. Robust two-stage Kalman filters for systems with unknown inputs. IEEE Trans. Autom. Control. 2000, 45, 2374–2378. [Google Scholar] [CrossRef]
- Jwo, D.J.; Wang, S.H. Adaptive Fuzzy Strong Tracking Extended Kalman Filtering for GPS Navigation. IEEE Sens. J. 2007, 7, 778–789. [Google Scholar] [CrossRef]
- Hamid, K.R.; Talukder, A.; Islam, A.K.M.E. Implementation of Fuzzy Aided Kalman Filter for Tracking a Moving Object in Two-Dimensional Space. Int. J. Fuzzy Log. Intell. Syst. 2018, 18, 85–96. [Google Scholar] [CrossRef]
- Zhang, M.; Shi, P.; Liu, Z.; Ma, L.; Su, H. H∞ filtering for discrete-time switched fuzzy systems with randomly occurring time-varying delay and packet dropouts. Signal Process. 2018, 143, 320–327. [Google Scholar] [CrossRef]
- Wang, H.; Xue, A. Adaptive event-triggered H∞ filtering for discrete-time delayed neural networks with randomly occurring missing measurements. Signal Process. 2018, 153, 221–230. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, C. Event-triggered H∞ filtering for networked Takagi–Sugeno fuzzy systems with asynchronous constraints. IET Signal Process. 2015, 9, 403–411. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, P.; Agarwal, R.K.; Shi, Y. Event-based mixed H∞ and passive filtering for discrete singular stochastic systems. Int. J. Control. 2020, 93, 2407–2415. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, Z. Finite-Time Extended Dissipative Filtering for Singular T-S Fuzzy Systems With Nonhomogeneous Markov Jumps. IEEE Trans. Cybern. 2022, 52, 4574–4584. [Google Scholar] [CrossRef]
- Shi, P.; Su, X.; Li, F. Dissipativity-Based Filtering for Fuzzy Switched Systems with Stochastic Perturbation. IEEE Trans. Autom. Control. 2016, 61, 1694–1699. [Google Scholar] [CrossRef]
- Cheng, J.; Park, J.H.; Chadli, M. Peak-to-peak fuzzy filtering of nonlinear discrete-time systems with Markov communication protocol. Inf. Sci. 2022, 607, 361–376. [Google Scholar] [CrossRef]
- Song, J.; Chang, X.H. Finite-Time Peak-To-Peak Filtering for Nonlinear Singular System. IEEE Trans. Circuits Syst. Ii: Express Briefs 2022, 69, 4369–4373. [Google Scholar] [CrossRef]
- Kchaou, M.; Regaieg, M.A.; Al-Hajjaji, A. Quantized asynchronous extended dissipative observer-based sliding mode control for Markovian jump TS fuzzy systems. J. Frankl. Inst. 2022, 359, 9636–9665. [Google Scholar] [CrossRef]
- Liu, J.; Gu, Y.; Cao, J.; Fei, S. Distributed event-triggered H∞ filtering over sensor networks with sensor saturations and cyber-attacks. ISA Trans. 2018, 81, 63–75. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Christofides, P.D.; He, X.; Wu, Z.; Zhang, Z.; Zhou, D. Event-triggered filtering and intermittent fault detection for time-varying systems with stochastic parameter uncertainty and sensor saturation. Int. J. Robust Nonlinear Control. 2018, 28, 4666–4680. [Google Scholar] [CrossRef]
- Wu, Y.; Cheng, J.; Wu, Z.G. Fuzzy-Affine-Model-Based Filtering Design With Memory-Based Dynamic Event-Triggered Protocol. IEEE Trans. Fuzzy Syst. 2022, 1–11. [Google Scholar] [CrossRef]
- Peng, C.; Zhang, J.; Yan, H. Adaptive Event-Triggering H∞ Load Frequency Control for Network-Based Power Systems. IEEE Trans. Ind. Electron. 2018, 65, 1685–1694. [Google Scholar] [CrossRef]
- Gu, Z.; Yue, D.; Liu, J.; Ding, Z. H∞ tracking control of nonlinear networked systems with a novel adaptive-event-triggered communication scheme. J. Frankl. Inst. 2017, 354, 3540–3553. [Google Scholar] [CrossRef]
- Zhang, Z.; Liang, H.; Wu, C.; Ahn, C.K. Adaptive Event-Triggered Output Feedback Fuzzy Control for Nonlinear Networked Systems With Packet Dropouts and Actuator Failure. IEEE Trans. Fuzzy Syst. 2019, 27, 1793–1806. [Google Scholar] [CrossRef]
- Chang, X.H.; Liu, Y. Robust H∞ Filtering for Vehicle Sideslip Angle With Quantization and Data Dropouts. IEEE Trans. Veh. Technol. 2020, 69, 10435–10445. [Google Scholar] [CrossRef]
- Xia, W.; Zheng, W.X.; Xu, S. Event-triggered filter design for Markovian jump delay systems with nonlinear perturbation using quantized measurement. Int. J. Robust Nonlinear Control. 2019, 29, 4644–4664. [Google Scholar] [CrossRef]
- Li, F.; Cao, X.; Zhou, C.; Yang, C. Event-triggered asynchronous sliding mode control of CSTR based on Markov model. J. Frankl. Inst. 2021, 358, 4687–4704. [Google Scholar] [CrossRef]
- Chu, X.; Li, M. H∞ observer-based event-triggered sliding mode control for a class of discrete-time nonlinear networked systems with quantizations. ISA Trans. 2018, 79, 13–26. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, I.; Ge, X.; Han, Q.L. Decentralized Dynamic Event-Triggered Communication and Active Suspension Control of In-Wheel Motor Driven Electric Vehicles with Dynamic Damping. IEEE/CAA J. Autom. Sin. 2021, 8, 971–986. [Google Scholar] [CrossRef]
- Pan, Y.; Yang, G.H. Event-based output tracking control for fuzzy networked control systems with network-induced delays. Appl. Math. Comput. 2019, 346, 513–530. [Google Scholar] [CrossRef]
- Shen, H.; Jiao, S.; Huo, S.; Chen, M.; Li, J.; Chen, B. On energy-to-peak filtering for semi-Markov jump singular systems with unideal measurements. Signal Process. 2018, 144, 127–133. [Google Scholar] [CrossRef]
- Tao, J.; Xiao, Z.; Li, Z.; Wu, J.; Lu, R.; Shi, P.; Wang, X. Dynamic Event-Triggered State Estimation for Markov Jump Neural Networks With Partially Unknown Probabilities. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 7438–7447. [Google Scholar] [CrossRef]
- Zhang, B.; Zheng, W.X.; Xu, S. Filtering of Markovian Jump Delay Systems Based on a New Performance Index. IEEE Trans. Circuits Syst. Regul. Pap. 2013, 60, 1250–1263. [Google Scholar] [CrossRef]
- Shen, Y.; Wu, Z.G.; Shi, P.; Shu, Z.; Karimi, H.R. H∞ control of Markov jump time-delay systems under asynchronous controller and quantizer. Automatica 2019, 99, 352–360. [Google Scholar] [CrossRef]
- Chen, J.; Lu, J.; Xu, S. Summation inequality and its application to stability analysis for time-delay systems. IET Control. Theory Appl. 2016, 10, 391–395. [Google Scholar] [CrossRef]
- Hamidi, F.; Aloui, M.; Jerbi, H.; Kchaou, M.; Abbassi, R.; Popescu, D.; Ben Aoun, S.; Dimon, C. Chaotic Particle Swarm Optimisation for Enlarging the Domain of Attraction of Polynomial Nonlinear Systems. Electronics 2020, 9, 1704. [Google Scholar] [CrossRef]
- Moughamir, S.; Zaytoon, J.; Manamanni, N.; Afilal, L. A system approach for control development of lower-limbs training machines. Control. Eng. Pract. 2002, 10, 287–299. [Google Scholar] [CrossRef]
- Kaviarasan, B.; Kwon, O.M.; Park, M.J.; Sakthivel, R. Reduced-order filtering for semi-Markovian jump systems against randomly occurring false data injection attacks. Appl. Math. Comput. 2023, 444, 127832. [Google Scholar] [CrossRef]
- Wu, Z.; Chen, J.; Zhang, X.; Xiao, Z.; Tao, J.; Wang, X. Dynamic event-triggered synchronization of complex networks with switching topologies: Asynchronous observer-based case. Appl. Math. Comput. 2022, 435, 127413. [Google Scholar] [CrossRef]




| Symbol | Definition |
|---|---|
| set of real numbers | |
| n | dimension of the Euclidean space |
| real matrix | |
| real symmetric positive definite matrix | |
| norm of the matrix | |
| transpose of the matrix | |
| * | term that is induced by symmetry of a matrix |
| the maximal eigenvalue of a matrix | |
| mathematical expectation | |
| transition probability from states p to q | |
| r | number of if–then rules |
| discrete-time Markov process | |
| LMI | linear matrix inequalities |
| MJS | Markovian jump systems |
| NCS | networked control systems |
| ET | event-triggered |
| T-S | Takagi–Sugeno |
| IT-2 | interval Type-2 |
| Performance | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| −1 | 0 | 0 | 14.3165 | −8.4295 | 14.5129 | −9.4800 | 0.7327 | ||
| passivity | 0 | 1 | 0 | 10.0000 | −8.0000 | 14.5663 | −10.0000 | 0.1201 | |
| dissipativity | −1 | 1 | 0 | 10.6384 | −8.0000 | 12.7780 | −10.0000 |
| Filter Gains | (65) | (66) | (67) | [34] |
|---|---|---|---|---|
| Data transmission rate | 14.172 | 13.573 | 12.575 | 18.563 |
| ISE | 1.5152 | 1.4895 | 0.94308 | 8.7833 |
| IAE | 2.9001 | 2.8546 | 2.4904 | 5.8065 |
| Parameter | Physical Meaning | Value | Mode 1 | Mode 2 | Unit |
|---|---|---|---|---|---|
| a | Gravitational coefficient | 110 | - | - | (N) |
| b | Gravitational coefficient | 31 | - | - | (N) |
| l | Arm’s length | - | - | (m) | |
| Viscous friction | - | - | (N(rad/s)) | ||
| Coriolis coefficient | - | - | (Nm(rad/s)) | ||
| inertia | - | 33.8 | 35.2 | (kg m) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kchaou, M.; Regaieg, M.A. Event-Triggered Extended Dissipativity Fuzzy Filter Design for Nonlinear Markovian Switching Systems against Deception Attacks. Mathematics 2023, 11, 2064. https://doi.org/10.3390/math11092064
Kchaou M, Regaieg MA. Event-Triggered Extended Dissipativity Fuzzy Filter Design for Nonlinear Markovian Switching Systems against Deception Attacks. Mathematics. 2023; 11(9):2064. https://doi.org/10.3390/math11092064
Chicago/Turabian StyleKchaou, Mourad, and Mohamed Amin Regaieg. 2023. "Event-Triggered Extended Dissipativity Fuzzy Filter Design for Nonlinear Markovian Switching Systems against Deception Attacks" Mathematics 11, no. 9: 2064. https://doi.org/10.3390/math11092064
APA StyleKchaou, M., & Regaieg, M. A. (2023). Event-Triggered Extended Dissipativity Fuzzy Filter Design for Nonlinear Markovian Switching Systems against Deception Attacks. Mathematics, 11(9), 2064. https://doi.org/10.3390/math11092064







