Entropy-Optimized Fault Diagnosis Based on Unsupervised Domain Adaptation

Abstract

In practice, the cross-domain transfer of data distribution and the sample imbalance of fault status are inevitable, but one or both are often ignored, which restricts the adaptability and classification accuracy of the generated fault diagnosis (FD) model. Accordingly, an entropy-optimized method is proposed in this paper based on an unsupervised domain-adaptive technique to enhance FD model training. For the training, pseudosamples and labels corresponding to the target samples are generated through data augmentation and self-training strategies to diminish the distribution discrepancy between the source and target domains. Meanwhile, an adaptive conditional entropy loss function is developed to improve the data quality of the semisupervised learning, with which reliable samples are generated for the training. According to the experiment results, compared with other state-of-the-art algorithms, our method can achieve significant accuracy improvement in rolling bearing FD. Typically, the accuracy improvement compared with the baseline Convolutional Neural Network (CNN) is achieved by over 13.23%.

1. Introduction

A rolling bearing is a widely used key component in mechanical equipment. It serves under random noises, impact loads and thermal stresses persistently. Hence, failures from some hidden faults are not rare. Effective fault diagnosis (FD) ensures the reliable operation of rolling bearings and extends the service life of the equipment [1,2,3,4]. For instance, Qin et al. [5] applied the joint signal components and the improved logistic sigmoid units to diagnose the health condition of wind turbines. Shao et al. [6] introduced multisource signals as training data to enhance the robustness and accuracy of the FD model. Yang et al. [7] utilized graph theory for short-time Fourier transform and employed a Laplacian matrix to represent different features for data classification of FD.

Currently, most research findings are obtained by assuming that the distributions of the training and test data are consistent, as well as that the interclass data in the dataset are balanced. In practical scenarios, the first assumption is not always promised due to the varying working conditions and environment noises. Meanwhile, the fault-free data are generally more than the faulty ones from the industrial operation sites, which indicates high imbalance ratios (IRs) of the obtained data and a low possibility of the second assumption. An example is given in Figure 1 to illustrate these situations, where the data in the training and testing stages are set to cover the source domain and target domain, respectively. A large number of normal data (blue square) and a small number of failure data (blue circle) are chosen for the model training (Figure 1a). In a conventional way, the feature of the majority data from the same family is learned by the trained model, while the feature of the minority data is most probably ignored and incorrectly aligned into the family of the majority data (Figure 1b). These situations cause deviations between theory and practice. It is necessary to establish an effective FD scheme for mechanical components with high adaptability and strong classification ability.

The domain adaptation (DA) technique is an effective method to solve the distribution shift issue that arose in the first assumption, as it applies the object’s health knowledge from the source domain to the target domain, and the domain-invariant knowledge extracted between the source and target domains improves the model performance on the testing data [8,9]. Generally, the DA technique in the FD field contains adversarial-learning-based and moment-matching-based approaches. The first type is inspired by generative adversarial networks, which train the model antagonistically in two game classifiers and make it difficult for the model to distinguish features between the source and target domains [10]. The other type embeds various distance metrics into networks and minimizes them to mitigate distribution discrepancies. For example, Cui et al. [11] proposed a new feature distance metric method based on a stacked autoencoder (SAE) to minimize the distribution discrepancy between the source and target data and utilized a support vector machine as a classifier to detect faults. In [12], Qian et al. adopted the CORAL distance metric method based on a convolution autoencoder to resist the classification loss and diagnose the faults in the test data from the cross-domain bearings by combining the CORAL loss and domain classification loss. A cross-domain FD model was developed by Deng et al. [13] which extracts the features of a large number of source domain data based on SAE and is then fine-tuned with a small number of target domain data.

Concerning the imbalance issue that arose in the second assumption, only a few solutions have been proposed based on the aspects of data and algorithms [14,15,16,17,18]. Data-related methods focus on changing the data distribution, whereas algorithm-related methods tend to improve the precision of minority samples based on new algorithms [19,20]. For the algorithm aspect, the semisupervised learning (SSL) technique has been developed as an effective way to address the class-imbalanced issue of samples. Ge et al. [21] used an affinity propagation and spatial constraint algorithm that expanded the small number of labeled sample sets by selecting unlabeled samples with high confidence. Zhao et al. [22] proposed a new entropy perception algorithm to improve the self-training reliability on a small number of labels and limited node classification performance. In [23], an associative self-training classification approach is developed based on the ant colony optimization, which produces higher accuracy than the traditional self-training classification by using the correlation among the attribute values. From the related findings, it is found that the quality of the constructed pseudosample in the self-training algorithm is commonly poor, and hence the representation learning of the model would be misled.

To address the aforementioned issues, we consider eliminating the effect of the IRs for the target samples without obtaining additional samples in the process of applying the source knowledge to the target dataset (Figure 1c). To this end, an unsupervised-DA-based entropy optimization (UDA-EO) method is proposed for the FD of rolling bearings in this paper. In detail, a number of reliable pseudosamples are automatically constructed via a predicted consistency strategy; then, an entropy optimization algorithm under a leveraged entropy objective is designed to ensure the prediction consistency between the true and pseudosamples and minimize the distribution discrepancy across domains; and finally, the classification for FD is achieved, and the performance is improved by a progressively updated model, where the impacts from the class imbalance and distribution shift on the model are effectively reduced. Comparative experiments are performed to illustrate the effectiveness of the proposed UDA-EO method on the benchmarks of two industrial datasets. The results of 16 experiments indicate that UDA-EO has strong FD ability and robustness under different IRs and can handle the data in the processes with class imbalance. The main contributions of this study are listed as follows:

(1)

The issues of class imbalance and distribution discrepancy in datasets under different working conditions are simultaneously and effectively addressed.

(2)

The UDA-EO FD method is developed under a leveraged entropy objective that ensures prediction consistency.

(3)

By means of applying the source knowledge to the target samples, the predictive entropy of pseudosamples is selectively minimized to improve confidence on highly consistent target data.

The remainder of this paper is organized as follows. Section 2 introduces the basic knowledge and the motivation. In Section 3, the main methodologies are provided. Comparative experiments are presented in Section 4 to illustrate the effectiveness and superiority of the proposed method. Section 5 concludes the paper.

2. Preliminaries

2.1. Convolutional Neural Network

During the past decades, CNNs have been widely used for image processing and machine vision. As a mainstream of the deep learning network techniques, the CNN includes a structure of convolutional, pooling, fully connected and classification layers. In a convolutional layer, filters are used to perform convolution operations to generate the features of the input samples. The pooling layer is set for extracting the features. The fully connected layer and the classification layer are responsible for outputting the probability and classification results of the network predictions, respectively. The convolution operation is defined as

$$z\left(i\right)=g(w^{\mathrm{T}}x\left(i\right)+b),$$

where $x\left(i\right)\in \left\{x\right(1),x(2),x(3),\dots ,x(n\left)\right\}$ is an input datum, n denotes the length of the input data, $g(*)$ represents an activation function of the rectified linear unit (ReLU), w is a weight matrix, b indicates a bias and $z\left(i\right)$ is the feature output learned from the convolution kernel.

To reduce the dimension of the features extracted from the convolution layer, the maximum pooling function is set as

$$p_j\left(i\right)=\underset{j\in R_j}{max}\left\{z_j\left(i\right)\right\},$$

where $z_j\left(i\right)$ represents the feature extracted in the jth pooling layer, $p_j\left(i\right)$ is the pooling value of the ith neuron and $R_j$ indicates the pooling area.

2.2. Maximum Mean Discrepancy

In this study, the maximum mean discrepancy (MMD) technique is adopted to estimate the distribution discrepancy. MMD is defined as

$$\begin{array}{cc}\hfill MM{D}_H(X_S,X_{\mathcal{T}})& \hfill =\parallel \frac{1}{n}\sum _{i=1}^n(\varphi \left(x_i^S\right)-\varphi \left(x_i^{\mathcal{T}}\right)){\parallel }_H^2,\hfill \end{array}$$

and it is regarded as the distance metric of marginal distributions with kernel embedded, where $\varphi$ is the nonlinear mapping function of the reproducing kernel Hilbert space H [24], S and $\mathcal{T}$ represent the source and target domains, respectively, and $x_i^{*}$ and $X_{*}$ from S or $\mathcal{T}$ denote the data and the dataset, respectively. If the distributions of the source and target domains are consistent, $MM{D}_H(X_S,X_{\mathcal{T}})=0$.

In a DA process, MMD is usually considered as the regularization term of the representation learning to minimize the discrepancy between different domains. In this study, the embedding of multiple kernels is performed to ensure low testing errors. Additionally, the MMD optimization objective $L_M$ between two datasets is given as

$$L_M=\sum _{k=1}^{m}MM{D}_{Hk}(X_S,X_{\mathcal{T}}),$$

(1)

where $MM{D}_{Hk}$ indicates that k Gaussian kernels are embedded in H.

2.3. Self-Training

Self-training is a kind of semisupervised learning and a promising way for training a classifier to expand the labeled samples. In the original dataset, only a small proportion of labeled samples are contained by comparing them with the unlabeled ones. Traditional self-training methods take labeled samples (A) as training data to generate an initial classifier (C). With the initial classifier (C), the most reliable samples (B′) are selected from the unlabeled samples (B) and then classified as labeled ones (A). By restarting a new training process based on the updated labeled samples (A), the final classifier (C) is obtained [25].

2.4. Motivation

In practical applications, data imbalance and distribution shifts of collected data are always present, but they are partially ignored in most of the FD research findings. Only a focus on one situation may result in weak model generalization ability and poor FD performance. Accordingly, dealing with these two issues simultaneously is necessary, which gives birth to this study. Decreasing IRs and using the DA technique will balance the interclass distributions and reduce the discrepancy between distributions, respectively. Hence, our goal is to solve the mentioned issues by fusing these measures to obtain the health condition of rolling bearings in the target domain. More details are given as below.

3. Methodology

3.1. Notations

Define an input space X, the input random variable x, the set of n health conditions Y = $\left\{1,2,3,\dots ,n\right\}$ and the output random variable y. The CNN classifier is given as $y=f\left(x\right)$ (mapping $f:X\to Y$). The joint probability distributions of X and Y are set as $P(X,Y)$, and the joint probability distributions of the source domain S and target domain $\mathcal{T}$ are given as $P_S(X,Y)$ and $P_{\mathcal{T}}(X,Y)$, respectively. For the data from the source domain, the output probability predicted by the model is denoted as $p\left(y\right|x)$; for the data in the target domain, the estimated pseudolabel $\widehat{y}$ represents $maxp\left(y\right|x_{\mathcal{T}})$.

In a UDA process, we have access to the labeled source sample $(x_s,y_s)\sim P_S(X,Y)$ and unlabeled target sample $\left(x_{\mathcal{T}}\right)\sim P_{\mathcal{T}}\left(X\right)$. Concerning the data distribution shift case, it is known that $P_{\mathcal{T}}\left(Y\right|X=x)=P_S\left(Y\right|X=x)$, but $P_{\mathcal{T}}\left(X\right)\ne P_S\left(X\right)$. In the class-imbalanced domain, it gives $P_{\mathcal{T}}\left(X\right|Y=y)$ and $P_{\mathcal{T}}\left(Y\right)\ne P_S\left(Y\right)$.

3.2. Overall Architecture

To realize our purpose, it is required to classify the imbalanced samples from the target domain into the correct fault statuses by decreasing the IRs between the majority and minority classes. The pipeline of the UDA-EO method consists of two parts, i.e., to learn the knowledge from S and to optimize the entropy objective from $\mathcal{T}$, as shown in Algorithm 1. For the first part, UDA-EO learns the sample features in S and obtains a fault classifier. For the second part, it performs two steps to selectively minimize the predictive entropy of the pseudosamples and improve confidence on highly consistent target data. Firstly, UDA-EO constructs pseudosamples and labels of target samples with the data augmentation and self-training strategies to eliminate the IRs effects. Then, pseudosamples with high confidence are employed to train the model, with which the health condition in $\mathcal{T}$ is consequently classified. These two steps are executed continuously until the maximal epoch is reached.

Algorithm 1 Training of the UDA-EO model

Require: source domain data $X_S$, source domain label $Y_S$, unlabeled target domain data $X_{\mathcal{T}}$. Ensure: the network model $y=f\left(x\right)$ and the predicted health conditions for the target data. 1: Train an initial deep network on source dataset $(X_S,Y_S)$. 2: Obtain the cross-entropy loss $L_M$. 3: while maximum epochs do 4:    Initial m and n and predict the pseudolabels $\widehat{y_{\mathcal{T}}}=argmaxp\left(y\right|x_{\mathcal{T}})$ for the target data. 5:    Obtain $\left\{r_1\left(x_{\mathcal{T}}\right),r_2\left(x_{\mathcal{T}}\right),r_3\left(x_{\mathcal{T}}\right),\dots ,r_i\left(x_{\mathcal{T}}\right)\right\}$ from RandAugment, $predictio{n}_{+}$, and $predictio{n}_{-}$ 6:    if $predictio{n}_{+}$ then 7:      $L_{EO}=L_{predictio{n}_{+}}$ based on Equation (6) 8:    else 9:      $L_{EO}=L_{predictio{n}_{-}}$ based on Equation (6) 10:    end if 11:    Minimize the loss function defined in Equation (8). 12:    Update the network parameters by back propagation. 13: end while

The framework of the proposed method used for cross-domain FD with imbalanced data is shown in Figure 2. By concerning the available source dataset under multiple working conditions for data preprocessing, the samples from each condition are all put into the network. Reshaping operations are conducted based on Gramian angular field (GAF) technique for all input data to generate a 2D image [26,27,28]. Note that the following UDA-EO framework still works if no GAF-based preprocessing is given.

Considering the domain generalization error and the imbalanced class distribution, the feature extractor (FE), consistency discriminator (CD) and fault classifier (FC) are designed core components of the framework, as shown in Figure 2. A CNN backbone is customized to realize the functions of the above core components. In detail, FE is a combination of a $7\times 7$ convolutional layer, batch normalization (BN) layers, ReLU activation functions and block modules, which extracts domain-invariant features to alleviate the distribution discrepancies between domains. The CD is composed of data augmentation and a decider, which is trained by the proposed entropy-optimized objective function and aimed to reduce the interclass IRs and improve the reliability of pseudolabels from the unlabeled target samples. The FC consists of a linear layer, ReLU, and max pooling, which is applied to decrease the generalization error and identify the status of the target data. The pseudosamples augmented in CD and the truth samples are input into the FE via EO to extract features and to train the FC, with which it finally obtains a domain-adaptation classifier that focuses on the feature information of the minority class. The backbone could be adapted to other CNN models, e.g., LeNet.

3.3. Entropy-Optimized Strategy

The goal of UDA-EO in CD is to decrease the IRs impact on the target data by using the data augmentation and self-training techniques. RandAugment [29], the data augmentation technique adopted in this paper, is a useful way to promote the reliability of the model because of its diversity and randomness [30]. It has 14 predefined transformations of available images. We define set P = $\left\{r_1\left(x_{\mathcal{T}}\right),r_2\left(x_{\mathcal{T}}\right),r_3\left(x_{\mathcal{T}}\right),\dots ,r_i\left(x_{\mathcal{T}}\right)\right\}$ as the generated pseudosamples (see Figure 3), where $i\in [1,14]$.

If the pseudosamples from the real target data are directly utilized to train the model, the prediction performance of the model is not stable, since the quality of the constructed pseudosamples cannot be guaranteed. With high-quality pseudosamples, the performance is positively confirmed, whereas low-quality pseudosamples could lead to wrong learning directions and result in poor prediction accuracy.

In traditional UDA research, the FD method based on UDA is sufficient to address the data distribution shift problem while achieving mediocre results on the imbalanced class problems [31]. Concerning this situation, the method based on conditional entropy minimization (CEM) is able to achieve good results. By denoting the moving average $q\left(\widehat{y}\right)$ ($\widehat{y}\in [1,2,3,\cdots ,n]$) as an approximation of $p\left(y\right|x_{\mathcal{T}})$, the entropy objective $L_e$ is given as

$$\begin{array}{c}\hfill L_e=E_{x\sim P_{\mathcal{T}}}\left[\sum _{i=1}^{n}p\left(y\right|x_{\mathcal{T}})log\frac{1}{q\left(\widehat{y}\right)}\right]\end{array}$$

(2)

By minimizing $L_e$, a model with good initialization performs well on class-imbalanced problems, because it leads the model to learn data features in the right direction. Once the model is initialized in a negative direction, minimizing $L_e$ causes a catastrophic result, as the prediction error and the confidence of the wrong prediction are simultaneously increased, whereas the confidence of the correct target sample is decreased.

Accordingly, an entropy-optimized strategy with two steps is proposed to ensure that the high-quality pseudosamples are selected for model training, where the estimation of the prediction consistency between the pseudo and true labels is generated.

3.3.1. Decreasing IRs in the Target Domain

Given the samples of batch B, for each x in B, its pseudosample set $\mathbf{P}=\{r_1\left(x_{\mathcal{T}}\right),$$r_2\left(x_{\mathcal{T}}\right),r_3\left(x_{\mathcal{T}}\right),\dots ,r_i\left(x_{\mathcal{T}}\right)\}$ is generated in the data augmentation strategy under the CD module. The predicted labels and pseudolabels of the unlabeled truth sample x and pseudosample set $\mathbf{P}$ in B are predicted in the FC module, respectively. Define n and m to represent the degree of consistency between predicted labels and predicted pseudolabels, respectively. If the predicted label of x and all the corresponding predicted pseudolabels in $\mathbf{P}$ are the same, n counts; otherwise, m counts. The prediction consistency is evaluated by a majority strategy, that is,

$$\left\{\begin{array}{c}\hfill predictio{n}_{+},\mathrm{if}n>m,\hfill \\ \hfill predictio{n}_{-},\mathrm{if}n\le m,\hfill \end{array}\right.$$

(3)

where $predictio{n}_{+}$ measures the prediction accuracy between the true and pseudolabels, and $predictio{n}_{-}$ measures the prediction inaccuracy. A larger n indicates that the prediction results of pseudosamples are more consistent with the true samples. Explicitly, if the predictions are consistent, i.e., the majority of the prediction results falls into $predictio{n}_{+}$, more reliable samples will be noticed by the proposed EO function. Its prediction entropy will be minimized, which boosts the model to learn the features of the minority classes. The objective of the positive entropy minimization $L_{predictio{n}_{+}}$ can be defined as

$$L_{predictio{n}_{+}}=\sum _{i=1}^m\sum _{j=1}^{n}p(y=j|r_i\left(x_{\mathcal{T}}\right))log\frac{1}{p(\widehat{y}=j|r_i\left(x_{\mathcal{T}}\right))}$$

(4)

Conversely, if the predictions are inconsistent, i.e., the negative observation dominates the results, the entropy objective will be maximized by EO, which reduces the model learning of data features in a wrong direction. The objective of the negative entropy minimization $L_{predictio{n}_{-}}$ can be defined as

$$L_{predictio{n}_{-}}=-\sum _{i=1}^m\sum _{j=1}^{n}p(y=j|r_i\left(x_{\mathcal{T}}\right))log\frac{1}{p(\widehat{y}=j|r_i\left(x_{\mathcal{T}}\right))}.$$

(5)

With the above selection process for prediction consistency, the complete entropy minimization objective $L_{EO}$ can be defined as

$$L_{EO}=\left\{\begin{array}{c}\hfill L_{predictio{n}_{+}},\mathrm{if}predictio{n}_{+}\hfill \\ \hfill L_{predictio{n}_{-}},\mathrm{if}predictio{n}_{-}\hfill \end{array}\right.$$

(6)

By this means, not only can the class-imbalanced issue be efficiently addressed, but more consistent samples can also be encouraged to be a group by the selection strategy. Moreover, the misleading of the model by incorrect pseudolabels and the overfitting of minority data samples can be reduced.

3.3.2. Object Function Optimization

Provided with the source labeled data, a standard cross-entropy loss $L_C$ of the classifier FC is given as

$$L_C=-\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^m{y}_{ij}^{*}log{y}_{ij}$$

(7)

to correctly identify the data classes, where m is the total number of samples and $y_{ij}^{*}$ denotes the ground-truth label.

The integrated entropy objective of the model is defined as

$$min{L}_{\mathrm{final}}=L_C+\alpha L_M+\beta L_e+\gamma L_{EO}$$

(8)

where $\alpha$, $\beta$ and $\gamma$ denote the penalty coefficients. The default value of $\alpha$ is set to 1 [8]. Back propagation is employed to transfer the loss parameters and update the network parameters in every epoch.

4. Case Study

4.1. Dataset Description

(1) Case Western Reserve University (CWRU) Dataset: The CWRU dataset is obtained from [32]. In the experiment, the single-point damage of the electrodischarge machining (EDM) was artificially made. The signals from the bearings (model SKF6205) were collected at a sampling frequency of 12 kHz over 3 different rotational speeds of a motor drive. Except the normal state, the faults are set as the damages on the inner race, outer race and ball, where the damage diameters of $0.007$, $0.014$, $0.021$ and $0.028$ inches are contained. By considering the correspondences between the damage places and diameters, the 11 fault statuses shown in

Table 1. Fault statuses of the bearings from the CWRU dataset.

Bearing Condition	Fault Diameters (inch)	Label	Working Condition
Normal	0	0	1HP: 1772 rpm 2HP: 1750 rpm 3HP: 1730 rpm
Ball	0.007	1
Outer race	0.007	2
Ball	0.0014	3
Inner race	0.0014	4
Outer race	0.0014	5
Ball	0.0021	6
Inner race	0.0021	7
Outer race	0.0021	8
Ball	0.0028	9
Inner race	0.0028	10

are adopted.

(2) Xi’an Jiaotong University (XJTU) Dataset: The XJTU dataset is obtained from [33]. During the accelerated lifetime test, the data from the bearings (model LDK UER204) were collected at a sampling frequency of 64 kHz over 3 different working conditions of an AC motor. The faults are set as the damages on the outer race, inner race and cage. Three fault statuses are considered, as listed in

Table 2. Fault statuses of the bearings from the XJTU dataset.

Fault	Outer Race	Inner Race	Cage
Fault label	0	1	2
Working condition	1HP: 2100 rpm, 12 KN
	2HP: 2250 rpm, 11 KN
	3HP: 2400 rpm, 10 KN

. By comparison with the CWRU dataset, the rotational speeds from the XJTU dataset obviously change between different working conditions, which results in significant distribution differences in the collected data.

4.2. Detailed Settings

(1) CWRU Dataset: With this dataset, experiments covering 1HP → 2HP ($C_{12}$), 2HP → 1HP ($C_{21}$), 2HP → 3HP ($C_{23}$) and 3HP → 2HP ($C_{32}$) are designed for the 11 fault statuses. For each experiment situation, $1.8$ million sampling points are collected, where $80\%$ of the data are used for training and the rest of the data are used for testing. A range of datasets with different IRs from these data are further designed. IR $\triangleq N_{\max -\mathrm{class}}/N_{\min -\mathrm{class}}$ is subject to a power-law distribution [34], since some categories are more likely to occur than others, where $N_{\max -\mathrm{class}}$ and $N_{\min -\mathrm{class}}$ represent, respectively, the maximum and minimum numbers of samples from the fault classes. Detailed information is listed in

Table 3. Detailed data distributions (%) of Imbalance settings.

Label	IR1	IR2	IR3
0	22.30	26.28	28.92
1	17.72	19.65	20.64
2	14.05	14.69	14.95
3	11.15	10.98	10.75
4	8.84	8.21	7.72
5	7.01	6.13	5.55
6	5.56	4.58	3.99
7	4.41	3.43	2.87
8	3.50	2.56	2.06
9	3.17	2.01	1.48
10	2.19	1.43	1.07

and

Table 4. Detailed information of diagnosis experiments.

Transfer experiment	$C_{12}$, $C_{21}$, $C_{23}$, $C_{32}$, $X_{12}$, $X_{21}$, $X_{23}$, $X_{32}$
Data division	$80\%$ for training and $20\%$ for testing
IRs	IR1: $10.16$; IR2: $18.38$; IR3: $27.03$

.

(2) XJTU Dataset: With this dataset, experiments covering 1HP → 2HP ($X_{12}$), 2HP → 1HP ($X_{21}$), 2HP → 3HP ($X_{23}$) and 3HP → 2HP ($X_{32}$) are designed for the 3 fault statuses. For each experiment, $0.5$ million sampling points are collected. The detailed information is also listed in Table 4, which implements similar settings to that of the CWRU dataset.

In the model training procedure, the detailed parameter settings of UDA-EO are given as listed in

Table 5. Detailed parameters of UDA-EO in the experiments.

Learning Rate	Optimizer	Epoch	Batch Size	Transformation Number	Penalty Coefficients
				$\mathit{i}$	$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\gamma }$
$0.001$	SGD	90	16	3	1	$0.1$	1

, where the optimizer is set as the stochastic gradient descent (SGD).

4.3. Comparison Methods

All experiments are carried out on a PC with an Intel Core i9 CPU, 32 GB RAM and GeForce RTX 2080Ti GPU. The programming platform is PyTorch. In this paper, a CNN backbone is customized, where the last linear layer is replaced by a fully connected layer with Xavier-initialized weights and no bias.

To validate the competitiveness of the proposed method, 5 other methods are implemented below for comparisons, including the baseline CNN, domain adversarial NN (DANN, [35]), deep coral [36], deep adaptation network (DAN, [37]) and conditional domain adversarial network (CDAN, [38]). According to the detailed settings shown in the references, the experimental parameters of all the models are properly fine-tuned.

(1)

DANN is a typical adversarial learning method and a way to solve transfer learning under severe label imbalance.

(2)

Deep coral is a DA model that utilizes the second-order statistics to align features between the source and the target domains.

(3)

DAN is an adaptive model that selects the optimal kernel in the multicore Hilbert space to match the mean value of the distribution.

(4)

CDAN is an adaptive model that improves the discrimination ability of classifiers through multilinear conditions and conditional entropy.

4.4. Experimental Results

The overall average accuracy defined as the number of correctly identified samples divided by the total number of test samples is adopted to measure the performance of different methods. To eliminate the randomness in the experiments, the average values of 10 experimental results are collected for comparison.

(1)

Result analyses between different methods in terms of different working conditions

The overall classification results of these two datasets on the imbalanced experiments are listed in

Table 6. Average accuracies (%) of IR1 in terms of different transfer scenarios.

Tasks	CNN	DANN	DAN	Deep Coral	CDAN	Proposed
$C_{12}$	88.43 ± 1.93	81.79 ± 6.70	89.25 ± 2.03	90.46 ± 1.30	86.24 ± 3.31	96.94 ± 1.48
$C_{21}$	91.39 ± 4.14	81.76 ± 5.67	87.00 ± 2.05	89.83 ± 2.58	80.00 ± 1.35	94.58 ± 0.68
$C_{23}$	88.29 ± 3.02	84.12 ± 6.49	89.19 ± 1.05	89.59 ± 0.99	85.19 ± 4.08	97.28 ± 0.57
$C_{32}$	94.30 ± 1.09	85.00 ± 9.24	89.36 ± 1.68	90.84 ± 1.24	83.96 ± 2.49	97.03 ± 0.69
$X_{12}$	97.89 ± 1.89	82.88 ± 12.82	76.57 ± 3.86	100 ± 0.05	97.85 ± 1.32	100 ± 0.03
$X_{21}$	50.11 ± 0.33	86.82 ± 5.41	89.96 ± 1.63	94.74 ± 0.73	68.89 ± 12.6	98.68 ± 0.55
$X_{23}$	78.33 ± 7.65	82.98 ± 2.93	81.67 ± 4.12	76.52 ± 2.03	88.94 ± 4.41	99.26 ± 0.48
$X_{32}$	89.12 ± 8.64	96.71 ± 2.19	90.68 ± 3.28	99.78 ± 0.26	82.32 ± 2.74	99.89 ± 0.33
Average	84.73 ± 14.11	85.26 ± 4.61	86.71 ± 4.66	91.47 ± 6.92	84.17 ± 7.66	97.96 ± 1.73

,

Table 7. Average accuracies (%) of IR2 in terms of different transfer scenarios.

Tasks	CNN	DANN	DAN	Deep Coral	CDAN	Proposed
$C_{12}$	88.53 ± 1.80	80.29 ± 8.73	87.75 ± 1.52	90.26 ± 1.57	84.86 ± 2.26	96.47 ± 0.73
$C_{21}$	91.69 ± 3.05	75.30 ± 9.31	83.03 ± 2.44	86.11 ± 2.27	81.59 ± 3.71	94.96 ± 1.15
$C_{23}$	89.35 ± 1.84	85.97 ± 5.98	89.71 ± 1.30	91.33 ± 1.43	90.06 ± 3.59	98.01 ± 0.62
$C_{32}$	86.78 ± 0.56	84.80 ± 5.00	90.43 ± 1.79	91.47 ± 1.36	85.81 ± 1.68	97.13 ± 0.88
$X_{12}$	98.34 ± 1.17	72.93 ± 10.32	69.24 ± 1.65	98.84 ± 1.37	100 ± 0.02	100 ± 0.02
$X_{21}$	51.03 ± 1.00	41.01 ± 9.78	50.76 ± 1.34	34.14 ± 2.91	54.70 ± 12.44	99.47 ± 0.53
$X_{23}$	68.51 ± 3.55	73.84 ± 3.30	68.89 ± 3.02	70.96 ± 2.31	73.74 ± 4.21	97.29 ± 1.54
$X_{32}$	98.74 ± 0.94	84.64 ± 6.30	77.03 ± 2.27	99.45 ± 0.26	78.74 ± 2.34	99.97 ± 0.01
Average	84.12 ± 15.27	74.85 ± 13.68	77.11 ± 12.78	82.82 ± 20.18	81.19 ± 12.40	97.91 ± 1.69

and

Table 8. Average accuracies (%) of IR3 in terms of different transfer scenarios.

Tasks	CNN	DANN	DAN	Deep Coral	CDAN	Proposed
$C_{12}$	91.34 ± 0.64	81.61 ± 3.54	86.79 ± 1.95	89.10 ± 1.56	83.34 ± 1.95	96.27 ± 0.76
$C_{21}$	93.20 ± 2.85	81.62 ± 5.14	84.05 ± 2.91	86.83 ± 2.91	77.05 ± 0.76	94.81 ± 1.48
$C_{23}$	87.57 ± 3.17	83.63 ± 6.80	89.12 ± 1.50	90.71 ± 1.43	83.11 ± 3.19	97.98 ± 0.41
$C_{32}$	90.02 ± 0.40	78.96 ± 10.19	89.33 ± 2.22	89.22 ± 1.36	81.67 ± 4.94	96.25 ± 1.11
$X_{12}$	95.28 ± 1.32	73.93 ± 11.18	64.44 ± 2.53	96.96 ± 1.43	99.90 ± 0.2	99.94 ± 0.12
$X_{21}$	50.77 ± 0.46	43.22 ± 5.07	47.87 ± 0.74	32.12 ± 3.02	43.63 ± 1.98	98.51 ± 0.12
$X_{23}$	85.83 ± 2.71	94.88 ± 1.06	72.32 ± 6.60	78.58 ± 3.27	78.48 ± 5.75	99.69 ± 0.27
$X_{32}$	98.63 ± 0.83	79.39 ± 4.64	70.10 ± 4.33	82.12 ± 2.13	82.32 ± 2.74	99.82 ± 0.37
Average	86.58 ± 14.06	77.16 ± 13.99	75.50 ± 13.70	80.71 ± 19.07	76.87 ± 15.1	97.85 ± 1.91

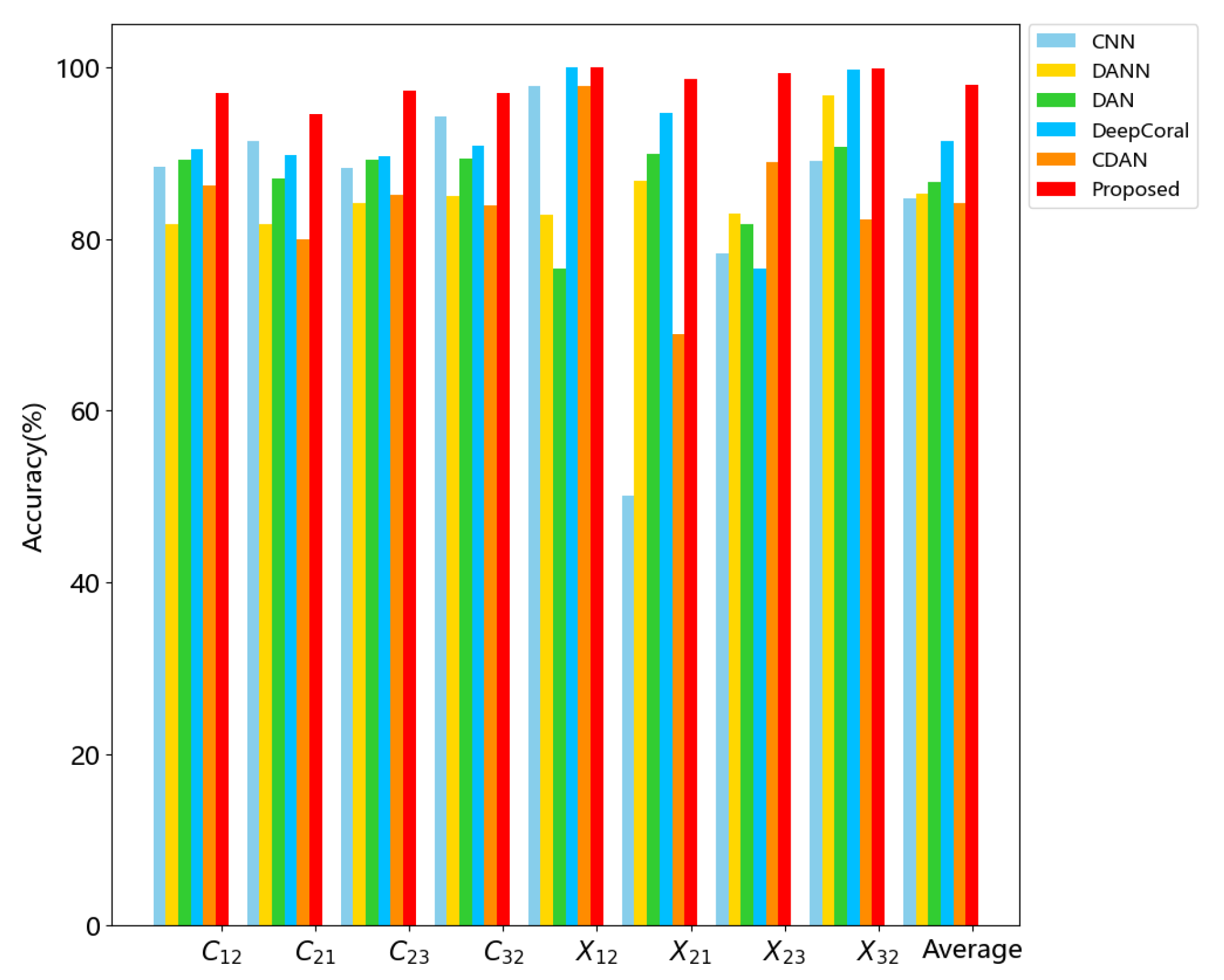
and shown in Figure 4, Figure 5 and Figure 6. As listed in Table 6, the proposed UDA-EO outperforms the other methods significantly at an average level of 8 transfer experiments with IR1. The average accuracy of UDA-EO for all transfer experiments exceeds $97.96\%$, which is a $6.49\%$ more accurate performance than the second best method. As shown in Figure 4, each method performs different degrees of fluctuations, among which CNN and the proposed UDA-EO show the largest and smallest degrees, respectively. These results indicate that the proposed UDA-EO is able to handle the class-imbalanced problem more effectively under variable working conditions.

In Table 7, the average accuracy of UDA-EO with IR2 for 8 transfer experiments is more than $97.91\%$, which improves the average accuracy over the next competing method by $15.09\%$. In Table 8, the classification accuracy of the proposed method with IR3 approximately reaches an 11.27% improvement compared with the baseline CNN method. This shows that the proposed UDA-EO retains the capability of shared-class classification, even with sharp IR in real applications. In addition, the proposed method still displays more robust performance and keeps relatively stable classification accuracy in all eight experiments, as shown in Figure 5 and Figure 6.

It should be noted that accurate classification for the imbalanced data is yielded based on two main reasons. Firstly, the proposed selection strategy promotes more reliable pseudosamples for model training, ensuring that the feature of the minority class can be effectively learned by the model on severely class-imbalanced conditions. Secondly, the data features across domains are well-aligned, which guarantees that the sample categories are correctly identified by the classifier.

(2)

Feature visualization

A result randomly selected from the $C_{23}$ experiment under IR2 is processed to visualize the classification effects. The 2D features are displayed by the t-SNE ([39]), as shown in Figure 7. It is observed from Figure 7a–e that the comparison methods have limited learning and separation effects on different health categories under severe class imbalance, resulting in quite a few incorrect classifications of the fault types. However, the classes shown in Figure 7f were effectively separated with a much clearer class boundary and a more compact learned class feature based on the proposed UDA-EO. The reasons come from the fact that UDA-EO well fits the distributions of the 11 fault types of the imbalanced samples in $\mathcal{T}$, and the overlaps of the class probability distributions are reduced under the conditional entropy minimization. These results indicate the effectiveness and feasibility of using the pseudolabel idea and the entropy minimization method to address the class-imbalanced problem.

(3)

Interclass performance study

To explore the detailed impact of the proposed framework on some minority class in the class-imbalanced datasets under a cross-domain condition, a single-class performance study is implemented on eight imbalanced experiments. By comparing with the baseline CNN, the average accuracies of all classes can be seen in Figure 8a, where it corresponds to the majority class, and the rest of the subfigures correspond to the minority classes. It is observed that both methods perform stably on the majority class, but only the proposed UDA-EO maintains good performances on the minority classes when IRs intensify; comparatively, the performances of the baseline CNN on the minority classes degrade significantly. This indicates that the proposed method substantially improves the classification accuracy of the minority classes while maintaining good classification ability on the majority class.

To display the role of the proposed UDA-EO more profoundly in $\mathcal{T}$ with imbalanced samples, we randomly visualize one result from $C_{23}$ by comparing with the baseline CNN, as shown in Figure 9. Clearly, the proposed selection strategy achieves a $4/5$ improvement in classification accuracy over the baseline CNN. As has been discussed in Section 3.3, UDA-EO is designed to assist the model in improving the confidence of pseudosamples and overcoming the performance degradation caused by ignoring the minority classes under class imbalance, which allows the model to maintain good classification ability in severe class imbalance.

(4)

Parameter sensitivity analysis

Because the penalty coefficients $\beta$ and $\gamma$ are critical for UDA-EO, these two hyperparameters are further discussed. Experimental results of $X_{23}$ are listed in

Table 9. Fault diagnosis performances under varying penalty coefficients.

Parameters	$\mathit{\beta }=0.1$	$\mathit{\beta }=0.3$	$\mathit{\beta }=0.5$	$\mathit{\beta }=1$
$\gamma =0.1$	89.41	95.19	91.63	97.99
$\gamma =0.5$	98.82	99.19	99.56	97.65
$\gamma =1$	99.59	99.41	98.30	98.64

, which indicate that the FD ability of the proposed method is relatively stable when $\beta$ and $\gamma$ vary in $[0,1]$. It is based on the fact that the model takes advantage of the predictive consistency and robustness of the proposed EO and data augmentation strategies to select reliable target samples for corresponding classes. The slight changes in the performances indicate that the best parameters could be found, such as the ones around $\beta =0.1$ and $\gamma =1$.

(5)

Ablation case analysis

To evaluate the effectiveness of the proposed optimized-entropy algorithm, ablation experiments are designed in this subsection. In particular, UDA-EO is compared with the following modifications. (1) w/o conditional entropy: the CNN is trained without conditional entropy loss function. (2) w/o $L_{EO}$: the model is trained without the proposed data augmentation strategy. (3) Ours: the proposed method is provided to train the model. The ablation results with IR3 settings are listed in

Table 10. Ablation case on IR3.

Ablation Case	${\mathit{C}}_{12}$	${\mathit{C}}_{21}$	${\mathit{C}}_{23}$	${\mathit{C}}_{32}$
W/o conditional entropy	91.34	93.20	87.57	90.02
W/o $L_{EO}$	96.28	93.47	94.97	94.43
Ours	96.27	94.36	97.98	96.25

.

In Table 10, the results of (1–3) show that the proposed method obtains relatively higher classification accuracy, which implies that the conditional entropy and the proposed data augmentation strategy have positive impacts on the UDA-EO model and improve FD precision with data imbalance settings. By comparing (2) with (3), it can be discovered that the precision of 3/4 FD drops when the data augmentation strategy is removed from the proposed method, which shows that the data augmentation strategy can effectively alleviate the model’s negative learning of minority class feature information in the initial state and improve the FD accuracy.

5. Conclusions

This paper investigated the application of the transfer learning technique for diagnosing the faults of rolling bearings in a fault-imbalanced scenario, where the common but not widely discussed class imbalance and distribution discrepancy of datasets exist. To address the problem, an EO method on the basis of UDA was proposed, which combines the construction of pseudobalanced class samples and the learning of domain-invariant features in a framework and encourages the FD model to learn the feature information of the minority class in variable conditions. Moreover, the predictive entropy of the pseudosamples is selectively minimized to improve confidence on highly consistent target data and improve the consistency prediction between the ground-truth labels and pseudolabels. Diverse FD experiments focusing on the classification accuracy of bearing faults with imbalanced data in various operating conditions were conducted based on the CWRU and XJTU datasets. The statistical and visual results indicate that UDA-EO effectively improves the feature learning of minority fault categories in imbalanced datasets. In future research, an open-set FD method will be developed to handle more practical issues.