Conditioning Theory for Generalized Inverse
Abstract
1. Introduction
2. Preliminaries
- (i)
- The normwise condition number of ℵ at v is given by
- (ii)
- The mixed condition number of ℵ at v is given by
- (iii)
- The componentwise condition number of ℵ at v is given by
3. Condition Numbers
4. Componentwise Perturbation Analysis
5. Statistical Condition Estimates
| Algorithm 1: Probabilistic condition estimator for the normwise condition number |
| Algorithm 2: Small-sample statistical condition estimation method for the normwise condition number |
|
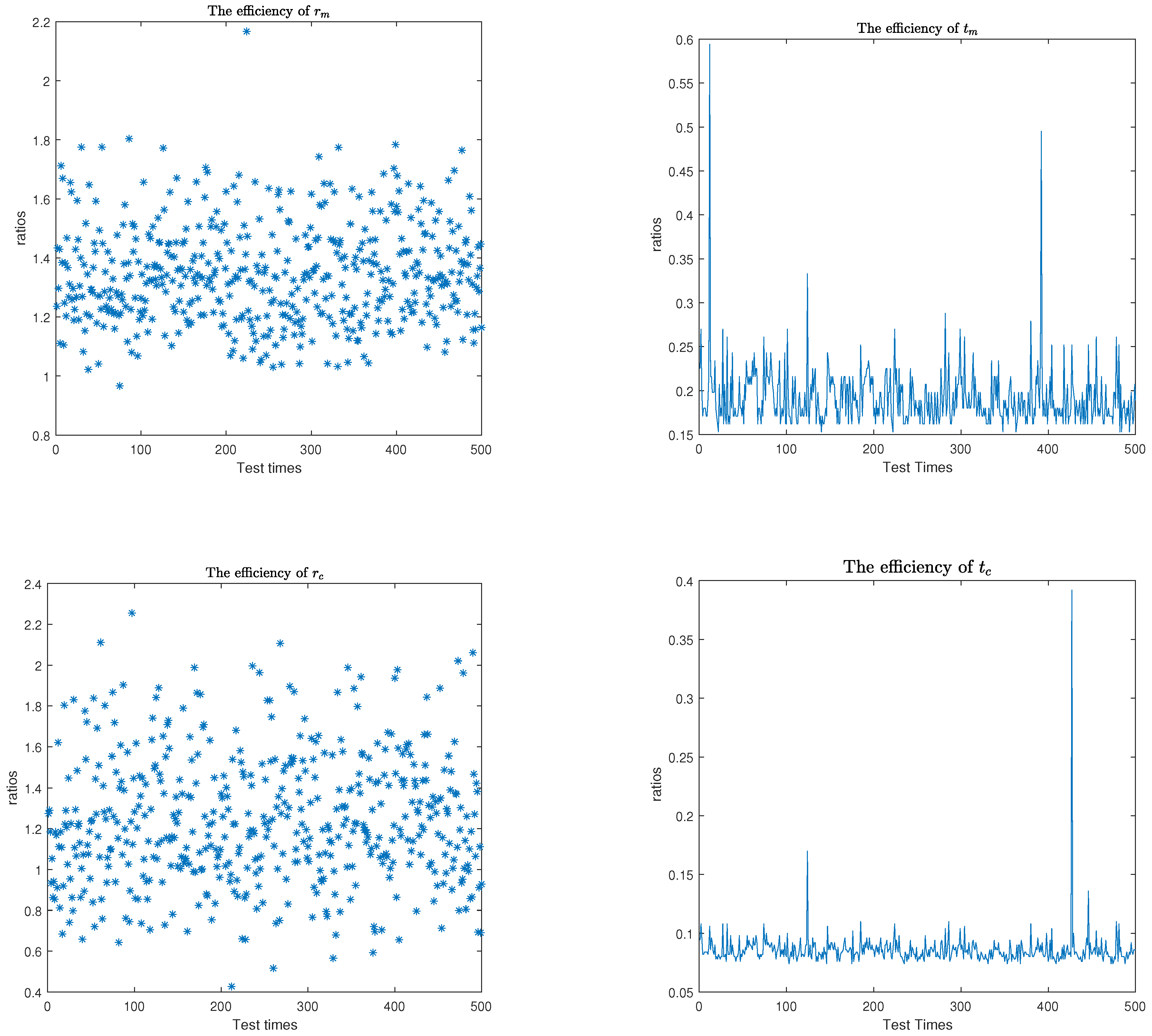
6. Numerical Experiments
| Algorithm 3: Small-sample statistical condition estimation method for the mixed and componentwise condition numbers |
|
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cucker, F.; Diao, H.; Wei, Y. On mixed and componentwise condition numbers for Moore–penrose inverse and linear least squares problems. Math. Comput. 2007, 76, 947–963. [Google Scholar] [CrossRef]
- Liu, Q.; Pan, B.; Wang, Q. The hyperbolic elimination method for solving the equality constrained indefinite least squares problem. Int. J. Comput. Math. 2010, 87, 2953–2966. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, M. Algebraic properties and perturbation results for the indefinite least squares problem with equality constraints. Int. J. Comput. Math. 2010, 87, 425–434. [Google Scholar] [CrossRef]
- Bjöorck, Å.; Higham, N.J.; Harikrishna, P. Solving the indefinite least squares problem by hyperbolic QR factorization. SIAM J. Matrix Anal. Appl. 2003, 24, 914–931. [Google Scholar]
- Bjöorck, Å.; Higham, N.J.; Harikrishna, P. The equality constrained indefinite least squares problem: Theory and algorithms. BIT Numer. Math. 2003, 43, 505–517. [Google Scholar]
- Wei, M.; Zhang, B. Structures and uniqueness conditions of MK-weighted pseudoinverses. BIT Numer. Math. 1994, 34, 437–450. [Google Scholar] [CrossRef]
- Bjöorck, Å. Algorithms for indefinite linear least squares problems. Linear Algebra Appl. 2021, 623, 104–127. [Google Scholar]
- Shi, C.; Liu, Q. A hyperbolic MGS elimination method for solving the equality constrained indefinite least squares problem. Commun. Appl. Math. Comput. 2011, 25, 65–73. [Google Scholar]
- Mastronardi, N.; Dooren, P.V. An algorithm for solving the indefinite least squares problem with equality constraints. BIT Numer. Math. 2014, 54, 201–218. [Google Scholar] [CrossRef]
- Mastronardi, N.; Dooren, P.V. A structurally backward stable algorithm for solving the indefinite least squares problem with equality constraints. IMA J. Numer. Anal. 2015, 35, 107–132. [Google Scholar] [CrossRef]
- Wang, Q. Perturbation analysis for generalized indefinite least squares problems. J. East China Norm. Univ. Nat. Sci. Ed. 2009, 4, 47–53. [Google Scholar]
- Diao, H.; Zhou, T. Linearised estimate of the backward error for equality constrained indefinite least squares problems. East Asian J. Appl. Math. 2019, 9, 270–279. [Google Scholar]
- Li, H.; Wang, S.; Yang, H. On mixed and componentwise condition numbers for indefinite least squares problem. Linear Algebra Appl. 2014, 448, 104–129. [Google Scholar] [CrossRef]
- Wang, S.; Meng, L. A contribution to the conditioning theory of the indefinite least squares problems. Appl. Numer. Math. 2022, 17, 137–159. [Google Scholar] [CrossRef]
- Skeel, R.D. Scaling for numerical stability in Gaussian elimination. J. ACM 1979, 26, 494–526. [Google Scholar] [CrossRef]
- Bjöorck, Å. Component-wise perturbation analysis and error bounds for linear least squares solutions. BIT Numer. Math. 1991, 31, 238–244. [Google Scholar] [CrossRef]
- Diao, H.; Liang, L.; Qiao, S. A condition analysis of the weighted linear least squares problem using dual norms. Linear Algebra Appl. 2018, 66, 1085–1103. [Google Scholar] [CrossRef]
- Diao, H.; Zhou, T. Backward error and condition number analysis for the indefinite linear least squares problem. Int. J. Comput. Math. 2019, 96, 1603–1622. [Google Scholar] [CrossRef]
- Diao, H. Condition numbers for a linear function of the solution of the linear least squares problem with equality constraints. J. Comput. Appl. Math. 2018, 344, 640–656. [Google Scholar] [CrossRef]
- Eldén, L. A weighted pseudoinverse, generalized singular values, and constrained least squares problems. BIT Numer. Math. 1982, 22, 487–502. [Google Scholar] [CrossRef]
- Wei, M. Algebraic properties of the rank-deficient equality-constrained and weighted least squares problem. Linear Algebra Appl. 1992, 161, 27–43. [Google Scholar] [CrossRef]
- Gulliksson, M.E.; Wedin, P.A.; Wei, Y. Perturbation identities for regularized Tikhonov inverses and weighted pseudoinverses. BITBIT Numer. Math. 2000, 40, 513–523. [Google Scholar] [CrossRef]
- Samar, M.; Li, H.; Wei, Y. Condition numbers for the K-weighted pseudoinverse and their statistical estimation. Linear Multilinear Algebra 2021, 69, 752–770. [Google Scholar] [CrossRef]
- Burgisser, P.; Cucker, F. Condition: The geometry of numerical algorithms. In Grundlehren der Mathematischen Wissenschaften; Springer: Heidelberg, Germany, 2013; Volume 349. [Google Scholar]
- Rice, J. A theory of condition. SIAM J. Numer. Anal. 1966, 3, 287–310. [Google Scholar] [CrossRef]
- Gohberg, I.; Koltracht, I. Mixed, componentwise, and structured condition numbers. SIAM J. Matrix Anal. Appl. 1993, 14, 688–704. [Google Scholar] [CrossRef]
- Hochstenbach, M.E. Probabilistic upper bounds for the matrix two-norm. J. Sci. Comput. 2013, 57, 464–476. [Google Scholar] [CrossRef]
- Kenney, C.S.; Laub, A.J. Small-sample statistical condition estimates for general matrix functions. SIAM J. Sci. Comput. 1994, 15, 36–61. [Google Scholar] [CrossRef]
- Xie, Z.; Li, W.; Jin, X. On condition numbers for the canonical generalized polar decomposition of real matrices. Electron. J. Linear Algebra 2013, 26, 842–857. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Topics in Matrix Analysis; Cambridge University Press: New York, NY, USA, 1991. [Google Scholar]
- Magnus, J.R.; Neudecker, H. Matrix Differential Calculus with Applications in Statistics and Econometrics, 3rd ed.; John Wiley and Sons: Chichester, UK, 2007. [Google Scholar]
- Diao, H.; Xiang, H.; Wei, Y. Mixed, componentwise condition numbers and small sample statistical condition estimation of Sylvester equations. Numer. Linear Algebra Appl. 2012, 19, 639–654. [Google Scholar] [CrossRef]
- Li, H.; Wang, S. On the partial condition numbers for the indefnite least squares problem. Appl. Numer. Math. 2018, 123, 200–220. [Google Scholar] [CrossRef]
- Samar, M. Condition numbers for a linear function of the solution to the constrained and weighted least squares problem and their statistical estimation. Taiwan J. Math. 2021, 25, 717–741. [Google Scholar] [CrossRef]
- Samar, M.; Lin, F. Perturbation and condition numbers for the Tikhonov regularization of total least squares problem and their statistical estimation. J. Comput. Appl. Math. 2022, 411, 114230. [Google Scholar] [CrossRef]
- Diao, H.; Wei, Y.; Xie, P. Small sample statistical condition estimation for the total least squares problem. Numer. Algor. 2017, 75, 435–455. [Google Scholar] [CrossRef]
- Samar, M.; Zhu, X. Structured conditioning theory for the total least squares problem with linear equality constraint and their estimation. AIMS Math. 2023, 8, 11350–11372. [Google Scholar] [CrossRef]
- Baboulin, M.; Gratton, S.; Lacroix, R.; Laub, A.J. Statistical estimates for the conditioning of linear least squares problems. In Parallel Processing and Applied Mathematics: 10th International Conference, PPAM 2013, Warsaw, Poland, September 8–11, 2013, Revised Selected Papers, Part I 10; Springer: Berlin/Heidelberg, Germany, 2014; Lecture Notes in Computer Science; Volume 8384, pp. 124–133. [Google Scholar]
- Higham, N.J. Accuracy and Stability of Numerical Algorithms, 2nd ed.; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Higham, N.J. J-Orthogonal matrices: Properties and generation. SIAM Rev. 2003, 45, 504–519. [Google Scholar] [CrossRef]


| Mean | Max | Mean | Max | Mean | Max | ||
|---|---|---|---|---|---|---|---|
| 1.0763 | 4.8422 | 1.0647 | 2.8373 | 1.1538 | 3.9657 | ||
| 1.3146 | 6.7089 | 1.0861 | 4.4630 | 1.2845 | 5.9123 | ||
| 1.7422 | 1.6402 | 1.1965 | 1.2847 | 1.0784 | 1.5766 | ||
| 2.6043 | 1.9461 | 1.4574 | 1.6783 | 1.7540 | 1.8452 | ||
| 1.4032 | 5.7654 | 1.2433 | 4.6501 | 1.3601 | 5.3752 | ||
| 1.7341 | 8.2074 | 1.5623 | 6.4738 | 1.7320 | 7.2004 | ||
| 2.5254 | 2.8732 | 1.8510 | 1.6062 | 2.0653 | 2.2903 | ||
| 2.7034 | 3.9543 | 2.0312 | 2.0106 | 2.3871 | 2.4803 | ||
| 1.7301 | 7.9662 | 1.4607 | 6.8606 | 1.5296 | 8.0651 | ||
| 1.9674 | 3.7649 | 1.7065 | 8.5963 | 1.8472 | 9.7063 | ||
| 2.7055 | 5.6570 | 2.0276 | 3.2613 | 2.3601 | 4.6904 | ||
| 2.9867 | 7.1601 | 2.2760 | 4.9013 | 2.5935 | 5.9721 | ||
| 1.8271 | 2.3021 | 1.6354 | 1.4032 | 1.7925 | 1.5102 | ||
| 2.3064 | 3.7632 | 1.9642 | 1.5210 | 1.9862 | 1.6082 | ||
| 2.8063 | 7.4310 | 2.0513 | 5.0471 | 2.6743 | 6.0437 | ||
| 2.9887 | 8.6501 | 2.3810 | 7.1089 | 2.7011 | 7.4810 | ||
| Mean | Variance | Mean | Variance | Mean | Variance | Mean | Variance | ||
|---|---|---|---|---|---|---|---|---|---|
| 1.0000 | 5.3577 | 1.0322 | 1.2063 | 1.0067 | 1.3505 | 1.2785 | 1.0431 | ||
| 1.0000 | 7.0635 | 1.1439 | 3.5027 | 1.0134 | 3.9054 | 1.3744 | 3.6397 | ||
| 1.0001 | 1.5165 | 1.2906 | 4.6021 | 1.1075 | 4.1653 | 1.5043 | 3.9428 | ||
| 1.0001 | 1.7940 | 1.3482 | 5.7803 | 1.2306 | 4.9563 | 1.8732 | 4.6543 | ||
| 1.0000 | 6.5102 | 1.2654 | 2.7360 | 1.3405 | 3.4605 | 1.2765 | 2.6123 | ||
| 1.0000 | 7.4738 | 1.4783 | 4.4925 | 1.7169 | 4.8543 | 1.5063 | 4.3326 | ||
| 1.0001 | 1.6062 | 1.6295 | 6.8732 | 1.8206 | 6.4890 | 1.7422 | 5.0542 | ||
| 1.0001 | 2.5106 | 1.8693 | 7.9543 | 2.1456 | 7.4293 | 2.0361 | 6.3702 | ||
| 1.0000 | 1.7029 | 1.2063 | 4.2083 | 1.6710 | 5.7862 | 1.3722 | 4.7031 | ||
| 1.0000 | 2.4771 | 1.7033 | 7.2035 | 1.8041 | 6.0165 | 1.5760 | 5.7402 | ||
| 1.0002 | 6.1041 | 2.0654 | 7.5293 | 2.2054 | 8.3014 | 2.0113 | 7.2461 | ||
| 1.0003 | 5.6854 | 2.1976 | 8.2063 | 2.2593 | 8.6458 | 2.1263 | 7.9432 | ||
| 1.0000 | 5.6321 | 1.6305 | 6.2092 | 1.9455 | 6.7402 | 1.8240 | 6.0461 | ||
| 1.0000 | 6.0573 | 1.7002 | 8.0210 | 1.9822 | 8.0549 | 1.9701 | 7.4322 | ||
| 1.0003 | 8.6021 | 2.1533 | 9.0425 | 2.4003 | 9.3614 | 2.2764 | 8.4681 | ||
| 1.0004 | 2.8543 | 2.4187 | 9.2054 | 2.6005 | 9.5370 | 2.5711 | 9.4502 | ||
| 0.1065 | 0.2742 | 0.7601 | 0.4643 | |
| 0.3784 | 0.5204 | 1.3644 | 1.1677 | |
| 0.4842 | 0.6032 | 1.4569 | 1.2658 | |
| 0.5643 | 0.7411 | 1.6345 | 1.5403 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samar, M.; Zhu, X.; Shakoor, A.
Conditioning Theory for Generalized Inverse
Samar M, Zhu X, Shakoor A.
Conditioning Theory for Generalized Inverse
Samar, Mahvish, Xinzhong Zhu, and Abdul Shakoor.
2023. "Conditioning Theory for Generalized Inverse
Samar, M., Zhu, X., & Shakoor, A.
(2023). Conditioning Theory for Generalized Inverse





