Amplitude and Phase Angle of Oscillatory Heat Transfer and Current Density along a Nonconducting Cylinder with Reduced Gravity and Thermal Stratification Effects
Abstract
:1. Introduction
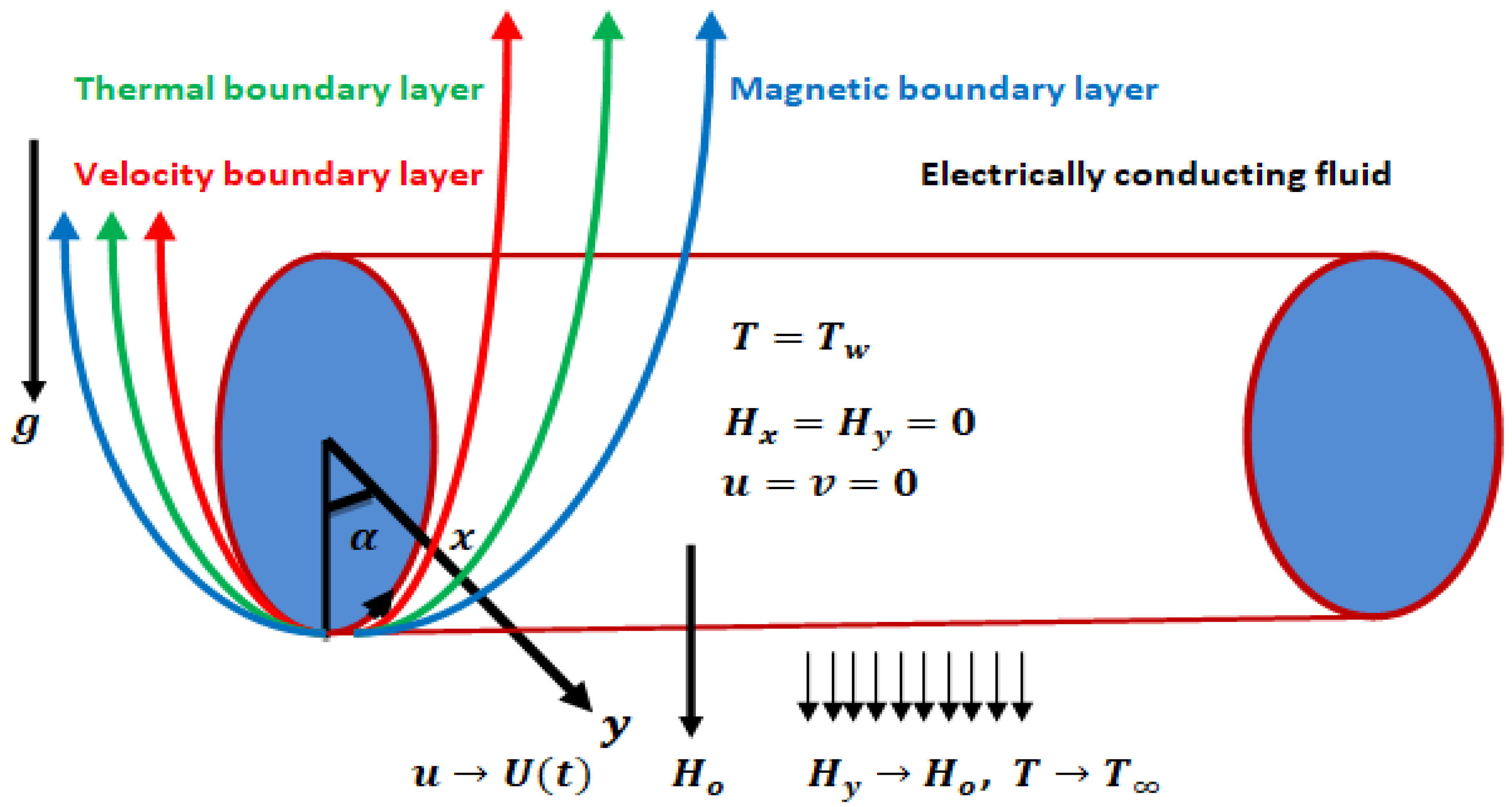
2. Flow Geometry and Mathematical Formulation
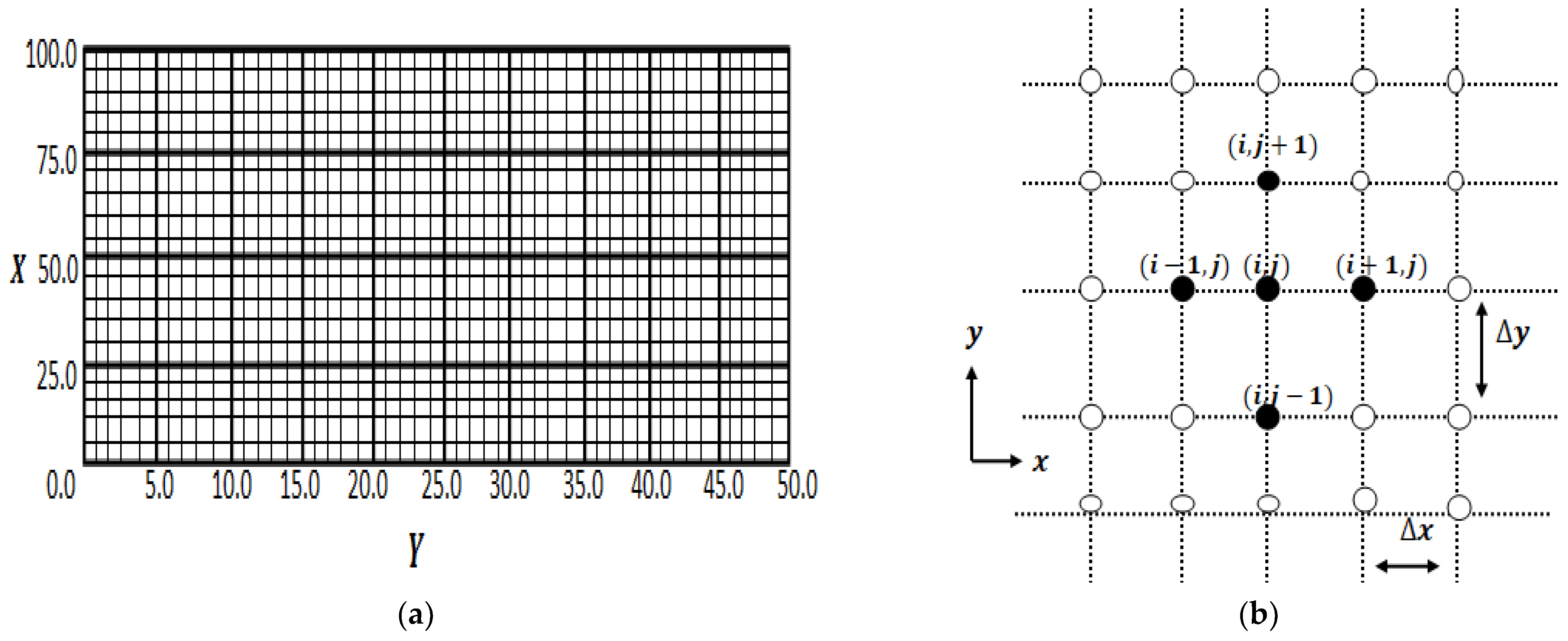
3. Computational Scheme and Solution Methodology
4. Results and Discussion
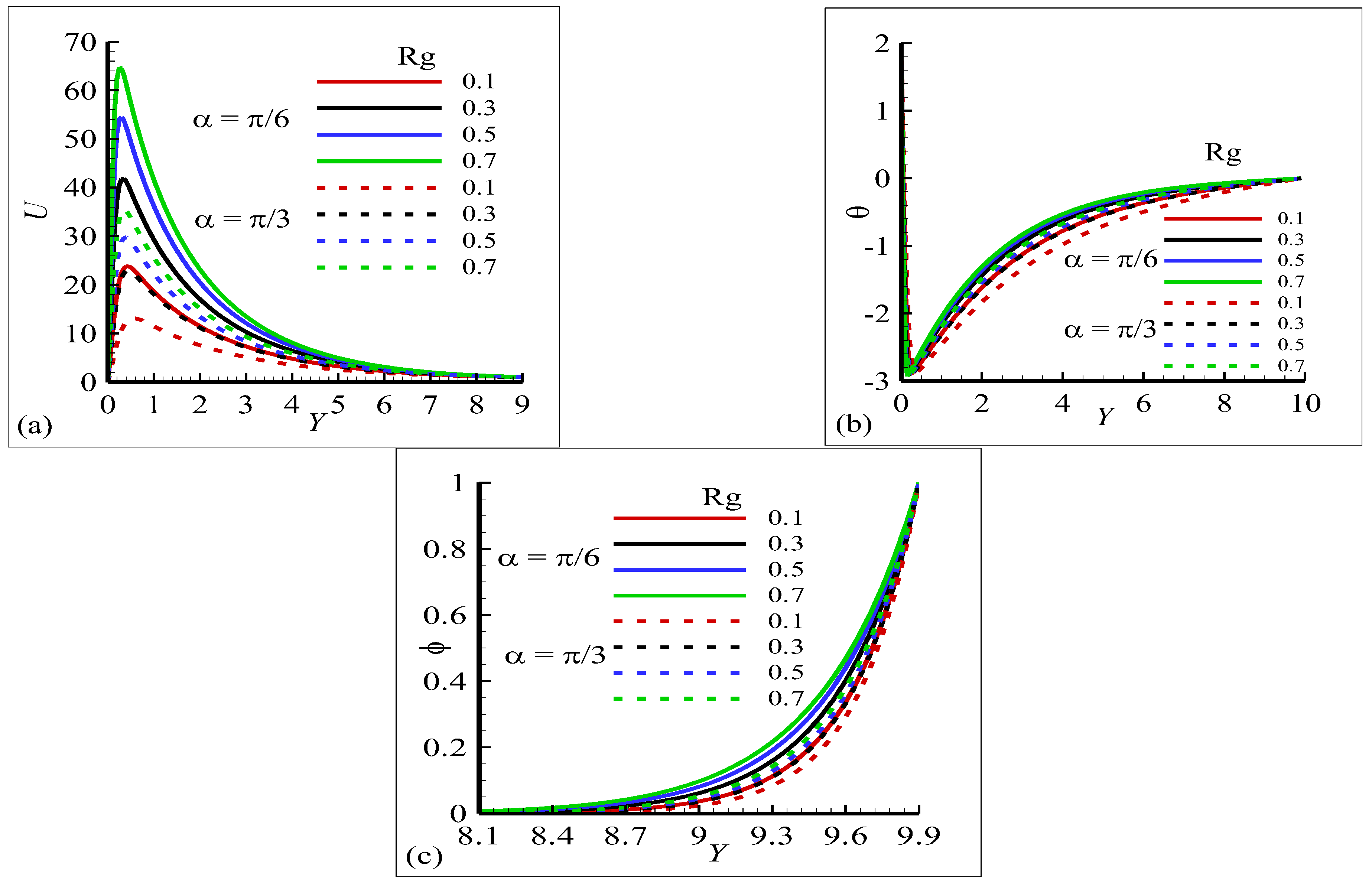
4.1. The Fluid’s Velocity , the Temperature , and the Magnetic Field Plots to Evaluate the Validity of Findings from Described Conditions
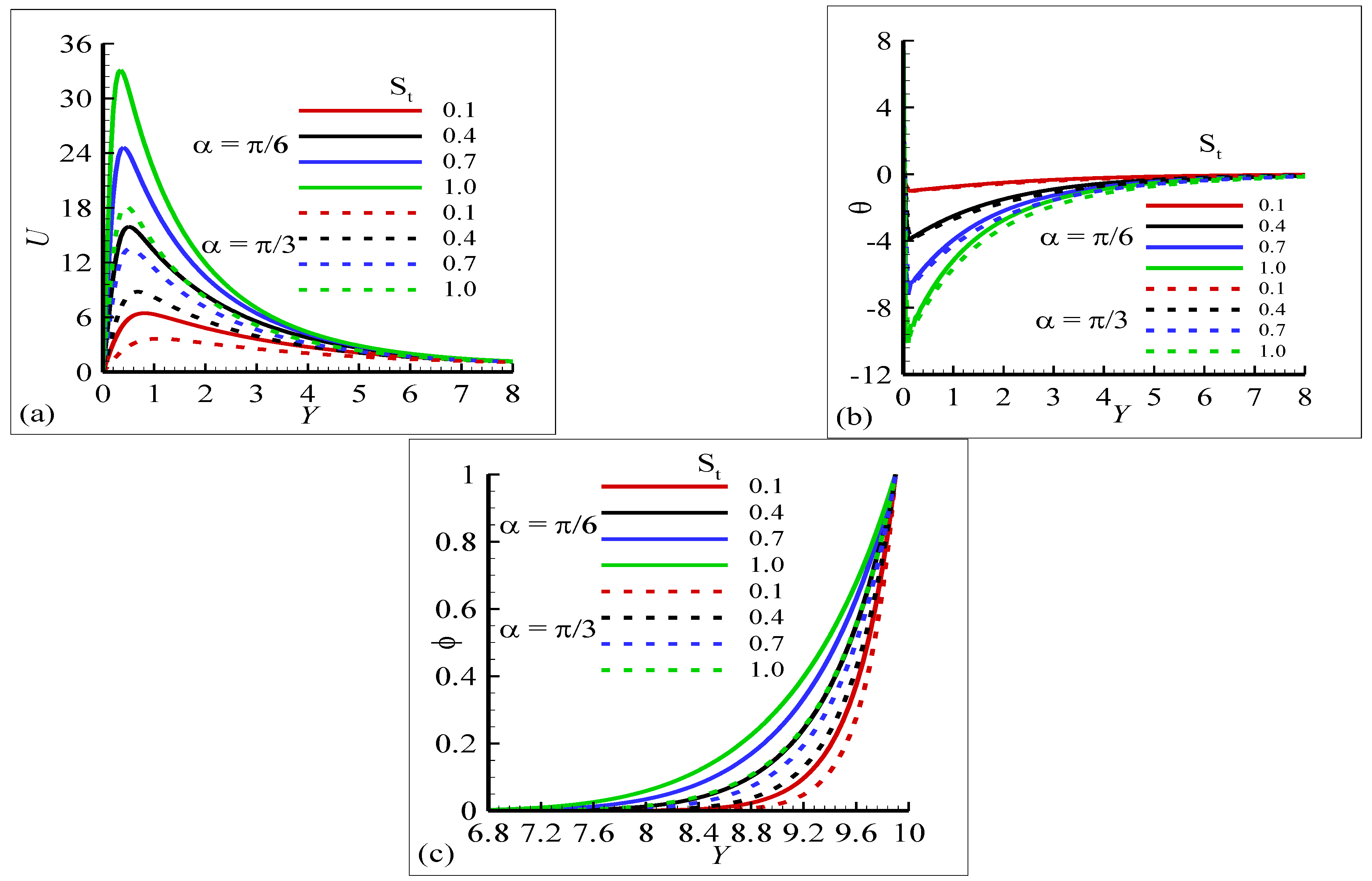
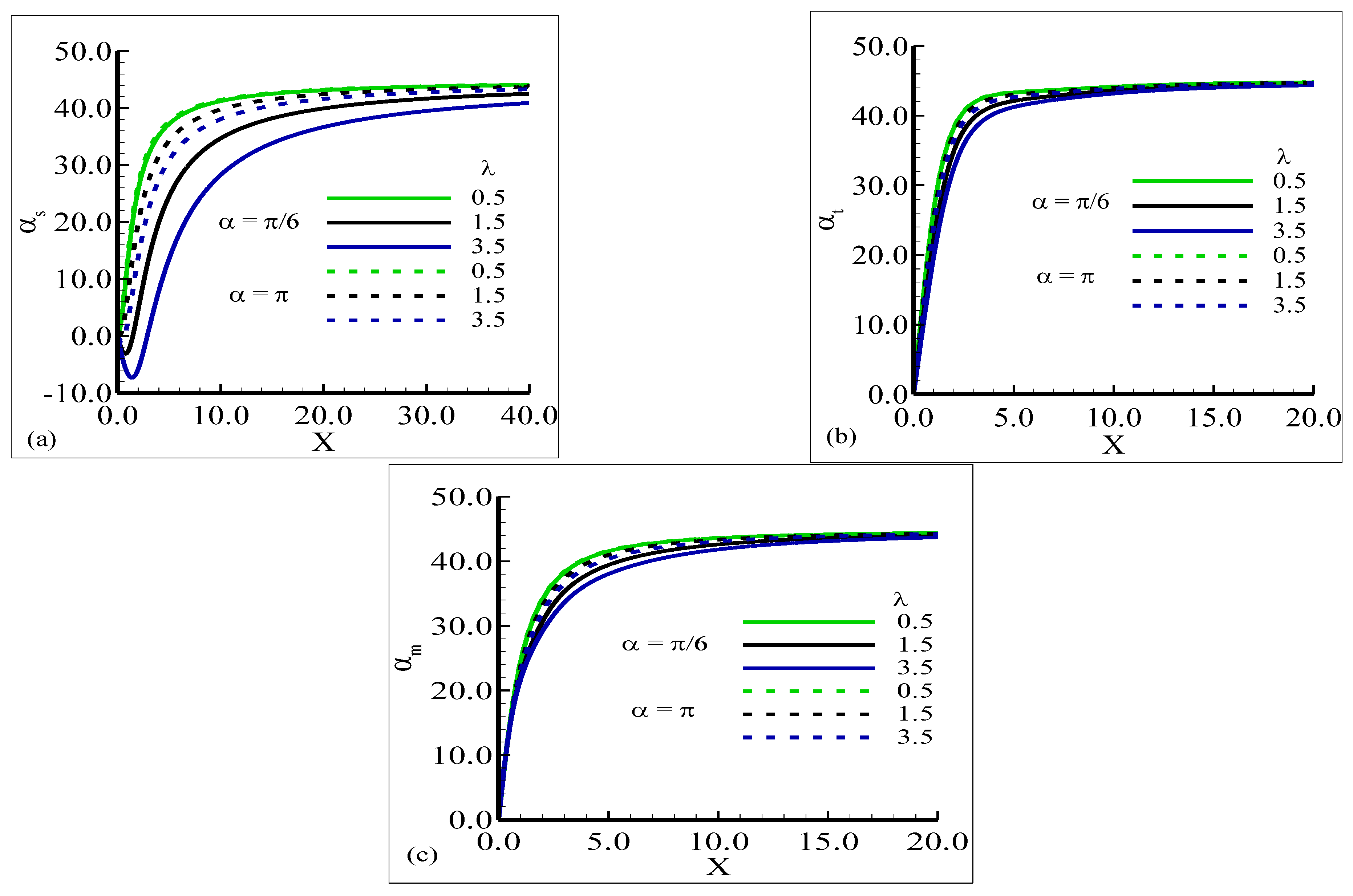
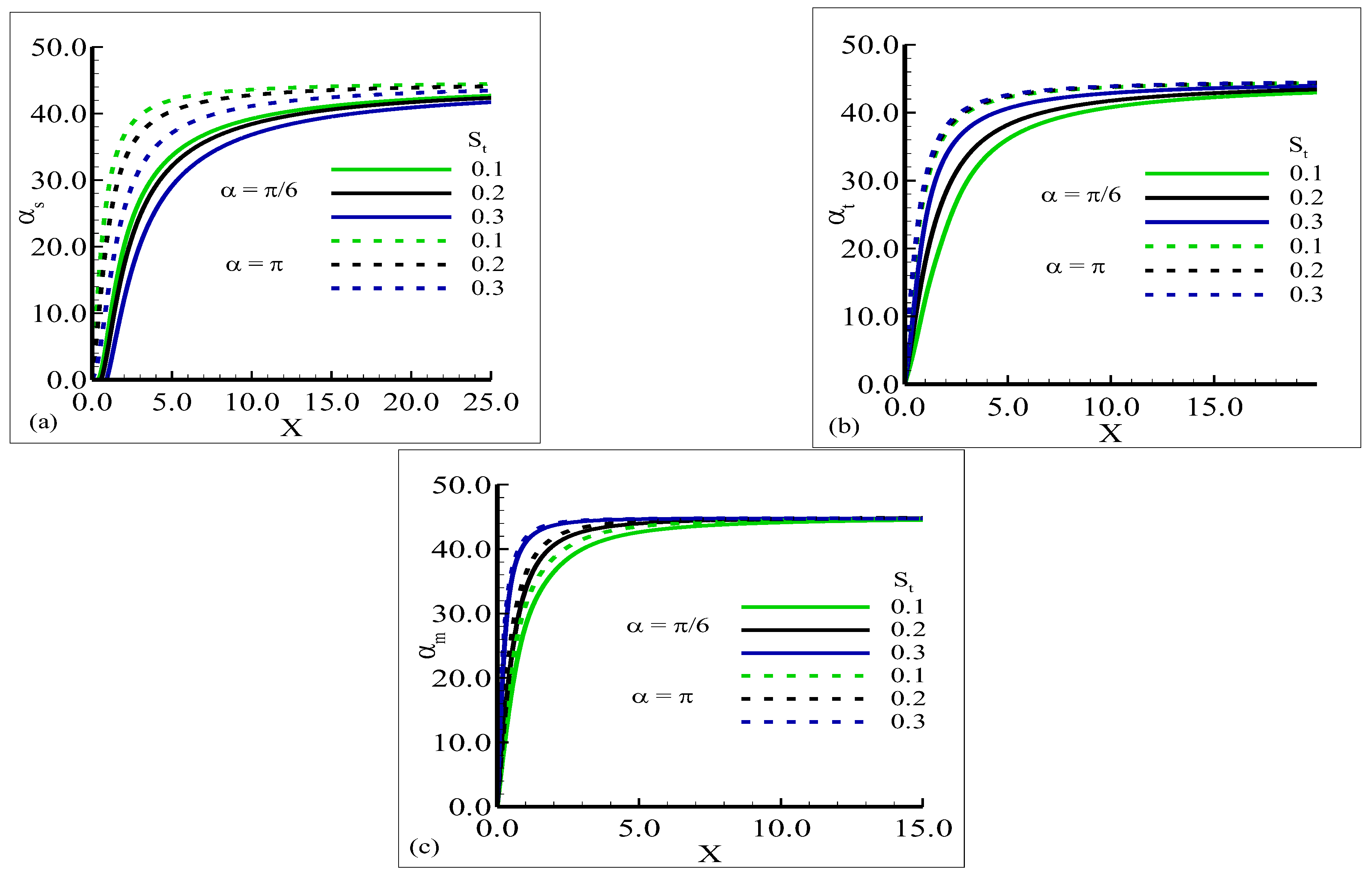
4.2. Phase Angle of Heat Transfer , Skin Friction and Current Density
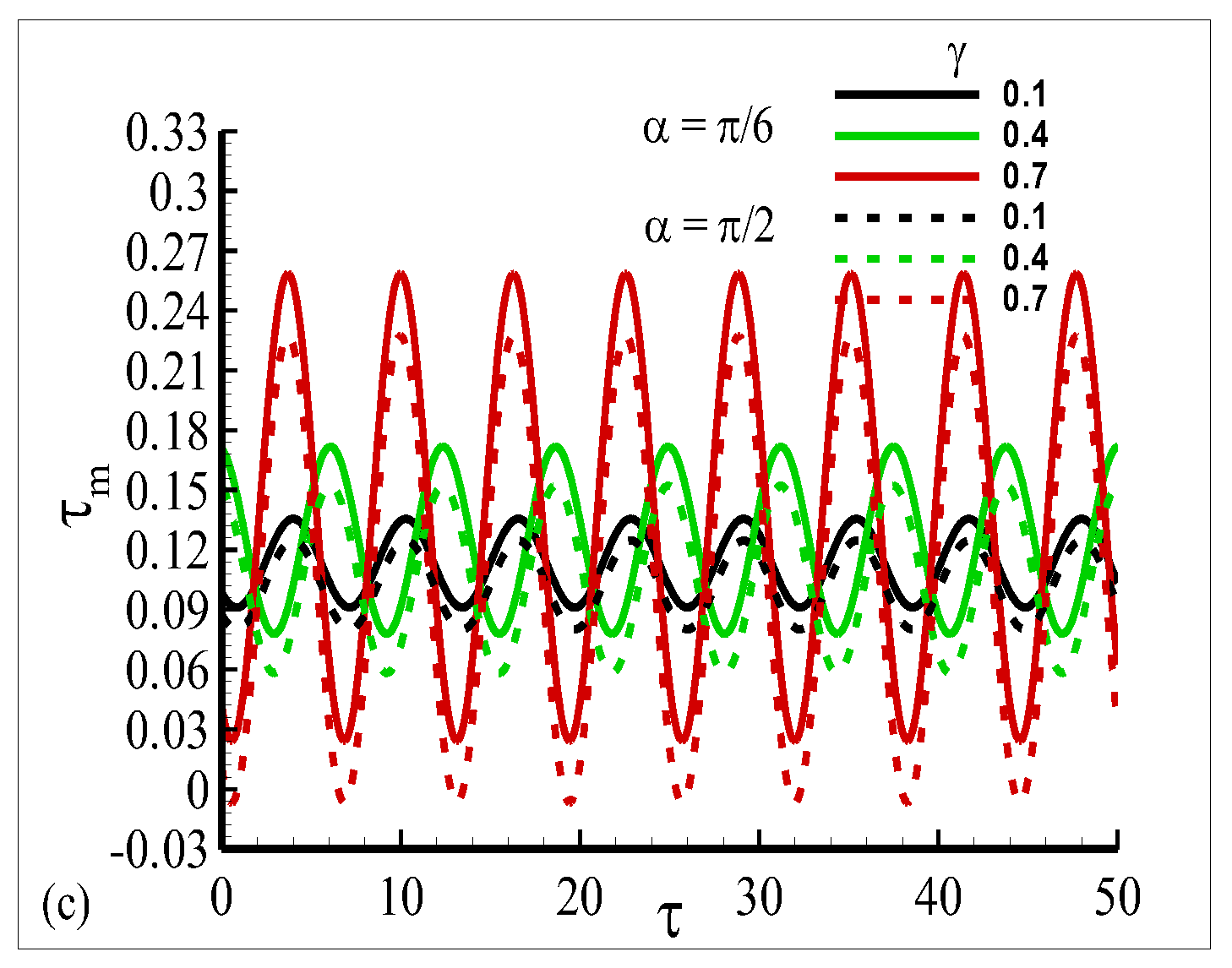
4.3. Amplitude Shapes of Oscillating Heat Transfer , Skin Friction , and Current Density
5. Concluding Remarks
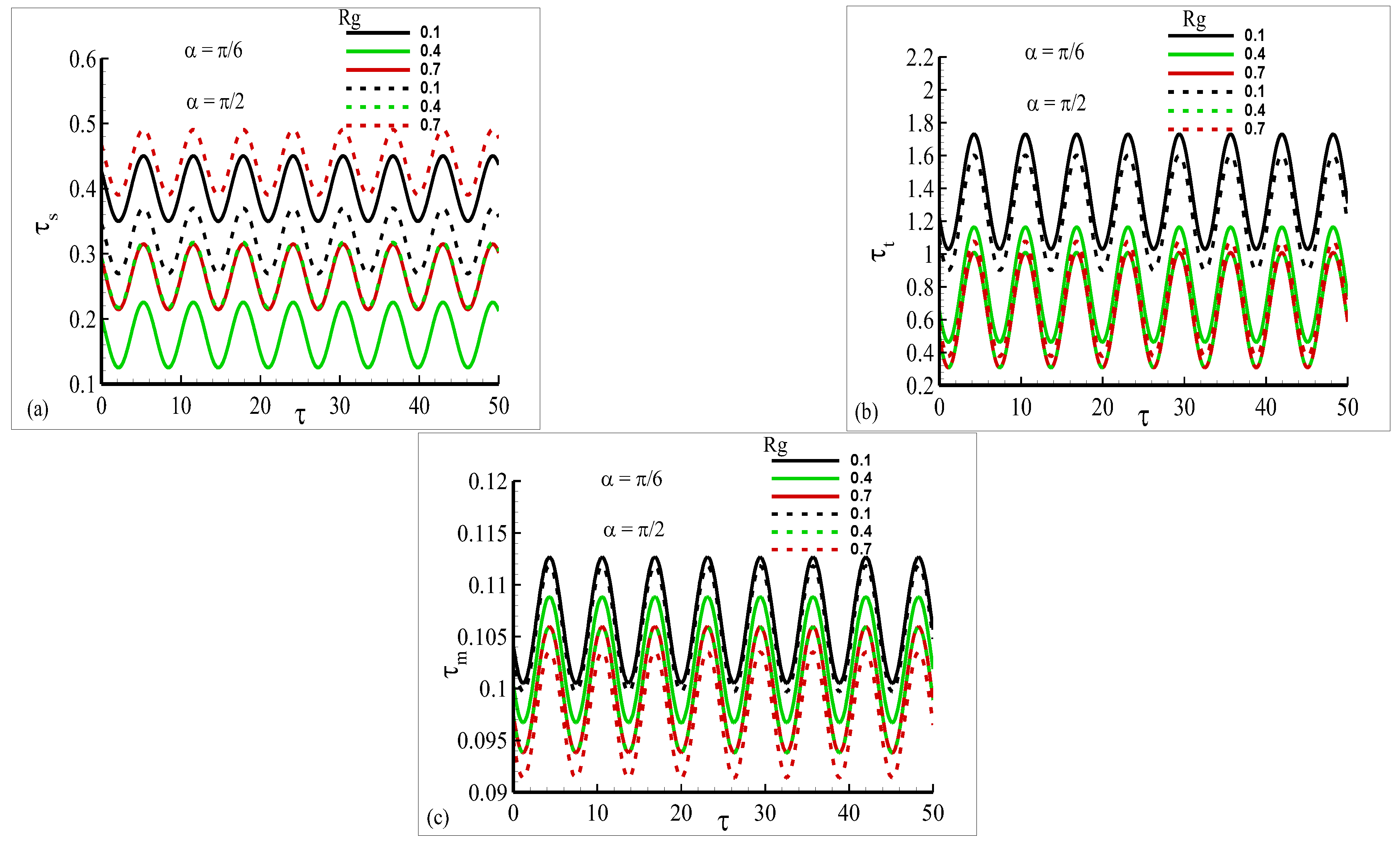
- The thermal boundary layer thickness and magnetic field increases at each angle as reduced gravity increases. It is also mentioned that the dimensionless velocity of the fluid increases as gravity factor decreases.
- It is noted that the fluid velocity and magnetic field decrease as thermal stratification increases at each position but the temperature distribution increases sharply in the presence of buoyancy forces.
- The phase angle of current density and heat transfer increases as the buoyancy force increases. In convection, buoyancy forces increase the pressure gradient and temperature increases due to the heated fluid (water) for Pr .
- The minimum enhancement in the phase angle is noted for increasing the values of thermal stratification but the current density of the fluid is increased at both angles.
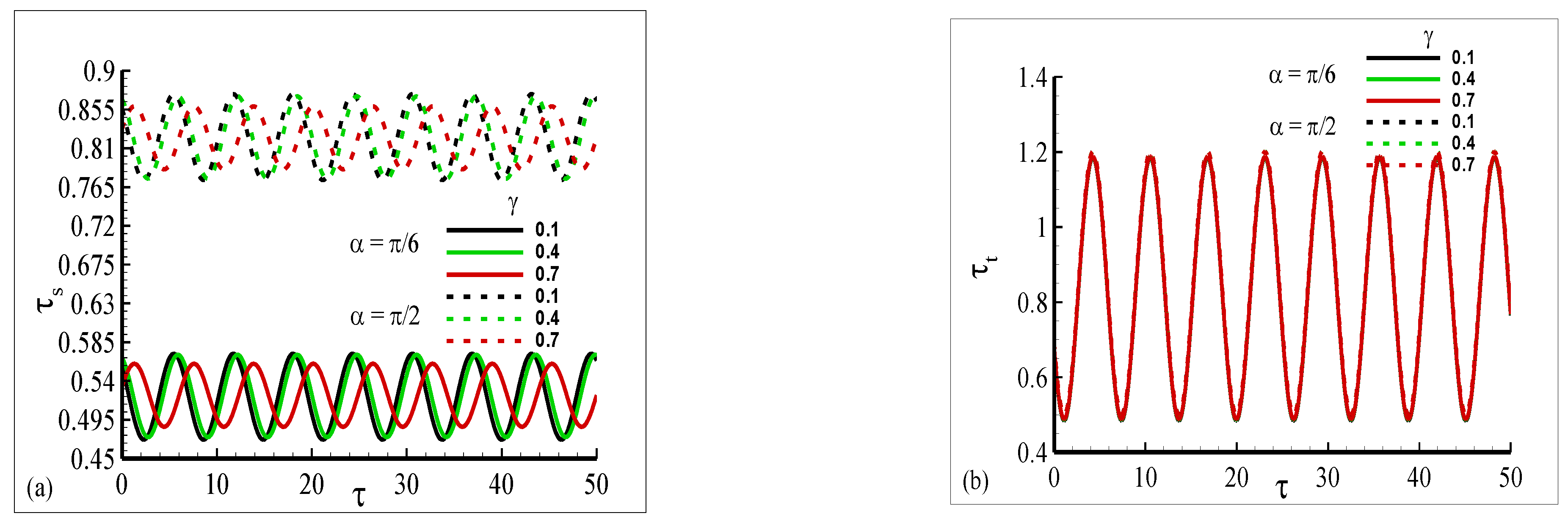
- The periodic heat transfer rate and current density increase with a prominent magnitude of oscillation in the presence of reduced gravity.
- The oscillating amplitude of current density increases with prominent variations as the magnetic Prandtl number increases. This was expected because the magnetic diffusion at the surface of the horizontal circular cylinder is decreased for a higher magnetic Prandtl number.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| , | Velocity along and -direction (m s−1) | Ambienttemperature (K) | |
| , | Magnetic velocities along and -direction (Tesla) | Reynolds number | |
| Dynamicviscosity (kg m−1 s−1) | Grashof number | ||
| Kinematicviscosity (m2 s−1) | Greek symbols | ||
| Fluid density (kg m−3) | Shearing stress (Pa) | ||
| Gravitational acceleration (m s−2) | Magnetic force parameter | ||
| Thermal expansion coefficient (K−1) | Mixed convection parameter | ||
| Magnetic permeability (H m−1) | Dimensionless temperature | ||
| Thermal diffusivity (m2 s−1) | Magnetic Prandtl number | ||
| T | Temperature (K) | Pr | Prandtl number |
| Specific heat (J kg−1 K−1) | Electrical conductivity (s m−1) | ||
| Reduced gravity parameter | Thermal stratification parameter | ||
References
- Millsaps, K.; Pohlhausen, K. The laminar free convective heat transfer from the outer surface of a vertical circular cylinder. J. Aeronaut. Sci. 1958, 25, 357–360. [Google Scholar] [CrossRef]
- Chawla, S.S. Fluctuating boundary layer on a magnetized plate. Proc. Camb. Phil. Soc. 1967, 63, 513–525. [Google Scholar] [CrossRef]
- Tamilzharasan, B.M.; Karthikeyan, S.; Kaabar, M.K.; Yavuz, M.; Özköse, F. Magneto mixed convection of Williamson nanofluid flow through a double stratified porous medium in attendance of activation energy. Math. Comput. Appl. 2022, 27, 46. [Google Scholar] [CrossRef]
- Rehman, S.U.; Mir, N.A.; Farooq, M.; Rafiq, N.; Ahmad, S. Analysis of thermally stratified radiative flow of Sutterby fluid with mixed convection. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 934–942. [Google Scholar] [CrossRef]
- Salahuddin, T.; Siddique, N.; Khan, M.; AlAlwan, B.; Almesfer, M. Outlining the influence of thermal and solutal stratifications on mixed convection second grade fluid flow near an irregular cylinder with induced magnetic field. Waves Random Complex Media 2021, 1–22. [Google Scholar] [CrossRef]
- Shah, S.; Hussain, S.; Sagheer, M. Thermal stratification effects on mixed convective Maxwell fluid flow with variable thermal conductivity and homogeneous/heterogeneous reactions. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 452. [Google Scholar] [CrossRef]
- Hayat, T.; Ullah, I.; Muhammad, T.; Alsaedi, A. Thermal and solutal stratification in mixed convection three-dimensional flow of an Oldroyd-B nanofluid. Results Phys. 2017, 7, 3797–3805. [Google Scholar] [CrossRef]
- Al-Farhany, K.; Al-Muhja, B.; Loganathan, K.; Periyasamy, U.; Ali, F.; Sarris, I.E. Analysis of Convection Phenomenon in Enclosure Utilizing Nanofluids with Baffle Effects. Energies 2022, 15, 6615. [Google Scholar] [CrossRef]
- Al-Mdallal, Q.; Prasad, V.R.; Basha, H.T.; Sarris, I.; Akkurt, N. Keller box simulation of magnetic pseudoplastic nano-polymer coating flow over a circular cylinder with entropy optimisation. Comput. Math. Appl. 2022, 118, 132–158. [Google Scholar] [CrossRef]
- Sofiadis, G.; Sarris, I. Reynolds number effect of the turbulent micropolar channel flow. Phys. Fluids 2022, 34, 075126. [Google Scholar] [CrossRef]
- Maranna, T.; Sneha, K.N.; Mahabaleshwar, U.S.; Sarris, I.E.; Karakasidis, T.E. An Effect of Radiation and MHD Newtonian Fluid over a Stretching/Shrinking Sheet with CNTs and Mass Transpiration. Appl. Sci. 2022, 12, 5466. [Google Scholar] [CrossRef]
- Mabood, F.; Fatunmbi, E.O.; Benos, L.; Sarris, I.E. Entropy Generation in the Magnetohydrodynamic Jeffrey Nanofluid Flow Over a Stretching Sheet with Wide Range of Engineering Application Parameters. Int. J. Appl. Comput. Math. 2022, 8, 98. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Hafidzuddin, E.H.; Wahi, N. Thermally Stratified Flow of Cu-Al2O3/Water Hybrid Nanofluid Past a Permeable Stretching/Shrinking Circular Cylinder. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 63, 154–163. [Google Scholar]
- Gireesha, B.J.; Venkatesh, P.; Shashikumar, N.S.; Prasannakumara, B.C. Boundary layer flow of dusty fluid over a radiating stretching surface embedded in a thermally stratified porous medium in the presence of uniform heat source. Nonlinear Eng. 2017, 6, 31–41. [Google Scholar] [CrossRef]
- Rehman, K.U.; Alshomrani, A.S.; Malik, M.Y. Carreau fluid flow in a thermally stratified medium with heat generation/absorption effects. Case Stud. Therm. Eng. 2018, 12, 16–25. [Google Scholar] [CrossRef]
- Koriko, O.K.; Oreyeni, T.; Omowaye, A.J.; Animasaun, I.L. Homotopy Analysis of MHD Free Convective Micropolar Fluid Flow along a Vertical Surface Embedded in Non-Darcian Thermally-Stratified Medium. Open J. Fluid Dyn. 2016, 6, 198–221. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Ishak, A. Mixed Convection Flow along a Stretching Cylinder in a Thermally Stratified Medium. J. Appl. Math. 2012, 2012, 491695. [Google Scholar] [CrossRef]
- Besthapu, P.; Haq, R.U.; Bandari, S.; Al-Mdallal, Q.M. Mixed convection flow of thermally stratified MHD nanofluid over an exponentially stretching surface with viscous dissipation effect. J. Taiwan Inst. Chem. Eng. 2017, 71, 307–314. [Google Scholar] [CrossRef]
- Abbas, A.; Sarris, I.E.; Ashraf, M.; Ghachem, K.; Hnaein, N.; Alshammari, B.M. The Effects of Reduced Gravity and Radiative Heat Transfer on the Magnetohydrodynamic Flow Past a Non-Rotating Stationary Sphere Surrounded by a Porous Medium. Symmetry 2023, 15, 806. [Google Scholar] [CrossRef]
- MatYasin, M.H.; Arifin, N.M.; Nazar, R.; Ismail, F.; Pop, I. Mixed Convection Boundary Layer Flow Embedded in a Thermally Stratified Porous Medium Saturated by a Nanofluid. Adv. Mech. Eng. 2013, 5, 121943. [Google Scholar] [CrossRef]
- Geetha, P.; Moorthy, M.B.K. Variable Viscosity, Chemical Reaction and Thermal Stratification Effects on Mixed Convection Heat and Mass Transfer along a Semi-Infinite Vertical Plate. Am. J. Appl. Sci. 2011, 8, 628. [Google Scholar] [CrossRef]
- Hayat, T.; Shehzad, S.A.; Al-Sulami, H.H.; Asghar, S. Influence of thermal stratification on the radiative flow of Maxwell fluid. J. Braz. Soc. Mech. Sci. Eng. 2013, 35, 381–389. [Google Scholar] [CrossRef]
- Moorthy, M.B.K.; Thangavelu, K.; Senthilvadivu, K. Free convection in non-newtonian power-law fluids along a vertical plate with variable viscosity and thermal stratification in the presence of internal heat generation. Heat Transf. Res. 2017, 48, 9–22. [Google Scholar] [CrossRef]
- Kay, A.; Kuiken, H.K.; Merkin, J.H. Boundary-layer analysis of the thermal bar. J. Fluid Mech. 1995, 303, 253–278. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Al-Mudhaf, A. Unsteady heat and mass transfer from a rotating vertical cone with a magnetic field and heat generation or absorption effects. Int. J. Therm. Sci. 2005, 44, 267–276. [Google Scholar] [CrossRef]
- Saleem, S.; Nadeem, S. Theoretical analysis of slip flow on a rotating cone with viscous dissipation effects. J. Hydrodyn. Ser. B 2015, 27, 616–623. [Google Scholar] [CrossRef]
- Malik, M.Y. Application of shooting method on MHD thermally stratified mixed convection flow of non-Newtonian fluid over an inclined stretching cylinder. J. Phys. Conf. Ser. 2017, 822, 012012. [Google Scholar] [CrossRef]
| Chamkha et al. [25] | Saleem and Nadeem [26] | Malik et al. [27] | Present Results | |
|---|---|---|---|---|
| 0.0 | 1.4110 | 1.4111 | 1.4110 | 1.4103 |
| 1.0 | 1.5662 | 1.5661 | 1.5660 | 1.5654 |
| 10.0 | 2.3580 | 2.3581 | 2.3581 | 2.3579 |
| 0.1 | 4.3565762 | 0.251481 | 0.340288 |
| 0.3 | 5.851118 | 0.281927 | 0.285282 |
| 0.5 | 7.019164 | 0.305644 | 0.251765 |
| 0.7 | 7.850729 | 0.321940 | 0.230962 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, Z.; Jabeen, N.; Khan, M.U. Amplitude and Phase Angle of Oscillatory Heat Transfer and Current Density along a Nonconducting Cylinder with Reduced Gravity and Thermal Stratification Effects. Mathematics 2023, 11, 2134. https://doi.org/10.3390/math11092134
Ullah Z, Jabeen N, Khan MU. Amplitude and Phase Angle of Oscillatory Heat Transfer and Current Density along a Nonconducting Cylinder with Reduced Gravity and Thermal Stratification Effects. Mathematics. 2023; 11(9):2134. https://doi.org/10.3390/math11092134
Chicago/Turabian StyleUllah, Zia, Nawishta Jabeen, and Muhammad Usman Khan. 2023. "Amplitude and Phase Angle of Oscillatory Heat Transfer and Current Density along a Nonconducting Cylinder with Reduced Gravity and Thermal Stratification Effects" Mathematics 11, no. 9: 2134. https://doi.org/10.3390/math11092134







