Maximum Power Point Tracker Controller for Solar Photovoltaic Based on Reinforcement Learning Agent with a Digital Twin
Abstract
:1. Introduction
- Continuous action space. Compared to other RL agents such as DQN, the continious action space handled by the DDPG agent is more suitable for control task, giving the precise control signal to achieve the MPP in each environmental case of temperature and irradiance.
- Instantaneous control action. Contrary to the work [35], after training, the DDPG agent instantly provides the optimal duty cycle to obtain the MPP, so the time needed to reach the MPP is only limited by the response of the system.
- Direct control. The DDPG agent in this case, is the only one in charge of providing the duty cycle to the converter without counting on other controllers or without being itself the one that provides help to other controllers as in the paper [36]. In this way, the computational cost is lower and the system is simplified.
- Training simplicity. Compared to any ANN or machine learning that works as an MPPT, an RL agent learns the correct control signal during training for a variety of irradiance and temperature values. A machine learning or supervised ANN needs to know in advance, what the optimal duty cycles are for each combination of irradiance and temperature, and thus presents a lengthy process using scanning or other types of controllers to obtain this large amount of data, in addition to the time to train the network afterwards. In the case of an RL agent, this initial process is eliminated at the cost of greater design difficulty.
- DT for the training of an RL agent. The use of the DT as part of the reward function of the DDPG training accelerates the training process.
2. Materials and Methods
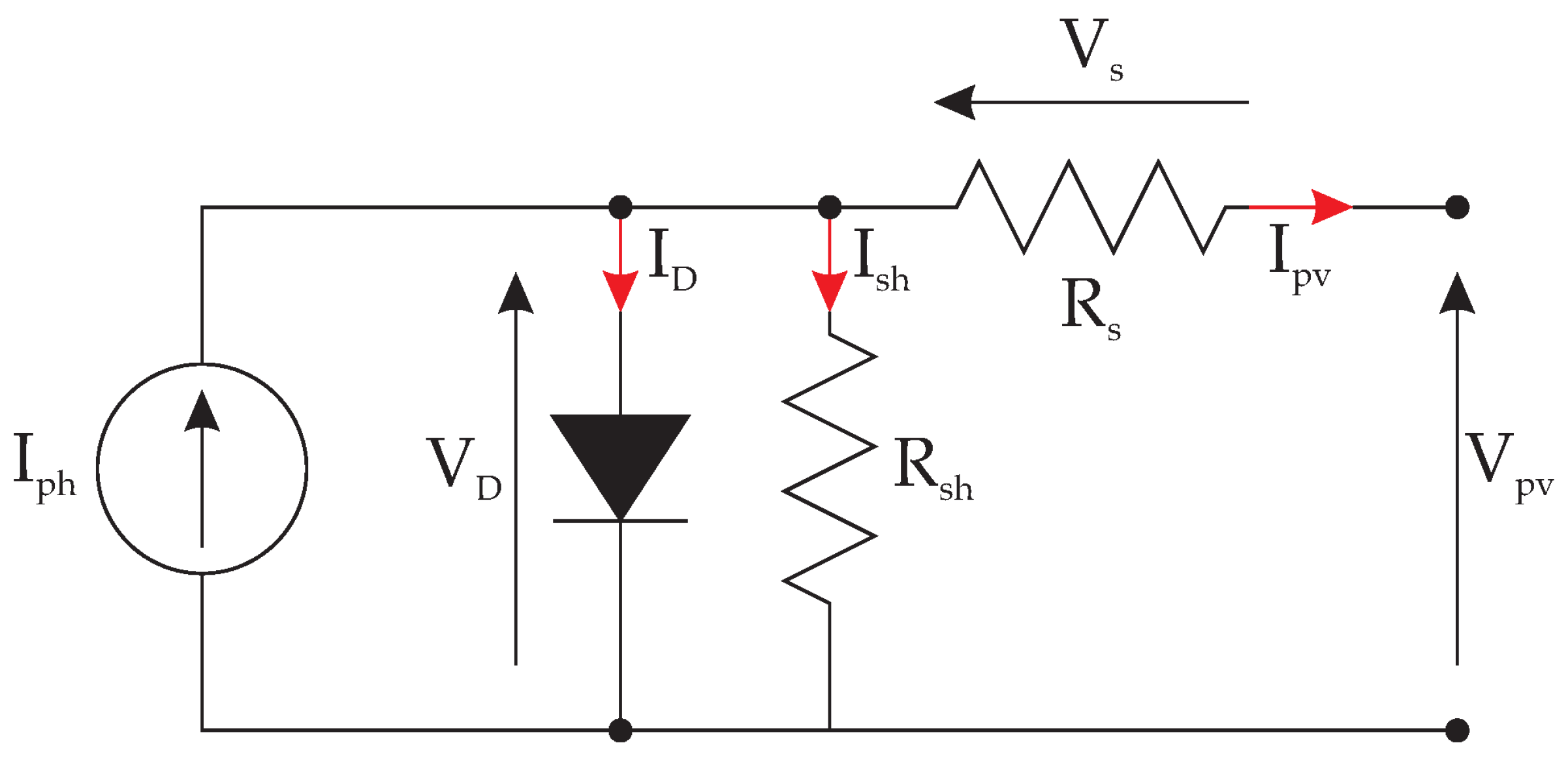
2.1. Digital Twin (PV Model)
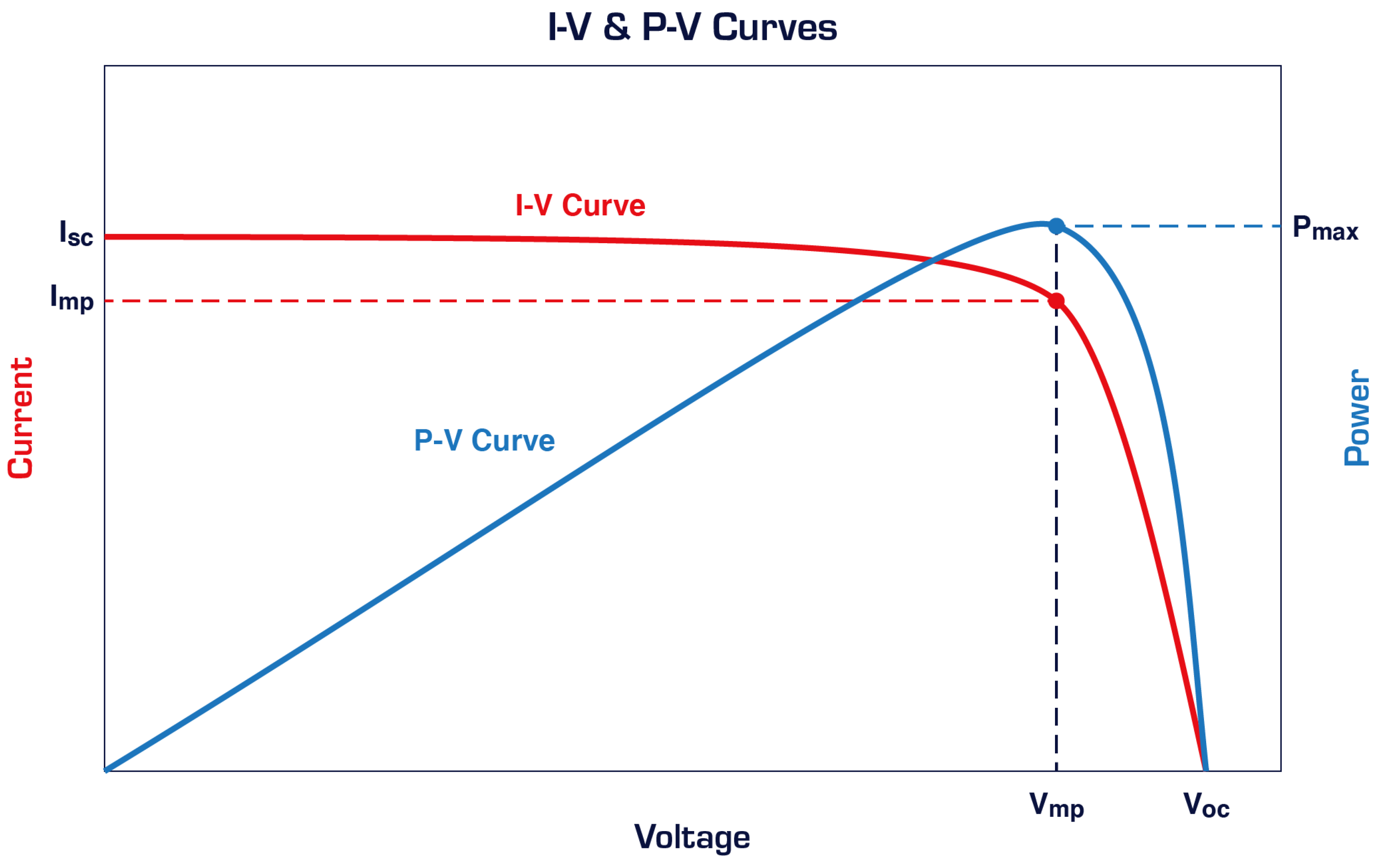
2.2. Maximum Power Point (MPP)
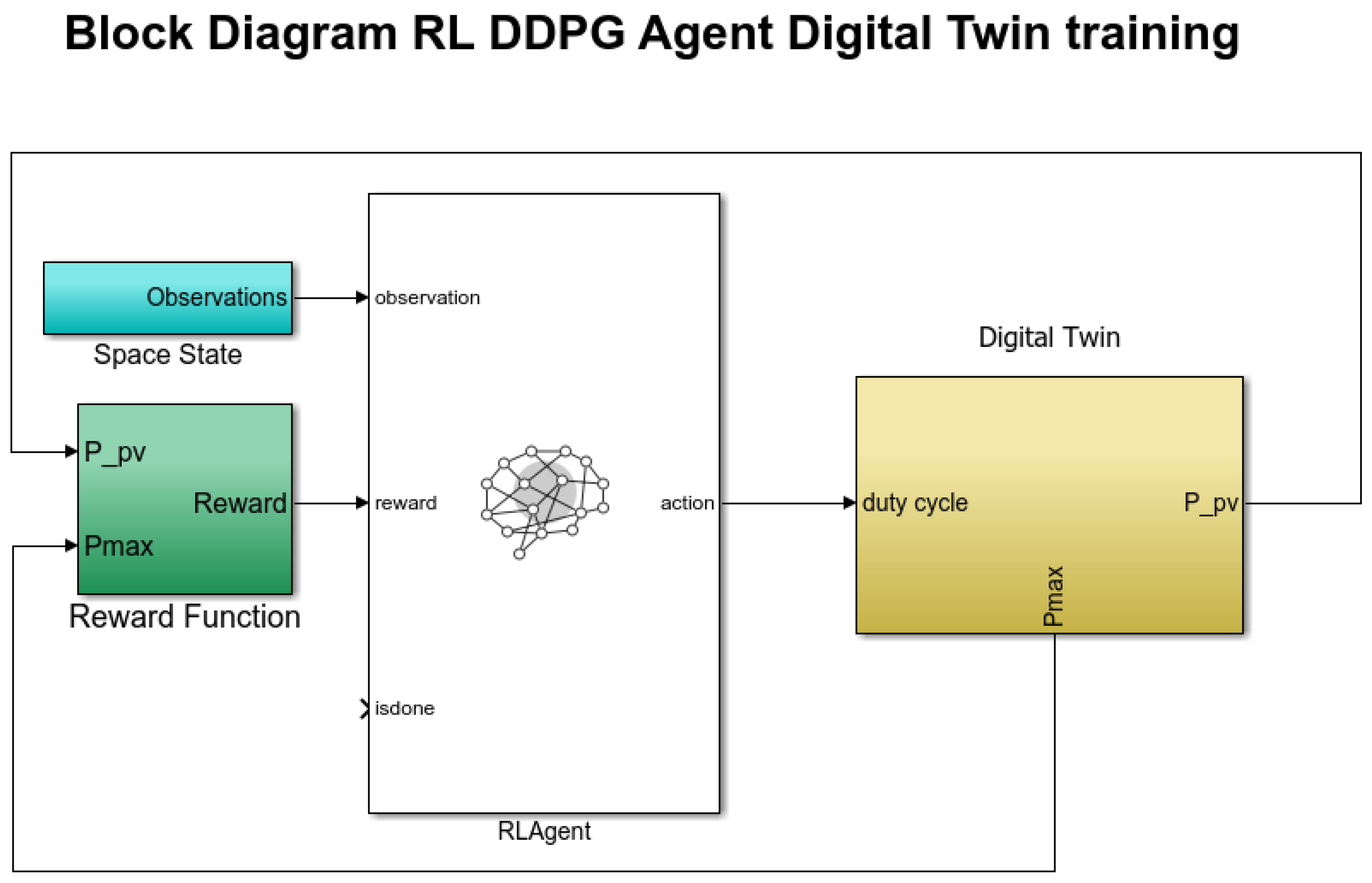
2.3. Reinforcement Learning
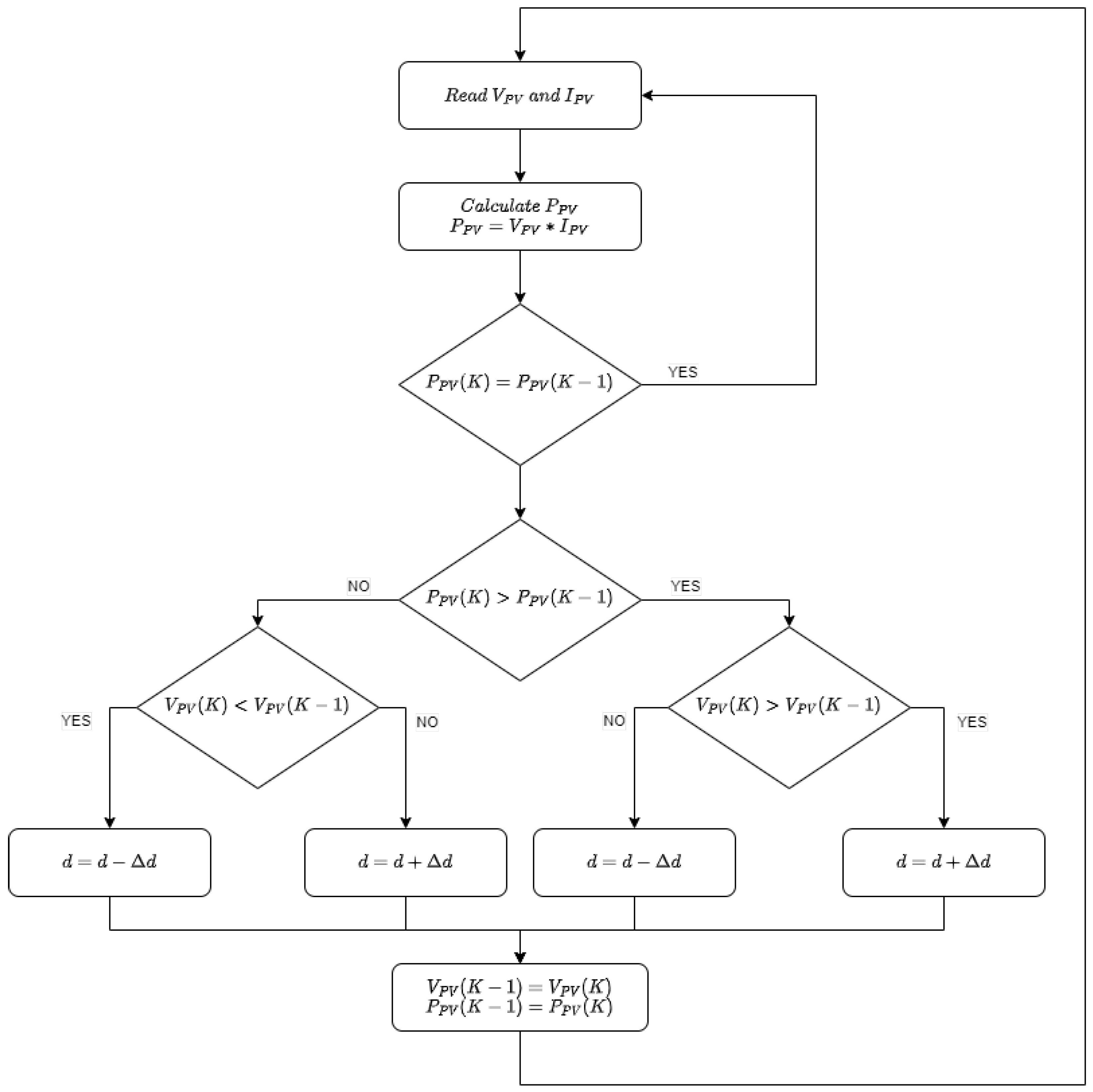
2.4. Perturb and Observe (P&O) Controller
2.5. Hardware
3. Results
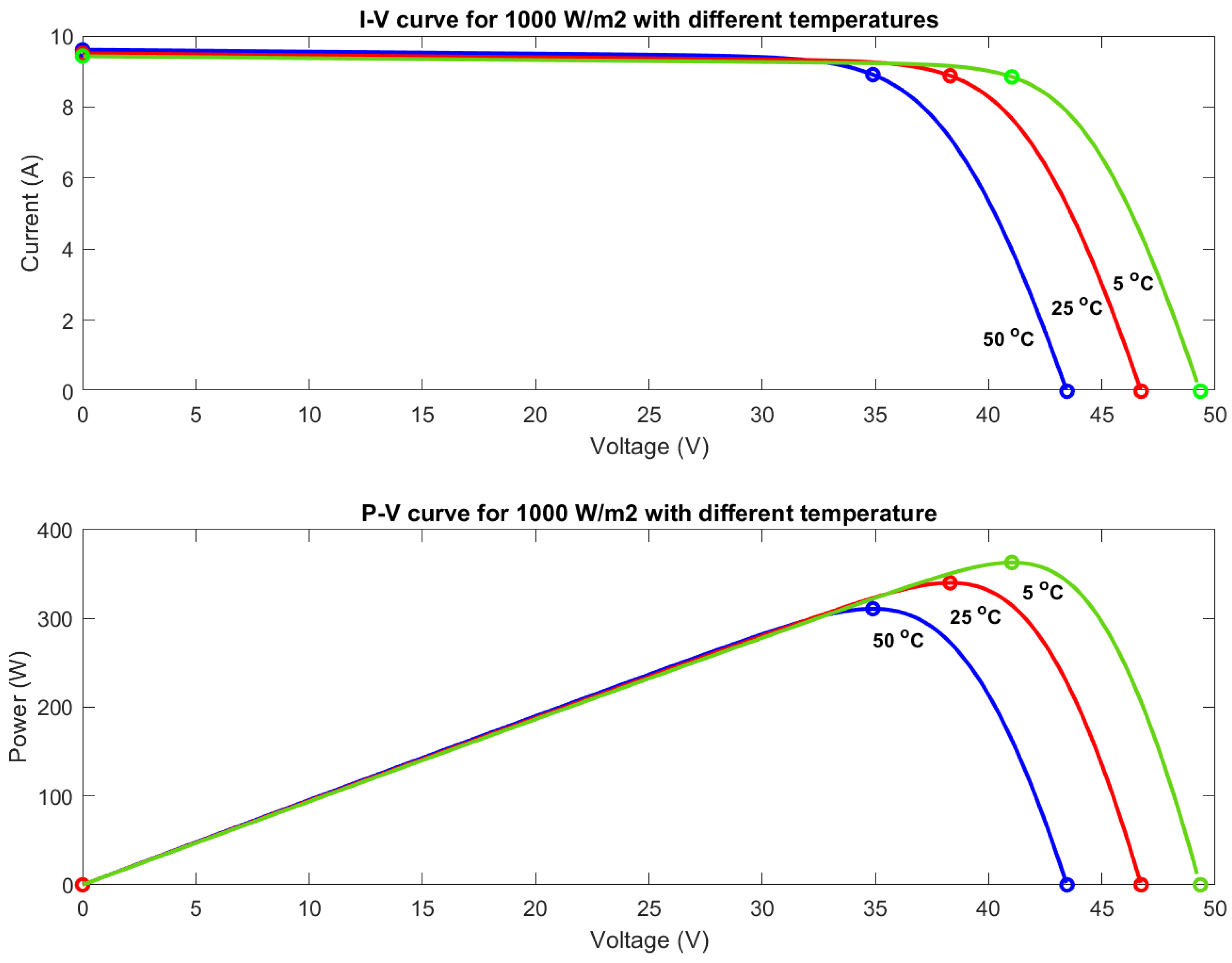
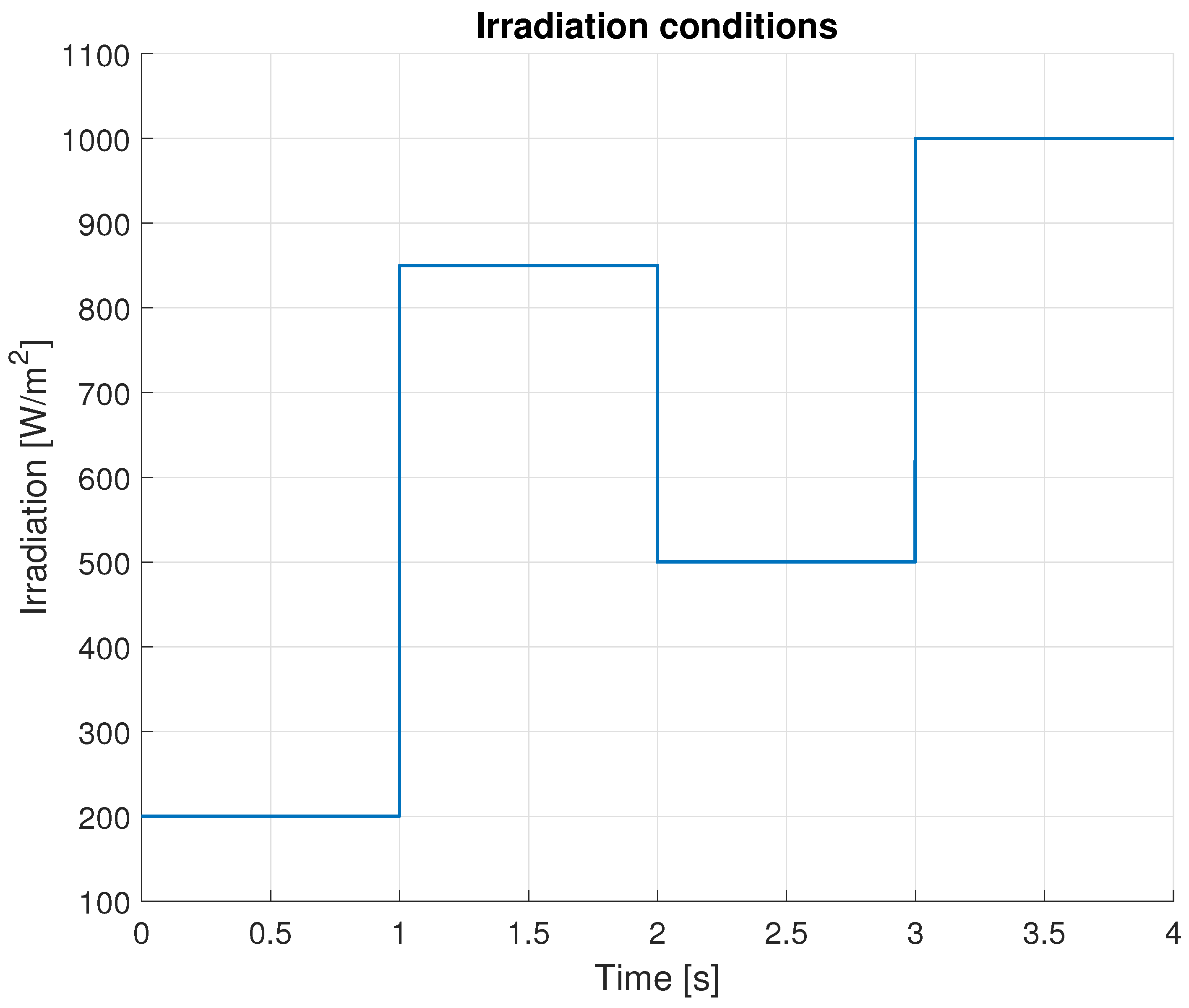
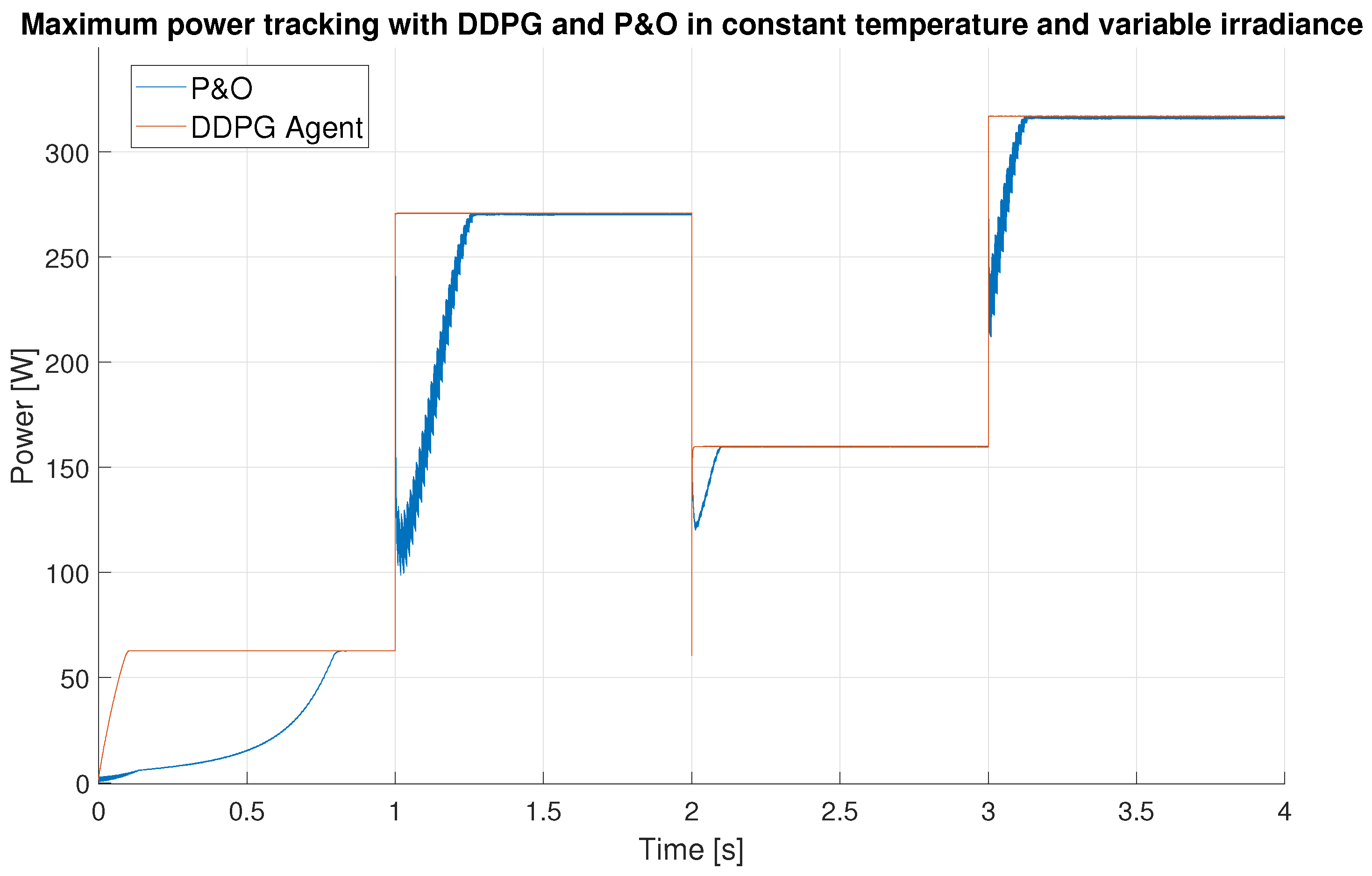
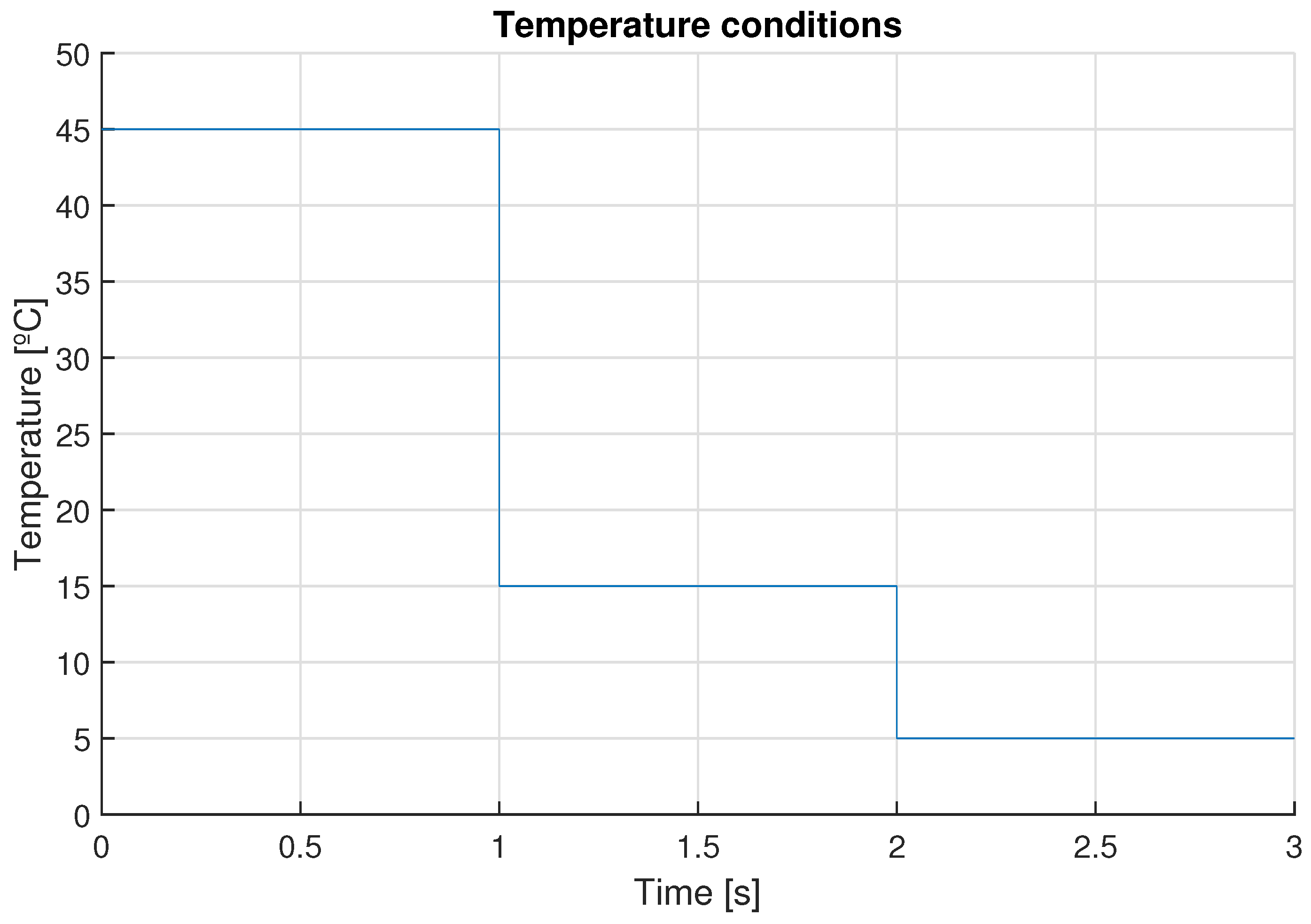
3.1. Simulation Results
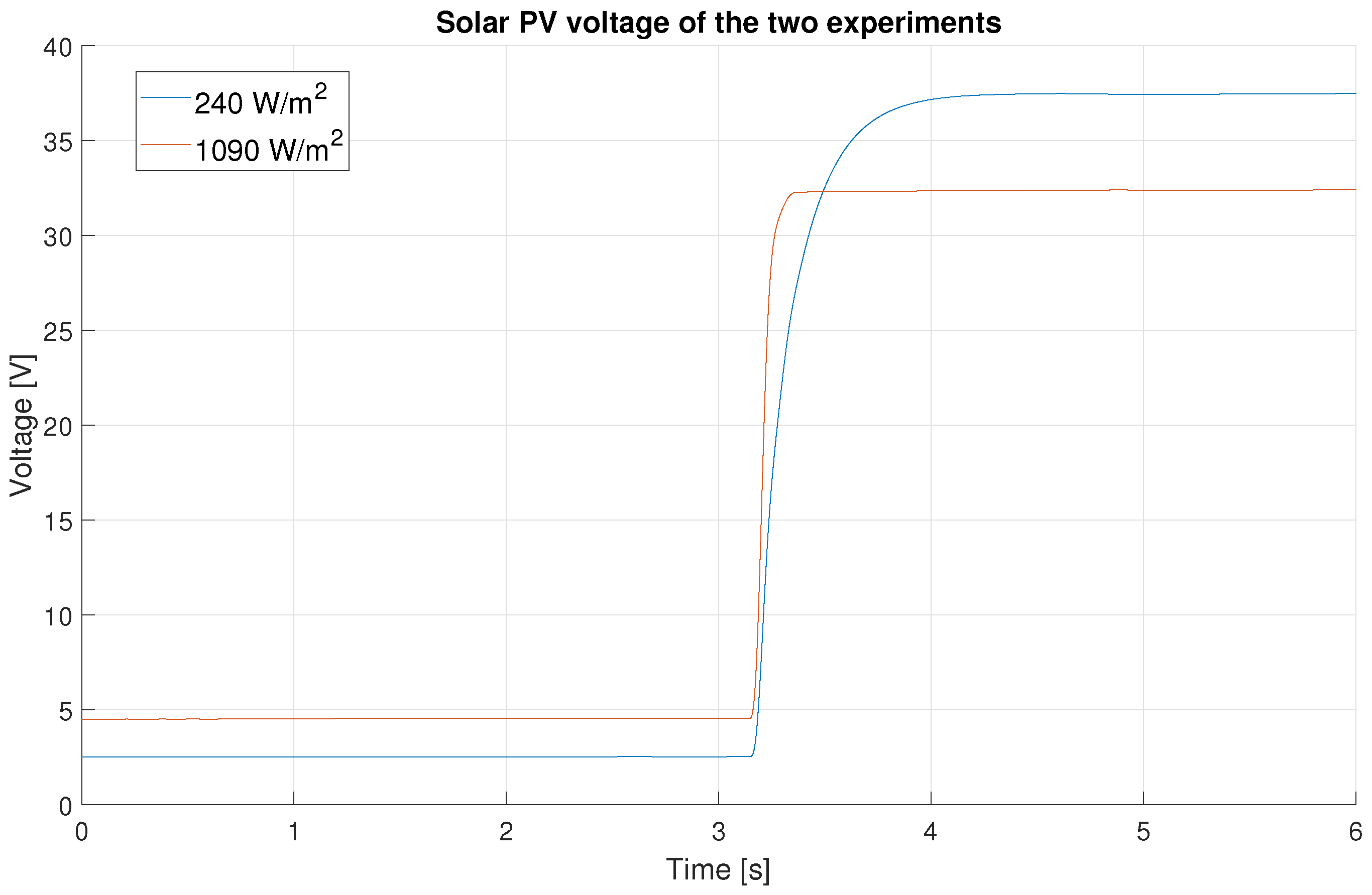
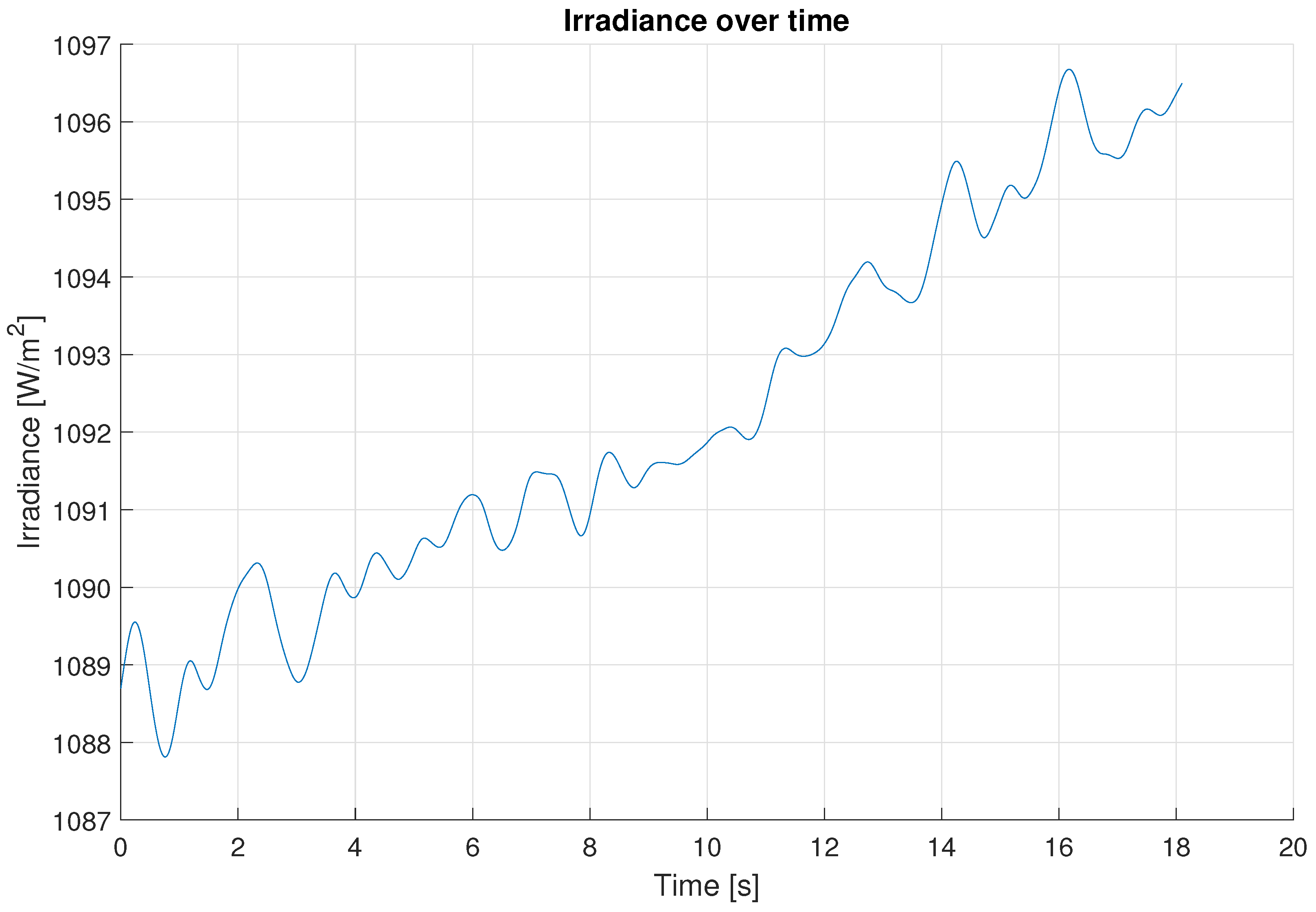
3.2. Real Solar PV Experiments Results
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEA. Energy Statistics Data Browser. 2022. Available online: https://www.iea.org/data-and-statistics/data-tools/energy-statistics-data-browser?country=WORLD&fuel=Energy%20consumption&indicator=TFCbySource (accessed on 18 April 2023).
- IEA. Global Primary Energy Demand Growth by Scenario, 2019–2030. 2022. Available online: https://www.iea.org/data-and-statistics/charts/global-primary-energy-demand-growth-by-scenario-2019-2030 (accessed on 18 April 2023).
- Goman, V.; Prakht, V.; Kazakbaev, V.; Dmitrievskii, V. Comparative Study of Energy Consumption and CO2 Emissions of Variable-Speed Electric Drives with Induction and Synchronous Reluctance Motors in Pump Units. Mathematics 2021, 9, 2679. [Google Scholar] [CrossRef]
- Brauers, H.; Oei, P.Y.; Walk, P. Comparing coal phase-out pathways: The United Kingdom’s and Germany’s diverging transitions. Environ. Innov. Soc. Transit. 2020, 37, 238–253. [Google Scholar] [CrossRef] [PubMed]
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Hrovatin, D.; Žemva, A. Exploiting Solar Energy during an Aerial Mapping Mission on a Lightweight UAV. Electronics 2021, 10, 2876. [Google Scholar] [CrossRef]
- Mukhtar, S.; Gul, T. Solar Radiation and Thermal Convection of Hybrid Nanofluids for the Optimization of Solar Collector. Mathematics 2023, 11, 1175. [Google Scholar] [CrossRef]
- Verduci, R.; Romano, V.; Brunetti, G.; Yaghoobi Nia, N.; Di Carlo, A.; D’Angelo, G.; Ciminelli, C. Solar energy in space applications: Review and technology perspectives. Adv. Energy Mater. 2022, 12, 2200125. [Google Scholar] [CrossRef]
- Alsadi, S.; Khatib, T. Photovoltaic power systems optimization research status: A review of criteria, constrains, models, techniques, and software tools. Appl. Sci. 2018, 8, 1761. [Google Scholar] [CrossRef]
- Parada-Salado, J.G.; Rodríguez-Licea, M.A.; Soriano-Sanchez, A.G.; Ruíz-Martínez, O.F.; Espinosa-Calderon, A.; Pérez-Pinal, F.J. Study on Multiple Input Asymmetric Boost Converters with Simultaneous and Sequential Triggering. Electronics 2021, 10, 1421. [Google Scholar] [CrossRef]
- Troudi, F.; Jouini, H.; Mami, A.; Ben Khedher, N.; Aich, W.; Boudjemline, A.; Boujelbene, M. Comparative Assessment between Five Control Techniques to Optimize the Maximum Power Point Tracking Procedure for PV Systems. Mathematics 2022, 10, 1080. [Google Scholar] [CrossRef]
- Shen, C.L.; Chen, L.Z.; Chuang, T.Y.; Liang, Y.S. Cascaded-like High-Step-Down Converter with Single Switch and Leakage Energy Recycling in Single-Stage Structure. Electronics 2022, 11, 352. [Google Scholar] [CrossRef]
- Danandeh, M.; Mousavi G., S. Comparative and comprehensive review of maximum power point tracking methods for PV cells. Renew. Sustain. Energy Rev. 2018, 82, 2743–2767. [Google Scholar] [CrossRef]
- Petrescu, C.; Sharma, A.K.; Pachauri, R.K.; Choudhury, S.; Minai, A.F.; Alotaibi, M.A.; Malik, H.; Márquez, F.P.G. Role of Metaheuristic Approaches for Implementation of Integrated MPPT-PV Systems: A Comprehensive Study. Mathematics 2023, 11, 269. [Google Scholar] [CrossRef]
- Grieves, M. Completing the Cycle: Using PLM Information in the Sales and Service Functions [Slides]. In Proceedings of the SME Management Forum, Troy, MI, USA, 31 October 2002. [Google Scholar]
- Wang, K.; Ma, J.; Wang, J.; Xu, B.; Tao, Y.; Man, K.L. Digital Twin based Maximum Power Point Estimation for Photovoltaic Systems. In Proceedings of the 2022 19th International SoC Design Conference (ISOCC), Gangneung-si, Republic of Korea, 19–22 October 2022; pp. 189–190. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, X. Digital Twin Modeling for Photovoltaic Panels Based on Hybrid Neural Network. In Proceedings of the 2021 IEEE 1st International Conference on Digital Twins and Parallel Intelligence (DTPI), Beijing, China, 15 July–15 August 2021; pp. 90–93. [Google Scholar] [CrossRef]
- Liu, H.D.; Lu, S.D.; Lee, Y.L.; Lin, C.H. A novel photovoltaic module quick regulate mppt algorithm for uniform irradiation and partial shading conditions. Processes 2021, 9, 2213. [Google Scholar] [CrossRef]
- Yildirim, M.A.; Nowak-Ocłoń, M. Modified maximum power point tracking algorithm under time-varying solar irradiation. Energies 2020, 13, 6722. [Google Scholar] [CrossRef]
- Zafar, M.H.; Al-shahrani, T.; Khan, N.M.; Feroz Mirza, A.; Mansoor, M.; Qadir, M.U.; Khan, M.I.; Naqvi, R.A. Group teaching optimization algorithm based MPPT control of PV systems under partial shading and complex partial shading. Electronics 2020, 9, 1962. [Google Scholar] [CrossRef]
- Ko, J.S.; Huh, J.H.; Kim, J.C. Overview of maximum power point tracking methods for PV system in micro grid. Electronics 2020, 9, 816. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. An enhanced adaptive P&O MPPT for fast and efficient tracking under varying environmental conditions. IEEE Trans. Sustain. Energy 2018, 9, 1487–1496. [Google Scholar]
- Macaulay, J.; Zhou, Z. A fuzzy logical-based variable step size P&O MPPT algorithm for photovoltaic system. Energies 2018, 11, 1340. [Google Scholar] [CrossRef]
- Farhat, M.; Barambones, O.; Sbita, L. A real-time implementation of novel and stable variable step size MPPT. Energies 2020, 13, 4668. [Google Scholar] [CrossRef]
- Alagammal, S.; Rathina Prabha, N. Combination of modified P&O with power management circuit to exploit reliable power from autonomous PV-battery systems. Iran. J. Sci. Technol. Trans. Electr. Eng. 2021, 45, 97–114. [Google Scholar] [CrossRef]
- Mendez, E.; Ortiz, A.; Ponce, P.; Macias, I.; Balderas, D.; Molina, A. Improved MPPT algorithm for photovoltaic systems based on the earthquake optimization algorithm. Energies 2020, 13, 3047. [Google Scholar] [CrossRef]
- Ajani, T.S.; Imoize, A.L.; Atayero, A.A. An overview of machine learning within embedded and mobile devices–optimizations and applications. Sensors 2021, 21, 4412. [Google Scholar] [CrossRef]
- Li, C.; Chen, Y.; Zhou, D.; Liu, J.; Zeng, J. A high-performance adaptive incremental conductance MPPT algorithm for photovoltaic systems. Energies 2016, 9, 288. [Google Scholar] [CrossRef]
- Khan, M.J.; Mathew, L.; Alotaibi, M.A.; Malik, H.; Nassar, M.E. Fuzzy-Logic-Based Comparative Analysis of Different Maximum Power Point Tracking Controllers for Hybrid Renewal Energy Systems. Mathematics 2022, 10, 529. [Google Scholar] [CrossRef]
- Al-Gizi, A.G.; Al-Chlaihawi, S.J. Study of FLC based MPPT in comparison with P&O and InC for PV systems. In Proceedings of the 2016 International Symposium on Fundamentals of Electrical Engineering (ISFEE), Bucharest, Romania, 30 June–2 July 2016; pp. 1–6. [Google Scholar]
- Roy, R.B.; Rokonuzzaman, M.; Amin, N.; Mishu, M.K.; Alahakoon, S.; Rahman, S.; Mithulananthan, N.; Rahman, K.S.; Shakeri, M.; Pasupuleti, J. A comparative performance analysis of ANN algorithms for MPPT energy harvesting in solar PV system. IEEE Access 2021, 9, 102137–102152. [Google Scholar] [CrossRef]
- Kofinas, P.; Doltsinis, S.; Dounis, A.I.; Vouros, G.A. A reinforcement learning approach for MPPT control method of photovoltaic sources. Renew. Energy 2017, 108, 461–473. [Google Scholar] [CrossRef]
- Chou, K.Y.; Yang, S.T.; Chen, Y.P. Maximum Power Point Tracking of Photovoltaic System Based on Reinforcement Learning. Sensors 2019, 19, 5054. [Google Scholar] [CrossRef]
- Singh, Y.; Pal, N. Reinforcement learning with fuzzified reward approach for MPPT control of PV systems. Sustain. Energy Technol. Assess. 2021, 48, 101665. [Google Scholar] [CrossRef]
- Phan, B.C.; Lai, Y.C.; Lin, C.E. A Deep Reinforcement Learning-Based MPPT Control for PV Systems under Partial Shading Condition. Sensors 2020, 20, 3039. [Google Scholar] [CrossRef] [PubMed]
- Nicola, M.; Nicola, C.I.; Selișteanu, D. Improvement of the Control of a Grid Connected Photovoltaic System Based on Synergetic and Sliding Mode Controllers Using a Reinforcement Learning Deep Deterministic Policy Gradient Agent. Energies 2022, 15, 2392. [Google Scholar] [CrossRef]
- Humada, A.M.; Hojabri, M.; Mekhilef, S.; Hamada, H.M. Solar cell parameters extraction based on single and double-diode models: A review. Renew. Sustain. Energy Rev. 2016, 56, 494–509. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar] [CrossRef]
- Raj, A.; Gupta, M. Numerical Simulation and Performance Assessment of ANN-INC Improved Maximum Power Point Tracking System for Solar Photovoltaic System Under Changing Irradiation Operation. Ann. Rom. Soc. Cell Biol. 2021, 25, 790–797. [Google Scholar]




| Properties | Values |
|---|---|
| Sample time | 0.01 |
| Experience buffer length | |
| Mini-batch size | 64 |
| Discount factor () | 0.99 |
| O-U noise variance | 0.15 |
| Smooth factor () | 0.001 |
| Properties | Values | Units |
|---|---|---|
| Dimensions | 156 × 156 | mm |
| Open-circuit voltage | 45 | V |
| Max power voltage | 37 | V |
| Max power current | 9 | A |
| Maximum power | 340 | W |
| Number of parallel cells | 12 | units |
| Number of series cells | 6 | units |
| Isc | 9.9 | A |
| Properties | Values | Units |
|---|---|---|
| Switching frequency | 20 | kHz |
| Max input voltage | 60 | V |
| Max output voltage | 250 | V |
| Max input current | 30 | A |
| Max output current | 30 | A |
| Properties | Values | Units |
|---|---|---|
| Power | 300 | W |
| Operating voltage | 0–120 | V |
| Rated current | 30 | A |
| Load range | 0.1–4 k | Ω |
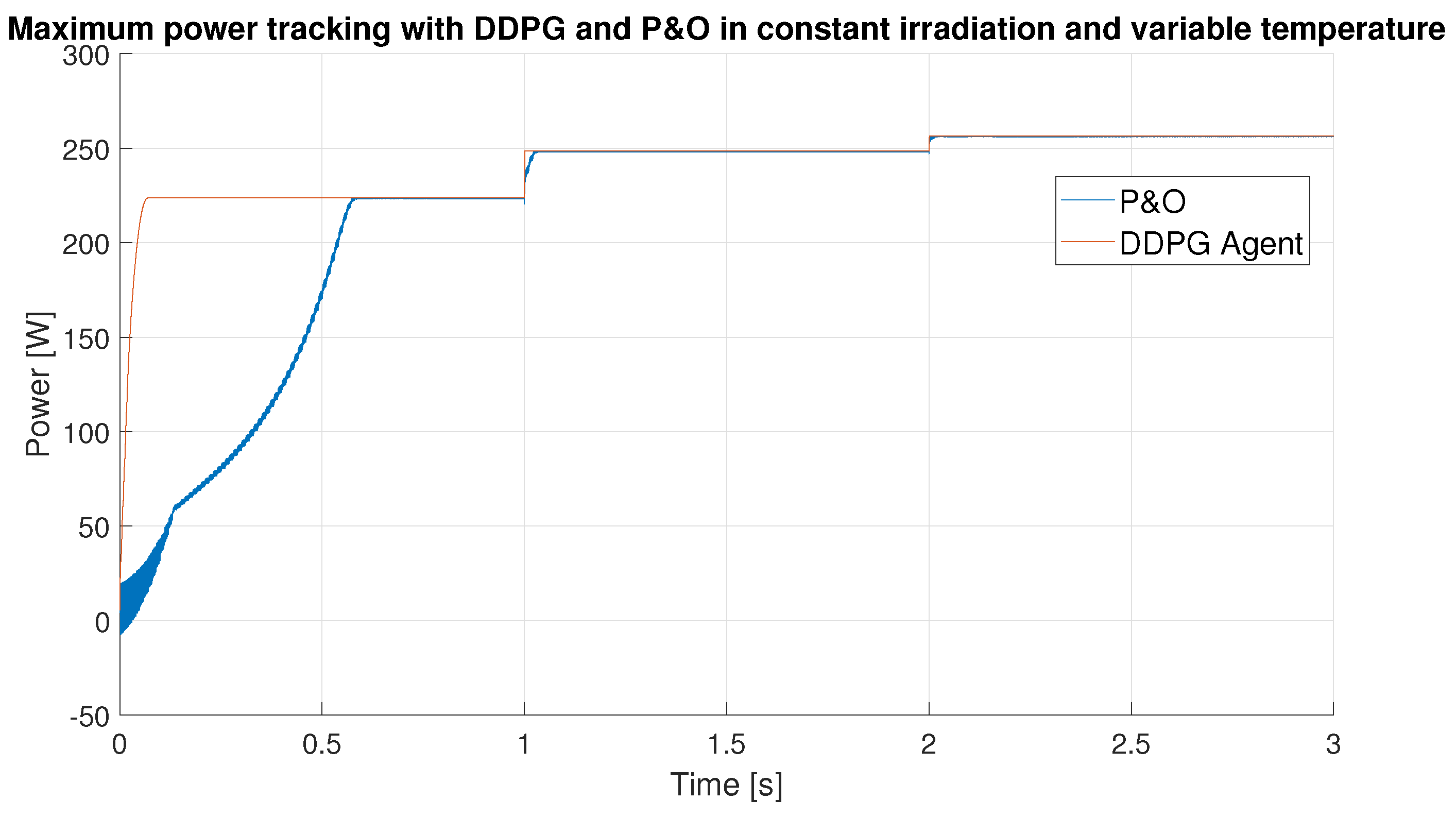
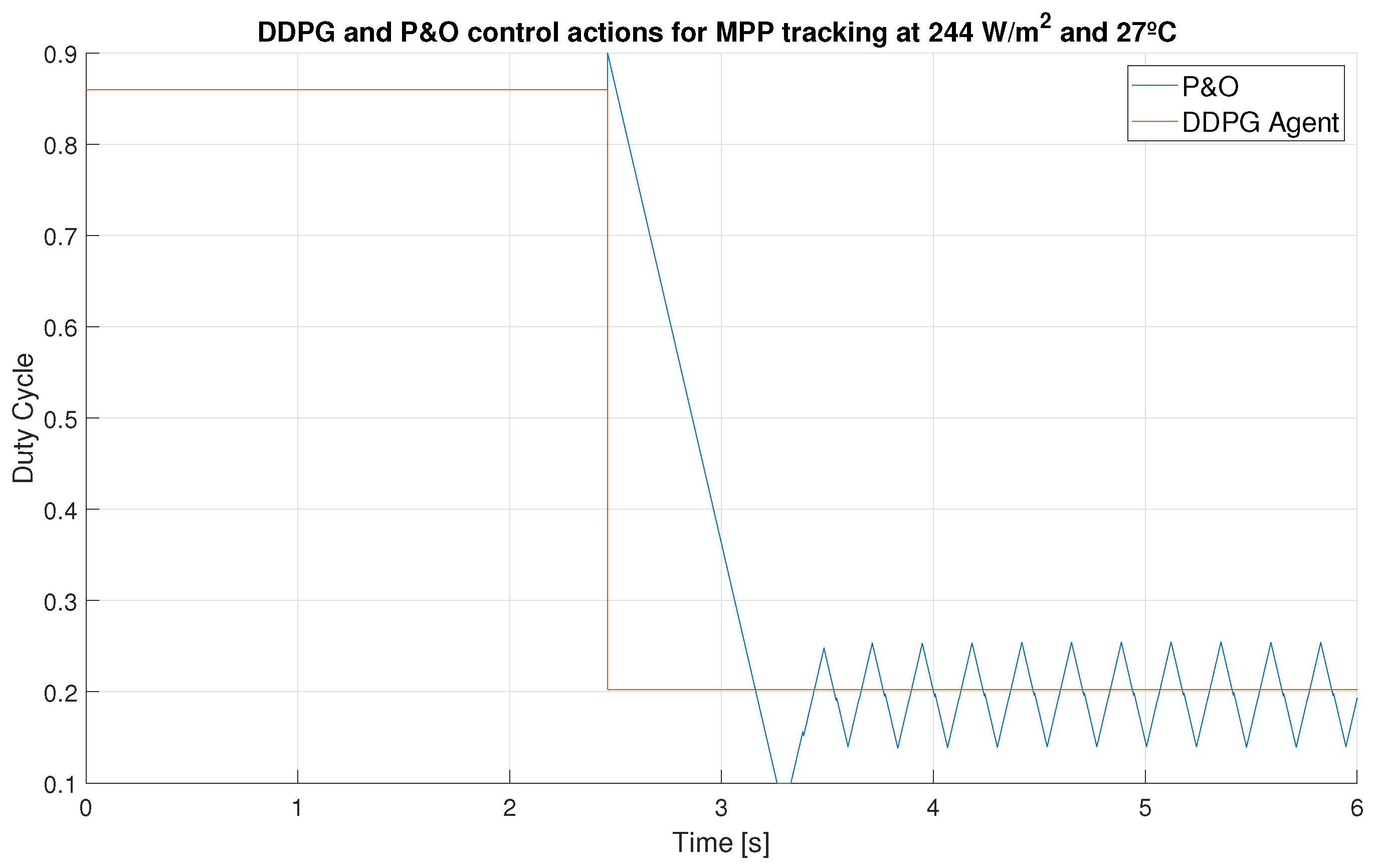
| Step | Step Time (s) | DDPG Settling Time (s) | P&O Settling Time (s) | Settling Time Improvement | Overall Efficiency Improvement |
|---|---|---|---|---|---|
| 1 | 0 | 0.096 | 0.81 | 843% | 8.59% |
| 2 | 1 | 0.011 | 0.28 | 2454% | |
| 3 | 2 | 0.014 | 0.1 | 714% | |
| 4 | 3 | 0.005 | 0.12 | 2400% |
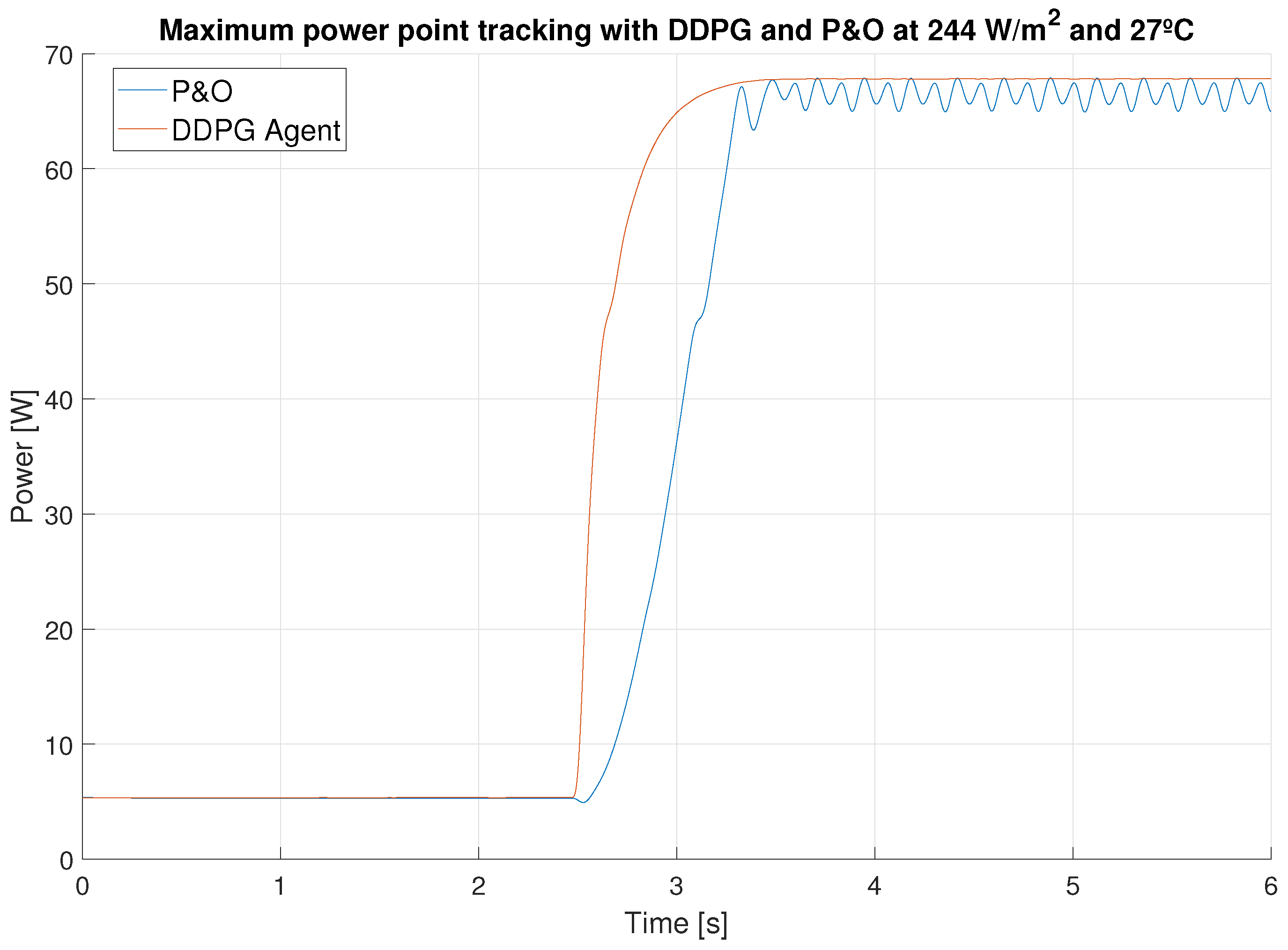
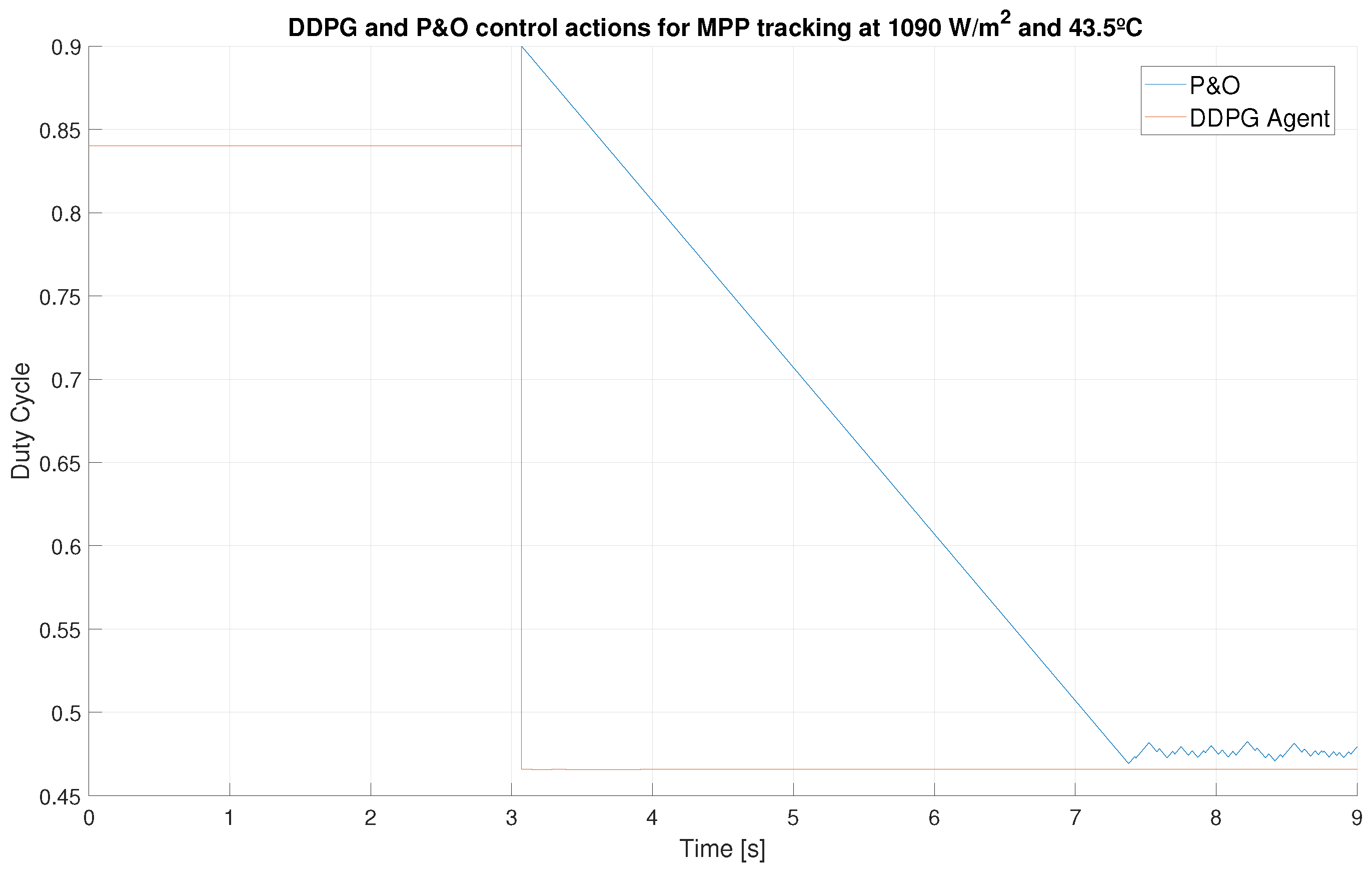
| Step | Step Time (s) | DDPG Settling Time (s) | P&O Settling Time (s) | Settling Time Improvement | Overall Effiency Improvement |
|---|---|---|---|---|---|
| 1 | 0 | 0.06 | 0.58 | 966% | 10.45 % |
| 2 | 1 | 0.003 | 0.32 | 10,667% | |
| 3 | 2 | 0.0025 | 0.012 | 428% |
| Test | Settling Time Improvement | Efficiency Improvement |
|---|---|---|
| 1st Simulation | 2454% | 8.59% |
| 2nd Simulation | 10,667% | 10.45% |
| 1st Real Test | 5% | 11.19% |
| 2nd Real Test | 1704% | 51.45% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Artetxe, E.; Uralde, J.; Barambones, O.; Calvo, I.; Martin, I. Maximum Power Point Tracker Controller for Solar Photovoltaic Based on Reinforcement Learning Agent with a Digital Twin. Mathematics 2023, 11, 2166. https://doi.org/10.3390/math11092166
Artetxe E, Uralde J, Barambones O, Calvo I, Martin I. Maximum Power Point Tracker Controller for Solar Photovoltaic Based on Reinforcement Learning Agent with a Digital Twin. Mathematics. 2023; 11(9):2166. https://doi.org/10.3390/math11092166
Chicago/Turabian StyleArtetxe, Eneko, Jokin Uralde, Oscar Barambones, Isidro Calvo, and Imanol Martin. 2023. "Maximum Power Point Tracker Controller for Solar Photovoltaic Based on Reinforcement Learning Agent with a Digital Twin" Mathematics 11, no. 9: 2166. https://doi.org/10.3390/math11092166
APA StyleArtetxe, E., Uralde, J., Barambones, O., Calvo, I., & Martin, I. (2023). Maximum Power Point Tracker Controller for Solar Photovoltaic Based on Reinforcement Learning Agent with a Digital Twin. Mathematics, 11(9), 2166. https://doi.org/10.3390/math11092166








