Modeling, Analysis and Evaluation of a Novel Compact 6-DoF 3-RRRS Needle Biopsy Robot
Abstract
:1. Introduction
1.1. Application Background
1.2. Related Works
1.3. Brief Summary
- (1)
- A kinematic model is established for a structure-specific parallel robot, which can be used to analytically solve its nonlinear kinematics problems and allows for fast and accurate feedback control calculations, including forward kinematics, inverse kinematics, and differential kinematics.
- (2)
- The correctness of the derivation kinematics is verified via a Simscape simulation model and a prototype. The results show that the model has high accuracy of robot calculation.
- (3)
- The first prototype was built based on simulation experiments. The rationality of the kinematic model we established was illustrated by demonstrating a puncture case.
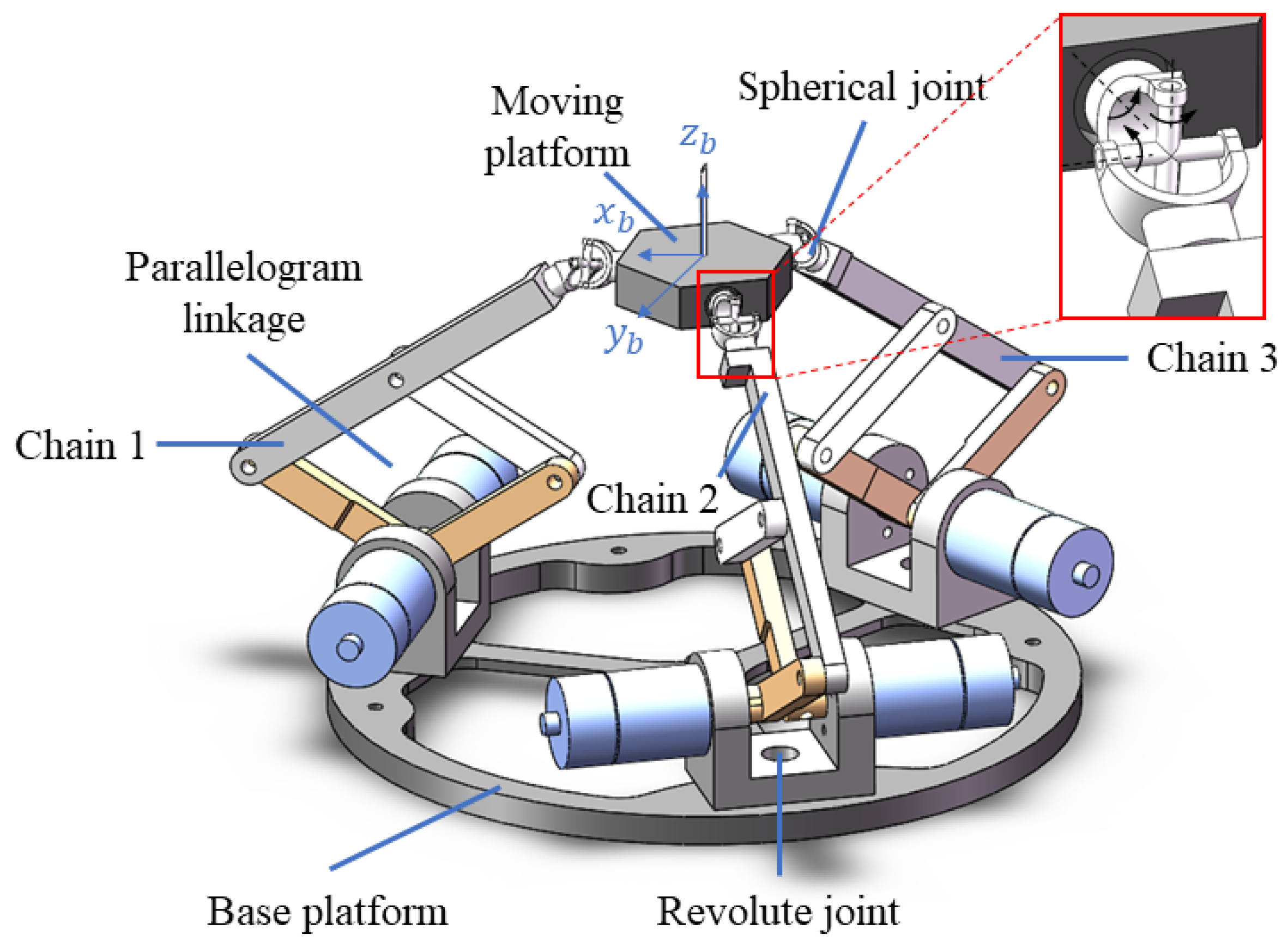
2. Design of the 3-RRRS Parallel Needle Biopsy Robot
2.1. Mechanical Structure
2.2. Degree of Freedom Analysis
2.3. Workspace Analysis
3. Kinematic Modeling
3.1. Inverse Kinematics
3.2. Forward Kinematics
3.3. Jacobian Matrix and Velocity-Level Kinematics
4. Singularity Analysis
4.1. Chain Singularity
4.2. Platform Singularity
- (1)
- If any passive joint axis passes precisely through its corresponding attachment point on the moving platform, a platform singularity occurs, as illustrated in Figure 5b. In this scenario, the velocity contribution of this passive joint to the velocity of the platform connection point diminishes. This singularity configuration is a consequence of particular robot structures and manifests across all configurations within the entire robot workspace. Therefore, this structural singularity can be circumvented through meticulous design considerations.
- (2)
- Considering the case where three driving links align in a straight line within a shared plane: Let and represent lines parallel to the driving links that traverse through point . A singularity configuration arises when line or of the jth supporting chain is part of supporting chain plane i and passes through point . Consequently, lines or must align with the edge of the moving platform. This circumstance is only realized when planes i and j coincide, as depicted in Figure 5c.
- (3)
- Considering the scenario of three interrelated supporting chains: when the constraint forces of the three supporting chains exhibit linear dependence, according to Grassmann linear geometry, it can be elucidated that the three supporting chain planes , , and share a common intersection line, as illustrated in Figure 5d. When the normal vectors of the three planes 1, 2 and 3 are coplanar, it satisfiesAccording to Equation (22), the conditions for the occurrence of such singularity are
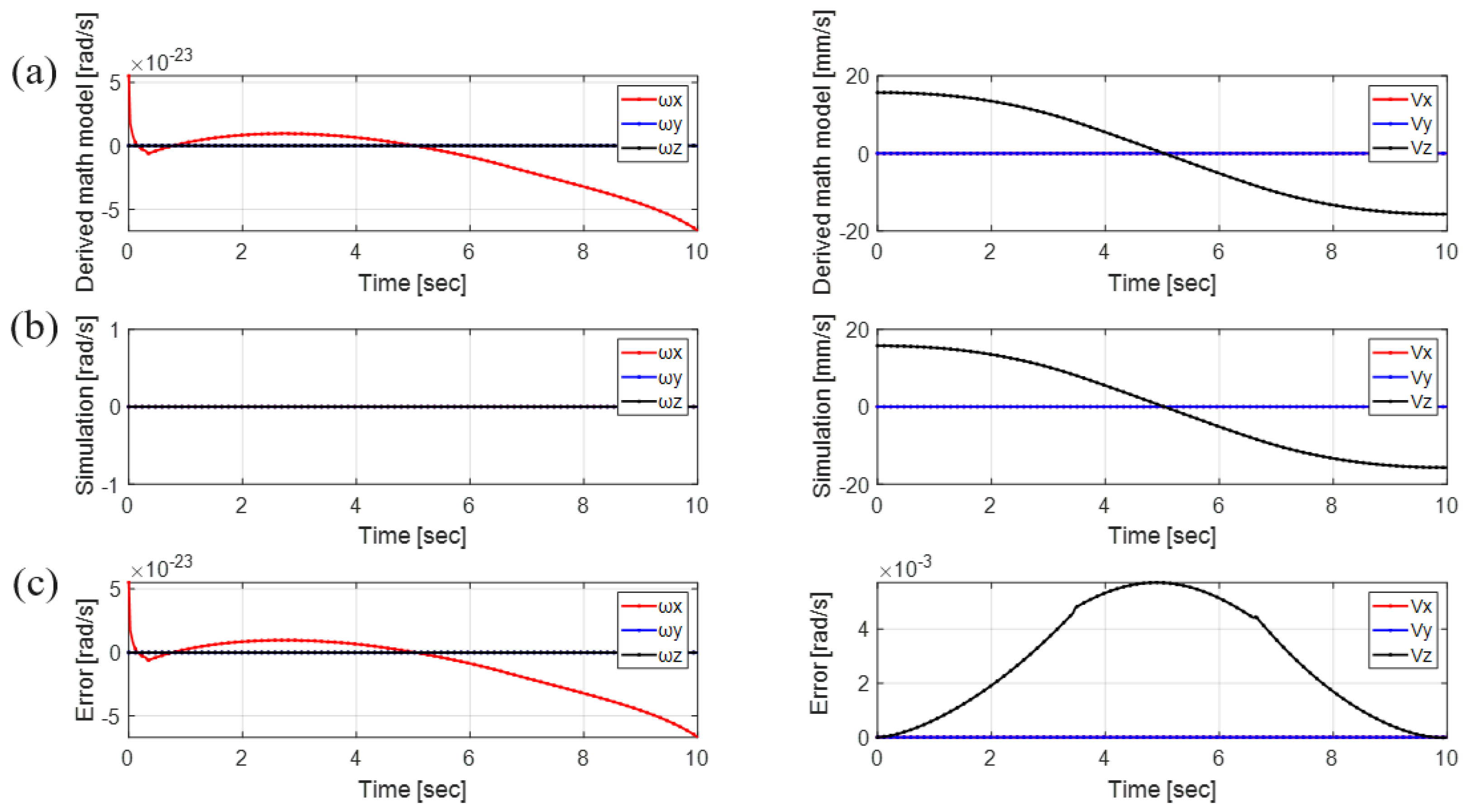
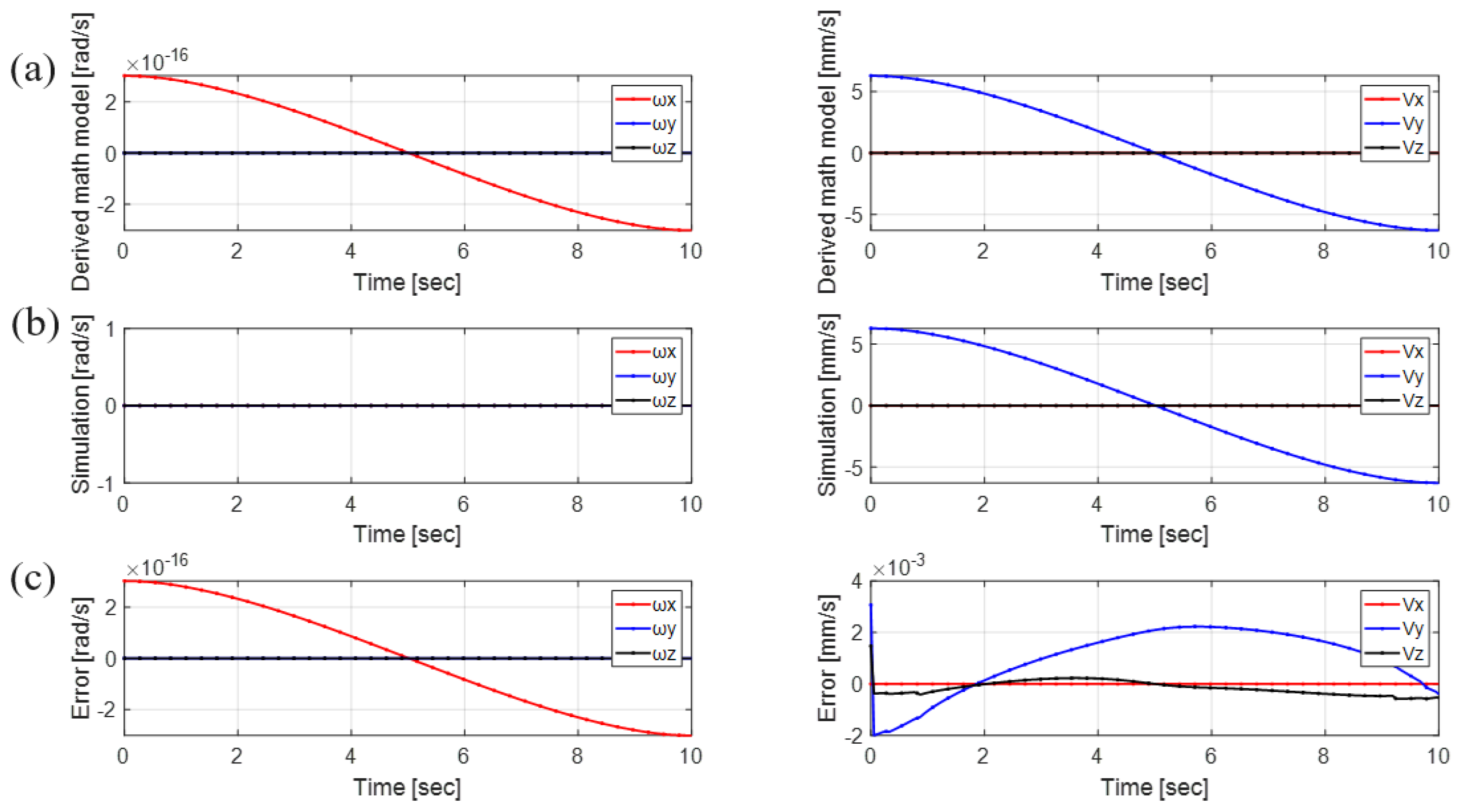
5. Simulation Experiments
5.1. Simulation Platform Setup
5.2. Simulation Test
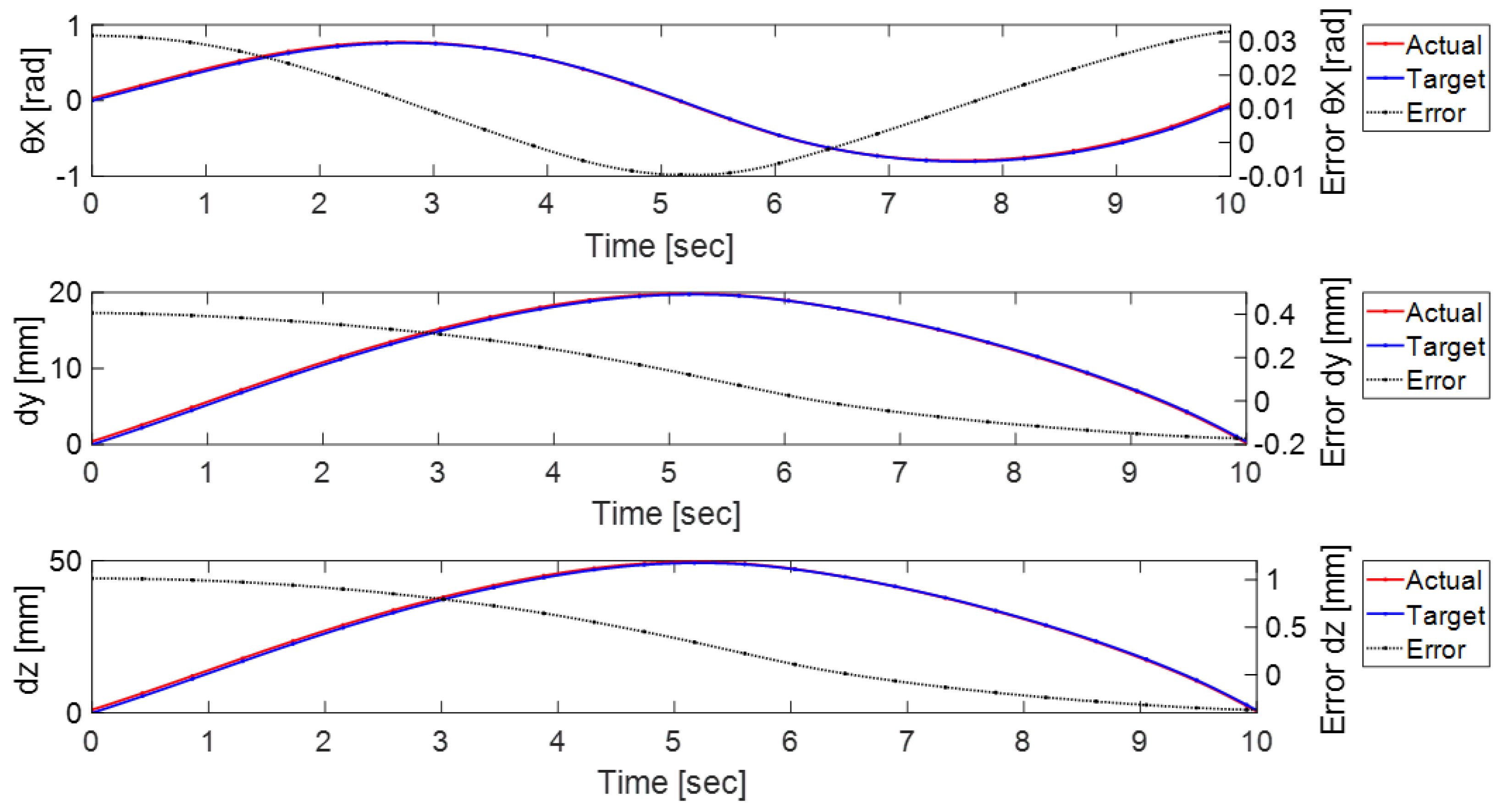
6. Prototype Experiments
6.1. Prototype Platform Setup
6.2. Realtime Robot Configuration Measurement Based on ArUco Tag
6.3. Experiment Results
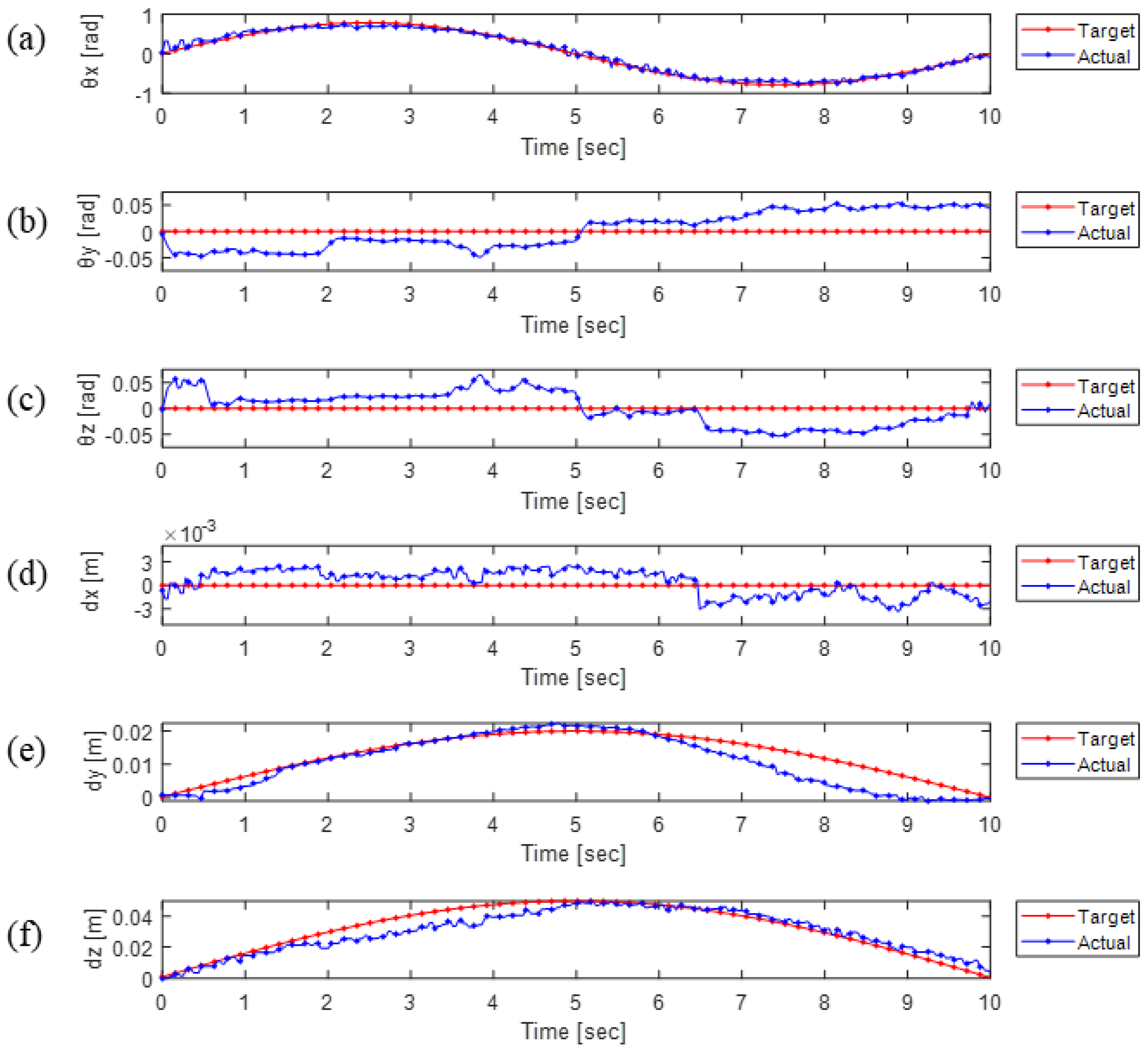
6.4. Puncture Experiment Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation
| Position vector of point relative to base platform | |
| Position vector of point relative to moving platform | |
| Position vector of point relative to base platform | |
| c | Number of parts in the mechanism |
| Line parallel to the driving links that traverse through point | |
| Degrees of freedom of joint k | |
| Singular value decomposition correlation matrix | |
| g | Number of joints |
| Jacobian coefficient matrix | |
| m | Degrees of freedom |
| Set of 3D points connected to the moving platform | |
| Direction of the moving platform represented by the normal vector | |
| Position vector of moving platform relative to base platform | |
| Attachment point between chain and platform | |
| Attachment point between chain and base | |
| Circumscribed circle radii of the moving platform | |
| Circumscribed circle radii of the base platform | |
| relative to base platform | |
| Velocity of the connection point of the moving platform | |
| Velocity component of perpendicular to the supporting chain plane | |
| Rotation matrix of moving platform relative to base platform | |
| Length of connecting rod i | |
| Homogeneous transformation matrix of the ArUco tag coordinate system relative to the camera | |
| Unit vector in the x-axis direction of chain i | |
| Rotation angle of the moving platform around the rotation axis | |
| Active rotational joint angle | |
| Passive rotational joint angle of chain i | |
| Active rotational joint angle of chain i | |
| Rotation matrix of moving platform relative to base platform | |
| Rotating axis of the moving platform | |
| Screw system of the i th supporting chain | |
| The plane in which supporting chain i is located | |
| Euler angle describing the direction of the moving platform |
Appendix A
Appendix A.1. Calculation of the forward Kinematics Model
Appendix A.2. Jacobian Analysis of Differential Kinematics
References
- Su, H.; Kwok, K.W.; Cleary, K.; Iordachita, I.; Cavusoglu, M.C.; Desai, J.P.; Fischer, G.S. State of the art and future opportunities in MRI-guided robot-assisted surgery and interventions. Proc. IEEE 2022, 110, 968–992. [Google Scholar] [CrossRef] [PubMed]
- Pan, Z.; Zhu, J.; Zhang, J.; Li, W.; Jia, G.; Luo, W.; Peng, J.; Li, M. An Eye Gaze Controlled Needle Deployment Robot: Design, Modeling and Experimental Evaluation. IEEE Trans. Instrum. Meas. 2024, 73, 3370751. [Google Scholar] [CrossRef]
- Siepel, F.J.; Maris, B.; Welleweerd, M.K.; Groenhuis, V.; Fiorini, P.; Stramigioli, S. Needle and biopsy robots: A review. Curr. Robot. Rep. 2021, 2, 73–84. [Google Scholar] [CrossRef]
- D’Souza, M.; Gendreau, J.; Feng, A.; Kim, L.H.; Ho, A.L.; Veeravagu, A. Robotic-assisted spine surgery: History, efficacy, cost, and future trends. Robot. Surg. Res. Rev. 2019, 6, 9–23. [Google Scholar] [CrossRef] [PubMed]
- Groenhuis, V.; Veltman, J.; Siepel, F.J.; Stramigioli, S. Stormram 3: A magnetic resonance imaging-compatible robotic system for breast biopsy. IEEE Robot. Autom. Mag. 2017, 24, 34–41. [Google Scholar] [CrossRef]
- Stoianovici, D.; Kim, C.; Petrisor, D.; Jun, C.; Lim, S.; Ball, M.W.; Ross, A.; Macura, K.J.; Allaf, M.E. MR safe robot, FDA clearance, safety and feasibility of prostate biopsy clinical trial. IEEE/ASME Trans. Mechatron. 2016, 22, 115–126. [Google Scholar] [CrossRef] [PubMed]
- Su, H.; Zervas, M.; Cole, G.A.; Furlong, C.; Fischer, G.S. Real-time MRI-guided needle placement robot with integrated fiber optic force sensing. In Proceedings of the 2011 IEEE International Conference on Robotics And Automation, Shanghai, China, 9–13 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1583–1588. [Google Scholar]
- Chen, Y.; Squires, A.; Seifabadi, R.; Xu, S.; Agarwal, H.K.; Bernardo, M.; Pinto, P.A.; Choyke, P.; Wood, B.; Tse, Z.T.H. Robotic system for MRI-guided focal laser ablation in the prostate. IEEE/ASME Trans. Mechatron. 2016, 22, 107–114. [Google Scholar] [CrossRef]
- Li, G.; Patel, N.A.; Liu, W.; Wu, D.; Sharma, K.; Cleary, K.; Fritz, J.; Iordachita, I. A fully actuated body-mounted robotic assistant for mri-guided low back pain injection. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 5495–5501. [Google Scholar]
- Pan, Z.; Jia, G.; Zhu, J.; Wang, J.; Luo, W.; Li, M. Design and Implementation of A Novel 4-DoF Robot for Assisted Needle Puncture Deployment. In Proceedings of the 2023 International Conference on Frontiers of Robotics and Software Engineering (FRSE), Changsha, China, 16–18 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 9–15. [Google Scholar]
- Stoianovici, D.; Kim, C.; Schäfer, F.; Huang, C.M.; Zuo, Y.; Petrisor, D.; Han, M. Endocavity ultrasound probe manipulators. IEEE/ASME Trans. Mechatron. 2012, 18, 914–921. [Google Scholar] [CrossRef]
- Nycz, C.J.; Gondokaryono, R.; Carvalho, P.; Patel, N.; Wartenberg, M.; Pilitsis, J.G.; Fischer, G.S. Mechanical validation of an MRI compatible stereotactic neurosurgery robot in preparation for pre-clinical trials. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1677–1684. [Google Scholar]
- Schreiber, D.A.; Shak, D.B.; Norbash, A.M.; Yip, M.C. An open-source 7-axis, robotic platform to enable dexterous procedures within CT scanners. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 386–393. [Google Scholar]
- Cheng, S.S.; Wang, X.; Jeong, S.; Kole, M.; Roys, S.; Gullapalli, R.P. Mechanical design and evaluation of a selectively-actuated MRI-compatible continuum neurosurgical robot. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 2498–2503. [Google Scholar]
- Welleweerd, M.K.; Siepel, F.J.; Groenhuis, V.; Veltman, J.; Stramigioli, S. Design of an end-effector for robot-assisted ultrasound-guided breast biopsies. Int. J. Comput. Assist. Radiol. Surg. 2020, 15, 681–690. [Google Scholar] [CrossRef]
- Gosselin, C.; Merlet, J. Parallel robots: Architecture, modeling, and design. In Encyclopedia of Robotics; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–6. [Google Scholar]
- Eslami, S.; Shang, W.; Li, G.; Patel, N.; Fischer, G.S.; Tokuda, J.; Hata, N.; Tempany, C.M.; Iordachita, I. In-bore prostate transperineal interventions with an MRI-guided parallel manipulator: System development and preliminary evaluation. Int. J. Med Robot. Comput. Assist. Surg. 2016, 12, 199–213. [Google Scholar] [CrossRef]
- Orhan, S.O.; Yildirim, M.C.; Bebek, O. Design and modeling of a parallel robot for ultrasound guided percutaneous needle interventions. In Proceedings of the IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 005002–005007. [Google Scholar]
- Moreira, P.; van de Steeg, G.; Krabben, T.; Zandman, J.; Hekman, E.E.; van der Heijden, F.; Borra, R.; Misra, S. The miriam robot: A novel robotic system for mr-guided needle insertion in the prostate. J. Med. Robot. Res. 2017, 2, 1750006. [Google Scholar] [CrossRef]
- Wang, X.; Ye, Y.; Pan, Z.; Wang, J.; Guo, R.; Li, M. Design and Kinematic Analysis of a 6-DoF Parallel Robot for Image-Guided Surgery. In Proceedings of the 2023 China Automation Congress (CAC), Chongqing, China, 17–19 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 2677–2682. [Google Scholar]
- Musa, M.; Sengupta, S.; Chen, Y. Design of a 6 dof parallel robot for mri-guided interventions. In Proceedings of the 2021 International Symposium on Medical Robotics (ISMR), Atlanta, GA, USA, 17–19 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–7. [Google Scholar]
- Huang, W.; Dai, S.; Xu, A.; He, X.; Huang, S.; Gao, A. Pneumatically actuated mr-safe parallel robot for deep brain stimulation electrode implantation. In Proceedings of the 2021 IEEE International Conference on Robotics and Biomimetics (ROBIO), Sanya, China, 27–31 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1743–1748. [Google Scholar]
- Monfaredi, R.; Cleary, K.; Sharma, K. MRI robots for needle-based interventions: Systems and technology. Ann. Biomed. Eng. 2018, 46, 1479–1497. [Google Scholar] [CrossRef]
- Michiels, C.; Jambon, E.; Bernhard, J. Measurement of the accuracy of 3D-printed medical models to be used for robot-assisted partial nephrectomy. Am. J. Roentgenol. 2019, 213, 626–631. [Google Scholar] [CrossRef] [PubMed]
- Li, M. Design and stability analysis of a nonlinear controller for MRI-compatible pneumatic motors. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 3–17. [Google Scholar] [CrossRef]
- Taghirad, H.D. Parallel Robots: Mechanics and Control; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Monsarrat, B.; Gosselin, C.M. Singularity analysis of a three-leg six-degree-of-freedom parallel platform mechanism based on Grassmann line geometry. Int. J. Robot. Res. 2001, 20, 312–328. [Google Scholar] [CrossRef]
- Monsarrat, B.; Gosselin, C.M. Workspace analysis and optimal design of a 3-leg 6-DOF parallel platform mechanism. IEEE Trans. Robot. Autom. 2003, 19, 954–966. [Google Scholar] [CrossRef]
- Takeda, Y.; Xiao, X.; Hirose, K.; Yoshida, Y.; Ichiryu, K. Kinematic analysis and design of 3-RPSR parallel mechanism with triple revolute joints on the base. Int. J. Autom. Technol. 2010, 4, 346–354. [Google Scholar] [CrossRef]
- Nguyen, A.V.; Bouzgarrou, B.C.; Charlet, K.; Béakou, A. Static and dynamic characterization of the 6-Dofs parallel robot 3CRS. Mech. Mach. Theory 2015, 93, 65–82. [Google Scholar] [CrossRef]
- Li, W.; Angeles, J. A novel three-loop parallel robot with full mobility: Kinematics, singularity, workspace, and dexterity analysis. J. Mech. Robot. 2017, 9, 051003. [Google Scholar] [CrossRef]
- Yiğit, A.; Breton, D.; Zhou, Z.; Laliberté, T.; Gosselin, C. Kinematic Analysis and Design of a Novel (6+ 3)-DoF Parallel Robot with Fixed Actuators. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 9693–9699. [Google Scholar]
- Chen, Y.; Godage, I.S.; Sengupta, S.; Liu, C.L.; Weaver, K.D.; Barth, E.J. MR-conditional steerable needle robot for intracerebral hemorrhage removal. Int. J. Comput. Assist. Radiol. Surg. 2019, 14, 105–115. [Google Scholar] [CrossRef]
- Ebert-Uphoff, I.; Gosselin, C.M. Kinematic study of a new type of spatial parallel platform mechanism. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Atlanta, GA, USA, 13–16 September 1998; American Society of Mechanical Engineers: New York, NY, USA, 1998; Volume 80302, p. V01AT01A020. [Google Scholar]
- Akritas, A.G.; Malaschonok, G.I. Applications of singular-value decomposition (SVD). Math. Comput. Simul. 2004, 67, 15–31. [Google Scholar] [CrossRef]
- Kim, J.; Gosselin, C. A Kinematically Redundant (6+ 1)-dof Hybrid Parallel Robot for Delicate Physical Environment and Robot Interaction (pERI). In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 9679–9685. [Google Scholar]
- Slavutin, M.; Shai, O.; Sheffer, A.; Reich, Y. A novel criterion for singularity analysis of parallel mechanisms. Mech. Mach. Theory 2019, 137, 459–475. [Google Scholar] [CrossRef]
- Chen, Q.; Li, M.; Wu, H.; Liu, W.; Peng, J. Design, self-calibration and compliance control of modular cable-driven snake-like manipulators. Mech. Mach. Theory 2024, 193, 105562. [Google Scholar] [CrossRef]
- Qiu, Q.; Zhu, J.; Gou, C.; Li, M. Eye gaze estimation based on stacked hourglass neural network for aircraft helmet aiming. Int. J. Aerosp. Eng. 2022, 2022. [Google Scholar] [CrossRef]
- Zhang, Z. Flexible camera calibration by viewing a plane from unknown orientations. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; IEEE: Piscataway, NJ, USA, 1999; Volume 1, pp. 666–673. [Google Scholar]
- Zhu, J.H.; Wang, J.; Wang, Y.G.; Li, M.; Guo, Y.X.; Liu, X.J.; Guo, C.B. Performance of robotic assistance for skull base biopsy: A phantom study. J. Neurol. Surg. Part B Skull Base 2017, 78, 385–392. [Google Scholar] [CrossRef] [PubMed]
- Carai, A.; Mastronuzzi, A.; De Benedictis, A.; Messina, R.; Cacchione, A.; Miele, E.; Randi, F.; Esposito, G.; Trezza, A.; Colafati, G.S.; et al. Robot-assisted stereotactic biopsy of diffuse intrinsic pontine glioma: A single-center experience. World Neurosurg. 2017, 101, 584–588. [Google Scholar] [CrossRef] [PubMed]
- Groenhuis, V.; Siepel, F.J.; Veltman, J.; van Zandwijk, J.K.; Stramigioli, S. Stormram 4: An MR safe robotic system for breast biopsy. Ann. Biomed. Eng. 2018, 46, 1686–1696. [Google Scholar] [CrossRef] [PubMed]
- Navarro-Alarcon, D.; Singh, S.; Zhang, T.; Chung, H.L.; Ng, K.W.; Chow, M.K.; Liu, Y. Developing a compact robotic needle driver for MRI-guided breast biopsy in tight environments. IEEE Robot. Autom. Lett. 2017, 2, 1648–1655. [Google Scholar] [CrossRef]
- Zhang, T.; Wen, Y.; Liu, Y.H. Developing a parallel robot for MRI-guided breast intervention. IEEE Trans. Med Robot. Bionics 2019, 2, 17–27. [Google Scholar] [CrossRef]
- Liu, W.; Yang, Z.; Jiang, S.; Feng, D.; Zhang, D. Design and implementation of a new cable-driven robot for MRI-guided breast biopsy. Int. J. Med Robot. Comput. Assist. Surg. 2020, 16, e2063. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, C.; Du, H.; Gu, B.; Yu, Y. A MRI compatible robot for breast intervention. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics (ROBIO), Zhuhai, China, 6–9 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 2472–2477. [Google Scholar]
- Hungr, N.; Bricault, I.; Cinquin, P.; Fouard, C. Design and validation of a CT-and MRI-guided robot for percutaneous needle procedures. IEEE Trans. Robot. 2016, 32, 973–987. [Google Scholar] [CrossRef]
- Alvara, A.N.; Looi, T.; Saab, R.; Shorter, A.; Goldenberg, A.; Drake, J. Development and validation of MRI compatible pediatric surgical robot with modular tooling for bone biopsy. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 4935–4941. [Google Scholar]
- Pan, Z.; Ye, Y.; Wang, J.; Wang, X.; Zhang, J.; Peng, J.; Li, M. Cornerstone for MRI-compatible robots: A continuous pneumatic actuator with easy-to-connect prismatic/revolute and bidirectional encoder modules. Measurement 2024, 232, 114685. [Google Scholar] [CrossRef]










| Items | Specifications (mm) |
|---|---|
| 80 | |
| 31.8 | |
| 50 | |
| 50 | |
| 62.5 | |
| 33.28 |
| Focus (mm) | |
| Center column () (pixel) | 340.4478 |
| Center row () (pixel) | 213.4719 |
| 2nd-order radial distortion (K1) (1/pixel2) | −0.3401 |
| 4th-order radial distortion (K2) (1/pixel4) | 0.1350 |
| 6th-order radial distortion (K3) (1/pixel6) | −0.0270 |
| 2nd-order tangential distortion (P1) (1/pixel2) | 0 |
| 2nd-order tangential distortion (P2) (1/pixel2) | 0 |
| Image width (pixel) | 640 |
| Image height (pixel) | 480 |
| Reprojection error (pixel) | 0.1172 |
| Robot System | Imaging | Mech Actuation | DoF | Accuracy | Control Modes 1 | ||||
|---|---|---|---|---|---|---|---|---|---|
| (mm) | P | C | T | ||||||
| Robot assistance skull base biopsy | [41] | CBCT | Electric | 5 | (0.56–1.73) | ✓ | |||
| Robot-assisted stereotactic biopsy | [42] | MRI/CT | Electric | 6 | Feasible | ✓ | |||
| Stormram 3: a MRI- compatible robotic system | [5] | MRI | Pneumatic | 5 | (2) | ✓ | |||
| Stormram 4: an MR- safe robotic system | [43] | MRI | Pneumatic | 4 | (1.29) | ✓ | ✓ | ||
| Compact robotic needle driver for MRI-guided biopsy | [44] | MRI | Piezoelectric and pneumatic actuation | 3 | Demonstration of functionality | ✓ | ✓ | ||
| Parallel robot for MRI- guided intervention | [45] | MRI | Cable-actuated system and piezoelectric motors | 2 | (0.84–1.99) | ✓ | |||
| Cable-driven robot for MRI-guided breast biopsy | [46] | MRI | Ultrasonic motors | 3 | (0.7) | ✓ | ✓ | ||
| MRI-compatible robot for intervention | [47] | MRI | Cables, belts | 7 | N/A | ✓ | ✓ | ||
| CT- and MRI-guided robot for percutaneous needle procedures | [48] | MRI/CT | Ultrasonic, Bowden cables, and pneumatics | 5 | (3.3 ± 1.7) | ✓ | ✓ | ||
| MRI-safe robot for biopsy MrBot | [6] | MRI | Pneumatic | 6 | (2.55) | ✓ | ✓ | ||
| MRI-compatible pediatric surgical robot with modular tooling for bone biopsy | [49] | MRI | Piezoelectric ultrasonic | 5 | (1.65 ± 1.77) | ✓ | ✓ | ||
| Proposed | MRI | Electrics for model validation, pneumatics for future clinical application | [50] | 6 | Demonstration of functionality | ✓ | ✓ | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Xiang, R.; Xiang, J.; Wang, B.; Wu, X.; Cai, M.; Pan, Z.; Li, M.; Li, X. Modeling, Analysis and Evaluation of a Novel Compact 6-DoF 3-RRRS Needle Biopsy Robot. Mathematics 2024, 12, 1461. https://doi.org/10.3390/math12101461
Wang J, Xiang R, Xiang J, Wang B, Wu X, Cai M, Pan Z, Li M, Li X. Modeling, Analysis and Evaluation of a Novel Compact 6-DoF 3-RRRS Needle Biopsy Robot. Mathematics. 2024; 12(10):1461. https://doi.org/10.3390/math12101461
Chicago/Turabian StyleWang, Jiangnan, Ruiqi Xiang, Jindong Xiang, Baichuan Wang, Xiyun Wu, Mingzhen Cai, Zhijie Pan, Mengtang Li, and Xun Li. 2024. "Modeling, Analysis and Evaluation of a Novel Compact 6-DoF 3-RRRS Needle Biopsy Robot" Mathematics 12, no. 10: 1461. https://doi.org/10.3390/math12101461
APA StyleWang, J., Xiang, R., Xiang, J., Wang, B., Wu, X., Cai, M., Pan, Z., Li, M., & Li, X. (2024). Modeling, Analysis and Evaluation of a Novel Compact 6-DoF 3-RRRS Needle Biopsy Robot. Mathematics, 12(10), 1461. https://doi.org/10.3390/math12101461





