Event-Triggered Tracking Control for Nonlinear Systems with Mismatched Disturbances: A Non-Recursive Design Approach
Abstract
1. Introduction
- (i)
- By integrating the event-triggering mechanism into a non-recursive design framework, the proposed controller features a concise form and effectively conserves system resources.
- (ii)
- The co-design approach for the controller and the triggering event enables the controller to compensate for errors induced by sampling. In practical applications, it is easy to determine the optimal parameters according to specific operating conditions, achieving a balance between control performance and the conservation of system resources.
2. Preliminaries and Problem Formulation
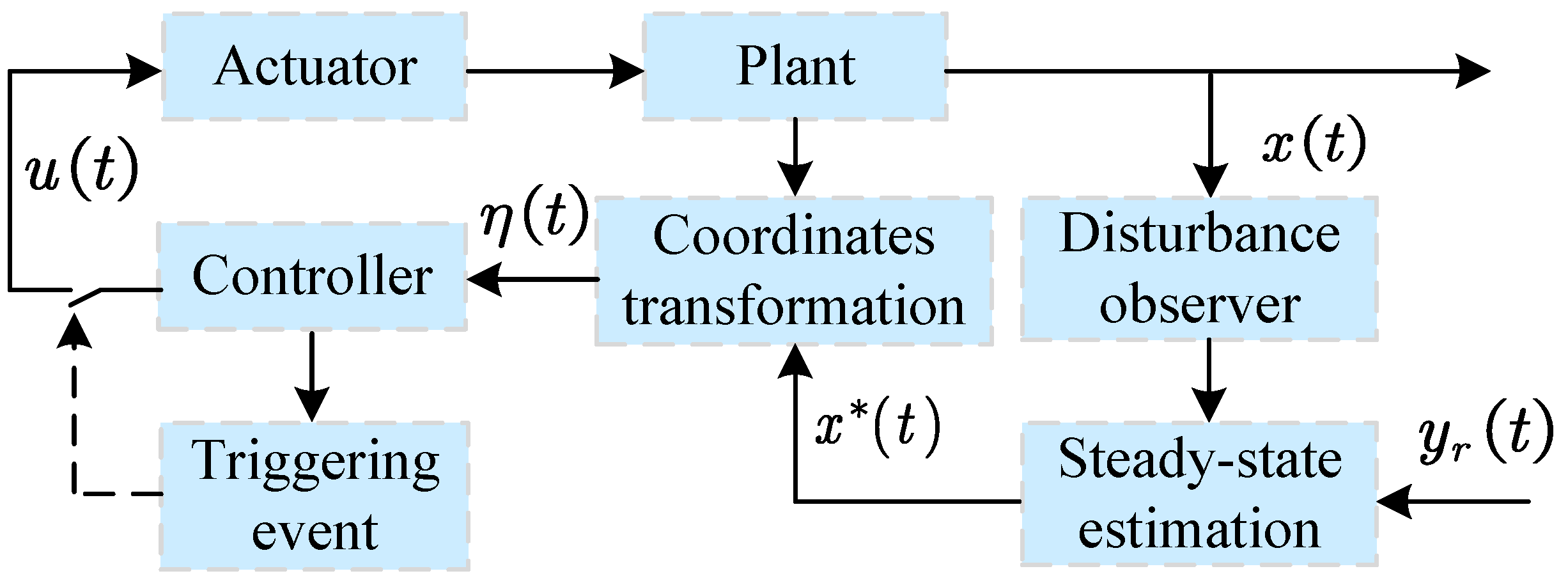
3. Non-Recursive Event-Triggered Control Design Framework
3.1. Disturbance Observation
3.2. Steady-State Estimations
3.3. Coordinates Transformation
3.4. Event-Triggered Controller Design
4. Main Result
- All signals in the resulting closed-loop system are bounded and the tracking error will exponentially converge to a set.
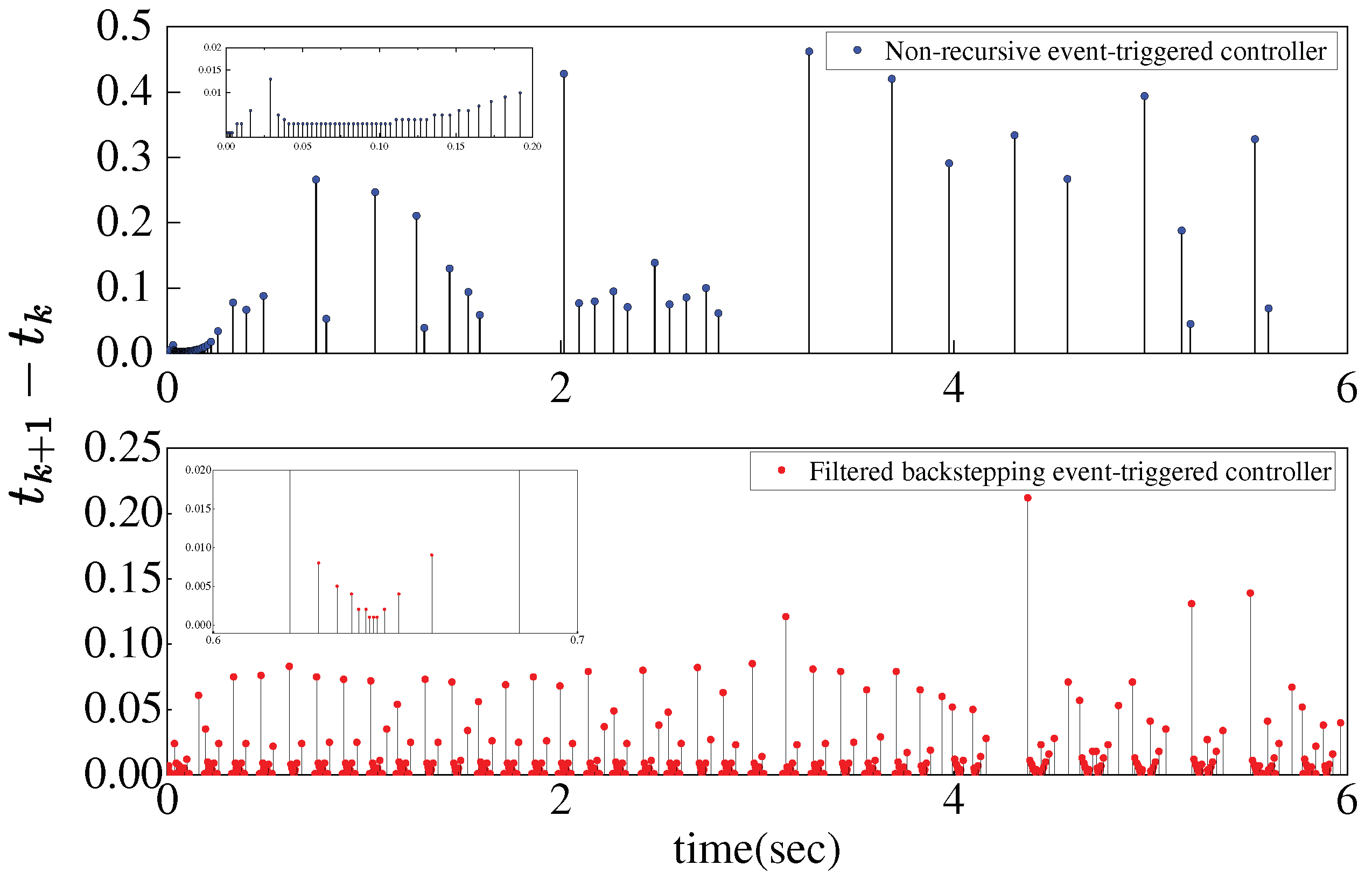
- The inter-execution intervals indicate the absence of the Zeno phenomenon.
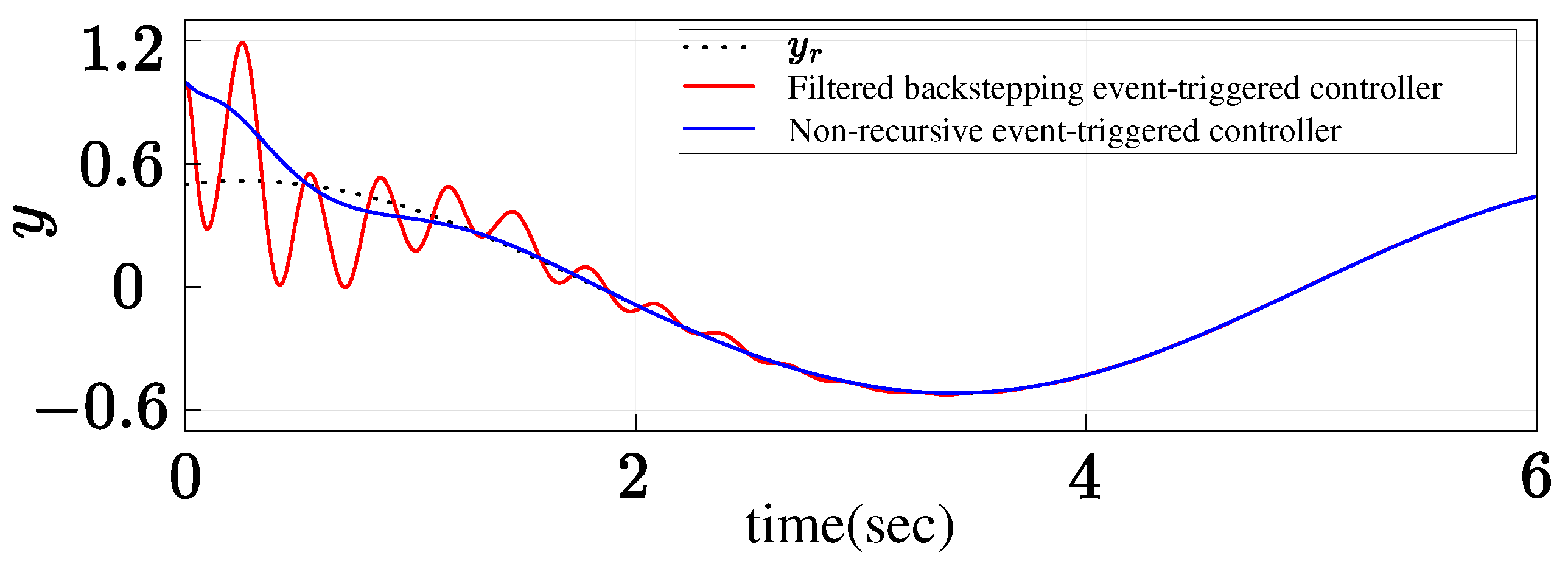
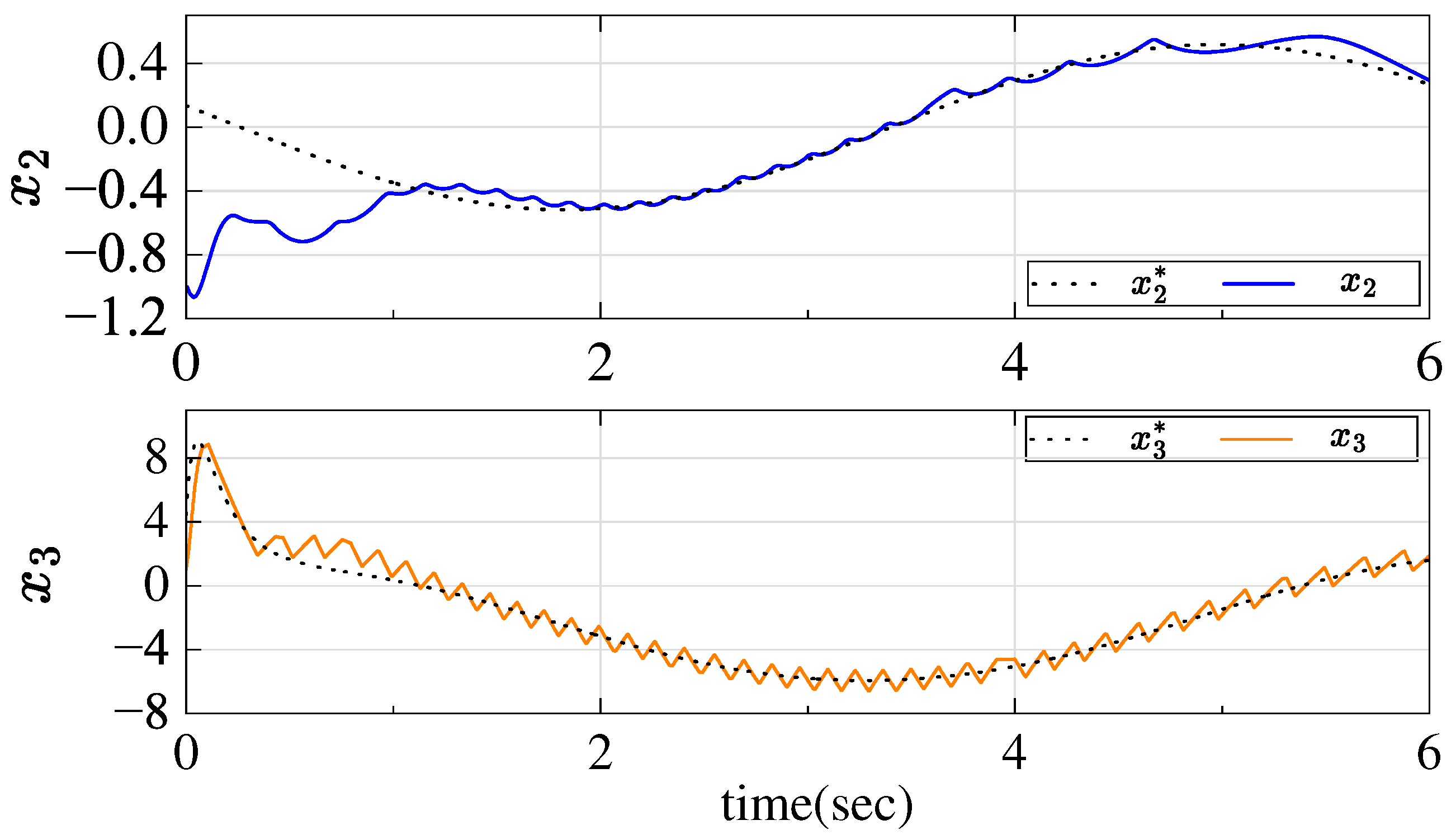
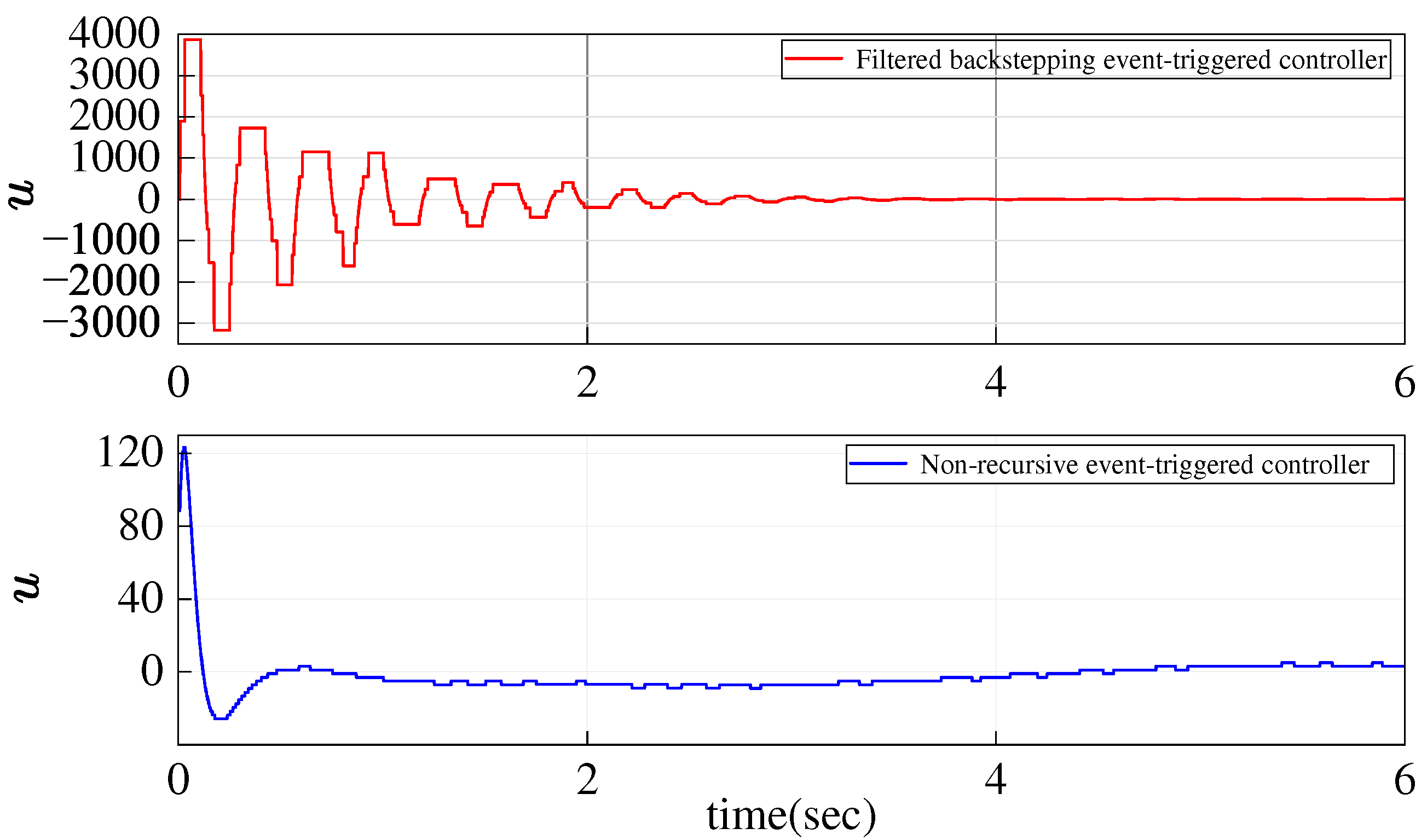
5. Numerical Simulations
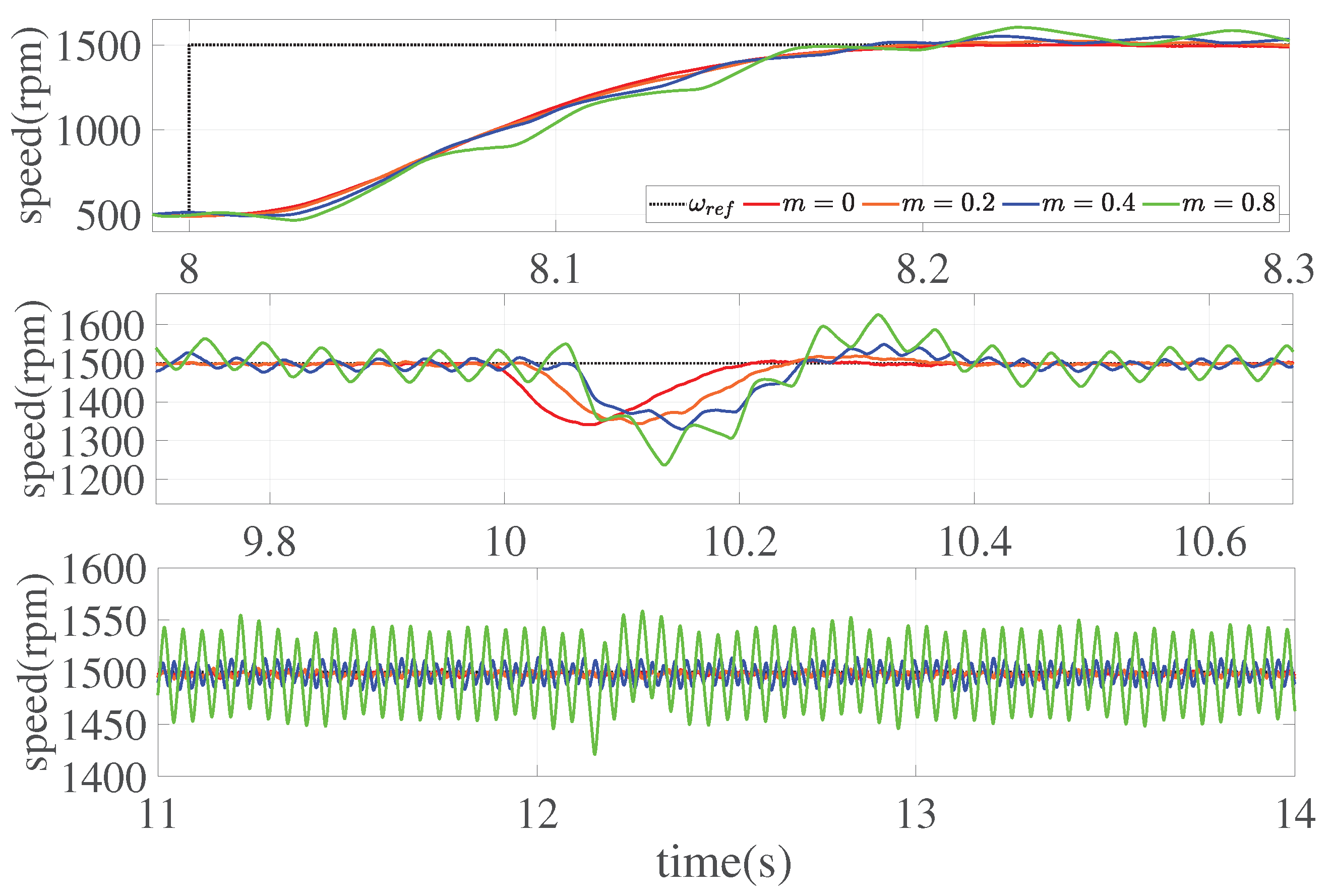
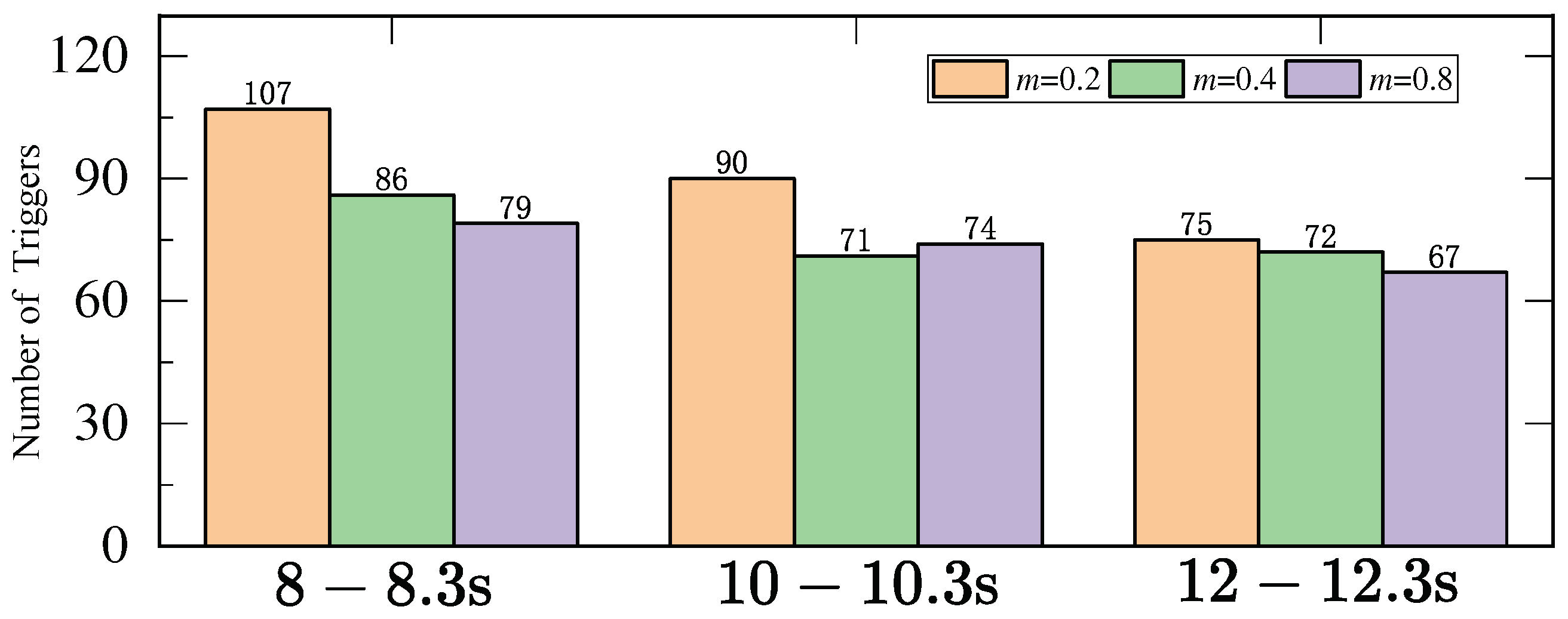
6. Application to Speed Regulation of PMSM
- The motor speed is switched from 500 to 1500 rpm at s;
- A sudden load torque of Nm is applied at s with the motor speed at 1500 rpm.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ding, Z. Global output regulation of uncertain nonlinear systems with exogenous signals. Automatica 2001, 37, 113–119. [Google Scholar] [CrossRef]
- Chalishajar, D.; Ramkumar, K.; Ravikumar, K.; Anguraj, A.; Anguraj, A. Optimal control of conformable fractional neutral stochastic integrodifferential systems with infinite delay. Results Control Optim. 2023, 13, 100293. [Google Scholar] [CrossRef]
- Davila, J. Exact tracking using backstepping control design and high-order sliding modes. IEEE Trans. Autom. Control 2013, 58, 2077–2081. [Google Scholar] [CrossRef]
- Nesic, D.; Teel, A.R.; Carnevale, D. Explicit computation of the sampling period in emulation of controllers for nonlinear sampled-data systems. IEEE Trans. Autom. Control 2009, 53, 619–624. [Google Scholar] [CrossRef]
- Qian, C.; Du, H. Global output feedback stabilization of a class of nonlinear systems via linear sampled-data control. IEEE Trans. Autom. Control 2012, 57, 2934–2939. [Google Scholar] [CrossRef]
- Arzen, K. A simple event-based PID controller. Trienn. World Congr. IFAC 1999, 32, 5006–5011. [Google Scholar]
- Tabuada, P. Event-triggered real-time scheduling of stabilizing control tasks. IEEE Trans. Autom. Control 2007, 52, 1680–1685. [Google Scholar] [CrossRef]
- Postoyan, R.; Tabuada, P.; Nesic, D.; Anta, A. A framework for the event-triggered stabilization of nonlinear systems. IEEE Trans. Autom. Control 2015, 60, 982–996. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, Y. Practical tracking via adaptive event-triggered feedback for uncertain nonlinear systems. IEEE Trans. Autom. Control 2019, 64, 3920–3927. [Google Scholar] [CrossRef]
- Li, H.; Liu, Y.; Huang, Y. Event-triggered controller via adaptive output-feedback for a class of uncertain nonlinear systems. Int. J. Control 2020, 94, 2575–2583. [Google Scholar] [CrossRef]
- Hua, C.; Li, K.; Guan, X. Decentralized event-triggered control for interconnected time-delay stochastic nonlinear systems using neural networks. Neurocomputing 2018, 272, 270–278. [Google Scholar] [CrossRef]
- Xing, L.; Wen, C.; Liu, Z.; Su, H.; Cai, J. Event-triggered adaptive control for a class of uncertain nonlinear systems. IEEE Trans. Autom. Control 2016, 64, 2071–2076. [Google Scholar]
- Li, S.; Yang, J.; Chen, W.; Chen, X. Disturbance Observer-Based Control: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Guo, L.; Cao, S. Anti-disturbance control theory for systems with multiple disturbances: A survey. ISA Trans. 2014, 53, 846–849. [Google Scholar] [CrossRef]
- Zhang, X.; Gu, X.; Yi, Y.; Zhang, T. Event-triggered anti-disturbance tracking control for systems with exogenous disturbances. Chin. Intell. Syst. Conf. 2020, 705, 117–126. [Google Scholar]
- Li, T.; Wen, C.; Li, S.; Guo, L. Event-triggered tracking control for nonlinear systems subject to time-varying external disturbances. Automatica 2020, 119, 109070. [Google Scholar] [CrossRef]
- Liu, J.; Yu, J.; Lin, C. Event-triggered and command-filter-based backstepping control for a class of uncertainty nonlinear systems. Control Decis. 2022, 37, 2733–2737. [Google Scholar]
- Pi, W.; Liu, W. Event-triggered finite-time neural control for uncertain nonlinear systems with unknown disturbances and its application in SVC. Trans. Inst. Meas. Control 2024, 46, 1803–1814. [Google Scholar] [CrossRef]
- Peng, Z.; Jiang, Y.; Wang, J. Event-triggered dynamic surface control of an underactuated autonomous surface vehicle for target enclosing. IEEE Trans. Ind. Electron. 2020, 68, 3402–3412. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, J. Nonrecursive Control Design for Nonlinear Systems: Theory and Applications; CRC Press: Roca Boton, FL, USA; London, UK, 2023. [Google Scholar]
- Xi, Z.; Ding, Z. Global adaptive output regulation of a class of nonlinear systems with nonlinear ecosystems. Automatica 2022, 43, 143–149. [Google Scholar] [CrossRef]
- Li, M.; Lang, J.; Zhang, C.; Cui, C.; Xu, L. Decentralized composite generalized predictive control strategy for DC microgrids with high PV penetration. Int. J. Robust Nonlinear Control 2022, 32, 7793–7808. [Google Scholar] [CrossRef]
- Sun, H.; Li, S.; Yang, J.; Guo, L. Non-linear disturbance observer-based back-stepping control for airbreathing hypersonic vehicles with mismatched disturbances. IET Control. Theory Appl. 2014, 8, 1852–1865. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, J.; Yan, Y.; Fridman, L.; Li, S. Semiglobal finite-time trajectory tracking realization for disturbed nonlinear systems via higher-order sliding modes. IEEE Trans. Autom. Control 2020, 65, 2185–2191. [Google Scholar] [CrossRef]
- Isidori, A.; Byrnes, C. Output regulation of nonlinear systems. IEEE Trans. Autom. Control 1990, 35, 131–140. [Google Scholar] [CrossRef]
- Dong, X.; Zhang, C. Nonrecursive robust/adaptive integrated control design framework for nonlinear systems with mismatched disturbances. Control. Theory Appl. 2022, 39, 1641–1650. [Google Scholar]
- Ho, H.; Wong, Y.; Rad, A. Adaptive fuzzy approach for a class of uncertain nonlinear systems in strict-feedback form. ISA Trans. 2008, 47, 286–299. [Google Scholar] [CrossRef]
- Dai, C.; Guo, T.; Yang, J.; Li, S. A disturbance observer-based current-constrained controller for speed regulation of PMSM systems subject to unmatched disturbances. IEEE Trans. Ind. 2020, 68, 767–775. [Google Scholar] [CrossRef]


| Symbol | Quantity | Nominal Values |
|---|---|---|
| Poles | 4 | |
| Stator inductance | H | |
| Stator resistance | ||
| B | Viscous damping | |
| Rated speed | 4107 rpm | |
| Rated current | 7 A | |
| Bus voltage | 24 V | |
| Sampling frequency | 20 kHz | |
| Flux linkage | 0.0064 Wb | |
| J | Rotor inertia |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, G.; Zhao, X. Event-Triggered Tracking Control for Nonlinear Systems with Mismatched Disturbances: A Non-Recursive Design Approach. Mathematics 2024, 12, 1716. https://doi.org/10.3390/math12111716
Dong G, Zhao X. Event-Triggered Tracking Control for Nonlinear Systems with Mismatched Disturbances: A Non-Recursive Design Approach. Mathematics. 2024; 12(11):1716. https://doi.org/10.3390/math12111716
Chicago/Turabian StyleDong, Gaofeng, and Xin Zhao. 2024. "Event-Triggered Tracking Control for Nonlinear Systems with Mismatched Disturbances: A Non-Recursive Design Approach" Mathematics 12, no. 11: 1716. https://doi.org/10.3390/math12111716
APA StyleDong, G., & Zhao, X. (2024). Event-Triggered Tracking Control for Nonlinear Systems with Mismatched Disturbances: A Non-Recursive Design Approach. Mathematics, 12(11), 1716. https://doi.org/10.3390/math12111716






