Guaranteed Performance Event-Triggered Adaptive Consensus Control for Multiagent Systems under Time-Varying Actuator Faults
Abstract
:1. Introduction
- Actuator faults are a common phenomenon in actual engineering that may impact the accomplishments of control objects. Especially for systems that require faster convergence while suffering from time-varying faults, it brings difficulty to compensation. With the aid of the transform function, an adaptive neural network compensation strategy is constructed to handle such an issue. When systems suffer from time-varying actuator faults, the investigated compensation strategy can guarantee systems prescribed time consensus;
- To improve the transient and steady performance in the control operation, the asymmetric barrier Lyapunov function is adopted to further restrain systems’ errors with minor overshoots. Moreover, considering that ensuring systems performance requires significant resources, the ASETC is developed based on the input characteristics of different periods. The presented method not only enhances systems control performance but relaxes the pressure of the communication of systems in the control operation.
- •
- and represent the set of real numbers and the real numbers in M × M size space, respectively;
- •
- denotes a diagonal matrix, and · is a symbol on behalf of all the elements located in the diagonal of the matrix;
- •
- denotes the transposed matrix of the original one A;
- •
- stands for the Euclidean norm of vector B;
- •
- is the maximal function, which is capable of catching the maximum value among ⋯, and ⋯ is a 1-dimension arbitrary array.
2. Preliminaries and Problem Description
2.1. Graph Theory
2.2. Model Description
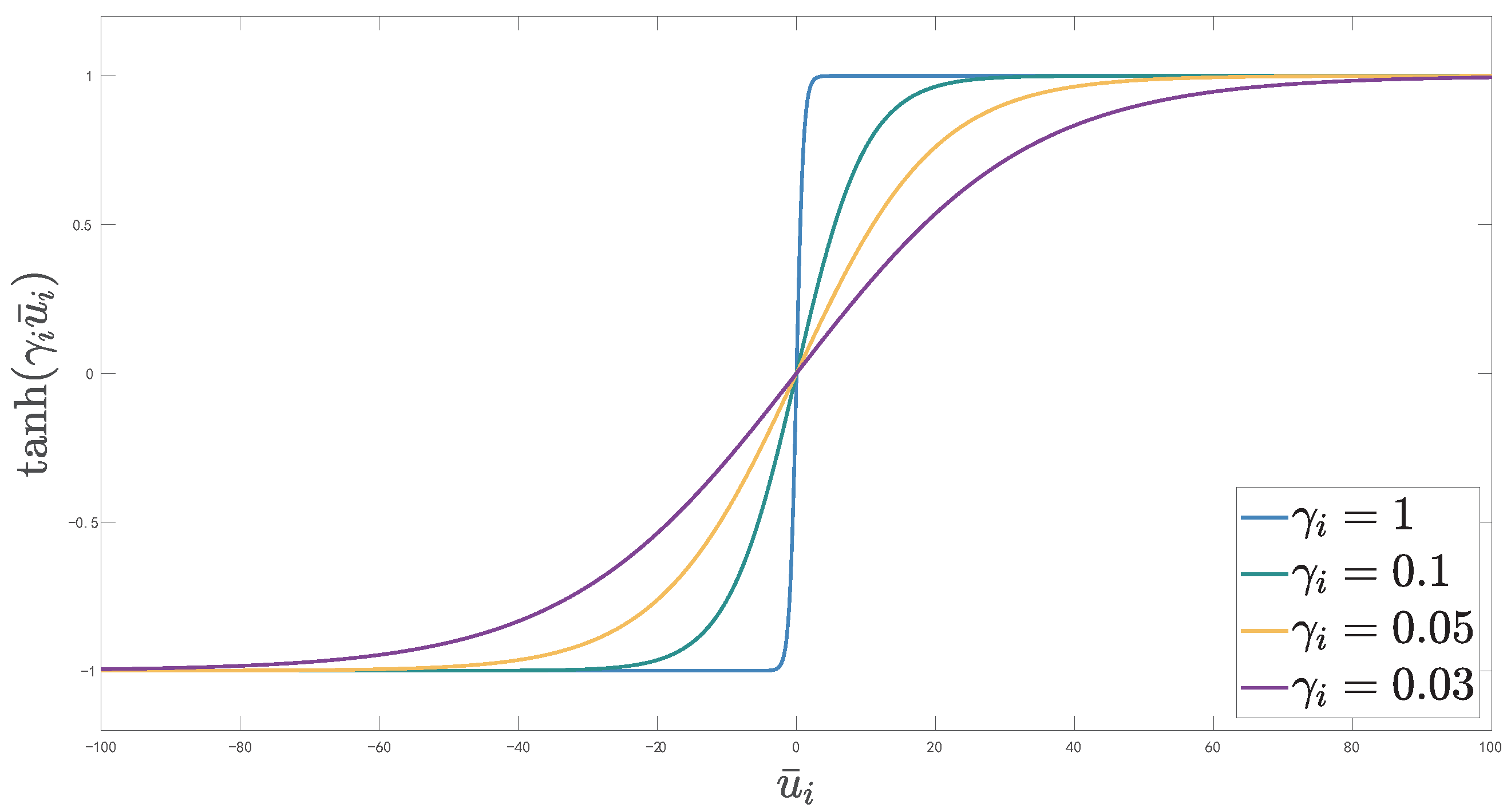
2.3. Transform Function
2.4. Radial Basis Function Neural Networks (RBFNNs)
3. Consensus Controller Design and Systems Stability Analysis
3.1. Consensus Control Design
3.2. Systems Stability Analysis
- (1)
- All the system signals of multiagent systems subject to time-varying actuator faults are bounded. The error of each agent can be a guaranteed prescribed time convergence into a preset range under the given performance;
- (2)
- The Zeno behavior is surely eliminated in the proposed triggered scheme.
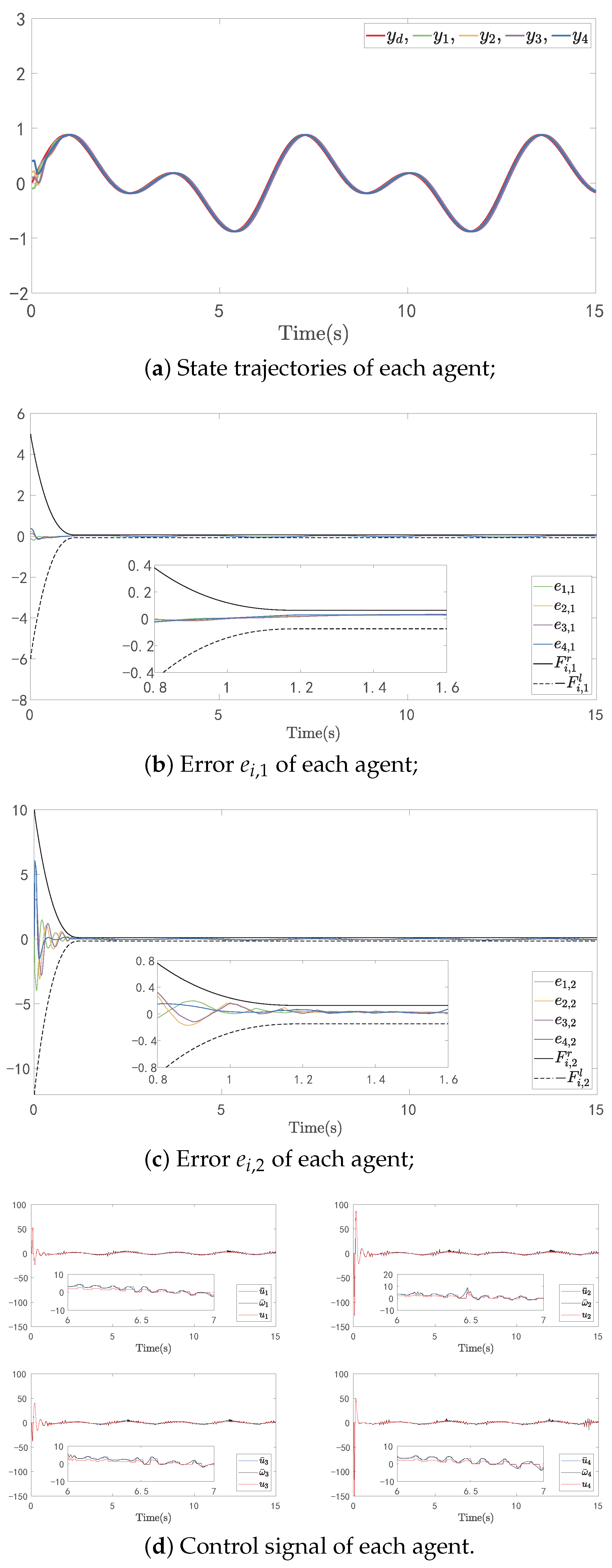
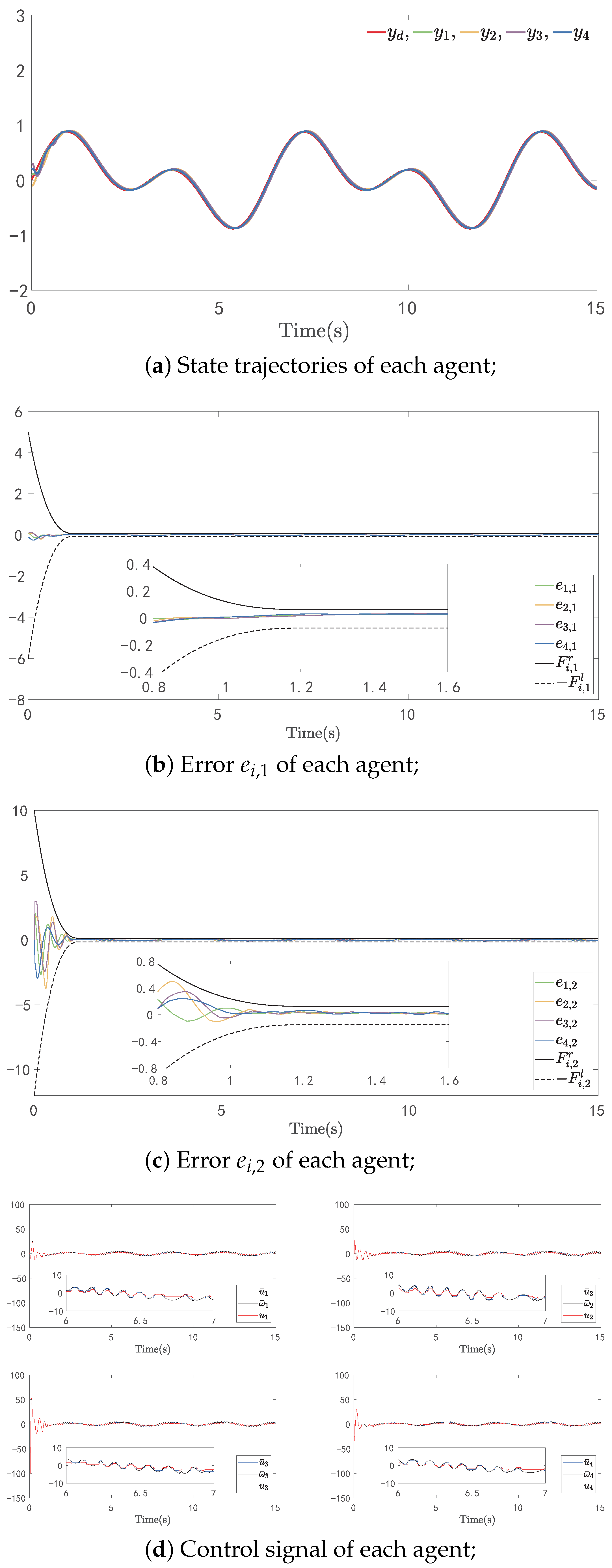
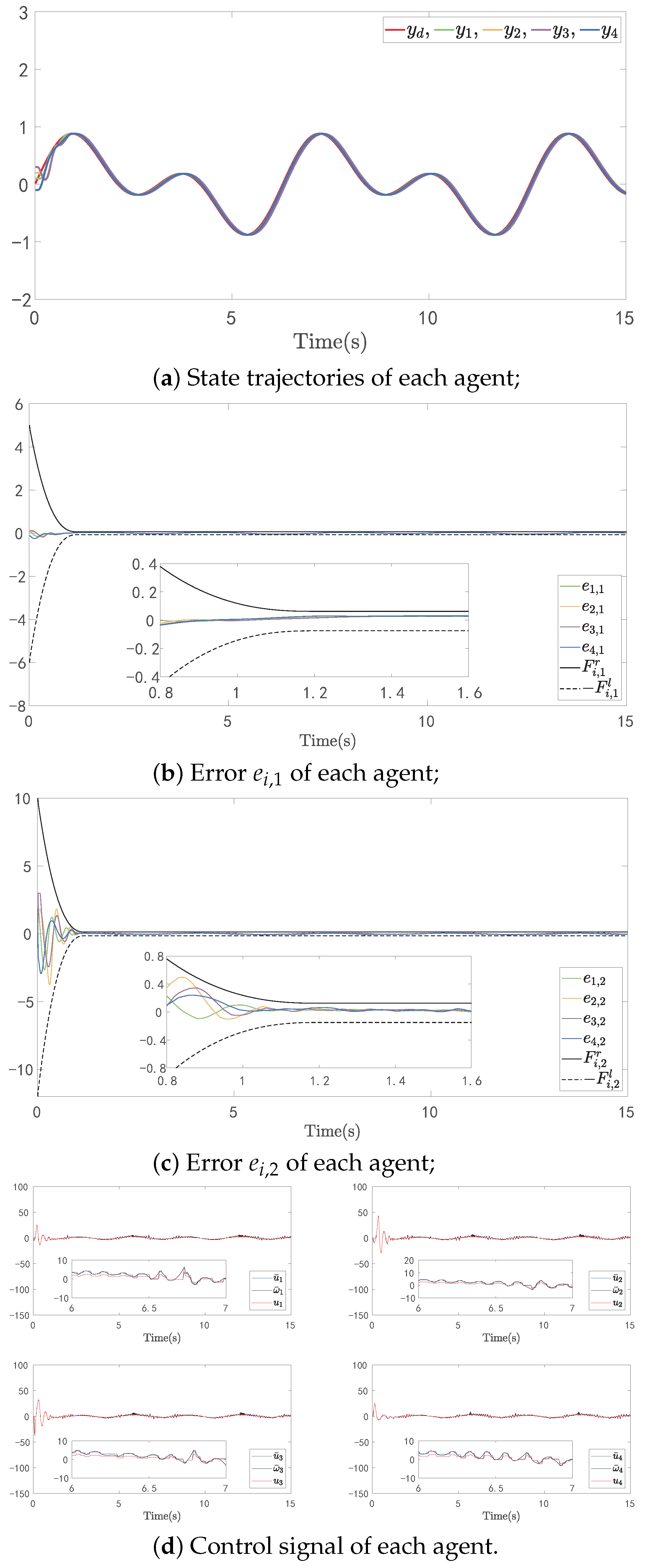
4. Simulation
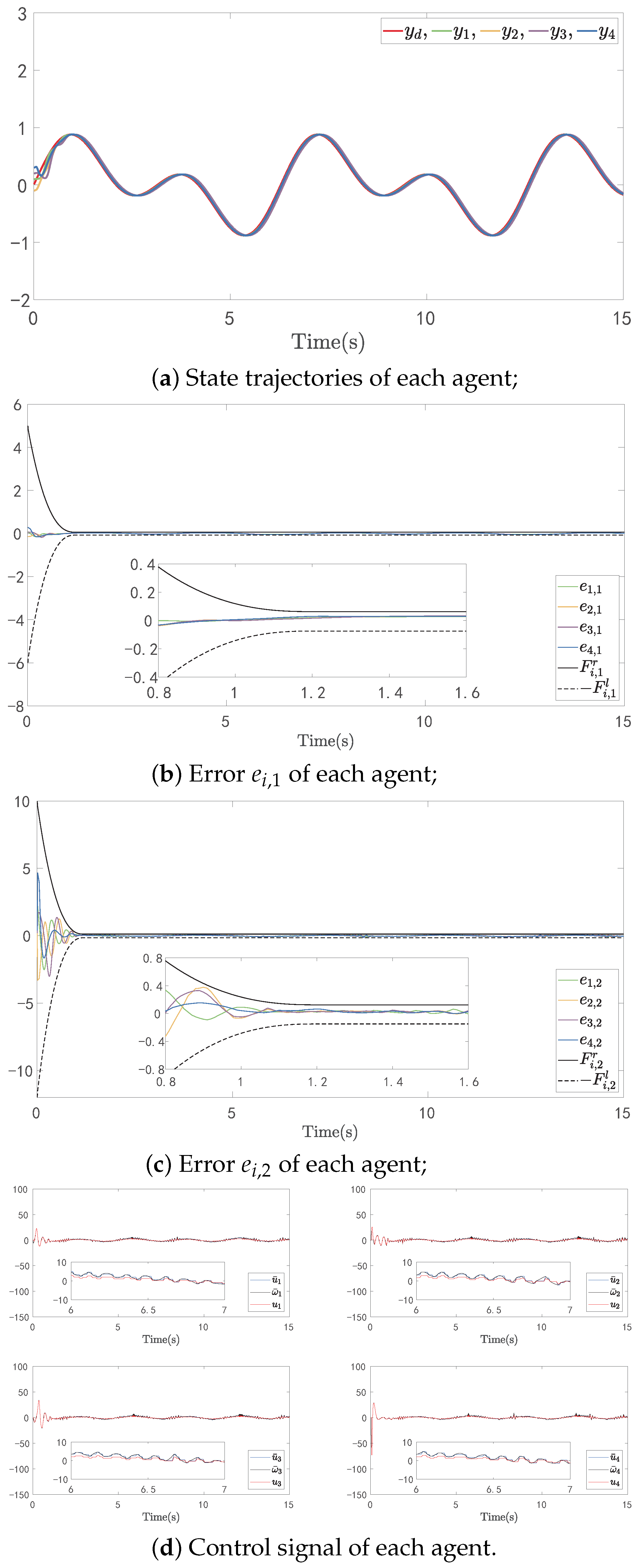
4.1. Numerical Example
4.2. Application Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tang, Y.; Zhang, D.; Shi, P.; Zhang, W.; Qian, F. Event-Based Formation Control for Nonlinear Multiagent Systems Under DoS Attacks. IEEE Trans. Autom. Control 2021, 66, 452–459. [Google Scholar] [CrossRef]
- Zou, W.; Shi, P.; Xiang, Z.; Shi, Y. Consensus Tracking Control of Switched Stochastic Nonlinear Multiagent Systems via Event-Triggered Strategy. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1036–1045. [Google Scholar] [CrossRef]
- Liang, H.; Zhang, L.; Sun, Y.; Huang, T. Containment Control of Semi-Markovian Multiagent Systems with Switching Topologies. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3889–3899. [Google Scholar] [CrossRef]
- Ma, Q.; Xu, S. Consensusability of First-Order Multiagent Systems under Distributed PID Controller with Time Delay. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 7908–7912. [Google Scholar] [CrossRef]
- Lu, M.; Liu, L. Consensus of Heterogeneous Second-Order Nonlinear Uncertain Multiagent Systems under Switching Networks. IEEE Trans. Autom. Control 2021, 66, 3331–3338. [Google Scholar] [CrossRef]
- Li, X.; Shi, P.; Wang, Y.; Wang, S. Cooperative Tracking Control of Heterogeneous Mixed-Order Multiagent Systems with Higher-Order Nonlinear Dynamics. IEEE Trans. Cybern. 2020, 52, 5498–5507. [Google Scholar] [CrossRef]
- Ma, Q.; Meng, Q.; Xu, S. Distributed Optimization for Uncertain High-Order Nonlinear Multiagent Systems via Dynamic Gain Approach. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 4351–4357. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Li, Y.; Chen, C.; Liu, Z.; Li, F. Prescribed time fuzzy adaptive consensus control for multiagent systems with dead-zone input and sensor faults. IEEE Trans. Autom. Sci. Eng. 2023. [Google Scholar] [CrossRef]
- Yang, H.; Luo, H.; Kaynak, O.; Yin, S. Adaptive SMO-Based Fault Estimation for Markov Jump Systems with Simultaneous Additive and Multiplicative Actuator Faults. IEEE Syst. J. 2021, 15, 607–616. [Google Scholar] [CrossRef]
- Ren, Y.; Zhao, Z.; Ahn, C.K.; Li, H.X. Adaptive Fuzzy Control for an Uncertain Axially Moving Slung-Load Cable System of a Hovering Helicopter with Actuator Fault. IEEE Trans. Fuzzy Syst. 2022, 30, 4915–4925. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, H.; Li, W.; Mu, Y.; He, Q. Distributed Bipartite Adaptive Event-Triggered Fault-Tolerant Consensus Tracking for Linear Multiagent Systems Under Actuator Faults. IEEE Trans. Cybern. 2021, 52, 11313–11324. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Wu, J.; Zhan, X.; Han, T.; Yan, H. Distributed Adaptive Predefined-Time Bipartite Containment Algorithm for Nonlinear Multi-Agent Systems with Actuator Faults. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 2141–2145. [Google Scholar] [CrossRef]
- Wu, W.; Li, Y.; Tong, S. Neural Network Output-Feedback Consensus Fault-Tolerant Control for Nonlinear Multiagent Systems with Intermittent Actuator Faults. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 4728–4740. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Li, Y.; Wu, Y.; Liu, Z.; Chen, K.; Chen, C. Fixed-Time Formation Control for Uncertain Nonlinear Multiagent Systems with Time-Varying Actuator Failures. IEEE Trans. Fuzzy Syst. 2024, 32, 1965–1977. [Google Scholar] [CrossRef]
- Wang, C.; Li, X.; Cui, L.; Wang, Y.; Liang, M.; Chai, Y. Tracking control of state constrained fractional order nonlinear systems. ISA Trans. 2021, 123, 240–250. [Google Scholar] [CrossRef] [PubMed]
- Tang, L.; Zhang, X.; Liu, Y.; Tong, S. Neural-Network-Based Adaptive Constrained Control for Switched Systems under State-Dependent Switching Law. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 4057–4067. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, C.; Chen, C.L.P.; Liu, Z.; Zhang, C. Fast Finite-Time Event-Triggered Consensus Control for Uncertain Nonlinear Multiagent Systems with Full-State Constraints. IEEE Trans. Circuits Syst. Regul. Pap. 2023, 70, 1361–1370. [Google Scholar] [CrossRef]
- Guo, G.; Gao, Z.; Dong, K. Prescribed-time formation control of surface vessels with asymmetric constraints on LOS range and bearing angles. Nonlinear Dyn. 2021, 104, 3701–3712. [Google Scholar] [CrossRef]
- Naderolasli, A.; Shojaei, K.; Chatraei, A. Platoon formation control of autonomous underwater vehicles under LOS range and orientation angles constraints. Ocean Eng. 2023, 271, 113674. [Google Scholar] [CrossRef]
- Fang, X.; Fan, H.; Liu, L.; Wang, B. Adaptive fixed-time fault-tolerant control of saturated MIMO nonlinear systems with time-varying state constrains. Nonlinear Dyn. 2022, 110, 3463–3483. [Google Scholar] [CrossRef]
- Sun, W.; Wang, L.; Wu, Y. Adaptive Dynamic Surface Fuzzy Control for State Constrained Time-Delay Nonlinear Nonstrict Feedback Systems with Unknown Control Directions. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 7423–7434. [Google Scholar] [CrossRef]
- Wang, N.; Wang, Y.; Wen, G.; Lv, M.; Zhang, F. Fuzzy Adaptive Constrained Consensus Tracking of High-Order Multi-agent Networks: A New Event-Triggered Mechanism. IEEE Trans. Syst. Man Cybern. Syst 2022, 52, 5468–5480. [Google Scholar] [CrossRef]
- Wei, Y.; Luo, J.; Yan, H.; Wang, Y. Event-triggered adaptive finite-time control for nonlinear systems under asymmetric time-varying state constraints. Front. Inf. Technol. Electron. Eng. 2021, 22, 1610–1624. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, J.; Zhang, Z.; Wu, Y. Output feedback control of nonlinear cascaded systems with external disturbance and asymmetric constraints. Nonlinear Dyn. 2022, 108, 3727–3743. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.; Zuo, Z.Y.; Li, X.; Lu, R. An Overview of Finite/Fixed-Time Control and its Application in Engineering Systems. IEEE/CAA J. Autom. Sin. 2022, 9, 2106–2120. [Google Scholar] [CrossRef]
- Wang, F.; Chen, B.; Sun, Y.; Gao, Y.; Lin, C. Finite-Time Fuzzy Control of Stochastic Nonlinear Systems. IEEE Trans. Cybern. 2020, 50, 2617–2626. [Google Scholar] [CrossRef]
- Bafghi, H.F.; Jahed-Motlagh, M.R.; Abooee, A.; Moarefianpur, A. Robust finite-time tracking for a square fully actuated class of nonlinear systems. Nonlinear Dyn. 2021, 103, 1611–1625. [Google Scholar] [CrossRef]
- Qi, W.; Gao, M.; Ahn, C.K.; Cao, J.; Cheng, J.; Zhang, L. Quantized Fuzzy Finite-Time Control for Nonlinear Semi-Markov Switching Systems. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 2622–2626. [Google Scholar] [CrossRef]
- Wang, D.; Liu, C.L.; Ding, D.; Gao, S.; Chu, M.H. Finite-time optimal tracking control using augmented error system method. Appl. Math. Comput. 2022, 424, 127013. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, F.; Liu, Z.; Zhang, Y.; Chen, C.L.P. Fixed-Time Fuzzy Control for a Class of Nonlinear Systems. IEEE Trans. Cybern. 2020, 52, 3880–3887. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, S.; Yan, Y. Fixed-time velocity-free sliding mode tracking control for marine surface vessels with uncertainties and unknown actuator faults. Ocean Eng. 2020, 201, 107107. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, H.; Zhang, J.; Wang, W. Fixed-time leader-following/containment consensus for a class of nonlinear multi-agent systems. Inf. Sci. 2021, 555, 58–84. [Google Scholar] [CrossRef]
- Li, D.; Ge, S.S.; heng Lee, T. Fixed-Time-Synchronized Consensus Control of Multiagent Systems. IEEE Trans. Control Network Syst. 2021, 8, 89–98. [Google Scholar] [CrossRef]
- Wu, W.; Tong, S. Fixed-Time Adaptive Fuzzy Containment Dynamic Surface Control for Nonlinear Multiagent Systems. IEEE Trans. Fuzzy Syst. 2022, 30, 5237–5248. [Google Scholar] [CrossRef]
- Wang, J.; Wang, C.; Liu, Z.; Chen, C.; Zhang, C. Practical Fixed-Time Adaptive ERBFNNs Event-Triggered Control for Uncertain Nonlinear Systems with Dead-Zone Constraint. IEEE Syst. Man CY.-S. 2024, 54, 342–351. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, X.; Ge, S.S. Prescribed-time control with explicit reference governor for a class of constrained cascaded systems. Int. J. Robust Nonlinear Control 2021, 31, 6422–6437. [Google Scholar] [CrossRef]
- Liu, D.; Liu, Z.; Chen, C.L.P.; Zhang, Y. Prescribed-time containment control with prescribed performance for uncertain nonlinear multi-agent systems. J. Frankl. Inst. 2021, 358, 1782–1811. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, S.; Guo, F.; Zhao, X.; Zhang, F. Prescribed time attitude containment control for satellite cluster with bounded disturbances. ISA Trans. 2022, 137, 160–174. [Google Scholar] [CrossRef]
- Chen, X.; Yu, H.; Hao, F. Prescribed-Time Event-Triggered Bipartite Consensus of Multiagent Systems. IEEE Trans. Cybern. 2020, 52, 2589–2598. [Google Scholar] [CrossRef]
- Wang, Y.; Song, Y.; Hill, D.J.; Krstić, M. Prescribed-Time Consensus and Containment Control of Networked Multiagent Systems. IEEE Trans. Cybern. 2019, 49, 1138–1147. [Google Scholar] [CrossRef]
- Gong, X.; Cui, Y.; Wang, T.; Shen, J.; Huang, T. Distributed Prescribed-Time Consensus Observer for High-Order Integrator Multi-Agent Systems on Directed Graphs. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 2216–2220. [Google Scholar] [CrossRef]
- Chen, S.; Jiang, H.; Yu, Z.; Zhao, F. Distributed Optimization of Single-Integrator Systems with Prescribed-Time Convergence. IEEE Syst. J. 2023, 17, 3235–3245. [Google Scholar] [CrossRef]
- Zhao, N.-N.; Ouyang, X.Y.; Wu, L.; Shi, F. Event-triggered adaptive prescribed performance control of uncertain nonlinear systems with unknown control directions. ISA Trans. 2020, 108, 121–130. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Che, W.; Deng, C.; Wu, Z. Prescribed Performance Control for Multiagent Systems via Fuzzy Adaptive Event-Triggered Strategy. IEEE Trans. Fuzzy Syst. 2022, 30, 5078–5090. [Google Scholar] [CrossRef]
- Wang, J.; Yan, Y.; Liu, J.; Chen, C.L.P.; Liu, Z.; Zhang, C. NN event-triggered finite-time consensus control for uncertain nonlinear Multi-Agent Systems with dead-zone input and actuator failures. ISA Trans. 2023, 137, 59–73. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Li, Y.; Tong, S.; Hou, Z. Event-Triggered Adaptive Fuzzy Asymptotic Tracking Control of Nonlinear Pure-Feedback Systems with Prescribed Performance. IEEE Trans. Cybern. 2021, 53, 2380–2390. [Google Scholar] [CrossRef]
- Li, T.; Li, S. Fixed-time adaptive dynamic event-triggered control of flexible-joint robots with prescribed performance and time delays. ISA Trans. 2023, 140, 198–223. [Google Scholar] [CrossRef]
- Shao, X.; Ye, D. Event-based adaptive fuzzy fixed-time control for nonlinear interconnected systems with non-affine nonlinear faults. Fuzzy Sets Syst. 2021, 432, 1–27. [Google Scholar] [CrossRef]
- Pang, N.; Wang, X.; Wang, Z. Event-Triggered Adaptive Control of Nonlinear Systems with Dynamic Uncertainties: The Switching Threshold Case. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3540–3544. [Google Scholar] [CrossRef]
- Zeng, Q.; Zhao, J. Adaptive Switching Event-Triggered Control for Active Suspension Systems with Acceleration Performance Constraint. IEEE Trans. Intell. Transp. Syst. 2023, 24, 8028–8037. [Google Scholar] [CrossRef]
- Li, J.; Liu, C.; Sun, Y.; Shao, L. A new event-triggered adaptive tracking controller for nonlinear systems with unknown virtual control coefficients. Eur. J. Control 2022, 69, 100759. [Google Scholar] [CrossRef]
- Wang, J.; Gong, Q.; Huang, K.; Liu, Z.; Chen, C.; Liu, J. Event-triggered prescribed settling time consensus compensation control for a class of uncertain nonlinear systems with actuator failures. IEEE Trans. Neural Networks Learn. Syst. 2023, 34, 5590–5600. [Google Scholar] [CrossRef] [PubMed]



| Case | ||||||||
|---|---|---|---|---|---|---|---|---|
| I | 1 | |||||||
| II | ||||||||
| III | 1 |
| Case | Scheme | Agent 1 | Agent 2 | Agent 3 | Agent 4 | Totally |
|---|---|---|---|---|---|---|
| The scheme in [48] | 476 | 581 | 522 | 498 | 2077 | |
| I | The switching scheme in [51] | 343 | 404 | 391 | 354 | 1492 |
| The ASETC | 339 | 406 | 354 | 340 | 1439 | |
| The scheme in [48] | 475 | 548 | 591 | 468 | 2082 | |
| II | The switching scheme in [51] | 369 | 444 | 417 | 354 | 1584 |
| The ASETC | 347 | 408 | 395 | 344 | 1494 | |
| The scheme in [48] | 457 | 563 | 526 | 465 | 2011 | |
| III | The switching scheme in [51] | 364 | 397 | 366 | 359 | 1486 |
| The ASETC | 327 | 393 | 350 | 354 | 1424 |
| Case | ||||||||
|---|---|---|---|---|---|---|---|---|
| I | ||||||||
| II | ||||||||
| III |
| Case | Scheme | Agent 1 | Agent 2 | Agent 3 | Agent 4 | Totally |
|---|---|---|---|---|---|---|
| The scheme in [48] | 561 | 669 | 667 | 562 | 2459 | |
| I | The switching scheme in [51] | 361 | 431 | 385 | 389 | 1566 |
| The proposed switching scheme | 356 | 416 | 367 | 374 | 1513 | |
| The scheme in [48] | 572 | 675 | 668 | 592 | 2507 | |
| II | The switching scheme in [51] | 376 | 431 | 416 | 402 | 1625 |
| The proposed switching scheme | 362 | 420 | 394 | 376 | 1552 | |
| The scheme in [48] | 561 | 759 | 653 | 566 | 2539 | |
| III | The switching scheme in [51] | 381 | 454 | 416 | 375 | 1626 |
| The proposed switching scheme | 380 | 420 | 391 | 364 | 1555 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.; Gu, Y.; Lin, H.; Zhang, Z.; Zhou, X.; Wang, X. Guaranteed Performance Event-Triggered Adaptive Consensus Control for Multiagent Systems under Time-Varying Actuator Faults. Mathematics 2024, 12, 1528. https://doi.org/10.3390/math12101528
Chen K, Gu Y, Lin H, Zhang Z, Zhou X, Wang X. Guaranteed Performance Event-Triggered Adaptive Consensus Control for Multiagent Systems under Time-Varying Actuator Faults. Mathematics. 2024; 12(10):1528. https://doi.org/10.3390/math12101528
Chicago/Turabian StyleChen, Kairui, Yixiang Gu, Hai Lin, Zhonglin Zhang, Xiaoyang Zhou, and Xiaodong Wang. 2024. "Guaranteed Performance Event-Triggered Adaptive Consensus Control for Multiagent Systems under Time-Varying Actuator Faults" Mathematics 12, no. 10: 1528. https://doi.org/10.3390/math12101528
APA StyleChen, K., Gu, Y., Lin, H., Zhang, Z., Zhou, X., & Wang, X. (2024). Guaranteed Performance Event-Triggered Adaptive Consensus Control for Multiagent Systems under Time-Varying Actuator Faults. Mathematics, 12(10), 1528. https://doi.org/10.3390/math12101528








